Егэ физика задачи на преломление света - ExamHelp.top

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

На рисунке  — опыт по преломлению света в стеклянной пластине. Чему равен показатель преломления стекла? Ответ укажите с точностью до сотых.

При переходе луча света из одной среды в другую угол падения равен а угол преломления Каков относительный показатель преломления первой среды относительно второй? (Ответ округлите до сотых.)

Синус предельного угла полного внутреннего отражения на границе стекло  — воздух равен Чему равен абсолютный показатель преломления стекла? (Ответ округлить до сотых.)

На рисунке изображено преломление светового пучка на границе воздух  — стекло. Чему равен показатель преломления стекла? (Ответ округлите до сотых.)

Пройти тестирование по этим заданиям

Источник

ОПТИКА
«Преломление света» 11 класс

Задания
№15

1. При переходе луча света из одной среды в другую угол падения равен 30⁰
угол преломления 60⁰. Каков относительный показатель преломления
первой среды относительно второй? (Ответ округлите до сотых.)

2. Синус предельного угла полного внутреннего отражения на границе стекло
— воздух равен 8/ 13.Чему равен абсолютный показатель преломления стекла?
(Ответ округлить до сотых.)

3. Луч света падает на плоскую границу раздела двух сред, проходя из среды
1 в среду 2. Угол падения равен 30°, скорость распространения света в среде 1
равна 2х10⁸ м/с, показатель преломления среды 2 равен 1,45.
Определите синус угла преломления луча света. Ответ округлите до сотых долей.

4. Луч света
падает из воздуха на поверхность стекла. Угол падения луча можно изменять. В
таблице приведена зависимость угла преломления β луча от угла падения α
луча (углы выражены в градусах). Чему равен показатель преломления стекла?
Ответ округлите до десятых долей.

α, °	10	20	30	40	50	60	70	80
β, °	6,23	12,34	18,21	23,69	28,61	32,77	35,97	37,99

5. В центр верхней грани прозрачного кубика под углом
α = 45° падает из воздуха луч света (см. рисунок). Плоскость падения луча
параллельна плоскости передней грани кубика (АВСD). Преломлённый
луч попадает в ребро АЕ кубика. Определите показатель преломления материала, из
которого изготовлен кубик. Ответ округлите до сотых долей.

6. Луч света от лазерной указки падает из воздуха на поверхность воды
бассейна под углом α. Затем преломленный луч попадает на плоское
зеркало, лежащее на дне бассейна. Расстояние от точки падения луча на
поверхность воды до точки выхода луча на поверхность равно 2 м, показатель
преломления воды равен 1,33. В воде свет проходит путь 376 см. Чему равен угол α?
Ответ выразите в градусах и округлите до целого числа.

7. Непрозрачный круг освещается точечным источником света и отбрасывает
круглую тень на экран. Определите диаметр тени, если диаметр круга 0,1 м.
Расстояние от источника света до круга в 3 раза меньше, чем расстояние от
источника до экрана. (Ответ дать в метрах.

8. Солнце находится над горизонтом на высоте 60⁰. Определите
длину тени, которую отбрасывает вертикально стоящий шест высотой 1 м.
(Ответ дать в метрах, округлив до десятых)

задание 17

9. Световой
пучок выходит из стекла в воздух (см. рисунок).

Что происходит при этом с частотой
электромагнитных колебаний в световой волне, скоростью их распространения,
длиной волны?

Для каждой величины определите
соответствующий характер изменения:

1) увеличивается; 2) уменьшается;
3) не изменяется.

Запишите выбранные цифры для каждой
физической величины. Цифры в ответе могут повторяться.

Частота	Скорость	Длина волны

10. Луч света падает
на границу раздела «стекло — воздух». Как изменятся при увеличении показателя
преломления стекла следующие три величины: длина волны света в стекле, угол
преломления, угол полного внутреннего отражения?

Для каждой величины определите соответствующий
характер изменения:

1) увеличится; 2)
уменьшится; 3) не изменится

Запишите в таблицу выбранные цифры
для каждой физической величины. Цифры в ответе могут повторяться.

Длина
волны

света в
стекле

Угол

преломления

Угол
полного

внутреннего
отражения

11. Установите
соответствие между разновидностями тонкой линзы и результатами преломления в
ней параллельных лучей. К каждой позиции первого столбца подберите нужную
позицию второго и запишите в таблицу выбранные цифры под соответствующими
буквами.

РАЗНОВИДНОСТИ
ТОНКОЙ ЛИНЗЫ

РЕЗУЛЬТАТ
ПРЕЛОМЛЕНИЯ ПАРАЛЛЕЛЬНЫХ ЛУЧЕЙ

А) Собирающая

Б) Рассеивающая

1) Лучи, параллельные главной
оптической оси линзы, пройдя через нее, пройдут затем через ее дальний фокус

2) Лучи, параллельные главной
оптической оси линзы, пройдя через нее, пересекутся затем в ее ближнем фокусе

3) Лучи, параллельные главной
оптической оси линзы, пройдя через нее, будут казаться расходящимися из ее
ближнего фокуса

4) Лучи, параллельные главной
оптической оси линзы, пройдя через нее, соберутся в ее дальнем фокусе

12. Пучок света
переходит из воздуха в стекло. Частота световой волны ν скорость света в
воздухе — с показатель преломления стекла относительно воздуха — n.
Установите соответствие между физическими величинами и комбинациями других
величин, по которым их можно рассчитать. К каждой позиции первого столбца
подберите нужную позицию второго и запишите в таблицу выбранные цифры под
соответствующими буквами.

ФИЗИЧЕСКИЕ
ВЕЛИЧИНЫ

РАВНЫЕ
ИМ КОМБИНАЦИИ ДРУГИХ ВЕЛИЧИН

А) Скорость света в стекле

Б) Длина волны света в стекле

1) сn

2) cnν

3) c/n

4) c/nν

13. На рисунке
изображены два квадратных плоских зеркала, касающиеся друг друга краями (см.
рис. слева). Угол раствора зеркал 90°. На линии OO’, проходящей через
линию касания зеркал перпендикулярно к ней, помещён точечный источник света S.
Точки S₁, S₂ и S₃ —
изображения источника в этих зеркалах при данном угле раствора. Угол раствора
зеркал увеличивают до 120° (см. рисунок справа).

Определите, как при этом изменятся
следующие величины: количество изображений источника в зеркалах; расстояние от
источника до ближайшего к нему изображения.

Для каждой величины определите
соответствующий характер изменения:

1) увеличится; 2) уменьшится; 3)
не изменится.

Запишите в таблицу выбранные
цифры для каждой физической величины. Цифры в ответе могут повторяться.

Количество
изображений источника

в
зеркалах

Расстояние
от источника до

ближайшего
к нему изображения

Задание
23

14. Школьник
экспериментально изучает получение изображений при помощи тонкой собирающей
линзы. Для этого он располагает тонкий предмет П перпендикулярно главной
оптической оси линзы на расстоянии a от линзы с фокусным расстоянием F.

Школьник проводит пять опытов,
используя для этого предметы с разной высотой H и разные линзы, а также
изменяя расстояние a. Какие два опыта позволят школьнику исследовать
зависимость размера изображения предмета от расстояния a? Запишите в
ответе номера выбранных опытов.

№ опыта	Высота предмета H, см	Фокусное расстояние линзы F, см	Расстояние от предмета до линзы a, см
1	6	10	12
2	4	10	12
3	10	8	17
4	4	8	15
5	4	10	17

Задание 32

15. Точечный источник света S находится в передней фокальной
плоскости собирающей линзы на расстоянии 2 см от ее главной оптической оси. За
линзой в ее задней фокальной плоскости находится плоское зеркало (см. рис.).
Построить действительное изображение источника в данной оптической системе и
найти расстояние между точками S и S^/

16. Луч от
лазерной указки проходит через стеклянную призму с показателем преломления n
= 1,5 и преломляющим углом θ = 30° так, что внутри призмы он идёт
перпендикулярно биссектрисе её преломляющего угла (см. рисунок). На какой угол
φ луч отклоняется призмой от своего первоначального направления?

Источник

Преломление света.

Закон преломления (частный случай).
Обратимость световых лучей.
Закон преломления (общий случай).
Полное внутреннее отражение.
Разберем задачи ЕГЭ по теме: Преломление света.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: закон преломления света, полное внутреннее отражение.

На границе раздела двух прозрачных сред наряду с отражением света наблюдается его преломление — свет, переходя в другую среду, меняет направление своего распространения.

Преломление светового луча происходит при его наклонном падении на поверхность раздела (правда, не всегда — читайте дальше про полное внутреннее отражение). Если же луч падает перпендикулярно поверхности, то преломления не будет — во второй среде луч сохранит своё направление и также пойдёт перпендикулярно поверхности.

к оглавлению ▴

Закон преломления (частный случай).

Мы начнём с частного случая, когда одна из сред является воздухом. Именно такая ситуация присутствует в подавляющем большинстве задач. Мы обсудим соответствующий частный случай закона преломления, а уж затем дадим самую общую его формулировку.

Предположим, что луч света, идущий в воздухе, наклонно падает на поверхность стекла, воды или какой-либо другой прозрачной среды. При переходе в среду луч преломляется, и его дальнейший ход показан на рис. 1.

Рис. 1. Преломление луча на границе «воздух–среда»

В точке падения проведён перпендикуляр (или, как ещё говорят, нормаль) к поверхности среды. Луч , как и раньше, называется падающим лучом, а угол alpha между падающим лучом и нормалью — углом падения. Луч — это преломлённый луч; угол beta между преломлённым лучом и нормалью к поверхности называется углом преломления.

Всякая прозрачная среда характеризуется величиной , которая называется показателем преломления этой среды. Показатели преломления различных сред можно найти в таблицах. Например, для стекла n=1,6 , а для воды n=1,33 . Вообще, у любой среды ; показатель преломления равен единице только в вакууме. У воздуха , поэтому для воздуха с достаточной точностью можно полагать в задачах n=1 (в оптике воздух не сильно отличается от вакуума).

Закон преломления (переход «воздух–среда»).

1) Падающий луч, преломлённый луч и нормаль к поверхности, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно показателю преломления среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=n$ . (1)

Поскольку из соотношения (1) следует, что , то есть — угол преломления меньше угла падения. Запоминаем: переходя из воздуха в среду, луч после преломления идёт ближе к нормали.

Показатель преломления непосредственно связан со скоростью распространения света в данной среде. Эта скорость всегда меньше скорости света в вакууме: . И вот оказывается,что

$n=frac{displaystyle c }{displaystyle v }$ . (2)

Почему так получается, мы с вами поймём при изучении волновой оптики. А пока скомбинируем формулы . (1) и (2):

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle c }{displaystyle v }$ . (3)

Так как показатель преломления воздуха очень близок единице, мы можем считать, что скорость света в воздухе примерно равна скорости света в вакууме . Приняв это во внимание и глядя на формулу . (3), делаем вывод: отношение синуса угла падения к синусу угла преломления равно отношению скорости света в воздухе к скорости света в среде.

к оглавлению ▴

Обратимость световых лучей.

Теперь рассмотрим обратный ход луча: его преломление при переходе из среды в воздух. Здесь нам окажет помощь следующий полезный принцип.

Принцип обратимости световых лучей. Траектория луча не зависит от того, в прямом или обратном направлении распространяется луч. Двигаясь в обратном направлении, луч пойдёт в точности по тому же пути, что и в прямом направлении.

Согласно принципу обратимости, при переходе из среды в воздух луч пойдёт по той же самой траектории, что и при соответствующем переходе из воздуха в среду (рис. 2) Единственное отличие рис. 2 от рис. 1 состоит в том, что направление луча поменялось на противоположное.

Рис. 2. Преломление луча на границе «среда–воздух»

Раз геометрическая картинка не изменилась, той же самой останется и формула (1): отношение синуса угла alpha к синусу угла beta по-прежнему равно показателю преломления среды. Правда, теперь углы поменялись ролями: угол beta стал углом падения, а угол alpha — углом преломления.

В любом случае, как бы ни шёл луч — из воздуха в среду или из среды в воздух — работает следующее простое правило. Берём два угла — угол падения и угол преломления; отношение синуса большего угла к синусу меньшего угла равно показателю преломления среды.

Теперь мы целиком подготовлены для того, чтобы обсудить закон преломления в самом общем случае.

к оглавлению ▴

Закон преломления (общий случай).

Пусть свет переходит из среды 1 с показателем преломления $n_{displaystyle 1}$ в среду 2 с показателем преломления $n_{displaystyle 2}$ . Среда с большим показателем преломления называется оптически более плотной; соответственно, среда с меньшим показателем преломления называется оптически менее плотной.

Переходя из оптически менее плотной среды в оптически более плотную, световой луч после преломления идёт ближе к нормали (рис. 3). В этом случае угол падения больше угла преломления: .

Наоборот, переходя из оптически более плотной среды в оптически менее плотную, луч отклоняется дальше от нормали (рис. 4). Здесь угол падения меньше угла преломления:

Оказывается, оба этих случая охватываются одной формулой — общим законом преломления, справедливым для любых двух прозрачных сред.

Закон преломления.
1) Падающий луч, преломлённый луч и нормаль к поверхности раздела сред, проведённая в точке падения, лежат в одной плоскости.
2) Отношение синуса угла падения к синусу угла преломления равно отношению показателя преломления второй среды к показателю преломления первой среды:

$frac{displaystyle sinalpha }{displaystyle sinbeta }=frac{displaystyle n_{displaystyle 2}}{displaystyle n_{displaystyle 1}}$ . (4)

Нетрудно видеть, что сформулированный ранее закон преломления для перехода «воздух–среда» является частным случаем данного закона. В самом деле, полагая в формуле (4) $n_{displaystyle 1}=1, n_{displaystyle 2}=n$ , мы придём к формуле (1).

Вспомним теперь, что показатель преломления — это отношение скорости света в вакууме к скорости света в данной среде: $n_{displaystyle 1}=c/v_{displaystyle1}, n_{displaystyle 2}=c/v_{displaystyle2}$ . Подставляя это в (4), получим:

$frac{displaystyle sinalpha}{displaystyle sinbeta }=frac{displaystyle v_{displaystyle 1}}{displaystyle v_{displaystyle 2}}$ . (5)

Формула (5) естественным образом обобщает формулу (3). Отношение синуса угла падения к синусу угла преломления равно отношению скорости света в первой среде к скорости света во второй среде.

к оглавлению ▴

Полное внутреннее отражение.

При переходе световых лучей из оптически более плотной среды в оптически менее плотную наблюдается интересное явление — полное внутреннее отражение. Давайте разберёмся, что это такое.

Будем считать для определённости, что свет идёт из воды в воздух. Предположим, что в глубине водоёма находится точечный источник света , испускающий лучи во все стороны. Мы рассмотрим некоторые из этих лучей (рис. 5).

Рис. 5. Полное внутреннее отражение

Луч $SO_{displaystyle 1}$ падает на поверхность воды под наименьшим углом. Этот луч частично преломляется (луч $O_{displaystyle 1} A_{displaystyle 1}$ ) и частично отражается назад в воду (луч $O_{displaystyle 1} B_{displaystyle 1}$ ). Таким образом, часть энергии падающего луча передаётся преломлённому лучу, а оставшаяся часть энергии -отражённому лучу.

Угол падения луча $S O_{displaystyle 2}$ больше. Этот луч также разделяется на два луча — преломлённый и отражённый. Но энергия исходного луча распределяется между ними по-другому: преломлённый луч $O_{displaystyle 2} A_{displaystyle 2}$ будет тусклее, чем луч $O_{displaystyle 1} A_{displaystyle 1}$ (то есть получит меньшую долю энергии), а отражённый луч $O_{displaystyle 2} B_{displaystyle 2}$ — соответственно ярче, чем луч $O_{displaystyle 1} B_{displaystyle 1}$ (он получит большую долю энергии).

По мере увеличения угла падения прослеживается та же закономерность: всё большая доля энергии падающего луча достаётся отражённому лучу, и всё меньшая — преломлённому лучу. Преломлённый луч становится всё тусклее и тусклее, и в какой-то момент исчезает совсем!

Это исчезновение происходит при достижении угла падения $alpha _{0}$ , которому отвечает угол преломления $90^{circ}$ . В данной ситуации преломлённый луч должен был бы пойти параллельно поверхности воды, да идти уже нечему — вся энергия падающего луча целиком досталась отражённому лучу .

При дальнейшем увеличении угла падения преломлённый луч и подавно будет отсутствовать.

Описанное явление и есть полное внутреннее отражение. Вода не выпускает наружу лучи с углами падения, равными или превышающими некоторое значение $alpha _{0}$ — все такие лучи целиком отражаются назад в воду. Угол $alpha _{0}$ называется предельным углом полного отражения.

Величину $alpha _{0}$ легко найти из закона преломления. Имеем:

$frac{displaystyle sinalpha _{0}}{displaystyle sin90^{circ}}=frac{displaystyle 1}{displaystyle n}$ .

Но $sin90^{circ}=1$ , поэтому

$sinalpha _{0}=frac{displaystyle 1}{displaystyle n}$ ,

откуда

$alpha _{0}=arcsinfrac{displaystyle 1}{displaystyle n}$ .

Так, для воды предельный угол полного отражения равен:

$alpha _{0}=arcsinfrac{displaystyle 1}{1,33} approx 48,8^{circ}$ .

Явление полного внутреннего отражения вы легко можете наблюдать дома. Налейте воду в стакан, поднимите его и смотрите на поверхность воды чуть снизу сквозь стенку стакана. Вы увидите серебристый блеск поверхности — вследствие полного внутреннего отражения она ведёт себя подобно зеркалу.

Важнейшим техническим применением полного внутреннего отражения является волоконная оптика. Световые лучи, запущенные внутрь оптоволоконного кабеля (световода) почти параллельно его оси, падают на поверхность под большими углами и целиком, без потери энергии отражаются назад внутрь кабеля. Многократно отражаясь, лучи идут всё дальше и дальше, перенося энергию на значительное расстояние. Волоконно-оптическая связь применяется, например, в сетях кабельного телевидения и высокоскоростного доступа в Интернет.

к оглавлению ▴

Разберем задачи ЕГЭ по теме: Преломление света.

Задача 1. Нижняя грань AC прозрачного клина посеребрена и представляет собой плоское зеркало. Угол при вершине клина $alpha = 30^{circ}$ . Луч света падает из воздуха на клин перпендикулярно грани AB, преломляется и выходит в воздух через ту же грань AB, но уэе под углом преломления $beta = 90^{circ}$ Определите показатель преломления материала клина. Сделайте рисунок, поясняющий ход луча в клине.

Дано:
$alpha = 30^{circ}$
$beta = 90^{circ}$
n-?
Решение. Решение задач по геометрической оптике необходимо начинать с построения чертежа (рисунка), моделирующего условия, описанные в тексте задачи.

Световой луч падает на прозрачный клин перпендикулярно стороне АВ (см.рис.1). В этом случае, световой луч не преломляется на границе раздела воздух-клин, так как угол падения равен 0, соответственно, угол преломления также равен 0. Следовательно, внутри клина световой луч попадает на нижнюю грань АС, которая представляет собой плоское зеркало. Согласно рис.1 величина угла $alpha_1=180^{circ}-(alpha+90^{circ})=90^{circ}-alpha.$

$alpha_1=90^{circ}-30^{circ}=60^{circ}.$

Тогда угол падения луча на плоское зеркало будет равен
$90^{circ}-alpha_1=90^{circ}-60^{circ}=30^{circ}.$

То есть угол падения равен $alpha=30^{circ}$ .
Согласно закону отражения света, угол падения светового луча равен углу отражения. В треугольнике МКО угол КОМ образован суммой двух углов α, поэтому он равен 60°. Тогда угол падения светового луча на грань АВ также будет равен $2alpha=60^{circ}$ (равенство накрест лежащих углов).
На следующем этапе задачи надо применить закон преломления света, так как луч переходит из одной среды в другую.
$frac{sin{2alpha}}{sinbeta}=frac{1}{n}$
При записи этой формулы учтено, что второй средой является воздух с показателем преломления равным 1, а первой средой является материал клина с показателем преломления n, который необходимо определить. Из последней формулы можно выразить и рассчитать n.

$n=frac{sinbeta}{sin2alpha}$

$n=frac{sin90^{circ}}{sin(2cdot 30^{circ})}=frac{sin90^{circ}}{sin60^{circ}}approx 1,15$

Ответ: 1,15

Задача 2. На тонкую собирающую линзу от удалённого источника падает пучок параллельных лучей (см. рисунок). Как изменится положение изображения источника, создаваемого линзой, если между линзой и её фокусом поставить
плоскопараллельную стеклянную пластинку с показателем преломления n (на рисунке положение пластинки отмечено пунктиром)? Ответ поясните, указав, какие физические закономерности Вы использовали. Сделайте рисунок, поясняющий ход лучей до и после установки плоскопараллельной стеклянной пластинки.

Решение. Рассмотрим ход световых лучей от удаленного источника через линзу при отсутствии плоскопараллельной стеклянной пластинки (см.рис.1).

Луч 1-1ʹ проходит через оптический центр линзы и не преломляется. Луч 2-2ʹ идет через фокус и после прохождения через линзу, идет параллельно главной оптической оси. Пересечение этих двух лучей дает действительное изображение удаленного источника, которое расположено в фокальной плоскости линзы. Этот факт также можно доказать, используя формулу тонкой линзы.

$frac{1}{d}+frac{1}{f}=frac{1}{F} (1)$

Так как источник света расположен на расстоянии то $frac{1}{d}rightarrow 0.$

Тогда формула тонкой линзы (1) примет вид $frac{1}{f}=frac{1}{F},$ следовательно, f=F, т.е. изображение формируется в фокальной плоскости линзы.

Рассмотрим ход световых лучей через плоскопараллельную стеклянную пластинку. Для этого необходимо использовать закон преломления света.

Рис.2

Согласно рис.2 угол падения луча на пластину равен α. Закон преломления света на границе раздела воздух-пластинка имеет вид:

$frac{sinalpha}{sinbeta}=frac{n}{1}=n (1).$

Здесь учтено, что показатель преломления воздуха равен 1, а пластинки n.
При переходе светового луча из пластинки в воздух, закон преломления света будет иметь вид:

$frac{sinbeta}{singamma}=frac{1}{n} (2).$

В этом случае первой средой является пластинка с показателем преломления n, а второй средой будет воздух с показателем преломления равным 1.
Из (1) и (2) выразим и .

Так как правые части этих уравнений равны, то

Отсюда вытекает равенство углов . Следовательно, луч, падающий на стеклянную пластину, выходит из нее, оставаясь параллельным входящему лучу. Но при этом выходящий луч немного смещается вверх.

Исходя из этого можно сделать вывод, что изображение удаленного источника после прохождения через плоскопараллельную стеклянную пластину, не изменится. Из удаленного источника выходит бесконечное количество параллельных лучей, которые собираются в фокальной плоскости линзы.

Ответ: не изменится.

Задача 3. Ученик провел опыт по преломлению света, представленный на фотографии. Как изменится при уменьшении угла падения угол преломления светового пучка и скорость света, распространяющегося в стекле? Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшиться
3) не изменится
Запишите в таблицу выбранные цифры для каждой величины. Цифры в ответе могут повторяться.

Угол преломления	Скорость света в стекле

Решение. Для ответа на первый вопрос задачи необходимо применить закон преломления света для границы раздела воздух-стекло.

$frac{sinalpha}{sinbeta}=frac{n}{1}=n.$

Показатель преломления стекла равен n, а воздуха 1.
При уменьшении угла падения α, будет уменьшаться и значение Так как показатель преломления стекла не изменяется, то значение sinbeta так же будет уменьшаться. Поэтому угол преломления уменьшится.

Для ответа на второй вопрос надо учесть, что скорость света в данной среде определяется значением показателя преломления $v_{cp}=frac{c}{n},$ где с – скорость света в вакууме, а n – показатель преломления среды (стекла). Так как эти обе величины не изменяются, то скорость света в стекле так же не изменяется.

Ответ: 23.

Задача 4. Чему равен синус предельного угла полного внутреннего отражения при переходе света из вещества с n_1=1,5 в вещество с n_2=1,2 ?

Решение.

Явление полного внутреннего отражения наблюдается при переходе светового луча из оптически более плотной среды в оптически менее плотную (см.рис.1). Источник света S должен находиться в среде с большим показателем преломления.

Для нахождения синуса угла полного внутреннего отражения необходимо воспользоваться законом преломления света.

$frac{sinalpha_{np}}{sinbeta}=frac{n_2}{n_1} (1)$

При полном внутреннем отражении преломленный луч скользит по границе раздела двух сред и угол преломления $beta=90^{circ}$ . С учетом того, что $sin90^{circ}=1$ уравнение (1) примет вид:

$sinalpha_{np}=frac{1,2}{1,5}=0,8$

$sinalpha_{np}=0,8$

Ответ: 0,8.

Если вам нравятся наши материалы — записывайтесь на курсы подготовки к ЕГЭ по физике онлайн

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Преломление света.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

15. Магнитное поле. Оптика

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

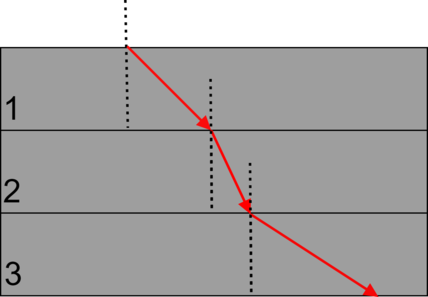
На рисунке изображен ход луча в трех средах. Найдите наименее оптически плотную среду. В ответ укажите цифру.

Чем среда менее оптически плотная, тем луч света больше отклоняется от перпендикуляра. В нашем случае ход луча наиболее отдаленный от перпендикуляра в среде под номером 3.

Ответ: 3

Скорость света в среде 1,5(cdot 10^8) м/c. Найдите абсолютный показатель преломления.

Абсолютный показатель преломления находится по формуле: [n=dfrac{c}{u}]

Где (c) — скорость света в вакууме, а (u) — скорость света в среде. Найдем абсолютный показатель преломления (n=dfrac{3 cdot 10^8 text{ м/c}}{1,5 cdot 10^8 text{ м/c}} =2)

Ответ: 2

Скорость света в среде 1 (u_1=1,5cdot10^8) м/c, а скорость света в среде 2 (u_2=0,75cdot10^8) м/c. Найдите относительный показатель преломления первой среды ко второй.

Абсолютный показатель преломления находится по формуле: [n=dfrac{c}{u}]

Для первой среды (n_1=dfrac{c}{u_1}), для второй (n_2=dfrac{c}{u_2}), следовательно [dfrac{n_1}{n_2}=dfrac{dfrac{c}{u_1}}{dfrac{c}{u_2}}=dfrac{u_2}{u_1}=dfrac{0,75cdot10^8text{ м/c}}{1,5cdot10^8text{ м/c}}=0,5]

Ответ: 0,5

Скорость света в среде 1 (u_1=1,5cdot10^8) м/c, а скорость света в среде 2 (u_2=0,75cdot10^8) м/c. Найдите относительный показатель преломления второй среды к первой.

Абсолютный показатель преломления находится по формуле: [n=dfrac{c}{u}]

Для первой среды (n_1=dfrac{c}{u_1}), для второй (n_2=dfrac{c}{u_2}), следовательно [dfrac{n_2}{n_1}=dfrac{dfrac{c}{u_2}}{dfrac{c}{u_1}}=dfrac{u_1}{u_2}=dfrac{1,5cdot10^8text{ м/c}}{0,75cdot10^8text{ м/c}}=2]

Ответ: 2

Угол между падающим лучом и границей раздела двух сред равен (alpha) = 30(^circ), а угол между преломленным лучом и границей раздела двух сред равен (beta) = 60(^circ). Найдите относительный показатель преломления второй среды к первой. Ответ округлить до десятых.

Относительный показатель преломления второй среды к первой найдем из закона преломления.

[dfrac{n_2}{n_1}=dfrac{sinalpha_1}{sinbeta_1} quad (1)]

Где (sinalpha_1) – синус угла падения луча, а (sinbeta_1) – синус угла преломления. Угол падения – это угол между падающим лучом и перпендикуляром, а угол преломления – угол между преломленным лучом и перпендикуляром.

Синус угла падения можно найти по формуле:

[sinalpha_1=sin(90-alpha) quad (2)]

Синус угла преломления можно найти по формуле:

[sinbeta_1=sin(90-beta) quad (2)]

Подставим (2) и (3) в (1)

[dfrac{n_2}{n_1}=dfrac{sin(90-alpha)}{sin(90-beta)}=dfrac{sin(90-30)}{sin(90-60)}=dfrac{sin60}{sin30}=dfrac{dfrac{sqrt{3}}{2}}{dfrac{1}{2}}=sqrt{3}thickapprox1,7]

Ответ: 1,7

Свет идет из среды с показателем преломления (n_1=2,1) под углом 30(^circ) в среду с показателем преломления (n_2=1). Найдите угол преломления луча, если наблюдается полное внутреннее отражение, то в ответ запишите 0.

По закону преломления: [dfrac{n_2}{n_1}=dfrac{sinalpha_1}{sinalpha_2}]

Где (sinalpha_1) – синус угла падения, а (sinalpha_2) – синус угла преломления.

Выразим из закона преломления синус угла преломления и найдем его [sinalpha_2 =dfrac{sinalpha_1 cdot n_1}{n_2}=dfrac{sin30cdot 2,1}{ 1}=dfrac{2,1}{2}=1,05]

Так как максимальный возможный синус угла равен 1, а у нас 1,05, то мы наблюдаем полное внутреннее отражение.

Ответ: 0

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Данная
тема будет посвящена решению задач, связанных с таким явлением, как преломление
света.

Задача
1.
Луч света падает на стекло под углом 45º. Известно, что угол преломления
данного луча равен 20º. Постройте соответствующий чертёж, найдите
показатель преломления данного стекла и примерное значение скорости света в
нём.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Откуда
абсолютный показатель преломления

Также
абсолютный показатель преломления света равен

Тогда
скорость света в стекле равна

Задача
2.
Два разных стёкла (с показателями преломления 1,5 и 2,1) сложены вплотную друг
к другу. Может ли луч света, пройдя сквозь одно из стёкол, полностью отразиться
от второго?

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Тогда

Как
известно, функция синуса принимает значения в пределах от минус 1 до 1,
поэтому, полученное уравнение не имеет решения. Это говорит о том, что нет
такого угла падения альфа, при котором луч света прошёл бы в одно стекло, но
полностью отразился от другого.

Ответ:
нет,
не может.

Задача
3.
В сосуде кубической форме лежит предмет, расположенный точно в центре дна. Глаз
наблюдателя расположен таким образом, что он видит нижний угол сосуда. Чтобы
наблюдатель мог увидеть предмет в сосуде, его заполняют некой жидкостью с
показателем преломления 1,7. Найдите минимальный уровень этой жидкости.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Ответ:
сосуд
нужно заполнить на 92%.

Задача
4.
Луч света выходит из некоторой среды в воздух таким образом, что угол падения
вдвое меньше угла преломления. Если угол падения увеличить на 10º, то он
достигнет своего предельного значения. Найдите показатель преломления данной
среды.

ДАНО:

РЕШЕНИЕ

Закон
преломления света

Предельный
угол полного отражения

Тогда

Левую
часть уравнения распишем, воспользовавшись формулой синуса суммы углов, а
правую часть уравнения распишем, воспользовавшись формулой синуса двойного
угла

Разделим
правую и левую части на cos a

Ответ:
1,88.

Задача
5.
Мальчик старается попасть палкой в предмет, находящийся на дне пруда глубиной 50
см. Точно прицелившись, он двигает палку под углом сорок 40º к поверхности
воды. На каком расстоянии от предмета палка ткнёт в дно пруда?

ДАНО:

СИ

РЕШЕНИЕ

Закон
преломления света

Ответ:
14
см.

Источник

Законы отражения и преломления света

12 баллов

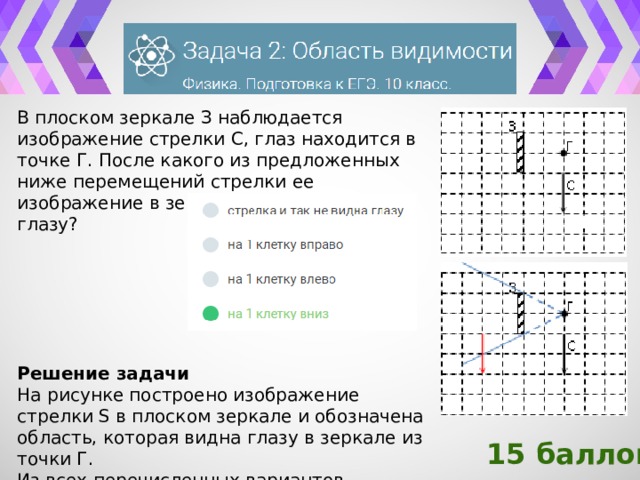
В плоском зеркале З наблюдается изображение стрелки C, глаз находится в точке Г. После какого из предложенных ниже перемещений стрелки ее изображение в зеркале не будет видно глазу?

Решение задачи

На рисунке построено изображение стрелки S в плоском зеркале и обозначена область, которая видна глазу в зеркале из точки Г.

Из всех перечисленных вариантов перемещения стрелки, только перемещение на одну клетку вниз сделает ее изображение невидимой из точки Г.

15 баллов

18 баллов

16 баллов

22 балла

Источник

Задачи по оптике с решениями

Отражение света

10.1.1 На какой угол повернется отраженный от зеркала солнечный луч при повороте зеркала
10.1.2 Предмет находился на расстоянии 20 см от плоского зеркала. Затем его отодвинули на 10 см
10.1.3 В плоскости экрана находится источник света, испускающий узкий пучок лучей под углом
10.1.4 От подъемного крана, освещенного солнцем, падает тень длиной 75 м, а тень от вертикально
10.1.5 Луч света падает на систему двух взаимно перпендикулярных зеркал. Угол падения
10.1.6 Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа
10.1.7 Высота Солнца над горизонтом 38°. Под каким углом к горизонту надо расположить
10.1.8 Солнечный луч, проходящий через отверстие в ставне, составляет с поверхностью стола
10.1.9 Небольшой предмет расположен между двумя плоскими зеркалами, образующими угол
10.1.10 На какой высоте находится аэростат, если с башни высотой 20 м он виден под углом 45°
10.1.11 Какова должна быть минимальная высота вертикального зеркала, в котором человек
10.1.12 Предмет помещен между двумя взаимно перпендикулярными зеркалами. Сколько
10.1.13 Под каким углом к поверхности стола надо расположить плоское зеркало, чтобы получить
10.1.14 Человек, стоящий на берегу озера, видит на гладкой поверхности воды изображение солнца
10.1.15 Светящаяся точка приближается к плоскому зеркалу со скоростью 4 м/с. С какой скоростью
10.1.16 Предмет находится от плоского зеркала на расстоянии 30 см. На каком расстоянии
10.1.17 Точечный источник света освещает тонкий диск диаметром 0,2 м. При этом на экране
10.1.18 На каком из приведенных ниже рисунков правильно построено изображение И предмета П
10.1.19 Горизонтальный луч падает на плоское вертикально расположенное зеркало. На какой
10.1.20 Вертикально стоящий шест высотой 1,1 м, освещенный Солнцем, отбрасывает
10.1.21 На горизонтальном столе по прямой движется шарик. Под каким углом к плоскости стола
10.1.22 Плоское зеркало AB движется поступательно со скоростью v1=2 м/с, а точка S движется
10.1.23 Светящаяся точка равномерно движется по прямой, образующей угол 30° с плоскостью

Показатель преломления и скорость света

10.2.1 Показатель преломления воды для света с длиной волны в вакууме λ₁=0,76 мкм
10.2.2 Как велика скорость света в алмазе?
10.2.3 На поверхность воды падает красный свет с длиной волны 0,7 мкм и далее распространяется
10.2.4 Во сколько раз изменится длина волны света при переходе из среды с абсолютным
10.2.5 Монохроматический свет с частотой 1,5·10¹⁵ Гц распространяется в пластинке
10.2.6 Длина световой волны в стекле 450 нм. Свет в стекле распространяется со скоростью
10.2.7 Световой луч проходит в вакууме расстояние 30 см, а в прозрачной жидкости за то же
10.2.8 Абсолютный показатель преломления алмаза равен 2,42, стекла – 1,5. Каково должно быть
10.2.9 Свет идет по кратчайшему пути из одной среды в другую. Каков показатель преломления
10.2.10 Показатель преломления света относительно воды равен 1,16. Найти скорость света в воде
10.2.11 При падении света на поверхность скипидара из вакуума угол падения равен 45°

Преломление света

10.3.1 Угол падения луча света на границу стекло-воздух равен 30°. Каков угол преломления?
10.3.2 Под каким углом следует направить луч на поверхность стекла, чтобы угол преломления
10.3.3 Определить скорость света внутри льда, если при угле падения луча на лед, равном
10.3.4 Луч света переходит из воды в стекло. Угол падения 38°. Найти угол преломления.
10.3.5 Скорость распространения света в некоторой жидкости равна 2,4·10^8 м/с. На поверхность
10.3.6 Определить абсолютный показатель преломления и скорость распространения света в слюде
10.3.7 Луч света при переходе изо льда в воздух падает на поверхность льда под углом 15
10.3.8 На горизонтальном дне водоема глубиной 1,2 м лежит плоское зеркало. На каком
10.3.9 Два взаимно перпендикулярных луча падают на поверхность воды. Угол падения
10.3.10 Водолазу, находящемуся под водой, кажется, что солнечные лучи падают под углом 60
10.3.11 Взаимно перпендикулярные лучи идут из воздуха в жидкость. Каков показатель преломления
10.3.12 Палка с изломом посередине погружена в пруд так, что наблюдателю, находящемуся
10.3.13 Под каким углом должен падать луч на поверхность стекла, чтобы угол преломления был
10.3.14 Найти угол падения луча на поверхность воды, если известно, что он больше угла
10.3.15 Луч белого света падает на поверхность воды под углом 60°. Чему равен угол
10.3.16 Определить на какой угол отклоняется узкий световой пучок от своего первоначального
10.3.17 На стеклянную пластинку падает луч света. Каков угол падения луча, если угол между
10.3.18 Луч света, падая из воздуха на поверхность воды, частично отражается и частично
10.3.19 Под каким углом должен падать луч света на плоскую поверхность льда, чтобы
10.3.20 Световой луч падает под углом 60° на пластинку с показателем преломления 1,73
10.3.21 Луч падает на границу раздела сред под углом 30°. Показатель преломления первой
10.3.22 Определить угол преломления луча, если при переходе из воздуха в этиловый спирт
10.3.23 В дно пруда вертикально вбита свая так, что она целиком находится под водой. Определите
10.3.24 В дно водоема глубиной 2 м вбита свая, выступающая из воды на 0,5 м. Найти длину тени
10.3.25 Высота солнца над горизонтом 60°. Высота непрозрачного сосуда 25 см. На сколько
10.3.26 Кубический сосуд с непрозрачными стенками расположен так, что глаз наблюдателя
10.3.27 На поверхности водоема глубиной 5,3 м плавает круг радиусом 1 м, над центром которого
10.3.28 Луч света падает на стеклянную пластинку толщиной 3 см под углом 60°. Определить
10.3.29 Луч света падает под углом 40° на систему из трех плоскопараллельных стеклянных
10.3.30 Поверх стеклянной горизонтально расположенной пластины налит тонкий слой воды
10.3.31 На плоскопараллельную стеклянную пластинку толщиной 2 см под углом 60° падает луч
10.3.32 На какое расстояние сместится луч, пройдя плоскопараллельную стеклянную пластинку
10.3.33 Определить смещение светового луча при прохождении его через стеклянную пластинку
10.3.34 Луч света падает под углом 30° на плоскопараллельную стеклянную пластинку
10.3.35 Луч света падает перпендикулярно на вертикальную грань прозрачной призмы
10.3.36 Показатель преломления стекла призмы для красных лучей равен 1,483. Преломляющий
10.3.37 Сечение стеклянной призмы имеет вид равностороннего треугольника. Луч света падает
10.3.38 Определить угол отклонения луча призмой. Преломляющий угол призмы равен 60°
10.3.39 Луч света входит в стеклянную призму под углом π/6 и выходит из призмы в воздух
10.3.40 Какова глубина бассейна, если человек, глядя под углом 30° к поверхности воды
10.3.41 Какова истинная глубина водоема, если камень, лежащий на дне его, при рассматривании
10.3.42 Кажущаяся глубина водоема h=4 м. Определить истинную глубину h0 водоема, если
10.3.43 На расстоянии 1,5 м от поверхности воды в воздухе находится точечный источник света
10.3.44 Угол падения луча на пластинку толщиной 6 мм и показателем преломления, равным

Полное внутреннее отражение

10.4.1 Предельный угол полного внутреннего отражения для воздуха и стекла 34°
10.4.2 Найти предельный угол падения луча на границу раздела стекла и воды
10.4.3 Определить угол полного внутреннего отражения для алмаза, погруженного в воду
10.4.4 Предельный угол полного внутреннего отражения для льда равен 50°. Определить
10.4.5 В системах бензин-воздух и стекло-воздух предельные углы полного внутреннего отражения
10.4.6 В алмазе свет распространяется со скоростью 1,22·10^8 м/с. Определить
10.4.7 Предельный угол полного внутреннего отражения для стекла 45°. Найти скорость
10.4.8 Предельный угол полного отражения в системе стекло-воздух равен 42°. Чему равна
10.4.9 Предельный угол полного отражения для алмаза 24°. Чему равна скорость
10.4.10 Предельный угол полного внутреннего отражения для бензола 45°. Определить
10.4.11 Чему равен предельный угол полного внутреннего отражения светового луча на границе
10.4.12 Предельный угол полного внутреннего отражения в системе скипидар-воздух равен 45°
10.4.13 На дне сосуда, заполненного водой до высоты 0,40 м, находится точечный источник света
10.4.14 Точечный источник света находится на дне сосуда с жидкостью с показателем преломления
10.4.15 Преломляющий угол трехгранной призмы равен 60°. Найти угол падения луча света
10.4.16 В водоем на некоторую глубину помещают источник белого света. Показатели преломления
10.4.17 Луч света переходит из воды в воздух. Угол падения луча 52°. Определить угол
10.4.18 Предельный угол полного внутреннего отражения для воздуха и стекла 34°. Определить
10.4.19 В алмазе свет распространяется со скоростью 1,22·10^8 м/с. Определить предельный
10.4.20 Световой луч падает на стеклянную пластинку квадратного сечения. Каким должен быть

Линзы

10.5.1 Найти оптическую силу собирающей линзы, если изображение предмета, помещенного
10.5.2 На расстоянии 25 см от двояковыпуклой линзы, оптическая сила которой 5 дптр
10.5.3 Предмет находится на расстоянии 8 см от переднего фокуса линзы, а его изображение
10.5.4 На каком расстоянии от собирающей линзы с фокусным расстоянием 20 см получится
10.5.5 Собирающая линза дает прямое изображение предмета с увеличением Γ=2
10.5.6 На каком расстоянии от выпуклой линзы с фокусным расстоянием 32 см следует поместить
10.5.7 Линза дает увеличение предмета в три раза, если предмет находится на расстоянии 10 см
10.5.8 Предмет помещен на расстоянии 25 см перед передним фокусом собирающей линзы
10.5.9 Светящийся предмет находится на расстоянии 3 м от экрана. На каком минимальном
10.5.10 Расстояние между лампой и экраном 3,2 м. Фокусное расстояние линзы 0,6 м. Определить
10.5.11 Предмет находится на расстоянии 12 см от двояковогнутой линзы, фокусное расстояние
10.5.12 Фокусное расстояние собирающей линзы равно 0,15 м. Определить высоту предмета
10.5.13 Оптическая сила тонкой линзы 5 дптр. Предмет поместили на расстоянии 60 см
10.5.14 Предмет находится на расстоянии 4F от собирающей линзы. Найдите коэффициент увеличения
10.5.15 На каком расстоянии от линзы с оптической силой 5 дптр необходимо поставить предмет
10.5.16 Фокусное расстояние собирающей линзы 0,2 м. На каком расстоянии от линзы следует
10.5.17 Когда предмет поместили на расстоянии 20 см от линзы, изображение получилось
10.5.18 Предмет находится на расстоянии 0,7 м от тонкой собирающей линзы. На каком
10.5.19 Каково главное фокусное расстояние линзы, если для получения изображения
10.5.20 Предмет и его прямое изображение, создаваемое тонкой собирающей линзой
10.5.21 Расстояние от предмета до экрана 5 м. Какой оптической силы надо взять линзу
10.5.22 Линза дает действительное изображение предмета с увеличением 3. Какое увеличение
10.5.23 Предмет находится на расстоянии 0,1 м от переднего фокуса собирающей линзы
10.5.24 Точечный источник света находится на расстоянии 50 см от собирающей линзы
10.5.25 Расстояние между предметом и экраном равно 120 см. На каком максимальном расстоянии
10.5.26 Изображение миллиметрового деления шкалы, расположенной перед линзой
10.5.27 Расстояние между лампой и экраном 3,2 м. Фокусное расстояние линзы 0,6 м.
10.5.28 Определить наименьшее возможное расстояние между светящимся предметом и его
10.5.29 Расстояние от предмета до экрана 90 см. Где нужно поместить между ними линзу
10.5.30 Светящийся предмет находится на расстоянии 420 см от экрана. На каком расстоянии
10.5.31 Расстояние от предмета до двояковыпуклой линзы d=kF, где F – фокусное расстояние
10.5.32 Найти наименьшее возможное расстояние между светящимся предметом и его
10.5.33 Расстояние между предметом и его равным, действительным изображением равно 2 м
10.5.34 С помощью линзы на экране получено изображение в 4 раза по площади больше самого
10.5.35 Перед собирающей линзой с оптической силой 2,5 дптр на расстоянии 30 см находится
10.5.36 Фокусное расстояние собирающей линзы 10 см, расстояние от переднего фокуса 5 см
10.5.37 Фокусное расстояние собирающей линзы равно 10 см, расстояние от предмета до фокуса
10.5.38 Мнимое изображение предмета находится на расстоянии 1 м от собирающей линзы
10.5.39 Величина прямого изображения предмета вдвое больше самого предмета. Расстояние
10.5.40 Линзой с оптической силой 4 дптр надо получить увеличенное в 5 раз мнимое изображение
10.5.41 Мнимое изображение предмета, получаемое с помощью линзы, в 4,5 раза больше
10.5.42 Предмет находится на расстоянии 1,5F от линзы. Его приблизили к линзе на расстояние 0,7F
10.5.43 Определить главное фокусное расстояние рассеивающей линзы, если известно, что
10.5.44 Предмет расположен на расстоянии 0,5F от рассеивающей линзы с фокусным расстоянием
10.5.45 Главное фокусное расстояние рассеивающей линзы 12 см. Изображение предмета
10.5.46 Предмет находится перед рассеивающей линзой на расстоянии 2 м. На каком расстоянии
10.5.47 Тонкая рассеивающая линза создает изображение предмета, находящегося в ее фокальной
10.5.48 Определите оптическую силу линзы, если изображение предмета, помещенного перед
10.5.49 Пучок лучей, параллельный главной оптической оси, после преломления в линзе
10.5.50 Расстояние от освещенного предмета до экрана 100 см. Линза, помещенная между ними
10.5.51 Высота пламени свечи 5 см. Линза дает на экране изображение этого пламени высотой
10.5.52 Предмет расположен на расстоянии 1,6F от линзы. Его переместили к линзе на расстояние
10.5.53 Собирающая линза дает изображение предмета, увеличенное в 5 раз. Экран придвинули
10.5.54 Собирающая линза дает двукратное изображение предмета. Когда линзу придвинули
10.5.55 Расстояние от предмета до линзы и от линзы до изображения предмета одинаковы
10.5.56 От предмета высотой 20 см при помощи линзы получили действительное изображение
10.5.57 Предмет расположен перпендикулярно оптической оси собирающей линзы. На сколько
10.5.58 Точечный источник света находится на расстоянии 40 см от собирающей линзы
10.5.59 На каком расстоянии от рассеивающей линзы с фокусным расстоянием 10 см находится
10.5.60 Изображение светящейся точки в рассеивающей линзе с оптической силой D=-5 дптр
10.5.61 Светящаяся точка находится в фокусе рассеивающей линзы. На каком расстоянии от линзы
10.5.62 Середина стержня, имеющего длину 10 мм, находится на расстоянии 18 см от собирающей
10.5.63 Точечный источник света находится на расстоянии 40 см от собирающей линзы с фокусным
10.5.64 На расстоянии 60 см от собирающей линзы с фокусным расстоянием 50 см находится
10.5.65 Какое линейное увеличение можно получить при помощи проекционного аппарата
10.5.66 Фотоаппаратом с расстояния 500 м сделан снимок телебашни. Фокусное расстояние
10.5.67 Линзой пользуются как лупой. Первоначально изображение было в 4 раза больше
10.5.68 С самолета, летящего на высоте 12 км, сфотографирована местность в масштабе 1:16000
10.5.69 При фотографировании предмета с расстояния 1 м высота изображения равна 6 см
10.5.70 Светящаяся точка приближается к собирающей линзе вдоль ее главной оптической оси
10.5.71 Небольшому шарику, который находится на поверхности горизонтально расположенной
10.5.72 Точечный предмет движется по окружности со скоростью 0,04 м/с вокруг главной
10.5.73 Укажите номер рисунка, на котором правильно изображен ход светового луча

Интерференция света

10.6.1 Разность хода двух волн, полученных от когерентных источников до данной точки равна
10.6.2 Разность хода двух интерферирующих лучей монохроматического света равна λ/4
10.6.3 Два когерентных источника звука колеблются в одинаковой фазе. В точке, отстоящей
10.6.4 Разность хода двух интерферирующих лучей монохроматического света равно четверти
10.6.5 Разность фаз двух интерферирующих световых волн равна 5π, разность хода между ними
10.6.6 Тонкая мыльная пленка освещается светом с длиной волны 0,6 мкм. Чему равна

Дифракция света

10.7.1 Определить угол отклонения лучей монохроматического света с длиной волны 0,55 мкм
10.7.2 Один миллиметр дифракционной решетки содержит 20 штрихов. На какой угол отклоняются
10.7.3 Дифракционная решетка имеет 250 штрихов на миллиметр. Под каким углом виден максимум
10.7.4 Определить число штрихов на 1 мм дифракционной решетки, если углу дифракции 30°
10.7.5 Сколько штрихов на 1 мм должна иметь дифракционная решетка, чтобы зеленая линия
10.7.6 Сколько штрихов на 1 мм должна иметь дифракционная решетка для того, чтобы второй
10.7.7 Период дифракционной решетки в два раза больше длины световой волны
10.7.8 На дифракционную решетку нормально падает монохроматический свет с длиной волны
10.7.9 На дифракционную решетку с периодом 6 мкм падает монохроматическая волна
10.7.10 Период дифракционной решетки 3 мкм. Найдите наибольший порядок спектра для желтого
10.7.11 На дифракционную решетку нормально падает монохроматический свет с длиной волны
10.7.12 Какой наибольший порядок спектра можно наблюдать с помощью дифракционной решетки
10.7.13 Период дифракционной решетки 3 мкм. Найдите наибольший порядок спектра
10.7.14 На дифракционную решетку нормально падает монохроматический свет с длиной
10.7.15 Какой наибольший порядок спектра можно наблюдать с помощью дифракционной
10.7.16 Вычислите максимальный порядок спектра дифракционной решетки с периодом 2 мкм
10.7.17 Найти наибольший порядок спектра для света с длиной волны 700 нм, если постоянная
10.7.18 Дифракционная линия для волны 546,1 нм в спектре первого порядка наблюдается под углом
10.7.19 Сколько максимумов можно будет увидеть на экране, если на дифракционную решетку
10.7.20 Постоянная дифракционной решетки в 3,7 раза больше длины световой волны, нормально
10.7.21 Определить длину волны для линии в дифракционном спектре третьего порядка
10.7.22 Определить длину волны для линии в дифракционном спектре второго порядка
10.7.23 На дифракционную решетку нормально падает пучок света от разрядной трубки. Какова
10.7.24 Период дифракционной решетки равен 1,5 мкм. Чему равна ширина прозрачных щелей
10.7.25 Определите оптическую разность хода волн длиной 540 нм, падающих на дифракционную
10.7.26 Дифракционная решетка, имеющая 100 штрихов на 1 мм, находится на расстоянии 1 м
10.7.27 На дифракционную решетку с периодом 4 мкм падает нормально монохроматическая волна
10.7.28 При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное
10.7.29 На каком расстоянии от дифракционной решетки надо поставить экран, чтобы расстояние
10.7.30 Для измерения длины световой волны применена дифракционная решетка, имеющая
10.7.31 Определить длину волны, падающей на дифракционную решетку, имеющую 400 штрихов
10.7.32 Найти период решетки, если дифракционный максимум 1-го порядка для волны 486 нм
10.7.33 Найдите наибольший порядок спектра для длины волны, равной 600 нм, если период
10.7.34 На дифракционную решетку с периодом 1 мкм падает нормально монохроматический свет
10.7.35 Дифракционная решетка длины 2 см имеет 10000 штрихов. Под каким углом наблюдается
10.7.36 На дифракционную решетку нормально падает пучок света от разрядной трубки
10.7.37 При нормальном падении белого света на дифракционную решетку зеленая линия

( 111 оценок, среднее 4.95 из 5 )

Источник

Преломление света.

Закон преломления (частный случай).

Обратимость световых лучей.

Закон преломления (общий случай).

Полное внутреннее отражение.

Разберем задачи ЕГЭ по теме: Преломление света.

Задачи по оптике с решениями

Отражение света

Показатель преломления и скорость света

Преломление света

Полное внутреннее отражение

Линзы

Интерференция света

Дифракция света

Новое и интересное на сайте: