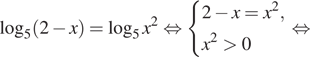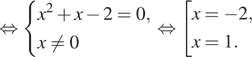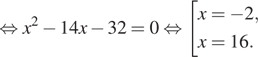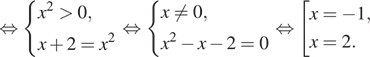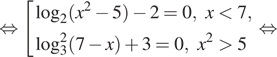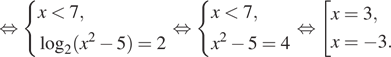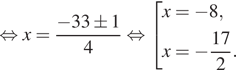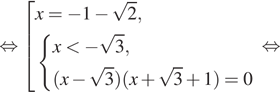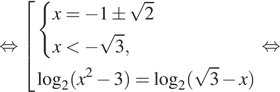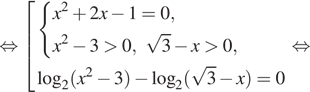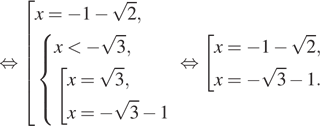Егэ по математике 514623

а)  Решите уравнение 6 логарифм по основанию 8 в квадрате x минус 5 логарифм по основанию 8 x плюс 1=0.

б)  Найдите все корни этого уравнения, принадлежащие отрезку левая квадратная скобка 2;2,5 правая квадратная скобка .

Спрятать решение

Решение.

а)  Запишем исходное уравнение в виде:

левая круглая скобка 3 логарифм по основанию 8 x минус 1 правая круглая скобка левая круглая скобка 2 логарифм по основанию 8 x минус 1 правая круглая скобка =0.

Значит, 3 логарифм по основанию 8 x=1, откуда x=2, или 2 логарифм по основанию 8 x=1, откуда x=2 корень из 2 .

б)  Заметим, что 2 меньше 2,5= корень из 6,25 меньше корень из 8 =2 корень из 2 .

Значит, указанному отрезку принадлежит корень 2.

Ответ: а) 2 и 2 корень из 2 ; б) 2.

Спрятать критерии

Критерии проверки:

Критерии оценивания выполнения задания Баллы
Обоснованно получены верные ответы в обоих пунктах. 2
Обоснованно получен верный ответ в пункте а),

ИЛИ

получены неверные ответы из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения пункта а) и пункта б).

 1
Решение не соответствует ни одному из критериев, перечисленных выше. 0
Максимальный балл 2

Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Вариант 701 (C часть).

Источник

Решу егэ профиль математика 517739

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Задание 12 № 517747

Ответ а 3 и 27; б 3.

Ege. sdamgia. ru

12.01.2020 13:48:01

2020-01-12 13:48:01

Источники:

Https://ege. sdamgia. ru/test? likes=517739

Решу егэ профиль математика 517739 — Математика и Английский » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 517746

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит корень −3.

Ответ: а) −3 и 27; б) −3.

Аналоги к заданию № 517739: 517746 517747 Все

Задание 12 № 517747

Задание 12 № 517746

Б Заметим, что Значит, указанному отрезку принадлежит корень 3.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах, если в одном дюйме 2,54 см. Результат округлите до целого числа сантиметров.

Источники:

ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword < color: red; >Решу егэ профиль математика 517739

Уско­рен­ная под­го­тов­ка к ЕГЭ с ре­пе­ти­то­ра­ми Учи. До­ма. За­пи­сы­вай­тесь на бес­плат­ное за­ня­тие!

Задание 12 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Запишем исходное уравнение в виде:

Б) Поскольку отрезку принадлежит единственный корень −2.

Ответ: а) −2; 1, б) −2.

Почему такое странное ОДЗ?? Где 2-х>0, х>0, следовательно х0; тогда х (0;2)

Екатерина, в решении не находили ОДЗ.

В решении было использован равносильный переход, при котором условия достаточно для решения примера

А у Вас ОДЗ найдено с ошибкой.

Задание 12 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

А) Из уравнения получаем:

Б) Заметим, что Значит, указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

В пункте «а» ответ только 16,вы не проверили ОДЗ

В этом уравнении не нужно искать ОДЗ. Это лишнее действие

Задание 12 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

А) Заметим, что преобразуем исходное уравнение:

Пусть тогда уравнение запишется в виде откуда или

При получим: откуда

При получим: откуда

Б) Корень не принадлежит промежутку Поскольку и корень принадлежит промежутку

Источник: ЕГЭ по математике 19.06.2013. Основная волна, резервный день. Центр. Вариант 502., Задания 13 (С1) ЕГЭ 2013

В строчке а) откуда-то взялась «3»

Путём каких преобразований мы получили ответ log(3)5 ?

1) Уравнение начинается с числе 9 в степени. Т. е. Мы раскладываем 9 как 3*3. Однако в первой строке решения мы видим 9*3. От туда и дальнейшее неверное вычисление.

2) Когда мы возвращаем замену (четвёртая строчка решения) вместо этого (если, допустим, t и правда равно 5/3) должно получиться Х-1= логорифм 5/3 по основанию 3. Верно?

Так ли это? Ибо мне свойственно ошибаться. Это правда ошибка, или я чего-то не понимаю? Если второе, то объясните, если можно.

Задание 12 № 517739

Задание 12 № 502094

Задание 12 502094.

Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.

Dankonoy. com

16.06.2020 6:45:22

2020-06-16 06:45:22

Источники:

Https://dankonoy. com/ege/ege11/archives/10087

Материал для подготовки к экзамену по математике 1 курс. » /> » /> .keyword { color: red; } Решу егэ профиль математика 517739

Материал для подготовки к экзамену по математике 1 курс

Материал для подготовки к экзамену по математике 1 курс.

нажмите, чтобы узнать подробности

Материал для подготовки к экзамену по математике для 1 курса СПО.

Просмотр содержимого документа
«Материал для подготовки к экзамену по математике 1 курс.»

Логарифмические уравнения

1. Задание 5 № 26646

Найдите корень уравнения

2. Задание 5 № 26647

Найдите корень уравнения

3. Задание 5 № 26648

Найдите корень уравнения

4. Задание 5 № 26649

Найдите корень уравнения

5. Задание 5 № 26657

Найдите корень уравнения

6. Задание 5 № 26658

Найдите корень уравнения

7. Задание 5 № 26659

Найдите корень уравнения

8. Задание 5 № 77380

Решите уравнение

9. Задание 5 № 77381

Решите уравнение

10. Задание 5 № 77382

Решите уравнение Если уравнение имеет более одного корня, в ответе укажите меньший из них.

11. Задание 5 № 315120

Найдите корень уравнения

12. Задание 5 № 315535

Найдите корень уравнения

13. Задание 5 № 525399

Решите уравнение

Тригонометрические уравнения

1. Задание 5 № 26669

Найдите корни уравнения: В ответ запишите наибольший отрицательный корень.


Значениям соответствуют положительные корни.

Если, то и

Если, то и

Значениям соответствуют меньшие значения корней.

Следовательно, наибольшим отрицательным корнем является число

2. Задание 5 № 77376

Решите уравнение В ответе напишите наибольший отрицательный корень.

Значению соответствует Положительным значениям параметра соответствуют положительные значения корней, отрицательным значениям параметра соответствуют меньшие значения корней. Следовательно, наибольшим отрицательным корнем является число −1.

3. Задание 5 № 77377

Решите уравнение В ответе напишите наименьший положительный корень.

Значениям соответствуют отрицательные корни.

Если, то и

Если, то и

Значениям соответствуют большие положительные корни.

Наименьшим положительным решением является 0,5.

Преобразования числовых логарифмических выражений

1. Задание 9 № 26843

Найдите значение выражения

2. Задание 9 № 26844

Найдите значение выражения

3. Задание 9 № 26845

Найдите значение выражения

4. Задание 9 № 26846

Найдите значение выражения

5. Задание 9 № 26847

Найдите значение выражения

6. Задание 9 № 26848

Найдите значение выражения

7. Задание 9 № 26849

Найдите значение выражения

8. Задание 9 № 26850

Найдите значение выражения

9. Задание 9 № 26851

Найдите значение выражения

10. Задание 9 № 26852

Найдите значение выражения

11. Задание 9 № 26853

Найдите значение выражения

12. Задание 9 № 26854

Найдите значение выражения

13. Задание 9 № 26855

Найдите значение выражения

14. Задание 9 № 26856

Найдите значение выражения

15. Задание 9 № 26857

Найдите значение выражения

16. Задание 9 № 26858

Найдите значение выражения

17. Задание 9 № 26859

Найдите значение выражения

18. Задание 9 № 26860

Найдите значение выражения

19. Задание 9 № 26861

Найдите значение выражения

20. Задание 9 № 26862

Найдите значение выражения

21. Задание 9 № 26882

Найдите значение выражения

22. Задание 9 № 26883

Найдите значение выражения

23. Задание 9 № 26885

Найдите значение выражения

24. Задание 9 № 26889

Найдите значение выражения

25. Задание 9 № 26892

Найдите значение выражения

26. Задание 9 № 26893

Найдите значение выражения

27. Задание 9 № 26894

Найдите значение выражения

28. Задание 9 № 26896

Найдите значение выражения

29. Задание 9 № 77418

Вычислите значение выражения:

30. Задание 9 № 505097

Найдите значение выражения

31. Задание 9 № 509086

Найдите значение выражения

32. Задание 9 № 510939

Найдите значение выражения

33. Задание 9 № 525403

Найдите значение выражения

Вычисление значений тригонометрических выражений

1. Задание 9 № 26775

Найдите, если и

2. Задание 9 № 26776

Найдите, если и

3. Задание 9 № 26777

Найдите, если и

4. Задание 9 № 26778

Найдите, если и

5. Задание 9 № 26779

Найдите, если

6. Задание 9 № 26780

Найдите, если

7. Задание 9 № 26783

Найдите значение выражения, если

8. Задание 9 № 26784

Найдите, если и

9. Задание 9 № 26785

Найдите, если и

10. Задание 9 № 26786

Найдите, если

11. Задание 9 № 26787

Найдите, если

12. Задание 9 № 26788

Найдите, если

13. Задание 9 № 26789

Найдите, если

14. Задание 9 № 26790

Найдите, если

15. Задание 9 № 26791

Найдите, если

16. Задание 9 № 26792

Найдите значение выражения, если

17. Задание 9 № 26793

Найдите значение выражения, если

18. Задание 9 № 26794

Найдите, если

19. Задание 9 № 316350

Найдите, если

20. Задание 9 № 501598

Найдите значение выражения

21. Задание 9 № 502014

Найдите значение выражения

22. Задание 9 № 502045

Найдите значение выражения

23. Задание 9 № 502106

Найдите значение выражения

24. Задание 9 № 502285

Найдите значение выражения

25. Задание 9 № 502305

Найдите значение выражения если и

26. Задание 9 № 504410

Найдите значение выражения:

27. Задание 9 № 504824

Найдите значение выражения

28. Задание 9 № 508966

Найдите если

29. Задание 9 № 510424

Найдите если и

30. Задание 9 № 549336

Найдите если и

Преобразования числовых тригонометрических выражений

1. Задание 9 № 26755

Найдите значение выражения

2. Задание 9 № 26756

Найдите значение выражения

3. Задание 9 № 26757

Найдите значение выражения

4. Задание 9 № 26758

Найдите значение выражения

5. Задание 9 № 26759

Найдите значение выражения

6. Задание 9 № 26760

Найдите значение выражения

7. Задание 9 № 26761

Найдите значение выражения

8. Задание 9 № 26762

Найдите значение выражения

9. Задание 9 № 26763

Найдите значение выражения

10. Задание 9 № 26764

Найдите значение выражения

11. Задание 9 № 26765

Найдите значение выражения

12. Задание 9 № 26766

Найдите значение выражения

13. Задание 9 № 26767

Найдите значение выражения

14. Задание 9 № 26769

Найдите значение выражения

15. Задание 9 № 26770

Найдите значение выражения

16. Задание 9 № 26771

Найдите значение выражения

17. Задание 9 № 26772

Найдите значение выражения

18. Задание 9 № 26773

Найдите значение выражения

19. Задание 9 № 26774

Найдите значение выражения

20. Задание 9 № 77412

Найдите значение выражения

21. Задание 9 № 77413

Найдите значение выражения

22. Задание 9 № 77414

Найдите значение выражения:

23. Задание 9 № 245169

Найдите значение выражения

24. Задание 9 № 245170

Найдите значение выражения

25. Задание 9 № 245171

Найдите значение выражения

26. Задание 9 № 245172

Найдите значение выражения

27. Задание 9 № 501701

Найдите значение выражения

28. Задание 9 № 502994

Найдите значение выражения

29. Задание 9 № 503310

Найдите значения выражения

30. Задание 9 № 510013

Найдите если и

31. Задание 9 № 510312

Найдите значение выражения

32. Задание 9 № 510386

Найдите значение выражения

33. Задание 9 № 510405

Найдите значение выражения

34. Задание 9 № 510824

Найдите значение выражения

35. Задание 9 № 510843

Найдите значение выражения

36. Задание 9 № 525113

Найдите значение выражения

37. Задание 9 № 526009

Найдите значение выражения

Ло­га­риф­ми­че­ские и по­ка­за­тель­ные уравнения

1. Задание 13 № 514082

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

2. Задание 13 № 517739

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

3. Задание 13 № 502094

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие промежутку

4. Задание 13 № 516760

А) Решите уравнение:

Б) Определите, какие из его корней принадлежат отрезку

5. Задание 13 № 514623

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

6. Задание 13 № 502053

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

7. Задание 13 № 525377

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

8. Задание 13 № 513605

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

9. Задание 13 № 503127

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

10. Задание 13 № 514081

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащего отрезку

11. Задание 13 № 502999

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−1; 2].

12. Задание 13 № 528517

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

13. Задание 13 № 550261

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие промежутку

14. Задание 13 № 555265

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

15. Задание 13 № 555583

А) Решите уравнение

Б) Укажите корни этого уравнения, принадлежащие отрезку

16. Задание 13 № 561853

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−2,5; −1,5].

17. Задание 13 № 562032

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку [−0,5; 0,5].

18. Задание 13 № 562757

А) Решите уравнение

Б) Найдите все корни этого уравнения, принадлежащие отрезку

б) Укажите корни этого уравнения, принадлежащие отрезку

Решите уравнение В ответе напишите наименьший положительный корень.

Просмотр содержимого документа «Материал для подготовки к экзамену по математике 1 курс.»

Б Укажите корни этого уравнения, принадлежащие отрезку.

Multiurok. ru

06.02.2020 18:29:01

2020-02-06 18:29:01

Источники:

Https://multiurok. ru/files/material-dlia-podgotovki-k-ekzamenu-po-matematike. html

Источник

Логарифмические
уравнения из материалов ЕГЭ профильного уровня.

 (Для
всех уравнений делается проверка или находится ОДЗ).

1. а)  Решите уравнение логарифм по основанию 5 левая круглая скобка 2 минус x правая круглая скобка = логарифм по основанию левая круглая скобка 25 правая круглая скобка x в степени 4 .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию 9 дробь: числитель: 1, знаменатель: { конец дроби 82; логарифм по основанию 9 8 правая квадратная скобка .

Решение. а)  Запишем
исходное уравнение в виде:

логарифм по основанию 5 левая круглая скобка 2 минус x правая круглая скобка = логарифм по основанию 5 x в квадрате равносильно система выражений 2 минус x=x в квадрате ,x в квадрате больше 0 конец системы равносильно
равносильно система выражений x в квадрате плюс x минус 2=0,x не равно 0 конец системы . равносильно совокупность выражений x= минус 2,x=1. конец совокупности .

б)  Поскольку логарифм по основанию целая часть: 9, дробная часть: числитель: 1, знаменатель: 82 меньше минус 2 меньше логарифм по основанию 9 8 меньше 1,отрезку
левая квадратная скобка логарифм по основанию целая часть: 9, дробная часть: числитель: 1, знаменатель: 82 ; логарифм по основанию 9 8 правая квадратная скобка принадлежит
единственный корень −2.

Ответ: а) −2; 1, б) −2.

2. а)  Решите уравнение логарифм по основанию 2 левая круглая скобка x в квадрате минус 14x правая круглая скобка =5.

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию 3 0,1; 5 корень из 10 правая квадратная скобка .

Решение. а)  Из
уравнения получаем:

логарифм по основанию 2 левая круглая скобка x в квадрате минус 14x правая круглая скобка =5 равносильно x в квадрате минус 14x=32 равносильно
равносильно x в квадрате минус 14x минус 32=0 равносильно совокупность выражений x= минус 2,x=16. конец совокупности .

б)  Заметим, что логарифм по основанию 3 0,1 меньше логарифм по основанию 3 дробь: числитель: 1, знаменатель: 9 конец дроби = минус 2 меньше 5 корень из 10= корень из 250 меньше корень из 256=16.Значит,
указанному отрезку принадлежит только корень −2.

Ответ: а) −2 и 16; б) −2.

3. а)  Решите уравнение 6 логарифм по основанию 8 в квадрате x минус 5 логарифм по основанию 8 x плюс 1=0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка 2;2,5 правая квадратная скобка .

Решение. а)  Запишем
исходное уравнение в виде:

левая круглая скобка 3 логарифм по основанию 8 x минус 1 правая круглая скобка левая круглая скобка 2 логарифм по основанию 8 x минус 1 правая круглая скобка =0.

Значит, 3 логарифм по основанию 8 x=1,откуда
x=2,или 2 логарифм по основанию 8 x=1,откуда
x=2 корень из 2 .

б)  Заметим, что 2 меньше 2,5= корень из 6,25 меньше корень из 8 =2 корень из 2 .

Значит, указанному отрезку принадлежит корень 2.

Ответ: а) 2 и 2 корень из 2 ;б) 2.

4.  а)  Решите уравнение 1 плюс логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию левая круглая скобка корень из 2 правая круглая скобка корень из 8x в степени левая круглая скобка 4 правая круглая скобка плюс 14.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка .

Решение. а)  Заметим,
что уравнение определено при любом x.Запишем исходное уравнение
в виде:

логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 8x в степени 4 плюс 14 правая круглая скобка минус логарифм по основанию 2 2 равносильно
равносильно логарифм по основанию 2 левая круглая скобка 9x в квадрате плюс 5 правая круглая скобка = логарифм по основанию 2 левая круглая скобка 4x в степени 4 плюс 7 правая круглая скобка равносильно равносильно 9x в квадрате плюс 5=4x в степени 4 плюс 7 равносильно 4x в степени 4 минус 9x в квадрате плюс 2=0 равносильно
равносильно левая круглая скобка 4x в квадрате минус 1 правая круглая скобка левая круглая скобка x в квадрате минус 2 правая круглая скобка =0.

Значит, либо 4x в квадрате минус 1=0,откуда x= дробь: числитель: 1, знаменатель: 2 конец дроби или x= минус дробь: числитель: 1, знаменатель: 2 конец дроби , либо x в квадрате минус 2=0,откуда x= корень из 2или x= минус корень из 2.

б)  Поскольку минус корень из 2 меньше минус 1 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 1, знаменатель: 2 конец дроби меньше дробь: числитель: 8, знаменатель: 9 конец дроби меньше корень из 2, отрезку
левая квадратная скобка минус 1; дробь: числитель: 8, знаменатель: 9 конец дроби правая квадратная скобка принадлежат
корни x= дробь: числитель: 1, знаменатель: 2 конец дроби и x= минус дробь: числитель: 1, знаменатель: 2 конец дроби .

Ответ: а) x=pm корень из 2,x=pm дробь: числитель: 1, знаменатель: 2 конец дроби ; б)
pm дробь: числитель: 1, знаменатель: 2 конец дроби .

5.   а)  Решите уравнение логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию левая круглая скобка 49 правая круглая скобка левая круглая скобка x в степени 4 правая круглая скобка .

б)  Найдите все корни этого уравнения, принадлежащие
отрезку левая квадратная скобка логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 7 ; логарифм по основанию 6 35 правая квадратная скобка .

Решение. а)  Поскольку
логарифм по основанию левая круглая скобка 7 в квадрате правая круглая скобка x в степени 4 = логарифм по основанию 7 x в квадрате ,получаем:

логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию левая круглая скобка 49 правая круглая скобка x в степени 4 равносильно логарифм по основанию 7 левая круглая скобка x плюс 2 правая круглая скобка = логарифм по основанию 7 x в квадрате равносильно
равносильно система выражений x в квадрате больше 0,x плюс 2=x в квадрате конец системы . равносильно система выражений x не равно 0,x в квадрате минус x минус 2=0 конец системы . равносильно совокупность выражений x= минус 1,x=2. конец совокупности .

б)  В силу цепочки соотношений логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 7 меньше логарифм по основанию целая часть: 6, дробная часть: числитель: 1, знаменатель: 6 = минус 1 меньше логарифм по основанию 6 35 меньше логарифм по основанию 6 36=2заданному
отрезку принадлежит только число −1.

Ответ: а) {−1, 2}, б) −1.

6. а)  Решите уравнение логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка минус 6=
=0.

б)  Укажите корни этого уравнения, принадлежащие
промежутку левая квадратная скобка логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 7 ; логарифм по основанию 2 9 правая квадратная скобка .

Решение. а)  Преобразуем
уравнение:

логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка минус 6=0 равносильно

равносильно логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка умножить на левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка минус 2 левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка =0 равносильно

равносильно левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 правая круглая скобка левая круглая скобка логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 правая круглая скобка =0 равносильно
равносильно совокупность выражений логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка минус 2 = 0, x меньше 7, логарифм по основанию 3 в квадрате левая круглая скобка 7 минус x правая круглая скобка плюс 3 = 0, x в квадрате больше 5 конец совокупности . равносильно

равносильно система выражений x меньше 7, логарифм по основанию 2 левая круглая скобка x в квадрате минус 5 правая круглая скобка = 2 конец системы . равносильно система выражений x меньше 7, x в квадрате минус 5 = 4 конец системы . равносильно совокупность выражений x=3,x= минус 3. конец совокупности .

б)  Заметим, что

минус 3 = логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 8 меньше логарифм по основанию целая часть: 2, дробная часть: числитель: 1, знаменатель: 7 меньше 3 = логарифм по основанию 2 8 меньше логарифм по основанию 2 9,

поэтому в указанный промежуток попадает только корень x=3.

Ответ: а) {−3; 3} б) 3.

7. а)  Решите
уравнение логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = дробь: числитель: 1, знаменатель: логарифм по основанию левая круглая скобка минус 33x правая круглая скобка левая круглая скобка левая круглая скобка 1 минус x правая круглая скобка левая круглая скобка x плюс 33 правая круглая скобка правая круглая скобка конец дроби .

б)  Укажите корни этого уравнения, принадлежащие
отрезку левая квадратная скобка минус корень из 333; минус корень из 33 правая квадратная скобка .

Решение. а)  Заметим,
что уравнение имеет смысл при минус 33 меньше x меньше 0,x не равно минус дробь: числитель: 1, знаменатель: конец дроби 33,x не равно минус 16 минус 12 корень из 2 (⁎). Преобразуем его при
этих условиях:

логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = дробь: числитель: 1, знаменатель: логарифм по основанию левая круглая скобка минус 33x правая круглая скобка левая круглая скобка левая круглая скобка 1 минус x правая круглая скобка левая круглая скобка x плюс 33 правая круглая скобка правая круглая скобка конец дроби равносильно

underset левая круглая скобка * правая круглая скобка mathop равносильно логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка 2x в квадрате плюс 136 правая круглая скобка = логарифм по основанию левая круглая скобка минус x в квадрате минус 32x плюс 33 правая круглая скобка левая круглая скобка минус 33x правая круглая скобка равносильно

underset левая круглая скобка * правая круглая скобка mathop равносильно 2x в квадрате плюс 136= минус 33x равносильно 2x в квадрате плюс 33x плюс 136=0 равносильно
равносильно x= дробь: числитель: минус 33pm1, знаменатель: 4 конец дроби равносильно совокупность выражений x= минус 8,x= минус дробь: числитель: 17, знаменатель: 2 конец дроби . конец совокупности .

б)  Заметим, что 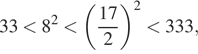33 меньше 8 в квадрате меньше левая круглая скобка дробь: числитель: 17, знаменатель: 2 конец дроби правая круглая скобка в квадрате меньше 333, поэтому
подходят оба корня.

Ответ: а) левая фигурная скобка минус 8; минус дробь: числитель: 17, знаменатель: 2 конец дроби правая фигурная скобка ; б)
минус 8, минус дробь: числитель: 17, знаменатель: 2 конец дроби .

8.     а)  Решите уравнение левая круглая скобка x в квадрате плюс 2x минус 1 правая круглая скобка левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 3 правая круглая скобка плюс логарифм по основанию левая круглая скобка 0,5 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка правая круглая скобка =0.

б)  Найдите все корни этого уравнения, принадлежащие
отрезку [−2,5; −1,5].

Решение. а)  Запишем
исходное уравнение в виде:

левая круглая скобка x в квадрате плюс 2x минус 1 правая круглая скобка левая круглая скобка логарифм по основанию 2 левая круглая скобка x в квадрате минус 3 правая круглая скобка плюс логарифм по основанию левая круглая скобка 0,5 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка правая круглая скобка =0 равносильно
равносильно совокупность выражений x = минус 1 минус корень из 2, система выражений x меньше минус корень из 3, левая круглая скобка x минус корень из 3 правая круглая скобка левая круглая скобка x плюс корень из 3 плюс 1 правая круглая скобка = 0 конец системы . конец совокупности . равносильно равносильно совокупность выражений система выражений x = минус 1 pm корень из 2x меньше минус корень из 3, конец системы логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка x в квадрате минус 3 правая круглая скобка = логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка конец совокупности . равносильно равносильно совокупность выражений система выражений x в квадрате плюс 2x минус 1 = 0,x в квадрате минус 3 больше 0, корень из 3 минус x больше 0, конец системы логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка x в квадрате минус 3 правая круглая скобка минус логарифм по основанию левая круглая скобка 2 правая круглая скобка левая круглая скобка корень из 3 минус x правая круглая скобка = 0 конец совокупности . равносильно

равносильно совокупность выражений x = минус 1 минус корень из 2, система выражений x меньше минус корень из 3, совокупность выражений x = корень из 3,x = минус корень из 3 минус 1 конец системы . конец совокупности . конец совокупности . равносильно совокупность выражений x = минус 1 минус корень из 2,x = минус корень из 3 минус 1. конец совокупности .

б)  Проверим корни на отрезке левая квадратная скобка минус 2,5; минус 1,5 правая квадратная скобка :

минус дробь: числитель: 5, знаменатель: 2 конец дроби меньше минус 1 минус корень из 2 меньше минус дробь: числитель: 3, знаменатель: 2 конец дроби равносильно минус дробь: числитель: 3, знаменатель: 2 конец дроби меньше минус корень из 2 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби равносильно
равносильно дробь: числитель: 1, знаменатель: 2 конец дроби меньше корень из 2 меньше дробь: числитель: 3, знаменатель: 2 конец дроби равносильно 1 меньше 2 корень из 2 меньше 3 равносильно 1 меньше 8 меньше 9.

Поскольку конечное неравенство верное, значение минус 1 минус корень из 2подходит и войдет в ответ.

Проверим следующее значение x:

минус дробь: числитель: 5, знаменатель: 2 конец дроби меньше минус корень из 3 минус 1 меньше минус дробь: числитель: 3, знаменатель: 2 конец дроби равносильно минус дробь: числитель: 3, знаменатель: 2 конец дроби меньше минус корень из 3 меньше минус дробь: числитель: 1, знаменатель: 2 конец дроби равносильно
равносильно дробь: числитель: 1, знаменатель: 2 конец дроби меньше корень из 3 меньше дробь: числитель: 3, знаменатель: 2 конец дроби равносильно 1 меньше 12 меньше 9.

Так как второе значение минус корень из 3 минус 1не дает правильного конечного неравенства, оно
не войдет в ответ.

Ответ: а) левая фигурная скобка минус 1 минус корень из 2, минус 1 минус корень из 3 правая фигурная скобка ;б)
минус 1 минус корень из 2.

Скачано с www.znanio.ru

Источник

Найдите трёхзначное натуральное число, большее 400, которое при делении на 5 и …

Разбор сложных заданий в тг-канале:

Найдите трёхзначное натуральное число, большее 400, которое при делении на 5 и 14 даёт равные ненулевые остатки и первая слева цифра которого является суммой двух других цифр. В ответе укажите какое-нибудь одно такое число.

Объект авторского права ООО «Легион»

Вместе с этой задачей также решают:

Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из второго числа вычли первое и получили 3546. В ответе укажите к…

Найдите трёхзначное число, кратное 80, все цифры которого различны, а сумма их квадратов делится на 9, но не делится на 81. В ответе укажите какое-нибудь одно такое число.

Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из второго числа вычли первое и получили 2178. В ответе укажите к…

Вычеркните в числе 212 729 263 три цифры так, чтобы получившееся число делилось на 18. В ответе укажите какое-нибудь одно такое число.

Источник

Пробные и тренировочные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.

Варианты составлены в соответствии с демоверсией 2023 года 

Тренировочные варианты ЕГЭ 2023 по математике (профиль)

vk.com/pezhirovschool
Вариант 1 решения
Вариант 2 решения
Вариант 3 решения
Вариант 4 решения
Вариант 5 (с ответами)
Вариант 6 (с ответами)
Вариант 7 (с ответами)
Вариант 8 (с ответами)
egemath.ru
вариант 1 скачать
вариант 2 скачать
вариант 3 скачать
вариант 4 скачать
вариант 5 скачать
вариант 6 скачать
вариант 7 скачать
вариант 8 скачать
вариант 9 скачать
вариант 10 скачать
вариант 11 скачать
вариант 12 скачать
вариант 13 скачать
вариант 14 скачать
вариант 15 скачать
вариант 16 скачать
вариант 17 скачать
вариант 18 скачать
вариант 19 скачать
вариант 20 скачать
time4math.ru
вариант 1-2 ответы
вариант 3-4 ответы
вариант 5-6 ответы
вариант 7-8
yagubov.ru
вариант 33 (сентябрь) ege2023-yagubov-prof-var33
вариант 34 (октябрь) ege2023-yagubov-prof-var34
вариант 35 (ноябрь) ege2023-yagubov-prof-var35
вариант 36 (декабрь) ege2023-yagubov-prof-var36
вариант 37 (январь) ege2023-yagubov-prof-var37
вариант 38 (февраль) ege2023-yagubov-prof-var38
math100.ru (с ответами)
variant 179 скачать
variant 180 скачать
variant 181 скачать
variant 182 скачать
variant 183 скачать
variant 184 скачать
variant 185 скачать
variant 186 скачать
variant 187 скачать
variant 188 скачать
variant 189 скачать
variant 190 скачать
variant 191 скачать
variant 192 скачать
variant 193 скачать
variant 194 скачать
variant 195 скачать
variant 196 скачать
variant 197 скачать
variant 198 скачать
variant 199 скачать
variant 200 скачать
variant 201 скачать
variant 202 скачать
variant 203 скачать
variant 204 скачать
variant 205 скачать
alexlarin.net 
Вариант 397 проверить ответы
Вариант 398 проверить ответы
Вариант 399 проверить ответы
Вариант 400 проверить ответы
Вариант 401 проверить ответы
Вариант 402 проверить ответы
Вариант 403 проверить ответы
Вариант 404 проверить ответы
Вариант 405 проверить ответы
Вариант 406 проверить ответы
Вариант 407 проверить ответы
Вариант 408 проверить ответы
Вариант 409 проверить ответы
Вариант 410 проверить ответы
Вариант 411 проверить ответы
Вариант 412 проверить ответы
Вариант 413 проверить ответы
vk.com/ege100ballov
вариант 1 скачать
вариант 2 скачать
вариант 3 скачать
вариант 4 скачать
вариант 5 скачать
вариант 6 скачать
вариант 7 скачать
вариант 8 скачать
вариант 9 скачать
вариант 10 скачать
вариант 11 скачать
vk.com/math.studying
Вариант 1 ответы
vk.com/marsel_tutor
Вариант 1 разбор
Вариант 2 конспект / разбор
Вариант 3 конспект / разбор
Вариант 4 конспект / разбор
Вариант 5 конспект / разбор
Вариант 6 разбор
vk.com/shkolkovo_easy_math
Вариант 1 решение
Вариант 2 решение
Вариант 3 решение
Вариант 5 решение
Вариант 6 решение
vk.com/mathlearn_ru
вариант 1 разбор
vk.com/ekaterina_chekmareva
Вариант 1 ответы
Вариант 2 ответы
Вариант 3 ответы
Вариант 4 ответы
Вариант 5 ответы
Вариант 6 ответы
Вариант 7 ответы
Вариант 8 ответы

Структура варианта КИМ ЕГЭ 2023 по математике профильного уровня

Экзаменационная работа состоит из двух частей и включает в себя 18 заданий, которые различаются по содержанию, сложности и количеству заданий:

– часть 1 содержит 11 заданий (задания 1–11) с кратким ответом в виде целого числа или конечной десятичной дроби;

– часть 2 содержит 7 заданий (задания 12–18) с развёрнутым ответом (полная запись решения с обоснованием выполненных действий).

Задания части 1 направлены на проверку освоения базовых умений и практических навыков применения математических знаний в повседневных ситуациях. Посредством заданий части 2 осуществляется проверка освоения математики на профильном уровне, необходимом для применения математики в профессиональной деятельности и на творческом уровне.

Задания части 1 предназначены для определения математических компетентностей выпускников образовательных организаций, реализующих программы среднего (полного) общего образования на базовом уровне. Задание с кратким ответом (1–11) считается выполненным, если в бланке ответов № 1 зафиксирован верный ответ в виде целого числа или конечной десятичной дроби.

Задания 12–18 с развёрнутым ответом, в числе которых 5 заданий повышенного уровня и 2 задания высокого уровня сложности, предназначены для более точной дифференциации абитуриентов вузов. 

Примеры заданий:

1. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 76 бадминтонистов, среди которых 22 спортсмена из России, в том числе Игорь Чаев. Найдите вероятность того, что в первом туре Игорь Чаев будет играть с каким-либо бадминтонистом из России.

2. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орёл не выпадет ни разу

3. На доске написали несколько не обязательно различных двузначных натуральных чисел без нулей в десятичной записи. Сумма этих чисел оказалась равной 363. Затем в каждом числе поменяли местами первую и вторую цифры (например, число 17 заменили на число 71).

а) Приведите пример исходных чисел, для которых сумма получившихся чисел ровно в 4 раза больше, чем сумма исходных чисел.

б) Могла ли сумма получившихся чисел быть ровно в 2 раза больше, чем сумма исходных чисел?

в) Найдите наибольшее возможное значение суммы получившихся чисел.

Смотрите также:

Источник

ГлавнаяШпаргалкиРазбор заданий ЕГЭ-2022 по профильной математике с Дальнего Востока

06 июня, 2022

5 мин

Мтмт 📈
Решение задач ✏️

4958

0

Разобрали задания, которые встретились на ЕГЭ-2022 по профильной математике на Дальнем Востоке.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!

Редакция Без Сменки

Редакция Без Сменки


44
подписчиков

+ Подписаться

Источник

адача №3 профильного ЕГЭ по математике. Сборник задач по теории вероятностей.ЕГЭ 2023. Задание №3 в ЕГЭ-2023 по математике. Теория и практика по математике для подготовки к экзамену. Вы можете скачать или решать задания онлайн на сайте.

Сборник задач по теории вероятностей: Скачать в PDF

Интересные задания:

Задача 1 На клавиатуре телефона 10 цифр, из них 5 четных (включая 0): 0, 2, 4, 6, 8. Поэтому вероятность того, что случайно будет нажата четная цифра, равна 5 10 = 0,5.

Задача 2 Всего дежурных 4 человека, из них 2 девочки: Ольга и Татьяна. Чтобы найти искомую вероятность, надо разделить кол-во девочек на общее число дежурных: 24 = 0,5.

Задача 3 Всего существует 6 возможных вариантов очереди: АБВ АВБ БАВ БВА ВАБ ВБА. Борис подойдет позже Андрея в трех случаях: АБВ ВАБ АВБ, значит искомая вероятность 36 =12 = 0,5. На самом деле существуют всего два случая, у которых равная вероятность: Борис
может подойти перед Андреем или после него. Из этих двух случаев благоприятным
является только один, и его вероятность: 12 = 0,5.

Задача 4 Натуральных чисел от 10 до 19 десять (19 − 10 + 1 = 10 или можно просто выписать все эти числа и убедиться в этом), из них на 3 делятся три числа: 12, 15, 18. Искомая вероятность равна: 3 10 = 0,3.

Задача 5 Будем считать, что жребий выглядит так: каждый турист достанет из шапки бумажку, на которой будет написано идёт ли он в магазин или нет. Всего бумажек 5. Вытянув две из них, турист пойдёт в магазин. Турист А с равной вероятностью может вытянуть любую из 5 бумажек. Для туриста A существует два благоприятных исхода из 5 возможных. Значит вероятность того, что турист А пойдёт в магазин 2 5 = 0,4. Всего в викторине участвуют 4 игрока. Из них двое получат приз. Тогда вероятность получения приза составляет 2 4 = 0,5.

Вам будет интересно:

ЕГЭ по математике (профиль) 11 класс 2023. Новый тренировочный вариант №11 — №221121 (задания и ответы)

* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР

Поделиться:

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Егэ по математике 510013
  • Егэ по математике 509781
  • Егэ по математике 509773
  • Егэ по математике 509208
  • Егэ по математике 508050

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии