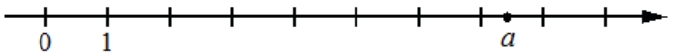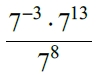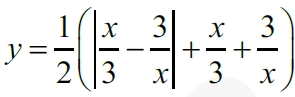Егэ по математике 9 класс 2021 ответы с решением - ExamHelp.top

Пробные тренировочные варианты по математике для 9 класса в формате ОГЭ 2021 с ответами из разных источников.

→ Тренировочные варианты ОГЭ 2022 года

time4math.ru
вариант 1-2	ответы 1-8
вариант 3-4
вариант 5-6
вариант 7-8
ОГЭ 100 баллов (с ответами)
вариант 1	скачать
вариант 2	скачать
вариант 3	скачать
вариант 4	скачать
вариант 5	скачать
вариант 6	скачать
вариант 7	скачать
вариант 8	скачать
вариант 9	скачать
вариант 10	скачать
вариант 11	скачать
yagubov.ru
вариант 18	Yagubov-oge-18
вариант 19	Yagubov-oge-19
на основе реального варианта	Yagubov-oge-real
math100.ru
вариант 13	math100-oge-13
вариант 14	math100-oge-14
вариант 15	math100-oge-15
Статград
Тренировочные варианты 1-4	критерии оценивания
alexlarin.net (усложненные варианты)
вариант 265	скачать
вариант 266	скачать
вариант 267	скачать

Работа состоит из двух частей, включающих в себя 25 заданий.

Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.

На выполнение работы по математике отводится 3 часа 55 минут (235 минут).

Если задание содержит рисунок, то на нём непосредственно в тексте работы можно выполнять необходимые Вам построения. Рекомендуем внимательно читать условие и проводить проверку полученного ответа.

При выполнении работы Вы можете воспользоваться справочными материалами, выданными вместе с вариантом КИМ, и линейкой.

Связанные страницы:

Прототипы заданий 1-5 ОГЭ по математике

Задание 7 ОГЭ по математике — неравенства

Задания 1-5 ОГЭ по математике — Зонт

Тренировочные варианты ОГЭ 2021 по математике с ответами

Решение заданий 11 и 22 ОГЭ по математике — функции и графики

Источник

04.11.2020

Сборник ответов для пособия ОГЭ 2021, 36 типовых вариантов по математике профильного уровня, под редакцией Ященко И.В., для выпускников 9 классов

Тренировочные варианты ОГЭ 2021 по математике
Работы СтатГрад 2020-2021

Выбирайте вариант и смотрите ответы. Вы можете скачать или сохранить их совершенно бесплатно.

Выберите свой номер варианта теста:

1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 / 13 / 14 / 15 / 16 / 17 / 18 / 19 / 20 / 21 / 22 / 23 / 24 / 25 / 26 / 27 / 28 / 29 / 30 / 31 / 32 / 33 / 34 / 35 / 36

Вариант 1

Видеоразбор варианта №1

1) 56,4

2) 8070

3) 62,5

4) 9813

5) 13

6) -2,8

7) 2

9) -2,5

10) 0,42

11) 213

12) 3

13) 3

14) 1031

15) 174

16) 5

17) 86

18) 12

19) 12

20) 2; 6

21) 16 км/ч

22) [ — 6,25; — 2,25],[0; + ∞)

23) 18

25) 3:10

Вариант 2

1) 60,6

2) 9910

3) 67,5

4) 11 445

5) 15

6) -7

7) 2

9) -0,5

10) 0,65

11) 123

12) 6

13) 4

14) 764

15) 216

16) 32

17) 54

18) 25

19) 23

20) -2; -5

21) 14 км/ч

22) [ — 4; — 1],[0; + ∞)

23) 15

25) 11:15

Вариант 3

Видеоразбор варианта №3

1) 61254

2) 160

3) 38

4) 225

5) 15,4

6) 1,25

7) 1

9) -4

10) 0,8

11) 231

12) 0,0003

13) 4

14) -53,7

15) 8

16) 23

17) 42

18) 4

19) 1

20) -4; -3; 2

21) 35 %

22) -4; 0; 4

23) 7

25) 20,8

Вариант 4

1) 24536

2) 120

3) 34

4) 12,5

5) 9,4

6) 1,65

7) 4

9) 10

10) 0,64

11) 123

12) 0,007

13) 3

14) -21,8

15) 12

16) 15

17) 65

18) 4

19) 3

20) -3; -1; 2

21) 55 %

22) -6,25; 0; 6,25

23) 8

25) 7,2

Вариант 5

Видео разбор 5 варианта ОГЭ 2021

1) 1243

2) 51

3) 39

4) 153

5) 148

6) -19,2

7) 1

240

9) -5

10) 0,45

11) 312

12) 8

13) 2

14) 740

15) 7

16) 147

17) 96

18) 4

19) 1

20) ( — 4 — √{10} ; — 4 + √{10} )

21) 173 км

22) -4; 5

23) 17

25) 924

Вариант 6

1) 1432

2) 25

3) 105

4) 17

5) 100

6) -18,2

7) 2

216

9) -6

10) 0,35

11) 231

12) 3

13) 3

14) 1230

15) 11

16) 118

17) 44

18) 8

19) 2

20) ( — ∞ ; — 2 — √5 )(√5 — 2; + ∞)

21) 218 км

22) -2,25; 4

23) 5

25) 1120

Вариант 7

Видеоразбор 7 варианта

1) 8

2) 14

3) 3,2

4) 120

5) 135-145

6) 20

7) 2

9) 5

10) 0,12

11) 231

12) 48

13) 2

14) 48

15) 0,7

16) 74

17) 51

18) 7

19) 13

20) -3; 1

21) 17 км/ч

22) -1; о

23) 8

25) 14,4

Вариант 8

1) 7

2) 7

3) 1,6

4) 13

5) 8,7-8,9

6) 12

7) 4

256

9) -5

10) 0,09

11) 312

12) 320

13) 2

14) 36

15) 0,7

16) 36

17) 60

18) 5

19) 23

20) -4; 1

21) 21 км/ч

22) -0,25; 0

23) 6

25) 13,5

Вариант 9

1) 195

2) 6

3) 65,24

4) 15,2

5) 2,3

6) 3,9

7) 4

9) -6,2

10) 0,375

11) 231

12) 24

13) 4

14) 12

15) 108

16) 40

17) 4,5

18) 0,6

19) 1

20) (7;7 + √{11} )

21) 14 л/мин.

22) -2; 2

23) 6

25) 28,8

Вариант 10

1) 185

2) 1

3) 60,3

4) 13,3

5) 2,2

6) 5,75

7) 3

9) -16

10) 0,24

11) 312

12) 0,8

13) 3

14) 10

15) 139

16) 57

17) 98

18) 3

19) 1

20) (5;5 + √{11} )

21) 10 л/мин.

22) 3; 4

23) 18

25) 37,1

Вариант 11

1) 3412

2) 64

3) 420

4) 310,8

5) 14

6) 8

7) 3

9) -3,5

10) 0,8

11) 321

12) 15

13) 3

14) 20

15) 13

16) 53

17) 91

18) 10

19) 13

20) -7; -2; 2

21) 21 т

22) -1; 0; 1

23) 10

25) 7,2

Вариант 12

1) 3142

2) 8

3) 594

4) 155,4

5) 0,7

6) 4,4

7) 4

125

9) 0,2

10) 0,875

11) 312

12) 3

13) 1

14) 30

15) 34

16) 79

17) 46

18) 9

19) 23

20) -4; -1; 1

21) 36 т

22) -4; 0; 1

23) 32

25) 6,5

Вариант 13

1) 46531

2) 120

3) 19

4) 3,36

5) 25

6) 44,9

7) 3

3,2

9) -10,25

10) 0,16

11) 312

12) 578

13) 3

14) 3

15) 24

16) 637

17) 18

18) 5

19) 1

20) (3; 4); (3; -4)

21) 700 м

22) -9; 4

23) 52

25) 8; 4

Вариант 14

1) 76324

2) 160

3) 17

4) 8,96

5) 22

6) 29,5

7) 2

40,5

9) -2,7

10) 0,12

11) 213

12) 32

13) 2

14) 5

15) 43

16) 119

17) 7

18) 10

19) 3

20) (2; 4); (2; -4)

21) 650 м

22) -2,25; 12,25

23) 33

25) 37; 3

Вариант 15

1) 14532

2) 54

3) 20

4) 34

5) 202

6) 0,9

7) 3

9) 0,4

10) 0,375

11) 123

12) 4

13) 3

14) 57 960

15) 21

16) 103

17) 56

18) 6

19) 13

20) 15

21) 38 %

22) -1; 1; 1,25

23) 76

25) 24√{13;} 48√{13;} 72√{5;}

Вариант 16

1) 34125

2) 25

3) 132

4) 78

5) 127

6) 1,8

7) 1

343

9) -1,8

10) 0,15

11) 213

12) 0,7

13) 1

14) 110 900

15) 24

16) 97

17) 61

18) 3

19) 12

20) 6

21) 30 %

22) -4; 4; 5

23) 58

25) 3√{13;} 6√{13;} 9√{5;}

Вариант 17

1) 61,5

2) 10 580

3) 94,1

4) 11 819

5) 12

6) 1,03

7) 2

9) 3,5

10) 0,24

11) 312

12) 66

13) 4

14) 530

15) 0,8

16) 9

17) 133

18) 12,5

19) 2

20) 2 — √{2;} 2 + √2

21) 23 км/ч

22) 1; 4

23) 6,5

25) 42

Вариант 18

1) 58,5

2) 8800

3) 65

4) 10 613

5) 8

6) 3,95

7) 1

9) -1,5

10) 0,34

11) 213

12) 11

13) 2

14) 570

15) 0,375

16) 13

17) 71

18) 7,5

19) 3

20) 4 — √{7;} 4 + √7

21) 17 км/ч

22) 0,5; 4

23) 15

25) 96

Вариант 19

1) 10

2) 23

3) 1,6

4) 100

5) 62-63

6) 1,25

7) 2

9) -12

10) 0,2

11) 312

12) 17

13) 1

14) -16

15) 17,5

16) 36,5

17) 138

18) 45,5

19) 2

20) (-3; 5)

21) 15 %

22) 4

23) 17√6

25) 3√2

Вариант 20

1) 9

2) 10

3) 3,2

4) 60

5) 9-9,3

6) 1,5

7) 3

9) -9

10) 0,04

11) 213

12) 32

13) 4

14) -30,9

15) 27,5

16) 57,5

17) 65

18) 38,5

19) 2

20) (-1; 4)

21) 12 %

22) 4

23) 25√3

25) frac{{38√3 }}{3}

Вариант 21

1) 275

2) 7,25

3) 77,52

4) 17,8

5) 2,3

6) -3

7) 4

9) -3

10) 0,3

11) 321

12) 3,2

13) 1

14) 1175

15) 53

16) 24

17) 20

18) 4

19) 13

20) (-1; 8); (1;

21) 84 км/ч

22) 0,5

23) 20,16

25) √{30}

Вариант 22

1) 225

2) 4,75

3) 66,44

4) 7,6

5) 1Д

6) -2

7) 1

0,2

9) -2

10) 0,74

11) 213

12) 85

13) 2

14) 642

15) 97

16) 12

17) 32

18) 6

19) 13

20) (2; 10); (0,75; 0)

21) 80 км/ч

22) 1

23) frac{{240}}{{13}}

25) 2√2

Вариант 23

1) 74632

2) 22,4

3) 4

4) 32

5) 55

6) 0,7

7) 4

9) -4

10) 0,7

11) 213

12) 4

13) 4

14) 700

15) 18

16) 46

17) 109

18) 7,5

19) 2

20) -2

21) 420 кг

22) 3; 3,5

23) 16

25) 112

Вариант 24

1) 62471

2) 240

3) 5

4) 6,24

5) 26,1

6) 1,2

7) 1

9) 2

10) 0,85

11) 231

12) 4

13) 3

14) 624

15) 24

16) 12

17) 91

18) 32

19) 3

20) -7

21) 44 кг

22) 3; 3,2

23) 4,8

25) 15

Вариант 25

1) 51432

2) 39

3) 17

4) 117

5) 116

6) -1,5

7) 1

9) 7

10) 0,3

11) 312

12) 72

13) 2

14) 45

15) 0,75

16) 95

17) 63

18) 1,5

19) 23

20) 40

21) 52,8 км/ч

22) -1; 4

23) 60°; 120°

25) 26

Вариант 26

1) 52314

2) 39

3) 117

4) 25

5) 116

6) -0,5

7) 2

9) -7

10) 0,32

11) 321

12) 150

13) 3

14) 68

15) 0,7

16) 50

17) 15

18) 2,5

19) 23

20) 2000

21) 76,5 км/ч

22) -1; 16

23) 60°; 120°

25) 17

Вариант 27

1) 3241

2) 32

3) 594

4) 1247,4

5) 1,4

6) -4

7) 3

0,5

9) -1

10) 0,15

11) 321

12) 3

13) 2

14) 40

15) 42

16) 73

17) 5

18) 9

19) 3

20) [1; 2]

21) 13%

22) 0; 1

23) 9

25) 6√{13}

Вариант 28

1) 4213

2) 16

3) 840

4) 623,7

5) 17

6) -24

7) 2

0,2

9) -0,4

10) 0,16

11) 132

12) 4

13) 1

14) 15

15) 44

16) 114

17) 9

18) 12

19) 2

20) ( — ∞ ; — 2] cup [frac{2}{7}; + ∞)

21) 16%

22) 2; 3

23) 15

25) √{751}

Вариант 29

1) 65,4

2) 11 470

3) 72,5

4) 13 204

5) 10

6) 78

7) 2

144

9) 2,5

10) 0,35

11) 231

12) 19

13) 4

14) 520

15) 43

16) 18

17) 21

18) 5

19) 2

20) -5

21) 14 км/ч

22) -6,75

23) 11

25) 78

Вариант 30

1) 60,6

2) 9890

3) 73

4) 11 461

5) 9

6) 84

7) 3

9) 1,5

10) 0,4

11) 123

12) 6

13) 2

14) 580

15) 27

16) 18

17) 8

18) 7

19) 2

20) -3

21) 15 км/ч

22) -1

23) 13

25) 300

Вариант 31

1) 9

2) 13

3) 3,8

4) 75-76

5) 1,6-1,7

6) -0,14

7) 3

9) -0,7

10) 0,05

11) 123

12) 29

13) 4

14) 8

15) 0,125

16) 8

17) 18

18) 4

19) 1

20) (-2; 6); (2; -6); (-6; 2); (6; -2)

21) 65 вопросов

22) -8;1/36

23) 40

25) 22

Вариант 32

1) 8

2) 14

3) 1,9

4) 80

5) 12,4-12,8

6) -0,55

7) 3

9) -0,6

10) 0,2

11) 123

12) 37

13) 1

14) 9

15) -0,2

16) 4

17) 13

18) 2

19) 3

20) (-1; 8); (1; -8); (-8; 1); (8; -1)

21) 57 вопросов

22) 0;1/4

23) 29

25) 9,6

Вариант 33

1) 53412

2) 120

3) 20

4) 10,08

5) 21

6) 1,3

7) 2

9) -0,8

10) 0,98

11) 123

12) 0,2

13) 1

14) 6

15) 1,6

16) 52

17) 289

18) 4

19) 23

20) -1;1/4

21) 14 км/ч

22) 0; 0,25

23) 36

25) 32

Вариант 34

1) 74132

2) 440

3) 50

4) 24,96

5) 120

6) 3,25

7) 3

9) -3

10) 0,95

11) 312

12) 0,5

13) 2

14) 2

15) 0,4

16) 13

17) 441

18) 1

19) 12

20) 2;13/4

21) 18 км/ч

22) 0; 4

23) 15

25) 56

Вариант 35

1) 4312

2) 105

3) 44

4) 75

5) 90

6) 0,47

7) 1

12,5

9) -0,8

10) 0,45

11) 132

12) 1260

13) 2

14) 49 380

15) 90

16) 41

17) 8

18) 5,5

19) 2

20) (8; -2)

21) 12 дет./ч

22) -1; 1

23) 7

25) 24

Вариант 36

1) 2341

2) 112

3) 60

4) 100

5) 96

6) 2,75

7) 3

1,8

9) -од

10) 0,35

11) 123

12) 850

13) 3

14) 65 030

15) 20

16) 11

17) 5

18) 3,5

19) 3

20) (-4; 13)

21) 27 дет./ч

22) -1; 1

23) 8

25) 13,5

Источник

Решение образца реального варианта с ответами ОГЭ по математике от сайта Ягубов.рф 27 мая 2021 года. КИМ 9 класс 27.05.21.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

ЧАСТЬ 1

Задание 1-5.
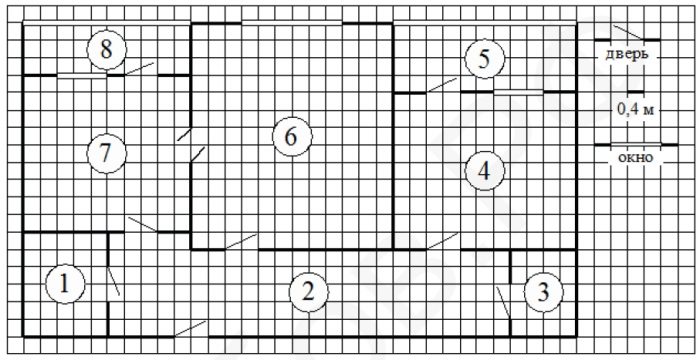
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.

Задание 6.
Найдите значение выражения 5,7 – 7,6.

Задание 7.
На координатной прямой отмечено число а. Какое из утверждений для этого числа является верным?

1) а – 6 < 0
2) a – 7 > 0
3) 6 – a > 0
4) 8 – a < 0

Задание 8.
Найдите значение выражения

Задание 9.
Решите уравнение х² – 121 = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

Задание 10.
На экзамене 25 билетов, Костя не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.

Задание 11.
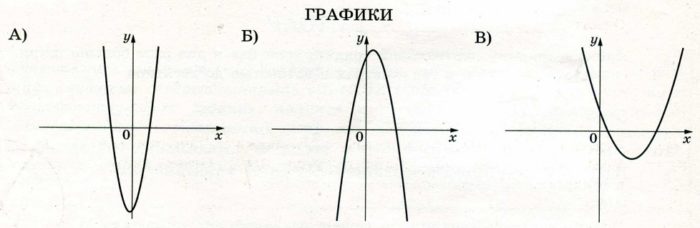
На рисунках изображены графики функций вида у = ах² + bх + c. Установите соответствие между графиками функций и знаками коэффициентов а и с.

КОЭФФИЦИЕНТЫ

1) а>0‚ с>0 2) а>0, с<0 3) а<0, с>0

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.
Площадь четырёхугольника можно вычислить по формуле , где d₁ и d₂ – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d₂, если d₁ = 14, sinα = , S = 8,75.

Задание 13.
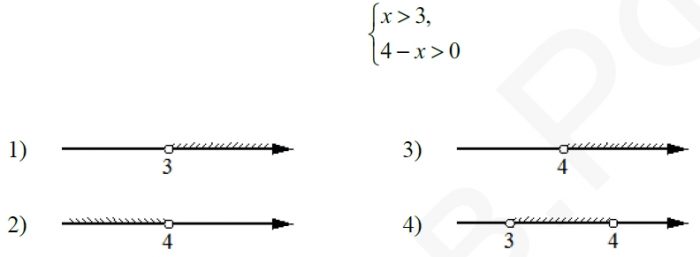
Укажите решение системы неравенств

Задание 14.
В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Задание 15.
Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Задание 16.
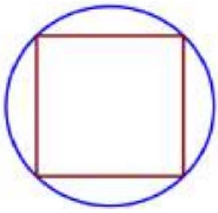
Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.

Задание 17.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.

Задание 18.
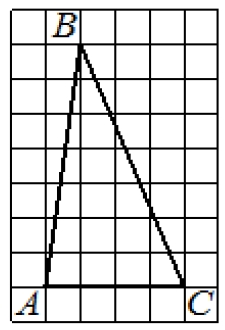
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Задание 19.
Какие из следующих утверждений верны?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Сумма углов равнобедренного треугольника равна 180 градусам.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Решите уравнение (x² – 49)² + (x² + 4x – 21)² = 0

Задание 21.
Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего по платформе параллельно путям со скоростью 3 км/ч навстречу поезду, за 36 секунд. Найдите длину поезда в метрах.

Задание 22.
Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.

Задание 23.
Точка H является основанием высоты, проведённой из вершины прямого угла В треугольника ABС к гипотенузе АС. Найдите АВ, если AH = 5, AC = 45.

Задание 24.
Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АВ и CD в точках E и F соответственно. Докажите, что отрезки АЕ и CF равны.

Задание 25.
Четырёхугольника ABCD со сторонами AB = 25 и CD = 16 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём ∠AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Источник варианта: Ягубов.рф

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 6

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

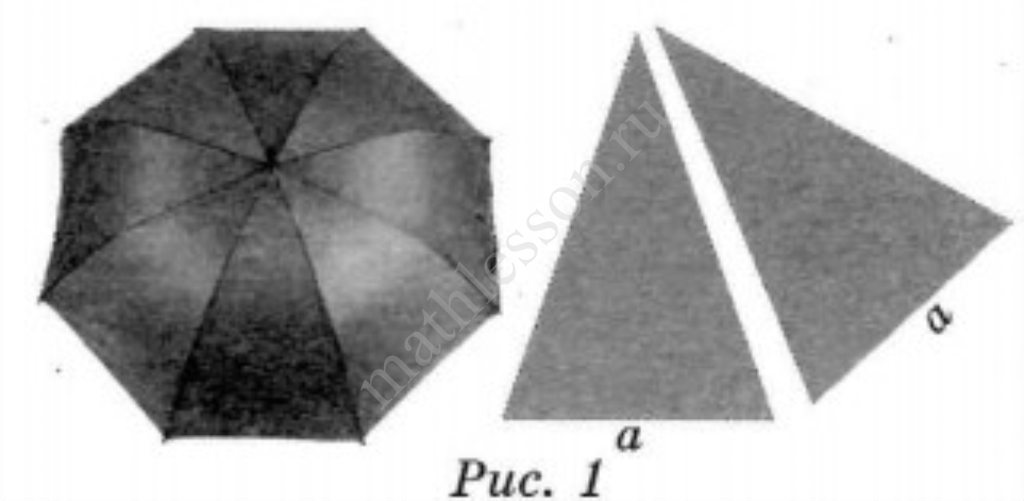
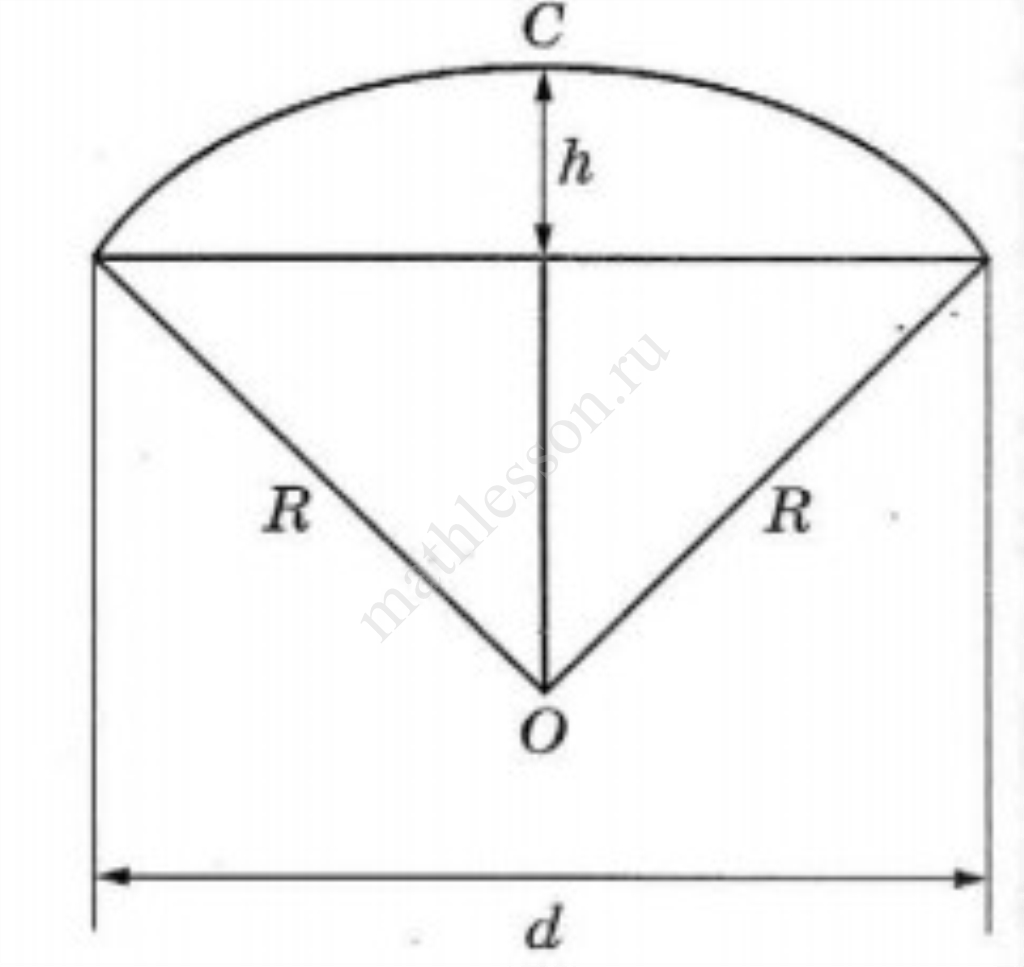
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта. На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счёт гибкости спиц и эластичности ткани, из которой изготовлен зонт. Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами спиц, образующих дугу окружности, проходящей через вершину зонта, — ровно 100 см.

1. Длина зонта в сложенном виде равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.

2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведённая к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.

3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус $$R$$ сферы купола, зная, что $$ОС = R$$ (рис. 2). Ответ дайте в сантиметрах.

4. Вася нашёл площадь купола зонта как площадь поверхности сферического сегмента по формуле $$S = 2pi Rh$$, где R — радиус сферы, a h — высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число $$pi$$ округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.

5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учётом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошло в обрезки?

Источник

Тренировочная работа №1 ОГЭ 2022 статград по математике для 9 класса. Ответы, решения и задания для вариантов МА2190101, МА2190102, МА2190103, МА2190104 официальная дата проведения работы: 05.10.2021 (5 октября 2021 год).

Варианты (МА2190101-МА2190102): скачать

Варианты (МА2190103-МА2190104): скачать

Все ответы для вариантов: скачать

Работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.

Тренировочная работа №1 по математике 9 класс ОГЭ 2022 статград

Варианты МА2190103-МА2190104

Задания с 1 варианта

Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово. Шоссе и просёлочные дороги образуют прямоугольные треугольники.

По шоссе Таня с дедушкой едут со скоростью 50 км/ч, а по просёлочным дорогам — со скоростью 30 км/ч. Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км.

1)Пользуясь описанием, определите, какими цифрами на плане обозначены деревни. Заполните таблицу, в бланк ответов перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.

2)Найдите расстояние от Антоновки до Егорки по шоссе. Ответ дайте в километрах.

3)Найдите расстояние от Антоновки до Горюново по прямой. Ответ дайте в километрах.

4)За какое наименьшее количество минут Таня с дедушкой могут добраться из Антоновки в Богданово?

5)На просёлочных дорогах машина дедушки расходует 9,1 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Горюново мимо пруда ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

10)В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 — из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Швеции.

14)В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 22 квадратных столика вдоль одной линии?

15)В треугольнике ABC угол C равен 90° , M — середина стороны AB, AB = 24 , BC =14 . Найдите CM .

16)Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K , BK =12 , DK =16, BC = 24. Найдите AD .

17)Сумма двух углов равнобедренной трапеции равна 196° . Найдите меньший угол этой трапеции. Ответ дайте в градусах.

19)Какое из следующих утверждений верно? 1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны. 2) Точка пересечения двух окружностей равноудалена от центров этих окружностей. 3) Диагонали ромба точкой пересечения делятся пополам.

21)Первый велосипедист выехал из посёлка по шоссе со скоростью 20 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 8 часов после этого догнал первого.

23)Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB =14, DC = 42, AC = 52 .

24)В выпуклом четырёхугольнике ABCD углы ABD и ACD равны. Докажите, что углы DAC и DBC также равны.

25)В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 44. Найдите стороны треугольника ABC.

Задания с 2 варианта

10)В соревнованиях по толканию ядра участвуют 6 спортсменов из Северной Ирландии, 8 спортсменов из Англии, 7 спортсменов из Шотландии и 4 — из Уэльса. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Англии.

11)В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 15 квадратных столиков вдоль одной линии?

15)В треугольнике ABC угол C равен 90° , M — середина стороны AB, AB = 26 , BC =18 . Найдите CM .

16)Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K , BK = 8, DK = 24 , BC =18. Найдите AD .

17)Сумма двух углов равнобедренной трапеции равна 102° . Найдите больший угол этой трапеции. Ответ дайте в градусах.

19)Какое из следующих утверждений верно? 1) Боковые стороны любой трапеции равны. 2) Площадь ромба равна произведению двух его смежных сторон на синус угла между ними. 3) Всякий равнобедренный треугольник является остроугольным.

21)Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.

23)Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB =12, DC = 48, AC = 35.

24)В выпуклом четырёхугольнике ABCD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.

25)В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 24. Найдите стороны треугольника ABC.

Задания с 3 варианта

На рисунке изображён план сельской местности. Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданово. Шоссе и просёлочные дороги образуют прямоугольные треугольники.

2)Найдите расстояние от Ванютино до Богданово по шоссе. Ответ дайте в километрах.

3)Найдите расстояние от Егорки до Жилино по прямой. Ответ дайте в километрах.

4)За какое наименьшее количество минут Таня с дедушкой могут добраться из Егорки в Жилино?

5)На просёлочных дорогах машина дедушки расходует 9,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь через Доломино и Горюново мимо конюшни ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

10)В соревнованиях по толканию ядра участвуют 4 спортсмена из Японии, 5 спортсменов из Южной Кореи, 8 спортсменов из Китая и 3 — из Монголии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Монголии.

14)В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 23 квадратных столика вдоль одной линии?

15)В треугольнике ABC угол C равен 90° , M — середина стороны AB, AB = 36, BC = 20. Найдите CM .

16)Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K , BK = 4, DK =12, BC = 21. Найдите AD .

17)Сумма двух углов равнобедренной трапеции равна 178° . Найдите больший угол этой трапеции. Ответ дайте в градусах.

19)Какое из следующих утверждений верно? 1) Касательная к окружности параллельна радиусу, проведённому в точку касания. 2) Диагонали ромба точкой пересечения делятся пополам. 3) Внешний угол треугольника равен сумме его внутренних углов.

21)Первый велосипедист выехал из посёлка по шоссе со скоростью 22 км/ч. Через час после него со скоростью 12 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 8 часов после этого догнал первого.

23)Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB =18, DC = 54 , AC = 48.

24)В выпуклом четырёхугольнике ABCD углы BCA и BDA равны. Докажите, что углы ABD и ACD также равны.

24)В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 32. Найдите стороны треугольника ABC.

Задания с 4 варианта

2)Найдите расстояние от Горюново до Жилино по шоссе. Ответ дайте в километрах.

3)Найдите расстояние от Доломино до Горюново по прямой. Ответ дайте в километрах.

4)За какое наименьшее количество минут Таня с дедушкой могут добраться из Доломино в Горюново?

5)На просёлочных дорогах машина дедушки расходует 8,2 литра бензина на 100 км. Известно, что на путь из Антоновки до Богданово через Ванютино и путь напрямик ей необходим один и тот же объём бензина. Сколько литров бензина на 100 км машина дедушки расходует на шоссе?

10)В соревнованиях по толканию ядра участвуют 4 спортсмена из Казахстана, 7 спортсменов из Узбекистана, 6 спортсменов из Таджикистана и 3 — из Туркменистана. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что последним будет выступать спортсмен из Таджикистана.

14)В кафе есть только квадратные столики, за каждый из которых могут сесть 4 человека. Если сдвинуть два квадратных столика, то получится стол, за который могут сесть 6 человек. На рисунке изображён случай, когда сдвинули 3 квадратных столика вдоль одной линии. В этом случае получился стол, за который могут сесть 8 человек. Сколько человек может сесть за стол, который получится, если сдвинуть 21 квадратный столик вдоль одной линии?

15)В треугольнике ABC угол C равен 90° , M — середина стороны AB, AB = 42 , BC = 30. Найдите CM .

16)Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K , BK = 6 , DK =10, BC =12 . Найдите AD .

17)Сумма двух углов равнобедренной трапеции равна 50° . Найдите больший угол этой трапеции. Ответ дайте в градусах.

19)Какие из следующих утверждений верны? 1) Если три угла одного треугольника равны соответственно трём углам другого треугольника, то такие треугольники равны. 2) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой. 3) Расстояние от точки, лежащей на окружности, до центра окружности равно радиусу.

21)Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.

23)Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M . Найдите MC , если AB =10, DC = 25, AC = 56 .

24)В выпуклом четырёхугольнике ABCD углы CDB и CAB равны. Докажите, что углы BCA и BDA также равны.

25)В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 8. Найдите стороны треугольника ABC.

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

Тренировочный вариант №21 ОГЭ 2022 по математике 9 класс с ответами

Тренировочный вариант Ларина №293 ОГЭ 2022 по математике 9 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Пробный ОГЭ №2 по математике 2021г.

Вариант 1

Вариант 2

Вариант 3

вариант 4

Вариант 5

вариант 6

Вариант 7

Вариант 8

Ответы

Скачать:

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 1

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

На рисунке изображён план однокомнатной квартиры в 16-этажном жилом доме (сторона одной клетки на плане равна 0,5м). Окна квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел, а слева – вход в комнату. Санузел имеет общую стену с кухней, отмеченную на плане цифрой 2. Комната имеет наибольшую площадь из всех помещений. Из кухни есть выход на балкон. Пол санузла выложен плиткой размером 25см х 25см.

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр.

Объекты	санузел	прихожая	балкон	комната
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 8 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?

Ответ: ________________

3. Найдите площадь, которую занимает балкон. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Во сколько раз площадь прихожей меньше, чем площадь комнаты?

Ответ: ________________

5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с фронтальной загрузкой, по глубине не превосходящую 42см.

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа х, у и z.

Какая из разностей z – x, x – y, z – y положительна?

1) z – x 2) x – y 3) z – y 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,28. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

11. На рисунках изображены графики функций вида . Установите соответствие между графиками функций и знаками коэффициентов a и с.

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 4 с-1, а центростремительное ускорение равно 96 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) 4) нет решений

Ответ:

14. Вере надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.

Ответ: ________________

15. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 27. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 360.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 32.

Найдите площадь этого квадрата.

Ответ: ________________

18. На клетчатой бумаге размером клетки 1х1 изображён треугольник АВС. Найдите длину его средней линии, параллельной стороне АС.

Ответ: ________________

19. Какое из следующих утверждений верно?

1) В прямоугольном треугольнике гипотенуза равна сумме катетов.

2) Всегда один из двух смежных углов острый, а другой тупой.

3) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

20. Решите уравнение .

21. Моторная лодка прошла против течения реки 221км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4км/ч.

22. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

23. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.

24. Точка К – середина боковой стороны СD трапеции АВСD. Докажите, что площадь треугольника КАВ равна половине площади трапеции.

25. Четырёхугольник АВСD со сторонами АВ = 34 и СD = 22 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 2

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

На рисунке изображён план однокомнатной квартиры в 22-этажном жилом доме (сторона одной клетки на плане равна 0,5м). Окна квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел, а слева – вход в комнату. Санузел имеет общую стену с кухней, отмеченную на плане цифрой 5. Комната имеет наибольшую площадь из всех помещений, из неё есть выход на просторную лоджию. Пол лоджии выложен плиткой размером 25см х 25см.

Объекты	комната	лоджия	прихожая	санузел
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол лоджии?

Ответ: ________________

3. Найдите площадь, которую занимает санузел. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами кухни (длину диагонали) в метрах.

Ответ: ________________

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа a, b и c.

Какая из разностей a – b, a – c, c – b отрицательна?

1) a – b 2) a – c 3) c – b 4) ни одна из них

Ответ:

13. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,09. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 6 с-1, а центростремительное ускорение равно 216 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) нет решений 4)

Ответ:

14. Маше надо подписать 385 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Маша подписала 8 открыток. Определите, сколько открыток было подписано за шестой день, если вся работа была выполнена за 14 дней.

Ответ: ________________

15. Сторона треугольника равна 29, а высота, проведённая к этой стороне, равна 12. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 520.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 68.

Найдите площадь квадрата

Ответ: ________________

19. Какое из следующих утверждений верно?

1) В треугольнике против большего угла лежит большая сторона.

2) Диагонали ромба равны.

3) Площадь параллелограмма равна половине произведения его диагоналей.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

20. Решите уравнение .

21. Моторная лодка прошла против течения реки 255км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 1км/ч.

22. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

23. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.

25. Четырёхугольник АВСD со сторонами АВ = 44 и СD = 8 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 3

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

На рисунке изображён план однокомнатной квартиры в 15-этажном жилом доме (сторона одной клетки на плане равна 0,5м). Окна квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел. Пол санузла выложен плиткой размером 25см х 25см. Санузел имеет общую стену с кухней. Слева от прихожей находится гардеробная, отмеченная на плане цифрой 5, и вход в комнату. Из кухни и комнаты есть выход на просторную лоджию, отмеченную на плане цифрой 4.

Объекты	комната	кухня	прихожая	санузел
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 10 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?

Ответ: ________________

3. Найдите площадь, которую занимает лоджия. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами кухни (длину диагонали) в метрах.

Ответ: ________________

5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой, по высоте не превосходящую 85см.

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа x, y и z.

Какая из разностей z – x, y – z, x – y отрицательна?

1) z – x 2) y – z 3) x – y 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,11. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) 4) нет решений

Ответ:

14. Наде надо подписать 828 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Надя подписала 12 открыток. Определите, сколько открыток было подписано за пятый день, если вся работа была выполнена за 18 дней.

Ответ: ________________

15. Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 380.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 84.

Найдите площадь квадрата

Ответ: ________________

19. Какие из следующих утверждений верны?

1) Смежные углы всегда равны.

2) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

3) Любые два равносторонних треугольника подобны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ: ________________

Часть 2

20. Решите уравнение .

21. Моторная лодка прошла против течения реки 132км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5км/ч.

22. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

23. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.

25. Четырёхугольник АВСD со сторонами АВ = 5 и СD = 17 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 4

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

На рисунке изображён план однокомнатной квартиры в 12-этажном жилом доме (сторона одной клетки на плане равна 0,5м). Окна квартиры выходят на юг. При входе в квартиру располагается прихожая. Справа от прихожей находится санузел. Пол санузла выложен плиткой размером 25см х 25см. В квартире имеется спальная, отмеченная на плане цифрой 5, и кухня, совмещённая с гостиной. Из спальни есть выход на балкон.

Объекты	кухня	балкон	прихожая	санузел
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 6 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол санузла?

Ответ: ________________

3. Найдите площадь, которую занимает прихожая. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами спальни (длину диагонали) в метрах.

Ответ: ________________

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа p, q и r.

Какая из разностей q – p, q – r, r – p положительна?

1) q – p 2) q – r 3) r – p 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,13. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 8,5 с-1, а центростремительное ускорение равно 289 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) нет решений 4)

Ответ:

14. Лере надо подписать 615 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Лера подписала 6 открыток. Определите, сколько открыток было подписано за семь день, если вся работа была выполнена за 15 дней.

Ответ: ________________

15. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 860.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 24.

Найдите площадь этого квадрата

Ответ: ________________

19. Какое из следующих утверждений верно?

1) Смежные углы всегда равны.

2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

3) Площадь параллелограмма равна половине произведения его диагоналей.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

20. Решите уравнение .

21. Моторная лодка прошла против течения реки 208км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5км/ч.

22. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

23. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68. Найдите углы ромба.

24. Точка Е – середина боковой стороны АВ трапеции АВСD. Докажите, что площадь треугольника ЕСD равна половине площади трапеции.

25. Четырёхугольник АВСD со сторонами АВ = 39 и СD = 12 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 5

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

На рисунке изображён план однокомнатной квартиры в 9-этажном жилом доме (сторона одной клетки на плане равна 0,5м). Окна квартиры выходят на север. При входе в квартиру располагается прихожая. Справа от прихожей находится ванная, а около ванной – туалет, отмеченный на плане цифрой 2. Пол в ванной и туалете выложен плиткой размером 25см х 25см. Налево из прихожей – вход в комнату. Комната имеет наибольшую площадь из всех помещений. Из комнаты есть выход на балкон. Ещё в квартире имеется кухня, отмеченная на плане цифрой 1.

Объекты	комната	прихожая	ванная	балкон
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 5 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол ванной?

Ответ: ________________

3. Найдите площадь, которую занимает кухня. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами балкона (длину диагонали) в метрах.

Ответ: ________________

5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6кг.

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа х, у и z.

Какая из разностей z – x, x – y, z – y положительна?

1) z – x 2) z – y 3) x – y 4) ни одна из них

Ответ:

13. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,16. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) 4) нет решений

Ответ:

14. Алине надо подписать 425 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Алина подписала 9 открыток. Определите, сколько открыток было подписано за седьмой день, если вся работа была выполнена за 17 дней.

Ответ: ________________

15. Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 15. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 480.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 36.

Найдите площадь этого квадрата.

Ответ: ________________

19. Какое из следующих утверждений верно?

1) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

2) В прямоугольном треугольнике гипотенуза равна сумме катетов.

3) Всегда один из двух смежных углов острый, а другой тупой.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

21. Решите уравнение .

22. Моторная лодка прошла против течения реки 221км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4км/ч.

23. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

24. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 15, а одна из диагоналей ромба равна 60. Найдите углы ромба.

25. Точка К – середина боковой стороны СD трапеции АВСD. Докажите, что площадь треугольника КАВ равна половине площади трапеции.

26. Четырёхугольник АВСD со сторонами АВ = 34 и СD = 22 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 6

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

Объекты	балкон	прихожая	санузел	комната
Цифры

Ответ: ________________

3. Найдите площадь, которую занимает кухня. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Во сколько раз площадь прихожей меньше, чем площадь комнаты?

Ответ: ________________

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа х, у и z.

Какая из разностей z – x, x – y, z – y положительна?

1) z – x 2) y – x 3) z – y 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = – .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,15. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 5 с-1, а центростремительное ускорение равно 100 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) 4) нет решений

Ответ:

14. Ирине надо подписать 640 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Ирина подписала 10 открыток. Определите, сколько открыток было подписано за четвертый день, если вся работа была выполнена за 16 дней.

Ответ: ________________

15. Сторона треугольника равна 18, а высота, проведённая к этой стороне, равна 21. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 440.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 40.

Найдите площадь этого квадрата.

Ответ: ________________

19. Какое из следующих утверждений верно?

1) В прямоугольном треугольнике гипотенуза равна сумме катетов.

2) Через любую точку, лежащую вне окружности, можно провести две касательные к этой окружности.

3) Всегда один из двух смежных углов острый, а другой тупой.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

21. Решите уравнение .

23. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 7

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

Объекты	прихожая	лоджия	санузел	комната
Цифры

Ответ: ________________

2. Плитка для пола продаётся в упаковках по 8 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол лоджии?

Ответ: ________________

3. Найдите площадь, которую занимает санузел. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами кухни (длину диагонали) в метрах.

Ответ: ________________

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа a, b и c.

Какая из разностей a – b, a – c, c – b отрицательна?

1) c – b 2) a – b 3) a – c 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 7 с-1, а центростремительное ускорение равно 245 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) 2)

3) нет решений 4)

Ответ:

14. Инне надо подписать 385 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Инна подписала 8 открыток. Определите, сколько открыток было подписано за шестой день, если вся работа была выполнена за 14 дней.

Ответ: ________________

15. Сторона треугольника равна 23, а высота, проведённая к этой стороне, равна 14. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 500.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 60.

Найдите площадь квадрата

Ответ: ________________

19. Какое из следующих утверждений верно?

1) Диагонали ромба равны.

2) Площадь параллелограмма равна половине произведения его диагоналей.

3) В треугольнике против большего угла лежит большая сторона.

В ответ запишите номер выбранного утверждения.

Ответ: ________________

Часть 2

21. Решите уравнение .

22. Моторная лодка прошла против течения реки 255км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 1км/ч.

23. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

24. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 16, а одна из диагоналей ромба равна 64. Найдите углы ромба.

26. Четырёхугольник АВСD со сторонами АВ = 44 и СD = 8 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Пробный ОГЭ № 2. 9 кл. Апрель 2021г.

Вариант 8

Часть 1

Прочитайте внимательно текст и выполните задания 1 – 5.

Объекты	санузел	кухня	комната	прихожая
Цифры

Ответ: ________________

3. Найдите площадь, которую занимает лоджия. Ответ дайте в квадратных метрах.

Ответ: ________________

4. Найдите расстояние между противоположными углами кухни (длину диагонали) в метрах.

Ответ: ________________

5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой, по высоте не превосходящую 85см.

Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
А	7	вертикальная	28 000	1700	бесплатно	85х60х45
Б	5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х40
В	5	фронтальная	25 000	5000	10% от стоимости машины (без учёта подключения)	85х60х40
Г	6,5	фронтальная	24 000	4500	10% от стоимости машины (без учёта подключения)	85х60х44
Модель	Вместимость барабана (кг)	Загрузка белья	Цена машины (руб.)	Подключение (руб.)	Условия доставки	Габариты (высота, ширина, глубина)
Д	6	фронтальная	28 000	1700	бесплатно	85х60х45
Е	6	вертикальная	27 600	2300	бесплатно	89х60х40
Ж	6	вертикальная	27 585	1900	10% от стоимости машины (без учёта подключения)	89х60х40
З	6	фронтальная	20 000	6300	10% от стоимости машины (без учёта подключения)	85х60х42
И	5	фронтальная	27 000	1800	бесплатно	85х60х40
К	5	вертикальная	27 000	1800	бесплатно	85х60х40

Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

Ответ: ________________

6. Найдите значение выражения .

Ответ: ________________

7. На координатной прямой отмечены числа x, y и z.

Какая из разностей z – x, y – z, x – y отрицательна?

1) y – z 2) x – y 3) z – x 4) ни одна из них

Ответ:

8. Найдите значение выражения при х = , y = .

Ответ: ________________

9. Найдите корень уравнения . Если уравнение имеет более одного корня, в ответ запишите меньший из корней.

Ответ: ________________

10. Вероятность того, что новая шариковая ручка пишет плохо (или не пишет), равна 0,07. Покупатель в магазине выбирает одну шариковую ручку. Найдите вероятность того, что эта ручка пишет хорошо.

Ответ: ________________

КОЭФФИЦИЕНТЫ

А) Б) В)

ГРАФИКИ

Втаблице под каждой буквой укажите соответствующий номер.

Ответ:

12. Центростремительное ускорение при движении по окружности (в м/с2) вычисляется по формуле , где — угловая скорость (в с-1), R – радиус окружности (в метрах). Пользуясь этой формулой, найдите радиус R, если угловая скорость равна 3 с-1, а центростремительное ускорение равно 81 м/с2. Ответ дайте в метрах.

Ответ: ________________

13. Укажите решение системы неравенств

1) нет решения 2)

3) 4)

Ответ:

14. Люсе надо подписать 828 открыток. Ежедневно она подписывает на одно и то же количество открыток больше по сравнению с предыдущим днем. Известно, что за первый день Люся подписала 12 открыток. Определите, сколько открыток было подписано за пятый день, если вся работа была выполнена за 18 дней.

Ответ: ________________

15. Сторона треугольника равна 16, а высота, проведённая к этой стороне, равна 25. Найдите площадь этого треугольника.

Ответ: ________________

16. Касательная в точках А и В к окружности с центром в точке О пересекается под углом 420.

Найдите угол АВО. Ответ дайте в градусах.

Ответ: ________________

17. Периметр квадрата равен 52.

Найдите площадь квадрата

Ответ: ________________

19. Какие из следующих утверждений верны?

1) Через точку, не лежащую на данной прямой, можно провести прямую, перпендикулярную этой прямой.

2) Любые два равносторонних треугольника подобны.

3) Смежные углы всегда равны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

Ответ: ________________

Часть 2

21. Решите уравнение .

22. Моторная лодка прошла против течения реки 132км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5км/ч.

23. Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

24. Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 14, а одна из диагоналей ромба равна 56. Найдите углы ромба.

26. Четырёхугольник АВСD со сторонами АВ = 5 и СD = 17 вписан в окружность. Диагонали АС и ВD пересекаются в точке К, причём

∠АКВ = 600. Найдите радиус окружности, описанной около этого четырёхугольника.

Предварительный просмотр:

Ответы:

Вариант 1

1) 5431; 2) 8; 3) 3; 4) 4; 5) 29900; 6) 0,6; 7) 2; –8;

9) –2; 10) 0,72; 11) 312; 12) 6; 13) 3; 14) 22;

15) 216; 16) 18; 17) 64; 18) 4; 19) 3.

20) ; 21) 30; 22) См.рис. m = 1 и m = 4;

23) 600, 1200, 600, 1200; 25) .

Вариант 2

1) 1243; 2) 29; 3) 6; 4) 5; 5) 28800; 6) 1,2; 7) 3; –0,4;

9) –8; 10) 0,91; 11) 132; 12) 6; 13) 2; 14) 23;

15) 174; 16) 26; 17) 289; 18) 3; 19) 1.

20) ; 21) 16; 22) См.рис. m = –3,5 и m = 1,5;

23) 600, 1200, 600, 1200; 25) .

Вариант 3

1) 3126; 2) 8; 3) 10,5; 4) 5; 5) 28800; 6) 0,7; 7) 1; –5;

9) –6; 10) 0,89; 11) 132; 12) 3; 13) 4; 14) 28;

15) 198; 16) 19; 17) 441; 18) 5; 19) 23.

20) ; 21) 17; 22) См.рис. m = –1,5 и m = 0;

23) 600, 1200, 600, 1200; 25) .

Вариант 4

1) 3412; 2) 14; 3) 7; 4) 6,5; 5) 29300; 6) 1,1; 7) 2; –0,5;

9) –3; 10) 0,87; 11) 213; 12) 4; 13) 3; 14) 36;

15) 161; 16) 43; 17) 36; 18) 4; 19) 2.

20) 2; 21) 21; 22) См.рис. m = 0,5 и m = 4;

23) 600, 1200, 600, 1200; 25) .

Вариант 5

1) 4365; 2) 13; 3) 10,5; 4) 2,5; 5) 29700; 6) 1,4; 7) 3; –7;

9) –5; 10) 0,84; 11) 231; 12) 5; 13) 1; 14) 21;

15) 105; 16) 24; 17) 81; 18) 4; 19) 1.

Часть 2 – как вариант 1.

Вариант 6

1) 3451; 2) 8; 3) 7,5; 4) 4; 5) 29900; 6) 0,6; 7) 4; 5;

9) –5; 10) 0,85; 11) 321; 12) 4; 13) 2; 14) 22;

15) 189; 16) 22; 17) 100; 18) 4; 19) 2.

Часть 2 – как вариант 2.

Вариант 7

1) 4231; 2) 18; 3) 6; 4) 5; 5) 28800; 6) 1,2; 7) 1; –0,8;

9) –3; 10) 0,89; 11) 312; 12) 5; 13) 4; 14) 23;

15) 161; 16) 25; 17) 225; 19) 3; 19) 3.

Часть 2 – как вариант 3.

Вариант 8

1) 6132; 2) 9; 3) 10,5; 4) 5; 5) 28800; 6) 0,7; 7) 3; –11;

9) –4; 10) 0,73; 11) 123; 12) 9; 13) 1; 14) 28;

15) 200; 16) 21; 17) 169; 18) 5; 19) 12.

Часть 2 – как вариант 4.

По теме: методические разработки, презентации и конспекты

Мне нравится

Источник

Тренировочные варианты по математике в формате ОГЭ 2021 с ответами.

Источник — time4math.ru

Автор: Ширяева Елена Алексеевна (математик, профессиональный репетитор)

Варианты соответствуют новой демоверсии ОГЭ 2021 года по математике.

→ варианты 1-2

→ варианты 3-4

→ варианты 5-6

→ варианты 7-8

→ Скачать ответы

→ варианты 9-10

→ варианты 11-12

→ варианты 13-14

→ варианты 15-16

→ Скачать ответы

Варианты от oge100ballov

→ Вариант 1 с ответами

→ Вариант 2 с ответами

→ Вариант 3 с ответами

→ Вариант 4 с ответами

→ Вариант 5 с ответами

Изменения в КИМ 2021 года по сравнению с 2020 годом:

В рамках усиления акцента на проверку применения математических знаний в различных ситуациях количество заданий уменьшилось на одно за счет объединения заданий на преобразование алгебраических (задание 13 в КИМ 2020 г.) и числовых выражений (задание 8 в КИМ 2020 г.) в одно задание на преобразование выражений на позиции 8 в КИМ 2021 г.

Задание на работу с последовательностями и прогрессиями (задание 12 в КИМ 2020 г.) заменено на задание с практическим содержанием, направленное на проверку умения применять знания о последовательностях и прогрессиях в прикладных ситуациях (задание 14 в КИМ 2021 г.).

Скорректирован порядок заданий в соответствии с тематикой и сложностью.

Связанные страницы:

Математика ОГЭ Действия с корнями Задание 8 Практика

Площадь треугольника — ОГЭ по математике (задания для тренировки)

Карточки по теме «Действия с обыкновенными дробями» Задание 6 ОГЭ по математике

Графики функций — подготовка к ОГЭ по математике

Источник

Выберите свой номер варианта теста:

Вариант 1

Видеоразбор варианта №1

Вариант 2

Вариант 3

Видеоразбор варианта №3

Вариант 4

Вариант 5

Видео разбор 5 варианта ОГЭ 2021

Вариант 6

Вариант 7

Видеоразбор 7 варианта

Вариант 8

Вариант 9

Вариант 10

Вариант 11

Вариант 12

Вариант 13

Вариант 14

Вариант 15

Вариант 16

Вариант 17

Вариант 18

Вариант 19

Вариант 20

Вариант 21

Вариант 22

Вариант 23

Вариант 24

Вариант 25

Вариант 26

Вариант 27

Вариант 28

Вариант 29

Вариант 30

Вариант 31

Вариант 32

Вариант 33

Вариант 34

Вариант 35

Вариант 36

Тренировочная работа №1 по математике 9 класс ОГЭ 2022 статград

Варианты МА2190103-МА2190104

Другие тренировочные варианты ОГЭ 2022 по математике 9 класс:

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Скачать:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Новое и интересное на сайте: