Задание 1
Решите уравнение $$frac{3^{x^2}-81}{x-2}=0.$$ Если уравнение имеет более одного корня, в ответе укажите больший из них.
Ответ: -2
Скрыть
ОДЗ: $$xneq2$$
$$3x^2=81=3^4$$
$$x^2=4$$
$$x=−2$$
$$x=2$$ – не подходит под ОДЗ
Задание 2
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответ: 0,0579
Скрыть
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$ – вероятность наступления 2-х несовместных событий
$$A_1$$ – исправная батарейка забракована системой
$$A_2$$ – неисправная батарейка забракована системой
$$P(A_1)=0,97cdot0,03$$
$$P(A_2)=0,03cdot0,96$$
$$P(A)=0,97cdot0,03+0,03cdot0,96=0,0579$$
Задание 3
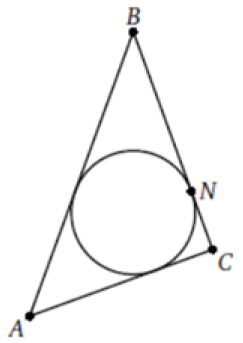
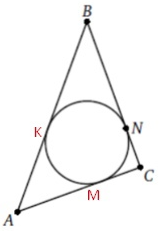
Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN = 15 и AC = 17. Найдите периметр треугольника.
Ответ: 64
Скрыть
$$P=AB+AC+BC$$
$$P=AK+BK+BN+NC+AC$$
По свойству касательных, проведенных из одной точки
$$AK=AM$$
$$NC=MC$$
$$BK=BN=15$$
$$AC=AM+MC=AK+NC$$
Значит
$$P=17+17+15+15=64$$
Задание 4
Найдите значение выражения $$frac{9^{x+11}cdot2^{3x+8}}{3^{2x+21}cdot4^{x+4}}$$ при $$x = 2$$
Ответ: 12
Скрыть
$$frac{3^{2x+22}cdot2^{3x+8}}{3^{2x+21}cdot2^{2x+8}}=3cdot2^x=12$$
Задание 5
Основанием наклонной призмы $$ABCDA_1B_1C_1D_1$$ является квадрат $$ABCD,$$ а диагональ $$AC_1$$ призмы перпендикулярна плоскости основания. Найдите площадь основания призмы, если $$AC_1=2sqrt{7}, AA_1=6.$$
Ответ: 4
Скрыть
Пусть $$a$$ — сторона квадрата
Если диагональ перпендикулярна плоскости основания, то из прямоугольного треугольника мы можем найти диагональ квадрата, который лежит в основании.
$$sqrt{36-14cdot7}=2sqrt{2}=asqrt{2}$$
$$a=2$$
$$S=4$$
Задание 6
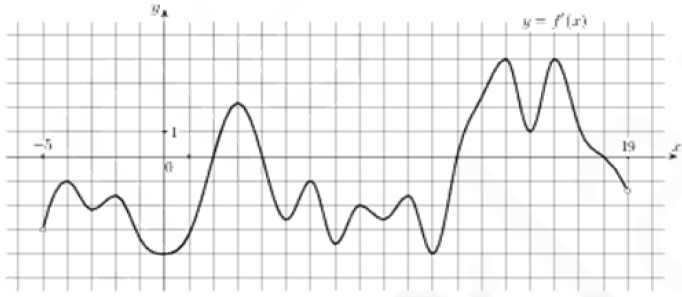
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x),$$ определенной на интервале $$(-5; 19).$$ Найдите количество точек максимума функции $$f(x),$$ принадлежащих отрезку $$[-3; 15].$$
Ответ: 1
Скрыть
Точка максимума будет там, где знак производной меняется с “+” на “-”
Задание 7
Скорость колеблющегося на пружине груза меняется по закону $$v(t)=3sinfrac{pi t}{4}$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 1,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,33
Скрыть
$$3cdotsinfrac{pi t}{4}>1,5$$
$$sinfrac{pi t}{4}>frac{1}{2}$$
$$frac{pi}{6}+2pi n<frac{pi t}{4}<frac{5pi}{6}+2pi n$$
$$frac{2}{3}+8n<t<frac{10}{3}+8n$$
$$n=0$$
$$frac{2}{3}<t<3frac{1}{3}$$
$$frac{2}{3}<t<1$$
Получаем, что $$1−frac{2}{3}=frac{1}{3}approx0,33$$ доля от первой секунды скорость была больше 1,5
Задание 8
Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой. «Если бы принтер стоил столько же, сколько компьютер, я бы получил 192 млн. рублей» — сказал Борис. «Если бы компьютер стоил столько же, сколько принтер, я бы получил 75 млн. рублей» — ответил Аркадий. На сколько процентов компьютер дороже принтера?
Ответ: 60
Скрыть
Пусть $$x, y$$ – цена принтера и компьютера соответственно, $$k,n$$ – кол-во проданных принтеров и компьютеров соответственно.
$$xcdot k=ycdot n$$
$$left{begin{matrix}
xcdot n=192\
ycdot k=75
end{matrix}right.$$
Решая систему, получаем $$frac{x}{y}=1,6$$
$$Rightarrow 60%$$
Задание 9
На рисунке изображен график функции $$f'(x)=acdottg x+b.$$ Найдите $$b.$$
Ответ: -3
Скрыть
$$1=acdottgfrac{pi}{4}+b$$
$$−3=acdottg0+b$$
$$b=−3$$
Задание 10
В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Ответ: 0,11
Скрыть
Всего благоприятных вариантов из 36 два: 5,6 и 6,5
Найдем вероятность того, что гостю ни разу не выпала комбинация 5,6:
$$P(A)=(1-frac{2}{36})cdot(1-frac{2}{36})$$
$$P_{иск}=1−P(A)=frac{35}{324}approx0,11$$
Задание 11
Найдите наибольшее значение функции $$y=12sin x-6sqrt{3}x+sqrt{3}pi+6$$ на отрезке $$[0;frac{pi}{2}].$$
Ответ: 12
Скрыть
Найдем критические точки:
$$y’=0$$
$$12cos x−6sqrt{3}=0$$
$$cos x=frac{sqrt{3}}{2}$$
$$x=pmfrac{pi}{6}+2pi n$$
Под отрезок попадает только $$x=frac{pi}{6}$$
Проверкой методом интервалов эта точка и является точкой максимума
$$y(frac{pi}{6})=12$$
Задание 12
А) Решите уравнение $$frac{4^{x+frac{1}{2}}=2^{x+1}-2^{x+frac{1}{2}}+sqrt{2}}{sin x+sin2x}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{pi}{2}]$$
Ответ: А)$$-0,5$$ Б)$$-0,5$$
Задание 13
В кубе ABCDA1B1C1D1 точки K, L и М — середины ребер АВ, В1С1 и DD1
А) Докажите, что сечение куба плоскостью KLM является правильным многоугольником.
Б) Найдите расстояние от точки А до плоскости KLM, если ребро куба равно 2.
Ответ: $$frac{1}{sqrt{3}}$$
Задание 14
Решите неравенство: $$(6+sqrt{35})^{2x}-frac{7-sqrt{35}}{(6-sqrt{35})^x}+6>sqrt{35}$$
Ответ: $$(-infty;-1),(0;infty)$$
Задание 15
В начале 1977 года Алишер положил в пустой сейф 1 млн. руб. В начале каждого последующего года он вынимает из сейфа m% имеющихся там рублей. При каком значении m он вынет из сейфа в начале 1982 года максимальную сумму?
Ответ: 20
Задание 16
В выпуклом четырехугольнике ABCD диагональ АС является биссектрисой угла BAD и пересекается с диагональю BD в точке Е. Известно, что около четырехугольника ABCD можно описать окружность.
А) Докажите, что $$AEcdot AC = ADcdot AB$$
Б) Найдите АЕ, если известно, что ВС=7, СЕ=4.
Ответ: 8,25
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$|log_5(x^2)-a|-|log_5 x+2a|=(log_5 x)^2$$
имеет ровно четыре решения.
Ответ: $$(-frac{1}{12};0),(0;frac{1}{12})$$
Задание 18
А) Можно ли в выражении $$ln 5 * ln 6 * ln 7 * ln8 * ln10 * ln12 * ln14$$ вместо всех знаков * так расставить знаки “+” и “-“, чтобы в результате получился ноль?
Б) Можно ли в выражении $$ln 6 * ln 7 * ln 8 * ln12 * ln14 * ln 24 * ln 32$$ вместо всех знаков * так расставить знаки “+” и “-“, чтобы в результате получился ноль?
В) Какое наибольшее количество попарно различных чисел можно выбрать из набора $$ln 7, ln 8,…ln 20$$ и расставить знаки “+” и “-“ так, чтобы их сумма стала равна нулю?
Ответ: А) да, Б) нет, В) 9
| 3043 | А) Можно ли в выражении ln5*ln6*ln7*ln8*ln10*ln12*ln14 вместо всех знаков * так расставить знаки «+» и «-«, чтобы в результате получился ноль? Б) Можно ли в выражении ln6*ln7*ln8*ln12*ln14*ln24*ln32 вместо всех знаков * так расставить знаки «+» и «-«, чтобы в результате получился ноль? В) Какое наибольшее количество попарно различных чисел можно выбрать из набора ln7, ln8, …, ln20 и расставить знаки «+» и «-» так, чтобы их сумма стала равна нулю? |
А) Можно ли в выражении ln5*ln6*ln7*ln8*ln10*ln12*ln14 вместо всех знаков * так расставить знаки ! Тренировочный вариант 365 от Ларина Задание 18 (19) # Решение — Кирилла Колокольцева # математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 12 Задание 18 | |
| 3042 | В кубе ABCDA1B1C1D1 точки K, L и M — середины рёбер AB, B1C1 и DD1. А) Докажите, что сечение куба плоскостью KLM является правильным многоугольником. Б) Найдите расстояние от точки A до плоскости KLM, если ребро куба равно 2 |
В кубе ABCDA1B1C1D1 точки K, L и M — середины рёбер AB, B1C1 и DD1 ! Тренировочный вариант 365 от Ларина Задание 13 (14) # Решение — Елены Ильиничны Хажинской | |
| 3041 | B выпуклом четырёхугольнике ABCD диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке E. Известно, что около четырёхугольника ABCD можно описать окружность. А) Докажите, что AE*AC=AD*AB. Б) Найдите AE, если известно, что ВС=7, СЕ=4 |
B выпуклом четырёхугольнике ABCD диагональ AC является биссектрисой угла BAD и пересекается с диагональю BD в точке E ! Тренировочный вариант 365 от Ларина Задание 16 | |
| 3040 | Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой. «Если бы принтер стоил столько же, сколько компьютер, я бы получил 192 млн. рублей» ‐ сказал Борис. «Если бы компьютер стоил столько же, сколько принтер, я бы получил 75 млн. рублей» ‐ ответил Аркадий. На сколько процентов компьютер дороже принтера? |
Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой ! Тренировочный вариант 365 от Ларина Задание 8 (11) ЕГЭ | |
| 3039 | Решите уравнение (3^(x^2)-81)/(x-2)=0. Если уравнение имеет более одного корня, в ответе укажите больший из них |
Тренировочный вариант 365 от Ларина Задание 1 | |
| 3038 | Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN =15 и AC =17. Найдите периметр треугольника |
Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N ! Тренировочный вариант 365 от Ларина Задание 3 (6) | |
| 3037 | Найдите значение выражения (9^(x+11)*2^(3x+8))/(3^(2x+21)*4^(x+4)) при x=2 |
Тренировочный вариант 365 от Ларина Задание 4 (9) | |
| 3036 | Основанием наклонной призмы ABCDA1B1C1D1 является квадрат ABCD, а диагональ AC1 призмы перпендикулярна плоскости основания. Найдите площадь основания призмы, если AC1=2sqrt7, A A1 =6 |
Основанием наклонной призмы ABCDA1B1C1D1 является квадрат ABCD, а диагональ AC1 призмы перпендикулярна плоскости основания ! Тренировочный вариант 365 от Ларина Задание 5 (8) ЕГЭ | |
| 3035 | На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале (‐5; 19). Найдите количество точек максимума функции f(x), принадлежащих отрезку [‐3; 15]
|
На рисунке изображен график y=f'(x) — производной функции f(x), определенной на интервале ! Тренировочный вариант 365 от Ларина Задание 6 (7) ЕГЭ | |
| 3034 | На рисунке изображен график функции f(x)=a*tg(x)+b. Найдите b
|
На рисунке изображен график функции f(x)=a tg(x)+b. Найдите b ! Тренировочный вариант 365 от Ларина Задание 9 ЕГЭ | |

Показана страница 1 из 2
| Clear |
Егэ математика профиль ларин вариант 365
1. Решите уравнение ( frac-81>=0 ) Если уравнение имеет более одного корня, в ответе укажите больший из них.
2. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
3. Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN =15 и AC =17. Найдите периметр треугольника.
4. Найдите значение выражения ( frac*2^>*4^> ) при ( x=2 )
5. Основанием наклонной призмы ABCD A1B1C1D1 является квадрат ABCD, а диагональ AC1 призмы перпендикулярна плоскости основания. Найдите площадь основания призмы, если ( AC_=2sqrt ) , ( AA_=6 )
6. На рисунке изображен график ( y=f'(x) ) — производной функции ( f(x) ) определенной на интервале (‐5; 19). Найдите количество точек максимума функции ( f(x) ) , принадлежащих отрезку [‐3; 15].
7. Скорость колеблющегося на пружине груза меняется по закону ( v(t)=3*sinfrac<pi t> ) (см/с), где t — время в секундах. Какую долю времени из первой секунды скорость движения превышала 1,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
8. Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой. «Если бы принтер стоил столько же, сколько компьютер, я бы получил 192 млн. рублей» ‐ сказал Борис. «Если бы компьютер стоил столько же, сколько принтер, я бы получил 75 млн. рублей» ‐ ответил Аркадий. На сколько процентов компьютер дороже принтера?
9. На рисунке изображен график функции ( f(x)=atgx+b ) . Найдите b.
10. В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш‐беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
11. Найдите наибольшее значение функции ( y+6=12sinx-6sqrtx+sqrtpi+6 ) отрезке [0;pi/2]
Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана чашку кофе или десерт бесплатно.
Gdz-larin. ru
08.04.2019 15:16:25
2019-04-08 15:16:25
Источники:
Https://gdz-larin. ru/?p=9776