Егэ по математике профиль 2021 основная волна

ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

В магазине вся мебель продаётся в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 10% от стоимости купленной мебели. Шкаф стоит 3300 рублей. Во сколько рублей обойдётся покупка этого шкафа вместе со сборкой?

Ответ:

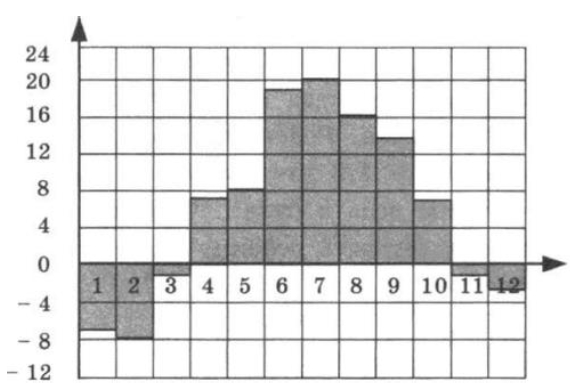
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали  — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой в 1973 году.

Ответ:

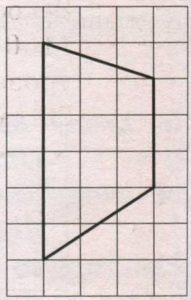
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Ответ:

В сборнике билетов по математике всего 25 билетов, в 10 из них встречается вопрос по теме «Неравенства». Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику не достанется вопроса по теме «Неравенства».

Ответ:

Найдите корень уравнения

Ответ:

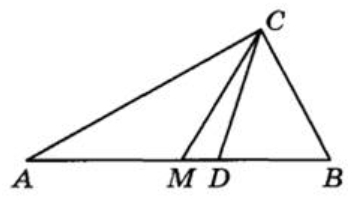
В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40°. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Ответ:

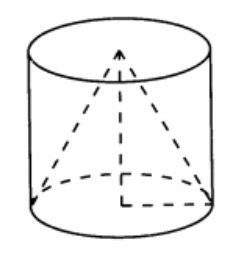
Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объем конуса равен 6. Найдите объем шара.

Ответ:

Найдите значение выражения

Ответ:

На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Ответ:

Найдите точку минимума функции

Ответ:

а)  Решите уравнение

б)  Укажите корни этого уравнения, принадлежащие отрезку

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

В правильной четырехугольной пирамиде SABCD проведена высота SH. K  — середина ребра SD, N  — середина ребра CD. Плоскость ABK пересекает ребро SC в точке P.

а)  Докажите, что прямая PK делит отрезок NS пополам.

б)  Найдите расстояние от точки P до плоскости ABS, если SH = 15, CD = 16.

Решите неравенство:

Дана трапеция ABCD с большим основанием AD, вписанная в окружность. Продолжение высоты трапеции BH пересекает окружность в точке K.

а)  Докажите, что отрезки AC и AK перпендикулярны.

б)  Найдите AD, если радиус описанной окружности равен 6, угол BAC составляет 30°, отношение площадей BCNH к NKH равно 35, где N  — точка пересечения отрезков AD и CK.

В июле 2025 года планируется взять кредит в банке на сумму 900 тысяч рублей на 10 лет. Условия его возврата таковы:

— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 12% по сравнению с концом предыдущего года;

— в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 8% по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;

— к июлю 2035 года кредит должен быть погашен полностью.

Найдите общую сумму выплат после полного погашения кредита.

Найдите все значения a, при каждом из которых уравнение

имеет ровно два различных корня.

Даны три различных натуральных числа такие, что второе число равно сумме цифр первого, а третье  — сумме цифр второго.

а)  Может ли сумма трех чисел быть равной 420?

б)  Может ли сумма трех чисел быть равной 419?

в)  Сколько существует троек чисел, таких что: первое число  — трехзначное, а последнее равно 5?

Завершить тестирование, свериться с ответами, увидеть решения.

Источник

12
Июн 2021

Категория: ЕГЭ (диагностич. работы)

2021-06-12
2021-08-27

№ 13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку

Решение: + показать

№ 14. В правильной четырехугольной пирамиде сторона основания , высота . Точка — середина бокового ребра , а точка — середина ребра . Плоскость пересекает боковое ребро в точке .

а) Докажите, что прямая пересекает отрезок в его середине.

б) Найдите расстояние от точки до плоскости .

Решение: + показать

№ 15. Решите неравенство: $16^{frac{1}{x}-1}-4^{frac{1}{x}-1}-2geq 0.$

Решение: + показать

№ 16. Трапеция с большим основанием и высотой вписана в окружность. Прямая вторично пересекает эту окружность в точке .

а) Докажите, что прямые и перпендикулярны.

б) Прямые и пересекаются в точке Найдите если радиус окружности равен $angle BAC=30^{circ},$ а площадь четырёхугольника в раз больше площади треугольника .

Решение: + показать

№ 17. В июле 2025 года планируется взять кредит в банке на сумму 700 тысяч рублей на 10 лет. Условия его возврата таковы:

— в январе 2026, 2027, 2028, 2029 и 2030 годов долг возрастает на 19% по сравнению с концом предыдущего года;

— в январе 2031, 2032, 2033, 2034 и 2035 годов долг возрастает на 16% по сравнению с концом предыдущего года;

— со февраля по июнь каждого года необходимо выплатить часть долга;

— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;

— к июлю 2035 года кредит должен быть погашен полностью.

Найдите общую сумму выплат после полного погашения кредита.

Решение: + показать

№18. Найдите все значения a, при каждом из которых уравнение

$|x^2-a^2|=|x+a|sqrt{x^2-ax+4a}$

имеет ровно два различных корня.

Решение: + показать

№19. Даны три различных натуральных числа такие, что второе число равно сумме цифр первого, а третье — сумме цифр второго.

а) Может ли сумма трех чисел быть равной 2022?

б) Может ли сумма трех чисел быть равной 2021?

в) Сколько существует троек чисел, таких что первое число трехзначное, а последнее равно 2?

Решение: + показать

Автор: egeMax |

комментария 2

Печать страницы

Источник

05.06.2021

Сборник реальных заданий с основной волны ЕГЭ 2021 по математике профильного уровня. Напомним, что базовую математику в 2021 году отменили.

Дата обновления: 21.07.21

Страница будет обновляться. СОХРАНИТЕ В ЗАКЛАДКИ!

Реальные задания ЕГЭ 2021 по всем предметам

Сначала идут задания с Дальнего востока. Это горячие задания, которые появлялись сразу после проведения ЕГЭ 2021.

Потом ниже уже идут PDF сборники целиком. Листайте до конца!

Реальные задания с Дальнего востока

Первая часть

Задание 1. Кто-то там получает 60.000 зп, из них вычитается 13% налогов, сколько будет конечная зп

ПРОТОТИП:

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.

ОБРАТНАЯ ЗАДАЧА:

Налог на доходы составляет 13% от заработной платы. После удержания налога на доходы Мария Константиновна получила 7830 рублей. Сколько рублей составляет заработная плата Марии Константиновны?

Задание 4. Завод делает детали (кол-во), шанс того, что деталь будет плохой (%) . Какова вероятность, что деталь будет /хорошей/

Задание 5. 9^(x-1)=81

Задание 6. Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Задание 7. Найти количество точек минимума / максимума

Задание 8. В цилиндре конус, у них одинаковое высота и основание общее, S цилиндра 9,найти S конуса

ПРОТОТИП:

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 27√2. Найдите площадь боковой поверхности конуса.

Смотрите ниже, как решать подобное задание

Задание 9. 9sin128/cos64*cos26

Смотрите ниже, как решать подобное задание

Задание 11. Про трубы. Первая труба пропускает на 5 литров воды в минуту больше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 704 литра она заполняет на 10 минут медленнее, чем первая труба заполняет резервуар объёмом 864 литра?

РЕШЕНИЕ ПОХОЖЕЙ ЗАДАЧИ НИЖЕ

Задание 12. Натуральный логарифм

Вторая часть

Задание 13. Были именно ЭТИ задачи

Вариант 1

Вариант 2

Задание 14.

Дана треугольная пирамида ????. Точка ? – середина ??, точка ? – середина ??. Плоскость ?, параллельная плоскости основания,
проходит через точку ? и пересекает ребра ?? и ?? в точках ? и ? соответственно.

Докажите, что ?? пересекает ?? в середине.
Найдите угол между плоскостью основания и плоскостью ???

Задание 15.

Вариант 1

Вариант 2

Вариант 3

Задание 16.

Дан параллелограмм ???? с острым углом ?. На продолжении стороны ?? за точку ? взята точка ? такая, что ?? = ??, а на продолжении стороны ?? за точку ? взята точка ? такая, что ?? = ??.

Докажите, что ?? = ??.
Найдите ??, если ?? = 7, sin, ??? = 7/25 .

Задание 17. В июле 2025 года планируется взять кредит на 8 лет. Условия его возврата таковы:

в январе 2026, 2027, 2028 и 2029 долг возрастает на 15% по сравнению с концом предыдущего года;
в январе 2030, 2031, 2032 и 2033 долг возрастает на 11%;
долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
к июлю 2033 года долг должен быть погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат составит 650 тыс. рублей?

Решение

Задание 18. Три модуля

Задание 19. ПРОТОТИП: Дано трёхзначное натуральное число (число не может начинаться с нуля) А, сумма цифр равна S.

а) Может ли произведение A*S быть равным 1106?
б) Может ли произведение A*S быть равным 1105?

Решение №1

Решение №2

Полный сборник всех заданий из второй части реального ЕГЭ по математике 2021

Посмотрите видеоразбор к каждому из заданий из второй части реального ЕГЭ. Пошагово разбираем все ошибки, способы решения и правильные ответы.

Сами задания из видео расположены ниже.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сборник заданий №2

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сборник заданий №3

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Источник


3111	В параллелограмме ABCD тангенс угла A равен 1,5. На продолжениях сторон AB и BC параллелограмма за точку B выбраны точки N и M соответственно, причём BC=CN и AB=AM. а) Докажите, что DN = DM. б) Найдите MN, если AC = sqrt13 Решение	В параллелограмме ABCD тангенс угла A равен 1,5 ! 36 вариантов ФИПИ Ященко 2022 Вариант 4 Задание 16 # ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 # Задача-аналог 3094 2862

3094	В параллелограмме ABCD угол A острый. На продолжениях сторон AD и СD за точку D выбраны точки M и N соответственно, причём AM=AD и CM=CD. а) Докажите, что BN = BM. б) Найдите MN, если AC = 5, sin/_BAD = 5/13 Решение	В параллелограмме ABCD угол A острый. На продолжениях сторон AD и СD за точку D ! 36 вариантов ФИПИ Ященко 2022 Вариант 3 Задание 16 # ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 # Задача-аналог 3111 2862

3084	В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12. Точка K — середина бокового ребра SD. Плоскость AKB пересекает боковое ребро SC в точке P. а) Докажите, что площадь четырёхугольника CDKP равна составляет 3/4 площади треугольника SCD. б) Найдите объем пирамиды ACDKP Решение	В правильной четырёхугольной пирамиде SABCD сторона основания AD равна 10, высота SH равна 12 ! 36 вариантов ФИПИ Ященко 2022 Вариант 2 Задание 13 #ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 14 # Задача-аналог 2866

3083	Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC=CD=DE, а AC перпендикулярна BE. Точка K — пересечение прямых BE и AD. а) Докажите, что прямая CE делит отрезок KD пополам. б) Найдите площадь треугольника ABK, если AD=4, DC=sqrt(3) Решение	Точки A, B, C, D и E лежат на окружности в указанном порядке, причем BC=CD=DE ! 36 вариантов ФИПИ Ященко 2022 Вариант 2 Задание 16 # Задача-аналог 2871

2902	Найдите все значения параметра а, при каждом из которых уравнение abs(a-2)x^4-2ax^2+abs(a-12)=0 имеет хотя бы два различных корня Решение График	Найдите все значения параметра а, при каждом из которых уравнение \|a -2\| x 4 — 2ax 2 + \|a — 12\| = 0 имеет хотя бы два различных корня ! ЕГЭ по математике 2021 Резервный день 29-06-2021 Задание 18

2897	Отрезок CH — высота прямоугольного треугольника ABC с прямым углом C. На катетах AC и BC выбраны точки N и M соответственно такие, что /_ MHN = 90^@. a) Докажите, что треугольник MNH подобен треугольнику ABC. б) Найдите CN, если BC = 3, AC = 5, CM = 2 Решение	Отрезок CH — высота прямоугольного треугольника ABC с прямым углом C ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 (16.4.2) Запад, Центр # Решение пункта б двумя способами # Задача-аналог 2896

2896	Треугольник ABC прямоугольный с прямым углом C. Опущена высота CH. На AC и BC соответственно отмечены точки M и N так, что угол MHN прямой. а) Докажите, что треугольники MNH и ABC подобны. б) Найдите CN, если AC = 5, CM = 2, BC = 3 Решение	Треугольник ABC прямоугольный с прямым углом C. Опущена высота CH ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 (16.4) Запад, Центр # Задача-аналог 2897 — решение пункта б вторым способом

2895	Трапеция ABCD с большим основанием AD и высотой BH вписана в окружность. Прямая BH вторично пересекает эту окружность в точке K. а) Докажите, что прямые AC и AK перпендикулярны. б) Прямые CK и AD пересекаются в точке N. Найдите AD, если радиус окружности равен 10, /_ BAC = 30^@, а площадь четырёхугольника BCNH в 24 раза больше площади треугольника KNH Решение	Найдите AD, если радиус окружности равен 10, угол BAC = 30 град, а площадь четырёхугольника BCNH в 24 раза больше площади треугольника KNH ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 (16.10) Санкт-Петербург, Запад, Центр # Задача-аналог 2894

2894	Трапеция ABCD с большим основанием AD и высотой BH вписана в окружность. Прямая BH вторично пересекает эту окружность в точке K. а) Докажите, что прямые AC и AK перпендикулярны. б) Прямые CK и AD пересекаются в точке N. Найдите AD, если радиус окружности равен 12, /_ BAC = 30^@, а площадь четырёхугольника BCNH в 8 раз больше площади треугольника KNH Решение	Трапеция ABCD с большим основанием AD и высотой BH вписана в окружность ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 16 (16.3) Санкт-Петербург # Задача-аналог 2895

2893	В правильной четырехугольной пирамиде SABCD сторона основания AD = 14, высота SH = 24. Точка K — середина бокового ребра SD, а точка N — середина ребра CD. Плоскость ABK пересекает боковое ребро SC в точке P. а) Докажите, что прямая KP пересекает отрезок SN в его середине. б) Найдите расстояние от точки P до плоскости ABS Решение	В правильной четырехугольной пирамиде SABCD сторона основания AD = 14, высота SH = 24 ! ЕГЭ по математике профильного уровня 07-06-2021 основная волна Задание 14 Санкт-Петербург

Источник

Варианты составлены из реальных заданий ЕГЭ 2021 по математике от 7 июня. Все задания взяты из открытых источников

В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.

Скачать 1 вариант: Скачать
Скачать 2 вариант: Скачать

Смотреть 1 вариант онлайн:
Смотреть 2 вариант онлайн:

Интересные задания:

1. Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 30 000 рублей. Сколько рублей он получит после вычета налога на доходы?

2. Показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 2020 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 2020 года. Ответ дайте в градусах Цельсия.

4. В среднем из 1000 садовых насосов, поступивших в продажу, 7 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.

11. Первая труба пропускает на 5 литров воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 375 литров она заполняет на 10 минут быстрее, чем первая труба заполняет резервуар объемом 500 литров?

14. Дана правильная треугольная пирамида SABC, AB = 24, высота SH, проведённая к основанию, равна 14, точка K — середина AS, точка N — середина BC. Плоскость, проходящая через точку K и параллельная основанию пирамиды, пересекает ребра SB и SC в точках Q и P соответственно.
а) Докажите, что PQ проходит через середину отрезка SN.
б) Найдите угол между плоскостью основания и плоскостью APQ.

17. В июле 2025 года планируется взять кредит на 600 тыс. рублей. Условия его возврата таковы:
— в январе 2026, 2027 и 2028 годов долг возрастает на r% по сравнению с концом предыдущего года;
— в январе 2029, 2030 и 2031 годов долг возрастает на 15% по сравнению с концом предыдущего года;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года;
— к июлю 2031 года долг должен быть полностью погашен. Чему равно r, если общая сумма выплат составит 930 тысяч рублей?

19. Дано трёхзначное число А, сумма цифр которого равна S.
а) Может ли выполняться равенство A · S = 1105?
б) Может ли выполняться равенство A · S = 1106?
в) Какое наименьшее значение может принимать выражение, если оно больше 1503?

Вам будет интересно:

ЕГЭ по математике (профиль) 11 класс 2021. Новый тренировочный вариант №37 — №210517 (задания и ответы)

* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР

Источник

25 июня 2021

В закладки

Обсудить

Жалоба

Основная волна ЕГЭ 2021.

Задания 1-12

Задание №1 — 01:00
Задание №2 — 03:29
Задание №3 — 04:15
Задание №4 — 06:46
Задание №5 — 08:17
Задание №6 — 08:43
Задание №7 — 12:37
Задание №8 — 14:02
Задание №9 — 15:24
Задание №10 — 18:43
Задание №11 — 20:48
Задание №12 — 28:24

Задания 13-15

Каждое верно решённое задание оценивается в 2 первичных балла.

Задание №13 — 00:25
Задание №14 — 11:34
Задание №15 — 35:42

Задания 16, 17

Каждое верно решённое задание оценивается в 3 первичных балла.

Задание №16 — 00:51
Задание №17 — 24:45

Задания 18, 19

Каждое верно решённое задание оценивается в 4 первичных балла.

Задание №18 — 00:30
Задание №19 — 11:52

Автор: Matesha Plus — Татьяна Колесникова.

Источник: youtube.com/c/MateshaPlus

Источник

Решение заданий и ответы вариантов Москвы и Дальнего Востока реального ЕГЭ от 7 июня 2021 года по математике (профильный уровень). Основная волна КИМ МСК, ДВ, Дальневосточный, Владивосток, профиль.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

Задание 1.
Ивану Кузьмичу начислена заработная плата 20 000 рублей. Из этой суммы вычитается налог на доходы физических лиц в размере 13%. Сколько рублей он получит после уплаты подоходного налога?

ИЛИ

Задачу №1 правильно решили 24840 человек, что составляет 72% от выпускников города. Сколько всего выпускников в этом городе?

Задание 2.
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются номера месяцев, по вертикали – температура в градусах Цельсия. Определите по диаграмме, сколько месяцев второго полугодия 1999 года средняя температура была ниже 14 °С.

Задание 3.
На клетчатой бумаге с размером клетки 1х1 изображена трапеция. Найдите её площадь.

Задание 4.
В среднем из 1000 садовых шлангов, поступивших в продажу, 16 подтекают. Найдите вероятность того, что один случайно выбранный для контроля шланг не подтекает.

ИЛИ

В сборнике билетов по химии всего 60 билетов, в 3 из них встречаются вопрос по теме белки. Найдите вероятность того что в случайно выбранном на экзамене билете школьнику достанется вопрос по теме белки.

Задание 5.
Найдите корень уравнения

Задание 6.
Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

ИЛИ

Острый угол В прямоугольного треугольника АВС равен 50°. Найдите угол между биссектрисой СD и медианой СМ, проведёнными из вершины прямого угла С. Ответ дайте в градусах.

Задание 7.
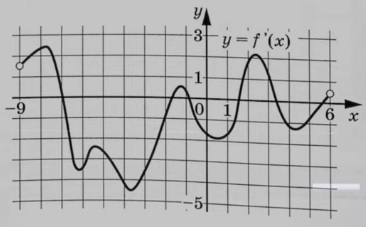
На рисунке изображен график y = f´(x) – производной функции f(x), определенной на интервале (−9; 6). Найдите количество точек минимума функции f(x), принадлежащих отрезку [−8; 5].

Задание 8.
Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 162. Найдите объём конуса.

ИЛИ

Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 188. Найдите объём конуса.

Задание 9.
Найдите значение выражения

ИЛИ

Найдите значение выражения

Задание 10.
Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

где с = 1500 м/с – скорость звука в воде, f₀– частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

ИЛИ

К источнику с ЭДС E = 95 В и внутренним сопротивлением r = 0,5 Ом хотят подключить нагрузку с сопротивлением R (в Ом). Напряжение (в В) на этой нагрузке вычисляется по формуле . При каком значении сопротивления нагрузки напряжение на ней будет равно 90 В? Ответ дайте в омах.

ИЛИ

В розетку электросети подключены приборы, общее сопротивление которых составляет R₁ = 90 Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление R₂ этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями R₁ Ом и R₂ Ом их общее сопротивление дается формулой R_общ = (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.

ИЛИ

При сближении источника и приёмника звуковых сигналов, движущихся в некоторой среде по прямой навстречу друг другу со скоростями u и v (в м/с) соответственно, частота звукового сигнала f (в Гц), регистрируемого приёмником, вычисляется по формуле: , где f₀ = 170 Гц – частота исходного сигнала, c – скорость распространения сигнала в среде (в м/с), а u = 2 м/с и v = 17 м/с – скорости приёмника и источника относительно среды. При какой скорости c (в м/с) распространения сигнала в среде частота сигнала в приёмнике f будет равна 180 Гц? Ответ дайте в м/с.

ИЛИ

В ходе распада радиоактивного изотопа его масса уменьшается по закону , где m₀ – начальная масса изотопа, t – время, прошедшее от начального момента, Т – период полураспада. В начальный момент времени масса изотопа 20 мг. Период его полураспада составляет 10 мин. Найдите, через сколько минут масса изотопа будет равна 5 мг.

Задание 11.
Первая труба пропускает на 16 литров воды в минуту меньше, чем вторая труба. Сколько литров воды в минуту пропускает первая труба, если резервуар объёмом 105 литров она заполняет на 4 минуты дольше, чем вторая труба?

ИЛИ

На изготовление 63 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 72 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?

Задание 12.
Найдите точку минимума функции y = 11x – ln(x + 4)¹¹ – 3

Задание 13.
а) Решите уравнение cos x(2cos² –1) = cos(x + π).
б) Найдите все корни этого уравнения, принадлежащие отрезку [; 2π].

ИЛИ

а) Решите уравнение 2cos³x + cosx + 2√2sin²x = 2√2
б) Найдите все корни этого уравнения, принадлежащие отрезку [–4π; ].

ИЛИ

а) Решите уравнение 2sin³x + 4√3cos²x + 3sinx = 4√3
б) Найдите все корни этого уравнения, принадлежащие отрезку [π; ].

Задание 15.
Решите неравенство (9^х – 3^х+1)² + 8·3^х+1 < 8·9^x + 20

ИЛИ

Решите неравенство

Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.

а) Докажите, что прямая BD пересекает отрезок CE в середине DT.
б) Найдите площадь треугольника ABT, если BD = 12, АЕ = 2√3.

Задание 17.
В июле 2025 года планируется взять кредит на 8 лет. Условия его возврата таковы:

– в январе 2026, 2027, 2028, 2029 годов долг возрастает на 15% по сравнению с концом предыдущего года;
– в январе 2030, 2031, 2032, 2033 годов долг возрастает на 11% по сравнению с концом предыдущего года;
– долг в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат за 8 лет составит 650 тысяч рублей?

Задание 18.
При каких значениях параметра а уравнение |x² – a²| + 8 = |x + a| + 8|x – a| имеет два положительных корня.

Задание 19.
Дано трехзначное число 𝐴, сумма цифр которого равна 𝑆.

а) Может ли выполняться равенство 𝐴 · 𝑆 = 1105?
б) Может ли выполняться равенство 𝐴 · 𝑆 = 1106?
в) Какое наименьшее значение может принимать выражение 𝐴 · 𝑆, если оно больше 1503?

Источник варианта: беседы vk.com и telegram.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 3.8 / 5. Количество оценок: 4

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

Реальные задания с Дальнего востока

Первая часть

Вторая часть

Полный сборник всех заданий из второй части реального ЕГЭ по математике 2021

Сборник заданий №2

Сборник заданий №3

Интересные задания:

Вам будет интересно:

Поделиться:

Новое и интересное на сайте: