Ответы к пособию для подготовки ЕГЭ-2021 по математике. Профильный уровень. Типовые экзаменационные варианты. Под редакцией И. В. Ященко. 36 вариантов.
| Вариант 1 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 725.2 | 11 | 14 |
| 2 | 9 | 12 | 7 |
| 3 | 12 | 13 | 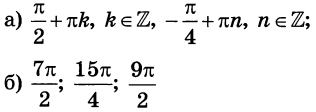 |
| 4 | 0.25 | 14 | 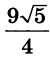 |
| 5 | 5.5 | 15 | 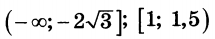 |
| 6 | 113 | 16 | 4.8 |
| 7 | 2 | 17 | 500 тыс. рублей |
| 8 | 60 | 18 | 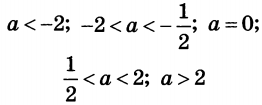 |
| 9 | 324 | 19 | а) да; б) нет; в) 232/21 |
| 10 | 6250 |
| Вариант 2 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 14.5 | 11 | 5 |
| 2 | 2 | 12 | 1.2 |
| 3 | 2 | 13 | 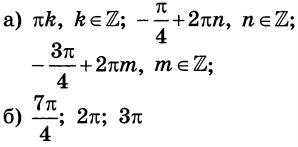 |
| 4 | 0.22 | 14 | 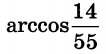 |
| 5 | 11 | 15 | 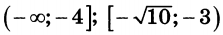 |
| 6 | 0.75 | 16 | 7.5 |
| 7 | 7 | 17 | 20 |
| 8 | 45 | 18 | 1 ⩽ a < 9 |
| 9 | -7.5 | 19 | а) да; б) нет; в) 10 |
| 10 | 1.3 |
| Вариант 3 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 27 | 11 | 75 |
| 2 | 2 | 12 | 18 |
| 3 | 2.5 | 13 | 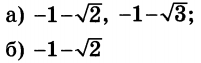 |
| 4 | 0.375 | 14 | 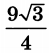 |
| 5 | -2 | 15 | 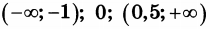 |
| 6 | 62 | 16 | 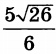 |
| 7 | 6 | 17 | 35700 рублей |
| 8 | 25 | 18 | 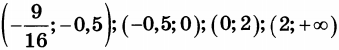 |
| 9 | 80 | 19 | а) 7; б) 15; в) 14 |
| 10 | 60 |
| Вариант 4 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 7 | 11 | 10 |
| 2 | 31 | 12 | -2 |
| 3 | 2 | 13 | 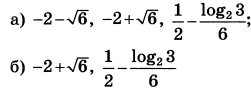 |
| 4 | 0.32 | 14 | 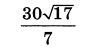 |
| 5 | 0 | 15 |  |
| 6 | 78 | 16 | 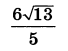 |
| 7 | 6 | 17 | 53 820 рублей |
| 8 | 20 | 18 | 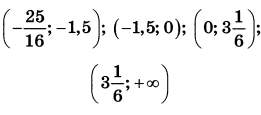 |
| 9 | 28 | 19 | а) 12; б) 15; в) 6 |
| 10 | 30 |
| Вариант 5 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 8 | 11 | 35 |
| 2 | 4 | 12 | 14 |
| 3 | 9 | 13 | 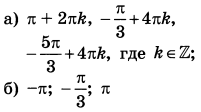 |
| 4 | 0.46 | 14 | 36 |
| 5 | 0.8 | 15 | 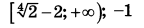 |
| 6 | 37 | 16 | 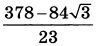 |
| 7 | -0.2 | 17 | 1 080 000 рублей |
| 8 | 135 | 18 | 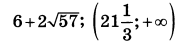 |
| 9 | 0.4 | 19 | а) нет; б) 21; в) 82 |
| 10 | 6 |
| Вариант 6 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 22.5 | 11 | 28 |
| 2 | 4 | 12 | 1 |
| 3 | 17 | 13 | 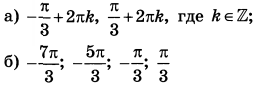 |
| 4 | 0.36 | 14 | 189 |
| 5 | -4 | 15 | (-0.5; 0.5); (0.5; 624.5) |
| 6 | 53 | 16 | 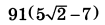 |
| 7 | -0.75 | 17 | 1 706 400 рублей |
| 8 | 72 | 18 | 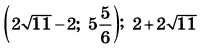 |
| 9 | -0.3 | 19 | а) нет; б) 36; в) 182 |
| 10 | 96 |
| Вариант 7 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 758 | 11 | 77 |
| 2 | 12 | 12 | -3 |
| 3 | 7.5 | 13 | 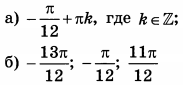 |
| 4 | 0.24 | 14 | 45° |
| 5 | 4 | 15 | 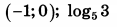 |
| 6 | 29 | 16 | 8 |
| 7 | 6 | 17 | 54 925 рублей |
| 8 | 315 | 18 | 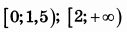 |
| 9 | 2.72 | 19 | а) да; б) нет; в) 16 |
| 10 | 7 |
| Вариант 8 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 7 | 11 | 6 |
| 2 | 4 | 12 | 38 |
| 3 | 13.5 | 13 | 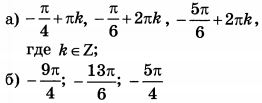 |
| 4 | 0.32 | 14 | 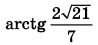 |
| 5 | -1 | 15 | 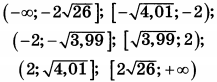 |
| 6 | 6 | 16 | 18 |
| 7 | -3 | 17 | 78 125 рублей |
| 8 | 176 | 18 | 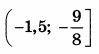 |
| 9 | -3 | 19 | а) да; б) нет; в) 12 |
| 10 | 28 |
| Вариант 9 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 4 | 11 | 6.4 |
| 2 | 200 | 12 | -21 |
| 3 | 4 | 13 | 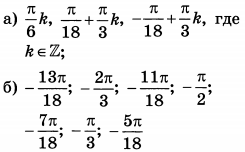 |
| 4 | 0.44 | 14 | 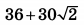 |
| 5 | 3 | 15 | [2; 5) |
| 6 | 60 | 16 | 1 |
| 7 | 4 | 17 | 126 694,4 рублей |
| 8 | 18 | 18 | 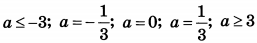 |
| 9 | 4 | 19 | а) да; б) нет; в) 2805 |
| 10 | 6.5 |
| Вариант 10 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 8 | 11 | 22 |
| 2 | 9 | 12 | -8 |
| 3 | 2.5 | 13 | 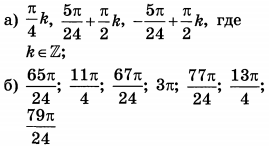 |
| 4 | 0.18 | 14 | 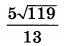 |
| 5 | 4 | 15 | (0; 5] |
| 6 | 64 | 16 | 50 |
| 7 | 14 | 17 | 1-й объект — 7 человек; 2-й объект — 23 человека; 43 150 рублей |
| 8 | 4 | 18 | 4 < a ⩽ 16 |
| 9 | 8 | 19 | а) да; б) нет; в) 2220 |
| 10 | 9.6 |
| Вариант 11 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 540 | 11 | 54 |
| 2 | 6 | 12 | 8 |
| 3 | 28 | 13 | 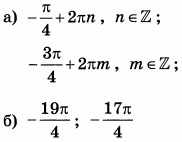 |
| 4 | 0.3 | 14 | 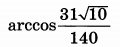 |
| 5 | 2 | 15 | [-2; 2) |
| 6 | 6.5 | 16 | 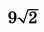 |
| 7 | 2 | 17 | 39 |
| 8 | 54 | 18 | -2 < a < -1; -1 < a < 0; 0 < a < 3; 3 < a < 8; a > 8 |
| 9 | -10 | 19 | а) нет; б) нет; в) 676 г |
| 10 | 25 |
| Вариант 12 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 2640 | 11 | 12 |
| 2 | 26 | 12 | -9 |
| 3 | 27 | 13 | 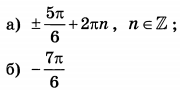 |
| 4 | 0.34 | 14 | 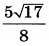 |
| 5 | -2 | 15 | (-2; 1); (1; 2) |
| 6 | 30 | 16 | 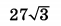 |
| 7 | 3 | 17 | 1,6 млн рублей |
| 8 | 27 | 18 | a < 0; 0 < a < 3; 3 < a < 4; 4 < a < 5; 5 < a < 6 |
| 9 | 91 | 19 | а) нет; б) нет; в) 240 г |
| 10 | 17 |
| Вариант 13 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 4320 | 11 | 48 |
| 2 | 0.3 | 12 | 26 |
| 3 | 13.5 | 13 | 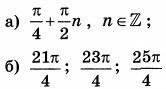 |
| 4 | 0.4 | 14 | 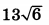 |
| 5 | -5 | 15 | 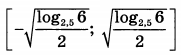 |
| 6 | 72.5 | 16 | 5 : 7 |
| 7 | 3 | 17 | 2.58 |
| 8 | 47 | 18 | 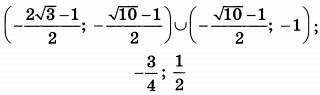 |
| 9 | 65 | 19 | а) нет; б) нет; в) 3 |
| 10 | 8 |
| Вариант 14 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 18000 | 11 | 64 |
| 2 | 2420 | 12 | -1 |
| 3 | 6 | 13 | 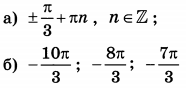 |
| 4 | 0.556 | 14 | 48.5 |
| 5 | 6 | 15 | 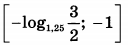 |
| 6 | 68 | 16 | 10 : 11 |
| 7 | 6 | 17 | 4.05 |
| 8 | 76 | 18 | 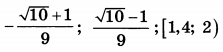 |
| 9 | 16 | 19 | а) да; б) нет; в) 5 |
| 10 | 633 |
| Вариант 15 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 84 | 11 | 20 |
| 2 | 485 | 12 | 9 |
| 3 | 26 | 13 | 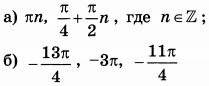 |
| 4 | 0.0595 | 14 | 4√3 |
| 5 | -2 | 15 | 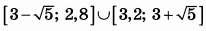 |
| 6 | 21 | 16 | 1:3:1 |
| 7 | 0.5 | 17 | 20 |
| 8 | 200 | 18 | [-3;22] |
| 9 | 7.5 | 19 | а) да; б) 180; в) 546 |
| 10 | 0.31 |
| Вариант 16 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 13 | 11 | 756 |
| 2 | 960 | 12 | 30 |
| 3 | 31.5 | 13 | 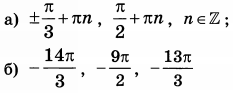 |
| 4 | 0.973 | 14 | 6√3 |
| 5 | -5 | 15 |  |
| 6 | 35 | 16 | 4:5:4 |
| 7 | 5.5 | 17 | 3 |
| 8 | 88 | 18 | 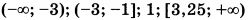 |
| 9 | 2.5 | 19 | а) да; б) 270; в) 17 |
| 10 | 1.728 |
| Вариант 17 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6 | 11 | 5 |
| 2 | 1.2 | 12 | -81 |
| 3 | 53 | 13 | 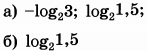 |
| 4 | 0.2 | 14 | 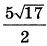 |
| 5 | 1.5 | 15 | 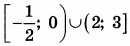 |
| 6 | 13 | 16 | 44 |
| 7 | 6 | 17 | 7 и 12 млн руб. |
| 8 | 10.5 | 18 | 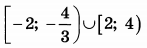 |
| 9 | 1 | 19 | а) да; б) да; в) 20 |
| 10 | 0.32 |
| Вариант 18 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 196 | 11 | 3 |
| 2 | 2.5 | 12 | 1.5 |
| 3 | 240 | 13 | 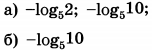 |
| 4 | 0.875 | 14 | 5√5 |
| 5 | 0.75 | 15 | 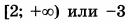 |
| 6 | 165 | 16 | 13.5 |
| 7 | 3 | 17 | 7 и 3 млн руб. |
| 8 | 216 | 18 | 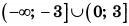 |
| 9 | -1 | 19 | а) да; б) да; в) 10 |
| 10 | 60 |
| Вариант 19 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 26 | 11 | 7 |
| 2 | -11 | 12 | -8 |
| 3 | 20 | 13 | 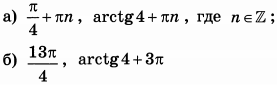 |
| 4 | 0.09 | 14 | 1 |
| 5 | -1 | 15 | [-1; ∞) |
| 6 | 2 | 16 | 12 |
| 7 | 11 | 17 | 5.35 |
| 8 | 96 | 18 | 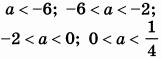 |
| 9 | 9 | 19 | а) нет; б) да; в) 9 x 16 и 12 x 12; 3 x 12 и 6 x 6; 1 x 16 и 4 x 4 |
| 10 | 0.006 |
| Вариант 20 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 34500 | 11 | 14 |
| 2 | 9 | 12 | -18 |
| 3 | 6 | 13 | 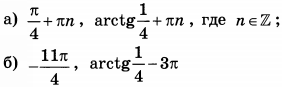 |
| 4 | 2.5 | 14 | √2 |
| 5 | -2 | 15 | [-3; 1) |
| 6 | 10 | 16 | 9 |
| 7 | 7 | 17 | 2 и 5 млн руб. |
| 8 | 111 | 18 | 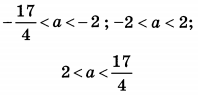 |
| 9 | 10 | 19 | а) нет; б) да; в) 4 x 9 и 6 x 6; 2 x 8 и 4 x 4; 1 x 9 и 3 x 3; |
| 10 | 120 |
| Вариант 21 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 6670 | 11 | 60 |
| 2 | 16 | 12 | 31 |
| 3 | 5 | 13 | 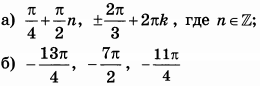 |
| 4 | 0.26 | 14 | 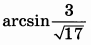 |
| 5 | -8.25 | 15 | 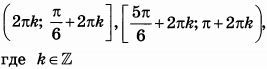 |
| 6 | 86 | 16 | 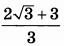 |
| 7 | -2 | 17 | 5000000 рублей |
| 8 | 24 | 18 | 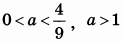 |
| 9 | 81 | 19 | а) да; б) нет; в) 7 |
| 10 | 62 |
| Вариант 22 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 11 | 11 | 78 |
| 2 | 15 | 12 | 13 |
| 3 | 8 | 13 | 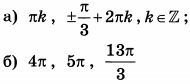 |
| 4 | 0.48 | 14 | 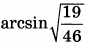 |
| 5 | -1.8 | 15 | 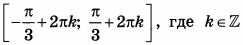 |
| 6 | 103 | 16 | 8√3 |
| 7 | 7 | 17 | 5000000 рублей |
| 8 | 39 | 18 | 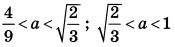 |
| 9 | -20 | 19 | а) да; б) нет; в) 6 |
| 10 | 58 |
| Вариант 23 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 26950 | 11 | 14 |
| 2 | 1678 | 12 | 6 |
| 3 | 11 | 13 | 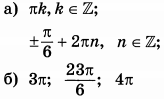 |
| 4 | 0.25 | 14 |  |
| 5 | 17 | 15 | (√2; +∞) |
| 6 | 73 | 16 | 30 |
| 7 | 7 | 17 | 3 |
| 8 | 72 | 18 | (-3; -1) |
| 9 | 27 | 19 | а) нет; б) да; в) 1347 |
| 10 | 24 |
| Вариант 24 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 24.2 | 11 | 65 |
| 2 | 4 | 12 | 40 |
| 3 | 16 | 13 | 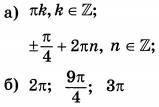 |
| 4 | 0.15 | 14 | 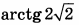 |
| 5 | 4 | 15 | 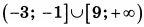 |
| 6 | 28 | 16 | 16 |
| 7 | 4 | 17 | 1200000 рублей |
| 8 | 13 | 18 | 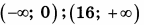 |
| 9 | 16 | 19 | а) нет; б) да; в) 989 |
| 10 | 44 |
| Вариант 25 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 19 | 11 | 13 |
| 2 | 4 | 12 | -5 |
| 3 | 4 | 13 | 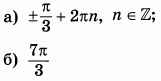 |
| 4 | 0.76 | 14 | 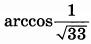 |
| 5 | 3 | 15 | 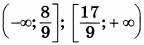 |
| 6 | 15 | 16 | 67.5 |
| 7 | 6 | 17 | 411 000 рублей |
| 8 | 4.8 | 18 | -2 < a < -1; 1 < a < 2 |
| 9 | 10 | 19 | а) да; б) нет; в) 26 |
| 10 | 3 |
| Вариант 26 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 188 | 11 | 13 |
| 2 | 9 | 12 | -3 |
| 3 | 3 | 13 | 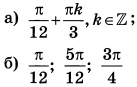 |
| 4 | 0.28 | 14 | 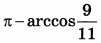 |
| 5 | 87 | 15 | 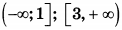 |
| 6 | 17 | 16 | 42+18√5 |
| 7 | 13 | 17 | 9282000 рублей |
| 8 | 61 | 18 | 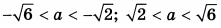 |
| 9 | 63 | 19 | а) нет; б) нет; в) 16 |
| 10 | 0.87 |
| Вариант 27 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 145 | 11 | 11 |
| 2 | 650 | 12 | -36 |
| 3 | 4 | 13 | 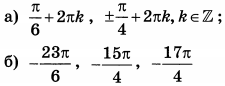 |
| 4 | 0.2 | 14 | 1.5√6 |
| 5 | 5 | 15 | (0;√2] |
| 6 | 21 | 16 | 5 |
| 7 | 4 | 17 | 1300000рублей |
| 8 | 72 | 18 | 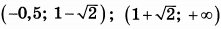 |
| 9 | 12 | 19 | а) нет; б) нет; в) 11.75 |
| 10 | 17 |
| Вариант 28 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 180 | 11 | 15 |
| 2 | 44.4 | 12 | 5 |
| 3 | 4 | 13 | 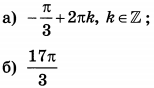 |
| 4 | 0.25 | 14 | 8√2π |
| 5 | 58 | 15 | [0; 2] |
| 6 | 56 | 16 | 7 |
| 7 | 1.6 | 17 | 2 |
| 8 | 32 | 18 | (-∞; -3) |
| 9 | 64 | 19 | 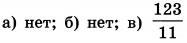 |
| 10 | 20 |
| Вариант 29 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 37.5 | 11 | 75 |
| 2 | 68.2 | 12 | 7 |
| 3 | 2.5 | 13 | 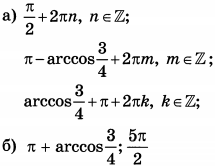 |
| 4 | 0.3125 | 14 | 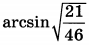 |
| 5 | 5.3 | 15 | 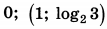 |
| 6 | 7 | 16 | 30 |
| 7 | 1 | 17 | 6 |
| 8 | 13 | 18 | 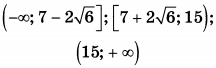 |
| 9 | 3 | 19 | 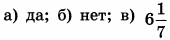 |
| 10 | 1200 |
| Вариант 30 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 61 | 11 | 27 |
| 2 | 420 | 12 | -1 |
| 3 | 5 | 13 | 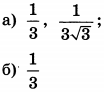 |
| 4 | 0.096 | 14 | 5 |
| 5 | 3 | 15 | 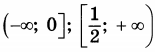 |
| 6 | 10 | 16 | 7 |
| 7 | 6 | 17 | 125000 рублей |
| 8 | 18 | 18 | b=-1, b ⩾ 0 |
| 9 | 3 | 19 | а) нет; б) да; в) 6(310-210) |
| 10 | 4974 |
| Вариант 31 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 611 | 11 | 18 |
| 2 | 1500 | 12 | -5 |
| 3 | 3.5 | 13 | 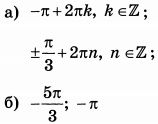 |
| 4 | 0.995 | 14 | 17:127 |
| 5 | 2 | 15 | (0; 1); 9; (27; +∞) |
| 6 | 38 | 16 | 71º |
| 7 | 5 | 17 | 20 |
| 8 | 84 | 18 | 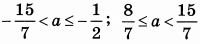 |
| 9 | -7 | 19 | а) да; б) нет; в) 6 |
| 10 | 42 |
| Вариант 32 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 186 | 11 | 20 |
| 2 | 56 | 12 | -6 |
| 3 | 20 | 13 | 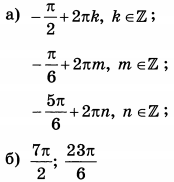 |
| 4 | 0.996 | 14 | 7:11 |
| 5 | 2 | 15 | (0;1) 2; (8; +∞) |
| 6 | 2 | 16 | 78º |
| 7 | 6 | 17 | 10 |
| 8 | 48 | 18 | 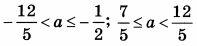 |
| 9 | -0.56 | 19 | а) да; б) нет; в) 5 |
| 10 | 100 |
| Вариант 33 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 31140 | 11 | 250 |
| 2 | 3 | 12 | 4 |
| 3 | 26 | 13 | 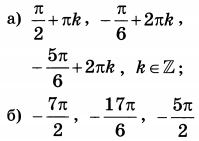 |
| 4 | 0.01 | 14 | 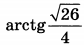 |
| 5 | 5 | 15 | 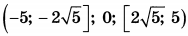 |
| 6 | 4.5 | 16 | 6√3 |
| 7 | 4.5 | 17 | 12.5 |
| 8 | 24 | 18 | [-1.5; -0.375); 0 |
| 9 | -63 | 19 | а) 42; б) положительных; в) 24 |
| 10 | 2642 |
| Вариант 34 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 28 | 11 | 48 |
| 2 | -21 | 12 | 32 |
| 3 | 5 | 13 | 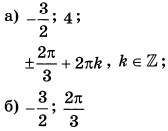 |
| 4 | 0.09 | 14 | 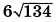 |
| 5 | 3 | 15 | 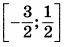 |
| 6 | 40 | 16 | 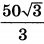 |
| 7 | 6 | 17 | 1029000 |
| 8 | 9 | 18 | 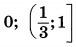 |
| 9 | -22 | 19 | а) 60; б) положительных; в) 36 |
| 10 | 2408 |
| Вариант 35 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 140 | 11 | 3 |
| 2 | 5 | 12 | 5 |
| 3 | 4 | 13 | 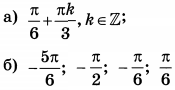 |
| 4 | 0.9 | 14 | √166 |
| 5 | 11 | 15 | 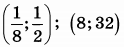 |
| 6 | 66 | 16 | 4 |
| 7 | -1 | 17 | 1171280 |
| 8 | 500 | 18 | 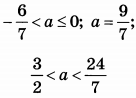 |
| 9 | -3 | 19 | а) да; б) нет; в) 1632 |
| 10 | 12 |
| Вариант 36 | |||
| Номер задания | Ответ | Номер задания | Ответ |
| 1 | 200 | 11 | 1 |
| 2 | 6 | 12 | 11 |
| 3 | 6 | 13 | 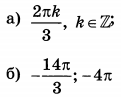 |
| 4 | 0.2 | 14 | 3√59 |
| 5 | 13 | 15 | 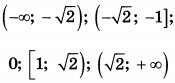 |
| 6 | 130 | 16 | 2 |
| 7 | 1 | 17 | 656250 |
| 8 | 1372 | 18 | 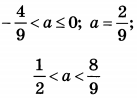 |
| 9 | -3 | 19 | а) да; б) нет; в) 1711 |
| 10 | 18 |
Задание 1
Показания счётчика электроэнергии 1 января составляли 53848 кВт*ч, а 1 февраля — 54107 кВт*ч. Сколько нужно заплатить за электроэнергию за январь, если 1 кВт*ч электроэнергии стоит 2 руб. 80 коп.? Ответ дайте в рублях.
Ответ: 725,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Разница в кВт*ч: $$54107-53848=259$$.
Стоимость: $$259cdot 2,8=725,2$$ рубля.
Задание 2
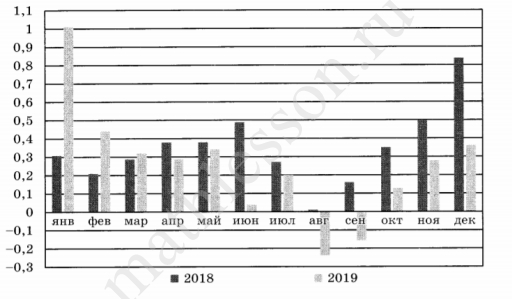
На диаграмме показан уровень инфляции в России в 2018 и 2019 годах. По горизонтали указаны месяцы, по вертикали — уровень инфляции (в процентах) за каждый месяц соответствующего года. Определите количество месяцев, когда инфляция в 2019 году была ниже, чем инфляция в соответствующем месяце 2018 года.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Это месяцы с апреля по декабрь: 9 месяцев.
Задание 3
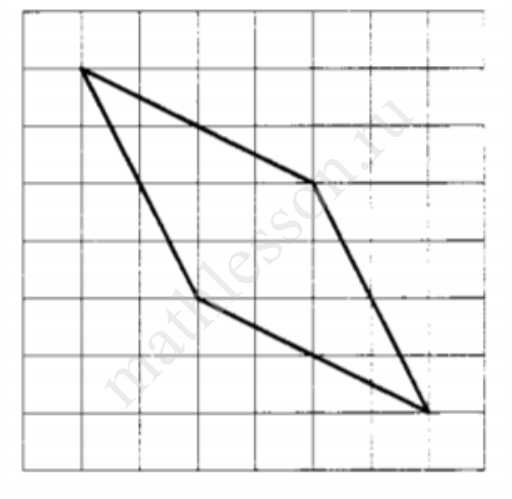
На клетчатой бумаге с размером клетки 1×1 изображён ромб. Найдите его площадь.
Ответ: 12
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем диагонали по теореме Пифагора $$d_1=sqrt{2^2+2^2}=2sqrt{2}; d_2=sqrt{6^2+6^2}=6sqrt{2}$$. $$S=frac{1}{2} d_1cdot d_2=frac{1}{2} cdot 2sqrt{2} cdot 6sqrt{2}=12$$
Задание 4
В гонке с раздельным стартом участвуют 25 лыжников, среди которых 7 спортсменов из Норвегии. Порядок старта определяется с помощью жребия случайным образом. Один из норвежских лыжников получил стартовый номер «5». Найдите вероятность, что он будет стартовать за своим соотечественником.
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вероятность, что 4-ый будет из Норвегии: $$Pleft(Aright)=frac{6}{24}$$ (т.к. после того, как один получит номер «5» лыжников из Норвегии осталось 6, а всего лыжников 24). Т.е. 0,25.
Задание 5
Найдите корень уравнения $$frac{1}{2x-3}=frac{1}{8}$$.
Ответ: 5,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{1}{2x+3}=frac{1}{8}leftrightarrow 2x-3=8leftrightarrow 2x=11leftrightarrow x=5,5$$
Задание 6
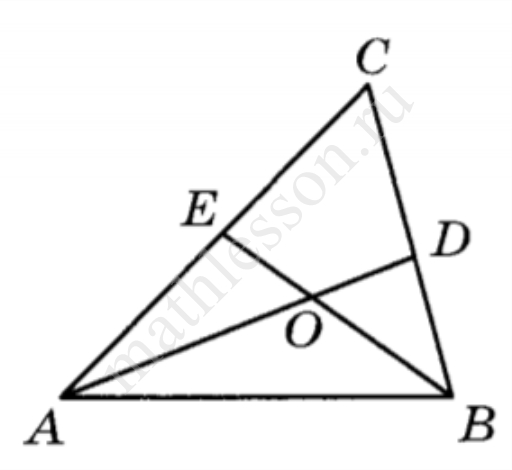
В треугольнике АВС угол С равен $$46{}^circ $$, AD и BE — биссектрисы, пересекающиеся в точке О. Найдите угол АОВ. Ответ дайте в градусах.
Ответ: 113
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$angle A+angle B=180{}^circ -angle C=134{}^circ to frac{angle A}{2}+frac{angle B}{2}=frac{134}{2}=67{}^circ to$$ $$to angle AOB=180-67=113{}^circ $$
Задание 7
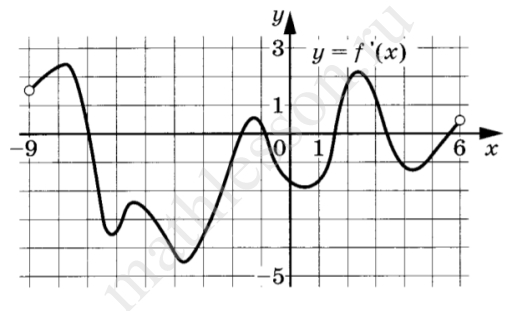
На рисунке изображён график $$у = f'(x)$$ — производной функции $$f(x)$$, определённой на интервале (-9; 6). Найдите количество точек минимума функции $$f(x)$$, принадлежащих отрезку $$[-8; 5].$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Точка минимума там, где $$f’left(xright)=0$$ при возрастании $$f’left(xright)$$, т.е. $$approx -1,8; approx 1,5; approx 5,6$$. Но на $$xin [-8;5]$$ их 2 точки.
Задание 8
В кубе $$ABCDA_1B_1C_1D_1$$ найдите угол между прямыми $$DC_1$$ и $$BD$$. Ответ дайте в градусах.
Ответ: 60
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим $$triangle BC_1D:BC_1=DC_1=BC_1=BD$$ (диагонали равных квадратов)$$to triangle BC_1D$$ — равносторонний $$to angle BDC_1=60{}^circ $$.
Задание 9
Найдите значение выражения $$4^{1-2{{log }_{0,5} 3 }}$$
Ответ: 324
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$4^{1-2{{log }_{0,5} 3 }}=frac{4^1}{4^{2{{log }_{0,5} 3 }}}=frac{4^1}{{(2^2)}^{{{log }_{2^{-1}} 3 }}}=frac{4}{2^{-2{{log }_2 9 }}}=frac{4}{2^{{{log }_2 frac{1}{81} }}}=frac{4}{frac{1}{81}}=324$$
Задание 10
Автомобиль разгоняется на прямолинейном участке шоссе с постоянным ускорением $$a$$ в км/ч$${}^{2}$$. Скорость $$v$$ (в км/ч) вычисляется по формуле $$v=sqrt{2la}$$, где $$l$$ — пройденный автомобилем путь (в км). Найдите ускорение, с которым должен двигаться автомобиль, чтобы, проехав 0,8 км, приобрести скорость 100 км/ч. Ответ дайте в км/ч$${}^{2}$$.
Ответ: 6250
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим известные в формулу: $$100=sqrt{2cdot 0,8cdot a}leftrightarrow 10000=1,6aleftrightarrow a=6250$$.
Задание 11
Катер в 8:40 вышел из пунтка А в пункт В, расположенный в 48 км от А. Пробыв 40 минут в пункте В, катер отправился назад и вернулся в пункт А в 16:20 того же дня. Найдите собственную скорость катера (в км/ч), если известно, что скорость течения реки 2 км/ч.
Ответ: 14
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Прошло времени: 7 часов 40 минут. При этом 40 минут стоял, т.е. в движении 5 часов. Пусть $$x$$ км/ч — собственная скорость катера.
Тогда: $$frac{48}{x+2}+frac{48}{x-2}=7leftrightarrow 48x-96+48x+96=7x^2-28leftrightarrow 7x^2-96x-28=0to $$ $$to frac{D}{4}=2304+196=2500to left[ begin{array}{c}
x_1=frac{48+50}{7} \
x_2<0 end{array}
right.leftrightarrow x=14$$
Задание 12
Найдите наименьшее значение функции $$y=4{sin x }-6x+7$$ на отрезке $$left[-frac{3pi }{2};0right]$$
Ответ: 7
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную: $$y’=4{cos x }-6$$. Т.к. $$left|{cos x }right|le 1$$, то $$y'<0$$ при любом $$x$$, тогда функция убывает на всем $$Dleft(xright)to y_{min}=y(0)$$. $$yleft(0right)=4{sin 0 }-6cdot 0+7=7$$
Задание 13
а) Решите уравнение $$2{{sin }^{{rm 2}} (frac{pi }{2}-x) }+{sin 2x }=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[3pi ;frac{9pi }{2}]$$
Ответ: а)$$frac{pi }{2}+pi n,nin Z$$; $$-frac{pi }{4}+pi n,nin Z$$ б) $$1)3pi +frac{pi }{2}=frac{7pi }{2};2)4pi +frac{pi }{2}=frac{9pi }{2} ;3)4pi -frac{pi }{4}=frac{15pi }{4} $$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
а) $$2{{sin }^{{rm 2}} (frac{pi }{2}-x) }+{sin 2x }=0leftrightarrow 2{{cos }^{{rm 2}} x }+2{sin x }{cos x }=0leftrightarrow$$ $$leftrightarrow 2{cos x }left({cos x }+{sin x }right)=0leftrightarrow left[ begin{array}{c} {cos x=0 } \ {cos x }+{sin x }=0 end{array} right.leftrightarrow left[ begin{array}{c} {cos x=0 } \ 1+{tan x }=0 end{array} right.leftrightarrow$$ $$leftrightarrow left[ begin{array}{c} x=frac{pi }{2}+pi n,nin Z \ x=-frac{pi }{4}+pi n,nin Z end{array} right.$$
б) С помощью единичной окружности отберем корни на $$left[3pi ;frac{9pi }{2}right]:1)3pi +frac{pi }{2}=frac{7pi }{2};2)4pi +frac{pi }{2}=frac{9pi }{2} ;3)4pi -frac{pi }{4}=frac{15pi }{4} $$
Задание 14
В правильной шестиугольной пирамиде SABCDEF сторона основания АВ равна 2, а боковое ребро SA равно 8. Точка М — середина ребра АВ. Плоскость $$alpha $$ перпендикулярна плоскости АВС и содержит точки М и D. Прямая SC пересекает плоскость $$alpha $$ в точке К.
а) Докажите, что KM = KD.
б) Найдите объём пирамиды CDKM.
Ответ: $$frac{3sqrt{5}}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) 1) Пусть $$FCcap DM=L$$. Т.к. $$alpha bot ABC$$, то ч/з L пойдет $$LKbot ABC$$. Пусть $$CBcap DM=H$$, $$KHcap SB=Rto left(DKRMright)$$ — искомая плоскость.
2) FC равноудалена от ED и AB $$to $$ т.к. $$EDparallel AB$$, то $$angle XDL=angle LZB$$ (накрест лежащие) $$to triangle XDL=triangle LMZto DL=LMto KL$$ — высота и медиана $$to $$ $$triangle DKM$$ — равнобедренный $$to KM=KD$$.
Б) 1) $$V_{CDKM}=frac{1}{3}S_{CDKM}cdot KL$$. $$S_{ABCDEF}=6S_{AOB}=6cdot frac{1}{2}cdot 2cdot 2cdot frac{sqrt{3}}{2}=6sqrt{3}to S_{MNDCB}=3sqrt{3}.$$ $$S_{MND}=frac{1}{2}MNcdot ND=frac{1}{2}cdot 2cdot 2cdot frac{sqrt{3}}{2}=6sqrt{3}.$$ $$S_{MBC}=frac{1}{2}MBcdot BC{sin angle B }=frac{1}{2}cdot 1cdot 2cdot frac{sqrt{3}}{2}=frac{sqrt{3}}{2}to S_{CDM}=3sqrt{3}-sqrt{3}-frac{sqrt{3}}{2}=$$ $$=frac{3sqrt{3}}{2}.$$
2) $$NX=OLto LC=2-frac{1}{2}=frac{3}{2}to frac{KL}{SO}=frac{LC}{OC}=frac{frac{3}{2}}{2}=frac{3}{4}$$ (т.к. $$triangle SOCsim triangle KLC$$ по острому углу) — $$SO=sqrt{SB^2-OB^2}=sqrt{8^2-2^2}=sqrt{60}=2sqrt{15}to KL=frac{3sqrt{15}}{2}to$$ $$to V_{CDKM}=frac{1}{3}cdot frac{3sqrt{3}}{2}cdot frac{3sqrt{15}}{2}=frac{3sqrt{5}}{4}$$.
Задание 15
Решите неравенство $$x^2{{log }_{64} (3-2x) }ge {{log }_2 left(4x^2-12x+9right) }$$
Ответ: $$xin left(-infty ;-sqrt{12}right];[1;1,5)$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$x^2{{log }_{64} (3-2x) }ge {{log }_2 left(4x^2-12x+9right) }leftrightarrow frac{x^2}{6}{{log }_2 left(3-2xright) }-{{log }_{64} {left(2x-3right)}^2 }ge 0leftrightarrow $$ $$leftrightarrow $$ т.к. $$3-2x>0$$, то: $$frac{x^2}{6}{{log }_2 left(3-2xright) }-2{{log }_2 left(3-2xright) }ge 0leftrightarrow (x^2-12)({{log }_2 (3-2x) })ge 0leftrightarrow $$ $$leftrightarrow left{ begin{array}{c}
3-2x>0 \
(x^2-12)(3-2x-1)ge 0 end{array}
right.leftrightarrow left{ begin{array}{c}
x<1,5 \
(x-sqrt{12})(x+sqrt{12})(x-1)le 0 end{array}
right.$$.
$$xin left(-infty ;-sqrt{12}right];[1;1,5)$$
Задание 16
Две окружности касаются внутренним образом в точке С. Вершины А и В равнобедренного прямоугольного треугольника АВС с прямым углом С лежат на меньшей и большей окружностях соответственно. Прямая АС вторично пересекает большую окружность в точке Е, а прямая ВС вторично пересекает меньшую окружность в точке D.
а) Докажите, что прямые AD и BE параллельны.
б) Найдите АС, если радиусы окружностей равны 3 и 4.
Ответ: 4,8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
а) По т.о. касательной и хорде $$angle LCD=angle CAD$$ (для меньшей) и $$angle LCD=angle CED$$ (для большей) $$to angle CAD=angle CED$$, а они накрест лежащие $$to ADparallel BE$$.
б) $$angle CDA$$ и $$angle EBE$$ — прямоугольные, $$angle CAD=angle CEDto triangle CDAsim triangle CBEto frac{CD}{CB}=frac{CA}{CE}=frac{AD}{BE}$$. При этом AD и BE — диаметры ($$angle C$$ — вписан и прямой) $$to AD=6;BE=8to frac{CD}{CB}=frac{3}{4}$$. Пусть $$CA=CB=xto CD=frac{3}{4}x$$. Из $$triangle ADC:AD^2=CD^2+CA^2to 36=x^2+frac{9x^2}{16}to x^2=frac{36cdot 16}{25}to x=4,8$$.
Задание 17
В июле 2022 года планируется взять кредит на пять лет в размере 1050 тыс. рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле 2023, 2024 и 2025 годов долг остаётся равным 1050 тыс. рублей;
— выплаты в 2026 и 2027 годах равны;
— к июлю 2027 года долг будет выплачен полностью.
На сколько рублей последняя выплата будет больше первой?
Ответ: 500 т.р.
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Раз первые 3 года долг не менялся, то платили только проценты, т.е. $$1050cdot 0,1=105$$ т.р. Пусть крайние 2 выплаты по $$x$$ т.р. Тогда: $$left(1050cdot 1,1-xright)cdot 1,1-x=0leftrightarrow 1270,5-2,1x=0to x=605$$ т.р. Тогда разница: $$605-105=500$$ т.р.
Задание 18
Найдите все значения $$a$$, при каждом из которых система уравнений $$left{ begin{array}{c} sqrt{16-y^2}=sqrt{16-a^2x^2} \ x^2+y^2=8x+4y end{array} right.$$ имеет ровно два различных решения.
Ответ: $$ain left(-infty ;-2right);(-2;+infty )$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$left{ begin{array}{c} sqrt{16-y^2}=sqrt{16-a^2x^2} \ x^2+y^2=8x+4y end{array} right.leftrightarrow left{ begin{array}{c} 16-y^2ge 0 \ 16-y^2=16-{left(axright)}^2 \ x^2+y^2-8x-4y=0 end{array} right.leftrightarrow$$ $$leftrightarrow left{ begin{array}{c} yin [-4;4] \ y=ax \ y=-ax \ x^2+y^2-8x-4y=0 end{array} right.$$
При $$y=ax:x^2+{a^2x}^2-8x-4ax=0leftrightarrow xleft(x+a^2x-8-4aright)=0leftrightarrow left[ begin{array}{c} x=0 \ x=frac{4a+8}{a^2+1} end{array} right.leftrightarrow $$ $$leftrightarrow left[ begin{array}{c} y=0 \ y=frac{4a^2+8a}{a^2+1} end{array} right.$$.
При $$y=-ax: x^2+{a^2x}^2-8x+4ax=0leftrightarrow left[ begin{array}{c} x=0 \ x=frac{-4a+8}{a^2+1} end{array} right.leftrightarrow left[ begin{array}{c} y=0 \ y=frac{4a^2-8a}{a^2+1} end{array} right.$$.
Получим: $$left(0:0right):left(frac{4a+8}{a^2+1};frac{4a^2+8a}{a^2+1}right);(frac{8-4a}{a^2+1};frac{4a^2-8a}{a^2+1})$$.
При этом $$left(0:0right)$$ всегда, т.к. $$yin [-4;4]$$ выполняется.
Вторая пара существует при: $$-4le frac{4a^2+8a}{a^2+1}le 4to left{ begin{array}{c} 4a^2+8age -4a^2-4 \ 4a^2+8ale 4a^2+4 end{array} right.leftrightarrow left{ begin{array}{c} 8a^2+8a+4ge 0 \ ale frac{1}{2} end{array} right.leftrightarrow ale frac{1}{2}$$.
Третья пара существует при: $$-4le frac{4a^2-8a}{a^2+1}le 4to left{ begin{array}{c} 4a^2-8age -4a^2-4 \ 4a^2-8age 4a^2+4 end{array} right.$$$$leftrightarrow left{ begin{array}{c} 8a^2-8a+4ge 0 \ age -frac{1}{2} end{array} right.leftrightarrow age -frac{1}{2}$$.
При этом первая и вторая совпадают при $$frac{4a+8}{a^2+1}=0to a=-2.$$
Первая и третья: $$frac{8-4a}{a^2+1}=0to a=2$$.
Вторая и третья: $$frac{4a+8}{a^2+1}=frac{8-4a}{a^2+1}to a=0$$. т.е. должно быть только 2: $$ain left(-infty ;-2right);(-2;+infty )$$.
Задание 19
На доске было написано несколько различных натуральных чисел. Эти числа разбили на три группы, в каждой из которых оказалось хотя бы одно число. К каждому числу из первой группы приписали справа цифру 3, к каждому числу из второй группы — цифру 7, а числа из третьей группы оставили без изменений.
а) Могла ли сумма всех этих чисел увеличиться в 8 раз?
б) Могла ли сумма всех этих чисел увеличиться в 17 раз?
в) В какое наибольшее число раз могла увеличиться сумма всех этих чисел?
Ответ: а)да б)нет в)$$frac{232}{21}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
А) Пусть было три числа $$A,B,Cin N,Ane Bne Cle 9$$. Получим $$Ato 10A+3;Bto 10B+7$$. Следовательно, $$frac{10A+3+10B+7+C}{A+B+C}=8to 2A+2B+10-7C=0$$. Пусть $$A=2,B=8,C=4to $$ Да, могла.
Б) Пусть в 1-ой группе $$x$$ чисел, их сумма $$A$$, во 2-ой $$y$$ чисел, сумма $$B$$, в 3-ей $$Z$$ чисел, сумма $$C$$. Тогда $$frac{10A+3x+10B+7y+C}{A+B+C}=17to 3x+7y=7A+7B+16C.$$ При этом $$Age x,Bge y$$, тогда $$3x+7y<7A+7Bto $$ равенство невозможно.
В) Пусть в 1,2 и 3 группах x, y и 7 чисел соответственно, их сумма $$A,B,C$$. Тогда $$frac{10A+3x+10B+7y+C}{A+B+C}=Qto frac{10left(A+B+Cright)+3x+7y-9C}{A+B+C}=Qto$$ $$to Q=10+frac{3x+7y-9c}{A+B+C}$$ т.к. при переносе чисел из первой или третьей группы во вторую $$A+B+C$$ не меняется, но $$3x+7y-9C$$ увеличивается, то и Q увеличится. Следовательно, $$Qto max$$, при $$xto min$$. А $$x_{min}=1$$. $$Cto min$$, т.е. $$Zto min, Z=1(C=1)$$. При этом общее число чисел тогда $$y+2$$. Получим: $$Q=10+frac{3x+7y-9c}{A+B+C}$$. Т.к. числа разные натуральные, то $$A+B+Cge 2+1+frac{2cdot 3+1left(y-1right)}{2}cdot y$$ (т.к. минимальная сумма будет у подряд идущих натуральных чисел с единицы). Т.е. $$A+B+Cge 3+frac{left(5+yright)y}{2}$$ или $$A+B+Cge frac{y^2+5y+6}{2}=frac{left(y+2right)left(y+3right)}{2}$$. Тогда: $$Q=10+frac{left(7y-6right)cdot 2}{(y+2)(y+3)}$$. Найдем максимальное значение $$frac{14y-12}{(y+2)(y+3)}=f(y)$$ при $$yin N$$. $$f’left(yright)=frac{14left(y^2+5y+6right)-left(14y-12right)left(2y+5right)}{{left((y+2)(y+3)right)}^2}=0to $$ $$to 14y^2+70y+84-28y^2-70y+24y+60=0$$. $$-14y^2+24y+144=0to -7y^2+12y+72=0to frac{D}{4}=540in ({23}^2;{24}^2)$$. $$left[ begin{array}{c} y_1=frac{-6+sqrt{540}}{-7} \ y_2=frac{-6-sqrt{540}}{-7}-max end{array} right..$$
При этом $$y_2=frac{6+sqrt{540}}{7}approx frac{6+23}{7}approx frac{29}{7}to y=4$$ или $$y=5$$. При $$y=4:fleft(4right)=frac{14cdot 4-12}{6cdot 7}=frac{44}{6cdot 7}=frac{22}{21}$$.
При $$y=5:fleft(5right)=frac{14cdot 5-12}{7cdot 8}=frac{58}{7cdot 8}=frac{29}{28}$$. $$fleft(4right)>fleft(5right)to Q_{max}=10+frac{22}{21}=frac{232}{21}.$$
Ответы к 36 вариантам профильного ЕГЭ по математике. Сборник ЕГЭ-2023 «Типовые экзаменационные варианты».
Вариант 1
1) 5,5
2) 2048
3) 0,06
4) 0,89
5) -0,2
6) 0,5
7) 5

9) 2
10) -4
11) -2910
Вариант 2
1) 7,5
2) 4
3) 0,12
4) 0,91
5) -0,9
6) 0,2
7) 1

9) 16
10) -8
11) 12,25
Вариант 3
1) 2,5
2) 30
3) 0,37
4) 0,375
5) -2,5
6) 4
7) 2

9) 14
10) 32
11) 204
Вариант 4
1) 1,5
2) 12
3) 0,24
4) 0,125.
5) 0,375
6) 125
7) 8

9) 18
10) -56
11) -10,9
Вариант 5
1) 99,5
2) 12
3) 0,004 /или/ -0,004
4) 0,9409
5) -0,5
6) 2
7) -19

9) 17
10) 16
11) -52
Вариант 6
1) 55
2) 18
3) 0,006 /или/ -0,006
4) 0,8464
5) -5,5
6) 3
7) -4

9) 24
10) -1
11) -6
Вариант 7
1) 0,2
2) 10
3) 0,2
4) 0,56
5) -0,4
6) -1
7) 9

9) 55
10) 6
11) 0,5
Вариант 8
1) 0,4
2) 5
3) 0,125
4) 0,46
5) -7
6) -1
7) 7

9) 11
10) 0,25
11) 17
Вариант 9
1) 3
2) 15 625
3) 0,01
4) 0,28
5) -12
6) 144
7) -1

9) 20
10) -3
11) 9
Вариант 10
1) 0,6
2) 150
3) 0,28
4) 0,17
5) -2,6
6) 625
7) -18

9) 9
10) 253
11) -23,25
Вариант 11
1) -0,7
2) 72
3) 0,25
4) 0,043
5) -0,2
6) -5
7) -1

9) 17,5
10) 78
11) 6,75
Вариант 12
1) 0,75
2) 24
3) 0,55
4) 0,02
5) -1,5
6) -4
7) 4

9) 13,5
10) -23
11) 6,25
Вариант 13
1) 8
2) 48
3) 0,4
4) 0,6
5) -9
6) 0,5
7) 4

9) 9
10) -0,5
11) 77
Вариант 14
1) 14
2) 40,5
3) 0,28
4) 0,78
5) -2
6) 0,04
7) 39

9) 24
10) 0,4
11) 37
Вариант 15
1) 11,55
2) 432
3) 0,014
4) 0,06
5) -9
6) 0,25
7) 2

9) 3
10) 2,5
11) 208
Вариант 16
1) 12
2) 192
3) 0,29
4) 0,02
5) -8
6) 0,125
7) 4

9) 1
10) -15
11) 5
Вариант 17
1) 10
2) 80
3) 0,08
4) 0,2
5) -2,5
6) 216
7) -2

9) 18
10) 16
11) -24
Вариант 18
1) 35
2) 10
3) 0,2
4) 0,24
5) -0,2
6) 3,5
7) 28

9) 21
10) 2,25
11) -15
Вариант 19
1) 2,5
2) 7,28
3) 0,25
4) 0,22
5) -1,5
6) 1
7) 0,2

9) 135
10) 2
11) -34
Вариант 20
1) 6
2) 7,68
3) 0,75
4) 0,27
5) -4,5
6) 10
7) -0,25

9) 52
10) 27
11) 0
Вариант 21
1) 113
2) 60
3) 0,2
4) 0,973
5) 5,5
6) 324
7) 2

9) 14
10) 15
11) 7
Вариант 22
1) 0,75
2) 45
3) 0,3
4) 0,9744
5) 11
6) -7,5
7) 7

9) 5
10) 3,4
11) 1,2
Вариант 23
1) 62
2) 25
3) 0,25
4) 0,3
5) -2
6) 80
7) 6

9) 75
10) 28
11) 18
Вариант 24
1) 78
2) 20
3) 0,2
4) 0,82
5) 0
6) 28
7) 6

9) 10
10) -28
11) -2
Вариант 25
1) 37
2) 135
3) 0,18
4) 3
5) 0,8
6) 0,4
7) -0,2

9) 1 35
10) -0,4
11) 14
Вариант 26
1) 53
2) 72
3) 0,38
4) 5
5) -4
6) -0,3
7) -0,75

9) 28
10) -13
11) 1
Вариант 27
1) 29
2) 315
3) 0,14
4) 0,03
5) 4
6) 2,72
7) 6

9) 77
10) 76
11) -3
Вариант 28
1) 6
2) 176
3) 0,375
4) 0,012
5) -1
6) -3
7) -3

9) 6
10) -5
11) 38
Вариант 29
1) 60
2) 18
3) 0,24
4) 0,2
5) 3
6) 4
7) 4

9) 6,4
10) 67
11) -21
Вариант 30
1) 64
2) 4
3) 0,28
4) 0,6
5) 4
6) 8
7) 14

9) 22
10) 3
11) -8
Вариант 31
1) 6,5
2) 54
3) 0,98
4) 0,2
5) 2
6) -10
7) 2

9) 54
10) -7
11) 8
Вариант 32
1) 30
2) 27
3) 0,024
4) 0,15
5) -2
6) 91
7) 3

9) 12
10) 13
11) -9
Вариант 33
1) 72,5
2) 47
3) 0,28
4) 0,097
5) -5
6) 65
7) 3

9) 48
10) -2,5
11) 26
Вариант 34
1) 68
2) 76
3) 0,16
4) 0,068
5) 6
6) 16
7) 6

9) 64
10) -0,25
11) -1
Вариант 35
1) 21
2) 200
3) 0,56
4) 0,9
5) -2
6) 7,5
7) 0,5

9) 20
10) 0,75
11) 9
Вариант 36
1) 35
2) 88
3) 0,12
4) 12
5) -5
6) 2,5
7) 5,5

9) 756
10) -0,5
11) 30

Читать онлайн и скачать сборник в формате PDF: Скачать
* Еще больше пособий ЕГЭ и ОГЭ
* Учебные материалы
Поделиться:
- 31.10.2020
Сборник ответов для пособия ЕГЭ 2021, 36 типовых вариантов по математике профильного уровня, под редакцией Ященко И.В.
- Тренировочные варианты ЕГЭ 2021 по математике
- Реальные варианты ЕГЭ 2020 по математике
- Работы СтатГрад 2020-2021
Выбирайте вариант и смотрите ответы по PDF файлу. Вы можете скачать их совершенно бесплатно.
Видеоразбор варианта №7 из сборника Ященко
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Видеоразбор варианта №5, Ященко
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
- Математика ЕГЭ
- Математика ОГЭ
- Биология ОГЭ
- Биология ЕГЭ
- Физика ОГЭ
- Физика ЕГЭ
- Химия ЕГЭ
- Химия ОГЭ
- Русский язык ОГЭ
- Русский язык ЕГЭ
- Английский язык ОГЭ
- Английский язык ЕГЭ
- Литература ЕГЭ
- Литература ОГЭ
- История ЕГЭ
- История ОГЭ
- Информатика ЕГЭ
- Информатика ОГЭ
- География ЕГЭ
- География ОГЭ
Вы здесь: ✔️ Главная сайта ГДЗ 

👀 Просмотров: 2243
Инфо
Автор: И.В. Ященко
Предмет (категория): 36 экзаменационных вариантов
Класс:
Читать онлайн: Да
Скачать бесплатно: Да
Формат книги: jpg
Размер книги/ГДЗ: 47.1 Мб
Год публикации (выпуска): 2021
Читать онлайн или скачать 36 тренировочных вариантов для подготовки к Единому государственному экзамену по математике под редакцией Ященко 2021 года:
Самые популярные статьи:
- ЕГЭ 2015. Ященко Математика. 36 вариантов.
- Лысенко, Калабухова ЕГЭ-2019 профильный уровень 40 тренировочных вариантов математика
- Ященко ЕГЭ-2019 36 типовых экзаменационных вариантов профильный уровень математика
- Подготовка к ЕГЭ-2016. Математика. 40 тренировочных вариантов по демоверсии на 2016 год. Профильный уровень. Лысенко Ф.Ф., Кулабухов С.Ю.
- Ященко ЕГЭ-2019 50 вариантов заданий профильный уровень математика
Новые материалы для вашего класса:
- Семенов ЕГЭ-2022 готовимся к итоговой аттестации базовый уровень математика
- Математика ЕГЭ-2021 диагностические работы профильный уровень
- Семенов, Высоцкий ЕГЭ-2021 базовый уровень готовимся к итоговой аттестации математика
- Ященко ЕГЭ-2021 профильный уровень 10 вариантов типовые варианты математика
< НазадВперёд >
Вам это пригодится
Барашкова английский язык на каникулах н…
Узорова английский язык в схемах и табл…
Державина английский язык для начальной …
Барашкова английский язык на каникулах н…
Карачаева 100 тестов по лексике и грамма…
Мордкович учебник алгебра углубленный ур…
| 3631 | В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75°. Точка P лежит вне прямоугольника, а угол APB равен 150°. а) Докажите, что углы BAP и POB равны. б) Прямая PO пересекает сторону CD в точке F. Найдите CF, если AP=6sqrt3 и BP=4 |
В прямоугольнике ABCD диагонали пересекаются в точке O, а угол BDC равен 75° ! 36 вариантов ФИПИ Ященко 2023 Вариант 25 Задание 16 # Задача-аналог 2559 | |
| 3577 | В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23. Длины боковых рёбер пирамиды SA = 2sqrt15, SB=sqrt85, SD=sqrt83. а) Докажите, что SA — высота пирамиды SABCD. б) Найдите угол между прямыми SC и BD |
В основании четырёхугольной пирамиды SABCD лежит прямоугольник ABCD со сторонами AB=5 и BC=sqrt23 ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 13 Вариант МА2210209 #Задача-аналог 2525 | |
| 3244 | В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt3. На ребрах C1D1 и DD1 отмечены соответственно точки K и M так, что D1K=KC1, а DM:MD1=1:3. а) Докажите, что прямые MK и BK перпендикулярны. б) Найдите угол между плоскостями BMK и ABB1 |
В правильной четырёхугольной призме ABCDA1B1C1D1 сторона основания AB равна 3, а боковое ребро AA1 равно sqrt 3 ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 18 Задание 13 # Задача-аналог 2574 | |
| 2881 | Точка O — центр вписанной в треугольник ABC окружности. Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P. а) Докажите, что /_POA=/_PAO. б) Найдите площадь треугольника APO, если радиус описанной около треугольника ABC окружности равен 6, /_BAC=75^@, /_ABC=60^@ |
Прямая BO вторично пересекает описанную около этого треугольника окружность в точке P ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 16 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 16 # Задача-аналог 2623 | |
| 2877 | В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7. На рёбрах AB и SC отмечены точки K и M соответственно, причем AK:KB=SM:MC=1:5. Плоскость alpha содержит прямую KM и параллельна прямой BC. a) Докажите, что плоскость alpha параллельна прямой SA. б) Найдите угол между плоскостями alpha и SBC |
В правильной треугольной пирамиде SABC сторона основания AB равна 6, а боковое ребро SA равно 7 ! 36 вариантов ФИПИ Ященко 2022 Вариант 21 Задание 13 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 11 Задание 14 # Задача-аналог 1669 | |
| 2874 | Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1). а) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 9 нулями? б) Существует ли такое натуральное число n, что десятичная запись числа n! оканчивается ровно 23 нулями? в) Сколько существует натуральных чисел n, меньших 100, для каждого из которых десятичная запись числа n∙ (100 — n)! оканчивается ровно 23 нулями |
Для каждого натурального числа n обозначим через n! произведение первых n натуральных чисел (1! = 1) ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 18 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 19 | |
| 2873 | Найдите, при каких неотрицательных значениях a функция f(x)=3ax^4-8x^3 +3x^2-7 на отрезке [-1; 1] имеет ровно одну точку минимума |
Найдите, при каких неотрицательных значениях a функция f(x) на отрезке [-1; 1] имеет ровно одну точку минимума ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 17 Задание 17 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 18 | |
| 2872 | Александр хочет купить пакет акций быстрорастущей компании. В начале года у Александра не было денег на покупку акций, а пакет стоил 100 000 рублей. В середине каждого месяца Александр откладывает на покупку пакета акций одну и ту же сумму, а в конце месяца пакет дорожает, но не более чем на 30 %. Какую наименьшую сумму нужно откладывать Александру каждый месяц, чтобы через некоторое время купить желаемый пакет акций? |
Александр хочет купить пакет акций быстрорастущей компании ! 36 вариантов ЕГЭ 2022 ФИПИ школе Ященко Вариант 15 Задание 15 # 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 7 Задание 17 | |
| 2853 | а) Решите уравнение 2sin^2(x)+cos(x)-1=0 б) Найдите все корни этого уравнения, принадлежащие отрезку [-5pi; -4pi]. |
а) Решите уравнение 2sin2 x + cosx -1 = 0 ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 36 Задание 13 | |
| 2852 | За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки. Найдите вероятность того, что девочки не окажутся на соседних местах |
За круглый стол на 21 стул в случайном порядке рассаживаются 19 мальчиков и 2 девочки ! 36 вариантов ЕГЭ 2021 ФИПИ школе Ященко Вариант 35 Задание 4 | |

Показана страница 1 из 21