Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Задание 1
Магазин закупает мужские шорты по цене 600 рублей за штуку, а продает по 870 рублей. Сколько процентов составляет торговая наценка в этом магазине?
Ответ: 45
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Разница в цене: $$870-600=270$$ рублей, что составляет $$frac{270}{600}cdot 100=45%$$
Задание 2
На рисунке жирными точками показаны продажи ювелирных изделий сетью магазинов в течение 7 лет (для наглядности точки соединены линией). По горизонтали указываются года, по вертикали — число проданных ювелирных изделий за год, в тыс. штук. Определите по рисунку суммарное число проданных ювелирных изделий (в тыс.штук) в сети за 2001, 2003 и 2007 годы.
Ответ: 28
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В 2001 — 4 тысячи, в 2003 — 8 тысяч, в 2007 — 16 тысяч, всего 28 тысяч.
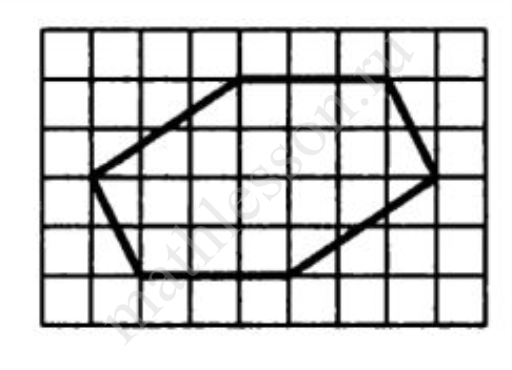
Задание 3
Найдите площадь шестиугольника, изображенного на клетчатой бумаге с размером клетки
2 см $$times$$ 2 см. Ответ дайте в квадратных сантиметрах.
Ответ: 80
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Площадь клетки $$2cdot 2=4$$ см$${}^{2}$$. Площадь фигуры $$frac{3+7}{2}cdot 2cdot 2=20$$ клеток или 80 см$${}^{2}$$
Задание 4
В одном из регионов производством школьной формы занимаются две фабрики. Первая фабрика выпускает $$40%$$ школьной формы, реализуемой в данном регионе, вторая -$$60%$$. Среди комплектов школьной формы, произведенной первой фабрикой, дефекты пошива имеют $$5%$$ комплектов, у второй фабрики дефекты пошива имеют $$9%$$ комплектов. Найдите вероятность того, что случайно купленный в данном регионе комплект школьной формы не имеет дефект.
Ответ: 0,926
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x комплектов всего выпущено, тогда дефектных из первого: $$0,4xcdot 0,05$$, из второго $$0,6xcdot 0,09$$. Тогда вероятность купить без дефекта: $$1-frac{0,02x+0,054x}{x}=0,926$$
Задание 5
Решить уравнение: $$sqrt[3]{2x-1}+sqrt[3]{x-1}=1$$
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sqrt[3]{2x-1}+sqrt[3]{x-1}=1$$. Пусть $$fleft(xright)=sqrt[3]{2x-1};gleft(xright)=1-sqrt[3]{x-1}to fleft(xright)=g(x) $$при $$x=1$$.
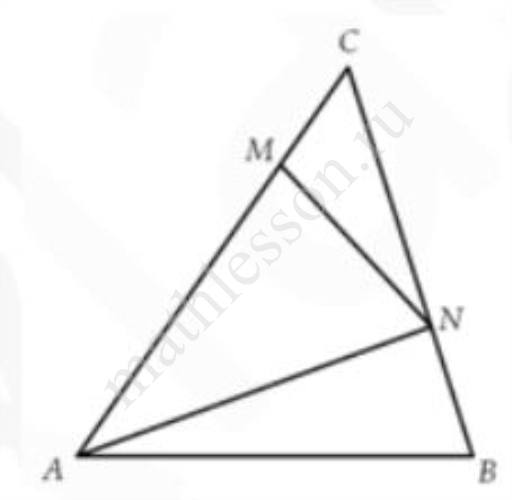
Задание 6
На сторонах АС и ВС треугольника АВС взяты точки M и N так, что $$AM:CM=3:1, BN:CN=1:2$$ (cм. рисунок). Площадь треугольника АВС равна 36. Найдите площадь четырехугольника AMNB.
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$S_{CMN}=frac{CMcdot CN}{CAcdot CB}cdot S_{ABC}=frac{1}{4}cdot frac{2}{3}cdot 36=6to S_{AMNB}=36-6=30.$$
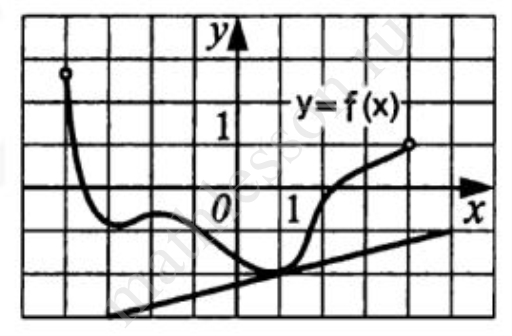
Задание 7
Функция $$y=fleft(xright)$$ определена на промежутке $$(-4;4)$$. На рисунке изображен её график и касательная к этому графику в точке с абсциссой $$x_0=1$$. Вычислите значение производной функции $$gleft(xright)=16cdot fleft(xright)-6$$ в точке $$x_0=1$$.
Ответ: 0,25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$g’left(xright)=16f’left(xright)=16cdot frac{1}{4}=4$$. Найдем $$f’left(xright):{ f}’left(xright)={tan alpha }=frac{1}{4}=0,25$$
Задание 8
Апофема правильной треугольной пирамиды равна $$2sqrt{7}$$, а боковое ребро 7. Найдите угол между плоскостью боковой грани пирамиды и плоскостью ее основания. Ответ дайте в градусах.
Ответ: 60
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$AH=sqrt{7^2-{left(2sqrt{7}right)}^2}=sqrt{21}to AC=2sqrt{21}$$
$$BH=AC{sin 60{}^circ }=2sqrt{21}cdot frac{sqrt{3}}{2}=sqrt{63}$$
$${cos DHB=frac{DH^2+HB^2-DB^2}{2DHcdot HB} }=frac{28+63-49}{2cdot 3sqrt{7}cdot 2sqrt{7}}=frac{42}{2cdot 42}=frac{1}{2}to angle DHB=60{}^circ $$
Задание 9
Найдите значение выражения: $$frac{{{log }_2 800 }}{{{log }_{800} 2 }}-frac{{{log }_2 625 }}{{{log }_{160} 2 }}$$
Ответ: 25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{{{log }_2 800 }}{{{log }_{800} 2 }}-frac{{{log }_2 625 }}{{{log }_{160} 2 }}={left({{log }_2 800 }right)}^2-{{log }_2 625 }cdot {{log }_2 160 }=$$ $$={left({{{{log }_2 160 }{rm +log}}_2 5 }right)}^2-4{{log }_2 5 }cdot {{log }_2 160 }={left({{log }_2 160 }right)}^2+2{{log }_2 160 }cdot {{log }_2 5 }+$$ $$+{left({{log }_2 5 }right)}^2-4{{log }_2 5 }{{log }_2 160 }={left({{log }_2 160 }-{{log }_2 5 }right)}^2={left({{log }_2 32 }right)}^2=5^2=25$$
Задание 10
Два тела массой $$m=10$$ кг каждое, движутся с одинаковой скоростью 6 м/с под углом $$alpha >0$$ друг к другу. Энергия Q (в джоулях),выделяющаяся при их абсолютно неупругом соударении, определяется выражением: $$Q=mv^2{({sin frac{alpha }{2} })}^2$$. Под каким наименьшим углом $$alpha $$ (в градусах) могли двигаться тела, если в результате соударения выделилось не менее 180 джоулей?
Ответ: 90
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим имеющиеся значения: $$180=10cdot 6^2{left({sin frac{alpha }{2} }right)}^2to {left({sin frac{alpha }{2} }right)}^2=frac{1}{2}to {sin frac{alpha }{2} }=pm frac{sqrt{2}}{2}$$ т.к. $$0{}^circ le alpha le 90{}^circ $$, то $$frac{alpha }{2}=45{}^circ to alpha =90{}^circ $$
Задание 11
В двух бочках содержится сахарный сироп различной концентрации. В первой бочке содержится 150 кг сиропа, а во второй 250 кг. Если перемешать весь сироп, находящийся в этих бочках, то получится сироп, в котором $$30%$$ сахара. А если смешать равные массы сиропа из каждой бочки, то полученный сироп будет содержать $$28%$$ сахара. Сколько килограммов сахара содержится в сиропе из второй бочки?
Ответ: 90
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть x — концентрация в первой $$to 150x$$ кг — масса сахара, y — во второй $$to 250y$$ кг — масса сахара во второй. Получим $$150x+250y=0,3cdot 400$$. Возьмем по 150 кг, тогда $$150x+150y=0,28cdot 300$$. Получим: $$left{ begin{array}{c}
15x+25y=0,3cdot 40 \
15x+15y=0,28cdot 30 end{array}
to 10y=12-8,4to y=0,36right.$$
Масса сахара во второй: $$0,36cdot 250=90$$ кг.
Задание 12
Найдите наименьшее значение функции $$y=4x-frac{8sqrt{3}}{3}{sin x }+2+frac{4sqrt{3}}{3}-frac{2pi }{3}$$ на отрезке $$left[0;pi right]$$.
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем производную: $$y’={left(4xright)}’-frac{8sqrt{3}}{3}{left({sin x }right)}’=4-frac{8sqrt{3}}{3}{cos x }=0to {cos x }=frac{4cdot 3}{8sqrt{3}}=frac{sqrt{3}}{2}to$$ $$to x=pm frac{pi }{6}+2pi n, nin Z.$$ На $$left[0;pi right]$$ имеем $$x=frac{pi }{6}$$. При этом это точка минимума $$to yleft(frac{pi }{6}right)=4cdot frac{pi }{6}-frac{8sqrt{3}}{3}cdot frac{1}{2}+2+frac{4sqrt{3}}{3}-frac{2pi }{3}=2$$ — наименьшее значение.
Задание 13
а) Решите уравнение $$sqrt{{cos 2x }-{left({sin x }right)}^3+3}={sin x }$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$left(frac{73pi }{2};left.41pi right]right.$$
Ответ: а)$$frac{pi}{2}+2pi n, nin Z$$ б)$$frac{77pi}{2};frac{81pi}{2}$$
Задание 14
В правильной четырехугольной призме $$ABCDA_1B_1C_1D_1$$ на боковых ребрах $$AA_1$$ и $$DD_1$$ взяты соответственно точки K и М так, что $$AK:A_1K=2:3, DM:D_1M=4:1$$.
а) Докажите, что плоскость ВМК параллельна прямой АС.
б) Найдите расстояние от точки А до плоскости ВМК, если $$AB=8,AA_1=10.$$
Ответ: $$frac{4sqrt{6}}{3}$$
Задание 15
Решите неравенство: $$frac{{{{{rm (log}}_{2x-1} (9x^2-12x+4) })}^2-10{{log }_{2x-1} left(3x-2right) }+18}{3{{log }_{2x-1} (6x^2-7x+2) }-2}le 2$$
Ответ: 0,75
Задание 16
Точка Е — середина боковой стороны CD трапеции ABCD. На стороне АВ взяли точку К так, что прямые СК и АЕ параллельны. Отрезки ВЕ и СК пересекаются в точке L.
а) Докажите, что EL — медиана треугольника КСЕ
б) Найдите отношение площади треугольника ВLC к площади четырехугольника AKCD, если площадь трапеции ABCD равна 100, а $$BC:AD=2:3$$.
Ответ: 2:21
Задание 17
Петр Иванович получил кредит в банке под определенный процент годовых. Ровно через год (после начисления процентов) Петр Иванович в счет погашения кредита вернул $$frac{2}{13}$$ той суммы, которую задолжал к тому моменту. А еще через год он внес сумму, на $$43%$$ превышающую величину займа, и тем самым полностью погасил кредит. Каков был процент годовых?
Ответ: 30
Задание 18
Найдите все значения параметра $$a$$, при каждом из которых система $$left{ begin{array}{c} x^2+left(2-5aright)x+4a^2-2ale 0 \ x^2+a^2=4 end{array} right.$$ имеет хотя бы одно решение.
Ответ: $$[-sqrt{2};0]; [frac{16}{17};sqrt{2}]$$
Задание 19
За прохождение каждого уровня платной сетевой игры можно получить от одной до трех звезд. При этом со счета участника игры списывается 75 рублей при получении одной звезды, 60 рублей — при получении двух звезд и 45 рублей при получении трех звезд. Миша прошел несколько уровней игры подряд.
а) Могла ли сумма на его счете уменьшиться при этом на 330 рублей?
б) Сколько уровней игры прошел Миша, если сумма на его счете уменьшилась на 435 рублей, а число полученных им звезд равно 13?
в) За пройденный уровень начисляется 5000 очков при получении трех звезд, 3000 — при получении двух звезд и 2000 — при получении одной звезды. Какую наименьшую сумму (в рублях) мог потратить на игру Миша, если он набрал 50000 очков, получив при этом 32 звезды?
Ответ: да;7;780
Решение и ответы заданий № 1–12 варианта №346 Александра Ларина. Разбор ЕГЭ 2021 по математике (профильный уровень).
Задание 1.
Сергей и Николай вместе весят 92 кг, Сергей и Костя – 95 кг, а Николай и Костя – 97 кг. Сколько весят вместе Сергей, Николай и Костя?
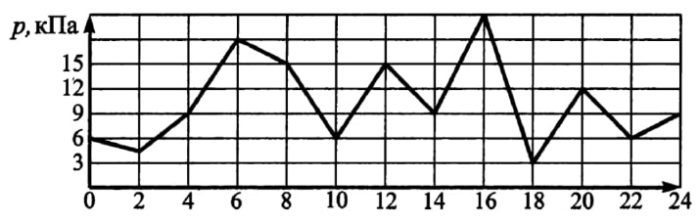
Задание 2.
На графике показано изменение давления в некотором физическом эксперименте, длящемся ровно сутки. По оси абсцисс откладывается время (в часах), прошедшее от начала эксперимента, по оси ординат – давление (в кПа). Определите по графику, сколько раз после начала эксперимента давление было в 3 раза больше, чем его минимальное значение в течение эксперимента.
Задание 3.
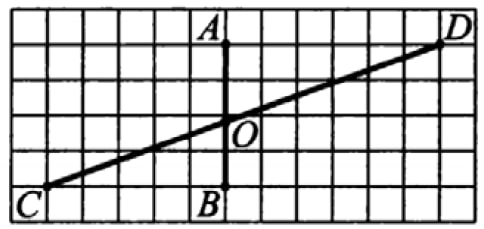
На клетчатой бумаге с размером клеток 1см х 1см отмечены отрезки АВ и CD, пересекающиеся в точке О (см. рисунок). Найдите длину отрезка АО. Ответ выразите в сантиметрах, округлив до сотых.
Задание 4.
Абонент забыл последнюю цифру номера телефона и поэтому набирает её наугад. Определить вероятность того, что ему придётся звонить не более чем в 4 места.
Задание 5.
Решите уравнение: 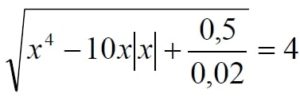
Задание 6.
В трапеции KLMT LM || KT, KL = MT, диагональ МК = 8 и ∠MKT = 75°. Найдите площадь трапеции.
Задание 7.
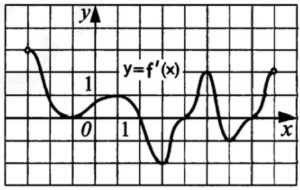
Функция y = f(x) определена на промежутке (‐3;8). На рисунке изображен график ее производной. Укажите точку минимума функции y = f(x) на промежутке (‐2;7)
Задание 8.
Шар вписан в цилиндр. Объем шара равен 2021. Найдите объем цилиндра.
Задание 9.
Найдите tg272°·ctg254°
Задание 10.
Прокладывая пути, между рельсами оставили зазор в 1,8 миллиметра. При возрастании температуры происходит тепловое расширение рельса, и его длина l меняется по закону l(t) = l0·(1 + α·t), где l0 = 15 метров – первоначальная длина рельса, α = 1,2·10–5 °С–1 – коэффициент теплового расширения, t – температура в °С. Какова минимальная температура t (в °С), при которой зазор между рельсами отсутствует?
Задание 11.
Из бака, наполненного спиртом, вылили часть спирта и долили водой. Потом из бака вылили столько же литров смеси. После этого в баке осталось 49 л чистого спирта. Сколько литров спирта вылили во второй раз, если вместимость бака 64 л?
Задание 12.
Найдите наибольшее значение функции
Источник варианта: alexlarin.net
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 0 / 5. Количество оценок: 0
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |
| 3462 | Решите неравенство 2^(x/(x+1))-2^((5x+3)/(x+1))+8<=2^((2x)/(x+1)) |
Решите неравенство 2 x/x+1 -2 5x+3 / x+1 +8 <= 2 2x/x+1 ! Тренировочный вариант 398 от Ларина Задание 14 |
|

Показана страница 1 из 89
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Новый тренировочный вариант №397 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, который вышел на сайте 10 сентября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Демоверсия ЕГЭ 2023 по математике
Тренировочный вариант 397 Ларина ЕГЭ 2023 по математике профиль
ларин-егэ2023-вариант-397-ответы
Ответы для варианта
1)Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
2)В прямоугольном параллелепипеде АВСDА1B1C1D1 известны длины ребер: АВ = 11, AD = 20, AA1 = 4. Найдите расстояние от вершины С до центра грани АА1D1D.
Ответ: 15
3)Из слова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
4)Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
9)Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
13)В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4. А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды. Б) Найдите объем пирамиды CDKM.
15)В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы: — каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.; — к июлю 2029 года долг должен быть выплачен полностью. Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
16)Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. А) Докажите, что прямые АС и BD параллельны. Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
18)Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из‐за чего количество книг с бирками «выгодно» уменьшилось.
А) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
Б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
В) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Видео решение варианта Ларина
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
12 сентября 2020
В закладки
Обсудить
Жалоба
Тренировочный вариант ЕГЭ по математике
Первый вариант в новом учебном году от сайта alexlarin.net.
Варианты публикуются на сайте alexlarin каждую неделю.
trvar321.pdf