Егэ по математике вариант 1 часть 1

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Версия для печати и копирования в MS Word

1

В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

Ответ:

2

На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали  — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.

Ответ:

3

Найдите корень уравнения log }_2} левая круглая скобка 15 плюс x правая круглая скобка =log _23.

Ответ:

4

5

Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?

Перевозчик Стоимость перевозки одним автомобилем
(руб. на 100 км) 		Грузоподъемность автомобилей
(тонн)
А 3200 3,5
Б 4100 5
В 9500 12

Ответ:

6

Найдите сумму координат вектора oversetto mathopa минус oversetto mathopb.

Ответ:

7

Найдите значение выражения дробь: числитель: 3 в степени левая круглая скобка 6,5 правая круглая скобка , знаменатель: 9 в степени левая круглая скобка 2,25 правая круглая скобка конец дроби .

Ответ:

8

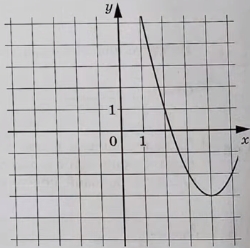
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.

Ответ:

9

Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите V/ Пи .

Ответ:

10

11

Найдите наименьшее значение функции y=3x минус натуральный логарифм левая круглая скобка x плюс 3 правая круглая скобка в кубе на отрезке [−2,5; 0].

Ответ:

12

Даша и Маша пропалывают грядку за 12 минут, а одна Маша  — за 20 минут. За сколько минут пропалывает грядку одна Даша?

Ответ:

13

а)  Решите уравнение | косинус x плюс синус x|= корень из 2 синус 2x.

б)  Найдите решения уравнения, принадлежащие отрезку [3; 5].

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

14

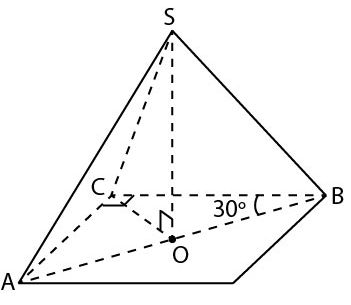
В правильной треугольной пирамиде SABC с основанием ABC известны ребра AB=7 корень из 3, SC  =  25. M  — середина ребра SA.

а)  Докажите, что проекции точек S и M на плоскость основания делят высоту AN треугольника ABC на три равные части.

б)  Найдите угол, образованный плоскостью основания и прямой MN.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

15

Решите неравенство логарифм по основанию левая круглая скобка 3x минус 3 правая круглая скобка 3 плюс логарифм по основанию левая круглая скобка левая круглая скобка x минус 1 правая круглая скобка в квадрате правая круглая скобка 27 больше или равно 2.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

16

Прямая касается окружностей радиусов R и r в точках A и B. Известно, что расстояние между центрами равно a причем r < R и r + R < a. Найдите AB.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

17

Найдите все значения a при каждом из которых система система выражений новая строка дробь: числитель: x минус ax минус a, знаменатель: x плюс 2a минус 2 конец дроби больше или равно 0, новая строка x минус ax больше 8 конец системы . не имеет решений.

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

18

Перед каждым из чисел 14, 15, . . ., 20 и 4, 5, . . ., 8 прозвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?

Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.

Чтобы отправить работу учителю, перейдите на следующую страницу, сверьте ваши решения заданий с развернутым ответом с образцами, оцените ваши решения и сохраните выставленные баллы.

Источник

Задание 1

Боковые стороны трапеции, описанной около окружности, равны 7 и 4. Найдите среднюю линию трапеции.

Ответ: 5,5

Скрыть

Задание 2

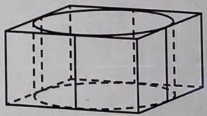
Цилиндр вписан в прямоугольный параллелепипед. Радиус основания и высота цилиндра равны 8. Найдите объём параллелепипеда.

Ответ: 2048

Скрыть

Задание 3

Вероятность того, что на тестировании по физике учащийся К. верно решит больше 9 задач, равна 0,79. Вероятность того, что К. верно решит больше 8 задач, равна 0,85. Найдите вероятность того, что К. верно решит ровно 9 задач.

Ответ: 0,06

Скрыть

Задание 4

При выпечке хлеба производится контрольное взвешивание свежей буханки. Известно, что вероятность того, что масса окажется меньше, чем 810 г, равна 0,96. Вероятность того, что масса окажется больше, чем 790 г, равна 0,93. Найдите вероятность того, что масса буханки больше, чем 790 г, но меньше, чем 810 г.

Ответ: 0,89

Скрыть

Задание 5

Найдите корень уравнения $$log_3(5-2x)=log_3(1-4x)+1$$

Ответ: -0,2

Скрыть

Задание 6

Найдите значение выражения $$frac{sin 126^{circ}}{4sin 63^{circ}cdot sin 27^{circ}}$$

Ответ: 0,5

Скрыть

Задание 7

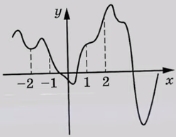
На рисунке изображён график $$y=f'(x)$$ — производной функции $$f(x)$$, определённой на интервале $$(-2;20)$$. Найдите количество точек экстремума функции $$f(x)$$, принадлежащих отрезку $$[1;15]$$.

Ответ: 5

Скрыть

Задание 8

При адиабатическом процессе для идеального газа выполняется закон $$pV^k=1,3122cdot 10^7$$ Па$$cdot$$м4, где $$p$$ — давление в газе в паскалях, $$V$$ — объём газа в в кубических метрах, $$k=frac{4}{3}$$. Найдите, какой объём $$V$$ (в куб. м) будет занимать газ при давлении $$p$$, равном $$1,25cdot 10^6$$ Па.

Ответ: 5,832

Скрыть

Задание 9

Моторная лодка прошла против течения реки 96 км и вернулась в. пункт отправления, затратив на обратный путь на 4 часа меньше. Найдите скорость течения, если скорость лодки в неподвижной воде равна 10 км/ч. Ответ дайте в км/ч.

Ответ: 2

Скрыть

Задание 10

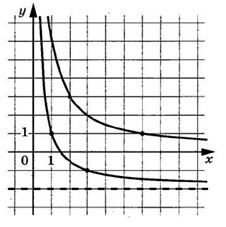
На рисунке изображены части графиков функций $$f(x)=frac{k}{x}$$ и $$g(x)=frac{c}{x}+d$$. Найдите ординату точки пересечения графиков этих функций.

Ответ: -4

Скрыть

Задание 11

Найдите наименьшее значение функции $$y=xsqrt{x}-27x+6$$ на отрезке $$[1;422]$$

Ответ: -2910

Скрыть

Задание 12

а) Решите уравнение $$2sin^{2}x-3cos(-x)-3=0$$

б) Найдите все корни этого уравнения, принадлежащие отрезку $$[2pi;frac{7pi}{2}]$$

Ответ: а)$$pi+2pi k; pmfrac{2pi}{3}+2pi n, n,k in Z$$ б)$$frac{8pi}{3};3pi; frac{10pi}{3}$$

Скрыть

Задание 13

В основании пирамиды $$SABCD$$ лежит трапеция $$ABCD$$ с большим основанием $$AD$$. Диагонали трапеции пересекаются в точке $$O$$. Точки $$M$$ и $$$$ — середины боковых сторон $$AB$$ и $$CD$$ соответственно. Плоскость $$alpha$$ проходит через точки $$M$$ и $$N$$ параллельно прямой $$SO$$.

а) Докажите, что сечение пирамиды $$SABCD$$ плоскостью $$alpha$$ является трапецией.

б) Найдите площадь сечения пирамиды $$SABCD$$ плоскостью $$alpha$$, если $$AD=9$$, $$BC=7$$, $$SO=6$$, а прямая $$SO$$ перпендикулярна прямой $$AD$$.

Ответ: 24

Скрыть

Задание 14

Решите неравенство $$4^x+frac{112}{4^{x}-32}leq 0$$

Ответ: $$(-infty;1];[log_{4} 28;2,5)$$

Скрыть

Задание 15

В июле 2027 года планируется взять кредит на три года в размере 1200 тыс. рублей. Условия его возврата таковы:

— каждый январь долг будет возрастать на 10 % по сравнению с концом предыдущего года;

— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;

— платежи в 2028 и 2029 годах должны быть равными;

— к июлю 2030 года долг должен быть выплачен полностью.

Известно, что платёж в 2030 году составит 673,2 тыс. рублей. Сколько рублей составит платёж 2028 года?

Ответ: 400 тыс. руб.

Скрыть

Задание 16

В параллелограмме $$ABCD$$ угол $$BAC$$ вдвое больше угла $$CAD$$. Биссектриса угла $$BAC$$ пересекает отрезок $$BC$$ в точке $$L$$. На продолжении стороны $$CD$$ за точку $$D$$ выбрана такая точка $$E$$, что $$AE=CE$$.

а) Докажите, что $$AL:AC=AB:BC$$.

б) Найдите $$EL$$, если $$AC=21$$, $$tgangle BCA=0,4$$.

Ответ: 14,2

Скрыть

Задание 17

Найдите все значения $$a$$, при каждом из которых уравнение $$(a-x)^2+4a+1=(2x+1)^2-8|x|$$ имеет четыре различных корня.

Ответ: (-4;-3);(-3;-1);(-1;0)

Скрыть

Задание 18

Есть три коробки: в первой коробке 112 камней, во второй — 99, а третья — пустая. За один ход берут по одному камню из любых двух коробок и кладут в оставшуюся. Сделали некоторое количество таких ходов.

а) Могло ли в первой коробке оказаться 103 камня, во второй — 99, а в третьей — 9?

б) Могло ли в третьей коробке оказаться 211 камней?

в) Во второй коробке оказалось 4 камня. Какое наибольшее число камней могло оказаться в третьей коробке?

Ответ: а)да б)нет в)195

Скрыть

Источник

Решение и ответы заданий Варианта №1 из сборника ЕГЭ 2022 по математике (профильный уровень) И.В. Ященко. ГДЗ Решебник профиль для 11 класса. Полный разбор. Ответы с решением.

Задание 1.
Найдите корень уравнения 45х+2 = 0,8·55х+2.

Задание 2.
На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Тригонометрия», равна 0,1. Вероятность того, что это вопрос по теме «Внешние углы», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Задание 3.
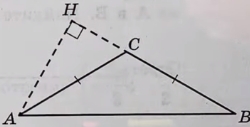
В тупоугольном треугольнике ABC известно, что  AC = BC = 10, высота AH равна √51. Найдите косинус угла ACB.

В тупоугольном треугольнике ABC известно, что  AC = BC = 10, высота AH равна √51.

Задание 4.
Найдите значение выражения frac{5sin61^{circ}}{sin299^{circ}}.

Задание 5.
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3. Найдите площадь боковой поверхности призмы.
Цилиндр вписан в правильную четырёхугольную призму. Радиус основания и высота цилиндра равны 3.

Задание 6.
На рисунке изображён график функции y = f(x). На оси абсцисс отмечены точки −2, –1, 1, 2. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.

На рисунке изображён график функции 𝑦 = 𝑓(𝑥). На оси абсцисс отмечены точки −2, –1, 1, 2.

Задание 7.
При температуре 0°С рельс имеет длину l0 = 10 м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону l(𝑡°) = l0(1 + α∙t°), где α = 1,2∙10−5(°С )−1 – коэффициент теплового расширения, t° – температура (в градусах Цельсия). При какой температуре рельс удлинится на 6 мм? Ответ дайте в градусах Цельсия.

Задание 8.
Велосипедист выехал с постоянной скоростью из города А в город В, расстояние между которыми равно 105 км. На следующий день он отправился обратно в А со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 4 часа. В результате велосипедист затратил на обратный путь столько же времени, сколько на путь из А в B. Найдите скорость велосипедиста на пути из B в А. Ответ дайте в км/ч.

Задание 9.
На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые. Найдите значение f(−5).

На рисунке изображён график функции вида f(x) = ax2 + bx + c, где числа a, b и c – целые.

Задание 10.
Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 30% этих стекол, вторая – 70%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Задание 11.
Найдите наименьшее значение функции y = frac{4}{3}x√x – 3x + 9 на отрезке [0,25; 30].

Задание 12.
а) Решите уравнение 2sin3(π + x) = frac{1}{2}cos(x – frac{3pi }{2}).
б) Найдите все корни уравнения, принадлежащие отрезку [-frac{7pi }{2};-frac{5pi }{2}].

Задание 13.
Дана правильная треугольная пирамида SABC, сторона основания AB = 16, высота SH = 10, точка K – середина бокового ребра SА. Плоскость, параллельная плоскости АВС, проходит через точку K и пересекает ребра SB и SC в точках Q и P соответственно.

а) Докажите, что площадь четырёхугольника BCPQ составляет frac{3}{4} площади треугольника SBC
б) Найдите объем пирамиды KBCPQ.

Задание 14.
Решите неравенство (4х – 5·2х)2 – 20(4х – 5·2х) ≤ 96.

Задание 15.
В июле 2025 года планируется взять кредит на 8 лет. Условия его возврата таковы:
– в январе 2026, 2027, 2028, 2029 годов долг возрастает на 20% по сравнению с концом предыдущего года;
– в январе 2030, 2031, 2032, 2033 годов долг возрастает на 18% по сравнению с концом предыдущего года;
– с февраля по июнь каждого года необходимо выплатить часть долга;
– в июле каждого года должен быть на одну и ту же величину меньше долга на июль предыдущего года;
– к июлю 2033 года долг должен быть полностью погашен.
Какую сумму планируется взять в кредит, если общая сумма выплат до полного его погашения составит 1125 тысяч рублей?

Задание 16.
Точки A, B, C, D и E лежат на окружности в указанном порядке, причем AE = ED = CD, а прямые AC и BE перпендикулярны. Отрезки AC и BD пересекаются в точке T.

а) Докажите, что прямая EC пересекает отрезок TD в его середине.
б) Найдите площадь треугольника ABT, если BD = 6, АЕ = √6.

Задание 17.
Найдите все значения 𝑎, при каждом из которых уравнение

|x^{2}-a^{2}|=|a+x|cdot sqrt{x^{2}-4ax+5a}

имеет ровно один корень.

Задание 18.
На доске написаны три различных натуральных числа. Второе число равно сумме цифр первого, а третье равно сумме цифр второго.

а) Может ли сумма этих чисел быть равна 2022?
б) Может ли сумма этих чисел быть равна 2021?
в) В тройке чисел первое число трёхзначное, а третье равно 2. Сколько существует таких троек?

Источник варианта: Сборник ЕГЭ 2022. ФИПИ школе. Математика профильный уровень. Типовые экзаменационные варианты. Под редакцией И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.1 / 5. Количество оценок: 17

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Источник

Алякина Елена Ивановна

Пробный ЕГЭ № 1 по математике. 11 класс

Вариант 1
Вариант 2
Вариант 3
Вариант 4
Ответы

Скачать:

Предварительный просмотр:

МБОУ «Апраксинская СОШ»

ЕГЭ по МАТЕМАТИКЕ   №1

Профильный уровень.        2022г.

Вариант 1

C:UsersUserDesktopРисунок1.jpg

C:UsersUserDesktopРисунок2.jpg

Часть 1

1.         Найдите корень уравнения        .

        Ответ: ___________________

2.        Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом все три раза.

        Ответ: ___________________

3.        В треугольнике АВС  СD – медиана, угол С равен 900, угол В равен 350. Найдите угол АСD.  Ответ дайте в градусах.

        Ответ: ___________________

4.        Найдите значение выражения                .

        Ответ: ___________________

5.        Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 28. Найдите площадь боковой поверхности исходной призмы.

        Ответ: ___________________

6.        На рисунке изображён график функции . На оси абсцисс отмечены десять точек: х1, х2, х3, х4, х5, х6, х7, х8. В скольких из этих точек производная функции  положительна?

C:UsersUserDesktopант.jpg

        Ответ: ___________________

7.         Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле        , где t – время в минутах, ,  ,  b = 98К/мин.  Известно, что при температуре нагревателя свыше 1720К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

        Ответ: ___________________

8.        Имеется два сплава. Первый сплав содержит 5% никеля, второй – 20% никеля. Из этих двух сплавов получили третий сплав массой 225кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

        Ответ: ___________________

9.        На рисунке изображён график функции        . Найдите .

C:UsersUserDesktopигно.jpg

        Ответ: ___________________

10.        Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 25% этих стекол, вторая – 75%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

        Ответ: ___________________

11.        Найдите наибольшее значение функции

          на отрезке        .

        Ответ: ___________________

C:UsersUserDesktopне заб.jpg

Часть 2

12.        а) Решите уравнение:        .

        б) Найдите корни этого уравнения, принадлежащие отрезку .

13.        На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.

        а) Докажите, что точка М является серединой ребра СС1.

        б) Найдите расстояние от точки С1 до плоскости А1РQ.

14.        Решите неравенство        .

15.        15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:

        – 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;

        – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

        – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг (в млн рублей)

1

0,6

0,4

0,3

0,2

0,1

0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

16.        В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.

        а) Докажите, что ВМ = СМ.

        б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.

17.        Найдите значения a, при каждом из которых уравнение

 

        имеет ровно два различных корня.

18.        Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.

Предварительный просмотр:

МБОУ «Апраксинская СОШ»

ЕГЭ по МАТЕМАТИКЕ   №1

Профильный уровень.        2022г.

Вариант 2

C:UsersUserDesktopРисунок1.jpg

C:UsersUserDesktopРисунок2.jpg

Часть 1

1.         Найдите корень уравнения        .

        Ответ: ___________________

2.        Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом ровно один раз.

        Ответ: ___________________

3.        В треугольнике АВС  СD – медиана, угол С равен 900, угол В равен 410. Найдите угол АСD.  Ответ дайте в градусах.

        Ответ: ___________________

4.        Найдите значение выражения                .

        Ответ: ___________________

5.        Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 32. Найдите площадь боковой поверхности исходной призмы.

        Ответ: ___________________

6.        На рисунке изображён график функции . На оси абсцисс отмечены десять точек: х1, х2, х3, х4, х5, х6, х7, х8. В скольких из этих точек производная функции  отрицательна?

C:UsersUserDesktopант.jpg

        Ответ: ___________________

7.         Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле        , где t – время в минутах, ,  ,  b = 69К/мин.  Известно, что при температуре нагревателя свыше 1736К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

        Ответ: ___________________

8.        Имеется два сплава. Первый сплав содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 270кг, содержащий 20% никеля. На сколько килограммов масса первого сплава меньше массы второго?

        Ответ: ___________________

9.        На рисунке изображён график функции        . Найдите .

C:UsersUserDesktopигно.jpg

        Ответ: ___________________

10.        Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 35% этих стекол, вторая – 65%. Первая фабрика выпускает 4% бракованных стекол, а вторая – 2%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

        Ответ: ___________________

11.        Найдите наибольшее значение функции

          на отрезке        .

        Ответ: ___________________

C:UsersUserDesktopне заб.jpg

Часть 2

12.        а) Решите уравнение:        .

        б) Найдите корни этого уравнения, принадлежащие отрезку .

13.        На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.

        а) Докажите, что точка М является серединой ребра СС1.

        б) Найдите расстояние от точки С1 до плоскости А1РQ.

14.        Решите неравенство        .

15.        15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:

        – 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;

        – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

        – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг (в млн рублей)

1

0,6

0,4

0,3

0,2

0,1

0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

16.        В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.

        а) Докажите, что ВМ = СМ.

        б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.

17.        Найдите значения a, при каждом из которых уравнение

 

        имеет ровно два различных корня.

18.        Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.

Предварительный просмотр:

МБОУ «Апраксинская СОШ»

ЕГЭ по МАТЕМАТИКЕ   №1

Профильный уровень.        2022г.

Вариант 3

C:UsersUserDesktopРисунок1.jpg

C:UsersUserDesktopРисунок2.jpg

Часть 1

1.        Найдите корень уравнения        .

        Ответ: ___________________

2.        Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» начнёт игру с мячом ровно два раза.

        Ответ: ___________________

3.        В треугольнике АВС  СD – медиана, угол С равен 900, угол В равен 370. Найдите угол АСD.  Ответ дайте в градусах.

        Ответ: ___________________

4.        Найдите значение выражения                .

        Ответ: ___________________

5.        Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 36. Найдите площадь боковой поверхности исходной призмы.

        Ответ: ___________________

6.        На рисунке изображён график функции . На оси абсцисс отмечены десять точек: х1, х2, х3, х4, х5, х6, х7, х8. В скольких из этих точек производная функции  положительна?

C:UsersUserDesktopант.jpg

        Ответ: ___________________

7.         Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле        , где t – время в минутах, ,  ,  b = 96К/мин.  Известно, что при температуре нагревателя свыше 1700К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

        Ответ: ___________________

8.        Имеется два сплава. Первый сплав содержит 5% никеля, второй – 20% никеля. Из этих двух сплавов получили третий сплав массой 240кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

        Ответ: ___________________

9.        На рисунке изображён график функции        . Найдите .

C:UsersUserDesktopигно.jpg

        Ответ: ___________________

10.        Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 40% этих стекол, вторая – 60%. Первая фабрика выпускает 5% бракованных стекол, а вторая – 3%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

        Ответ: ___________________

11.        Найдите наибольшее значение функции

          на отрезке        .

        Ответ: ___________________

C:UsersUserDesktopне заб.jpg

Часть 2

12.        а) Решите уравнение:        .

        б) Найдите корни этого уравнения, принадлежащие отрезку .

13.        На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.

        а) Докажите, что точка М является серединой ребра СС1.

        б) Найдите расстояние от точки С1 до плоскости А1РQ.

14.        Решите неравенство        .

15.        15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:

        – 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;

        – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

        – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг (в млн рублей)

1

0,6

0,4

0,3

0,2

0,1

0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

16.        В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.

        а) Докажите, что ВМ = СМ.

        б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.

17.        Найдите значения a, при каждом из которых уравнение

 

        имеет ровно два различных корня.

18.        Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.

Предварительный просмотр:

МБОУ «Апраксинская СОШ»

ЕГЭ по МАТЕМАТИКЕ   №1

Профильный уровень.        2022г.

Вариант 4

C:UsersUserDesktopРисунок1.jpg

C:UsersUserDesktopРисунок2.jpg

Часть 1

1.         Найдите корень уравнения        .

        Ответ: ___________________

2.        Перед началом футбольного матча судья бросает монету, чтобы определить, какая из команд начнёт игру с мячом. Команда «Биолог» играет три матча с разными командами. Найдите вероятность того, что в этих матчах команда «Биолог» ни разу не начнёт игру с мячом.

        Ответ: ___________________

3.        В треугольнике АВС  СD – медиана, угол С равен 900, угол В равен 390. Найдите угол АСD.  Ответ дайте в градусах.

        Ответ: ___________________

4.        Найдите значение выражения                .

        Ответ: ___________________

5.        Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 35. Найдите площадь боковой поверхности исходной призмы.

        Ответ: ___________________

6.        На рисунке изображён график функции . На оси абсцисс отмечены десять точек: х1, х2, х3, х4, х5, х6, х7, х8. В скольких из этих точек производная функции  отрицательна?

C:UsersUserDesktopант.jpg

        Ответ: ___________________

7.         Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально. На исследуемом интервале температура вычисляется по формуле        , где t – время в минутах, ,  ,  b = 196К/мин.  Известно, что при температуре нагревателя свыше 1800К прибор может испортиться, поэтому его нужно отключить. Определите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ дайте в минутах.

        Ответ: ___________________

8.        Имеется два сплава. Первый сплав содержит 10% никеля, второй – 25% никеля. Из этих двух сплавов получили третий сплав массой 210кг, содержащий 15% никеля. На сколько килограммов масса первого сплава меньше массы второго?

        Ответ: ___________________

9.        На рисунке изображён график функции        . Найдите .

C:UsersUserDesktopигно.jpg

        Ответ: ___________________

10.        Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая – 55%. Первая фабрика выпускает 6% бракованных стекол, а вторая – 4%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

        Ответ: ___________________

11.        Найдите наибольшее значение функции

          на отрезке        .

        Ответ: ___________________

C:UsersUserDesktopне заб.jpg

Часть 2

12.        а) Решите уравнение:        .

        б) Найдите корни этого уравнения, принадлежащие отрезку .

13.        На ребрах DD1 и ВВ1 куба АВСDА1В1С1D1 с ребром 12 отмечены точки Р и Q соответственно, причём DP= 10, а В1Q = 4. Плоскость А1РQ пересекает ребро СС1 в точке М.

        а) Докажите, что точка М является серединой ребра СС1.

        б) Найдите расстояние от точки С1 до плоскости А1РQ.

14.        Решите неравенство        .

15.        15-го января планируется взять кредит в банке на шесть месяцев в размере 1 млн. рублей. Условия его возврата таковы:

        – 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;

        – со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;

        – 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.

Дата

15.01

15.02

15.03

15.04

15.05

15.06

15.07

Долг (в млн рублей)

1

0,6

0,4

0,3

0,2

0,1

0

Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.

16.        В трапеции АВСD основание АD в два раза меньше основания ВС. Внутри трапеции взяли точку М так, что углы ВАМ и СDМ прямые.

        а) Докажите, что ВМ = СМ.

        б) Найдите угол АВС, если угол ВСD равен 640, а расстояние от точки М до прямой ВС равно стороне АD.

17.        Найдите значения a, при каждом из которых уравнение

 

        имеет ровно два различных корня.

18.        Задумано несколько (не обязательно различных) натуральных чисел. Эти числа и их все возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке неубывания. Если какое-то число n, выписанное на доску, повторяется несколько раз, то на доске оставляется одно такое число n, а остальные числа, равные n, стираются. Например, если задуманы числа 1, 3, 3, 4, то на доске будет записан набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

а) Приведите пример задуманных чисел, для которых на доске будет записан набор 1, 2, 3, 4, 5, 6, 7.

б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 6, 7, 8, 10, 11, 12, 13, 15, 16, 17, 19, 20, 22?

в) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 7, 9, 11, 14, 16, 18. 20, 21, 23, 25, 27, 30, 32, 34, 41.

Предварительный просмотр:

МБОУ «Апраксинская СОШ»

ЕГЭ по МАТЕМАТИКЕ   №1

Профильный уровень.        2022г.

Ответы

Часть 1

Вариант 1

1) 7;   2) 0,125;   3) 55;   4) – 10;   5) 56;   6) 5;   7) 6   8) 75;   9) 34;   10) 0,025;   11) 28.

Вариант 2

1) 11;   2) 0,375;   3) 49;   4) – 6;   5) 64;   6) 3;   7) 7   8) 90;   9) 7;   10) 0,027;   11) 23.

Вариант 3

1) 8;   2) 0,375;   3) 53;   4) – 20;   5) 72;   6) 5;   7) 5   8) 80;   9) 23;   10) 0,038;   11) 30.

Вариант 4

1) 3;   2) 0,125;   3) 51;   4) – 16;   5) 70;   6) 3;   7) 8   8) 70;   9) 47;   10) 0,049;   11) 11.

Часть 2

12) а) .         13)       мой ответ: .

14) .            15) 7%.               16) 710.            17)      мой ответ: .

18) а) 1, 2, 4 (1,1,1,1,1,1,1;    1,1,2,3);   б) нет;   в) 7, 7, 7, 9, 11  или  7, 9, 11, 14.

По теме: методические разработки, презентации и конспекты

  • Мне нравится 

 

Источник

Видеоразбор варианта 1:

Часть 1. Задания с кратким ответом

1. Анна Малкова На Пробном ЕГЭ по математике Гриша получил некоторое количество баллов. Если бы его результат увеличить на 80%, получилось бы 90 баллов. На сколько баллов Гриша написал Пробный ЕГЭ?

Решение:

Пусть количество баллов, полученное Гришей на Пробном ЕГЭ, равно х.

Увеличив х на 80%, получим x + 0,8 x = 1,8 x,

1,8 x = 90, отсюда х = 50 баллов — первоначальный результат Гриши.

Ответ: 50

2. На графике показано изменение напряжения на конденсаторе в зависимости по времени. Определите, за какое время напряжение на конденсаторе уменьшилось от 1 В до нуля. Ответ выразите в мс.

Решение:

Напряжение на конденсаторе было равно 1 В при t_1 = 0,6 мс и стало равно нулю при t_2 = 1,4 мс. Уменьшение напряжения от 1 В до нуля произошло за 1,4 — 0,6 = 0,8 мс.

Ответ: 0,8

3. Ольга Чемезова

В прямоугольном треугольнике ABC длина отрезка AH = 40, tg A = 0,7. Найдите AB.

Решение:

Из vartriangle AHC, CH={90}^{circ }:

displaystyle tgA=frac{CH}{AH}, отсюда CH=40cdot 0,7=28

По свойству высоты прямоугольного треугольника, проведённой к гипотенузе,
CH^2=AHcdot BH;
displaystyle BH=frac{CH^2}{AH}=frac{{28}^2}{40}=19,6
AB=AH+BH=40+19,6=59,6

Ответ: 59,6

4. Анна Малкова Маша купила для всей семьи пирожков: 3 с капустой, 3 с вареньем и 4 с рисом. Пирожки лежат в одном пакете и внешне совершенно одинаковы. По дороге домой Маша чувствует непреодолимое желание съесть 2 пирожка, причем разных и не с рисом. С какой вероятностью ей удастся выбрать нужные пирожки из пакета?

Решение: Благоприятными для Маши будут следующие варианты:

1) Первый пирожок, который она вытащит, будет с капустой, а второй с вареньем.

2) Наоборот — первый с вареньем, второй с капустой.

Вероятность достать пирожок с капустой из пакета, в котором всего 10 пирожков, равна 3/10. После того как этот пирожок вытащен, в пакете остается 9 пирожков, из которых 3 с вареньем. Значит, вероятность вытащить пирожок с вареньем равна 3/9 = 1/3, а вероятность достать пирожки с капустой и с вареньем равна 3/10 * 1/3 =1/10, поскольку эти события независимы.

Во втором варианте вероятность достать пирожок с вареньем равна 3/10, а вероятность вытащить после этого пирожок с капустой равна 3/9, произведение этих вероятностей также равно 1/10.

Сложив полученные вероятности, получаем: 0,1 + 0,1 = 0,2.

Ответ: 0,2

5. Решите уравнение x^2-6x+sqrt{6-x}= sqrt{6-x}+7

Если уравнение имеет несколько корней, в ответе запишите больший корень.

Решение:

Ответ: -1

6. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Решение:

Сложив 3 и 5, мы получим, что длина боковой стороны равна 8. Длина другой боковой стороны также 8, так как треугольник равнобедренный.

Длины отрезков касательных, проведенных из одной точки, равны. Значит, длины отрезков касательных, проведенных из точки B, равны 3. Тогда длина стороны АС равна 3+ 3 = 6.

Ответ: 22

7. На рисунке изображён график функции y=fleft(xright). Найдите количество точек максимума функции y=fleft(xright) на отрезке [-4; 6]

Решение:

По определению, точка максимума — такая внутренняя точка области определения функции, значение в которой больше, чем во всех достаточно близких к ней соседних точках.

Таких точек на графике четыре.

Ответ: 4

8. Площадь основания конуса равна 112. Плоскость, параллельная плоскости основания конуса, делит его высоту на отрезки длиной 2 и 6, считая от вершины. Найдите площадь сечения конуса этой плоскостью.

Решение:

Плоскость, параллельная основанию, отсекает от конуса меньший конус, все линейные размеры которого в 4 раза меньше, чем у большого. Поэтому площадь сечения в 16 раз меньше площади основания. Она равна 7.

Ответ: 7

9. Найдите значение выражения. displaystyle sqrt{32}-sqrt{128}{{sin}^2 frac{7pi }{8} }.

Решение:

displaystyle sqrt{32}-sqrt{128}{{sin}^2 frac{7pi }{8} }=sqrt{32}-2sqrt{32}{{sin}^2 frac{7pi }{8}=4sqrt{2}left(1-{2{sin}^2 frac{7pi }{8} }right)= }

displaystyle =4sqrt{2}{cos left(2cdot frac{7pi }{8}right)=4sqrt{2}{cos frac{7pi }{4}=4sqrt{2}cdot frac{sqrt{2}}{2}=4. } }

Ответ: 4

10. Анна Малкова

Численность популяции глупых пингвинов описывается уравнением Pleft(tright)=P_0cdot {1,1}^{kt}, где P_0 — начальная численность популяции, t — время в десятилетиях, прошедшее с момента начала наблюдений. Известно, что через 20 лет после начала наблюдений численность популяции пингвинов увеличилась примерно в 1,331 раза. Найдите k.

Решение:

Pleft(tright)=P_0cdot {1,1}^{kt};
t=20 лет=2 десятилетия,
Pleft(tright)=1,331P_0={1,1}^3cdot P_0
Получим:
{1,1}^3cdot P_0=P_0cdot {1,1}^{2k}
2k=3; k=1,5.

Ответ: 1,5

11. Анна Малкова

В течение двух месяцев «самоизоляции», вызванной пандемией Covid-19, оборот фирмы предпринимателя Ивана уменьшался на p процентов ежемесячно. Иван подсчитал, что для возвращения к первоначальному уровню оборот необходимо увеличить на 56,25 %. Найдите р.

Решение:

Обозначим X — оборот формы Ивана до «самоизоляции»

displaystyle xcdot {left(1-frac{p}{100}right)}^2 — оборот фирмы Ивана после двух месяцев «самоизоляции», если величину xcdot {left(1-frac{p}{100}right)}^2 увеличить на 56,25%, то есть умножить на 1,5625, получим x.

displaystyle xcdot {left(1-frac{p}{100}right)}^2cdot left(1+frac{56,25}{100}right) = x;

displaystyle {left(1-frac{p}{100}right)}^2cdot frac{156,25}{100} = 1;

displaystyle {left(1-frac{p}{100}right)}^2 =frac{100}{156,25}

Так как {12,5}^2 = 156,25, получим:

displaystyle {left(1-frac{p}{100}right)}^2 =frac{{10}^2}{{left(12,5right)}^2};

displaystyle 1-frac{p}{100} =frac{10}{12,5} =frac{20}{25} =frac{4}{5}

displaystyle frac{p}{100} = 1 -frac{4}{5} =frac{1}{5};

p=20

Ответ: 20

12. Найдите наибольшее значение функции displaystyle y= frac{1}{x^2-10x+21} на отрезке [4; 6].

Решение:

Функция displaystyle yleft(xright)=frac{1}{x^2-10x+21} определена при всех x, кроме x=3 и x=7 (так как x=3 и x=7 — нули знаменателя); на отрезке [4; 6] функция y(x) непрерывна.

Наибольшее значение функции displaystyle y =frac{1}{x^2-10x+21} на отрезке [4; 6] достигается при наименьшем значении знаменателя дроби, т.е. выражения t(x)=x^2-10x+21.

Так как t(x) — квадратичная парабола с ветвями вверх, её наименьшее значение достигается в вершине параболы, то есть при displaystyle x_0 =frac{10}{2} = 5;

4 textless 5 textless 6, то есть вершина параболы лежит на отрезке [4; 6].

t_{min}(x)=t(5)=25-50+21=-4,

y_{max}(x)=y(-4)=-0,25

Ответ: -0,25

Часть 2. Задания с развернутым ответом

13. Ольга Чемезова

а) Решите уравнение
displaystyle sin2x+2{sin}^2x=2sqrt{2}sin(x+frac{pi }{4});
б) Найдите все его корни на отрезке
[-2pi ; frac{-pi} {2}]

Решение:

а) displaystyle 2{sin x }{cos x }+2{{sin}^2 x } = 2sqrt{left(2right)}left({sin x }+{cos x }right)cdot frac{sqrt{2}}{2}

{sin x }{cos x }+{{sin}^2 x } ={sin x } +{cos x }

{sin x } left({sin x } +{cos x }right)={sin x }+{cos x }

б) displaystyle xin left[-2pi ; -frac{pi }{2}right]; Отберём корни с помощью тригонометрического круга.

Отметим на тригонометрическом круге отрезок  [displaystyle -2pi; -frac{pi}{2};] и найденные серии решений. Видим, что указанному отрезку принадлежат точки displaystyle -frac{3pi}{2};-frac{5pi}{4}.

Ответ: а) 

б) displaystyle -frac{3pi }{2}; -frac{5pi }{4}

14. Анна Малкова

В основании треугольной пирамиды SABC лежит треугольник АВС, причем его углы А, В и С относятся как 1 : 2 : 3, SO — высота пирамиды.

Известно, что SA = SC = АВ = SB

а) Докажите, что треугольники SCO и ABC равны.

б) Найдите расстояние от точки С до плоскости SAB, если АВ = 8.

Решение:


angle A:angle B:angle C=1:2:3Rightarrow angle A={30}^{circ }, angle B={60}^{circ }, angle C={90}^{circ },

Если боковые ребра пирамиды равны, ее вершина проецируется в центр описанной окружности основания.

SA=SB=SC Rightarrow O — центр описанной окружности vartriangle ABC,

O — середина AB, OB=OC=AC.

vartriangle SCO=vartriangle ABC по катету и гипотенузе.

б) Найдём h — расстояние от C до (SAB), если AB=SA=SB=SC=8.

Применим метод объёмов. Рассмотрим треугольную пирамиду SABC:

displaystyle V_{SABC}=frac{1}{3}S{vartriangle }_{ABC}cdot SO=frac{1}{3} S{vartriangle }_{SAB}cdot h

displaystyle S_{vartriangle SAB}=frac{AB^2sqrt{3}}{4}=frac{64sqrt{3}}{4}=16sqrt{3}
(vartriangle SAB — правильный )

8sqrt{3}cdot 4sqrt{3}=16sqrt{3}cdot h

h=2sqrt{3}

Ответ: 2sqrt{3}

15.

Решить неравенство
displaystyle sqrt{9x+frac{1}{2x+1}}cdot left(9-25x^2right)geq 0.

Решение:

displaystyle sqrt{9x+frac{1}{2x+1}}cdot left(9-25x^2right)geq 0Leftrightarrow

Решим отдельно уравнение:

18x^2+9x+1=0
D=81-72=9

displaystyle x=frac{-9pm 3}{36}; x_1 = - frac{1}{3}, x_2 = -frac{1}{6}

Получим:

Ответ: displaystyle left(-frac{1}{2}; -frac{1}{3}right] или left[-frac{1}{6}; frac{3}{5}right]

16. Анна Малкова Биссектрисы AA_1, BB_1 и CC_1 треугольника ABC продолжены до пересечения с его описанной окружностью, причем A_1, B_1, C_1 — точки пересечения.

В треугольнике A_1B_1C_1 углы A_1, B_1и C_1 равны 75, 60 и 45 градусов соответственно.

а) Докажите, что AB^2 = 2 A_1B_1^2

б) Пусть О — центр описанной окружности треугольника АВС, Р — точка пересечения его биссектрис. Найдите угол РОВ. Ответ выразите в градусах.

Решение:


angle A={75}^{circ }
angle B_1={60}^{circ }
angle C_1={45}^{circ }
Доказать: AB^2=2A_1B^2_1

Пусть angle A=2alpha , angle B=2beta , angle C=2 gamma

Вписанные углы, которые опираются на равные дуги, равны

left{ begin{array}{c}angle A_1=beta +gamma ={75}^{circ } \angle B_1=alpha +gamma ={60}^{circ } \angle C_1=alpha +beta ={45}^{circ } end{array}right.

Тогда alpha ={15}^{circ }, angle A={30}^{circ },
beta ={30}^{circ }, angle B={60}^{circ }
gamma ={45}^{circ }, angle C={90}^{circ },
AB — диаметр окружности, AB =2R;

vartriangle A_1B_1C_1 —вписан в окружность.

По теореме синусов: displaystyle frac{A_1B_1}{sinangle C}=2R; frac{A_1B_1}{AB}=frac{sqrt{2}}{2},

AB^2=2A_1B^2_1.

б) vartriangle ABC — прямоугольный, angle C={90}^{circ },

angle A={30}^{circ }

P — центр вписанной окружности; O — центр описанной окружности vartriangle ABC.

Проведём PHbot AB, PH=r (радиус вписанной окружности);
PLbot BC, PL=PH

Тогда BL=BH (отрезки касательных, проведенных из одной точки к вписанной окружности, равны). Пусть BC=a, тогда AC=asqrt{3}, AB=2a,

BL=BH=a-r,

OH=OB-BH=a-left(a-rright)=r

Рассмотрим vartriangle OPH:

OH=PH=r, angle H={90}^{circ },

angle POH=angle POB={45}^{circ }

Ответ: 45

17. Ольга Чемезова

В начале 2017 года Михаил положил сумму X рублей на депозит в банке. Банк начисляет 10% годовых в конце каждого года на имеющуюся сумму. Начисленные проценты остаются на депозите. В начале 2018 и 2019 годов Михаил пополнял вклад на такую же сумму X, в результате в конце 2019 года сумма на вкладе составила 152922 руб. Найдите сумму X.

Решение:

Составим схему пополнения вклада.

k=1,1  коэффициент, показывающий, во сколько раз увеличилась сумма вклада после начисления процентов;

К концу 2019 года сумма на депозите Михаила z = 152922 рубля;

left(left(xk+xright)cdot k+xright)k=z

xleft(k^3+k^2+kright)=z

displaystyle x=frac{152922}{{1,1}^3+{1,1}^2+1,1}=frac{10cdot 152922}{11cdot left({1,1}^2+1,1+1right)}=frac{10cdot 13902}{3,31}=frac{1000cdot {1390}^2}{331}=42000

Ответ: 42 000 рублей

18. Анна Малкова Найдите все значения параметра k, при каждом из которых система уравнений
displaystyle left{ begin{array}{c}{left(x-aright)}^2+{left(y-aright)}^2=frac{a^2}{4} \y=kx end{array}right. 
имеет единственное решение для любого a textgreater 0.

Решение:

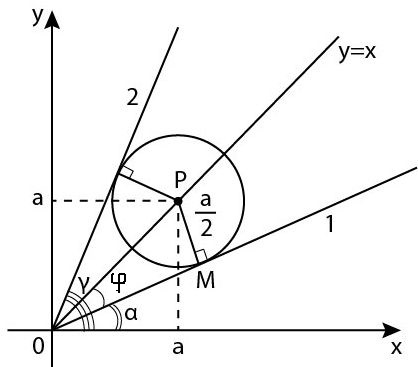
Решим систему графически в координатах Х, Y.

Первое уравнение задаёт окружность, центр left(a; aright) радиус displaystyle frac{a}{2}

Система имеет единственное решение, если y=kx — касательная к окружности.

Центр окружности displaystyle (x-a)^2+(y-a)^2 =frac{a^2}{4} лежит на прямой у = х – биссектрисе угла между положительными направлениями осей Х и Y.

Это значит, что если прямая y=kx касается окружности displaystyle {left(x-a_0right)}^2+{left(y-a_0right)}^2=frac{a^2_0}{4}, то она будет касаться всех окружностей такого вида для любого a.

Рассмотрим vartriangle OPM:

displaystyleangle M={90}^{circ }, PM=r=frac{a}{2}, OP=asqrt{2}

displaystyle {sin angle varphi =frac{PM}{OP}=frac{1}{2sqrt{2}}=frac{1}{sqrt{8}}, } тогда
displaystyle {cos angle varphi =frac{sqrt{7}}{sqrt{8}} }; tg varphi =frac{1}{sqrt{7}}

Для прямой 1:

k_1=tg a ;

a ={45}^{circ }-varphi .

displaystyle tg a =tgleft({45}^{circ }-varphi right)=frac{tg{45}^{circ }-tgvarphi }{1+tg{45}^{circ }tgvarphi}=frac{1-tgvarphi }{1+tgvarphi }=frac{1-frac{1}{sqrt{7}}}{1+frac{1}{sqrt{7}}}=frac{sqrt{7}-1}{sqrt{7}+1}==frac{{left(sqrt{7}-1right)}^2}{6}=frac{8-2sqrt{7}}{6}=frac{4-sqrt{7}}{3}.

Для прямой 2:

displaystyle k_2tggamma =tgleft({45}^{circ }+varphi right)=frac{tg{45}^{circ }+tgvarphi }{1-tg{45}^{circ }tgvarphi }=
displaystyle =frac{1+tgvarphi }{1-tgvarphi }=frac{sqrt{7}+1}{sqrt{7}-1 }=frac{{left(sqrt{7}+1right)}^2}{6}=frac{4+sqrt{7}}{3}

Ответ: frac{4pmsqrt{7}}{3}

19. На доске написаны 3 натуральных числа. К первому числу приписали справа цифру 6, ко второму — цифру 9, третье оставили без изменений.

а) Могла ли сумма этих чисел увеличиться в 9 раз?

б) Могла ли сумма этих чисел увеличиться в 19 раз?

в) В какое наибольшее целое число раз могла увеличиться сумма этих чисел?

Решение:

Вначале на доске написаны числа: a, b, c, их сумма равна a + b + c.

После того, как к ним приписали цифры, их сумма стала равна

10a+6+10b+9+c

а) Да, могла.

Предположим, что 10a+6+10b+9+c=9left(a+b+cright)
a+b+15=8c

Пусть c=3, тогда a+b=9.

Возьмём a=2, b=7.
2+7+3=12;
26+79+3=108=9cdot 12.

б) Предположим, что

10a+6+10b+9+c=19left(a+b+cright)

9a+9b+18c=15

Так как ageq 1, bgeq 1, cgeq 1,

9a+9b+18cgeq 36 textgreater 15 — противоречие

в) Пусть

10a+10b+15+c=mleft(a+b+cright)

displaystyle m=frac{10a+10b+c+15}{a+b+c}=frac{10a+10b+10c+15-9c}{a+b+c}=10+frac{15-9c}{a+b+c}

Так как ageq 1, bgeq 1, cgeq 1,

a+b+cgeq 3;

displaystyle frac{1}{a+b+c}leq frac{1}{3};

displaystyle mleq 10+frac{15-9c}{3}

Так как cgeq 1, -9cleq -9.

displaystyle mleq 10+frac{15-9}{3}

mleq 12 (оценка)

Приведём пример для m=12.

Пусть a=b=c=1;
16+19+1=36=12cdot left(1+1+1right).

Ответ:

а) да

б) нет

в) 12

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Вариант 1, решения» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.03.2023

Источник
Skip to content

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.

Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.admin2023-03-05T21:56:54+03:00

Используйте LaTeX для набора формулы
Источник

Задача 3. Начала теории вероятностей

Задача 3. Начала теории вероятностей

Задача 4. Вероятности сложных событий

Задача 4. Вероятности сложных событий

Задача 5. Простейшие уравнения

Задача 5. Простейшие уравнения

Задача 6. Вычисления и преобразования

Задача 6. Вычисления и преобразования

Задача 7. Производная и первообразная

Задача 7. Производная и первообразная

Задача 8. Задачи с прикладным содержанием

Задача 8. Задачи с прикладным содержанием

Задача 9. Текстовые задачи

Задача 9. Текстовые задачи

Задача 10. Графики функций

Задача 10. Графики функций

Задача 11. Наибольшее и наименьшее значение функций

Задача 11. Наибольшее и наименьшее значение функций

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Егэ по математике базовый уровень сдам егэ
  • Егэ по математике базовый уровень продолжительность экзамена
  • Егэ по математике базовый уровень онлайн решать онлайн
  • Егэ по математике базовый уровень задачи на вероятность
  • Егэ по математике базовый уровень 2022 ященко 30 вариантов скачать фипи

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии