Ответы на тренировочный вариант №182 профильного ЕГЭ
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Стоимость полугодовой подписки на журнал составляет 450 рублей, а стоимость одного номера журнала — 24 рубля. За полгода Аня купила 25 номеров журнала. На сколько рублей меньше она бы потратила, если бы подписалась на журнал?
Ответ:
2
На рисунке жирными точками показано суточное количество осадков, выпадавших в Казани с 3 по 15 февраля 1909 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, какого числа впервые выпало миллиметров осадков.
Ответ:
3
При строительстве сельского дома можно использовать один из двух типов фундамента: каменный или бетонный. Для каменного фундамента необходимо 9 тонн природного камня и 13 мешков цемента. Для бетонного фундамента необходимо 7 тонн щебня и 50 мешков цемента. Тонна камня стоит 1450 рублей, щебень стоит 700 рублей за тонну, а мешок цемента стоит 220 рублей. Сколько рублей будет стоить материал для фундамента, если выбрать наиболее дешевый вариант?
Ответ:
4
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ:
5
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Ответ:
6
Найдите корень уравнения:
Ответ:
7
8
На рисунке изображен график производной функции f(x). Найдите абсциссу точки, в которой касательная к графику y = f(x) параллельна прямой y = 6x или совпадает с ней.
Ответ:
9
В правильной треугольной пирамиде SABC с вершиной S биссектрисы треугольника ABC пересекаются в точке O. Площадь треугольника ABC равна 2; объем пирамиды равен 6. Найдите длину отрезка OS.
Ответ:
10
Найдите значение выражения
Ответ:
11
Независимое агентство намерено ввести рейтинг новостных интернет-изданий на основе оценок информативности In, оперативности Op, объективности публикаций Tr, а также качества сайта Каждый отдельный показатель оценивается читателями по 5-балльной шкале целыми числами от 1 до 5.
Аналитики, составляющие формулу рейтинга, считают, что объективность ценится втрое, а информативность публикаций — вдвое дороже, чем оперативность и качество сайта. Таким образом, формула приняла вид
Каким должно быть число A, чтобы издание, у которого все оценки наибольшие, получило бы рейтинг 1?
Ответ:
12
Объем треугольной пирамиды равен 30. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 7:8, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.
Ответ:
13
Митя, Антон, Гоша и Борис учредили компанию с уставным капиталом 200 000 рублей. Митя внес 14% уставного капитала, Антон − 42 000 рублей, Гоша − 12% уставного капитала, а оставшуюся часть капитала внес Борис. Учредители договорились делить ежегодную прибыль пропорционально внесенному в уставной капитал вкладу. Какая сумма от прибыли 1 000 000 рублей причитается Борису? Ответ дайте в рублях.
Ответ:
14
Найдите наибольшее значение функции на отрезке
Ответ:
15
Найдите наибольшее значение функции на отрезке
Ответ:
16
Каждому из четырёх неравенств в левом столбце соответствует одно из решений из правого столбца. Установите соответствие между неравенствами и множествами их решениями.
РЕШЕНИЯ
Впишите в приведённую в ответе таблицу под каждой буквой соответствующую цифру.
Ответ:
17
Какое из приведённых ниже утверждений равносильно утверждению «Если Вы ― слон, значит, Вы ничего не забываете»?
(1) Если Вы ничего не забываете, значит, Вы ― слон.
(2) Если Вы ― не слон, значит, Вы все забываете.
(3) Если Вы ― не слон, значит, Вы что-то забываете.
(4) Если Вы что-то забываете, значит, Вы ― не слон.
Ответ:
18
Приведите пример четырёхзначного числа, кратного 12, произведение цифр которого равно 10. В ответе укажите ровно одно такое число.
Ответ:
19
Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
ЕГЭ по математике, Вариант № 182, 11 класс, 2010.
На выполнение экзаменационной работы по математике дается 4 часа (240 мин). Работа состоит из двух частей и содержит 18 заданий. Часть 1 содержит 12 заданий с кратким ответом (В1–В12) базового уровня по материалу курса математики. Задания части 1 считаются выполненными, если экзаменуемый дал верный ответ в виде целого числа или конечной десятичной дроби.
Часть 2 содержит 6 более сложных заданий (С1–С6) по материалу курса математики. При их выполнении надо записать полное решение и ответ.
Примеры.
1. Магазин закупает цветочные горшки по оптовой цене 110 рублей за штуку. Торговая наценка составляет 25%. Какое наибольшее число таких горшков можно купить в этом магазине на 900 рублей?
2. На рисунке жирными точками показана цена серебра на момент закрытия биржевых торгов во все рабочие дни с 9 по 22 января 2008 года. По горизонтали указываются числа месяца, по вертикали – цена унции серебра в долларах США. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшую цену серебра на момент закрытия торгов в указанный период (в долларах США за унцию).
3. В треугольнике ABC угол C равен 90° , AB = 30, AC = 24. Найдите sin A.
4. Строительной фирме нужно приобрести 60 кубометров строительного бруса. У неё есть три поставщика. Сколько рублей придется заплатить за самую дешевую покупку с доставкой? Цены и условия доставки приведены в таблице.
5. Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рисунок). Ответ дайте в квадратных сантиметрах.
6. Для одного из предприятий-монополистов зависимость объема спроса на продукцию q (единиц в месяц) от ее цены p (тыс. руб.) задается формулой: q =160 −10 p . Определите максимальный уровень цены p (в тыс. руб.), при котором значение выручки предприятия за месяц r = q ⋅ p составит не менее 550 тыс. руб.
7. Перед каждым из чисел 4, 5, …, 8 и 14, 15, …, 20 произвольным образом ставят знак плюс или минус, после чего к каждому из образовавшихся чисел первого набора прибавляют каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Бесплатно скачать электронную книгу в удобном формате, смотреть и читать:
Скачать книгу ЕГЭ по математике, Вариант № 182, 11 класс, 2010 — fileskachat.com, быстрое и бесплатное скачивание.
Скачать pdf
Ниже можно купить эту книгу по лучшей цене со скидкой с доставкой по всей России.Купить эту книгу
Скачать книгу ЕГЭ по математике, Вариант № 182, 11 класс, 2010 — pdf — depositfiles.
Скачать книгу ЕГЭ по математике, Вариант № 182, 11 класс, 2010
— pdf — Яндекс.Диск.
Дата публикации: 31.05.2013 16:37 UTC
Теги:
математика :: ЕГЭ по математике :: 11 класс
Следующие учебники и книги:
- ЕГЭ по математике, Вариант № 186, 11 класс, 2010
- ЕГЭ по математике, Вариант № 185, 11 класс, 2010
- ЕГЭ по математике, Вариант № 184, 11 класс, 2010
- ЕГЭ по математике, Вариант № 183, 11 класс, 2010
Предыдущие статьи:
- ЕГЭ по математике, Вариант № 181, 11 класс, 2010
- ЕГЭ по математике, Вариант № 180, 11 класс, 2010
- ЕГЭ по математике, Вариант № 179, 11 класс, 2010
- ЕГЭ по математике, Вариант № 178, 11 класс, 2010
Задание 1
Найдите значение выражения $$(1frac{1}{12}+frac{1}{15})div1frac{2}{3}$$
Ответ: 0,69
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(frac{13}{3*4}+frac{1}{3*5})div frac{5}{3}=$$$$frac{13*5+1*4}{3*4*5}*frac{3}{5}=$$$$frac{69}{4*5*5}=0,69$$
Задание 2
В таблице приведены размеры штрафов за превышение максимальной разрешённой скорости, зафиксированное с помощью средств автоматической фиксации, установленных на территории России с 1 сентября 2013 года.
| Превышение скорости, кмч | 21-40 | 41-60 | 61-80 | 81 и более |
| Размер штрафа, руб. | 500 | 1000 | 2000 | 5000 |
Какой штраф должен заплатить владелец автомобиля, зафиксированная скорость которого составила 95 км/ч на участке дороги с максимальной разрешённой скоростью 60 км/ч?
Варианты ответа:
1) 500;
2) 1000;
3) 2000;
4) 5000.
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Превышение составляет 35 км/ч, что входит в интервал 21-40, и штраф в таком случае составляет 500 руб. Тогда ответ под номером 1
Задание 3
Между какими числами заключено число $$sqrt{30}$$
Варианты ответа:
1) 2 и 3;
2) 4 и 5;
3) 5 и 6;
4) 25 и 36.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sqrt{25} < sqrt{30} < sqrt{36} Leftrightarrow$$$$ 5 < sqrt{30} < 6$$. То есть правильный ответ будет под номером 3
Задание 4
Найдите значение выражения $$(3-sqrt{7})^{2}$$
Варианты ответа:
1) $$2$$;
2) $$16$$;
3) $$16-3sqrt{7}$$;
4) $$16-6sqrt{7}$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(3-sqrt{7})^{2}=$$$$3^{2}-2*3*sqrt{7}+(sqrt{7})^{2}=$$$$9+7-6sqrt{7}=$$$$16-6sqrt{7}$$
Задание 5
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На рисунке показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечается время работы фонарика в часах, на вертикальной оси – напряжение в вольтах. Определите по рисунку на сколько вольт упадет напряжение с конца 6-го по конец 56-го часа фонарика.
Ответ: 0,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Конец 6го — 1,4В, конец 56го — 1В. Тогда разница составляет: $$1,4-1=0,4$$
Задание 6
Решите уравнение $$(2x+3)^{2}+(x-5)^{2}=5x^{2}$$
Ответ: -17
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(2x+3)^{2}+(x-5)^{2}=5x^{2}$$ $$4x^{2}+12x+9+x^{2}-10x+25-5x^{2}=0$$ $$2x+34=0$$ $$x=-17$$
Задание 7
После уценки электрического чайника его новая цена составила 0,65 старой. На сколько процентов уменьшилась цена чайника в результате уценки?
Ответ: 35
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если проценты переводить в доли единицы, то получаем, что 1 процент соответствует 0,01, тогда 0,65 это 65 процентов, и , следовательно, уменьшение произошло на $$100-65=35%$$
Задание 8
На диаграмме представлены семь крупнейших по площади территории (в млн км2) стран мира.
Какие из следующих утверждений верны?
1. Алжир входит в семёрку крупнейших по площади территории стран мира
2. Площадь территории Канады составляет 9,6 млн км2.
3. Площадь Австралии меньше площади Бразилии.
4. Площадь Канады больше площади Индии более чем в три раза.
Ответ: 34
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. Алжир входит в семёрку крупнейших по площади территории стран мира — неверно, такой страны на диаграмме нет
2. Площадь территории Канады составляет 9,6 млн км2 — неверно, составляет 10 млн км2
3. Площадь Австралии меньше площади Бразилии. — верно
4. Площадь Канады больше площади Индии более чем в три раза. — верно
Задание 9
Конкурс исполнителей проводится в 4 дня. Всего заявлено 65 выступлений — по одному от каждой страны. В первый день 26 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса?
Ответ: 0,2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В оставшиеся дни ежедневно будет по : $$frac{65-26}{3}=13$$ выступлений. Тогда вероятность выступить в третий день ( как и в любой другой, кроме первого ) : $$P=frac{13}{65}=0,2$$
Задание 10
Найдите значение с по графику функции $$y=ax^{2}+bx+c$$, изображенному на рисунке.
Варианты ответа:
1) 1;
2) -1;
3) 2;
4) -2.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Значение коэффициента $$c$$ соответствует ординате точки пересечения оси $$oY$$ графиком квадратичной функции, то есть в приведенном примере $$c=2$$ (3 вариант ответа)
Задание 11
Выписаны первые несколько членов арифметической прогрессии: — 3; 1; 5; … Найдите сумму первых тридцати её членов.
Ответ: 1650
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Первый член прогрессии : $$a_{1}=-3$$ ; разность арифметической прогрессии: $$d=1-(-3)=4$$. Найдем сумму первых тридцати ее членов: $$S_{30}=frac{2*(-3)+4(30-1)}{2}*30=$$$$110*15=1650$$
Задание 12
Упростите выражение $$frac{6b}{7a}-frac{49a^{2}+36b^{2}}{42ab}+frac{7a-36b}{6b}$$ и найдите его значение при $$a=-39$$, $$b=99$$
Ответ: -6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{6b}{7a}-frac{49a^{2}+36b^{2}}{42ab}+frac{7a-36b}{6b}=$$$$frac{36b^{2}-49a^{2}-36b^{2}+49a^{2}-36*7ab}{42ab}=$$$$frac{-6*6*7ab}{6*7ab}=-6$$
Задание 13
Площадь четырёхугольника можно вычислить по формуле $$S=frac{d_{1}d_{2}sinalpha}{2}$$, $$d_{1},d_{2}$$ — длины диагоналей четырёхугольника, $$alpha$$ — угол между диагоналями. Пользуясь этой формулой найдите длину диагонали $$d_{2}$$, если $$d_{1}=9$$, $$sinalpha=frac{1}{6}$$, $$S=15$$
Ответ: 20
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$d_{2}=frac{2S}{d_{1}sinalpha}=$$$$frac{2*15}{9*frac{1}{6}}=$$$$frac{2*15*6}{9}=20$$
Задание 14
На каком рисунке изображено множество решений неравенства $$18-5(x+3)>1-7x$$ ?
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$18-5(x+3)>1-7x Leftrightarrow$$$$18-5x-15-1+7x> 0 Leftrightarrow$$$$2x> -2|:2 Leftrightarrow$$$$x> -1$$. Данный ответ соответствует 3 варианту.
Задание 15
От столба к дому натянут провод длиной 10 м, который закреплён на стене дома на высоте 3 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 8 м. Ответ дайте в метрах.
Ответ: 9
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Сделаем дополнительное построение:
$$CB=NH=8$$. Тогда по теореме Пифагора из треугольника ABC: $$AC=sqrt{10^{2}-8^{2}}=6$$
$$CN=BH=3$$, тогда $$AN=6+3=9$$
Задание 16
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=75° и ∠OAB=18°. Найдите угол BCO. Ответ дайте в градусах.
Ответ: 57
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Угол ABC вписанный, угол AOC — центральный, они опираются на одну дугу, значит угол AOC в два раза больше, то есть 150 градусов. Тогда внутренний угол $$AOC=360-150=210$$. Тогда по свойству углов четырехугольника $$angle BCO = 360-210-75-18 =57^{circ}$$
Задание 17
Высота равностороннего треугольника равна $$3sqrt{3}$$. Найдите его периметр.
Ответ: 18
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть а — сторона треугольника, h — высота, тогда: $$h=asin 60^{circ} Leftrightarrow$$$$a=frac{h}{sin 60^{circ}}=frac{3sqrt{3}}{frac{sqrt{3}}{2}}=6$$. Периметр — сумма длин всех сторон, тогда : $$P=3*6=18$$
Задание 18
Площадь ромба равна 60, а периметр равен 30. Найдите высоту ромба.
Ответ: 8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Раз периметр равен 30, то одна сторона ромба: $$a=frac{30}{4}=7,5$$. Высоту ромба можно найти через его площадь: $$h=frac{S}{a}=frac{60}{7,5}=8$$
Задание 19
В треугольнике $$ABC$$ $$AB=BC=3sqrt{5}$$, высота СН равна 3. Найдите $$tg A$$.
Ответ: 0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
По теореме Пифагора из треугольника BCH: $$BH=sqrt{(3sqrt{5})^{2}-3^{2}}=6$$. Вероятнее всего необходимо найти тангенс угла B, его можно найти как отношение CH к BH из треугольника BCH: $$tg A=frac{3}{6}=0,5$$ Если же надо именно угла А, то найдем AH : $$AH=AB-BH=3sqrt{5}-6$$. Тогда из треугольника AHC: $$tgA=frac{CH}{AH}=frac{3}{3sqrt{5}-6}$$
Задание 20
Какие из следующих утверждений верны?
1. Все углы ромба равны.
2. Диагонали ромба взаимно перпендикулярны
3. Высота ромба в два раза больше радиуса вписанной в него окружности.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 23
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. Все углы ромба равны — неверно, только противоположные 2. Диагонали ромба взаимно перпендикулярны — верно 3. Высота ромба в два раза больше радиуса вписанной в него окружности — верно
Задание 21
Решите уравнение $$(x-2)^{3}-(x-3)^{3}=37$$
Ответ: $$left { -1;6 right }$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Разложим левую часть уравнения по формуле сокращенного умножения разность кубов: $$((x-2)-(x-3))((x-2)^{2}+(x-2)(x-3)+(x-3)^{2})=37 Leftrightarrow$$$$(x-2-x+3)(x^{2}-4x+4+x^{2}-5x+6+x^{2}-6x+9)=37 Leftrightarrow$$$$1*(3x^{2}-15x+19)=37Leftrightarrow$$$$3x^{2}-15x-18=0 |:3 Leftrightarrow$$$$x^{2}-5x-6=0$$ Воспользуемся теоремой Виета: $$left[begin{matrix}x_{1}+x_{2}=5\ x_{1}*x_{2}=-6end{matrix}right.Leftrightarrow $$$$left[begin{matrix}x_{1}=6\ x_{2}=-1end{matrix}right.$$
Задание 22
Первый велосипедист выехал из поселка по шоссе со скоростью 15 км/ч. Через час после него со скоростью 10 км/ч из того же поселка в том же направлении выехал второй велосипедист, а еще через час после этого — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 2 часа 20 минут после этого догнал первого.
Ответ: 25
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Чтобы найти время, за которое догоняет первый объект второго, при учете различного времени выезда, необходимо воспользоваться формулой: $$t=frac{v_{2}t_{1}}{v_{1}-v_{2}}$$, где $$v_{1}$$-скорость того, кто догоняет, $$v_{2}$$ — скорость того, которого догоняют, $$t_{1}$$-разница во времени выезда. Пусть x км/ч — скорость третьего. Тогда, время, за которое третий догонит второго: $$t_{1}=frac{10*1}{x-10}$$,- время, за которое третий догонит первого: $$t_{2}=frac{15*2}{x-15}$$. При этом $$t_{2}-t_{1}=2frac{20}{60}$$ часов. $$frac{15*2}{x-15}-frac{10*1}{x-10}=2frac{20}{60} Leftrightarrow$$$$frac{30}{x-15}-frac{10}{x-10}=frac{7}{3} |*3(x-15)(x-10) Leftrightarrow$$$$3(30x-300-10x+150)=7(x^{2}-25x+150)Leftrightarrow$$$$60x-450-7x^{2}+175x-1050=0|*(-1)Leftrightarrow$$$$7x^{2}-235x+1500=0$$ Найдем корни уравнения через дискриминант: $$D=55225-42000=13225=115^{2}$$ $$x_{1}=frac{235+115}{14}=25$$ $$x_{2}=frac{235-115}{14}=frac{60}{7}$$ — не подходит, так как скорость третьего должна быть больше, чем скорости первого и второго (иначе он их не сможет догонять)
Задание 23
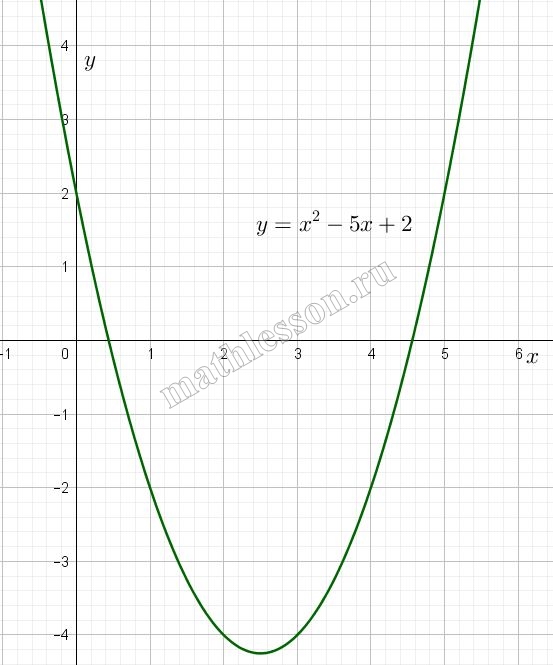
Постройте график функции $$y=|x^{2}-5x+2|$$ . Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Рассмотрим график функции $$y_{1}=x^{2}-5x+2$$. Искомый будет отличаться от данного тем, что та часть параболы, которая находится под осью Ох симметрично отобразиться относительно оси Ох (в силу того, что модуль все отрицательные значения сделает положительными).
Найдем вершину параболы: $$x_{0}=-frac{b}{2a}=-frac{-5}{2}=2,5$$ , $$y_{1}(2,5)=2,5^{2}-5*2,5+2=-4,25$$.
Найдем еще несколько значений для функции $$y_{1}$$: $$y_{1}(2)=-4 ; y_{1}(1)=-2 ; y_{1}(0)=2$$. График квадратичной функции симметричен относительно оси $$x=x_{0}$$, в нашем случае относительно $$x=2,5$$. Начертим график функции $$y_{1}$$:
Отобразим симметрично относительно оси Ох ту часть параболы, которая располагается под осью Ох и получим график функции $$y=|x^{2}-5x+2|$$:
Очевидно, что прямая параллельная оси Оу будет иметь максимально четыре точки пересечения с графиком данной функции, например:
Задание 24
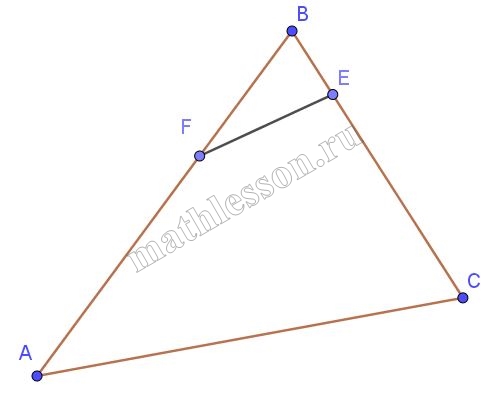
На сторонах ВС и ВА треугольника АВС взяты точки E и F такие, что ВE:EС=1:3, ВF:FА=1:2. Площадь треугольника BEF равна 10. Найти площадь треугольника АВС
Ответ: 120
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{S_{ABC}}{S_{BEF}}=frac{AB*BC}{BF*BE}(1)$$. Так как ВE:EС=1:3, то BC=4BE, так как ВF:FА=1:2, то AB=3BF. Подставим данные выражения в формулу (1): $$frac{S_{ABC}}{S_{BEF}}=frac{3BF*4BE}{BF*BE}=12$$, тогда $$S_{ABC}=12S_{BFE}=12*10=120$$
Задание 25
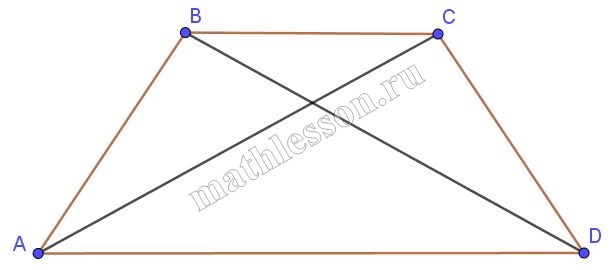
Докажите, что в трапеции, диагонали которой являются биссектрисами углов при одном из оснований, длины трёх сторон равны.
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1)$$angle BDA=angle DBC$$(накрестлежащие при параллельных BC и AD) ; $$angle BDA=angle BDC$$ (BD — биссеткриса) , тогда $$angle BDC=angle DBC$$, тогда треугольник BDC — равнобедренный и BC=BD(1)
2)аналогично рассматривается равенство углов BAC и BCA, тогда треугольник ABC — равнобедренный, и AB=BC, но с учетом равенства (1) получаем AB=BC=CD.
ч.т.д.
Задание 26
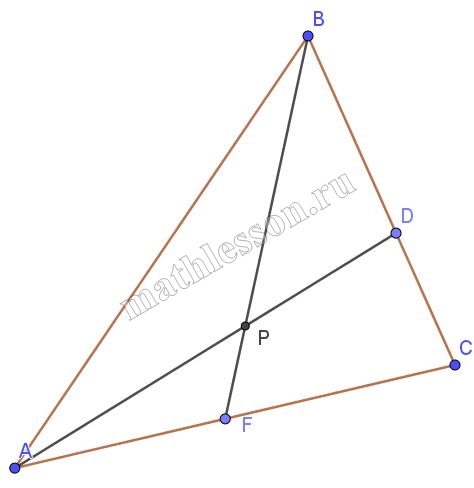
В треугольнике АВС точка D на стороне ВС и точка F на стороне АС расположены так, что ВD:DC=3:2, AF:FC=3:4. Отрезки AD и BF пересекаются в точке Р. Найдите отношение АР:PD.
Ответ: $$frac{5}{4}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
ВD:DC=3:2, пусть BD=3x, тогда DC=2x, а BC=5x. AF:FC=3:4, пусть AF=3y, тогда FC=4y. По теореме Менелая для треугольника BFC: $$frac{AP}{PD}*frac{BD}{BC}*frac{CF}{AF}=1Leftrightarrow$$$$frac{AP}{PD}*frac{3x}{5x}*frac{4y}{3y}=1Leftrightarrow$$$$frac{AP}{PD}=frac{5}{4}$$
Регистрация Форум Текущее время: 10 мар 2023, 22:39 Сообщения без ответов | Активные темы Страница 1 из 19 [ Сообщений: 190 ] На страницу 1, 2, 3, 4, 5 … 19 След. Начать новую тему»> Ответить Тренировочный вариант №182
Тренировочный вариант №182
Страница 1 из 19 [ Сообщений: 190 ] На страницу 1, 2, 3, 4, 5 … 19 След. Текущее время: 10 мар 2023, 22:39 | Часовой пояс: UTC + 3 часа Удалить cookies форума | Наша команда | Вернуться наверх Кто сейчас на форуме
|









 Для печати
Для печати
 Предыдущая тема | Следующая тема
Предыдущая тема | Следующая тема 




