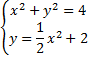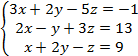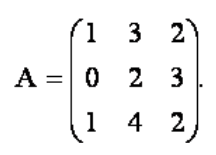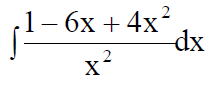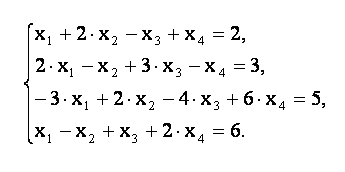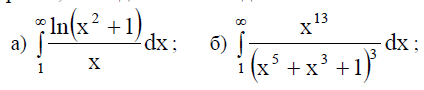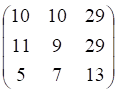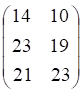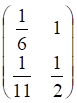Экзамен по элементам высшей математике

ДЕПАРТАМЕНТ
ОБРАЗОВАНИЯ ГОРОДА МОСКВЫ

Государственное
бюджетное профессиональное

образовательное
учреждение города Москвы

«МОСКОВСКИЙ
КОЛЛЕДЖ БИЗНЕС-ТЕХНОЛОГИЙ»

(ГБПОУ
КБТ)

УТВЕРЖДАЮ

Заместитель
директора по содержанию образования                    ГБПОУ
КБТ

_________      Ю.А.
Медведева                                              

  2015г

  
ЗАДАНИЯ ИТОГОВОЙ
АТТЕСТАЦИИ                                                                  

по
дисциплине

«ЭЛЕМЕНТЫ
ВЫСШЕЙ МАТЕМАТИКИ»

2014/2015
учебный год

для
студентов 2 курса, обучающихся по специальности

230115 «Программирование
и компьютерные системы»

Преподаватели:
Маковкина Н.П.

СОГЛАСОВАНО                                                                                                                                    

Протокол
заседания  предметной (цикловой) комиссии (кафедры)                                            
Естественнонаучных дисциплин 

от 
12 мая 2015г.   № 13

Председатель
предметной (цикловой) комиссии (кафедры) ___________Кузнецова Е.В.

12
мая  2015г.


Пояснительная записка

Цель экзамена:проверка
уровня предметной компетентности студентов2 курса

 по дисциплине «Элементы высшей
математики» за 2014-2015 учебный год в рамках проведения  промежуточной   аттестации.

Форма экзамена:
письменно, по контрольно-измерительным материалам.

Количество вариантов 2.

Структура экзаменационной работы:

На
выполнение экзаменационной работы отводится 2 часа (90 минут).

Экзаменационная
работа состоит из одной части, включающей 9 заданий с полным решением и ответом
базового уровня сложности. Задания: №4 содержит 4 примера, №8 – 2 примера. При
выполнении заданий 1-13  необходимо записать ход решения и полученный ответ.

Критерии оценивания работы:

Отметка

Количество
баллов

«5»

11-13

«4»

9—10

«3»

7—8

«2»

0-6

Вариант
№1.

1. Вычислите .

2. Решить систему уравнений по
формулам Крамера

3. Прямая, проходящая через точку
(-4;-1) пересекает ось Оу в точке (0;3).     Составьте уравнение
этой прямой.

4. Даны векторы: . Найти:

         а)

5. Каноническое уравнение эллипса
имеет вид:

а)                           в)

         б)                        г)

6. Вычислите:

7. Найти производную первого
порядка  функции

8. Вычислите:   а) ,

                           б) , 1

9. Найдите частные решения
дифференциального уравнения, удовлетворяющие начальным условиям:

Вариант 2.

1. Вычислите .

2. Решить систему уравнений по
формулам Крамера

3. Прямая, проходящая через точку
(-2;4) пересекает ось Ох в  точке (2;0). Составьте уравнение этой прямой.

4. Даны векторы: . Найти:

         а)

5. Каноническое уравнение гиперболы
 имеет вид:

а)                           в)

         б)                        г)

6. Вычислите:

7. Найти производную первого
порядка  функции

8. Вычислите:  a)  ;

                          б)  , 1

9. Найдите частные решения
дифференциального уравнения, удовлетворяющие начальным условиям:

Ответы к
заданиям.

Вариант
I

Вариант
II

1.       

1.

2.           
(3; -1)

2.
(2;
-4)

3.     

3.

     
4.    
а) (15; 8; -23);

б);

в)
62;

г)

4.
a) (-1;
0; 1);

б);

в)
24;

г)

               5.          в

                  
5.
      в

                 
6.          6

                 
6.        

7.

7.

                 
8.
  a) 
10;

                       
б)  9,5

                 
8.;

                      
б)  6

                
9.

                 
9.
Источник

Министерство образования и науки Хабаровского края

Краевое государственное бюджетное

профессиональное образовательное учреждение

«Хабаровский технический колледж»

Рассмотрено и рекомендовано ПЦК

«Математических и естественнонаучных дисциплин»

Протокол № ___ от «___» ___________ 2017г.

Председатель ПЦК __________ ___________________

Утверждаю

директора по УР

____________ Клюева В.Н.

«___» ___________ 2017 г.

СОГЛАСОВАНО

Руководитель по ИМР

_______________ Павленко Е.В.

«___» ___________ 2017 г.

КОМПЛЕКТ ОЦЕНОЧНЫХ СРЕДСТВ

по учебной дисциплине

«Элементы высшей математики»

для проведения итогового контроля и соответствия уровня и качества подготовки обучающихся КГБ ПОУ ХТК

по специальности(ям):

Информационные системы

курс 2 (на базе основного общего образования)

Форма проведения оценочной процедуры: экзамен

Разработчик: Адливанкина А.М., преподаватель математики, физики, информатики и ИТ.

2015

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 1

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Элементы высшей математики. Основные разделы и их значение в специальности.

2. Умножить матрицу  на матрицу 

3. При помощи двойного интеграла вычислить площадь плоской фигуры D, ограниченной линиями .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 2

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Обратная матрица. Миноры. Вычисление обратной матрицы.

2. Решить предел 

3. Решить графически систему уравнений:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 3

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Приращение аргумента и функции. Точки разрыва.

2. Найти частные производные первого порядка функции 

3. Составить параметрическое уравнение прямой, если известна точка А(1; 0,5) и

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 4

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Геометрический смысл производной. Правила нахождения производных.

2. Решить дифференциальное уравнение .

3. Решить систему уравнений матричным методом:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 5

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Приближение функции. Системы уравнений.

  2. Дан двойной интеграл  с областью интегрирования . Перейти к повторным интегралам и расставить пределы интегрирования.

  3. 3. Найти общее решение дифференциального уравнения:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 6

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Метод координат на плоскости. Уравнение прямой на плоскости.

2. Решить дифференциальное уравнение первого порядка  .

3. Решить систему уравнений методом Гаусса:

Преподаватель __________ А.М. Адливанкина

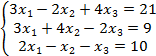
Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 7

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Решение систем уравнений методом Крамера.

2. Решить дифференциальное уравнение 

3. Найти обратную матрицу данной:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 8

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Определители. Вычисление определителей.

2. Найти действительную и мнимую часть функции .

3. При помощи приближенных вычислений найти

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 9

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Вычисление приближенного числового значения функции. Формулы приближенного вычисления.

2. Вычислить предел 

3. Решить систему уравнений методом Крамера:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 10

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Непрерывность функции, ее свойства. Асимптоты.

2. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию 

3. При помощи приближенных вычислений вычислить .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 11

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Производные и дифференциалы высших порядков.

2. Найти действительную и мнимую часть функции 

3. Найти определитель матрицы

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 12

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Понятие знакочередующегося, степенного ряда. Абсолютная и условная сходимость.

2. Найти интервал сходимости исследуемого степенного ряда .

3. Вычислить предел функции

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 13

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Понятие положительного ряда. Признак Даламбера.

  2. Найти y(3) для функции .

  3. Исследовать ряд на сходимость:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 14

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Решение систем уравнений методом Гаусса.

2. Даны комплексные числа , . Найти частное .

3. Используя признак предельного сравнения исследовать на сходимость рад:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 15

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Абсолютная и относительная погрешность приближенного значения числа, округление.

2. Найти неопределенный интеграл (по частям).

.

3. Исследовать ряд на сходимость используя признак Даламбера:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 16

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Применение производной к исследованию функций.

2. Вычислить определенный интеграл

3. Вычислите предел функции .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 17

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

1. Действия над комплексными числами, заданными в алгебраической форме.

2. Найти производную функции 

3. Найти вторую производную функции

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 18

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Формула Ньютона – Лейбница. Вычисление площадей плоских фигур.

  2. Найти производную функции .

  3. Решить дифференциальное уравнение:

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 19

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Бесконечная числовая последовательность и ее предел.

  2. Умножить матрицу    на матрицу  .

  3. Вычислить интеграл .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 20

по дисциплине «Элементы высшей математики»

  1. курс (база 9 классов)

1. Понятие первообразной. Неопределенный интеграл.

2. Вычислить разность и сумму комплексных чисел: z=2i+5, z=-3+4i.

3. Найти , если .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 21

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Предел числовой последовательности. Замечательные пределы.

  2. Найти , если f(x)=(2x-4)5

  3. Вычислить произведение и сумму комплексных чисел: z=2i+5, z=-3+4i.

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 22

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Понятие числового ряда. Признаки сходимости.

  2. Найти неопределенный интеграл методом замены переменной и выполнить проверку.

3. Найти если

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 23

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Понятие обыкновенного дифференциального уравнения. Общее и частное решение.

  2. Вычислить приближенно , заменяя приращения функции ее дифференциалом.

  3. 2. Вычислить неопределенный интеграл

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 24

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Вычисление дифференциала функции. Абсолютная и относительная погрешность.

  2. Найти неопределенный интеграл. .

  3. Найти частное решение дифференциального уравнения , удовлетворяющее начальному условию .

Преподаватель __________ А.М. Адливанкина

Министерство образования и науки Хабаровского края

КГБ ПОУ «Хабаровский технический колледж»

Экзаменационный билет № 25

по дисциплине «Элементы высшей математики»

2 курс (база 9 классов)

  1. Приложения интегралов к нахождению объемов тел и вычислению величин.

  2. Найти неопределенный интеграл.

  3. Изобразите кривые второго порядка.

Преподаватель __________ А.М. Адливанкина

Источник

Государственное автономное профессиональное  образовательное  учреждение Новосибирской области

«Карасукский педагогический колледж»

УТВЕРЖДАЮ

Зам. директора по учебно-методической работе

……………………О.М. Кривушева

КОНТРОЛЬНО – ОЦЕНОЧНЫЕ СРЕДСТВА

учебной дисциплины

ЕН.01. Элементы высшей математики

  специальности  09.02.03 Программирование в компьютерных системах

Курс 3

Комплект   контрольно-оценочных   средств   по   учебной дисциплине  разработан на основе Федерального государственного образовательного стандарта среднего профессионального образования  (далее  –  ФГОС СПО)  по   специальности 09.02.03 Программирование в компьютерных системах

Организация – разработчик: ГАПОУ НСО «Карасукский педагогический колледж»

Разработчик: Шуст М.Н. преподаватель ГАПОУ НСО «Карасукский педагогический колледж».

Паспорт контрольно – оценочных средств

для  проведения экзамена по  учебной  дисциплине

ЕН.01. Элементы высшей математики

специальности  09.02.03 Программирование в компьютерных системах

для студентов 3 курса

КОС разработаны на основании:

— основной профессиональной образовательной программы по направлению подготовки специальности СПО 09.02.03 «Программирование в компьютерных системах»;

— программы учебной дисциплины ЕН.01. «Элементы высшей математики».

КОС предназначены для проведения промежуточной аттестации в форме экзамена.

Задания по экзамену направлены на проверку освоения предметных результатов освоения образовательной программы (умений) и практических навыков применения математических знаний в повседневных ситуациях.

В работе контролируются элементы содержания из следующих разделов  курса элементы высшей математики:

1. Раздел 5. Дифференциальное исчисление функций одной переменной.

2. Раздел 6.  Интегральное исчисление функции одной переменной.

3. Раздел 7. Обыкновенные дифференциальные уравнения, их виды и методы решения.

Экзаменационная работа проверяет освоение знаний и умений, формируемых при изучении курса элементы высшей математики:

знать:

З1— основы  математического анализа;

З3— основы  дифференциального и  интегрального исчисления;

уметь:

У4— применять методы дифференциального и  интегрального исчисления;

У5 — решать дифференциальные уравнения.

Результаты освоения дисциплины, подлежащие проверке

Результаты обучения (освоенные умения, усвоенные знания)

Основные показатели оценки результатов

Умение применять методы дифференциального и  интегрального исчисления.

— Нахождение производной функции.

— Нахождение производных высших порядков.

— Исследование функции и построение графика.

— Нахождение неопределенных интегралов.

— Вычисление определенных интегралов.

-Вычисление площадей фигур, объёмов  фигур, длин дуги кривой.

Умение решать дифференциальные уравнения.

— Решение дифференциальных уравнений первого и второго порядка.

Знание основ  математического анализа

— Исследование функций при построении.

— Классификация точек разрыва.

Знание основ  дифференциального и  интегрального исчисления.

— Формулировка понятия производной, свойств.

— Формулировка правил дифференцирования и перечисление производных основных элементарных функций.

— Перечисление табличных интегралов.

— Приложение определенного интеграла к вычислению площадей фигур, объемов тел вращения.

В ходе проведения экзамена оценивается освоение общих компетенций (ОК):

Общие компетенции

Показатели оценки результата

ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес.

Аргументированность и полнота объяснения сущности и социальной значимости будущей профессии.

Активность, инициативность в процессе освоения профессиональной деятельности.

ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.

Обоснованность выбора методов и приемов при выполнении внеаудиторной самостоятельной работы; способов решения профессиональных задач. Умение оценивать свою деятельность по предложенной преподавателем шкале.

ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

Объективность оценки степени риска и принятие оптимальных решений в нестандартной ситуации на основе оперативного анализа.

Своевременное проведение эффективных профилактических мер для снижения риска в профессиональной деятельности на основе прогнозирования развития ситуации.

ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.

Оперативность и самостоятельность поиска, анализа, оптимальность выбора информационных ресурсов различного типа (текстовых, графических, числовых и т.п.), необходимых для постановки и решения профессиональных задач в области информационных технологий и личностного роста.

Объективная оценка значимости и возможности применения информации для решения профессиональных задач и личностного роста.

Грамотное применение  методов обработки информации и результатов исследований, систематизация, представление и интерпретация полученных данных.

ОК 5. Использовать информационно-коммуникационные технологии в профессиональной деятельности.

Оптимальный отбор и эффективность использования информационно-коммуникационных технологий, информационных ресурсов сети Интернет в совершенствовании профессиональной деятельности.

Эффективное использование программного обеспечения для совершенствования профессиональной деятельности.

ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями.

Эффективность и целесообразность общения с коллегами, руководством (совместное решение профессиональных задач).

Соблюдение норм делового общения и деловой этики во взаимодействии с руководством, коллегами и социальными партнерами.

Аргументированная трансляция своей точки зрения.

ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий.

Эффективность организации коллективной (командной) работы в профессиональной деятельности.

Объективность анализа успешности коллективной (групповой) работы, путей ее совершенствования.

ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно планировать повышение квалификации.

Самостоятельное, систематическое, осознанное планирование самообразования, саморазвития, профессионального самосовершенствования, и повышения квалификации в соответствии с современными требованиями и на основе анализа собственной деятельности

ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.

Проявление устойчивого интереса к инновациям в области профессиональной деятельности.

Быстрая адаптация к изменяющимся условиям.

Своевременное обновление методологического и технологического содержания профессиональной деятельности в области информационных технологий

Распределение типов и количества контрольных заданий по элементам знаний и умений, контролируемых на промежуточной аттестации

Содержание учебного материала по программе УД

Тип контрольного задания

У4

применять методы дифференциального и  интегрального исчисления

У5

решать дифференциальные уравнения

З1

основы  математического анализа

З3

основы  дифференциального и  интегрального исчисления

Раздел 5. Дифференциальное исчисление функций одной переменной

Тема 5.1. Производная функции, свойства и формулы дифференцирования.

расчетное задание 1

расчетное задание 3

расчетное задание 1

расчетное задание 3

Тема 5.2. Производные и дифференциалы высших порядков.  

Тема 5.3. Приложения производной к исследованию функции на монотонность, экстремумы.

Тема 5.5. Исследования функций и построение графиков.

Раздел 6.  Интегральное исчисление функции одной переменной

Тема 6.1. Неопределённый интеграл и его свойства.

расчетное задание 2

расчетное задание 3

расчетное задание 3

расчетное задание 2

расчетное задание 3

Тема 6.2. Основные методы интегрирования.

Тема 6.3. Интегрирование  рациональных дробей.

Тема 6.4. Определённый интеграл, свойства, формула Ньютона-Лейбница.  

Тема 6.5. Замена переменной в  определенном интеграле.

Тема 6.6. Интегрирование по частям в определённом  интеграле.

Тема 6.7. Несобственные интегралы.

Тема 6.8. Вычисление площадей плоских фигур.

Тема 6.9. Вычисление объёмов тел.

Тема 6.10. Вычисление длины дуги кривой.

Раздел 7. Обыкновенные дифференциальные уравнения, их виды и методы решения.

Тема 7.1. Дифференциальные уравнения первого порядка.

расчетное задание 4

расчетное задание 4

Тема 7.2. Дифференциальные уравнения с разделяющимися переменными.

Тема 7.3. Однородные дифференциальные уравнения.

Тема 7.4. Линейные дифференциальные уравнения.

Тема 7.5. Уравнения в полных дифференциалах.

Тема 7.6. Линейные однородные дифференциальные уравнения второго   порядка с постоянными коэффициентами.

Оценочные средства

1 вариант

1. Найдите монотонность функции  

2. Найдите интеграл методом подстановки  

3. Найдите площадь фигуры, ограниченной линиями:

y=4x-x2 и  y=4-x

4.Найдите общее решение дифференциального уравнения с разделяющимися переменными  

(2-у) ·dу=хdх

2 вариант

1. Найдите экстремумы функции  

2. Найдите интеграл методом по частям  

3. Найдите площадь фигуры, ограниченной линиями:

y=x2 и  y=2x-x2

4.Найдите общее решение линейного дифференциального уравнения первого порядка  

Условия выполнения: данные задания выполняются в форме проведения письменной работы; к выполнению письменной работы допускаются студенты, прошедшие инструктаж по выполнению заданий, критерии оценивания; работа выполняется студентами самостоятельно на листах; при выполнении работы обучающемуся предоставляется возможность в течение всего времени, отведенного на выполнение заданий, вносить изменения в свои решения и ответы, пропускать ряд заданий с возможностью последующего возврата к пропущенным заданиям; выполненные задания сдаются учителю.

Время на выполнение: 90 минут.

Критерии оценивания к заданиям

1 задание

Наименование объектов контроля и оценки

Основные показатели оценки результата

Критерии оценивания выполнения задания

Баллы

Знание основ  дифференциального исчисления

— Формулировка правил дифференцирования и перечисление производных основных элементарных функций.

-правильно воспроизведены правила дифференцирования и производные основных элементарных функций.

-правильно воспроизведен алгоритм монотонности, экстремумов функций с помощью производной.

-верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

-решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

-рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

-решение неверное, продвижение или решение отсутствует.

2

1

0

Умение применять методы дифференциального исчисления.

— Нахождение производной функции.

— Исследование функции на монотонность, экстремумы.

2 задание

Наименование объектов контроля и оценки

Основные показатели оценки результата

Критерии оценивания выполнения задания

Баллы

Знание основ  интегрального исчисления.

— Перечисление табличных интегралов

-правильно воспроизведены табличные интегралы.

— правильно решены интегралы методом замены переменной, интегрированием по частям.

-верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

-решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

-доказаны вспомогательные утверждения, помогающие в решении задачи.

-рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

-решение неверное, продвижение или решение отсутствует.

2

1

0

Умение применять методы интегрального исчисления.

— Нахождение неопределенных интегралов методами замены переменной, по частям

3 задание

Наименование объектов контроля и оценки

Основные показатели оценки результата

Критерии оценивания выполнения задания

Баллы

Знание основ математического анализа

— Исследование функций при построении.

— Классификация точек разрыва, если имеются.

-правильное определение вида функции;

-правильно построили графики функции, применяя полученные данные;

-правильно воспроизведены табличные интегралы.

-правильно использовали приложение определенного интеграла к вычислению площадей плоских фигур.

-выбран правильный путь решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ, соответствующий данному заданию.

-верно выполнено задание, но нет обоснований.

-ход выполнения  заданий верный, но допущены вычислительные ошибки.

-ход выполнения  заданий верный, но неверно составлена запись вычисления искомой площади

-начато решение, но не закончено.

-другие случаи, не соответствующие указанным критериям.

2

1

0

Знание основ  интегрального исчисления.

— Приложение определенного интеграла к вычислению площадей плоских фигур

Умение применять методы интегрального исчисления.

-Вычисление площадей плоских фигур

4 задание

Наименование объектов контроля и оценки

Основные показатели оценки результата

Критерии оценивания выполнения задания

Баллы

Знание основ  дифференциального и  интегрального исчисления

— Формулировка правил дифференцирования, интегрирования и перечисление производных, интегралов основных элементарных функций.

-правильно воспроизведены правила дифференцирования и производные основных элементарных функций.

-правильно воспроизведены табличные интегралы.

-правильно воспроизведены способы решения дифференциальных уравнений первого и второго порядка.

-верное решение. Имеются небольшие недочеты, в целом не влияющие на решение.

-решение в целом верное. Однако оно содержит ряд ошибок, либо не рассмотрение отдельных случаев, но может стать правильным после небольших исправлений или дополнений.

-доказаны вспомогательные утверждения, помогающие в решении задачи.

-верно рассмотрен один из двух (более сложный) существенных случаев, или в задаче типа «оценка + пример» верно получена оценка.

-рассмотрены отдельные важные случаи при отсутствии решения (или при ошибочном решении).

-решение неверное, продвижение или решение отсутствует.

2

1

0

Умение решать дифференциальные уравнения.

— Решение дифференциальных уравнений первого и второго порядка.

Универсальная шкала оценки выполнения экзаменационной работы

Количество полученных баллов

Процент результативности

Качественная оценка индивидуальных образовательных достижений

балл (отметка)

вербальный аналог

8

90 — 100

5

отлично

6-7

75-89

4

хорошо

4-5

60 – 74,9

3

удовлетворительно

менее 4

менее 60

2

неудовлетворительно
Источник

Пакет экзаменационных материалов содержит банк заданий для проведения промежкточной аттестации студентов средних профессиональных учреждений по дисциплине ЕН. 01 Элементы высшей математики. Материалы предназначены для подготовки к экзамену, а также будут полезны преподавателям.

Вы уже знаете о суперспособностях современного учителя?

Тратить минимум сил на подготовку и проведение уроков.

Быстро и объективно проверять знания учащихся.

Сделать изучение нового материала максимально понятным.

Избавить себя от подбора заданий и их проверки после уроков.

Наладить дисциплину на своих уроках.

Получить возможность работать творчески.

Источник

Решение математики

Экзаменационные билеты, вопросы и задачи по курсу высшей математики для студентов 1 курса (1 и 2 учебный семестр) и 2 курса (3 и 4 семестр) очной и заочной форм обучения технических и гуманитарных специальностей ВУЗов.

Допуск к экзамену получают учащиеся, выполнившие и сдавшие все контрольные и расчетные работы, предусмотренные учебным планом кафедры математики.

Для успешной сдачи экзамена необходимо выполнить 60 или более процентов заданий указанных в билете, решив минимум одну задачу.

Ответы на теоретические вопросы экзамена должны включать точные определения и основные положения рассматриваемой темы с выводами соответствующих формул.

Если Вам требуется помощь в решении задач, наши специалисты готовы ответить на все вопросы по математике.

Экзаменационный билет по высшей математике

Билет для сдачи экзамена по высшей математике включает решение задач и ответы на вопросы по темам, изучавшимся в пройденном учебном семестре, и может содержать от трех до 5, а в некоторых случаях и до 10 пунктов.

Например, в билете могут быть три теоретических вопроса и две задачи, либо задание в виде теста.

Пример экзаменационного билета

Примерный билет содержит задачи и вопросы по разделам высшей математики:

1. Определители. Свойства определителей.

2. Угол между векторами. Проекция вектора на ось.

3. Векторное произведение двух векторов и его свойства.

4. Найти обратную матрицу A-1, если:

5. Вычислить неопределенный интеграл

Вопросы к экзаменам по математике

Примерный перечень экзаменационных вопросов по теории курса высшей математики, включаемых в билет:

Раздел матрицы и векторы

  1. Матрицы. Виды матриц. Действия над матрицами.
  2. Алгебраические дополнения и миноры.
  3. Вычисление определителей методом треугольников и разложением по элементам строки или столбца.
  4. Невырожденная матрица. Обратная матрица. Нахождение обратной матрицы.
  5. Матричный метод решения систем линейных уравнений. Формулы Крамера.
  6. Метод Гаусса решения систем алгебраических линейных уравнений.
  7. Действия над векторами.
  8. Линейная зависимость и независимость векторов.
  9. Векторный базис. Координаты вектора.
  10. Прямоугольная декартова система координат. Деление отрезка в заданном отношении. Определение расстояния между точками.
  11. Скалярное произведение двух векторов и его свойства.
  12. Смешанное произведение трех векторов и его свойства.

Неопределённый интеграл

  1. Первообразная функция и неопределенный интеграл.
  2. Простейшие свойства неопределенного интеграла и его геометрический смысл.
  3. Интегрирование методом разложения и методом замены переменной.
  4. Метод интегрирования по частям.
  5. Интегрирование простейших дробей.
  6. Интегрирование дробно-рациональной функции.
  7. Интегрирование тригонометрических функций.
  8. Интегрирование иррациональных функций.

Определённый интеграл

  1. Определение определенного интеграла. Свойства определенного интеграла.
  2. Определенный интеграл с переменным верхним пределом интегрирования. Формула Ньютона-Лейбница.
  3. Замена переменной и интегрирование по частям в определенном интеграле.
  4. Несобственные интегралы с бесконечными пределами интегрирования и от неограниченных функций.
  5. Геометрические приложения определенного интеграла. Вычисление площадей фигур в декартовых и полярных координатах.
  6. Длина дуги плоской кривой в декартовых и полярных координатах, объем тела вращения.
  7. Решение физических задач с помощью определенных интегралов.

Кратные интегралы

  1. Определение двойного интеграла. Его геометрический смысл
  2. Свойства двойного интеграла
  3. Понятие о правильных областях. Двукратный интеграл
  4. Сведение двойного интеграла к двукратному
  5. Замена переменных в двойном интеграле. Вычисление двойного интеграла полярных координатах
  6. Вычисление объемов тел и площадей плоских областей
  7. Задачи механики
  8. Определение тройного интеграла. Его механический смысл. Свойства
  9. Вычисление тройного интеграла
  10. Вычисление тройного интеграла в декартовых координатах
  11. Замена переменных в тройном интеграле. Тройной интеграл в цилиндрических и сферических координатах
  12. Приложения тройных интегралов к задачам геометрии и механики
  13. Вычисление объемов тел
  14. Задачи механики

Криволинейные и поверхностные интегралы

  1. Криволинейные интегралы первого рода (или по длине дуги)
  2. Определение и физический смысл криволинейного интеграла первого рода. Свойства
  3. Вычисление криволинейного интеграла первого рода
  4. Криволинейный интеграл для пространственного случая
  5. Некоторые применения криволинейного интеграла первого рода
  6. Криволинейный интеграл второго рода (или по координатам)
  7. Задача о работе силового поля. Определение криволинейного интеграла второго рода
  8. Существование и вычисление криволинейного интеграла второго рода
  9. Связь между криволинейными интегралами первого и второго рода
  10. Формула Грина
  11. Условия независимости интеграла от пути интегрирования
  12. Поверхностный интеграл первого рода (или по площади поверхности). Теорема существования
  13. Вычисление поверхностного интеграла первого рода
  14. Некоторые применения поверхностного интеграла первого рода
  15. Поверхностный интеграл второго рода или по координатам. Физический смысл
  16. Применение поверхностного интеграла второго рода

Экзаменационные задачи по математике

Примеры экзаменационных задач по курсу высшей математики, которые могут быть включены в билет для сдачи экзамена:

1. Решить систему уравнений методом Гаусса

2. Используя признаки сходимости несобственных интегралов, исследовать на сходимость

3. Применяя основные правила дифференцирования, найти производную функции

Ответы на экзаменационные вопросы по математике

Ответы на некоторые теоретические вопросы в экзаменационных билетах по высшей математике:

  • Однородные функции, однородные дифференциальные уравнения
  • Линейное дифференциальное уравнение первого порядка
  • Уравнение Бернулли
  • Уравнение в полных дифференциалах
  • Интегрирующий множитель
  • Дифференциальные уравнения высших порядков. Задача Коши
  • Числовые ряды. Основные понятия
  • Ряд геометрической прогрессии со знаменателем
  • Остаток ряда
  • Свойства, сходящихся числовых рядов
  • Необходимый признак сходимости числового ряда
  • Признак сравнения рядов с неотрицательными членами
  • Признак Даламбера
  • Признак Коши

Другие ответы можно найти, воспользовавшись поиском на нашем сайте.

Наш коллектив математиков желает Вам успешной подготовки и сдачи экзамена, и в случае необходимости готов оказать студентам всю необходимую помощь.

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Комплексный сборник тестов с ответами по Высшей математике

Кривые второго порядка

Правильный ответ подчёркнут.

1. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

2. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

3. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

4. Кривой II порядка является

— эллипс, не вырожденный в окружность

— гипербола

— парабола

— окружность

Прямые и плоскости в пространстве

Правильный ответ выделен и подчёркнут.

1. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

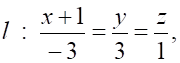
а.        б.       в.

2. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

3. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. £

4. Прямая, проходящая через точки и , перпендикулярна плоскости

а. 

б. 

в. 

г. 

5. Даны три прямых на плоскости: , и Верным является утверждение

а.  и перпендикулярны

б.   и перпендикулярны

в.   и перпендикулярны

г.  перпендикулярных прямых нет

6. Уравнением плоскости, проходящей через точку и перпендикулярной прямой является

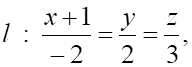
а. 

б. 

в. 

г. 

тест 7. Общее уравнение плоскости, содержащей точку и параллельной плоскости , имеет вид

а. 

б. 

в. 

г. 

8. Плоскость перпендикулярна плоскости

а. 

б. 

в. 

г. 

Прямые на плоскости

Правильный ответ выделен и подчёркнут.

1. Прямая, проходящая через точку и параллельная прямой имеет вид

а. 

б. 

в. 

г. 

2. Уравнением прямой, содержащей точку и параллельной прямой является

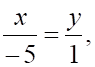
а. 

б. 

в. 

г.  

3. Общее уравнение прямой, содержащей точки и имеет вид

а. 

б. 

£

£

Треугольник на плоскости

Правильный ответ выделен и подчёркнут.

1. Длина стороны в треугольнике с вершинами , , равна

а.        б.          в.           г.  

2. Длина медианы в треугольнике с вершинами , , равна

а.          б.         в.           г.  

3. Угол в треугольнике с вершинами , и

а.  прямой     б. тупой        в. острый

4. В треугольнике , где , , , угол при вершине равен

а.          б.            в.            г. 

5. В треугольнике , где , , , угол

а. прямой         б. тупой         в. острый

Линейная алгебра. Алгебра матриц. Обратная матрица. Определители

Правильный ответ выделен и подчёркнут.

1тест. Обратной к матрице 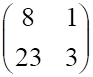является матрица

а.          б.             в.               г.  

2. Определитель матрицы 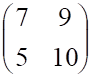равен

а.         б.          в.             г. 

3. Определитель матрицы 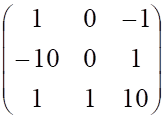равен

а.        б.          в.             г.  

4. Определитель матрицы 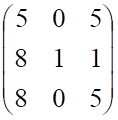равен

а.        б.          в.          г. 

5. Определитель матрицы 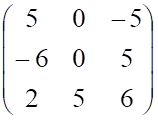равен

а.       б.       в.        г. 

6. Уравнение для нахождения собственных значений матрицы имеет вид

а. 

б. 

в. 

г. £

Сумма и произведение матриц

Правильный ответ выделен и подчёркнут.

1. Выражение эквивалентно

а.        б.        в.          г. 

2. Выражение эквивалентно

а.       б.        в.          г. 

3. Произведение матриц 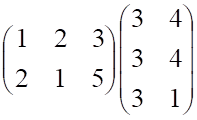равно

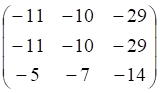
а.            б.                в.                 г. 

4. Заданы матрицы 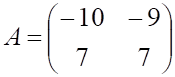и . Произведение равно

а.                б.                        в.                       г. 

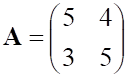
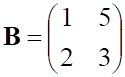
5. Заданы матрицы и . Произведение равно

а.             б.              в.                г. 

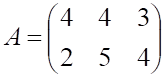
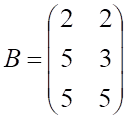
6. Заданы матрицы и . Сумма равна

а.            б.                 в.                    г. 

тест №7. Транспонированной к матрице 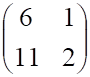является матрица

а.         б.          в.            г. 

Векторная алгебра

Правильный ответ выделен и подчёркнут.

1. Заданы векторы и . Выражение равно

а.       б.       в.        г. 

2. Заданы векторы и . Длина вектора равна

а.         б.          в.          г. 

3. Из векторов , и , ортогональными являются

а. и

б.  и

в.  и

г.  и , и

Комплексные числа

Правильный ответ выделен и подчёркнут.

1. Сумма если , , равна

а.         б.           в.           г. 

2. Произведение если , , равно

а.         б.        в.         г. 

Системы линейных уравнений

Правильный ответ выделен и подчёркнут.

1. Система линейных уравнений 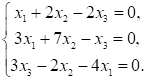имеет

а. одно нулевое решение

б. бесконечно много решений

в. одно ненулевое решение

г. нет решений

2. Частным решением системы линейных уравнений 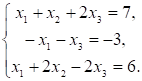является

а.         б.          в.            г. 

3. Система линейных уравнений 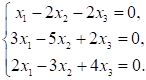имеет

а. одно решение£ два решения

б. бесконечно много решений

в. нет решений

4. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.         б.           в.         г.

5. Матричное уравнение с невырожденной квадратной матрицей А имеет решение

а.            б.           в.            г. 

Математический анализ. Дифференциальное исчисление

Правильный ответ выделен и подчёркнут.

1 — тест. Производная функции равна

а. 

б. 

в.  

г. 

2. Производная функции равна

а. 

б. 

в. 

г. 

3. Производная функции 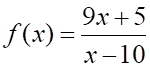равна

а.           б.            в.             г. 

4. Частной производной для функции является

а.           б.            в.           г. 

5. Производная функции равна

а.          б.         в.           г. 

6. Градиент функции равен

а. 

б. 

в. 

г. 

7. Смешанная производная для функции равна

а.            б.           в.           г. 

8. Достаточным условием выпуклости функции на интервале является

а.  на  

б.  на

в.  на

г.  на

9. Достаточным условием убывания функции на интервале является

а.  на

б.  на

в.  на

г.  на

10. Точкой локального экстремума функции является

а.       б.         в.         г.

11. Градиент функции равен

а. 

б. 

в. 

г. 

Дифференциальные уравнения

Правильный ответ выделен и подчёркнут.

тест — 1. Общим решением дифференциального уравнения является

а. 

б. 

в. 

г. 

Интегральное исчисление

Правильный ответ выделен и подчёркнут.

1. Определенный интеграл 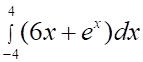равен

а.        б.        в.         г. 

2. Несобственный интеграл равен

а.       б.      в.        г. 

3. Несобственный интеграл 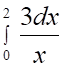равен

а.        б.      в.       г. 

4. Определенный интеграл 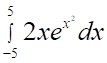равен

а.        б.       в.        г. 

5. Несобственный интеграл 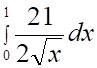равен

а.       б.         в. 

Последовательности

Правильный ответ выделен и подчёркнут.

1. Примером неограниченной последовательности является последовательность

а.      б.         в.      г. 

2. Примером сходящейся последовательности является последовательность

а.         б.          в.          г. 

3. Примером ограниченной последовательности является последовательность

а.       б.        в.         г. 

4. Примером бесконечно малой последовательности является последовательность

а.       б.        в.         г. 

5. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

6. Примером ограниченной последовательности является последовательность

а.        б.        в.        г. 

7. Примером бесконечно малой последовательности является последовательность

а.        б.        в.          г. 

8. Примером бесконечно большой последовательности является последовательность

а.        б.         в.        г. 

9_тест. Примером ограниченной последовательности является последовательность

а.       б.       в.        г. 

Предел функции

Правильный ответ выделен и подчёркнут.

1. Предел 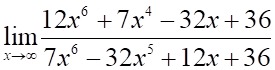равен

а.         б.           в.           г. 

2. Предел 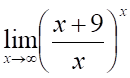равен

а.         б.        в.          г. 

3. Предел равен

а.        б.       в.          г. 

Ряды

Правильный ответ выделен и подчёркнут.

1. Радиус сходимости ряда 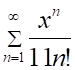равен

а.       б.        в.         г. 

2. Радиус сходимости ряда 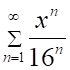равен

а.         б.         в.        г. 

3. Радиус сходимости ряда 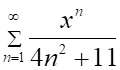равен

а.       б.        в.         г. 

Теория вероятностей

Правильный ответ выделен и подчёркнут.

1. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.        б.       в.        г. 

2. Распределение дискретной случайной величины задано таблицей

Математическое ожидание равно

а.      б.      в.      г. 

3. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.      б.       в.       г. 

тест_4. Распределение дискретной случайной величины задано таблицей

Дисперсия равна

а.        б.         в.        г. 

Классическая вероятность

Правильный ответ выделен и подчёркнут.

1. Вероятность, что кубик упадет на грань « «, при условии, что выпадет нечетная грань, равна

а.       б.       в.        г. 

2. В урне находится красных и черных шаров. Вероятность на удачу достать два красных шара равна

а.      б.      в.       г. 

3. Вероятность попадания в цель при одном выстреле равна Вероятность того, что из двух выстрелов попали оба раза, равна

а.       б.       в.         г. 

4. Урна содержит белых и черных шаров. Вероятность наудачу достать первым белый шар, а вторым черный, равна

а.        б.        в.         г. 

5. Количество способов, которыми можно выбрать экзаменационных билетa из , равно

а.      б.       в.        г.

Источник

Понравилась статья? Поделить с друзьями:

Новое и интересное на сайте:

  • Экзамен по электротехнике онлайн
  • Экзамен по электротехнике 1 семестр
  • Экзамен по электроприводу
  • Экзамен по электрооборудованию для проводников
  • Экзамен по электроматериаловедению

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии