Меню
-
ТулГу
- История
- Математика
- Материаловедение
- Начертательная геометрия
-
Педагогика
- Политология
- Русский язык
- Сопротивление материалов
- Социология
- Теоретическая механика
- Физика
- Философия
- Химия
- Экономика
-
Электротехника и электроника
- Информатика
-
Демография
- Учебники
- Лекции
- Шпаргалки
-
Иностранные языки
-
Английский язык
- Учебники
- Тесты
-
Английский язык
-
Информатика
-
C/C++
- Учебники
-
Delphi
- Учебники
-
C/C++
-
Концепции современного естествознания
- Учебники
- Лекции
- Шпаргалки
-
Математика
- Учебники
-
Лекции
- Шпаргалки
- Задачники
- Справочники
-
Материаловедение
- Учебники
- Лекции
- Шпаргалки
-
Общая электротехника
- Учебники
- Лекции
- Шпаргалки
-
Задачники
-
Политология
- Учебники
- Лекции
- Шпаргалки
-
Психология
- Учебники
- Лекции
- Шпаргалки
-
Русский язык и культура речи
-
Учебники
- Шпаргалки
- Справочники
-
Учебники
-
Сопротивление материалов
- Учебники
- Лекции
- Шпаргалки
- Справочники
-
Социология
- Учебники
-
Лекции
- Шпаргалки
-
Теоретическая механика
- Учебники
- Лекции
- Шпаргалки
-
Физика
- Учебники
- Лекции
- Шпаргалки
-
Задачники
- Справочники
-
Химия
- Учебники
- Лекции
- Шпаргалки
-
Экономика
- Учебники
- Лекции
- Шпаргалки
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА шпаргалка
|
СОДЕРЖАНИЕ |
. . . . . . . .29. Составное движение точки |
.29аб |
||||||||||||||||||||||||||
|
30. Основные понятия динамики. |
||||||||||||||||||||||||||||
|
1. Основные понятия |
Основные законы механики |
30аб |
||||||||||||||||||||||||||
|
и аксиомы статики . . . . . . . . . . . . . . . . . |
. . . .1аб |
31. |
Свободное падение тела |
|||||||||||||||||||||||||
|
2. Сходящиеся силы на плоскости |
2аб |
без учета сопротивления воздуха. |
||||||||||||||||||||||||||
|
3. Равнодействующая сходящихся |
Движение тела, брошенного |
|||||||||||||||||||||||||||
|
сил на плоскости. Леммы |
под углом к горизонту без учета |
|||||||||||||||||||||||||||
|
. . . . . . . . . . . . . . . .о нулевых стержнях |
. . . .3аб |
. . . . . . . . . . . . . .сопротивления воздуха |
.31аб |
|||||||||||||||||||||||||
|
4. Теория пар сил, лежащих в одной |
32. |
Движение падающего тела |
||||||||||||||||||||||||||
|
плоскости. Момент силы |
с учетом сопротивления воздуха . . . . . . |
.32аб |
||||||||||||||||||||||||||
|
относительно точки на плоскости . . . . |
. . . .4аб |
33. |
Колебательное движение точки. |
|||||||||||||||||||||||||
|
5. Система сил, произвольно |
. . . . . . . . . . . . . . .Свободные колебания |
.33аб |
||||||||||||||||||||||||||
|
. . . . . . .расположенных на плоскости |
. . . .5аб |
34. |
Затухающие колебания |
|||||||||||||||||||||||||
|
6. Условия равновесия сил, |
материальной точки, апериодическое |
|||||||||||||||||||||||||||
|
приложенных к рычагу. |
движение точки. Явление биений. |
|||||||||||||||||||||||||||
|
Сцепление и трение скольжения |
6аб |
Явление резонанса |
34аб |
|||||||||||||||||||||||||
|
7. Система сходящихся сил |
35. |
Математический маятник |
||||||||||||||||||||||||||
|
в пространстве. Уравнение |
и его малые колебания . . . . . . . . . . . . . . . |
.35аб |
||||||||||||||||||||||||||
|
равновесия сил |
7аб |
36. |
Динамика относительного |
|||||||||||||||||||||||||
|
. .8. Теория пары сил в пространстве |
. . . .8аб |
. . . . . . . .движения материальной точки |
.36аб |
|||||||||||||||||||||||||
|
9. Главные моменты системы сил . . . . |
. . . .9аб |
37. |
Система материальных точек . . . . . . |
.37аб |
||||||||||||||||||||||||
|
10. |
Приведение пространственной |
38. |
Твердое тело. Моменты инерции |
|||||||||||||||||||||||||
|
системы сил к главному вектору |
. . . . . . . . . . . . . . . . . . . . . . .твердого тела |
.38аб |
||||||||||||||||||||||||||
|
. . . . . . . . . . . . . .и к главному моменту |
. . .10аб |
. . .39. Центробежные моменты инерции |
.39аб |
|||||||||||||||||||||||||
|
11. |
Условия равновесия |
40. Теорема о движении центра масс |
||||||||||||||||||||||||||
|
пространственных систем сил. |
механической системы. |
|||||||||||||||||||||||||||
|
Сложение параллельных сил |
Дифференциальные уравнения |
|||||||||||||||||||||||||||
|
в пространстве. Центр тяжести тела . |
. . .11аб |
движения механической системы . . . . . |
.40аб |
|||||||||||||||||||||||||
|
12. |
Вспомогательные теоремы |
41. |
Импульс силы и его проекции |
|||||||||||||||||||||||||
|
для определения положения |
. . . . . . . . . . . . . . . .на координатные оси |
.41аб |
||||||||||||||||||||||||||
|
. . . . . . . . . . . . . . . . . . .центра тяжести |
. . .12аб |
42. |
Понятие о теле |
|||||||||||||||||||||||||
|
13. |
Центр тяжести некоторых |
переменной массы . . . . . . . . . . . . . . . . . . |
.42аб |
|||||||||||||||||||||||||
|
линий, плоских фигур и тел |
13аб |
43. |
Моменты количества движения |
|||||||||||||||||||||||||
|
14. |
Основные понятия кинематики . . . |
. . .14аб |
материальной точки относительно |
|||||||||||||||||||||||||
|
15. |
. . . . . . . . . . . . . . . .Скорость точки |
. . .15аб |
. . . . . . . . . . .центра и относительно оси |
.43аб |
||||||||||||||||||||||||
|
16. |
Ускорение точки . . . . . . . . . . . . . . . |
. . .16аб |
44. |
Работа. Теоремы о работе силы . . . . |
.44аб |
|||||||||||||||||||||||
|
17. |
Классификация движений точки |
45. |
Работа сил тяжести, |
|||||||||||||||||||||||||
|
по ускорениям ее движения |
17аб |
упругости, тяготения |
45аб |
|||||||||||||||||||||||||
|
18. |
Движение. Путь. Скорость |
46. |
Применение теоремы |
|||||||||||||||||||||||||
|
и касательное ускорение точки . . . . . |
. . .18аб |
об изменении кинетической |
||||||||||||||||||||||||||
|
19. |
Простейшие движения |
. . . . . . . . . .энергии материальной точки |
.46аб |
|||||||||||||||||||||||||
|
. . . . . . . . . . . . . . . . . . . . .твердого тела |
. . .19аб |
47. |
Кинетическая энергия |
|||||||||||||||||||||||||
|
20. |
Векторные выражения |
твердого тела . . . . . . . . . . . . . . . . . . . . . . . |
.47аб |
|||||||||||||||||||||||||
|
вращательной скорости, |
48. |
Силовое поле. Потенциальное |
||||||||||||||||||||||||||
|
вращательного |
силовое поле и силовая функция. |
|||||||||||||||||||||||||||
|
.и центростремительного ускорений |
. . .20аб |
. . . . . . . . . . . . . .Потенциальная энергия |
.48аб |
|||||||||||||||||||||||||
|
21. |
Плоское движение твердого тела |
. . .21аб |
49. |
Закон сохранения |
||||||||||||||||||||||||
|
22. |
План скоростей. |
. . . . . . . . . . . . . . .механической энергии |
.49аб |
|||||||||||||||||||||||||
|
Мгновенный центр скоростей |
22аб |
50. |
Динамика поступательного |
|||||||||||||||||||||||||
|
23. |
Уравнения неподвижной |
и вращательного движения |
||||||||||||||||||||||||||
|
и подвижной центроиды . . . . . . . . . . . . |
. . .23аб |
твердого тела . . . . . . . . . . . . . . . . . . . . . . . |
.50аб |
|||||||||||||||||||||||||
|
24. |
Теорема об ускорениях точек |
51. |
Физический маятник |
|||||||||||||||||||||||||
|
плоской фигуры и ее следствия. |
и его малые колебания |
51аб |
||||||||||||||||||||||||||
|
Положение мгновенного |
52. |
Динамика плоского движения |
||||||||||||||||||||||||||
|
. . . . . . . . . . . . . . . . .центра ускорений |
. . .24аб |
. . . . . . . . . . . . . . . . . . . . . . .твердого тела |
.52аб |
|||||||||||||||||||||||||
|
25. |
Определение ускорений точек |
53. |
Понятие о гироскопе . . . . . . . . . . . . . |
.53аб |
||||||||||||||||||||||||
|
и угловых ускорений звеньев |
54. |
. . . . . . . . . . . . . . . . . . . .Теория удара |
.54аб |
|||||||||||||||||||||||||
|
плоского механизма . . . . . . . . . . . . . . . |
. . .25аб |
55. |
Потеря кинетической энергии |
|||||||||||||||||||||||||
|
26. |
Сферическое движение |
при ударе двух тел |
55аб |
|||||||||||||||||||||||||
|
. . . . . . . . . . . . . . . . . . . . .твердого тела |
. . .26аб |
56. |
Общее уравнение динамики. |
|||||||||||||||||||||||||
|
27. |
Ускорения точек твердого тела |
Принцип возможных перемещений |
||||||||||||||||||||||||||
|
при сферическом движении . . . . . . . . |
. . .27аб |
в случае движения системы. |
||||||||||||||||||||||||||
|
28. |
Теорема о скоростях точек |
Примеры применения |
||||||||||||||||||||||||||
|
свободного твердого тела и ее |
общего уравнения динамики |
56аб |
||||||||||||||||||||||||||
|
следствия. Теорема об ускорениях |
||||||||||||||||||||||||||||
|
точек свободного твердого тела . . . . . |
. . .28аб |
|||||||||||||||||||||||||||

|
1. Основные понятия |
||
|
1а |
||
|
и аксиомы статики |
||
Статика — это раздел теоретической механики, в коF тором устанавливаются методы преобразования одF них систем сил в другие, им эквивалентные, а также условия равновесия различных систем сил, действуюF щих на твердое тело.
Материальная точка — это простейшая модель маF териального тела любой формы, размеры которого достаточно малы и которое можно принять за геометF рическую точку, имеющую определенную массу.
Механическая система — это любая совокупность материальных точек.
Абсолютно твердое тело — это механическая система, расстояние между точками которой не измеF няется при любых взаимодействиях.
Сила — это одна из векторных мер действия одного материального объекта на другой рассматриваемый объект. Сила характеризуется числовым значением, а также точкой приложения и направлением действия. Это векторная величина и обозначается она, наприF
мер, F.
Система сил — это совокупность сил, действующих на рассматриваемое тело.
Система сил, эквивалентная нулю (равновесная система сил), — это такая система сил, действие коF торой на твердое тело или точку, находящиеся в покое или движущиеся по инерции, не приводит к изменеF нию его состояния.
Существуют следующие аксиомы.
1. О равновесии системы двух сил. Для равновеF сия системы 2Fх сил, приложенных к точкам твердого тела, необходимо и достаточно, чтобы эти силы были
3а 3. Равнодействующая сходящихся сил на плоскости.
Леммы о нулевых стержнях
Равнодействующая сила при равновесии системы R =0 представляет собой замыкающую силового мноF гоугольника, или векторную сумму сил, однако, с друF гой стороны,
n
R =∑Fi .
i=1
Следовательно, условия равновесия системы схоF дящихся сил в аналитической форме будут
nn
|
∑Fix =0, |
∑Fiy =0. |
||||
|
i=1 |
i=1 |
Иными словами, для равновесия системы сходяF щихся сил, действующих на твердое тело, необходиF мо и достаточно, чтобы суммы проекции этих сил на каждую из двух прямоугольных координат осей, лежаF щих в плоскости, были равны нулю.
Фермы — это конструкции, которые состоят из прямолинейных стержней, соединенных между собой шарнирами и образующих неизменяемую геометриF ческую фигуру.
Существует определенная зависимость между коF личеством стержней (n) и количеством шарниров (k). В основном треугольнике имеются 3 стержня и 3 узла. При этом для образования одного узла требуются
2а 2. Сходящиеся силы на плоскости
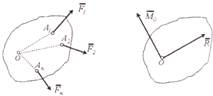
Система сходящихся сил — это такая система сил, линии действия которых пересекаются в одной точке — центре пучка. Пусть задана произвольная система сходящихся сил F1, F2, …, Fn, приложенных к твердому телу. Сложение двух сходящихся сил
графически осуществляется по правилу параллелоF грамма,
R12 = F 1 + F2.
По правилу параллелограмма складываем силы R12 и F3, и получаем их равнодействующую
R123 = R12 + F3 = F1 + F2 + F3;
n
R =∑Fi .
i=1
Для плоской системы сходящихся сил одну из коордиF натных осей (обычно OZ) выбирают перпендикулярF ной силам. Таким образом, каждая из сил пучка даст проекцию на эту ось, равную нулю, а значит, будет равна нулю и проекция равнодействующей силы на ось OZ. После этого проецируют векторы векторF ного равенства на прямоугольные оси координат. ТогF да в соответствии с теоремой о проекции замыкающей получится
nn
Rx =∑Fix , Ry =∑Fiy .
4а 4. Теория пар сил, лежащих в одной плоскости. Момент силы
относительно точки на плоскости
Система двух равных по модулю параллельных сил, направленных в противоположные стороны, называется парой сил. Пара сил, как правило, прилагается к телу (F1, F2), которое должно вращаться. Плоскость, в коF торой расположены пары сил, называется плоскос$ тью действия пары сил N. Кратчайшее расстояние между линиями действия сил пары называется пле$ чом пары h. Алгебраический момент пары сил —
это взятое со знаком плюс или минус произведение одной из сил пары на плечо пары сил:
M = M(F1, F2) =±Fd.
Алгебраический момент пары сил имеет знак плюс, если пара сил стремится вращать тело против часовой стрелки, и знак минус, если пара сил стремится враF щать тело по часовой стрелке. Алгебраический моF мент пары сил не зависит от переноса сил пары вдоль своих линий действия и может быть равен нулю, если линии действия пары сил совпадают. Произведение модуля силы на плечо силы относительно этой точки
M0 (F ) =±Fh
называют алгебраическим моментом пары отно$
сительно точки. Плечо пары h относительно точ$ ки — это кратчайшее расстояние между этой точкой и линией действия силы. Две пары сил называются
3
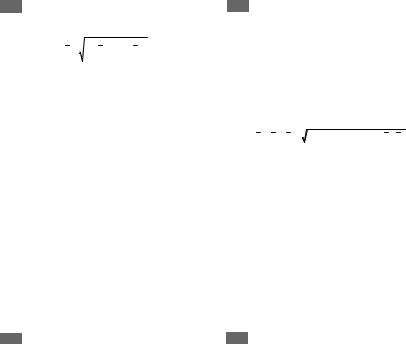
2б По проекциям определяют модуль равнодейстF вующей силы и косинусы углов ее с осями коорF
динат по формулам
nn
R = (∑Fix )2 +(∑Fiy )2
i=1 i=1
и
cos(Rx, x )=Rx / R, cos(Ry , y )= Ry / R.
Следовательно, система n сходящихся сил эквиваF лентна одной силе R, которая и является равнодейF ствующей этой системы сил. Процесс последовательF ного применения правила параллелограмма означает по сути построение многоугольника из заданных сил. Этот силовой многоугольник называют замкнутым.
Геометрическое условие равновесия системы сходящихся сил. Для равновесия системы сходяF щихся сил необходимо и достаточно, чтобы равнодейF ствующая сила равнялась нулю R = 0.
Теорема о трех силах. Если твердое тело под дейF ствием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таF ких трех сил пересекаются в одной точке. Для случая трех сходящихся сил при равновесии силовой треF угольник, построенный из трех сил, должен быть замкF нутым.
4б эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях, а также если они имеют одинаковые по модулю и наF
правлению векторные моменты.
Теорема об эквивалентности пары сил. Пару сил, действующую на твердое тело, можно заменить друF гой парой сил, расположенной в той же плоскости действия и имеющей одинаковый с первой парой алF гебраический момент.
Пару сил как жесткую фигуру можно поворачивать
ипереносить в плоскости ее действия как угодно. У пары сил можно изменять плечо и силы, сохраняя при этом алгебраический момент пары и плоскость действия. Эти операции над парами сил не изменяют их действия на твердое тело.
Теорема о сумме алгебраических моментов пары сил. Пары сил, действующие на твердое тело
ирасположенные в одной плоскости, можно привести к одной паре сил, алгебраический момент которой раF вен сумме алгебраических моментов составляющих пар сил:
n
M =∑Mi .
i=1
Пары сил, расположенные в параллельных плосF костях, также складываются, поскольку их предвариF тельно можно перенести в одну плоскость. Если сложеF ние выполнять графически, когда векторные моменты пары сил находятся в одной плоскости, то векторный момент эквивалентной пары сил будет иметь вид заF мыкающей векторного многоугольника, построенного из векторных моментов заданных пар сил.
1б равны по модулю и действовали вдоль одной прямой, проходящей через точки их приложеF
ния, в противоположных направлениях.
2.О добавлении системы сил, эквивалентной ну$ лю. Если на твердое тело действует система сил, то
кней можно добавить систему сил, эквивалентную нулю.
3.Аксиома параллелограмма сил. Две силы, дейF ствующие в одной точке твердого тела или на одну маF териальную точку, можно заменить одной равнодейF ствующей силой, равной по модулю и направлению диагонали параллелограмма, построенного на заданF ных силах:
R = F + F = F 2 + F 2 + 2F 2F 2 cos F , F .
1 2 1 2 1 2 1 2
4. Аксиома о равенстве сил действия и противо$ действия. Всякой силе действия есть равная протиF воположная сила противодействия.
Несвободное твердое тело — это тело, не имеюF щее возможность совершать в рассматриваемый моF мент любые перемещения в пространстве.
Аксиома связи: всякую связь можно отбросить или заменить силой, реакцией связей или систе$ мой сил. Реакция связи — это сила, с которой связь действует на систему материальных точек или тверF дое тело. Сила реакции связи направлена в сторону, противоположную направлению перемещения рассматF риваемого тела.
3б 2 стержня. Значит, для образования (k – 3) узлов нужно 2(k – 3). Общее число стержней:
n = 2 (k – 3) + 3,
n = 2k – 3.
Нулевыми называются стержни, ненагруженные силой, на концах которых находятся точечные шарниF ры и весом которых можно пренебречь.
Способ вырезания узлов заключается в том, что каждый узел вырезается из фермы и рассматриваетF ся отдельно, как находящийся в равновесии. Система сил, действующих на стержень, — это плоская систеF ма сходящихся сил, которая находится в равновесии. Построение силовых многоугольников всегда начиF нают с узла, в котором сходятся 2 стержня. Каждый последующий узел следует выбирать так, чтобы в нем сходилось не более двух стержней с неизвестными усилиями. Если усилия разрезанных стержней направF лены по стержням в сторону узла, то их называют сжи$ мающими, а если наоборот — растягивающими.
Леммы о нулевых стержнях.
1.Если в узле, не нагруженном внешними силами, сходятся три стержня, и которых два направлены вдоль одной прямой, то усилие в третьем стержне равно нулю, т. е. он является нулевым.
2.Стержень находится в равновесии под действием двух сил, приложенных в шарнирах, где силы равны по величине и противоположны по направлению, т. е. его реакция также будет направлена по оси стержня.
4

5а 5. Система сил, произвольно расположенных на плоскости
Приведение силы к заданному центру. Силу можно переносить параллельно самой себе в любую точку твердого тела, добавляя при этом пару сил, векF торный момент которой равен векторному моменту переносимой силы относительно новой точки прилоF жения силы.
Теорема Пуансо. Любую произвольную систему сил, действующих на твердое тело, можно в общем случае привести к силе и паре сил.
Главный вектор системы сил — это вектор, котоF рый равен векторной сумме этих сил. Главный вектор системы сил изображается вектором, замыкающим силовой многоугольник, построенный на силах:
n
R =∑Fi .
i=1
Главный момент системы сил относительно точ$ ки тела — это сумма векторных моментов всех сил системы относительно этой точки. Главный момент L0 равняется сумме векторных моментов присоединеF ния пар:
n
L0 =∑M0 (Fi ).
i=1
Уравнения равновесия системы сил, произ$ вольно расположенных на плоскости. Пусть кажF дая из сил расположена в одной плоскости с осями координат ОX, ОY, и потому ее моменты относительF
7а 7. Система сходящихся сил в пространстве. Уравнение
равновесия сил
Система сходящихся сил — это такая система сил, линии действия которых пересекаются в одной точке — центре пучка. Для аналитического опредеF ления равнодействующей силы выбирают систему прямоугольных осей координат. Проецируя векторы векторного равенства на прямоугольные оси коордиF нат, получают
|
n |
n |
n |
||||||||||||
|
R |
x =∑Fix , |
R |
y =∑Fiy , |
R |
z =∑Fiz . |
|||||||||
|
i=1 |
i=1 |
i=1 |
По проекциям определяют модуль равнодействуюF щей силы и косинусы углов ее с осями координат по формулам:
|
n |
n |
n |
||||||
|
R |
= (∑Fix )2 + (∑Fiy )2 + (∑Fiz )2 |
|||||||
|
i=1 |
i=1 |
i=1 |
и
cos(Rx, x )= Rx / R, cos (Ry, y )=Ry / R, cos(Rz, z)=Rz / R.
Для равновесия системы сходящихся сил, прилоF женных к твердому телу, равнодействующая сила должна обратиться в точку.
6а 6. Условия равновесия сил, приложенных к рычагу.
Сцеплениеи трение скольжения
Рычагом называется форма действия плоской систеF мы сил на объект, при которой соблюдаются те же усF ловия равновесия сил, что и для точки, на которую дейF ствует сила.
Алгебраический момент относительно точки —
это произведение модуля силы на плечо силы относиF тельно этой точки:
M0 (F ) =±Fh.
Плечо пары h относительно точки — это кратчайF шее расстояние между этой точкой и линией дейстF вия силы. Алгебраический момент относительно точки численно равен удвоенной площади треугольника, поF строенного на силе.
Векторное условие равновесия: для равновесия системы сил, приложенных к точке, необходимо и досF таточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно точки также был равен нулю.
Три условия равновесия:
n n n
∑Fix =0, ∑Fiy =0, ∑M0 (Fi ) =0.
i=1 i=1 i=1
В случае опрокидывания на устойчивое положение тела или системы тел действует возбуждающая сила, которая стремится опрокинуть объект. Положение равF
8а 8. Теория пары сил в пространстве
Пусть к тердому телу приложена пара сил (F, F′)
так, что F = −F′. Момент пары сил — это векторная величина, обозначаемая M (F, F′) и определяемая форF мулой
M (F , F ′) = A′A × F =AA′ × F ′.
Данный вектор, перпендикулярный плоскости дейF ствия пары сил, является свободным, иными слоF вами, он может быть перенесен параллельно сам себе и приложен в любой точке тела. Этот вектор направлен в ту сторону, откуда вращение, произвоF димое парой сил, происходит против хода часовой стрелки.
Плечо пары сил h — это расстояние между линиями действия сил, т. е.
|M (F, F ′)| = hF.
Теорема об эквивалентности пар сил.
1.Пару сил можно переносить, не меняя ее дейстF вия на тело, как единое целое в плоскости действия пары сил.
2.Не изменяя действий пары, плоскость действия можно переносить параллельно самой себе.
Доказательство. Пусть дана пара ( F 1, F 2) с плеF чом АВ. Если перенести плечо АВ в положение А1В1
ик точкам А1 и В1 приложить направленные в противоF положные стороны силы F3, F4 и F5, F6, равные по
5

6б новесия q0 называется устойчивым, если в кажF дой паре сколь угодно малых положительных фиксированных чисел е для моментов времени t > t0
выполняется неравенство:
q(t) – q(t0) < е.
Потенциальная энергия тела будет иметь минимум или равняться нулю, т. е.
П = 1/2∑Ciqi = 0,
где Ci — коэффициент устойчивости. Приближенные законы, препятствующие качению.
1.Наибольший момент пары сил, препятствующий качению, не зависит от радиуса катка.
2.Предельное значение момента пропорционально нормальному давлению, а значит, и равной ему норF
мальной реакции, т. е. Mmax = δN. Коэффициент треF ния качения δ при покое называется коэффициентом трения второго рода.
3.Этот коэффициент устойчивости (сцепления) заF висит от материала катка, плоскости и физического состояния поверхности.
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поF верхности соприкосновения возникает сила трения. Если поверхности абсолютно гладкие, то реакция поF верхности связи направлена по нормали к общей каF сательной в точке соприкосновения.
5б но этих осей равны нулю. Значит, условия равF новесия:
n
∑Mx (Fi ) = 0,
i=1
n
∑My (Fi ) = 0
i=1
будут тождествами.
Сложение параллельных сил на плоскости.
Пусть заданы две параллельные силы ( F1, F2), они направлены в одну (или разные) стороны. Если F1≠−F2, т. е. они не образуют пару сил, то они привоF дятся к равнодействующей с некоторым центром приведения О. Положение точки О можно найти, подF считав относительно нее момент равнодействующей, он равен нулю в каждом из приведенных случаев:
n
R =∑Fi ,
i=1
M0 (R) = F1 ×О1О −F2 ×ОО2 ,
F1 = ОО2
F2 О1О
следует, что система двух параллельных сил, не обраF зующих пару, имеет равнодействующую, параллельF ную этим силам.
8б напряжению силам пары ( F1, F2) и параллельF ные им, то
( F1, F2) ≈ ( F1, F2, F3, F4, F5, F6).
Сложив силы F2, и F4, получим равнодействующую, равную 2 F, которая будет приложена в середине параллелограмма и направлена вверх. Если сложить силы F1 и F5, можно получить их равнодействующую, равную 2F′ и направленную вниз. Тогда F1, F5, F2, F4 ≈ 0, поэтому система
(F1, F2, F3, F4, F5, F6) ≈ ( F3, F6)
ипара ( F3, F6) эквивалентна паре ( F1, F2).
Значит, плоскость пары можно переносить паралF
лельно ей самой, не изменяя при этом оказываемого на тело действия.
Сложение пар в пространстве. Пусть на твердое тело действует система пар сил:
(F1, F1′), (F2, F2′), … (Fn, Fn′).
Момент kFой пары сил обозначим через
M (Fk , Fk′), при k =1, n.
Данную систему пар сил можно заменить одной паF рой сил, такой, ( F, F′), тогда момент M ( F, F′) равен геометрической сумме моментов данных пар сил.
7б Проецирование силы на оси координат.
Пусть дана сила F, тогда ее проекции на пряF моугольные оси координат вычисляются по формулам:
Fx =Fi =F cos(F, x),
Fy =Fj =F cos(F, y),
Fz =Fk =F cos(F, z).
где i, j, к — единичные векторы, направленные по осям координат.
Косинусы углов силы с осями координат удовлетвоF ряют условию:
cos2 (F, x) +cos 2(F, y) +cos 2(F, z) =1.
Из трех углов независимыми будут только два. При проецировании силы на прямоугольные оси коF ординат лучше использовать два угла. Для этого силу нужно разложить на две взаимно перпендикулярные составляющие. При этом одна из них параллельна каF койFлибо оси координат, например OZ, а другая нахоF дится в координатной плоскости двух других осей, в нашем случае — координатной плоскости ОXY. Тогда получается
Fx = F sin αcos β, Fy = F sin αcos β, Fz = Fcos α.
Условие равновесия системы сходящихся сил: для равновесия системы сходящихся сил необходимо и достаточно, чтобы равнодействующая сила равняF лась нулю R =0.
6

9а 9. Главные моменты системы сил
Момент силы F относительно некоторого выбранF ного центра О — это векторная величина M 0( F ), определяемая формулой
M0 (F )=r ×F,
где r — радиусFвектор точки А, причем r =OA . Тогда
|M0 (F )| = hF, F = |F|,
где h — кратчайшее расстояние от точки О до линии действия силы, называемое плечом силы.
Вектор

и к главному моменту
Лемма о параллельном переносе сил. Пусть к абсолютно твердому телу в точке А приложена сила FA. Состояние твердого тела не изменится, если эту силу перенести параллельно самой себе в любую другую точку тела В и приложить к телу пару сил, моF мент которой равен:
M (F ′, FA )= BA ×FA,
где
F′=−FA, FB = FA .
M0 (F ) r , F
и направлен в ту сторону, откуда вращение произF водимой силой осуществляется против часовой стрелки. Сила измеряется в [H], а момент силы — в [H·м].
Пусть в точке О будет начало некоторой прямоугольF ной декартовой системы координат XYZ. СпроектиF руем векторную формулу на координатные оси, получим:
|
i |
j |
k |
|||||||||||||||||||||||||
|
M |
0 (F )= M0 x (F )i +M0y (F )j +M0k = |
x y z |
. |
||||||||||||||||||||||||
|
Fx |
Fy |
Fz |
Доказательство очевидно, так как
FB, (F ′, FA )≈ FB, F ′, FA,
адве силы FB и F′ взаимно уравновешиваются. Приведение пространственной системы сил к главF
ному вектору и к главному моменту. Пусть на абсоF лютно твердое тело действует произвольная простF ранственная система сил ( F1, F2, …, Fn). Эта система сил может быть заменена одной силой F и парой сил, момент которой M0, причем сила F — главный вектор пространственной системы сил
n
F = ∑Fk .
k=1
11а 11. Условия равновесия пространственных систем сил.
Сложение параллельных сил в пространстве. Центр тяжести тела
Для равновесия пространственных систем сил ( F1, F2, …, Fn), приложенных к абсолютно твердому телу, необходимо и достаточно выполнение двух условий:
n
1) F =∑Fk =0;
k=1
n
2) M0 =∑rk Fk =0,
k=1
которые говорят, что для любого центра приведения главный вектор и главный момент пространственных систем сил должны быть равны нулю.
Если ввести координатные оси с началом в центре приведения и спроектировать предыдущие векF торные равенства на эти оси, то получатся скалярF ные условия равновесия пространственной систеF мы сил:
Fx =∑Fkx =0, Fy =∑Fky =0, Fz =∑Fkz =0,

центра тяжести
Теорема 1. Площадь поверхности, полученной враF щением дуги плоской кривой вокруг оси, лежащей в ее плоскости, но не пересекающей, равна длине этой дуги, умноженной на длину окружности, описанF ной ее центром тяжести.
Теорема 2. Объем тела вращения, образованного вращением плоской фигуры вокруг оси, лежащей в плосF кости этой фигуры и ее не пересекающей, равен произF ведению площади этой фигуры на длину окружности, описанной центром тяжести площади фигуры.
Метод группировки. При нахождении центра тяжесF ти тела легче определить центры тяжести отдельных его частей, на которые можно разбить тело. Пусть теF ло разбили на несколько частей и определили центр тяжести каждой такой части тела, тогда будут иметь место равенства:
|
(∑Pi ri )1 |
(∑Pi ri )2 |
|||||||
|
r1 = |
, r2 = |
и т. д. |
||||||
|
(∑Pi )1 |
(∑Pi )2 |
Если сгруппировать слагаемые, то получится:
|
P1 |
r1 |
+P2 |
r2 |
+… |
|||
|
r0 = |
∑Pi |
. |
|
i |
j |
k |
|||||
|
rk Fk = |
xk |
yk |
zk |
. |
|||
|
Fkx |
Fky |
Fkz |
|||||
Метод отрицательных масс является частным случаем метода разбиения и применяется к телам, имеющим разрывы.
7

10б Момент M0 — главный момент пространстF венной системы сил, равный
n
M0 =∑rk ×Fk ,
k=1
т. е. момент равен геометрической сумме моментов всех сил системы относительно выбранного центра приведения.
Доказательство этого утверждения основывается на лемме о параллельном переносе сил. Все силы исF ходной системы переносят параллельно самим себе в выбранную точку приведения О, тогда получится система исходящих сил. Данная система может быть заменена равнодействующей F, приложенной в точке О. Чтобы состояние тела не изменилось при выполF ненном переносе сил, необходимо к телу приложить n пар сил, моменты которых относительно центра О определяются соотношениями:
M (F ) = r ×F , k =1, n.
0 k k k
Главный момент M0 этой результирующей пары обычF но изображают приложенным в центре О, хотя он явF ляется свободным вектором и может переноситься паF раллельно самому себе.
Теорема Вариньона. Для системы сходящихся сил момент равнодействующей силы относительно выбF ранного центра равен геометрической сумме моменF тов всех сил системы.
12б Используя метод разбиения и свойства центF ров тяжести симметричных однородных тел, можF но найти центр тяжести сложных тел, разбивая на таF
кие части, центры которых легче определяются. Пример. Можно рассматривать отверстие как плоF
щадь с отрицательной массой. Фигура имеет ось симF метрии, значит, будем определять только одну коорF динату х, взяв начало координат в центре большого круга, тогда получится:
|
πR2 ×O −πr2 ×c |
r 2 ×c |
|||
|
x0 = |
=− |
. |
||
|
π(R2 −r2 ) |
R2 −r2 |
Метод веревочного многоугольника. Пусть задаF на некоторая сила F. Возьмем произвольный полюс О, не лежащий на линии действия силы F, и соединим его с концами силы F. Тогда можно рассматривать силу F как равнодействующую двух сил, приложенF ных в той же точке, в которой будет приложена сила F. Возьмем нить АСВ так, что АС и СВ будут соответF ственно параллельны заданным силам. Закрепим конF цы А и В неподвижно, а к точке С приложим ту же силу F. Тогда эта сила может быть представлена как равF нодействующая заданных сил, приложенных к точке С. Первой фигурой будет план заданных сил, а втоF рой — веревочный многоугольник.
|
9б |
||||||
|
M0 x |
(F )= yFz |
− zFy |
||||
|
M0y |
(F )= zFx |
− xFz , |
||||
|
)= xFy − yFz |
||||||
|
M0 z (F |
где x, y, z — координаты точки приложения силы.
Момент силы относительно оси OZ — это проекF ция вектора момента силы относительно некоторого центра, взятого на этой оси, на эту же ось, т. е.
M0z (F ) = (z ×F )z —
моменты силы F относительно координатных осей X,
Y, Z.
Главным моментом системы сил относительно выбранного центра О будет называться вектор, равF ный геометрической сумме моментов всех сил систеF мы относительно выбранного центра:
nn
M0 = ∑M0 (Fi ) = ∑ri ×Fi .
Если все силы системы приложены в одной точке, то все ri = r, тогда
n
M = r + ∑Fi = z ×F .
i=1
11б Тогда
n
Mox = ∑(yk Fkx − zk Fky )= 0, k=1
n
Moy = ∑(zk Fkz − xk Fkz )= 0, k=1
n
Moz = ∑(xk Fky − yk Fkx )= 0. k=1
Следовательно, для равновесия пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил системы на координатные оси быF ли равны нулю и чтобы сумма моментов всех сил систеF мы относительно координатных осей тоже была равна нулю.
Если рассматривать условия равновесия несвободF ного твердого тела, находящегося под действием сил ( F1, F2, …, Fn), то связи, наложенные на тело, мысленF но отбрасываются, а к телу прикладываются реакции связей (R1, R2, …, Rl), после чего условия равновесия записываются для системы сил, объединяющей акF тивные силы и реакции связей:
(R1, R2, …, Rl), (F1, F2, …, Fn).
8

13а 13. Центр тяжести некоторых линий, плоских фигур и тел
Пусть имеется дуга AB окружности R. Радиус ОС будет осью симметрии, значит, центр тяжести будет лежать на оси х.
|
x0 |
= |
R2 ∫−αα cos ϕdϕ |
= |
R sin α |
, |
||
|
2Rα |
α |
||||||
|
R sin α |
|||||||
|
где |
, 0 — координаты центра тяжести дуги. |
||||||
|
α |
Центр тяжести площади кругового сектора. СоF средоточивая массы элементарных секторов в их центF рах тяжести, сведем нахождение центра тяжести плоF щади кругового сектора к нахождению центра тяжести дуги окружности радиуса 2/3R с центральным углом 2α.
Для дуги радиуса r имеем:
sin α x0 =r α .
В этом случае r = 2/3R, значит, абсцисса центра тяF жести площади кругового сектора будет равна:
|
2 |
sin α |
|||
|
x0 = |
R |
. |
||
|
3 |
α |
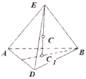
Центр тяжести тетраэдра. Разделим тетраэдр на элементарные пластинки плоскостями, параллельныF

Движущаяся точка описывает в пространстве некоF торую линию, которая называется траекторией точF ки. В зависимости от траектории движения точки быF вают прямолинейными и криволинейными.
Естественный способ движения точки применяетF ся в том случае, когда траектория точки заранее изF вестна. При движении точки M расстояние s от непоF движной точки O меняется с течением времени, s = f(t). Если в начальный момент времени t0 точка занимала положение M0, а в момент времени t занимает полоF жение M, то пройденный ею путь за промежуток вреF мени [0, t] при движении точки в одном направлении можно записать:
σ = M0 M = OM −OM0 = s −s0 .
Изменение дуговой координаты равно ds = f′(t)dt. Приращение пути:
dσ = ds = f ′(t )dt.
Путь, пройденный точкой за некоторый промежуток времени,
t
σ0t =∫ f′(t )dt.
0
Векторный способ задания движения точки. ПоF ложение точки в пространстве определяется задаF
Скорость — это векторная величина, которая хаF рактеризует быстроту и направление движения точки
вданной системе отсчета.
Векторный способ задания движения. ПоложеF
ние движущейся точки в каждыйrмомент времени опF ределяется радиусFвекторомr r r, который является функцией времени r = r (t). Допустим, в момент вреF мени t точка занимаетr положение М, определяемое радиусFвектором r, а в момент времени t1 = t + t r— положение М1, определяемое радиусFвектором r1, причем О — центр отсчета. Из треугольника OMM1 следует:
uuuuur uuuur uuuuur
OM1 =OM +MM1,
→ → → → →
r1 = r + r, vср = r/ t.
Вектор точки в момент времени t:
|
→ |
→ |
→ |
→ |
|
v = lim |
r/ |
t, lim r/ |
t =d r/ dt. |
|
t→0 |
t→0 |
Таким образом,
→→
v =d r/ dt,
аэто значит, что вектор скорости точки в данный момент равен производной от радиусFвектора точки во времени.
16а 16. Ускорение точки
Ускорение точки характеризует быстроту изменеF ния модуля и направления скорости точки. Пусть в моF
|
мент времени t точка занимает положение M и имеет |
||||||
|
r |
= t + |
t она заниF |
||||
|
скорость v , а в момент времени t |
r |
|||||
|
1 |
r |
r |
r |
|||
|
мает положение M и имеет скорость v |
, v |
= v + |
v. |
|||
|
1 |
r |
1 |
||||
|
Разделив приращение вектора |
v на промежуток вреF |
мени t, можем получить вектор среднего ускорения точки за этот промежуток:
|
→ |
→ |
→ |
→ |
|
|
aср =Δv |
t , a= lim |
v t. |
||
|
t→0 |
||||
|
→ → |
→ |
→ |
→ → |
→ |
|
v =v |
(t ) и v =d r dt , то a =d v dt =d 2 r dt 2 . |
Проекции ускорения точки на неподвижные оси деF картовых координат равны вторым производным от соответствующих координат точки по времени или перF вым производным по времени от проекции скорости на соответствующие оси.
Естественные координатные оси. Проведем в точF ке M кривой AB соприкасающуюся плоскость, норF мальную плоскость, перпендикулярную касательной, и спрямляющую плоскость, перпендикулярную соприF касающейся и нормальной плоскостям, образующую с этими плоскостями естественный трехгранник. Естественные координатные оси — это три взаимно перпендикулярные оси: касательная, направленная в сторону возрастания дуговой координаты; главная нормаль, направленная в сторону вогнутости кривой; бинормаль, направленная по отношению к касательF ной и главной нормали.
9

r
14б нием радиусFвектора r, проведенного из некоF торого неподвижного центра O в данную точку М.
Чтобы определить движение точки, необходимо знать, какr изменяется с течением времени радиусFr вектор r, должнаr r быть задана векторFфункция r арF гумента t: r = r (t). Траектория точки —rэто геометриF ческое место концов радиусFвектора r движущейся точки.
Координатный способ задания движения точки.
Положение точки М в системе отсчета Oxyz опредеF ляется декартовыми координатами точки x, y, z. При движении точки М ее координаты со временем меF няются: x = f1(t); y = f2(t); z = f3(t). Это уравнения дви$ жения точки в декартовых координатах. Уравнения движения, определяющие координаты точки в любой момент времени, можно рассматривать как параметF рические уравнения траектории точки. Например, уравнения движения точки М имеют вид x = f1(t); y = f2(t); z = f3(t). Решив 1Fе уравнение, получаем
t =ϕ(x ),
после чего можно вычислить уравнение траектории точки в координатной форме:
y =f2 ϕ(x ) ; z =f3 ϕ(x ) .
Пусть движение точки М в плоскости задано уравF нениями x = f1(t); y = f2(t); тогда, исключив параметр t, получим уравнение точки в координатной форме:
y =f2 ϕ(x ) .
16б Определим проекции ускорения точки на естестF венные координатные оси:
→→
v =τ ds
|
→ |
→ |
→ |
→d 2s |
|||||||||||||
|
→ |
d v d τ ds |
→ d 2s d τ ds ds |
||||||||||||||
|
a = |
= |
+ τ |
= |
+ τ |
. |
|||||||||||
|
dt |
dt |
dt |
dt 2 |
ds |
dt |
dt |
dt 2 |
→ → →
a=nv 2 ρ+τ d2s dt 2.
Ускорение точки равно геометрической сумме двух векторов, один из которых направлен по главной норF мали и называется нормальным ускорением, а другой направлен по касательной и называется касательным ускорением точки. Проекция ускорения точки на главF ную нормаль равна квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответстF вующей точке:
an =v 2 
Проекция ускорения точки на касательную равна второй производной от дуговой координаты точки по времени или первой производной от алгебраической величины скорости точки по времени:
→
aτ =d2 s dt 2 =d v dt .
13б ми основанию АСВ. Центры тяжести этих пластиF нок будут лежать на прямой SF, где F — центр тяF жести площади основания, который лежит на пересеF
чении медиан, т. е.
EF = 1 EC. 3
Теперь проделаем то же самое по отношению к граF ни ASB:
|
EK = |
1 |
ES. |
||||||||||||
|
3 |
||||||||||||||
|
Тогда KOF ≈ OSC, значит, из подобия: |
||||||||||||||
|
FO |
= |
KF |
, но |
KF |
= |
EK |
= |
EF |
= |
1 |
, |
|||
|
OS SC |
SC ES EC 3 |
значит, FO = 1OS = 1 SF.
34
Окончательно будет:
FO = 1 SF, SO = 3 SF.
44
Центр тяжести объема пирамиды лежит на прямой, соединяющей центр тяжести площади ее основания с вершиной на расстоянии 1/4 длины этой прямой.
15б Естественный способ задания движения.
Пусть известны траектория AB, начало и направF ление отсчета дуговой координаты, а также уравнеF ние движения точки s = f(t).
Из произвольногоr центра O проведем в точку М раF диусFвектор r и определим скорость в момент вреF мени t:
→→
v =dr/dt.
→
Вектор dr / ds направлен по касательной к кривой
в сторону увеличения дуговой координатыr.
→
Вектор dr / ds — от этого направления τ:
→→
τ=dr/ds.
Вектор скорости:
→→
v =τ ds / dt.
Значит,
→
v = v = ds dt —
модуль скорости равен абсолютному значению произF водной от дуговой координаты точки по времени.
10
Соседние файлы в предмете Теоретическая механика
- #
- #
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Теоретическая механика (шпаргалка)
Статика:
Уравновешенные
силы:
Система
сил, под действием которой свободное твердое тело может находится в покое,
называется уравновешенной.
Аксиомы
статики:
а) Аксиома о
уравновешенных силах (о абсолютном твердом теле) — две одинаковые силы,
приложенные к абс. твердому телу и действуют вдоль одной прямой в
противоположных направлениях назыв. уравновешенными силами. б) Аксиома
о прибавлении или вычитании уравновешенной системы сил — действие системы
сил на твердое тело не меняется, если если прибавить к ней уравновешенные силы.
в) Аксиома сложения сил — силы, которые действуют на точку, можно
складывать как векторы или аналитично. г) Аксиома о опорах (связи) и
их реакции — силы могут быть активными и пассивными. Первые стремятся
вызвать ускорение матер. точек. Другие — ограничивают движение. Они возникают
как реакции системы на движение или на действие активных сил. Движение матер.
точек может быть свободным или ограниченным. Во втором случае тело или точка
назыв. несвободной. Все, что ограничивает движение тел в пространстве
называется опорой (связью). д) Аксиома о освобождении от связи
(опоры) — механическое состояние системы материальных точек не изменится,
если освободить ее от связей, меняя их силами, действие которых такое же, как и
связей (опор). Эти силы назыв. реакциями связей — пассивные силы, которые
направлены в противоположную сторону относительно ограничения движения.
Момент
силы относительно точки.
Вращательный
эффект силы характеризуется ее эффектом. Моментом силы относительно центра О
называется величина, равная взятому с соотв. знаком произведению модуля силы на
длину плеча.
Момент
силы относительно оси.
Моментом
силы относительно оси называется скалярная величина, равная моменту проэкции
этой силы на плоскость, перпендикулярную оси, взятому относительно точки
пересечения оси с плоскостью.
Пара
сил, момент пары. Свойства пар сил.
Парой
сил называется система двух равных по модулю, параллельных и направленных в
противоположные стороны сил, действующих на абс. твердое тело. Моментом пары
наз. величина, равная взятому с соотв. знаком произведению модуля одной из сил
пары на ее плечо (Понятие момента силы связано с точкой, относительно к-рой
берется момент. Момент пары определяется только ее моментом и плечом; ни с
какой точкой плоскости эта величина не связана). Св-ва : сумма моментов сил
пары относительно точки не зависит от выбора точки и всегда равняется моменту
пары, Пара сил не имеет равнодействующей — нельзя уравновесить одной силой.
Сложение
пар сил.
Система
пар, лежащих в одной плоскости, эквивалентна одной паре, лежащей в той же
плоскости и имеющей момент, равный алгебраической сумме моментов слагаемых
пар.
Теорема
Вариньона.
О
моменте равнодействующей — момент равнодействующей плоской системы сходящихся
сил относительно любого центра равен алгебраической сумме моментов слагаемых
сил относительно того же центра.
Виды
нагрузок.
а)
Сосредоточенная, б) Рассредоточенная равномерная и неравномерная, в) Пара сил —
момент.
Параллельный
перенос сил. Приведение системы сил к одному центру.
Силу
можно переносить в любую точку тела, к-рая называется точкой приведения, если
прибавить при этом пару сил (в точку приведения).
Главный
вектор и главный момент произвольной системы сил.
Условия
равновесия произвольной пространственной системы сил.
S
— сумма,
Мгол = S Мi(F) = 0; Fгол = S Fi = 0;
Написать
проекции на все оси.
Условия
равновесия произвольной плоской системы сил.
а)Одной
проекции силы нет, зато есть один момент с индексом этой оси б) есть два
момента — нет двух сил в) Все моменты равны нулю.
Формы
условий равновесия. ??????
Центр
параллельных сил — это точка приложения равнодействующей системы параллельных
сил.
Центр
тяжести однородного тела.
Центр
тяжести плоской фигуры.
Трение
скольжения, угол трения.
Закон
Кулона-Амонтона — F=fN. Угол трения —
это угол, тангенс к-рого равен коэффициенту трения — предельный угол силы к
нормали пов-ти, чтобы тело поехало.
Кинематика:
Теоремы
о скоростях.
а)
Проекции скоростей (абсол. твердого тела) двух точек на прямую, которая
проходит через них равны. б) Скорость любой точки складывается из скорости
какой-либо другой точки, принятой за полюс, и скорости ее вращения вокруг этой
точки.
Мгновенный
центр скоростей. Связь скоростей точек с мгновенными радиусами при п.п.д.
МЦС
— это точка в плоскости движения, скорость к-рой в данный момент времени равна
нулю.
Способы
определения мгновенного центра скоростей.
Всего
— четыре.
Динамика точки и системы:
Основное
уравнение динамики для свободной и несвободной материальной точки в векторной,
координатной и естественной формах.
Теорема – о независимом
действии сил – если на точку действует несколько сил или равнодействующая
то точка будет двигаться с ускорением = сумме ускорений, к-рые возникают при
действии каждой силы отдельно.
Вывести
и сформулировать принцип Даламбера для точки.
ma
= F + N; F + N + (-ma) = 0; Ф = -ma; — сила инерции.
Решение
второй задачи динамики точки.
Это
— зная силы найти закон движения. а) Показываем начальное и конечное положение
тела. б) Направляем ось х из начального в конечное положение, ось у –
перпендикулярно х с начального положения, в) Показываем тело в свободном
положении и действующие на него силы, г) составляем дифур движения точки в
проекции на ось х, д) интегрируем это уравнение, е) находим постоянные
интегрирования с начальных условий и неизвестные величины. That all.
Две
основные меры механического движения точки.
Импульс (кол-во движения) и кинетическая
энергия.
Работа упругой силы. — Частный
случай
Работа
силы, когда тело вращается.
Теорема
об изменении кинетической энергии точки.
Изменение
кинетической энергии точки при некотором ее перемещении равно сумме работ
внешних сил, которые действуют на этом перемещении на точку.
Диф.
уравнение движения мех системы и св-во внутренних сил.
Теорема
об изменении кинетической энергии системы.
Идеальные
связи – сумма
возможных работ реакций которых равна нулю.
Возможные
перемещения, возможная работа силы.
Возможное
перемещение – это бесконечно малые перемещения точек мех. системы, которые мы
представляем и которые разрешены связями. Возможные работы находятся по таким
же правилам как и действительные, но вместо дифференциалов записываются их
вариации.
Принцип
Лагранжа-Даламбера (Общее уравнение динамики)
Необходимыми и достаточными условиями
действительного движения мех. системы на к-рую действуют голономные
двусторонние стационарные и идеальные связи есть равенство нулю суммы возможных
работ всех активных сил и сил инерции на любых возможных перемещениях системы.
Связи,
классификация связей.
а)
геометрические (без производных), б) кинематические (дифференциальные rj’=V), в) интегрируемые (это
кинемат. К-рые можно привести к геометрич. rj=s), г) односторонние, д) двухсторонние, е)
нестационарные –f(t).
Необходимыми и достаточными условиями
для равновесия мех. системы, к которой приложены двусторонние, стационарные и
идеальные связи, есть равенство нулю суммы возможных работ всех активных сил на
любых возможных перемещениях из положения равновесия.
Обобщенные
координаты, скорости, силы.
Называются независимые параметры, которые
однозначно определяют положение мех. системы (эти параметры – любой
размерности).
Обобщенная
сила – это коэффициент при вариации обобщенной координаты в выражении возможной
работы.
Обобщенная
сила инерции.
Уравнение
Лагранжа второго рода.
- Раздел: Механика → Теоретическая механика
Студенты группы ЕЕ-133, ТУМ, Кишинёв 2015 Основные понятия и определения статики. Аксиомы статики. Система сходящихся сил. Связи и их реакции. Задачи статики. Момент силы. Момент пары сил. Основная теорема статики. Условия равновесия произвольной системы сил. Теорема Вариньона. Равновесие плоской системы сил. Равновесие при наличии трения. Центр системы параллельных сил. Центр…
- №1
- 651,63 КБ
- добавлен 05.09.2021 15:24
- описание отредактировано 10.09.2021 07:08
- Раздел: Механика → Теоретическая механика
Составитель Каримов И. Ш., Башкирский государственный аграрный университет, Кафедра теоретической и прикладной механики, 2010 г. , 70 с. Содержание: Сила. Материальная точка. Абсолютно твердое тело. Эквивалентные системы сил. Аксиомы статики и их следствия. Теорема о приведении произвольной системы сил к двум силам. Момент силы относительно точки. Связь моментов одной и той же…
- №2
- 4,35 МБ
- дата добавления неизвестна
- описание отредактировано 10.02.2011 12:26
- Раздел: Механика → Теоретическая механика
Теорема о движении центра масс мех. системы
Определение динамических реакции при вращении твердого тела вокруг неподвижной оси
Теорема о моментах инерции твёрдого тела относительно параллельных осей
Вывод общего уравнения динамики
Вывод уравнения Лагранжа 2 рода
Теорема об изменении количества движения механической системы.
Теорема о работе силы
Дифференциальное уравнение…
- №3
- 24,13 КБ
- дата добавления неизвестна
- описание отредактировано 14.10.2010 12:13
- Раздел: Механика → Теоретическая механика
РГСУ ЗТВ 2-й курс, 4-й семестр, шпаргалка по теме Динамика, два файла в виде шпаргалки и для изучения в нормальном формате, раскрыты вопросы такие как: 1. Предмет динамики. Основные понятии: масса, материальная точка, сила. Законы механики Галилея-Ньютона. Инерционная система точки. Дифференциальные уравнения движения точки. Решение первой и второй задач. Начальные условия 2….
- №4
- 961,24 КБ
- дата добавления неизвестна
- описание отредактировано 18.06.2011 13:01
- Раздел: Механика → Теоретическая механика
Механика Ньютона: движение в центральном поле и рассеяние частиц, помимо прочего выведены законы Кеплера и формула Резерфорда.
Переход к механике Лагранжа.
Из механики абсолютно твердого тела: определения, координаты, физические величины, уравнения, отдельно рассмотрено вращение юлы с неподвижной точкой опоры.
Немного о колебаниях и нормальных координатах колебаний.
Механика…
- №5
- 231,21 КБ
- дата добавления неизвестна
- описание отредактировано 27.10.2018 06:25
- Раздел: Механика → Теоретическая механика
Основные понятия статики, Аксиомы статики Понятие о связях и реакциях связей. Типы связей в статике. Сходящаяся система сил. Способы геометрического сложения сил Теорема о равновесии 3-х непараллельных сил. Проекция силы на ось. Проекция равнодействующей силы на ось. Выражение равнодействующей силы через её проекции на оси координат. Условие равновесия сходящихся сил. Момент силы…
- №6
- 271,12 КБ
- дата добавления неизвестна
- описание отредактировано 28.10.2018 00:48
- Раздел: Механика → Теоретическая механика
2 курс, 3 семестр. УГАТУ. 90 вопросов. Статика Теоретическая механика и ее место среди естественных и технических наук. Объективный характер законов механики. Исходные положения и основные понятия статики Задачи и аксиомы статики. Связи и реакции связей. Основные виды связей и их реакции. Система сходящихся сил; геометрическое сложение системы сил; равнодействующая, правило…
- №7
- 10,50 МБ
- добавлен 06.02.2015 18:54
- описание отредактировано 06.01.2018 05:10
- Раздел: Механика → Теоретическая механика
Подробные ответы к вопросам по теоретической механике по разделу динамика. Вопросы:Предмет динамики.
Динамика.
Материальная точка.
Две основные задачи динамики.
Аксиомы классической механики.
Первая аксиома или закон инерции.
Вторая аксиома.
Третья аксиома.
Четвертая аксиома. Закон независимости действия сил.
Две основные задачи динамики.
Первая задача динамики.
Вторая…
- №8
- 238,34 КБ
- дата добавления неизвестна
- описание отредактировано 19.01.2009 18:14
- Раздел: Механика → Теоретическая механика
Ответы к некоторым вопросам по теоретической механике, разделу динамика к экзамену. Вопросы: Законы механики Ньютона Динамика Дифференц. уравнение движ. точки Колебания материальной точки Свободные колебания Затухающие колебания Дифференциальное уравнение движения Центр масс rc Момент инерции МС Момент инерции тв. тела Момент инерции относительно оси
- №9
- 5,39 КБ
- дата добавления неизвестна
- описание отредактировано 19.01.2009 17:33
- Раздел: Механика → Теоретическая механика
Ответы к некоторым вопросам по теоретической механике разделу кинематика к экзамену. Взято очень поверхностно всё только основное. никаких примеров и выводов. только теорема и формула! Вопросы:Способы задания движения: Векторный способ Координатный способ Естественный способ Поступательное движение Вращательным Скорость точки осью вращения Плоским называют Скорость любой точки…
- №10
- 6,84 КБ
- дата добавления неизвестна
- описание отредактировано 19.01.2009 17:36
- Раздел: Механика → Теоретическая механика
Ответы к некоторым вопросам теоретической механике по разделу статика к экзамену. Взято очень поверхностно всё только основное. никаких примеров и выводов. только теорема и формула! Вопросы: Сила Теор. механика Статика Кинематика Динамика Аксиома-1 Аксиома-2 Аксиома-3 Аксиома-4 Аксиома-5 Аксиома-6 Свободное тело Несвободное тело Уравновешенные силы Сходящиеся силы Связь…
- №11
- 8,46 КБ
- дата добавления неизвестна
- описание отредактировано 19.01.2009 17:50
- Раздел: Механика → Теоретическая механика
УГАТУ РГР по теор. механике №4 сдавалась Терешину Ю.Г вариант группы 5 вариант задания 6 на 2 листа А4
- №12
- 1,43 МБ
- добавлен 28.09.2011 18:18
- описание отредактировано 29.09.2011 03:15
- Раздел: Механика → Теоретическая механика
36 вопросов для подготовки к зачету или экзамену. Вопросы: Ретроспектива развития статики как раздела механики. Предмет статики. Основные задачи статики. Понятие материальной точки. Определение механической системы. Определение абсолютно твердого тела. Понятие силы и системы сил. Равновесная система сил. Эквивалентные системы сил. Равнодействующая сила. Уравновешивающая сила….
- №13
- 8,25 МБ
- дата добавления неизвестна
- описание отредактировано 09.02.2011 11:57
- Раздел: Механика → Теоретическая механика
УГАТУ. Преподаватель Ковган С. Т. Содержит формулы для векторного, естественного, координатного способа задания движения точки, а также для метода полярных координат и вращательного движения и формулы перехода от одного способа задания движения точки к другому.
- №14
- 23,58 КБ
- дата добавления неизвестна
- описание отредактировано 03.05.2010 16:02
- Раздел: Механика → Теоретическая механика
Минск, 2012 . — 4 с. Содержание Определение науки «Механика». История развития механике в строительстве и других областях. Понятие о науке – техническая механика и ее разделах. Основные понятия статики: Основные аксиомы статики. Методика решения задач на равновесие плоской системы сходящихся сил аналитическим способом. Основные виды опор балочных систем, их реакции…
- №15
- 46,50 КБ
- добавлен 31.01.2013 16:48
- описание отредактировано 01.02.2013 17:35
- Раздел: Механика → Теоретическая механика
Все разделы, 42 вопроса в принципе все есть удобно на телефон закачивать
- №16
- 1,04 МБ
- дата добавления неизвестна
- описание отредактировано 28.01.2010 12:01
- Раздел: Механика → Теоретическая механика
Основные понятия и задачи механики Векторный способ описания движения. Координатный способ описания движения. Естественный способ описания движения. Движение точки по окружности. Движение точки в цилиндрической системе координат. Плоско-параллельное движение твёрдого тела. Векторно-матричное описание движения твёрдого тела. Мгновенный центр скоростей. Мгновенный центр ускорений…
- №17
- 239,00 КБ
- дата добавления неизвестна
- описание отредактировано 18.07.2018 19:12
- Раздел: Механика → Теоретическая механика
Статика Предмет статики. Основные понятия и определения статики. Аксиомы статики. Связи и их реакции. Аксиома связей. Основные виды связей. Равнодействующая системы сходящихся сил. Геометрический и аналитический способы определения равнодействующей. Условия равновесия системы сходящихся сил в геометрической и аналитической формах. Векторный момент силы относительно центра….
- №18
- 148,35 КБ
- дата добавления неизвестна
- описание отредактировано 03.07.2011 00:13
- Раздел: Механика → Теоретическая механика
Шпаргалки по теоретической механике
Содержание: Разделение переменных, Одномерное движение под действием силы F(t), Одномерное движение под д-ем силы F(v), Движение частицы в поле, зависящем от координат F(x), Классификация одномерных движений, Понятие связи, Принцип Даламбера, Уравнение Лагранжа I рода, и т. д.
- №19
- 311,72 КБ
- дата добавления неизвестна
- описание отредактировано 09.10.2018 18:54
- Раздел: Механика → Теоретическая механика
Зачет. ТГУ, Россия, Глазунов А.А., 2004 г.
Как система сходящихся сил приводится к равнодействующей.
Вывод формул для вычисления равнодействующей системы сходящихся сил.
Условия равновесия системы сходящихся сил.
Обоснование векторной формулы момента силы относительно точки.
Обоснование определения момента силы относительно оси.
Зависимость между моментом силы относительно…
- №20
- 4,62 МБ
- добавлен 24.12.2011 09:49
- описание отредактировано 24.12.2011 16:11
- Раздел: Механика → Теоретическая механика
Динамика. Статика. Кинематика. Принцип Даламбера.
Принцип возможных (виртуальных) перемещений.
Ур-е Лагранжа 2го рода. Законы Ньютона. Теоремы динамики мех системы точек. Плоско-параллельное движение тела. Сложное движение точки. Типы связи. Пара сил. Пространственная система сил. Центр тяжести тела. Коэф-т трения качения
- №21
- 72,50 КБ
- дата добавления неизвестна
- описание отредактировано 15.05.2009 21:16
- Раздел: Механика → Теоретическая механика
Содержит все теоремы, готова для печати мелким шрифтом.
Некоторые из представленных вопросов:
Теорема о движении центра масс механической системы.
Теорема о моментах инерции твёрдого тела относительно параллельных осей.
Вывод общего уравнения динамики.
Вывод уравнения Лагранжа 2 рода.
Теорема об изменении количества движения механической системы.
Теорема о работе силы….
- №22
- 21,98 КБ
- дата добавления неизвестна
- описание отредактировано 25.05.2008 18:10
- Раздел: Механика → Теоретическая механика
Теоретические вопросы по термеху. Для сдачи экзамена. Все идеально подогнано под шпору 5 кегль, 3 столбика, все рисунки, формулы. все четко видно, готово к распечатке. присутствует удобное оглавление(по столбикам) короче все сделано с умом, а то обычно скачаешь, но убиваешь кучу времени на редактирование.
темы: статика, кинематика, динамика.
Статика.
Сила….
- №23
- 761,14 КБ
- дата добавления неизвестна
- описание отредактировано 20.01.2009 00:51
- Раздел: Механика → Теоретическая механика
Отличная шпора по теоретической механике. Включает в себя все основные разделы: Динамика.
Общие теоремы динамики точки.
Динамика плоского движения твердого тела.
Основы аналитической механики.
Динамика твердого тела.
Кинематика.
- №24
- 147,51 КБ
- дата добавления неизвестна
- описание отредактировано 02.11.2009 17:45
- Раздел: Механика → Теоретическая механика
БНТУ. МСФ 3 курс 1 сем. Богинская. Вся теория в мелком виде. Записать осн. уравн. динам. и диффер. уравн. движ. матер. точки в декарт. системе. Суть 1-й и 2-й задачи динамики: Записать диф. ур. свободных гармонич. колебаний. Пояснить физ. суть всех коэф. вошедших в диф. уравн. Зап. диф. ур. затух. колеб. Пояснить физ. суть всех коэф. вошедших в диф. уравн. Записать диф. ур. для…
- №25
- 40,51 КБ
- дата добавления неизвестна
- описание отредактировано 22.06.2011 01:34
- Раздел: Механика → Теоретическая механика
Шпора по теоретической механике — формат Word-35вопросов+(1общ. ) раскрыты полностью — оформлены аккуратно освещены следующие темы и вопросы: Статика Аксиомы статики Шарнирные опоры. Теорема о переносе силы вдоль линии действия Приведение к равнодействующей силе- Теорема о трех непараллельных силах Зависимость между моментом силы относительно оси и моментом силы относительно…
- №26
- 1,37 МБ
- дата добавления неизвестна
- описание отредактировано 09.10.2018 18:52
- Раздел: Механика → Теоретическая механика
Для техникума специальность электрики.
- №27
- 26,70 КБ
- дата добавления неизвестна
- описание отредактировано 12.06.2008 13:37
- Раздел: Механика → Теоретическая механика
Шпаргалка к экзамену по специальности АП 2курс . Собрано главное по кинематике, динамике, сопромату, детали машин и механизмов. Для сдачи экзамена нужная вещь.
- №28
- 1,10 МБ
- дата добавления неизвестна
- описание отредактировано 27.06.2008 13:08
- Раздел: Механика → Теоретическая механика
Теоретическая механика.
Сила. Система сил. Равновесие тела.
Аксиомы статики и их следствия.
активные силы и реакция связей.
Система сходящихся сил.
Сложение параллельных сил.
Пара сил. Момент пары сил. Теоремы о парах.
Основная теорема статики. Главный вектор и главный момент системы сил.
Условия равновесия системы сил.
Плоская система сил. Теорема Варионьона. Условия…
- №29
- 588,29 КБ
- дата добавления неизвестна
- описание отредактировано 09.01.2008 20:07
- Раздел: Механика → Теоретическая механика
Нормальные шпаргалки по термех.
Могилевский государственный университет продовольствия
- №30
- 27,96 КБ
- дата добавления неизвестна
- описание отредактировано 26.01.2008 04:23
- Раздел: Механика → Теоретическая механика
Определение реакций подшипников твердого тела, вращающегося вокруг неподвижной оси. Понятие статической и динамической уравновешенности твердого тела, вращающегося вокруг неподвижной оси. Основные положения теории удара. Теорема об изменении количества движения точки и системы точек при ударе. Теорема об изменении кинетического момента точки и механической системы при ударе….
- №31
- 555,48 КБ
- дата добавления неизвестна
- описание отредактировано 08.06.2007 01:41
- Раздел: Механика → Теоретическая механика
МАИ ГТУ
Основное уравнение динамики точки. Первая и вторая задача динамики
Теорема об изменении количества движения материальной точки
Теорема об изменении момента количества движения материальной точки
Работа силы. Мощность. Теорема об изменении кинетической энергии
Метод кинетостатики для точки (принцип Даламбера)
Центр масс. Теорема о движении центра масс…
- №32
- 675,54 КБ
- дата добавления неизвестна
- описание отредактировано 02.02.2010 15:37
- Раздел: Механика → Теоретическая механика
Кинематика — формулы
Основные формулы кинематики, механики жидкостей и газов и молекулярно-кинетической теории. Сила всемирного тяготения и сила тяжести. Закон Архимеда и Гука. Расчеты по электричеству и магнетизму. Последовательное и параллельное соединение проводников.
- №33
- 128,47 КБ
- дата добавления неизвестна
- описание отредактировано 27.01.2011 02:01
- Раздел: Механика → Теоретическая механика
Динамика
Законы механики
Пространство и время
Моментом инерции механической системы относительно неподвижной
Дифференциальные уравнения движения свободной материальной точки
Векторная форма записи уравнений движения
Координатная форма записи уравнения движения
Естественная форма записи уравнения движения
Две основные задачи динамики для мат. точки
Вторая задача динамики…
- №34
- 1,39 МБ
- дата добавления неизвестна
- описание отредактировано 03.01.2011 13:34
- Раздел: Механика → Теоретическая механика
Экзамен, БНТУ, 2013 г., 34 вопроса и ответа, 15 стр.
Общие сведения
Аксиомы статики
Связи и их реакции
Сложение плоской системы сходящихся сил
Определение равнодействующей системы сходящихся сил методом проекций. Аналитическое условие равновесия
Пара сил. Эквивалентность пар сил
Сложение пар сил. Условие равновесия пар
Момент пары относительно точки
Приведение силы к…
- №35
- 10,12 МБ
- добавлен 12.01.2014 02:40
- описание отредактировано 12.01.2014 16:56
- Раздел: Механика → Теоретическая механика
Зачет. ГГТУ имени Сухого, Гомель/Беларусь, 2013
Три способа задания движения точки: векторный, координатный и естественный. Траектория точки. Определение положения точки на траектории; скорость точки.
Ускорение точки при векторном и координатном способах задания движения точки. Построение вектора полного ускорения точки.
Ускорение точки при естественном способе задания…
- №36
- 3,73 МБ
- добавлен 02.12.2012 14:56
- описание отредактировано 11.01.2013 20:57
- Раздел: Механика → Теоретическая механика
(делал для себя)
КИНЕМАТИКА:
Плоское движение твердого тела., Способы задания движения точки, Естественный СП, Координатный СП, Векторный СП, Переход от координатного способа к естественному, Сложение поступательных движ, Естественный способ задания дв-я точки , Естественный способ задания движения точки, Определение скорости точки при естеств , Определение ускорения точки при…
- №37
- 118,97 КБ
- дата добавления неизвестна
- описание отредактировано 16.01.2009 23:12
- Раздел: Механика → Теоретическая механика
(Делал для себя)
СТАТИКА:
Предмет теоретической механики, Механическое движение , Механическое взаимодействие , Теоретическая механика , Статика, Аксиомы статики, Основные типы связей, Система сходящихся сил, Равнодействующая сходящихся сил , Условия равновесия сист. сходящихся сил, Теорема о трех силах, Момент силы относительно точки, Свойства момента силы, Теорема об…
- №38
- 47,48 КБ
- дата добавления неизвестна
- описание отредактировано 16.01.2009 23:07
- Раздел: Механика → Теоретическая механика
Для студентов высших учебных заведений (МГТУ) технических специальностей.Тарг С.М.»курс теоретической механики»Статика.Задачи статики.Связи и их реакции.Виды сил.Сложение-разложение сил.Проекция силы на ось и на плоскость.Момент силы относительно центра.Пара сил. Момент пары сил.Условия равновесия системы сил.Координаты центров тяжести однородных тел.Способы их определения.Трение…
- №39
- 156,66 КБ
- дата добавления неизвестна
- описание отредактировано 18.01.2009 06:37
- Раздел: Механика → Теоретическая механика
Все файлы в Word. Статика. Аксиомы статики. Система сходящихся сил. Теория пар сил. Плоская система сил. Силы трения. Пространственная система сил. Центр тяжести Кинематика. Способы задания движения. Скорость точки. Ускорение точки. Вращательное движение тела. Плоское движение твердого тела. Сферическое движение твердого тела. Движение свободного твердого тела. Сложное движение…
- №40
- 1,86 МБ
- дата добавления неизвестна
- описание отредактировано 27.02.2016 07:23
- Раздел: Механика → Теоретическая механика
УГАТУ, ЭСиС 2 курс 3 семестр, преподаватель Ильчанинов В. П… Имеется оглавление, около номера вопроса написаны страницы с ответами. Вопросы Основные задачи статики. Основные понятия статики. Аксиомы статики. Типы связей. Реакции связей. Проекции силы на ось в плоскости и пространстве. Теорема о проекции равнодействующей. Сходящаяся система сил. Определение равнодействующей….
- №41
- 16,32 МБ
- дата добавления неизвестна
- описание отредактировано 24.03.2010 22:49
- Раздел: Механика → Теоретическая механика
Вся теоретическая механика на трех страницах, в word. Разделы: статика, кинематика, динамика. Для студентов всех технических специальностей. Подготовлены преподавателем Владимиром Константиновичем.
- №42
- 572,94 КБ
- дата добавления неизвестна
- описание отредактировано 11.01.2010 15:09
- Раздел: Механика → Теоретическая механика
Представлены темы:
Сила и природа сил. Различные системы сил.
Принцип инерции и равновесие.
Аксиомы статики.
Сила как скользящий вектор.
Теорема о трех силах.
Связи и реакции связей. Аксиома связей.
Сходящаяся система сил и равнодействующая.
Силовой многоугольник и геометрическое условие равновесия.
Проекции силы на оси координат и проекции равнодействующей….
- №43
- 557,78 КБ
- дата добавления неизвестна
- описание отредактировано 18.06.2009 17:14
- Раздел: Механика → Теоретическая механика
Теоретическая механика и основы механики сплошных сред. Условие равновесия под действием сходящейся совокупности сил. Условие равновесия под действием не сходящейся совокупности сил. Пара сил. Момент пары сил. Теорема Вариньона. Сила трения скольжения. Конус трения. Сила трения качения. Сила трения верчения. Центр параллельных сил. Центр тяжести. Частные случаи центра тяжести….
- №44
- 809,37 КБ
- дата добавления неизвестна
- описание отредактировано 20.06.2009 14:31
- Раздел: Механика → Теоретическая механика
Включает разделы теоретической механики: кинематика и динамика.
Кинематика точки. Способы задания движения. Уравнения движения. Траектория. Закон движения точки. Связь между тремя способами задания движения. Скорость точки. Ускорение точки. Равнопеременное движение точки. Введение в динамику. Законы и аксиомы динамики материальной точки. Основное уравнение динамики. Уравнения…
- №45
- 143,06 КБ
- дата добавления неизвестна
- описание отредактировано 27.09.2009 19:20
- Раздел: Механика → Теоретическая механика
Шпоры по теоретической механике Способы задания движения точки. Определение скорости точки при задании ее движения векторным способом Определение скорости точки при задании ее естественным способом. Проекция на касательную к траектории. Определение точки при задании ее координатным способом. Проекции скорости точки на неподвижные оси декартовых координат. Годограф скорости…
- №46
- 9,93 МБ
- добавлен 28.12.2011 02:16
- описание отредактировано 28.12.2011 02:23
- Раздел: Механика → Теоретическая механика
Экзамен. Минск: БГУ, 2012. — 53 с. (электронный вид)
Импульс, закон изменения импульса системы материальных точек.
Момент импульса, закон изменения момента импульса с-мы материальных точек
Энергия, закон изменения кинетической энергии с-мы материальных точек
Система отсчета центра инерции. Преобразование импульса, момента импульса, энергии
Преобразование кинетической…
- №47
- 807,86 КБ
- добавлен 15.09.2012 18:15
- описание отредактировано 15.09.2012 21:34
- Раздел: Механика → Теоретическая механика
Сложение скоростей Поступательное движение твердого тела Вращательное движение твердого тела вокруг неподвижной оси. Угол поворота, угловая скорость, угловое ускорение Сложение параллельных сил. Момент силы относительно точки Плоская система сил. Теорема Вариньона. Условия равновесия плоской системы сил.
- №48
- 132,39 КБ
- дата добавления неизвестна
- описание отредактировано 27.05.2011 10:38
- Раздел: Механика → Теоретическая механика
1 курс, переработано, удобно распечатывать. Кинематика. Траектория точки. Естественный сп. Координатный сп. Векторный сп. Скорость точки. Ускорение точки. Поступательное движение. Вращательное движение. Угловая скорость. Плоским. Уравнения плоского движения. Скорости. Мгновенный центр скоростей. Ускорения. Мгновенный центр ускорений. Сложное движение точки (тела). Абсолютным…
- №49
- 149,27 КБ
- дата добавления неизвестна
- описание отредактировано 01.06.2007 21:27
- Раздел: Механика → Теоретическая механика
Статика. Уравновешенные силы Аксиомы статики Момент силы относительно точки. Момент силы относительно оси. Пара сил, момент пары. Свойства пар сил. Сложение пар сил. Теорема Вариньона. Виды нагрузок. Параллельный перенос сил. Приведение системы сил к одному центру. Главный вектор и главный момент произвольной системы сил. Частные случаи приведения произвольной системы сил к…
- №50
- 18,87 КБ
- дата добавления неизвестна
- описание отредактировано 14.09.2005 15:19
- Раздел: Механика → Теоретическая механика
Шпора по механике. Готова к распечатке.
Предмет динамики. Основные понятия и определения: масса, мат. точка, сила.
Дифф. ур-я движения мат. точки в поле центральной силы. Формула Бине.
Законы механики Галилея-Ньютона. Инерциальная система отсчета. Задачи динамики.
Движение мат. точки в поле тяготения Земли.
Дифференциальные ур-я движения свободной и несвободной точки в…
- №51
- 233,29 КБ
- дата добавления неизвестна
- описание отредактировано 08.12.2007 01:35
- Раздел: Механика → Теоретическая механика
85 вопросов и ответов на экзамен по теоретической механике. Преподаватель Ковган С.Т. УГАТУ, 2012
- №52
- 151,36 МБ
- добавлен 27.01.2013 01:04
- описание отредактировано 27.01.2013 05:48
- Раздел: Механика → Теоретическая механика
Векторный, координатный и естественный способы заданий движения точки.Поступательное движение, вращение вокруг неподвижной оси. Плоское движение твёрдых тел.Сложное движение точки. Абсолютная, относительная и переносная скорости и ускорения точки.Аксиомы статики. Геометрический и аналитический способы определения равнодействующей системы сходящихся сил. Момент силы относительно…
- №53
- 112,10 КБ
- дата добавления неизвестна
- описание отредактировано 29.01.2009 21:14
- Раздел: Механика → Теоретическая механика
Карагандинский государственный технический университет, кафедра механики.
Внутри 27 экзаменационных билетов и файл шпаргалка с ответами на эти билеты
- №54
- 197,12 КБ
- дата добавления неизвестна
- описание отредактировано 17.10.2010 23:26
В этом разделе нет файлов.
|
Билет №1. Статика – раздел механики, изучающий условия равновесия материальных тел, находящихся под действием сил. Абсолютно твердое тело – тело, расстояние между двумя точками которого всегда остается постоянным. Свободное тело – тело, перемещение в пространстве которого, ничем не ограничено. Несвободное тело – тело, перемещение в пространстве которого ограничено другими телами. Сила – мера механического воздействия одного тела на другое. Параметры, определяющие действие силы на твердое тело. Сила задается модулем, направлением и точкой приложения. Обозначается большими буквами латинского алфавита: Размерность сил. Основной единицей измерения силы в СИ является 1 ньютон (Н) или 1 килоньютон (кН). 1кН = 1000Н. Линия действия силы – линия, вдоль которой действует сила. Внешние силы – силы, которые действуют на тело со стороны других тел (не входящих в систему). Внутренние силы – силы, с которыми части данного тела дей-ствуют друг на друга. Сосредоточенная сила – сила, приложенная к телу какой-нибудь его точке. Распределенная сила – сила, действующая на все точки данного объема, данной части поверхности тела или линии. |
Билет №2. Система сил — совокупность нескольких сил, действующих на твердое тело. Виды систем сил: -Плоская система сил – совокупность сил, линии действия кото-рых лежат в одной плоскости. -Пространственная система сил – совокупность сил, линии действия которых не лежат одной плоскости. -Сходящееся система сил — совокупность сил, линии действия которых пересекаются одной точке. -Параллельная система сил – совокупность сил, линии действия которых параллельны друг другу. -Эквивалентная система сил – совокупность сил, при котором одну систему сил, можно заменить другой, не изменяя при этом покоя или движения, в которых находится тело. -Уравновешенная система сил – совокупность сил, под действи-ем которых свободное твердое тело может находится в покое. Равнодействующая сила – совокупность сил, при которой одна система сил эквивалентна другой. Задачи статики: Первая задача статики. Преобразование систем сил, действую-щих на твердое тело, системы им эквивалентные относительно некоторого центра О. Вторая задача статики. О равновесие: каким условиям должна удовлетворять система сил, приложенная к данному телу, чтобы она была уравновешенной? |
Билет №3. Аксиомы статики. 1.аксиома двух сил. Две силы, действующие на свободное твердое тело, являются уравновешенными тогда и только тогда, когда эти силы равны по модулю и действуют вдоль одной прямой в противоположные стороны. 2.аксиома присоединения. Действие данной системы сил на абсолютно твердое тело не изменяется, если прибавить к ней или отнять от нее уравновешенную систему сил: ( 3.аксиома параллелограмма. Система двух сил, приложенных к телу в одной точке, равна их геометрической сумме 4.аксиома равенства действия и противодействия. Всякому действию одного тела на другое составляет равное по величине, но противоположное по направлению противодействие. 5.аксиома отвердевания. Если деформируемое тело под действием системы сил находится в равновесии, то при отвердевании его равновесие сохраняется. |
|
Билет №4. Связи – тела, ограничивающие перемещение тела. Реакция связи – сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям. Реакция связи направлена в противоположную сторону действия силы. Основные виды связей: 1.Гладкая поверхность (без трения). Реакция гладкой поверхности направлена по нормали к этой поверхности (перпендикулярна общей касательной). 2.Опорная точка. Реакция перпендикулярна опирающейся поверхности. 3.Идеальная нить (гибкая, невесомая, нерастяжимая). Моделирует трос, канат, цепь, ремень, … . Реакция идеальной нити направлена по нити к точке подвеса. 4.Идеальный стержень (жесткий, невесомый стержень, на концах которого шарниры). Реакция связи направлена по стержню. В отличие от нити стержень может работать на сжатие. 5.Цилиндрический шарнир. Такая связь позволяет телу перемещаться вдоль оси, поворачиваться вдоль оси шарнира, но не позволяет точке закрепления перемещаться в плоскости, перпендикулярной оси шарнира, и проходит через нее. 6.Сферический шарнир. Такая связь не дает точке тела переме-щаться ни в одном из направлений. Положение реакции не опре- |
Билет №5. Сложение двух сил. Геометрическая сумма Или построением силового треугольника: Модуль силы Сложение трех сил, не лежащих в одной плоскости. Геометрическая сумма Сложение системы сил. Сложение системы сил сводится к нахождению ее главного век-тора. |
Билет №6. Проекция силы на ось. Проекция силы на ось – алгебраическая величина, равная произ-ведению модуля силы на косинус угла между силой и положи-тельным направлением оси: Fx = F · cosα = ab, Qx = Q · cosα1 = — Q · cosβ = — dc,
Проекция силы на плоскость. Проекция силы Модуль I В некоторых случаях для нахождения проекции силы на ось удобно найти сначала ее проекцию на плоскость, а затем найденную проекцию на плос- |
|
Билет №7. Аналитический способ задания силы. Для того, чтобы задать силу аналитически, достаточно задать ее проекции на оси системы координат. Пространственная система координат. Если заданы проекции Fx, Fy, Fz, то модуль силы определяется по формуле: I Направление силы находится че-рез вычисление углов α, β, γ с по-мощью направляющих косинусов: cosα = Fx/F, cosβ = Fy/F, cosγ = Fz/F
Плоская система координат. Если заданы проекции Fx, Fy,то модуль и направление силы определяется по фор-мулам: I α = arccos(Fx/F). Аналитический способ сложения сил. Аналитический способ сложения сил базируется на теореме геометрии: Теорема. Проекция вектора суммы на какую-нибудь ось равна ал-гебраической сумме проекций слагаемых векторов на ту же ось. |
Билет №8. Равновесие сходящейся системы сил. Геометрические условия равновесия сходящейся системы сил.
Равнодействующая Таким образом при равновесии: R = Так как Аналитические условия равновесия сходящийся системы сил. Пространственная система сходящихся сил. Для равновесия пространственной системы сходящихся сил необ-ходимо, чтобы сумма проекций этих сил на каждую из трех коор-динат осей была равна нулю: Эти условия называются аналитические условия равновесия пространственной сходящейся системы сил. Плоская система сходящихся сил. Для равновесия плоской сходящейся системы сил необходимо, |
Билет №9. Виды моментов сил. -алгебраический момент силы относительно центра; -векторный момент силы относительно центра; -момент силы относительно оси. Алгебраический момент силы относительно цен-тра – скалярная величии-на, равная произведению модуля силы на ее плечо: mO(
Плечо силы (h) – кратчайшее расстояние от моментальной точки до линии действия силы. Если сила поворачивает тело относительно точки против часовой стрелки, то знак момента «+» и наоборот – «-». Алгебраический момент силы относительно центра равен нулю если: -модуль силы равен нулю; -линия действия силы проходит через моментальную точку. Теорема Вариньона для плоской системы сил. Если данная система сил имеет равнодействующую, то ее момент Относительно центра О равен алгебраической сумме моментов сил системы относительно того же центра: |
|
Билет №10. Пара сил. Плоская система пар. Пара сил – система дух равных по модулю, параллельных и нап-равленных в противоположные стороны сил, дейстующих на абсолютно твердое тело. Пара сил не имеет равнодействующей. Плоскость, в которой действует пара сил, называется плоскостью действия пары. Виды моментов пары сил. -векторный момент; -алгебраический момент. Алгебраический момент пары сил. Алгебраический момент пары сил – взятое с соответствующим знаком произведение модуля одной из сил пары на плечо пары: m = ± F · d. Свойства пары сил. -пару, не изменяя оказываемого ею на твердое тело действия, можно переносить куда угодно в плоскости действия пары; -пару, не изменяя оказываемого ею на твердое тело действия, можно переносить из данной плоскости в любую другую плос-кость; -действие пары сил на твердое тело полностью характеризуется ее моментом, модуль которого равен m = ± F · d. Теорема о сложении пар, лежащих одной плоскости. Система пар, лежащих в одной плоскости и действующих на абсо-лютно твердое тело, эквивалентна одной паре с моментом, рав — |
Билет №11. Приведение произвольной плоской системы сил к неподвиж-ному центру (1-задача статики). Случаи приведения сил: -приведение произвольной пространственной системы сил; -приведение произвольной плоской системы сил. Главный момент произвольной плоской системы сил. Величина Mo равная алгебраической сумме моментов всех сил относительно неподвижного центра О, называется главным моментом произвольной плоской системы сил относительно данного центра: Mo =∑mo( Теорема о приведении плоской системы сил. Любая произвольная система сил, действующая на твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой |
Билет №12. Условия равновесия произвольной плоской системы сил. Геометрические условия равновесия. Для равновесия произвольной плоской системы сил необходимо, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю:
Основная форма аналитических условий равновесия произволь-ной плоской системы сил. Для равновесия произвольной плоской системы сил необходимо, чтобы сумма всех сил на каждую из двух координатных осей и сумма их моментов относительно любого центра, лежащего в плоскости действия сил, были равны нулю:
Первая вспомогательная форма аналитических условий равно-весия произвольной плоской системы сил. Для равновесия произвольной плоской системы сил необходимо, чтобы сумма моментов всех этих сил относительно каких-нибудь центров А и В и сумма их проекций на ось Оx, не перпендикуляр-ную прямой АВ, были равны нулю:
Аналитические условия равновесия плоской системы парал-лельных сил. Если все силы параллельны какой-нибудь оси, то аналитические условия равновесия системы сил имеют вид: |
|
Распределенные нагрузки характеризуются интенсивностью [q] (Н/м). Виды распределенной по линии нагрузки (силы). Равномерно распределенная нагрузка – заменяется сосредото-ченной силой Q = q · l, приложенной к середине участка. Распределенная по линейному закону – заменяется сосредото-ченной силой Q = q · l/2, приложенной на расстоянии 1/3 от конца участка распределения. Распределенная по произвольному закону – заменяется сосредо-точенной силой Q = ∫q(x)dx, приложенной в центре тяжести С фигуры. |
||
|
кость спроектировать: Fx = Fxy · cosϕ= F · cosθ · cosϕ, Fy = Fxy · sinϕ= F · cosθ · sinϕ. Иногда для нахождения проекции силы на ось удобно применять прямое проектирование: Fx = F · cosα, Fy = F · cosβ, Fz =F · cosγ. |
Главный вектор – геометрическая сумма всех сил, входящих в систему: Главный вектор можно найти посредством построения многоу-гольника, который строится посредством параллельного переноса сил. При этом каждая последующая сила откладывается в масшта-бе от конца предыдущей силы: Разложение силы по двум заданным направлениям. Для разложения силы Разложение силы по трем заданным направлениям. Для разложения силы |
делено, но она может быть представлена тремя взаимно перпендикулярными составляющими. 7.Жесткая заделка. Такая связь препятствует перемещению и повороту вокруг точки закрепления. Контакт тела со связью осуществляется по поверхности. Имеем распределенную систему сил реакции, которая может быть заменена одной силой и парой сил. Аксиома освобождаемости связей. Всякое несвободное тело можно считать свободным, если мысленно освободится от связей, а их действие заменить соответствующими реакциями. |
|
mo(
Если равнодействующие двух сил |
Теорема о трех силах. Теорема. Если твердое тело находит-ся в равновесии под действием трех сил, лежащих в одной плоскости, то линии действия этих сил пересекают-ся в одной точке. |
Сложение пространственной системы сил. Пусть силы
Согласно теореме (Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось) если Rx = I Направление равнодействующей силы находится через вычис-ление углов α, β, γ с помощью направляющих косинусов: cosα = Rx/IRI, cosβ = Ry/IRI, cosγ = Rz/IRI и α = arccos(Rx/IRI), β = arccos(Ry/IRI), γ = arccos(Rz/IRI). Сложение плоской системы сил. Пусть силы
Согласно теореме (Проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых векторов на ту же ось) если Rx = Модуль и направление
|
|
или
|
ным алгебраической сумме моментов складываемых пар: M = m1 + m2 + … + mn = ∑mk. Условия равновесия системы пар, лежащих в одной плоскости. Система пар, лежащих в одной плоскости и действующих на абсолютно твердое тело, эквивалентна нулю (находится в равновесии), если алгебраическая сумма моментов пар равна нулю: ∑mk = 0. |
|
|
Билет №13. Условия равновесия произвольной плоской системы сил, прило-женнойй к двум абсолютно твердым телам. Внешние и внутренние связи. Внутренние связи – связи, соединяющие части конструкции, а связи, присоединяющие ее к другим телам – внешние. Метод замораживания. При определении реакций внешних связей составляют одну из форм условий равновесия для «замороженной» конструкции АВС:
Однако этих условий равновесия не доста-точно для определения всех реакций вне-шних связей (4 реакции невозможно оп-ределить из 3-х уравнений). Такие системы называются статически неопределимые.
|
Билет №14. Определение центра тяжести.
Координаты центра тяжести неоднородного тела. Координаты центра тяжести определяются по формулам: ХС = где
Координаты центра тяжести однородных тел. Однородное тело – тело, вес одной из его части которого пропорционален объему этой части: pk = γ · Vk , а вес Р всего тела пропорционален объему V: Р = γ · V, где γ – вес единицы объема. Центр тяжести объема V. Координаты центра тяжести площади определяются по формулам ХС = где наты объемов частиц тела. |
Билет №15. Способы определения координат центров тяжести однород-ных тел. Способ симметрии. Если однородное тело имеет плоскость, ось или центр симметрии, то его центр тяжести лежит соответственно или в плоскости симметрии, или на оси симметрии, или в центре симметрии. Из свойств симметрии следует, что центр тяжести однородного кольца, круглой или прямоугольной пластины, прямоугольного параллелепипеда, шара и других однородных тел, имеющих центр симметрии, лежит в геометрическом центре этих сил. Способ разбиения. Суть метода разбиения заключается в том, что если тело можно разбить на конечное число таких частей, для каждой из которых положение центра тяжести известно, то координаты центра тяжести можно вычислить по формулам: ХС = Способ дополнения. Этот способ является частным случаем способа разбиения. Он применяется к телам, имеющих вырезы, если центры тяжести тел без выреза и вырезной части известны. При этом площади вырезанных частей принимаются отрицательными. Способ интегрирования. Способ заключается в том, что суммы в формулах заменяют интегралами: |
|
Билет №16. Центры тяжести однородных тел. Центр тяжести дуги окружности. Центр тяжести дуги окружности, радиусов R опирающейся на угол 2α имеет координаты: xC = (R · sinα)/α, y C = 0. Центр тяжести площади треугольника. Центр тяжести треугольника лежит на пересечении его медиан. Центр тяжести кругового сектора. Центр тяжести кругового сектора лежит на его оси симметрии на расстоянии от центра О равном: xC = (2R · sinα)/3α. |
Билет №17. Трение. Основные виды трения: трение скольжения и трение качения. Сила трения скольжения – сила сопротивления относительному скольжению при стремлении двигать одно тело по поверхности другого в плоскости сопротивления тел. Законы трения скольжения. 1.При стремлении сдвинуть одон тело по поверхности другого в плоскости соприкосновения тел возникает сила трения. 2.Сила трения приложенная к телу, направлена в противополож-ную сторону силам, которые стремятся сдвинуть тело. 3.Предельная сила трения равна произведению статического коэффициента трения на нормальную реакцию: Fпр = f0 · N. Трение скольжение при движении. При движении сила трения скольжения направлена в сторону, противоположную движению, и равна произведению динамичес-кого коэффициента трения на нормальную реакцию: F = f · N. Реакция шероховатой связи. Угол трения – наибольший угол ϕ0, который полная реакция шероховатой связи образует с нормалью к поверхности: tgϕ0 = Fпр/N = f0. |
Билет №18. Векторный момент силы относительно центра.
Момент силы относительно оси. Проекция момента силы относи-тельно центра, на какую-нибудь ось, проходящую через центр, называется моментом силы относительно оси: Векторный момент пары сил. Векторный момент пары сил – это вектор, модуль которого равен произведению модуля одной из сил пары на ее плечо: m = F · d, и который направлен перпендикулярно плоскости действия пары в ту сторону, откуда пара видна стремящейся повернуть тело против хода часовой стрелки. Свойства векторного момента пары сил. 1.действие пары сил на твердое тело полностью характеризуется |
|
Билет №19. Теорема Пуансо. Любая система сил, действующих на абсолютно твердое тело, при приведении к произвольно выбранному центру О заменяется одной силой Следствие из теоремы Пуансо. Две системы сил, имеющие одинаковые главные векторы и глав-ные моменты относительно одного и того же центра, эквива-лентны. Частные случаи приведения системы сил к центру. 1.Если для данной системы сил 2.Если для данной системы сил |
Билет №20. Геометрические условия равновесия произвольной простран-ственной системы сил. Для равновесия любой системы сил необходимо, чтобы главный вектор этой системы сил и ее главный момент относительно любого центра были равны нулю: Модули главного вектора. I Модуль главного момента. I Теорема Вариньона о моменте равнодействующей. Если данная система сил имеет равнодействующую, то момент равнодействующей относительно любого центра равен сумме моментов сил системы относительно того же центра: mo( Равновесие пространственной системы параллельных сил. Если все действующие силы параллельны друг другу, то можно выбрать оси координат так, что ось Оz будет параллельна силам. Тогда из шести уравнений равновесия останутся только три:
|
|
|
ХС = где
Экспериментальный способ. Различают два способа определения положения центра тяжести однородных и неоднородных тел произвольной формы: -метод подвешивания. Заключается в том, что тело подвешивают на нити или тросе за различные его точки. Направление нити, на которой подвешено тело будет каждый раз давать направление силы тяжести. Точка пересечения этих линий даст положение центра тяжести тела. -метод взвешивания. Заключается в том, что одну из реакций опор тяжелого неодно-родного тела произвольной конфигурации определяют посред-ством взвешивания на специальных весах, а другую реакцию находят из уравнений равновесия. |
Центр тяжести площади S. Координаты центра тяжести площади определяются по формулам ХС = где Центр тяжести линии L. Координаты центра тяжести линии определяются по формулам ХС = где наты частиц линии. |
частей конструкции (АС или ВС), расчленяя ее на части по внутрен-ней связи. При этом, как правило, необходимо составить уравнение моментов, принимая за моментную тоску ту точку, где тела соединяются связью (на рисунке т. С): Метод разбиения. При определении реакций внешних связей и внутренних связей конструкцию расчленяют по внутреннему шарниру, и для каждой части составляют уравнения равновесия. Для части АС: Для части ВС: С учетом того, что Для проверки правильности решения могут быть составлены уравнения равновесия для «замороженной» конструкции. |
|
ее векторным моментом. 2.Две пары сил, имеющие одинаковые векторные моменты экви-валентны. 3.Векторный момент можно приложить в любой точке, то есть этот вектор свободный. Теоремы о сложении пар сил, не лежащих в одной плоскости. Теорема1. Действие на твердое тело двух пар с моментами Теорема2. Система пар, действующих на тело, эквивалентна одной паре с моментом, равным геометрической сумме моментов складыва-емых пар: Геометрические условие равновесия системы пар. При равновесии систем пар момент равнодействующей пары будет равен нулю: Аналитические условия равновесия системы пар. В проекциях на оси координат векторное равенство где
|
Трение качения. Трение качения – сопротивление, возникающее при качении од-ного тела по поверхности другого. Трение качения возникает из-за деформации соприкасающихся тел. |
Центр тяжести объема пирамиды. Центр тяжести пирамиды С лежит на прямой С1Е, где С1 – центр тяжести площади основания пирамиды. |
А
Абсолютно твердое тело (1)
Аксиомы статики (3)
Аксиома освобождаемости связей (4)
Алгебраический момент пары сил (10)
Алгебраический момент силы относительно центра (9)
Аналитический способ задания силы (7)
Аналитический способ сложения сил (7)
Аналитические условия равновесия системы пар (18)
Аналитические условия равновесия плоской системы параллельных сил (12)
Аналитические условия равновесия сходящийся системы сил (8)
В
Векторный момент пары сил (18)
Векторный момент силы относительно центра (18)
Виды моментов сил (9)
Виды моментов пары сил (10)
Виды связей (4)
Внешние силы (1)
Внутренние силы (1)
Внешние и внутренние связи (13)
Г
Геометрические условия равновесия произвольной пространственной системы сил (20)
Геометрические условия равновесия сходящейся системы сил (8)
Геометрические условие равновесия системы пар (18)
Главный вектор (5)
Главный момент произвольной плоской системы сил (11)
З
Задачи статики (2)
Законы трения скольжения (17)
К
Координаты центра тяжести однородных тел (14)
Координаты центра тяжести неоднородного тела (14)
Л
Линия действия силы (1)
М
Метод замораживания (13)
Метод разбиения (13)
Модули главного вектора (20)
Модуль главного момента (20)
Модуль силы (5)
Момент силы относительно оси (18)
Моментальная точка (9)
Н
Несвободное тело (1)
О
Однородное тело (14)
Основная форма аналитических условий равновесия произвольной плоской системы сил (12)
П
Пара сил (10)
Параметры, определяющие действие силы на твердое тело (1)
Первая вспомогательная форма аналитических условий равновесия произвольной плоской системы сил (12)
Первая задача статики (11)
Плоская система координат (7)
Параллельная система сил (2)
Плечо силы (9)
Плоская система сил (2,8)
Плоская система пар (10)
Плоская система сходящихся сил (8)
Приведение произвольной плоской системы сил к неподвижному центру (11)
Проекция силы на ось (6)
Проекция силы на плоскость (6)
Пространственная система координат (7)
Пространственная система сил (2,7)
Пространственная система сходящихся сил (8)
Р
Равнодействующая сила (2,8)
Равновесие пространственной системы параллельных сил (20)
Равновесие сходящейся системы сил (8)
Равномерно распределенная нагрузка (1)
Разложение силы по двум заданным направлениям (5)
Разложение силы по трем заданным направлениям (5)
Размерность сил (1)
Распределенная сила (1)
Реакция связи (3)
Реакция шероховатой связи (17)
С
Свободное тело (1)
Свойства векторного момента пары сил (18)
Свойства пары сил (10)
Связи (3)
Сила (1)
Сила трения скольжения (17)
Система сил (2,5,7)
Система координат (7)
Сложение двух сил (5)
Сложение плоской системы сил (7)
Сложение пространственной системы сил (7)
Сложение системы сил (5)
Сложение трех сил, не лежащих в одной плоскости (5)
Сосредоточенная сила (1)
Способ симметрии (15)
Способ разбиения (15)
Способ дополнения (15)
Способ интегрирования (15)
Способы определения координат центров тяжести однородных тел (15)
Статика (1)
Статически неопределимые системы (13)
Сходящееся система сил (2,8)
Т
Теорема Вариньона для плоской системы сил (9)
Теорема Вариньона для плоской системы сил (случай двух сил) (9)
Теорема Вариньона о моменте равнодействующей (20)
Теорема Пуансо (19)
Теорема о приведении плоской системы сил (11)
Теоремы о сложении пар сил, не лежащих в одной плоскости (18)
Теорема о трех силах (8)
Теорема о сложении пар, лежащих одной плоскости (10)
Трение (17)
Трение качения (17)
Трение скольжение при движении (17)
У
Угол трения (17)
Уравновешенная система сил (2)
Условия равновесия произвольной плоской системы сил (12)
Условия равновесия произвольной плоской системы сил, приложенной к двум абсолютно твердым телам (13)
Условия равновесия системы пар, лежащих в одной плоскости (10)
Ц
Центр тяжести (14)
Центр тяжести объема V (14)
Центр тяжести площади S (14)
Центр тяжести линии L (14)
Центры тяжести однородных тел (16)
Центр тяжести дуги окружности (16)
Центр тяжести площади треугольника (16)
Центр тяжести кругового сектора (16)
Центр тяжести объема пирамиды (16)
Ч
Частные случаи приведения системы сил к центру (19)
Э
Эквивалентная система сил (2)

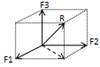
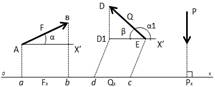
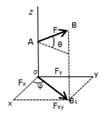 Px = 0.
Px = 0.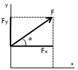
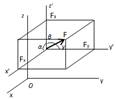 и α = arccos(Fx/F), β = arccos(Fy/F), γ = arccos(Fz/F).
и α = arccos(Fx/F), β = arccos(Fy/F), γ = arccos(Fz/F).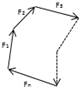 Сходящаяся система сил
Сходящаяся система сил 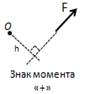
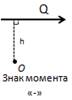 Центр О относительно которого вычисляется ал-гебраический момент, называется моментальной точкой.
Центр О относительно которого вычисляется ал-гебраический момент, называется моментальной точкой. 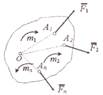
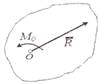
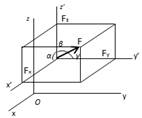
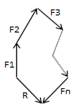
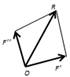 Теорема Вариньона для плоской системы сил (случай двух сил).
Теорема Вариньона для плоской системы сил (случай двух сил).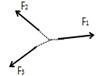 чтобы сумма проекций этих сил на каждую из двух координатных осей была равна нулю:
чтобы сумма проекций этих сил на каждую из двух координатных осей была равна нулю: 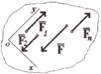
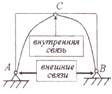
 Такую статическую неопределимость рас-крывают составлением дополнительного уравнения(ий) равновесия для одной из
Такую статическую неопределимость рас-крывают составлением дополнительного уравнения(ий) равновесия для одной из Центр тяжести – точка (на рисунке С), связанная с телом, через которую проходит линия действия равнодей-ствующей сил тяжести, действующих на частицы данного тела, при любом положении тела.
Центр тяжести – точка (на рисунке С), связанная с телом, через которую проходит линия действия равнодей-ствующей сил тяжести, действующих на частицы данного тела, при любом положении тела.
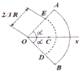
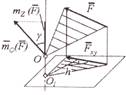
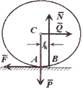 Векторный момент силы относительно центра – это приложенный в центре вектор, модуль которого равен произве-дению модуля силы на ее плечо и который направлен перпендикулярно плоскости, проходящей через центр и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра против хода часовой стрелки: I
Векторный момент силы относительно центра – это приложенный в центре вектор, модуль которого равен произве-дению модуля силы на ее плечо и который направлен перпендикулярно плоскости, проходящей через центр и силу, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра против хода часовой стрелки: I