Комитет общего и профессионального образования
Ленинградской области
ГБПОУ ЛО «Волховский колледж транспортного
строительства»
УТВЕРЖДАЮ
УТВЕРЖДАЮ
Заместитель директора
Заместитель
директора
по учебной работе
по учебной работе
__________ . «___»___________ 2017
г. «____»
_____________20___ г.
Экзаменационный материал
Дисциплина МАТЕМАТИКА
Группы 106, 111, 130 специальности 08.02.01,
08.02.05, 38.02.03
Преподаватель Петрова Людмила Львовна
Рассмотрено на заседании
цикловой Рассмотрено на заседании цикловой
комиссии .
комиссии . .
.
.
Протокол № от « »
2017г Протокол № ___ от «__» ______201 г
Председатель цикловой
комиссии Председатель цикловой комиссии
___________ _____________
г.
Волхов 2017
ВВЕДЕНИЕ
Экзамен по математике проводится письменно за
счет времени, выделяемого ФГОС СПО на промежуточную аттестацию, с
использованием экзаменационных материалов в виде набора контрольных заданий,
требующих краткого ответа и/или полного решения. На выполнение письменной
экзаменационной работы по математике дается 3 астрономических часа (180 минут).
Письменная
экзаменационная работа по математике составляется из 2-х частей: обязательной и
дополнительной. В обязательную часть включены задания минимально обязательного
уровня, в дополнительную часть — более сложные.
В обязательную часть работы включаются
задания базового уровня по всем основным разделам требований ФГОС — геометрия
(планиметрия и стереометрия), алгебра, начала математического анализа, теория
вероятностей, комбинаторика и статистика.
При выполнении заданий
обязательной
части обучающиеся должны продемонстрировать базовую математическую
компетентность. Задания этой группы проверяют базовые вычислительные и
логические умения и навыки, умение анализировать информацию, представленную в
графиках и таблицах, использовать простейшие вероятностные и статистические
модели, умение ориентироваться в простейших геометрических конструкциях,
владение основными алгоритмами, знание и понимание ключевых элементов
содержания (математических понятий, их свойств, приемов решения задач и пр.),
умение пользоваться математической записью, а также применять математические
знания в простейших практических ситуациях.
Обязательная часть содержит 15 заданий.
Дополнительная
часть направлена на проверку владения материалом на повышенном уровне и
умение решать математические задачи, не сводящиеся к прямому применению алгоритма.
Эта часть содержит 5 заданий повышенного уровня сложности из различных разделов
курса математики.
При выполнении
всех заданий дополнительной части обучающимся требуется представить описание
хода решения задачи и полученный ответ.
За правильное
выполнение любого задания из обязательной части обучающийся получает
один балл.
При выполнении задания из обязательной части,
где необходимо привести краткое решение, за неполное решение задания
(вычислительная ошибка, описка) выставляется 0,5 балла.
Если обучающийся
приводит неверное решение, неверный ответ или не приводит никакого ответа, он
получает 0 баллов.
За каждое задание дополнительной
части максимально можно получить 3 балла.
Максимальное
количество баллов за весь экзамен — 30 баллов.
За выполнение любого
задания из дополнительной части используются следующие
критерии оценки заданий:
|
Содержание критерия |
Баллы |
|
Приведено верное обоснованное решение, приведен правильный ответ |
3 |
|
Приведено верное решение, но допущена вычислительная |
2 |
|
Решение начато |
1 |
|
Неверное решение, |
0 |
Баллы, полученные за
все выполненные задания, суммируются.
Шкала перевода баллов
в отметки по пятибалльной системе
|
Отметка |
Число баллов, необходимое для получения |
|
«3» (удовлетворительно) |
15- 20 |
|
«4» (хорошо) |
21- 25 |
|
«5» (отлично) |
26 — 30 |
Тематика заданий
1 вопрос – задача на составление математической
модели;
2 вопрос – вычисление степенных выражений;
3 вопрос – решение иррациональных уравнений;
4 вопрос – решение систем уравнений;
5 вопрос – применение свойств логарифмов;
6-9 вопросы – определение свойств функции по
графику;
10 вопрос – нахождение значений
тригонометрических функций;
11 вопрос – определение нулей функции;
12 вопрос – производная или интеграл
элементарных функций;
13 вопрос – нахождение элементов
многогранников;
14 вопрос – тригонометрические уравнения;
15 вопрос – область определения функции;
16 вопрос – задача из раздела «Комбинаторика и
теория вероятностей»;
17 вопрос – показательное или логарифмическое
уравнение;
18 вопрос – нахождение объёмов или площадей
геометрических фигур;
19 вопрос – показательное или логарифмическое
неравенство;
20 вопрос– исследование функции с помощью
производной.
Примерный вариант
экзаменационной работы по математике за 1 курс
Обязательная часть
При выполнении заданий 1-5 запишите ход решения и полученный ответ.
1)
(1
балл) Стоимость одной поздравительной открытки 20 рублей. Сколько
открыток можно будет купить на 700 рублей во время распродажи, если скидка
составляет 35%?
2)
(1
балл) Вычислите значение выражения 
3)
(1
балл) Решите уравнение .
4)
(1
балл) Решите систему уравнений
5)

балл) Найдите значение выражения .
При выполнении заданий 6-9,
используя график функции
(см. рис. ниже) определите и запишите полученный ответ.
6)
(1
балл) Четность, нечетность функции.
7)
(1
балл) Нули функции.

(1
балл) Множество значений функции.
9)
(1
балл) При каких значениях
При выполнении заданий 10-15
укажите ход решения и запишите полученный ответ.
10)
(1
балл) Найдите значение , если известно,
что и
четверти.
11)
(1
балл) Найдите нули функции .
12)
(1
балл) Найти производную функции
13) (1 балл) В прямоугольном параллелепипеде известно,
что и
,
. Найдите длину
ребра .
14) (1 балл) (1 балл) Решите уравнение .
15) (1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-22
запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Сколькими
способами можно выбрать 5 человек на 5 различных должностей из 12 кандидатов
на эти должности?
17) (3 балла)
Найдите корень уравнения 
18) (3 балла) В правильной четырехугольной пирамиде точка
—
центр основания, вершина,
,
. Найдите боковое ребро
.
19) (3 балла) Решите неравенство .
20) (3 балла) Найдите наибольшее значение функции y =– 2x2 – 8х -12
на отрезке [–1; 7]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
10 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Налог на доходы составляет 13% от заработной платы. После удержания
налога на доходы Лариса Петровна получила 10440 рублей. Сколько рублей
составляет заработная плата Ларисы Петровны?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Наименьшее и наибольшее значения функции.

балл) Множество значений функции.
9) (1
балл) При каких значениях
При
выполнении заданий 10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1
балл) Найдите нули функции .
12) (1
балл) Найти производную функции
13) (1 балл) В правильной
четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите длину отрезка
.
14)
(1 балл) Решите уравнение sin 2x = 1.
15) (1 балл) Найдите область определения
функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 12
полицейских необходимо составить наряд из 5 человек. Сколькими способами это
можно сделать?
17) (3 балла)
Найдите корни уравнения .
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 15см,
высота пирамиды равна 12см. Найти объём и площадь полной поверхности пирамиды.
19)
(3
балла) Решите неравенство .
20) (3 балла) Найдите
наименьшее значение функции y = x2 – 12x + 12 на отрезке [-1 ; 3 ]
Преподаватель Петрова Л.Л.
Комитет общего и профессионального образования
Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
9 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Флакон шампуня стоит 80 рублей. Какое наибольшее количество флаконов
можно купить на 500 рублей во время распродажи, когда скидка составляет 25%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) На основании основного логарифмического тождества найдите
значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Наименьший положительный период функции.

балл) Множество значений функции.
9) (1
балл) Наименьшее и наибольшее значения функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1 балл) Найдите
нули функции
12) (1
балл) Найти производную функции
13) (1
балл) В прямоугольном параллелепипеде известно, что
,
,
.
Найдите длину ребра .
14) (1
балл) Решите уравнение cos x = –
.
15) (1
балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Сколько 3-значных чисел можно составить из множества цифр
1,2,3,4,5,6,7,8,9 а) без повторений; б) с повторениями?
17) (3 балла) Найдите корни уравнения .
18)
(3 балла) Сторона основания правильной четырехугольной пирамиды равна 12см,
высота пирамиды равна 8см. Найти площадь полной поверхности пирамиды.
19)
(3 балла) Решите неравенство.
20) (3 балла) Найти
интервалы возрастания и убывания функции y = x4 – 32x2
– 75
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
8 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Билет на автобус стоит 15 рублей. Какое наибольшее число билетов можно
будет купить на 100 рублей после повышения цены билета на 20%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Множество значений функции.

балл) Нули функции.
9) (1
балл) Четность, нечетность функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1
балл) Найдите нули функции
12) (1
балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14) (1 балл)
Решите уравнение cos3 x = –1.
15)
(1 балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Участники жеребьевки тянут из ящика
жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого
наудачу извлеченного жетона не содержит цифры 7.
17) (3 балла) Найдите корни уравнения .
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 10см,
высота пирамиды равна 8см. Найти объём и площадь полной поверхности пирамиды.
19)
(3 балла) Решите неравенство.
20) (3 балла) Найдите экстремумы функции y(x) = 2x3 – 3x2 – 12x + 5
выяснить их род.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
7 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Из 75 девятиклассников школы 15 человека приняли участие в городских
спортивных соревнованиях. Сколько процентов девятиклассников не принимали
участия в этих соревнованиях?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции 
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Область определения функции.
7) (1
балл) Четность, нечетность функции.

балл) Монотонность функции.
9) (1
балл) Нули функции.

При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10) (1
балл) Найдите значение , если известно,
что и
четверти.
11) (1 балл) Найдите нули
функции
12) (1
балл) Найти производную функции
13) (1
балл) В прямоугольном
параллелепипеде известно, что
,
,
.
Найдите длину ребра .
14) (1 балл)
Решите уравнение sin x = .
15) (1 балл)
Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) Из 100 билетов выигрышными
являются 15. Какова вероятность того, что среди 6-ти билетов, взятых на удачу,
будет два выигрышных?
17) (3 балла) Найдите корни уравнения
.
18) (3 балла) Апофема правильной четырехугольной пирамиды равна 5 м,
высота пирамиды равна 4 м. Найти объём и площадь полной поверхности пирамиды.
19 (3
балла) Решите неравенство
20 (3 балла) Найдите
наибольшее значение функции y =– 2x2 – 8х -12 на отрезке [–2; 6]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
6 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Дневная норма потребления витамина C
составляет 60 мг. Один мандарин в среднем содержит 35 мг витамина С. Сколько
примерно процентов дневной нормы витамина С получил человек, съевший один
мандарин?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение.
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Промежутки возрастания функции.
9) (1
балл) Нули функции.

При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр
основания, вершина,
,
. Найдите боковое ребро
14) (1 балл) Решите уравнение
cos 2x = 0
15)(1
балл) Найдите область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В магазин поступило 25 телевизоров,
4 среди которых имеют скрытые дефекты. Наудачу отбираются 2 телевизора для
проверки. Какова вероятность того, что оба они не имеют дефектов?
17) (3 балла) Найдите корни
уравнения .
18) (3 балла) Апофема
правильной четырехугольной пирамиды равна 15см, высота пирамиды равна 12см.
Найти объем пирамиды и площадь ее полной поверхности.
19) (3 балла) Решите неравенство 
20) (3 балла) Найти
интервалы возрастания и убывания функций y = x4 – 2x2
+ 64.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
5 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения
и полученный ответ.
1) (1
балл) Стоимость проезда в пригородном электропоезде составляет 198 рублей.
Школьникам предоставляется скидка 50 процентов. Сколько рублей стоит проезд
группы из 4 взрослых и 12 школьников?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .
При
выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В прямоугольном параллелепипеде известно, что
,
,
. Найдите длину
ребра .
14) (1 балл) Решите
уравнение sin 3x = –1.
15) (1 балл) Найдите
область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход обоснование решения и полученный ответ.
16) (3 балла) В
партии деталей 25 изделий высшего сорта, 35 изделий первого сорта и 5 нестандартных.
Деталь, выбранную наудачу, проверяют на соответствие стандарту. Найти
вероятность того, что она окажется нестандартной.
17) (3 балла) Найдите корни уравнения
.
18) (3 балла) Высота конуса равна 9
см., радиус основания 4 см. Найти объем конуса и площадь его полной
поверхности.
19) (3 балла)
Решите неравенство .
20) (3 балла) Найти экстремумы функции y(x) = 2x4 – 4x2 + 20, выяснить их род.
Преподаватель
Петрова Л.Л.
Комитет общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
4 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход решения
и полученный ответ.
1) (1
балл) Тетрадь стоит 20 рублей. Сколько тетрадей можно купить на 200 рублей
после повышения цены на 25%?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Наименьший положительный период функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В
прямоугольном параллелепипеде известно, что
,
,
. Найдите длину ребра
.
14) (1 балл) Решите
уравнение sin x = – .
15) (1 балл)
Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-18 запишите ход, обоснование решения и
полученный ответ.
16) (3 балла) Из 40 полицейских необходимо составить наряд из 8
человек. Сколькими способами это можно сделать?
17) (3 балла) Найдите корень уравнения .
18)
(3 балла) Стороны основания
правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите
площадь боковой поверхности этой пирамиды.
19)
(3 балла) Решите неравенство – 1
0.
.
20) (3 балла) Найдите
наибольшее значение функции y =– x2 + 4х + 8 на отрезке [ 3; 5]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
3 вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) После повышения цены на 20% тетрадь стоит 30 рублей. Сколько стоила
тетрадь до повышения цены?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Множество значений функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14)
(1 балл) Решите уравнение cos x = .
15)
(1 балл) Найдите область определения функции
Дополнительная часть
При выполнении заданий 16-20 запишите ход, обоснование решения и
полученный ответ.
16)(3 балла) Сколькими способами можно выбрать 6 человек
на 6 различных должностей из 10 кандидатов на эти должности?
17) (3 балла) Найдите корень уравнения .
18)
(3 балла) Стороны основания
правильной четырехугольной пирамиды равны 8, боковые ребра равны 5. Найдите
площадь поверхности этой пирамиды.
19)
(3 балла) Решите неравенство – 1
0.
20)(3 балла) Найти
интервалы возрастания и убывания функций
y =– x4 + 32x2 + 12.
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
2 Вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Коробка конфет стоит 60 рублей. Какое наибольшее количество коробок
можно купить на 400 рублей вовремя распродажи, когда скидки составляет 20%
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение .
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения 

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Значения переменной х, при .
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Нули функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите
значение , если известно, что
и
четверти.
11)
(1 балл) Найдите нули функции
12)
(1 балл) Найти производную функции
13)
(1 балл) В
прямоугольном параллелепипеде известно, что
,
,
. Найдите длину ребра
.
14) (1 балл)
Решите уравнение sin 2x = -1.
15) (1 балл) Найдите область
определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В магазин поступило
26 телевизоров, 4 среди которых имеют скрытые дефекты. Наудачу
отбираются 2 телевизора для проверки. Какова вероятность того, что оба они не
имеют дефектов?
17) (3 балла) Найдите корень
уравнения .
18) (3 балла) Найти объем прямоугольного
параллелепипеда, диагональ которого равна 13см, а длина сторон основания равны
3см и 4см.
19)
(3 балла) Решите неравенство –
1 0.
20) (3 балла) Найдите
наибольшее значение функции y =– 2x2 – 8х – 12 на отрезке [–1; 7]
Преподаватель
Петрова Л.Л.
Комитет
общего и профессионального образования Ленинградской области
ГБПОУ
ЛО «Волховский колледж транспортного строительства»
1 Вариант
Обязательная часть
При выполнении заданий 1-5 запишите ход
решения и полученный ответ.
1) (1
балл) Стоимость проезда в электричке составляет 240 рублей. После нового года
ожидается повышение стоимости на 15%. Сколько будет стоить проезд после нового
года?
2) (1
балл) Вычислите значение выражения .
3) (1
балл) Решите уравнение.
4) (1
балл) Решите систему уравнений
5) (1
балл) Найдите значение выражения .

выполнении заданий 6-9, используя график функции (см.
рис. ниже) определите и запишите полученный ответ.
6) (1
балл) Нули функции.
7) (1
балл) Четность, нечетность функции.

балл) Область определения функции.
9) (1
балл) Множество значений функции.
При выполнении заданий
10-15 укажите ход решения и запишите полученный ответ.
10)
(1 балл) Найдите значение , если известно, что
и
четверти.
11)
(1 балл) Найдите
нули функции
12)
(1 балл) Найти производную функции
13) (1 балл) В правильной четырехугольной пирамиде точка
— центр основания,
вершина,
,
. Найдите боковое ребро
.
14) (1 балл)
Решите уравнение sin 2x = 0.
15)(1 балл) Найдите
область определения функции
Дополнительная часть
При
выполнении заданий 16-20 запишите ход, обоснование решения и полученный ответ.
16) (3 балла) В партии деталей 80 изделий высшего
сорта, 90 изделий первого сорта и 7 нестандартных. Деталь, выбранную
наудачу, проверяют на соответствие стандарту. Найти вероятность того, что она
окажется нестандартной.
17) (3 балла) Найдите корень
уравнения .
18) (3 балла) Стороны основания правильной
четырёхугольной пирамиды равны 6, боковые рёбра равны 5. Найдите площадь
поверхности этой пирамиды.
19)
(3 балла) Решите неравенство ≤16.
20) (3 балла) Найти
экстремумы функции y(x) = 3x4 + 4x3
– 12x2
+ 17, выяснить их род.
Преподаватель
Петрова Л.Л.
Инструкция для обучающихся по выполнению
экзаменационной работы
На выполнение
письменной экзаменационной работы по математике дается
3 астрономических часа
(180 минут).
Экзаменационная работа
состоит из 2-х частей: обязательной и дополнительной.
Обязательная часть содержат задания минимально
обязательного уровня, а дополнительная часть — более сложные задания.
При выполнении
большинства заданий обязательной части требуется представить ход решения и
указать полученный ответ. Только в нескольких заданиях достаточно представить
ответ. За правильное выполнение любого задания из обязательной части Вы
получаете один балл. Если Вы приводите неверное решение, неверный ответ или не
приводите никакого ответа, получаете 0 баллов за задание.
При выполнении любого задания дополнительной
части необходимо подробно описать ход решения и дать ответ.
Правильное выполнение заданий дополнительной
части оценивается
3 баллами.
Баллы, полученные за
все выполненные задания, суммируются. Постарайтесь правильно выполнить как можно
больше заданий и набрать как можно больше баллов.
Перед началом работы
внимательно ознакомьтесь со шкалой перевода баллов в отметки и обратите
внимание, что начинать работу следует с заданий обязательной части.
|
Отметка |
Число баллов, необходимое для получения |
|
«3» (удов.) |
9-15 |
|
«4» (хорошо) |
16-21 |
|
«5» (отлично) |
Более 21 |
Желаем успехов!
Преподаватель
Петрова Л.Л.
Министерство образования Республики Башкортостан
Государственное бюджетное профессиональное образовательное учреждение
Зауральский агропромышленный колледж
РАССМОТРЕНО УТВЕРЖДАЮ
на заседании ПЦК ООД И.о.директора
Председатель ПЦК
________Р.А.Кашкаров _________А.Р.Валеев
«____»____________2020 «____»____________2020
Варианты экзаменационных работ по учебной дисциплине
«МАТЕМАТИКА: АЛГЕБРА И НАЧАЛА МАТЕМАТИЧЕСКОГО
АНАЛИЗА; ГЕОМЕТРИЯ»
35.01.13 «Тракторист-машинист сельскохозяйственного производства»
15.01.05 «Сварщик (электросварочные и газосварочные работы)»
23.01.13 «Автомеханик»
35.01.23 «Хозяйка(ин) усадьбы»
Подготовила:
преподаватель математики
Сулейманова Г.З.
Баймак-2020
Пояснительная записка.
Целью проведения письменного экзамена по математике является обобщение и систематизация знаний, умений, навыков, установление уровня и качества знаний студентов требованиям к уровню подготовки выпускников, предусмотренным стандартом среднего (полного) общего образования по математике и зафиксированным в учебной программе по математике для студентов по ППССЗ.
На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240 минут). Уровень сложности и содержание заданий определяется требованиями к математической подготовке обучающихся, предусмотренными учебной программой по математике. Экзаменационные материалы для проведения письменного экзамена с использованием набора контрольных заданий сформированы включающей задания минимально обязательного уровня, правильное выполнение которых достаточно для получения удовлетворительной оценки (3). Оценка результатов выполнения экзаменационной работы осуществляется согласно утвержденным критериям оценки, которые открыты для обучающихся до конца экзамена.
Требования (умения и виды деятельности), проверяемые заданиями письменной экзаменационной работы
Уметь выполнять вычисления и преобразования:
— выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;
— вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования; — проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции.
Уметь решать уравнения и неравенства:
— решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы;
— решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод;
— решать рациональные, показательные и логарифмические неравенства.
Уметь выполнять действия с функциями:
— определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения; строить графики изученных функций;
— вычислять производные и первообразные элементарных функций;
— исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций.
Уметь выполнять действия с геометрическими фигурами, координатами и векторами:
— решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей);
— решать простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов); использовать при решении стереометрических задач планиметрические факты и методы;
— определять координаты точки.
Уметь строить и исследовать простейшие математические модели:
— моделировать реальные ситуации на языке алгебры, составлять уравнения и неравенства по условию задачи; исследовать построенные модели с использованием аппарата алгебры;
— моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин; — проводить доказательные рассуждения при решении задач, оценивать логическую правильность рассуждений, распознавать логически некорректные рассуждения.
Уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
— анализировать реальные числовые данные; осуществлять практические расчеты по формулам, пользоваться оценкой и прикидкой при практических расчетах;
— описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики; извлекать информацию, представленную в таблицах, на диаграммах, графиках;
— решать прикладные задачи, в том числе социально-экономического и физического характера, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Экзаменационная письменная работа по математике.
Инструкция для студентов по выполнению работы.
На выполнение письменной экзаменационной работы по математике дается 4 астрономических часа (240 минут). Экзаменационная работа состоит из двух частей, включающих в себя 23 заданий. Часть 1 содержит 20 заданий с выбором ответа, часть 2 содержит 3 задания с развёрнутым ответом. Правильное выполнение заданий оценивается баллами. Правильное выполнение задания части 1оценивается 1 баллом, части 2- 2 баллами. Баллы указываются в скобках около номера задания. Если приводится неверный ответ или ответ отсутствует, ставится 0 баллов. Баллы, полученные за все выполненные задания, суммируются. Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов. Перед началом работы внимательно изучите критерии оценивания
Критерии оценки выполнения работы.
Оценка. Число баллов, необходимое для получения оценки «3» (удовлетворительно) 8-14, «4» (хорошо) 15–20 , «5» (отлично) 21–26 (не менее одного задания из части 2). Желаем успехов!
|
Оценка |
Число баллов, необходимое для получения оценки |
|
«2»(неудовлетворительно) |
0-7 |
|
«3» (удовлетворительно) |
8-14 |
|
«4» (хорошо) |
15-20 |
|
«5» (отлично) |
21-26 |
Вариант 1.
Часть 1.
1. Представить в виде степени и найти значение выражения при а = 6.
1 ) 6; 2) ; 3) – 6; 4)
.
2. В прямоугольном треугольнике гипотенуза равна 10 см, а один из катетов
6 см. Найти второй катет.
1) 4 см; 2) 16 см; 3) 8 см; 4) √136 см;
3. Банк выплачивает ежегодно 8% от суммы вклада. Какой станет сумма через
год, если первоначальный вклад составлял 7600 рублей?
1) 8208 руб.; 2) 608 руб.; 3) 8200 руб.; 4) 7600 руб.
4.Найдите корень уравнения log 2(3x +1) = 3
1) 11; 2) 1; 3) -10; 4) .
5. Укажите промежуток, которому принадлежит корень уравнения
log4 (4 – х ) + log4 2 = 1
1) ( -3; -1 ); 2) ( 0; 2 ); 3) [ 2; 3 ]; 4) [ 4; 8 ].
6. Решите неравенство log3( 4 – 2х ) 1
1) ( -∞; 0,5 ]; 2) ( -∞; 2 ]; 3) [ 2; + ∞ ); 4) [ 0,5; + ∞ ).
7. Какой не может быть призма?
1) Прямой; 2)Наклонной; 3) Правильной; 4) Усеченной.
8. Ребро куба равно 2 см. Вычислите сумму длин всех ребер куба.
1) 24 см; 2) 48 см; 3) 12 см; 4) 60 см.
9. Площадь грани куба равна 16 см . Вычислите его объем.
1) 24 см ; 2) 48 см
; 3) 56 см
; 4) 64 см
.
10. Укажите производную функции .
1) ; 2)
; 3)
; 4)
.
11. Уравнение касательной к графику функции в точке с абсциссой х0 = -3 имеет вид:
1) ; 2)
; 3)
; 4)
.
12. Тело движется по прямой так, что расстояние S (в метрах) от него до точки B этой прямой изменяется по закону (t – время движения в секундах). Через сколько секунд после начала движения мгновенная скорость тела будет равна 72 м/с.
1) 16; 2)15; 3) 14; 4) 13.
13.Найдите значение выражения 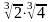
1) 2; 2) 4; 3) 10; 4)5.
14. Представьте в виде степени выражение: 
1) 
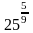
15. Решите показательное уравнение: 5х = 625
1) х = 125; 2) х = 25; 3) х = 4; 4) х = 5.
16. Сколько точек максимума имеет функция
1) 1; 2) 2; 3) 3; 4) таких точек нет.
17. Найдите значение выражения , если
1) 0,8; 2) 0,2; 3) 0,4; 4) 0,6.
18. Сколько нулей имеет функция
1) 1; 2) 2; 3) 3; 4) таких точек нет.
19.В сборнике по географии всего 35 билетов, в семи из них встречается вопрос о материках. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете будет вопрос о материках?
1)0,2; 2) 0,8; 3) 0,5; 4) 5
20. Найдите значение выражения log816 + log84
1) log820; 2) 1; 3) 2; 4) 0.
Часть 2.
1. Решите уравнение: 2sin 2 х-3cos х-3=0
2. Моторная лодка прошла против течения реки 210 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
3. Найдите наибольшее значение функции у=х3-3х+4 на отрезке [-2;0]
Вариант 2.
Часть 1.
1. .Представить в виде степени и найти значение выражения при с = 4.
1а) 16; 2) ; 3) 4; 4)
.
2. В прямоугольном треугольнике гипотенуза равна 10 см, а один из катетов 8 см. Найти второй катет.
1) 4 см; 2) 6 см; 3) 8 см; 4) √136 см;
3. Банк выплачивает ежегодно 8% от суммы вклада. Какой станет сумма через
год, если первоначальный вклад составлял 8600 рублей?
1) 8208 руб.; 2) 688 руб.; 3) 9288 руб.; 4) 8600 руб.
4.Найдите корень уравнения log 5(2x — 4) = 2
1) 11; 2) 14,5; 3) -10 ; 4) .
5. Укажите промежуток, которому принадлежит корень уравнения
lоg0,4 (5 – 2х ) – lоg0,4 2 = 1
1) ( -∞; -2 ); 2) [ -2; 1 ]; 3) [ 1; 2 ]; 4) ( 2; +∞).
6. Решите неравенство log8 (5 – 2х) 1
1) (-∞; -1,5); 2) (-10; 2,5); 3) (2,5; + ∞); 4) ( -10; + ∞).
7. Прямоугольный параллелепипед – это
1) Пирамида; 2) Призма; 3) Октаэдр; 4) Тетраэдр.
8. Измерения прямоугольного параллелепипеда равны 2 см, 3 см и 5 см. Вычислите его объем.
1) 30 см3; 2) 15 см ; 3) 20 см
; 4) 25 см
.
9. Ребро куба равно 2 см. Вычислите площадь поверхности куба.
1) 12 см ; 2) 24 см
; 3) 16 см
; 4) 18 см
.
10. Укажите производную функции .
1) ; 2)
; 3)
; 4)
.
11. Уравнение касательной к графику функции в точке с абсциссой х0 = -3 имеет вид:
1) ; 2)
; 3)
; 4)
.
12. Тело движется по прямой так, что расстояние от начальной точки изменяется по закону (м), где t – время движения в секундах. Найдите скорость тела через 10 секунд после начала движения .
1) 10; 2)9; 3) 8; 4) 7.
13. Найдите значение выражения
1) 2; 2) 4; 3) 10; 4)5.
14. Представьте в виде степени выражение:
1) ; 2)
; 3) 42; 4) 162.
15. Решите показательное уравнение: 3х = 27
1) х = 9; 2) х = 3; 3) х = 4; 4) х = 5.
16. Сколько точек минимума имеет функция
1) 1; 2) 2; 3) 3; 4) таких точек нет.
17. Найдите значение выражения , если
1) -0,4; 2) -0,6; 3) -1,4; 4) 0,6.
18. Сколько нулей имеет функция
1) 1; 2) 2; 3) 3; 4) таких точек нет.
19. В сборнике по биологии всего 25 билетов, в двух из них встречается вопрос о грибах. На экзамене школьнику достается один случайно выбранный билет из этого сборника. Какова вероятность того, что в этом билете не будет вопроса о грибах?
1) 0,92; 2) 0,08; 3) 0,80; 4) 0,25
20. Найдите значение выражения lg25 + lg4
1) 2; 2) 1; 3) lg29; 4)3.
Часть 2.
1. Решите уравнение: 4sin2 х+11sin х-3=0
2. Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.
3. Найдите наименьшее значение функции у=х3-3х2+2 на отрезке [1;4]
Ответы части 1:
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Вар.1 |
4 |
3 |
1 |
4 |
3 |
1 |
4 |
1 |
2 |
2 |
2 |
3 |
1 |
4 |
3 |
2 |
1 |
2 |
1 |
3 |
|
Вар.2 |
4 |
2 |
3 |
2 |
4 |
1 |
2 |
1 |
2 |
2 |
4 |
2 |
2 |
3 |
2 |
1 |
1 |
3 |
2 |
1 |
Ответы части 2:
Вариант 1.
2.Моторная лодка прошла против течения реки 210 км и вернулась в пункт отправления, затратив на обратный путь на 4 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
Ответ: 18.
3. Найдите наибольшее значение функции у=х3-3х+4 на отрезке [-2;0]
Ответ: −54.
Вариант 2.
2. Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.
Ответ: 4 км/ч.
3. Найдите наименьшее значение функции у=х3-3х2+2 на отрезке [1;4]
Ответ: −2.
Оборудование, приспособления, инструменты
Для реализации программы дисциплины имеется учебный кабинет математики.
Оборудование учебного кабинета:
— учебная мебель;
— рабочее место преподавателя;
— доска;
— модели по темам геометрии;
Технические средства обучения:
— компьютер;
-мультимедийный проектор;
— аудивизуальные средства- схемы и таблицы к лекциям в виде слайдов и электронных презентаций.
Основная литература:
1. Алимов Ш. А. и др. Математика: алгебра и начала математического анализа, геометрия.
Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 клас-
сы. — М., 2014.
2.Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Математика: алгебра и начала
математического анализа. Геометрия. Геометрия (базовый и углубленный уровни). 10—11
классы. — М., 2014.
Дополнительные источники:
1. Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. —М., 2014.
2. Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. — М., 2014.
3. Башмаков М. И. Математика. Задачник: учеб. пособие для студ. учреждений сред. проф.
образования. — М., 2014.
4. Башмаков М. И. Математика. Электронный учеб.-метод. комплекс для студ. учреждений сред. проф. образования. — М., 2015.
5. Башмаков М. И. Математика (базовый уровень). 10 класс. — М., 2014.
6. Башмаков М. И. Математика (базовый уровень). 11 класс. — М., 2014.
7. Башмаков М. И. Алгебра и начала анализа, геометрия. 10 класс. — М., 2013.
8. Башмаков М. И. Математика (базовый уровень). 10 класс. Сборник задач: учеб. посо-
бие. — М., 2008.
9. Башмаков М. И. Математика (базовый уровень). 11 класс. Сборник задач: учеб. посо-
бие. — М., 2012.
10. Колягин Ю.М., Ткачева М. В, Федерова Н. Е. и др. Математика: алгебра и начала мате-
матического анализа. Алгебра и начала математического анализа (базовый и углубленный
уровни). 10 класc / под ред. А. Б. Жижченко. — М., 2014.
11. Колягин Ю.М., Ткачева М. В., Федерова Н. Е. и др. Математика: алгебра и начала мате
матического анализа. Алгебра и начала математического анализа (базовый и углубленный
уровни). 11 класc / под ред. А. Б. Жижченко. — М., 2014.
- Общие положения
Экзамен по математике в образовательном учреждении при реализации
программ подготовки квалифицированных рабочих по профессиям с получением среднего (полного) общего образования является обязательным.
На выполнение экзаменационной работы по математике дается
4 астрономических часа (240 минут).
Экзамен по математике проводится письменно с использованием
экзаменационных материалов в виде набора контрольных заданий. В письменную экзаменационную работу по математике не включены задания с выбором ответа, что отвечает традициям преподавания математики и позволяет более качественно проверить освоение математических знаний, умений и навыков на базовом уровне. Экзаменационная работа состоит из двух частей: обязательной и дополнительной. Обучающиеся выполняют два выбранных варианта. Задания, включенные в разные варианты под одним и тем же номером, проверяют одни и те же элементы содержания одинакового уровня сложности.
Начинать выполнять экзаменационную работу все обучающиеся должны с заданий обязательной части.
Текст экзаменационной работы сопровождается критериями оценивания результатов ее выполнения для получения каждой из положительных оценок и краткой инструкцией для обучающихся, которые остаются открытыми для них в течение всего времени экзамена.
Экзаменационные материалы дополняются критериями оценки. Содержание экзаменационных материалов и критерии оценки разработаны преподавателями математики данного образовательного учреждения.
Все листы подписываются обучающимися и после завершения работы сдаются экзаменационной комиссии.
2.Контрольно-оценочные материалы (КОМ)
Содержание экзаменационного материала отвечает требованиям к уровню подготовки выпускников, предусмотренным стандартом среднего (полного) общего образования по соответствующей общеобразовательной дисциплине,
согласовано с методической комиссией и утверждено в установленном порядке.
Контрольно-оценочные материалы составлены по следующим параметрам:
по структуре — наличию обязательной и дополнительной части;
по наполнению – обязательной, включающей задания минимально обязательного уровня, правильное выполнение которых достаточно для получения удовлетворительной оценки «3», и дополнительной части с более сложными заданиями, выполнение которых позволяет повысить удовлетворительную оценку до «4» или «5»;
по содержанию — с точки зрения представленности заданий разных
содержательных линий курса математики, соответствующих умений и видов
деятельности;
по расположению заданий — по возрастающей степени сложности в обязательной и дополнительной части.
3. Критерии оценивания выполнения работы.
Оценка результатов выполнения экзаменационной работы осуществляется согласно утвержденным критериям оценки. Критерии оценки остаются открытыми для обучающихся в течение всего времени, отведенного на экзамен.
Основные требования к выполнению заданий состоят:
- из представленного решения был понятен ход рассуждений обучающегося;
- ход решения был математически грамотным;
- представленный ответ был правильным.
При этом метод и форма описания решения задачи могут быть произвольными.
Число баллов, которое обучающийся может получить за правильное выполнение того или иного задания проставлено в скобках около номера.
За правильное выполнение любого задания из обязательной части обучающийся получает один балл. При выполнении задания из обязательной части, где необходимо привести краткое решение, за недочёты в решении задания (вычислительная ошибка, описка) можно выставить 0,5 балла. Если обучающийся приводит неверное решение, неверный ответ или не приводит никакого ответа, он получает 0 баллов.
При выполнении любого задания дополнительной части используются следующие критерии оценки заданий:
- Найден правильный ход решения, все его шаги выполнены верно и получен правильный ответ (3 балла)
- Приведено верное решение, но допущена вычислительная ошибка или описка, при этом может быть получен неверный ответ (2 балла)
- Решение начато логически верно, но допущена ошибка, либо решение не доведено до конца, при этом ответ неверный или отсутствует (1 балл)
- Неверное решение. Неверный ответ или отсутствие решения (0 баллов)
Баллы, полученные за все выполненные задания, суммируются.
Для получения любой из положительных оценок сначала надо правильно выполнить определенное число заданий обязательной части (это число определяют по таблице перевода баллов в оценки). При этом для получения удовлетворительной оценки не обязательно выполнять все задания обязательной части. При выполнении заданий дополнительной части обучающимся следует также проследить по таблице перевода баллов в оценки, сколько заданий достаточно правильно выполнить, чтобы получить оценку «4» или «5».
Таблица перевода баллов в оценки по пятибалльной шкале.
|
оценки |
5 (отлично) |
4 (хорошо) |
3 (удовлетво-рительно) |
2 (неудовлетво-рительно) |
|
Количество баллов |
||||
|
Обязательная часть |
18 |
15-18 |
9-14 |
8 |
|
Дополнительная часть |
(не менее двух заданий) |
(не менее одного задания) |
_ |
_ |
Инструкция для обучающихся
по выполнению экзаменационной работы по математике.
На выполнение письменной экзаменационной работы по математике
дается 240 минут (4 астрономических часа).
Экзаменационная работа состоит из 2-х частей: обязательной и
дополнительной. Обязательная часть содержит задания обязательного уровня, дополнительная часть – более сложные задания.
При выполнении 1-3 заданий и 10-18 заданий обязательной части требуется
представить ход решения и указать полученный ответ, в 4-9 заданиях достаточно представить ответ.
При выполнении любого задания дополнительной части требуется привести развернутый ответ с полной записью анализа решения.
Правильное выполнение заданий оценивается баллами. Правильное выполнение любого задания обязательной части оценивается одним баллом, правильное выполнение каждого задания дополнительной части – тремя баллами. Баллы указаны в скобках около номера задания. Если приводится неверный ответ или ответ отсутствует, ставится ноль баллов.
Баллы, полученные за все выполненные задания, суммируются.
Постарайтесь правильно выполнить как можно больше заданий и набрать как можно больше баллов.
Перед началом работы внимательно изучите критерии оценивания и
обратите внимание, что начинать работу следует с заданий обязательной
части. И только после того, как Вы наберете необходимое количество баллов для удовлетворительной оценки, можете переходить к заданиям
дополнительной части, чтобы повысить оценку до «хорошо» или «отлично».
Желаем успехов!
Таблица перевода баллов в оценки по пятибалльной шкале.
|
оценки |
5 (отлично) |
4 (хорошо) |
3 (удовлетво-рительно) |
2 (неудовлетво-рительно) |
|
Количество баллов |
||||
|
Обязательная часть |
18 |
15-18 |
9-14 |
8 |
|
Дополнительная часть |
(не менее двух заданий) |
(не менее одного задания) |
_ |
_ |
Задания
для проведения промежуточной аттестации
по предмету «Математика»
для профессий:
(15.01.05) «Сварщик (электросварочные и газосварочные работы)»
(35.01.13) «Тракторист-машинист сельскохозяйственного производства» (19.01.17) «Повар, кондитер»
(23.01.03) «Автомеханик»
4 вариант
Обязательная часть
При выполнении заданий 1-3 запишите ход решения и полученный ответ
1. (1 балл) Два пешехода одновременно вышли в противоположных направлениях из одного пункта. Скорость первого 4 км/ч, скорость второго 5 км/ч. Какое расстояние будет между ними через 3 ч?
2. (1 балл) Сколько четырёхзначных чисел можно составить из четырёх карточек с цифрами 0,5,7,9?
3. (1 балл) Билет на автобус стоит 15 рублей. Определите, на сколько поездок хватит 100 рублей, если стоимость билета снизят на 10%.
При выполнении заданий 4-9 запишите полученный ответ
4. (1 балл) Определите, какие из перечисленных точек
А (1; 1); В (0; –1); С (2; 4); Д (3; 5) принадлежат графику функции у = 2x – 1.
5. (1 балл) На рисунке 1 изображен график функции f (x). В какой точке отрезка [4; 9] f (x) принимает наибольшее и наименьшее значения.

6. (1 балл) При каких значениях х, f (x)≥0.(Рис. 1)
7. (1 балл) При каких значениях х, f (x)≤ 0.(Рис. 1)
8. (1 балл) При каких значениях х, f ‘(x)=0.(Рис. 1)
9. (1 балл) На клетчатой бумаге с клетками размером 1см×1 см (рис. 2) изображён треугольник. Найдите его площадь в квадратных сантиметрах.

При выполнении заданий 10-18 запишите ход решения и полученный ответ
10. (1 балл) Найдите производную функции: y=2x3+2
11. (1 балл) Вычислите:
12. (1 балл) Докажите тождество: 

13. (1 балл) Решите уравнение: lg (2x+1)
14. (1 балл) Найдите все первообразные функции f(x)=2x+x3
15. (1 балл) Вычислите:
16. (1 балл) Решите уравнение: cos (

17. (1 балл) Решите неравенство: 
18. (1балл) Тело движется по прямой так, что расстояние S от начальной точки изменяется по закону S = t + 0.5t2 (м), где t – время движения в секундах. Найдите скорость тела через 4 с после начала движения.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
19.(3 балла) Найдите корни уравнения sin2x- cos2x =1, принадлежащие
отрезку [0;2
20.(3 балла) Решите уравнение:
21.(3 балла) Радиус основания цилиндра равен 8 см, площадь боковой
поверхности вдвое меньше площади основания. Найдите объём цилиндра.
22.(3балла) Решите систему уравнений x-y=7
log2(2x+y)=3
Задания
для проведения промежуточной аттестации
по предмету «Математика»
для профессий:
(15.01.05) «Сварщик (электросварочные и газосварочные работы)»
(35.01.13) «Тракторист-машинист сельскохозяйственного производства» (19.01.17) «Повар, кондитер»
(23.01.03) «Автомеханик»
1 вариант
Обязательная часть
При выполнении заданий 1-3 запишите ход решения и полученный ответ
1. (1 балл) Два велосипедиста выехали одновременно навстречу друг другу из двух пунктов, расстояние между которыми 36 км. Скорость первого 10 км/ч, второго 8 км/ч. Через сколько часов они встретятся?
2. (1 балл) У мамы 2 яблока и 3 груши. Каждый день в течение 5 дней подряд она выдает по одному фрукту. Сколькими способами это может быть сделано?
3. (1 балл) Товар на распродаже уценили на 20%, при этом он стал стоить 680 р. Сколько стоил товар до распродажи?
При выполнении заданий 4-9 запишите полученный ответ
4. (1 балл) Определите, какие из перечисленных точек
А (1; 1); В (0; –1); С (2; 5); Д (3; 5) принадлежат графику функции у = 2x + 1
.
5. (1 балл) На рисунке 1 изображен график функции f(x).
В какой точке отрезка [-3; 2 ] f(x) принимает наибольшее и наименьшее значения?

6. (1 балл) При каких значениях х, f (x)≥0.(Рис. 1)
7. (1 балл) При каких значениях х, f (x)≤ 0.(Рис. 1)
8. (1 балл) При каких значениях х, f ‘(x)=0.(Рис. 1)
9. (1 балл) На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок 2). Найдите его площадь в квадратных сантиметрах.

При выполнении заданий 10-18 запишите ход решения и полученный ответ
10. (1 балл) Найдите производную функции: y=2x – ctg x
11. (1 балл) Вычислите:
12. (1 балл) Докажите тождество:
13. (1 балл) Решите уравнение: 2 lg x = 1
14. (1 балл) Найдите все первообразные функции f(x)=x5-x2
15. (1 балл) Вычислите:
- (1 балл) Решите уравнение: 2cos (
=
.
- (1 балл) Решите неравенство:
.
- (1 балл) Тело движется по прямой так, что расстояние S от начальной точки изменяется по закону S = 5t — 0.5t2 (м), где t – время движения в секундах. Найдите скорость тела через 2 с после начала движения.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
19. (3балла) Найдите все решения уравнения (sinx-cosx)2 – 1 = 0, принадлежащие отрезку [0;2
20. (3 балла) Решите уравнение:
21. (3 балла) В основании прямой призмы – ромб; диагонали призмы составляют с плоскостью основания углы 30

22. (3 балла) Решите систему уравнений 4х + у = -10,
log3(3y – x) = 2
Задания
для проведения промежуточной аттестации
по предмету «Математика»
для профессий:
(15.01.05) «Сварщик (электросварочные и газосварочные работы)»
(35.01.13) «Тракторист-машинист сельскохозяйственного производства» (19.01.17) «Повар, кондитер»
(23.01.03) «Автомеханик»
2 вариант
Обязательная часть
При выполнении заданий 1-3 запишите ход решения и полученный ответ
1. (1 балл) Две гоночные машины выехали навстречу друг другу. Расстояние между ними было 660 км. Одна ехала со скоростью 100 км/ч, а другая 120 км/ч. Через какое время они встретятся?
2. (1 балл) Сколько слов можно получить, переставляя буквы в слове Гора и Институт?
3. (1 балл) После повышения цены на 25% товар стал стоить 250 рублей. Определите стоимость товара до повышения цены.
При выполнении заданий 4-9 запишите полученный ответ
4. (1 балл) Определите, какие из перечисленных точек
А (1; 2); В (0; –1); С (2; 4); Д (3; 5) принадлежат графику функции у = 3x – 1.
5. (1 балл) На рисунке 1 изображен график функции f(x). В какой точке отрезка [5; 9] f(x) принимает наибольшее и наименьшее значения?

6. (1 балл) При каких значениях х, f (x)≥0.(Рис. 1)
7. (1 балл) При каких значениях х, f (x)≤ 0.(Рис. 1)
8. (1 балл) При каких значениях х, f ‘(x)=0.(Рис. 1)
9. (1 балл) На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок 2). Найдите его площадь в квадратных сантиметрах.

При выполнении заданий 10-18 запишите ход решения и полученный ответ
10. (1 балл) Найдите производную функции: f (x) = x2
11. (1 балл) Вычислите:
12. (1 балл) Докажите тождество: 
13. (1 балл) Решите уравнение: lg (x+3) = 3 + 2 lg 5
14. (1 балл) Найдите все первообразные функции f(x)=x3-3x2 +x-1
15. (1 балл) Вычислите:
16. (1 балл) Решите уравнение: sin (

- (1 балл) Решите неравенство:
.
- (1 балл) Тело движется по прямой так, что расстояние S от начальной точки изменяется по закону S = 0.5t2 + 3t + 4 (м), где t – время движения в секундах. Найдите скорость тела через 2 с после начала движения.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
19. (3 балла) Найдите все решения уравнения sinx + cosx=0, принадлежащие отрезку[

20. (3 балла) Решите уравнение:
21. (3 балла) Образующая конуса равна 12 см и составляет с плоскостью основания угол 30
22. (3 балла) Решите систему уравнений 3х + у = 3,
log3(5x +4y) = log3(y + 5)
Задания
для проведения промежуточной аттестации
по предмету «Математика»
для профессий:
(15.01.05) «Сварщик (электросварочные и газосварочные работы)»
(35.01.13) «Тракторист-машинист сельскохозяйственного производства» (19.01.17) «Повар, кондитер»
(23.01.03) «Автомеханик»
3 вариант
Обязательная часть
При выполнении заданий 1-3 запишите ход решения и полученный ответ
1. (1 балл) Из одного логова одновременно в противоположных направлениях выбежало два тигра. Скорость одного тигра 48 км / ч., а другого– 54 км ч. Какое расстояние будет между тиграми через 3 часа?
2. (1 балл) Сколько четных двузначных чисел можно составить из цифр 0, 2, 3, 6, 7, 9?
3. (1 балл) Сбербанк начисляет на срочный вклад 10% годовых. Вкладчик положил на счёт 5000 рублей. Сколько денег будет через 2 года на этом счёте?
При выполнении заданий 4-9 запишите полученный ответ
4. (1 балл) Определите, какие из перечисленных точек
А (1; 2); В (0; –1); С (2; 4); Д (3; 
5. (1 балл) На рисунке 1 изображен график функции f(x). В какой точке отрезка [-2; 2] f(x) принимает наибольшее и наименьшее значения?

6. (1 балл) При каких значениях х, f (x)≥0.(Рис. 1)
7. (1 балл) При каких значениях х, f (x)≤ 0.(Рис. 1)
8. (1 балл) При каких значениях х, f ‘(x)=0.(Рис. 1)
9. (1 балл) На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок 2). Найдите его площадь в квадратных сантиметрах.

При выполнении заданий 10-18 запишите ход решения и полученный ответ
10. (1 балл) Найдите производную функции: y=x3
11. (1 балл) Вычислите:
12. (1 балл) Докажите тождество:
13. (1 балл) Решите уравнение: lg (2-x) = 2 lg 4 – lg 2
14. (1 балл) Найдите все первообразные функции f(x)=x4-4x2+1
15. (1 балл) Вычислите:
16. (1 балл) Решите уравнение: 2 

17. (1 балл) Решите неравенство: 103x+1
18. (1балл) Тело движется по прямой так, что расстояние S до него от некоторой точки А этой прямой изменяется по закону S = t3 — 3t + 4 (м), где t – время движения в секундах. Найдите скорость тела через 3 с после начала движения.
Дополнительная часть
При выполнении заданий 19-22 запишите ход решения и полученный ответ
19.(3 балла) Найдите корни уравнения 2 cosx – 1 = 0, принадлежащие
отрезку [0;2
20. (3 балла) Решите уравнение:
21.(3 балла) Радиус основания конуса равен 5 см, а образующая конуса
равна 13 см. Найти объем конуса.
22. (3 балла) Решите систему уравнений y – 2x = 2,
log5(y — x) = log5(x + 2)

Тесты
/
Математика
/
Прочее
/ Экзамен по учебной дисциплине «Организация обучения математике» (Билет № 1)
01.06.2020.
Тест. Математика, Прочее
Внимание! Все тесты в этом разделе разработаны пользователями сайта для собственного
использования.
Администрация сайта не
проверяет возможные ошибки,
которые могут встретиться в тестах.
Экзаменационные материалы содержат задания, направленные на определение уровня итоговых знаний обучающихся по учебной дисциплине. Тест содержит теоретические и методические вопросы по материалу первого и второго курсов изучения дисциплины
Список вопросов теста
Вопрос 1
Изучение сложения и вычитания в пределах десяти проводится по следующему плану:
Варианты ответов
- Подготовительный этап: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи прибавить и вычесть 1, где результаты находятся на основе знания свойства натурального ряда чисел
- Изучение приемов присчитывания и отсчитывания по одному и группами для случаев прибавления и вычитания чисел 2, 3, 4
- Изучение приема перестановки слагаемых для случаев + 5, 6, 7, 8, 9. Таблица сложения и состав чисел из слагаемых
- Изучение приема вычитания на основе знания связи между суммой и слагаемыми для случаев – 5, 6, 7, 8, 9
Вопрос 2
На уроке по ознакомлению с новыми приёмами вычислений учитель опирается на такое предметное действие: «Пусть ручки на учительском столе изображают число 5, а карандаши на парте — число 3. Ученица Лиза переносит карандаши на учительский стол: сначала один карандаш, затем второй, а затем и третий». Фрагмент какого урока представлен в описании? Укажите тему этого урока.
Варианты ответов
- Прибавление и вычитание числа 5
- Переместительное свойство сложения
- Прибавление и вычитание числа 3
- Число и цифра 5
Вопрос 3
Представьте методический план знакомства учащихся с приёмом сложения для случаев «прибавить 5, 6, 7, 8, 9»:
Варианты ответов
- Раскрыть приём перестановки слагаемых
- Показать, как использовать прием перестановки слагаемых при решении примеров и задач на сложение в пределах 10
- Составление таблицы сложения в пределах 10
Вопрос 4
Вы зашли на урок математики к первоклассникам по теме «Приёмы вычислений в пределах десяти». На доске учителем сделаны записи: (4+3=4+2+1 и 5-4=5-2-2)
Какие приёмы вычислений разбираются учащимися на этом уроке?
Варианты ответов
- Присчитывание группами
- Присчитывание по одному
- Отсчитывание группами
- Отсчитывание по одному
Вопрос 5
Установите соответствие между текстовой задачей, решаемой учащимися 1 класса, и вычислительным приёмом, с помощью которого она решается:
1.
Задача на уменьшение числа на несколько единиц
2.
Задача на увеличение числа на несколько единиц
3.
Задача на нахождение неизвестного слагаемого
4.
Задача на нахождение разности двух чисел
Варианты ответов
- У Тани было 5 открыток, а у Светы на 2 открытки больше. Сколько открыток было у Светы?
- В городе было 10 школ. В этом году построили еще новые школы, и всего стало 12 школ. Сколько новых школ построили?
- У Клавдии было 7 игрушек, а у Александры на 4 игрушки меньше. Сколько открыток было у Александры?
- Над лягушкой летело 5 комаров. 2 она съела. Сколько комаров ей осталось съесть?
Вопрос 6
Сколько методических ступеней выделяется в изучении нумерации чисел в пределах 100?
Ответ запишите числом
Вопрос 7
В рамках изучения какого материала в начальной школе впервые вводится понятие дециметра, как единицы длины?
Варианты ответов
- Сложение и вычитание в пределах 100
- Измерение отрезков
- Нумерация чисел второго десятка
- Сложение и вычитание в пределах второго десятка
Вопрос 8
Методика работы учителя над каждым вычислительным приёмом в пределах 100 строится по следующему плану:
Варианты ответов
- Подготовка к ознакомлению с приёмом
- Ознакомление с вычислительным приёмом
- Формирование вычислительных навыков
Вопрос 9
Определите теоретическую основу вычислительного приёма: (9+8)
Варианты ответов
- Свойство прибавления суммы к числу
- Свойство прибавления суммы к сумме
- Свойство состава чисел второго десятка
- Свойство сложения двух однозначных чисел
Вопрос 10
Определите теоретическую основу вычислительного приёма: (43-9)
Варианты ответов
- Свойство вычитания числа из суммы
- Свойство записи числа в виде суммы разрядных слагаемых
- Свойство вычитания суммы из числа
- Свойство вычитания однозначного числа из двузначного
Вопрос 11
Определите теоретические основы приёмов поразрядного сложения и вычитания двузначных чисел:
Варианты ответов
- Свойство прибавления числа к сумме
- Свойство прибавления суммы к сумме
- Свойство прибавления разности к разности
- Свойство вычитания суммы из суммы
Вопрос 12
Составление таблицы сложения с переходом через десяток входит в содержание обучения:
Варианты ответов
- Первого класса
- Второго класса
- Третьего класса
- Четвертого класса
Вопрос 13
Укажите тематические вопросы, которые изучаются в контексте умножения и деления в пределах 100
Варианты ответов
- Деление с остатком
- Табличное умножение
- Табличное деление
- Внетабличное умножение
- Умножение, деление с единицей и нулем
- Внетабличное деление
- Переместительное свойство умножения
- Свойство умножения числа на сумму
Вопрос 14
Теоретической основой к переходу от таблицы умножения двух к таблице умножения на 2 является изучение:
Варианты ответов
- Сочетательного свойства
- Распределительного свойства
- Переместительного свойства
- Свойства умножения числа на сумму
Вопрос 15
Учащемуся необходимо найти значение выражения (40cdot7cdot3cdot25) рациональным способом. Назовите свойства, которые помогут ему это сделать.
Варианты ответов
- Распределительное
- Сочетательное
- Переместительное
- Дистрибутивное
Вопрос 16
Установите соотвествие между простой задачей и её типом:
1.
Простая задача на деление по содержанию
2.
Простая задача на деление на равные части
Варианты ответов
- 12 кустов астр посадили на 4 клумбах. Сколько астр на одной клумбе?
- 12 яблок разделили по 4 яблока между детьми. Сколько детей получили яблоки?
Вопрос 17
Теоретическим основанием для изучения внетабличного умножения двузначного числа на однозначное является знание:
Варианты ответов
- Ассоциативного свойства умножения
- Переместительного свойства умножения
- Дистрибутивного свойства умножения
- Сочетательного свойства умножения
Вопрос 18
Оперируя с конкретными предметными множествами (демонстрационные и индивидуальные средства наглядности), учащиеся самостоятельно приходят к выводу: если из суммы двух слагаемых вычесть одно слагаемое, то получим другое слагаемое.
Данный вывод является базовым для изучения следующего вычислительного приёма:
Варианты ответов
- Вычитание в случаях «вычесть 5, 6, 7, 8, 9»
- Сложение в случаях «прибавить 2, 3, 4»
- Сложение в случаях «прибавить 5, 6, 7, 8, 9»
- Вычитание в случаях «вычесть 2, 3, 4»
Вопрос 19
Способ подбора лежит в основе:
Варианты ответов
- Деления двузначного числа на однозначное
- Умножения двузначного числа на однозначное
- Умножения двузначного числа на двузначное
- Деления двузначного числа на двузначное
Вопрос 20
С формирования какой счетной единицы начинается изучение нумерации в пределах 1000?
Варианты ответов
- Десяток
- Сотня
- Тысяча
Вопрос 21
Установите соответствие между разрядными единицами:
1.
1 десяток
2.
1 сотня
3.
1 тысяча
Варианты ответов
- 10 сотен
- 10 единиц
- 10 десятков
Вопрос 22
При изучении письменной нумерации чисел в пределах 1000, ученик должен усвоить, что единицы ТРЕТЬЕГО РАЗРЯДА записываются:
Варианты ответов
- На третьем месте, считая слева направо
- На втором месте справа налево
- На третьем месте справа налево
Вопрос 23
Соотнесите выражения с приёмами вычислений их значений:
1.
(540+30)
2.
(540-300)
3.
(800-600)
4.
(140-60)
Варианты ответов
- 54 дес. + 3 дес. = 57 дес.
- 54 дес. — 30 дес. = 24 дес.
- 8 сот. — 6 сот. = 2 сот.
- 14 дес. — 6 дес. = 8 дес.
Вопрос 24
Письменное сложение в пределах 1000 изучается в таком порядке:
Варианты ответов
- Случаи, где сумма единиц и сумма десятков меньше 10
- Случаи, где сумма единиц или сумма десятков (либо и та, и другая) равны 10
- Случаи, где сумма единиц или сумма десятков (либо и та, и другая) больше 10
Вопрос 25
Восстановите порядок начала алгоритма нахождения суммы чисел 544 и 218
Варианты ответов
- К 4 единицам прибавим 8 единиц, получится 12 единиц
- Это можно представить, как 1 десяток и 2 единицы
- 2 единицы пишем под единицами
- Один десяток прибавим к десяткам
Вопрос 26
Укажите выражения, при нахождении значения которого преобразование одних разрядных единиц в другие приходится выполнять несколько раз:
Варианты ответов
-
(540-126)
-
(875-528)
-
(800-537)
-
(906-637)
-
(1000-546)
Вопрос 27
С двух полей собрали 900 кг картофеля. Со второго поля собрали на 472 кг картофеля больше, чем с первого. Сколько килограммов картофеля собрали со второго поля?
Ответ запишите числом. Наименование в ответе записывать не нужно
Вопрос 28
Для удобного вычисления в выражении (85 : 5) делимое может быть представлено учащимся в виде:
Варианты ответов
- Суммы разрядных слагаемых
- Суммы двузначного разрядного числа и двузначного неразрядного числа
- Суммы разрядных двузначных чисел
- Суммой удобных двузначных чисел, не являющихся разрядными числами
«ВЛАДИМИРСКИЙ АГРАРНЫЙ КОЛЛЕДЖ»
|
Рассмотрены цикловой комиссией технико-математических дисциплин Протокол №__ от «____» ______20__г. Председатель: ________ |
УТВЕРЖДАЮ Заместитель директора по учебной работе _____________ |
МАТЕРИАЛЫ ПИСЬМЕННОЙ ЭКЗАМЕНАЦИОННОЙ РАБОТЫ учебной дисциплины «Математика»
Специальности 120714 Земельно — имущественные отношения
1 курс, группы 1 «З»
Составлены в соответствии с письмом Департамента государственной политики и нормативно-правового регулирования в сфере образования Минобрнауки России от 29.95.2007 № 03-1180
Подготовила преподаватель высшей категории ГБОУ СПО ВО «Владимирский аграрный колледж» Стародубцева А.И.
2011- 2012 учебный год
Письменная экзаменационная работа по учебной дисциплине «Математика» составлена в соответствии с ФГОС, а также в соответствии с рабочей программой, составленной на основе примерной программы учебной дисциплины «Математика», утвержденной 16.04.2008г. директором Департамента госполитики и нормативно правового регулирования в сфере образования Минобрнауки России И. М. Реморенко по специальности СПО 120714 Земельно — имущественные отношения
Письменная экзаменационная работа рассчитана на 2 часа (90 мин), состоит из 15 вариантов. Каждый вариант включает в себя 8 заданий по основным темам «Алгебры и начала анализа» за курс средней (полной) общеобразовательной школы. Они распределены на 2 части.
Первые пять заданий – это задания обязательного уровня по материалу курса «Алгебра и начала анализа». За правильное выполнение каждого из этих заданий ставится 1 балл.
Задания 6, 7, 8 – задания повышенного уровня, они должны быть представлены полным решением.
За выполнение любого из этих заданий ставится 2 балла.
Критерии оценивания работы
-
ниже 5 баллов – оценка «2» (неудовлетворительно)
-
5 – 6 баллов — оценка «3» (удовлетворительно)
-
7 – 8 баллов — оценка «4» (хорошо)
-
9- 11 баллов — оценка 5 (отлично)
Задания рекомендуется выполнять в том порядке, в котором они даны. Для экономии времени можно пропускать задание, которое не удается выполнить сразу, и переходить к следующему.























