Переводной экзамен по геометрии за 8 класс
Билеты по геометрии для переводного экзамена в 8 классе
(учебник Геометрия 7 – 9 Л. С. Атанасян.)
Каждый билет содержит 4 вопроса. В первом вопросе предлагается сформулировать и доказать теорему. Во втором вопросе даётся одно из следующих заданий: дать определение понятия, указать его основные свойства или привести примеры, описать этапы построения геометрических фигур. Третий и четвертый вопросы — практические, они содержат задачи за курс 8 класса. Задачи к билетам необходимо решить в тетради. К каждой задаче выполнить рисунок и необходимые пояснения. На экзамен надо принести эту тетрадь с решением и необходимые инструменты: линейка, карандаш, циркуль, ручка. Все билеты надо выучить, уметь ответить у доски и быть готовым к дополнительным вопросам.
Билет №1.
1.Параллелограмм. Свойства параллелограмма. Доказать, что диагонали параллелограмма точкой пересечения делятся пополам.
2.Определение синуса острого угла прямоугольного треугольника. Чему равны значения синуса для углов 300 , 450 , 600?
3. В выпуклом пятиугольнике длины сторон относятся как 5: 7: 8 : 9: 10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
4. В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Билет №2.
1.Параллелограмм. Признаки параллелограмма (доказать один из признаков).
2.Определение косинуса острого угла прямоугольного треугольника. Чему равны значения косинуса для углов 300 , 450 , 600?
3. В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
4. Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
Билет №3.
1.Прямоугольник. Свойства прямоугольника. Доказать, что диагонали прямоугольника равны.
2.Определение тангенса острого угла прямоугольного треугольника. Чему равны значения тангенса для углов 300 , 450 , 600?
3. В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4. Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
Билет №4.
1.Ромб. Свойства ромба. Доказать, что диагонали ромба взаимно перпендикулярны.
2.Определение подобных треугольников. Признаки подобия треугольников.
3.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
4. Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
Билет №5.
1.Квадрат. Свойства квадрата. Доказать, что если в ромбе диагонали равны, то ромб является квадратом.
2.Центральный угол. Свойство центрального угла.
3. Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
4. В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
Билет №6.
1.Доказать теорему о вычислении площади параллелограмма.
2. Вписанная окружность, центр вписанной окружности. Свойство сторон четырёхугольника, описанного около окружности.
3.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
4. Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
Билет №7.
1.Доказать теорему о вычислении площади треугольника. Как вычислить площадь прямоугольного треугольника?
2. Описанная окружность, центр описанной окружности. Свойство углов четырёхугольника, вписанного в окружность.
3. Основания прямоугольной трапеции равны 10см и 22см, а большая боковая сторона15см. Найти площадь трапеции.
4. Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
Билет №8.
1.Доказать теорему о вычислении площади трапеции.
2.Вписанный угол. Следствия, вытекающие из теоремы о вписанном угле.
3. Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
4. Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
Билет №9.
1.Доказать теорему Пифагора.
2.Биссектриса угла. Свойство биссектрисы угла.
3. Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
4. Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
Билет №10.
1.Определение средней линии треугольника. Доказать теорему о средней линии треугольника.
2.Серединный перпендикуляр. Свойство серединного перпендикуляра к отрезку.
3. АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
4. Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
Билет №11.
1.Доказать, что высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на подобные треугольники. Сформулировать утверждения о пропорциональных отрезках в прямоугольном треугольнике.
2.Сформулировать теорему обратную теореме Пифагора.
3. Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
4. Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
Билет №12.
1.Касательная к окружности, точка касания прямой к окружности. Доказать теорему о свойстве касательной.
2.Дать определение подобных треугольников. Теорема об отношении площадей подобных треугольников.
3. В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
4. Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
Билет №13.
1.Доказать, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют углы с прямой, проходящей через эту точку и центр окружности.
2.Сформулировать свойство медиан треугольника пересекающихся в одной точке.
3. Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
4. Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
Билет №14.
1.Вписанный угол. Теорема о вписанном угле.
2.Трапеция. Виды трапеции. Свойства равнобокой трапеции.
3. Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
4. Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см,
ДС =4см. Найти основание АС и высоту АД.
Билет №15.
1.Доказать теорему об отрезках пересекающихся хорд.
2.Теорема Фалеса. Деление отрезка на п-равных отрезков.
3. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
4. АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
Задачи к билетам
1.В выпуклом пятиугольнике длины сторон относятся как 5:7:8:9:10, а его периметр равен 117 см. Найти наибольшую сторону пятиугольника.
2.В параллелограмме АВСД высота, опущенная на сторону СД, делит её пополам и образует со стороной ВС угол 300, АВ = 12см. Найти периметр параллелограмма.
3.В равнобедренной трапеции АВСД диагональ ВД перпендикулярна боковой стороне, угол А равен 600 , АД = 24см., ВС = 12см. Найти периметр трапеции.
4.В ромбе АВСД биссектриса угла ВАС пересекает сторону ВС и диагональ ВД соответственно в точках М и К, угол АМС равен 1200 . Найти величину угла АКВ.
5.Высота ВД треугольника АВС делит сторону АС на отрезки, равные 7 см. и 4 см. Площадь треугольника равна 55см» . Найти длину ВД.
6.В треугольнике АВС угол А = 750 , угол В = 300 , АВ = 10см. Найти площадь треугольника.
7.Основания равнобедренной трапеции равны 10см и 24см, а большее основание 15см. Найти площадь трапеции.
8.Периметр треугольника равен 40см, две его стороны равны 15см и 9см. Найти отрезки, на которые биссектриса треугольника делит его третью сторону.
9.Стороны параллелограмма равны 6см и 7см, угол между ними 600 . Найти высоты параллелограмма.
10.АВ и ВС отрезки касательных, проведённых к окружности с центром О радиуса 6см. Найти периметр четырёхугольника АВСО, если угол АВС равен 600 .
11.Хорды АВ и СД пересекаются в точке Е. Найти длину АВ, если СЕ = 8см, ДЕ = 9см, а длина АЕ в 2 раза больше длины ВЕ.
12.В равнобедренном треугольнике основание равно 20см. а угол между боковыми сторонами равен 1200 . Найти высоту, проведённую к основанию.
13.Один из углов ромба на 400 больше другого. Найти углы треугольника ВОС, если О – точка пересечения диагоналей.
14.Найти площадь равнобедренного треугольника, если его основание равно 30см, боковая сторона равна 17см.
15.АМ и ВК – медианы треугольника АВС. Определить вид четырёхугольника АВМК и найти его периметр, если АВ =14см, ВС = 12см, АС = 18см.
16. Найдите периметр прямоугольника, если его площадь равна 40 см2 и одна сторона больше другой на 3 см
Задачи к билетам
1.АВСД – ромб, угол АВС равен 1400 . Найти углы треугольника СОД, где точка О – пересечение диагоналей.
2.Треугольник АВС – равнобедренный с основанием АС, АД – его высота, ВД = 16см, ДС =4см. Найти основание АС и высоту АД.
3.Найти площадь равнобедренной трапеции, если её основания равны 5см и 17см, а боковая сторона равна 10см.
4.Площадь прямоугольного треугольника равна 24см2 , а один из его катетов равен 6см. Найти длину средней линии, параллельной другому катету.
5.Одна из диагоналей ромба на 4см больше другой, а площадь ромба равна 96см2 . Найти сторону ромба.
6.Смежные стороны параллелограмма равны 32см и 26см., а один из его углов равен 1500 . Найти площадь параллелограмма.
7.Площадь прямоугольной трапеции равна 120см2 , а её высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.
8.Найти площадь прямоугольника, если одна из его сторон 5 см, а угол между диагоналями равен 600.
9.Трапеция ВСНМ с основанием ВМ вписана в окружность. Найти углы С, Н, М, если угол В равен 760 , и определите вид трапеции.
10.Найти сторону равностороннего треугольника, если радиус описанной окружности около него окружности равен 10см.
11.В окружность вписан равнобедренный треугольник АВС с основанием ВС. Найти углы треугольника, если дуга ВС равна 1020.
12.Центральный угол АОВ на 300 больше вписанного угла, опирающегося на дугу АВ. Найти каждый из этих углов.
13.Через концы хорды АВ, равной радиусу окружности, проведены две касательные, пересекающие в точке С. Найти угол АСВ.
14.Дан треугольник, стороны которого равны 5см, 8см, 7см. Найти периметр треугольника, вершинами которого являются середины сторон данного треугольника.
15.В трапеции АВСД с большим основанием АД диагональ АС перпендикулярна к боковой стороне СД, углы ВАС и САД равны. Найти АД, если периметр трапеции равен 20см, а угол Д равен 600.
Переводной экзамен по геометрии 8 класс
Пояснительная записка.
С 2008 года в список предметов, по которым государственная итоговая аттестация по курсу основной школы проводится в новой форме, включена и геометрия. С 2011 года задания по геометрии включаются в экзамен по математике. С 2013 года КИМы по математике (за курс основной школы) состоят из трех модулей («Алгебра», «Геометрия», «Реальная математика»). Модуль «Геометрия» содержит 8 заданий: в первой части – 6 заданий, во второй части – 2 задания. Причем оценка за экзамен будет неудовлетворительной, если не выполнено два задания по геометрии. Чтобы успешно сдать экзамен по математике за курс основной школы, необходимо провести экзамен на промежуточной аттестации за курс геометрии 8 класса.
Билеты составлены по курсу геометрии 8 класса. Всего 18 билета по четыре вопроса: первый вопрос предполагает, что учащийся должен сформулировать теорему, свойство (без доказательства), правильно и грамотно сформулировать определение, записать необходимую формулу, привести пример, или выполнить необходимый рисунок, второй вопрос требует развернутого, доказательного ответа, третий и четвертый вопросы практические – состоит из двух задач (одна базового уровня, вторая повышенного уровня).
Критерии оценивания:
Отметка 5 (отлично) – ставится за полный, логически обоснованный ответ на все четыре вопроса билета.
Отметка 4 (хорошо) – выставляется за обоснованный полный ответ на 1-2 вопросы и решение одной из задач третьего или четвертого вопросов; или за решение двух задач третьего и четвертого вопросов и правильно сформулированные теоремы, свойства, определения первого и второго вопросов (без доказательства).
Отметка 3 (удовлетворительно) – ставится за решение задачи базового уровня третьего вопроса и правильно сформулированные теоремы, свойства, определения первого и второго вопросов (без доказательства).
Отметка 2 (неудовлетворительно) – выставляется во всех остальных случаях.
Экзаменационные вопросы по геометрии 8 класс.
Вопрос 1.
1. Квадрат. Свойства квадрата.
2. Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
3. Подобные треугольники. Определение. Коэффициент подобия.
4. Описанная окружность. Центр окружности, описанной около треугольника.
5. Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
6. Прямоугольник. Свойства прямоугольника. Квадрат.
7. Значения синуса, косинуса и тангенса для углов 30° , 45° , 60° .
8. Вписанная окружность. Центр окружности, вписанной в треугольник.
9. Ромб. Свойства ромба. Квадрат.
10. Сформулируйте определение выпуклого многоугольника (периметр, диагональ). Сформулируйте теорему о сумме углов выпуклого многоугольника.
11. Свойство вписанного четырехугольника.
12. Свойства площадей.
13. Медиана треугольника. Определение. Свойство точки пересечения медиан треугольника.
14. Параллелограмм. Определение. Свойства.
15. Центральный угол. Вписанный угол.
16. Пропорциональные отрезки в прямоугольном треугольнике.
17. Четырехугольник. Сумма углов четырёхугольника.
18. Свойство описанного четырехугольника.
Вопрос 2.
1. Площадь трапеции (формулировка и доказательство).
2. Свойство серединного перпендикуляра к отрезку (доказательство).
3. Свойство отрезков касательных, проведенных из одной точки (формулировка и доказательство).
4. Теорема, обратная теореме Пифагора (формулировка и доказательство).
5. Свойство касательной к окружности (формулировка и доказательство).
6. Площадь треугольника (формулировка и доказательство).
7. Признаки подобия треугольников. Доказать второй признак подобия.
8. Свойства ромба (формулировка и доказательство).
9. Свойства прямоугольника (формулировка и доказательство).
10. Свойства параллелограмма (формулировка и доказательство).
11. Теорема об окружности, описанной около треугольника (формулировка и доказательство).
12. Теорема о средней линии треугольника (формулировка и доказательство).
13. Теорема о вписанном угле (формулировка и доказательство).
14. Теорема Пифагора (формулировка и доказательство). Пифагоровы треугольники.
15. Площадь прямоугольника (формулировка и доказательство).
16. Площадь параллелограмма (формулировка и доказательство).
17. Свойство биссектрисы угла (формулировка и доказательство).
18. Теорема об окружности, вписанной в треугольник(доказательство).
Вопрос 3.
1. В треугольнике АВС угол С=900 , катет АС=6 дм, угол А =α. Найдите гипотенузу АВ.
2. Центральный угол опирается на дугу в 800 , найдите вписанный угол, опирающийся на эту же дугу.
3. Угол В параллелограмма АВСD в 5 раз больше угла А. Найдите углы параллелограмма.
4. Из точки В к окружности с центром О проведена касательная, А – точка касания. Найдите радиус окружности, если ВО = 18 см. АВ= 9√3 см.
5. Сторона треугольника равна 14 см, а высота, проведенная к данной стороне равна 6 см. Найдите площадь треугольника.
6. Найдите синус, косинус и тангенс острого угла А прямоугольного треугольника АВС (∟С=900), если АВ = 13 см, ВС = 12 см.
7. Найдите среднюю линию трапеции, основания которой равны 6 и 8 см.
8. Найдите площадь ромба, диагонали которого равны 6 см и 10 см.
9. Начертите отрезок и, используя циркуль, линейку и чертежный угольник разделите его в отношении 3:2.
10. Сторона треугольника равна 14 см, а высота, проведенная к данной стороне равна 6 см. Найдите площадь треугольника.
11. В окружности с центром О проведена хорда МК. Найдите угол МОК, если угол ОМК равен 510.
12. В треугольнике АВС угол С равен 900, катеты равны 5 см и 12 см. Найдите гипотенузу.
13. Найдите площадь трапеции основания, которой равны 10 см и 16 см, а высота — 5 см.
14. В треугольнике АВС: угол С равен 900 , угол А равен 450 , гипотенуза равна 6√2 см. Найдите катеты треугольника.
15. Основания трапеции 18 см и 7 см, высота трапеции в 3 раза меньше большего основания. Найдите площадь трапеции.
16. Стороны прямоугольника равны 3 см и 4 см. Найдите углы, которые образует диагональ со сторонами прямоугольника.
17. Окружность разделена точками А, В и С на три дуги пропорциональные числам 2:3:4. Найдите вписанный угол, опирающийся на меньшую дугу.
18. Через точку М окружности с центром О проведена касательная МК. Найдите радиус окружности, если ОК = 10 см, угол МОК равен 600.
Вопрос 4.
1. Найдите площадь равнобедренной трапеции, если её диагональ равна √10 см , а высота 2√2 см.
2. Площадь параллелограмма равна 25 см2, а периметр 20 см. Найдите стороны параллелограмма, если высота, проведенная к одной из них, в 4 раза меньше этой стороны.
3. Из вершины А острого угла параллелограмма проведены перпендикуляры АН1 и АН2 к прямым ВС и СD. Найдите углы параллелограмма, если угол Н1АН2 равен 1300.
4. Найдите площадь треугольника, две стороны которого равны 6 и 8 см, а угол между ними 300 .
5. В окружности радиуса 10,5 см проведены диаметр АВ и хорда СD, пересекающиеся в точке К, причем, АК=18см, СК= 9 см. Найдите длину хорды CD.
6. В прямоугольной трапеции меньшее основание равно 6, а меньшая боковая сторона 2√3. Найдите площадь трапеции, если один из её углов равен 1200.
7. В прямоугольном треугольнике с углом 300 и меньшим катетом 8 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.
8. Продолжения боковых сторон трапеции АВСD, с основаниями ВС и АD, пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и АОD, если АD = 5 см, ВС=2 см, АО = 25 см.
9. Площадь параллелограмма равна 48 см2, а периметр 40 см. Найдите стороны параллелограмма, если высота, проведенная к одной из них, в 3 раза меньше этой стороны.
10. В равнобедренной трапеции тупой угол равен 1350, меньшее основание равно 4 см, а высота 2 см. Найдите площадь трапеции.
11. В прямоугольном треугольнике с углом 300 и меньшим катетом 6 см проведены средние линии. Найдите периметр треугольника, образованного средними линиями.
12. Продолжения боковых сторон трапеции АВСD, с основаниями ВС и АD, пересекаются в точке О. Найдите ВО и отношение площадей треугольников ВОС и АОD, если АD = 10 см, ВС= 6 см, АО = 30 см.
13. В треугольнике АВС угол А равен 450, а высота ВD = 2 см. Найдите площадь треугольника, если прямая ВС составляет с прямой АD угол 600.
14. Из точки М к окружности с центром О и радиусом 8 см проведены касательные МА и МВ ( А и В – точки касания). Найдите периметр треугольника АВМ, если угол АОВ равен 1200.
15. В треугольнике АВС угол А равен 450, а высота ВD = 2 см. Найдите площадь треугольника, если прямая ВС составляет с прямой АD угол 300.
16. Две окружности с центрами в точках О и О1 и радиусами 5 см и 3 см соответственно касаются сторон угла А (В и В1 – точки касания). Найдите расстояние между центрами окружностей, если АВ1=4 см.
17. В треугольнике АВС проведен отрезок МК, параллельный стороне АС ( М лежит на стороне АВ, К – на стороне ВС). Найдите АВ, если МК = 16 см, АС = 24 см, АМ = 6 см.
18. Из точки А к окружности с центром О проведены касательные АВ и АС (В и С – точки касания). Отрезки АО и ВС пересекаются в точке К. Найдите радиус окружности, если ВС = 16 см, АК = 8 см.
Переводной экзамен по геометрии за курс 8
класса.
Пояснительная
записка.
С
2008 года в список предметов, по которым государственная итоговая аттестация по
курсу основной школы проводится в новой форме, включена геометрия. С 2011 года
задания по геометрии включаются в экзамен по математике. С 2013 года КИМы по
математике (за курс основной школы) состоят из трех модулей («Алгебра»,
«Геометрия», «Реальная математика»). Всего экзамен включает 11 заданий по
геометрии: в первой части – 5 заданий в модуле «Геометрия» и 3 задания в модуле
«Реальная математика», во второй части – 3 задания. Причем оценка за экзамен
будет неудовлетворительной, если не выполнено два задания по геометрии. Чтобы
успешно сдать экзамен по математике за курс основной школы, необходимо провести
экзамен на промежуточной аттестации за курс геометрии 8 класса.
Билеты
составлены по курсу геометрии 8 класса. Всего 17 билетов по три вопроса в
каждом: первый вопрос предполагает, что учащийся должен сформулировать
теорему, свойство и доказать его, правильно сформулировать определение, привести
пример или выполнить необходимый рисунок. Второй вопрос предполагает, что
учащийся правильно и грамотно должен сформулировать определение, записать
необходимую формулу, привести пример, или выполнить необходимый рисунок.
Третий
вопрос практический – состоит из задачи, которую нужно правильно оформить,
составить к ней чертеж и решить, обосновывая каждое действие известными
геометрическими сведениями.
Билеты
формируются произвольно с использованием данных вопросов.
Содержание
заданий экзаменационных билетов разработано по основным темам курса геометрии 8
класса: «Четырехугольники», «Параллелограмм и
трапеция», «Прямоугольник, ромб, квадрат», «Площадь многоугольника», «Площадь
параллелограмма, треугольника, трапеции», «Теорема Пифагора», «Подобные треугольники», «Признаки
подобия треугольников», «Применение подобия треугольников к доказательству
теорем и решению задач», «Соотношение между сторонами и углами треугольника», «Касательная
к окружности», «Центральные и вписанные углы», «Четыре замечательные точки
треугольника», «Вписанные и описанные окружности».
Критерии
оценивания:
Отметка 5
(отлично) – ставится за полный, логически обоснованный ответ на все три вопроса
билета.
Отметка 4 (хорошо)
– выставляется за обоснованный полный ответ на 1 вопрос, изложенный второй
вопрос с небольшими недочетами и решение задачи, но возможны, допустимы
вычислительные ошибки или неточности в доказательстве теоремы.
Отметка 3 (удовлетворительно)
– ставится за решение задачи и правильно сформулированные теоремы, свойства,
определения (без доказательства).
Отметка 2 (неудовлетворительно)
– выставляется во всех остальных случаях.
Вопрос
1 (привести подробное доказательство).
- Определение
параллелограмма. Признаки параллелограмма, доказательство любого признака. - Определение
прямоугольника. Признаки прямоугольника, доказательство любого признака - Определение
ромба. Доказательство свойства ромба. - Понятие
многоугольника. Выпуклый многоугольник. Сумма его углов. - Определение
подобных треугольников. Доказать теорему об отношении площадей подобных
треугольников. - Площадь
треугольника (с доказательством). - Площадь
трапеции (с доказательством). - Теорема
Пифагора (с доказательством). - Признаки
подобия треугольников, доказательство любого признака. - Средняя
линия треугольника (определение и теорема с доказательством). - Касательная
к окружности, свойства касательной (доказательство любого свойства). - Свойства
серединного перпендикуляра к отрезку (определение и теорема). - Свойство
биссектрисы угла. - Теорема
о вписанном угле. - Взаимное
расположение прямой и окружности (три случая). - Площадь
прямоугольника (теорема с доказательством). - Признаки
подобия треугольников, доказательство любого признака.
Вопрос
2 (сформулировать и записать).
- Запишите
формулу площади треугольника. - Запишите
формулу площади трапеции. - В
равнобедренной трапеции ABCD углы, прилежащие к стороне AD, равны 45°.
Найдите площадь трапеции, если основания равны 13 и 27 см. - Формула
площади параллелограмма. - Трапеция.
Определение, виды. Свойства равнобедренной трапеции. - Значения
синуса, косинуса и тангенса для углов 30°, 45° и 60°. - Синус,
косинус и тангенс острого угла прямоугольного треугольника. - Вписанная
и описанная окружности (определение с примерами) - Площадь
квадрата. - Формула
Герона (формулировка). - Формула
площади ромба через его диагонали. - Площадь
параллелограмма. - Центральная
и осевая симметрия. - Подобные
треугольники. Отношение периметров и площадей подобных треугольников. - Формула
площади прямоугольного треугольника - Пропорциональные
отрезки (определение). Подобные треугольники (сходственные стороны,
коэффициент подобия). - Синус,
косинус и тангенс острого угла прямоугольного треугольника.
Вопрос
3. Решить задачу.
- В
прямоугольной трапеции АВСК большая боковая сторона равна З√2 см, угол К равен
45°,а высота СН делит основание АК пополам. Найдите площадь трапеции. - В
трапеции ABCD проведены диагонали АС и BD. Докажите, что ∆ СОB ~ ∆ AOD. - Пропорциональные
отрезки в прямоугольном треугольнике (формулировка и формулы). - В треугольнике
угол
равен 90°,
. Найдите
.
- В
параллелограмме АВСД проведены биссектрисы АК и ДМ (К, М лежат на ВС),
которые делят сторону на три равные части. Найдите периметр
параллелограмма, если АВ = 20 см. - В
равнобедренной трапеции основания равны 8 см и 14 см, боковая сторона — 5
см. Найдите: а) высоту трапеции; б) синус острого угла при основании
трапеции. - ABCD — прямоугольник. О — точка пересечения диагоналей.
Найдите стороны ∆АОВ, если CD = 5 см, а АС= 8 см. - В
прямоугольном треугольнике АВС (<С = 90˚) АВ = 41 см, АС = 9 см. Точки
М и К — середины сторон АВ и АС соответственно. Найдите: а) длину отрезка
МК; б) тангенсы острых углов. - Сторона
ромба равна 18 см, а один из углов равен 120°. Найдите расстояние между
противолежащими сторонами ромба. - Прямоугольник вписан в окружность радиуса 5 см. Одна из его
сторон равна 8 см. Найдите другие стороны прямоугольника. - Высота
ВК, проведенная к стороне АД параллелограмма АВСД делит эту сторону на два
отрезка АК = 7 см, КД = 15 см. Найдите площадь параллелограмма, если <А
= 45°. - Точки
Аи В делят окружность на две дуги ,длины которых относятся как
9:11.Найдите величину центрального угла, опирающегося на меньшую из дуг. - Мальчик прошел от дома по направлению на восток
800 м. Затем повернул на север и прошел 600 м. На каком расстоянии
(в метрах) от дома оказался мальчик? - Угол
DFG вписан в окружность с центром в точке Q. Найдите градусную меру
<DQG. - Хорды
АВ и СД пересекаются в точке Е. Найдите ЕД, если АЕ=0,2, ВЕ=0,5, СД=0,65. - Человек стоит на расстоянии 12 м от столба, на котором
висит фонарь, расположенный на высоте 9,5 м. Тень человека равна
3 м. Какого роста человек (в метрах)? - Сторона AC треугольника ABC содержит центр описанной
около него окружности. Найдите, если
. Ответ дайте в градусах.
18. Найти площадь трапеции ABCD с основаниями АВ и СD если угол D
равен 30, АВ=2 см, СD=10 см, DА=8 см.
19. В прямоугольнике ABCD найдите АD, если АВ= 5 см, АС=13 см.
20. Диагонали трапеции ABCD с основаниями АВ и СD пересекаются в
точке О. Найдите АВ, если ОВ=4 см, ОD=10 см, DС=25 см.
21. На одной из сторон данного угла А отложены отрезки Ав=5 см и
АС=16 см.На другой стороне этого же угла отложены отрезки АD=8 см и АF= 8 см.
Подобны ли треугольники АСD и АFВ ?
22. Подобны ли треугольники ABC и А 1В 1С 1, если АВ = 3 см, ВС =
5 см, СА = 7 см, А 1В 1=4,5 см, В 1С = 7,5 см, А 1С 1= 10,5 см ?
23. В треугольнике ABC медианы AA 1 и ВВ 1 пересекаются в точке
О. Найдите площадь треугольника ABC, если площадь треугольника АВО равна S.
24. Центральный угол АОВ на 30° больше вписанного угла,
опирающегося на дугу АВ. Найдите каждый из этих углов.
25. Докажите, что выпуклый четырехугольник ABCD является
параллелограммом, если: ∟BAC= ∟ACD и ∟BCA = ∟DAC
26. Найдите стороны прямоугольника, если: его площадь равна 250
см2, а одна сторона в 2,5 раза больше другой
27. Точка касания окружности, вписанной в равнобедренный
треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см,
считая от основания. Найдите периметр треугольника.
28. Стороны угла А касаются окружности с центром О радиуса г. Найдите:
г, если ОА = 14 дм, ∟А= 90°.
29. Треугольники ABC и А 1В1 С1 подобны, и их сходственные
стороны относятся как 6:5. Площадь треугольника ABC больше площади треугольника
А 1В1 С1 на 77 см2. Найдите площади треугольников.
- В подобных треугольниках ABC и KMN стороны АВ и КМ, ВС и
MN являются сходственными. Найдите стороны треугольника KMN, если АВ=4 см,
ВС = 5 см, СА = 7 см, KM/AB=2,1
31. Найдите синус, косинус и тангенс углов А и В треугольника АВС
с прямым углом С, если: ВС=8, АВ=17
32. Найдите углы В и D трапеции ABCD с основаниями AD и ВС, если
∟А = 36°, ∟С=117°.
33. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14
см, образует с ней угол в 30°. Найдите площадь параллелограмма.
34. Найдите углы параллелограмма ABCD, если: ∟А + ∟С=142°
35. Стороны АВ и ВС треугольника ABC равны соответственно 16 см и
22 см, а высота, проведенная к стороне АВ, равна 11 см. Найдите высоту,
проведенную к стороне ВС.
36. В прямоугольнике ABCD диагонали пересекаются в точке О.
Найдите периметр треугольника АОВ, если ∟CAD = 30°, АС=12 см.
- В окружность вписан треугольник ABC так, что
АВ — диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°;
- Сумма двух противоположных сторон описанного
четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5
см. Найдите площадь четырехугольника - Стороны прямоугольника равны 3 см и
см. Найдите углы, которые
образует диагональ со сторонами прямоугольника. - Докажите, что середины сторон произвольного
четырехугольника являются вершинами параллелограмма. - Точка касания окружности, вписанной в равнобедренный
треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см.
считая от основания. Найдите периметр треугольника. - Подобны ли треугольники ABC и МКР если: АВ=3 см, ВС=5
см, СА=7 см, МК=4,5 см, КР=7,5 см, РМ = 10,5 см. - Диагонали трапеции ABCD с основаниями АВ и CD
пересекаются в точке О. Найдите: АВ, если ОВ=4 см, OD=10 см, DC=25
см. - Площади двух подобных треугольников равны 75 и 300.
Одна из сторон второго треугольника равна 9 . Найдите сходственную ей
сторону первого треугольника. - Найдите сторону и площадь ромба, если его диагонали
равны 10 см и 24 см. - Найдите площадь прямоугольной трапеции, у которой две
меньшие стороны равны 6 см. а больший угол равен 135°. - Две стороны треугольника равны 7,5 см и 3,2 см. Высота,
проведенная к большей стороне, равна 2,4 см. Найдите высоту, проведенную к
меньшей из данных сторон. - Найдите площадь прямоугольника, если одна из его сторон
равна 5 см, а угол между диагоналями равен - Найдите углы выпуклого четырехугольника, если они
пропорциональны числам 1,2,4,5. - Найдите периметр параллелограмма, если биссектриса
одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см. - Найдите площадь равнобедренного треугольника, если его
основание равно 10см, а боковая сторона равна 13см. - Катеты прямоугольного треугольника равны 6 и 8см.,
гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе. - Найдите площадь трапеции с основаниями AD и BC, если
АD=12см, ВС=6см, СD=5см, АС=13см. - Найдите площадь параллелограмма, если АD =12см, ВD=5см,
АВ=13см.
Пояснительная записка.
В 2020 -2021учебном году промежуточную аттестацию по геометрии в 8 классе рекомендуем организовать в форме устного экзамена.
Целью устного экзамена является проверка уровня предметной компетентности учащихся 8 классов по геометрии за курс 8 класса.
Основные цели изучения геометрии:
-
Развитие пространственных представлений, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как умение:
-
читать и делать чертежи, необходимые для решения;
-
выделять необходимую конфигурацию при чтении чертежа;
-
определять необходимость дополнительных построений при решении задач и выполнять их;
-
различать взаимное расположение геометрических фигур.
-
Формирование и развитие логического мышления, что в требованиях, предъявляемых к знаниям и умениям учащихся стандартом, формулируется как владение методами доказательств, применяемыми при обосновании геометрических утверждений (теорем, лемм, следствий и т.д.), а также при проведении аргументации и доказательных рассуждений в ходе решения задач.
Структура экзаменационного билета.
Билеты содержат три вопроса по различным темам курса геометрии за 8 класс (два теоретических вопроса и одна задача).
Первый вопрос. Базовый уровень.
В первом вопросе от учащихся требуется выполнить одно из трех возможных заданий: первое – дать определение фигуры; второе – воспроизвести одну из формул для вычисления длин отрезков, градусных мер углов, площадей; третье – воспроизвести формулировку одной из теорем о свойствах или признаках фигур, их элементов, отношениях фигур.
При ответе на первый вопрос учащиеся должны:
— дать четкое определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж, а также привести пример применения этого определения, верно иллюстрирующий его смысл.
-правильно воспроизвести одну из формул для вычисления значений геометрических величин (площадей), при этом, кроме записи формулы, необходимо выполнить чертеж и объяснить смысл формулы. Привести пример применения этой формулы, позволяющий сделать вывод об уровне сформированности умения применять эту формулу.
— воспроизвести формулировку теоремы, проиллюстрировав содержание теоремы выполнением чертежа; привести пример применения этой теоремы, верно отражающий ее содержание и смысл.
Второй вопрос. Продвинутый уровень.
Во втором вопросе учащиеся должны, как правило, дать определение фигуры, сформулировать ее свойство или признак, указанный в теореме, и доказать эту теорему.
При ответе на второй вопрос учащиеся должны:
-
дать определение фигуры, включающее в себя как вербальное определение, так и графическое – чертеж;
-
правильно воспроизвести формулировку теоремы, проиллюстрировав ее выполнением чертежа по условию теоремы;
-
привести доказательство теоремы, при этом доказательство считается выполненным верно, если учащийся правильно привел схему доказательства, обосновал все логические шаги, выполнил чертежи, которые правильно отражают, кроме условия, еще и ход доказательства.
Практическая часть. Третий вопрос билета – задача. Цель включения этих заданий – проверка овладения учащимися основными практическими умениями, полученными в ходе изучения курса, эти задачи соответствуют уровню базовой подготовки.
С помощью заданий третьих вопросов проверяются знание и понимание важных элементов содержания (геометрических понятий, свойств основных фигур, отношений между фигурами, методов доказательств и пр.), владение основными формулами, умение применять полученные знания к решению геометрических задач. При выполнении этих заданий учащиеся также должны продемонстрировать определенную системность знаний и широту представлений, узнавать стандартные задачи в разнообразных формулировках.
Время подготовки выпускника. Система оценивания ответа.
Примерное время, отводимое на подготовку выпускника к ответу, – 20–30 минут.
Оценивание ответа осуществляется по традиционной пятибалльной шкале. Ученик у доски отвечает на теоритические вопросы, дополняя свой ответ необходимыми чертежами и записями. Далее на доске рассматривается подробное решение задач, с ссылками на все используемые факты.
Критерии оценивания:
Отметка 5 (отлично) – ставится за полный, логически обоснованный ответ на все три вопроса билета.
Отметка 4 (хорошо) – выставляется за обоснованный полный ответ, но с допущением 1-2 негрубых недочетов на 1-2 вопросы с доказательством и решение задачи;
Отметка 3 (удовлетворительно) – ставится за решение задачи и правильно сформулированные теоремы, свойства, определения первого и второго вопросов (без доказательства).
Отметка 2 (неудовлетворительно) – выставляется во всех остальных случаях.
-
Вопросы без доказательства:
-
Сформулируйте определение многоугольника. Элементы многоугольника. Виды многоугольников. Сформулировать теорему о сумме углов выпуклого многоугольника.
-
Сформулируйте определение трапеции. Виды трапеции.Сформулируйте свойства равнобедренной трапеции.
-
Сформулировать определение квадрата и перечислить все его свойства.
-
Приведите формулы площадей ромба, квадрата, параллелограмма, трапеции. Для ромба приведите несколько формул.
-
Сформулируйте определение подобных треугольников. Сформулируйте признаки подобия треугольников.
-
Сформулируйте теорему Фалеса. Начертите чертеж.
-
Сформулируйте утверждения о пропорциональных отрезках в прямоугольном треугольнике.
-
Сформулируйте определение синуса, косинуса и тангенса острого угла прямоугольного треугольника. Запишите основное тригонометрическое тождество.
-
Сформулируйте определение окружности. Взаимное расположение прямой и окружности. Сформулируйте определение касательная к окружности и свойство касательной.
-
Сформулируйте свойство отрезков касательных, проведенных из одной точки.
-
С
формулируйте формулу нахождения величины угла между пересекающимися хордами через дуги окружности.
С формулируйте формулу нахождения величины угла между секущими, пересекающимися вне окружности
-
Назовите формулу Герона. В каких случаях данную формулу применяют?
-
Назовите значение синуса, косинуса и тангенса для углов 30
, 45
, 60
.
-
Сформулируйте определения центрального угла окружности и угла, вписанного в окружность. Сформулируйте теорему об измерении вписанного угла и следствия из нее.
-
Сформулируйте условия, когда в четырехугольник можно вписать окружность и условие, когда около четырехугольника можно описать окружность.
-
Вопросы с доказательством
-
Сформулируйте определение параллелограмма. Сформулируйте признаки параллелограмма и докажите один признак по выбору.
-
Сформулируйте определение параллелограмма. Сформулируйте и докажите свойства углов и сторон параллелограмма.
-
Сформулируйте определение параллелограмма. Сформулируйте и докажите свойство диагоналей параллелограмма.
-
Сформулируйте определение ромба. Сформулируйте и докажите свойство диагоналей ромба.
-
Сформулируйте определение прямоугольника. Сформулируйте и докажите свойство диагоналей прямоугольника.
-
Приведите формулы площади прямоугольника и площади параллелограмма. Выведите одну из формул по выбору.
-
Запишите формулу площади треугольника и докажите теорему площади треугольника. Сформулируйте теорему об отношении площадей двух треугольников, имеющих по равному углу.
-
Выведите формулу площади трапеции.
-
Сформулируйте определение прямоугольного треугольника. Сформулируйте и докажите теорему Пифагора.
-
Сформулируйте определение подобных треугольников. Докажите теорему об отношении площадей подобных треугольников.
-
Сформулируйте определение средней линии треугольника. Сформулируйте и докажите теорему о средней линии треугольника.
-
Сформулируйте определение касательной к окружности. Сформулируйте и докажите свойство касательной к окружности.
-
Сформулируйте и докажите теорему об отрезках пересекающихся хорд.
-
Сформулируйте определение окружности, вписанной в многоугольник. Сформулируйте и докажите теорему об окружности, вписанной треугольник. Каким свойством обладают стороны четырехугольника, описанного около окружности?
-
Сформулируйте определение окружности, описанной около многоугольника. Сформулируйте и докажите теорему об окружности, описанной около треугольника. Каким свойством обладают углы четырехугольника, вписанного в окружность?
-
Задача.
Задачи из образовательного портала по подготовке к экзаменам «РЕШУ ОГЭ»:
16.Треугольники, четырехугольники, многоугольники и их элементы
-
Многоугольники
-
Параллелограмм
-
Ромб
-
Трапеция
17.Окружность, круг и их элементы
-
Касательная, хорда, секущая, радиус
-
Окружность, описанная вокруг многоугольника
-
Центральные и вписанные углы
18.Площади фигур
-
Квадрат
-
Прямоугольник
-
Трапеция
-
Параллелограмм
19.Фигуры на квадратной решётке
-
Многоугольники
-
Параллелограмм
-
Ромб
-
Трапеция
5
Муниципальное бюджетное образовательное учреждение
дополнительного образования детей дом детского творчества
г. Зверева Ростовской области.
Муниципальное бюджетное образовательное учреждение
средняя образовательная школа №1
г.Зверева Ростовской области.
Билеты к устному экзамену по геометрии 8 класс
Работа педагога дополнительного
образования МБОУ ДОД ДДТ,
учителя математики МБОУ СОШ №1
Куца Фёдора Ивановича
г. Зверево
2014 г.
Билет №1.
1. Сформулируйте определение выпуклого многоугольника ( периметр, диагональ). Сформулируйте теорему о сумме углов выпуклого многоугольника.
2.Признаки подобия треугольников. Доказать один признак на выбор обучающегося.
3. В окружность вписан треугольник ABC так, что АВ — диаметр окружности. Найдите углы треугольника, если: дуга ВС=134°;
Билет №2.
1.Определение синуса, косинуса и тангенса острого угла прямоугольного треугольника.
2.Площадь прямоугольника (формулировка и доказательство).
3. Сумма двух противоположных сторон описанного четырехугольника равна 12 см. а радиус вписанной в него окружности равен 5 см. Найдите площадь четырехугольника
Билет №3
1.Параллелограмм. Определение. Свойства.
2.Теорема об окружности, вписанной в треугольник.
3. Стороны прямоугольника равны 3 см и 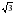
Билет № 4.
1.Четырехугольник. Сумма углов четырёхугольника.
2.Свойство касательной к окружности (формулировка и доказательство).
3. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Билет № 5.
1.Свойства площадей.
2.Теорема о средней линии треугольника (формулировка и доказательство).
3. Точка касания окружности, вписанной в равнобедренный треугольник, делит одну из боковых сторон на отрезки, равные 3 см и 4 см. считая от основания. Найдите периметр треугольника.
Билет № 6
1.Трапеция. Определение. Виды трапеций. Свойство равнобедренной трапеции.
2.Свойство отрезков касательных, проведенных из одной точки (формулировка и доказательство).
3. Подобны ли треугольники ABC и МКР если:
АВ=3 см, ВС=5 см, СА=7 см, МК=4,5 см, КР=7,5 см, РМ = 10,5 см.
Билет № 7
1.Прямоугольник. Свойства прямоугольника. Квадрат.
2.Теорема о вписанном угле (формулировка и доказательство).
3. Диагонали трапеции ABCD с основаниями АВ и CD пересекаются в точке О. Найдите: АВ, если ОВ=4 см, OD=10 см, DC=25 см.
Билет № 8
1.Ромб. Свойства ромба. Квадрат.
2.Свойство биссектрисы угла (формулировка и доказательство).
3. Площади двух подобных треугольников равны 75 и 300. Одна из сторон второго треугольника равна 9 . Найдите сходственную ей сторону первого треугольника.
Билет № 9
1.Квадрат. Свойства квадрата.
2.Свойство серединного перпендикуляра к отрезку (доказательство).
3. Найдите сторону и площадь ромба, если его диагонали равны 10 см и 24 см.
Билет № 10.
1.Подобные треугольники. Определение. Коэффициент подобия.
2.Свойства прямоугольника.
3. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см. а больший угол равен 135°.
Билет № 11.
1.Медиана треугольника. Определение. Свойство точки пересечения медиан треугольника.
2.Площадь параллелограмма (формулировка и доказательство).
3. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведенная к большей стороне, равна 2,4 см. Найдите высоту, проведенную к меньшей из данных сторон.
Билет № 12.
1.Пропорциональные отрезки в прямоугольном треугольнике.
2.Теорема об окружности, описанной около треугольника (формулировка и доказательство).
3. Найдите площадь прямоугольника, если одна из его сторон равна 5 см, а угол между диагоналями равен
Билет № 13.
1. Свойство описанного четырехугольника.
2.Свойства ромба (формулировка и доказательство).
3. Найдите углы выпуклого четырехугольника, если они пропорциональны числам 1,2,4,5.
Билет № 14.
1. Свойство вписанного четырехугольника.
2. Площадь треугольника (формулировка и доказательство).
3. Найдите периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см.
Билет № 15.
1. Центральный угол. Вписанный угол.
2.Площадь трапеции (формулировка и доказательство).
3. Найдите площадь равнобедренного треугольника, если его основание равно 10см, а боковая сторона
равна 13см.
Билет № 16.
1.Значения синуса, косинуса и тангенса для углов 30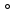
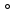
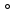
2.Теорема, обратная теореме Пифагора (формулировка и доказательство).
3.Катеты прямоугольного треугольника равны 6 и 8см., гипотенуза 10 см. Вычислите высоту, проведённую к гипотенузе.
Билет № 17
1.Описанная окружность. Центр окружности, описанной около треугольника.
2.Свойства параллелограмма (формулировка и доказательство).
3. Найдите площадь трапеции с основаниями AD и BC, если АD=12см, ВС=6см, СD=5см, АС=13см.
Билет № 18
1.Вписанная окружность. Центр окружности, вписанной в треугольник.
2. Теорема Пифагора (формулировка и доказательство). Пифагоровы треугольники.
3. Найдите площадь параллелограмма, если АD =12см, ВD=5см, АВ=13см.
.
Билеты по геометрии для 8 класса (Атанасян) 2018 год
Билет №1.
-
Определение четырёхугольника. Виды четырёхугольников.
-
Доказать теорему Фалеса.
-
Задача.
Найти площадь ромба, если его высота 15 см, а острый угол 30°.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет №2.
-
Параллелограмм. Определение. Свойства параллелограмма.
-
Доказать теорему о средней линии треугольника.
-
Задача. В равнобокой трапеции боковая сторона 17 см, основания равны 10 см и 26 см. Найти площадь трапеции.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №3.
-
Квадрат. Определение. Свойства.
-
Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
-
Задача. В равнобедренном треугольнике основание равно 80 см, и угол при нём 45°. Найти площадь треугольника.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №4.
-
Пропорциональность отрезков в прямоугольном треугольнике.
-
Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
-
Задача. Площадь равнобедренного треугольника равна 4800 см2, а его высота, проведённая к основанию, равна 80 см. Найти боковую сторону треугольника.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №5.
-
Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
-
Ромб. Доказательство теоремы о диагоналях ромба.
-
Задача. В окружности проведены две пересекающиеся хорды. Одна из них делится на отрезки 3 см и 12 см, а другая – пополам. Найдите длину второй хорды.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Билет № 6.
-
Касательная к окружности. Свойства.
-
Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
-
Задача. Определить площадь равнобедренного треугольника, если его основание 8 см и боковая сторона 5 см.
-
В треугольнике АВС
=90
,cosВ=
, АВ=45
Найдите АС.
Билет № 7.
-
Площадь четырехугольников: параллелограмма, трапеции
-
Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
-
Задача. В равнобедренный треугольник с основанием 12 см и периметром 32 см вписана окружность. Найдите радиус этой окружности.
-
В треугольнике АВС
=90
,ВС=
21, АВ=5. Найдите sinВ.
Билет №8.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Докажите свойство противолежащих сторон и углов параллелограмма.
-
Задача. Периметр равнобедренного треугольника равен 50 см, а его боковая сторона на 11 см меньше основания. Найти высоту треугольника, опущенную на основание.
-
В треугольнике АВС
=90
,АВ=13, АС=5. Найдите tgА.
Билет №9.
-
Признаки параллельности прямых.
-
Докажите теорему об отношении площадей треугольников.
-
Задача. Меньшее основание трапеции относится к средней линии как 1:3, а большее основание равно 30 см. Найдите среднюю линию трапеции.
-
В треугольнике АВС
=90
,cosВ=
, АВ=25
Найдите АС.
Билет №10.
-
Вписанная и описанная окружности в треугольники и четырехугольники.
-
Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
-
Задача. Одна из сторон параллелограмма в 3 раза больше проведённой к ней высоты. Вычислите их, если площадь параллелограмма равна 48 см2.
-
В треугольнике АВС
=90
,АВ=15, АС=12. Найдите tgА.
Билет №11.
-
Вписанный и центральный углы, дуга окружности.
-
Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
-
Задача. Боковая сторона равнобокой трапеции образует с большим её основанием угол 45°. Вычислите площадь трапеции, если основания её равны 24 см и 60 см.
-
В треугольнике АВС
=90
,АВ=20, АС=12. Найдите sinА
Билет №12.
-
Признаки равенства треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Длины диагоналей ромба относятся, как 3 : 4. Площадь ромба равна 150 см2. Вычислить высоту ромба.
-
В треугольнике АВС
=90
,sinА=
, АС=4
Найдите АВ.
Билет № 13.
-
Понятие площади многоугольника. Свойства площадей.
-
Докажите теорему Пифагора.
-
Задача. В треугольник, углы которого относятся как 1:3:5, вписана окружность. Найдите углы между радиусами, проведёнными в точки касания.
-
В треугольнике АВС
=90
,sinА=
, АС=5
Найдите АВ.
Билет №14.
-
Формулы для вычисления площади параллелограмма.
-
Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
-
Задача. В равнобокой трапеции, один из углов которой равен 45°, большее основание равно 70 см, высота равна 10 см. Вычислить площадь трапеции.
-
В треугольнике АВС
=90
,АВ=182, АС=70. Найдите tgА.
Билет №15.
-
Признаки равенства прямоугольных треугольников.
-
Вписанный угол. Докажите теорему о вписанном угле.
-
Задача. Боковая сторона равнобокой трапеции, равная 20 см, образует с меньшим её основанием угол 150°. Вычислите площадь трапеции, если её основания равны 12 см и 30 см.
-
В треугольнике АВС
=90
,ВС=28, АВ=35. Найдите sinВ.
Билет №16.
-
Треугольник. Свойства равнобедренного треугольника.
-
Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
-
Задача. Площадь параллелограмма равна 24 см2, каждая из его сторон равна 6 см. Найти расстояние между противоположными сторонами.
-
В треугольнике АВС
=90
,cosВ=
, АВ=5
Найдите АС.
Вопросы, предлагаемые для устного экзамена по геометрии в 8 классах
1 часть
1.Определение четырёхугольника. Виды четырёхугольников.
2.Параллелограмм. Определение. Свойства параллелограмма.
3.Квадрат. Определение. Свойства.
4. Пропорциональность отрезков в прямоугольном треугольнике.
5. Соотношения между сторонами и углами в прямоугольном треугольнике (определение синуса, косинуса и тангенса острого угла в прямоугольном треугольнике). Основное тригонометрическое тождество.
6. Касательная к окружности. Свойства
7. Площадь четырехугольников: параллелограмма, трапеции
8. Вписанная и описанная окружности в треугольники и четырехугольники.
9. Признаки параллельности прямых
10. Вписанный и центральный углы, дуга окружности.
11. Признаки равенства треугольников.
12. Понятие площади многоугольника. Свойства площадей.
13. Формулы для вычисления площади параллелограмма
14. Признаки равенства прямоугольных треугольников.
15. Треугольник. Свойства равнобедренного треугольника.
2 часть.
1. Доказать теорему Фалеса.
2. Доказать теорему о средней линии треугольника.
3. Вписанная окружность. Доказать теорему об окружности, вписанной в треугольник.
4. Прямоугольник. Доказательство теоремы о равенстве диагоналей прямоугольника.
5. Ромб. Доказательство теоремы о диагоналях ромба.
6. Параллелограмм. Свойства параллелограмма. Доказательство одного из свойств параллелограмма (на выбор учащегося).
7. Значения синуса, косинуса и тангенса некоторых углов. Вывод нахождения значений синуса, косинуса и тангенса углов в 45°, 30° и 60°.
8. Докажите свойство противолежащих сторон и углов параллелограмма.
9. Докажите теорему об отношении площадей треугольников.
10. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
11. Площадь треугольника. Формулы для вычисления площади треугольника (общие и частные случаи).
12. Признаки подобия треугольников. Докажите один из признаков подобия треугольников (по выбору учащегося).
13. Докажите теорему Пифагора.
14. Касательная к окружности. Докажите теорему о свойстве касательной к окружности.
15. Вписанный угол. Докажите теорему о вписанном угле.
16. Описанная окружность. Докажите теорему об окружности, описанной около треугольника.
ЭКЗАМЕН. МАТЕМАТИКА 8 КЛАСС.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Содержание экзаменационной работы определяется на основе Федерального компонента государственного стандарта основного общего образования по математике (приказ Минобразования России от 05.03.2004 № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования») и разработана с использованием материалов размещенных на сайте «Решу ОГЭ» https://oge.sdamgia.ru/.
Структура КИМ отвечает цели построения системы дифференцированного обучения математике в современной школе.
Работа состоит из трёх модулей: «Алгебра», «Геометрия», «Реальная математика». В модули «Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровнях, в модуль «Реальная математика» – одна часть, соответствующая проверке на базовом уровне.
Части 2 модулей «Алгебра» и «Геометрия» направлены на проверку владения материалом на повышенном уровне.
Работа состоит из трех модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 17 заданий. Модуль «Алгебра» содержит 7 заданий: в части 1 – шесть заданий; в части 2 – 1 задание. Модуль «Геометрия содержит пять заданий: части 1 – четыре задания, части 2 – одно задание. Модуль «Реальная математика» содержит пять заданий: все задания этого модуля – части 1.
На выполнение экзаменационной работы по математике отводится 90 минут.
Следует иметь в виду, что включённые в экзамен задания не отражают всех элементов, изученных обучающимися 8 класса.
ОЦЕНИВАНИЕ РАБОТЫ
Минимальное количество баллов по математике, которое подтверждает освоение обучающимся образовательной программы 8 класса, составляет 6 баллов, набранные в сумме за выполнение заданий трёх модулей, при условии, что из них не менее 2 балла по модулю «Алгебра», не менее 1 балла по модулю «Геометрия» и не менее 2 баллов по модулю «Реальная математика».
Максимальное количество баллов, которое может получить обучающийся за выполнение всей экзаменационной работы, – 19 баллов, из них:
за модуль «Алгебра» — 8 баллов; за модуль «Геометрия» — 6 баллов; за модуль «Реальная математика» — 5 баллов.
Критерии оценивания задания №16.
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Правильно составлено уравнение, получен верный ответ |
|
1 |
Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учетом решение доведено до ответа |
|
0 |
Другие случаи, не соответствующие указанным критериям |
Критерии оценивания задания №17.
|
Баллы |
Критерии оценки выполнения задания |
|
2 |
Получен верный обоснованный ответ |
|
1 |
При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу |
|
0 |
Другие случаи, не соответствующие критериям |
Далее перевод первичного балла в отметку по предмету выполняется в соответствии со шкалами, указанными ниже.
Шкала пересчета суммарного балла за выполнение работы в целом в отметку по математике в соответствии со шкалами, указанными ниже
|
Отметка по пятибалльной шкале |
«2» |
«3» |
«4» |
«5» |
|
Балл за работу в целом |
0 — 5 |
6 — 11 |
12 — 15 |
16 — 19 |
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Алгебра» (все задания модуля «Алгебра» и задания 14, 15, 16, 18, 19, 20 модуля «Реальная математика»), в отметку по алгебре
|
Отметка по пятибалльной шкале |
«2» |
«3» |
«4» |
«5» |
|
Балл за работу в целом |
0 — 4 |
5 — 7 |
8 — 11 |
12 — 13 |
Шкала пересчета суммарного балла за выполнение заданий, относящихся к разделу «Геометрия» (все задания модуля «Геометрия» и задание 17 модуля «Реальная математика»), в отметку по геометрии
|
Отметка по пятибалльной шкале |
«2» |
«3» |
«4» |
«5» |
|
Балл за работу в целом |
0 |
1 — 2 |
3 — 4 |
5 — 6 |
ОТВЕТЫ К ЗАДАНИЯМ 1 ЧАСТИ
|
№ задания |
Ответ 1 вариант |
Ответ 2 вариант |
Ответ 3 вариант |
Ответ 4 вариант |
|
1 |
8,4 |
1,38 |
15,3 |
3,44 |
|
2 |
2 |
3 |
4 |
2 |
|
3 |
2 |
4 |
4 |
4 |
|
4 |
0,5;1 |
1 |
0,5 |
1;0,5 |
|
5 |
243 |
243 |
243 |
243 |
|
6 |
1 |
1 |
2 |
3 |
|
7 |
70 |
80 |
70 |
80 |
|
8 |
6 |
3 |
5 |
4 |
|
9 |
35 |
15 |
20 |
18 |
|
10 |
610 |
130 |
730 |
1000 |
|
11 |
2 |
2 |
3 |
2 |
|
12 |
40 |
50 |
10 |
30 |
|
13 |
960 |
1610 |
1755 |
1320 |
|
14 |
0,5 |
0,75 |
0,6 |
0,5 |
|
15 |
8 |
8 |
8 |
8 |
ОТВЕТЫ К ЗАДАНИЯМ 2 ЧАСТИ
|
№ задания |
Ответ 1 вариант |
Ответ 2 вариант |
Ответ 3 вариант |
Ответ 4 вариант |
|
16 |
21 |
20 |
18 |
78 |
|
17 |
20 |
15 |
20 |
15 |
ОБРАЗЕЦ РЕШЕНИЯ ЧАСТИ 2
№16. Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
Решение. Пусть х км/ч скорость лодки в стоячей воде, (х-5) км/ч – скорость против течения, (х+5) км/ч – скорость по течению. 



Ответ. 21
№17. В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
|
|
Решение. Из треугольника АВС угол В = 180 – (20+50)= 110; <ABD = <DBC = 100:2 = 55; <HBC = 90-50= 40; <DBH =55-40 = 15/ Ответ. 15 |
Инструкция по выполнению работы
Работа состоит из трех модулей: «Алгебра», «Геометрия», «Реальная математика». Всего в работе 17 заданий. Модуль «Алгебра» содержит 7 заданий: в части 1 – шесть заданий; в части 2 – 1 задание. Модуль «Геометрия содержит пять заданий: части 1 – четыре задания, части 2 – одно задание. Модуль «Реальная математика» содержит пять заданий: все задания этого модуля – части 1.
На выполнение экзаменационной работы по математике отводится 90 минут.
Ответы к заданиям 2, 3, 6, 10 запишите в бланк ответов №1 в виде одной цифры, которая соответствует номеру правильного ответа.
Для остальных заданий части 1 ответом является число или последовательность цифр. Если в ответе получена обыкновенная дробь, превратите её в десятичную.
Решения заданий части 2 и ответы к ним запишите на бланке ответов №2. Задания можно выполнять в любом порядке, начиная с любого модуля. Текст задания переписывать не надо, необходимо указать только его номер.
Сначала выполняйте задания части 1. Начать советуем с тех заданий, которые вызывают у вас наименьшие затруднения. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у вас останется время, вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления и преобразования выполняйте на черновике.
Баллы, полученные за верно выполненные задания, суммируются. Для успешного прохождения экзамена необходимо в сумме набрать не менее 7 баллов, из них не менее 3 баллов в модуле «Алгебра», не менее 2 баллов в модуле «Геометрия», не менее 2 баллов в модуле «Реальная математика». За каждое правильно выполненное задание части 1 выставляется 1 балл. Задания части 2 оцениваются в 2 балла.
1 ВАРИАНТ
«Алгебра»
Найдите значение выражения: 2,5 * 3,5 – 0,35.
На координатной прямой отмечены числа a и b.
Какое из следующих чисел наибольшее? В ответе укажите номер правильного варианта.
1) a + b; 2) –a; 3) 2b; 4) a – b.
Население Австралии составляет 1,8·107 человек, а площадь их территории равна 7,7·106 кв. км. Сколько в среднем приходится жителей на 1 кв. км? В ответе укажите номер правильного варианта.
1) примерно 2,5 человека
2) примерно 2,3 человека
3) примерно 0,23 человека
4) примерно 2 человека
Решите уравнение 8x2 − 12x + 4 = 0. Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Укажите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Решите неравенство 20 — 3(х-5) < 19 -7x и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
«Геометрия»
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Центральный угол AOB опирается на хорду AB длиной 6. При этом угол OAB равен 60°. Найдите радиус окружности.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Мальчик прошел от дома по направлению на восток 110 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
«Реальная математика»
В таблице приведены нормативы по бегу на лыжах на 1 км для 10 класса.
|
мальчики |
девочки |
|||||
|
Отметка |
«3» |
«4» |
«5» |
«3» |
«4» |
«5» |
|
Время (мин. и сек.) |
5:30 |
5:00 |
4:40 |
7:10 |
6:30 |
6:00 |
Какую отметку получит девочка, пробежавшая на лыжах 1 км за 6 минут
15 секунд? В ответе укажите номер правильного варианта.
1) Неудовлетворительно
2) «4»
3) «3»
4) «5»
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 60 км/ч. Ответ дайте в метрах.
Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 800 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
Родительский комитет закупил 20 пазлов для подарков детям на окончание года, из них 10 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Коле достанется пазл с машиной.
Объём пирамиды вычисляют по формуле 


2 часть.
Моторная лодка прошла против течения реки 208 км и вернулась в пункт отправления, затратив на обратный путь на 5 часов меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 5 км/ч.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
2 ВАРИАНТ
«Алгебра»
Найдите значение выражения: 3,4 * 0,6 – 0,66.
На координатной прямой отмечены числа a и x .
Какое из следующих чисел наибольшее? В ответе укажите номер правильного варианта.
1) a+x; 2) 2a; 3) −x; 4) ax
Население Австралии составляет 1,8·107 человек, а площадь их территории равна 7,7·106 кв. км. Сколько в среднем приходится жителей на 1 кв. км? В ответе укажите номер правильного варианта.
1) примерно 2,5 человека
2) примерно 2 человека
3) примерно 0,23 человека
4) примерно 2,3 человека
Решите уравнение 8x2 − 12x + 4 = 0. Если корней несколько, запишите больший из них..
Укажите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Решите неравенство 2x – 5 < 9 – 6(x – 3) и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
«Геометрия»
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Центральный угол AOB, равный 60°, опирается на хорду АВ длиной 3. Найдите радиус окружности.
На клетчатой бумаге с размером клетки 1см × 1см изображен параллелограмм. Найдите его площадь.
Мальчик прошел от дома по направлению на восток 120 м. Затем повернул на север и прошел 50 м. На каком расстоянии (в метрах) от дома оказался мальчик?
«Реальная математика»
В таблице приведены нормативы по бегу на 30 метров для учащихся 9-х классов.
|
Мальчики |
Девочки |
|||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Время, секунды |
4,6 |
4,9 |
5,3 |
5,0 |
5,5 |
5,9 |
Какую отметку получит девочка, пробежавшая эту дистанцию за 5,36 секунды? В ответе укажите номер правильного варианта.
1) Отметка «5».
2) Отметка «4».
3) Отметка «3».
4) Норматив не выполнен.
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 70 км/ч. Ответ дайте в метрах.
Сберегательный банк начисляет на срочный вклад 15% годовых. Вкладчик положил на счет 1400 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
У бабушки 20 чашек: 5 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.
Объём пирамиды вычисляют по формуле 


2 часть.
Моторная лодка прошла против течения реки 297 км и вернулась в пункт отправления, затратив на обратный путь на 3 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 2 км/ч.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
3 ВАРИАНТ
«Алгебра»
Найдите значение выражения: 4,6 * 3,4 – 0,34.
На координатной прямой отмечены числа b и c .
Какое из следующих чисел наибольшее? В ответе укажите номер правильного варианта.
1) b+c; 2) –c; 3) 2b; 4) c−b
Население Канады составляет 2,2·107 человек, а площадь их территории равна 7,7·106 кв. км. Сколько в среднем приходится жителей на 1 кв. км? В ответе укажите номер правильного варианта.
1) примерно 3,5 человека
2) примерно 3 человека
3) примерно 0,29 человека
4) примерно 2,9 человека
Решите уравнение 8x2 − 12x + 4 = 0. Если корней несколько, запишите меньший из них
Укажите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Решите неравенство 4x +23 < 3 – 2(x – 4) и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
«Геометрия»
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 40° соответственно.
Центральный угол AOB равен 60°. Найдите длину хорды AB, на которую он опирается, если радиус окружности равен 5.
На клетчатой бумаге с размером клетки 1см × 1см изображен параллелограмм. Найдите его площадь.
Мальчик прошёл от дома по направлению на восток 550 м. Затем повернул на север и прошёл 480 м. На каком расстоянии (в метрах) от дома оказался мальчик?
«Реальная математика»
В таблице приведены нормативы по прыжкам с места для учеников 11 класса.
|
Мальчики |
Девочки |
|||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Расстояние, см |
230 |
220 |
200 |
185 |
170 |
155 |
Какую оценку получит девочка, прыгнувшая на 167 см?
В ответе укажите номер правильного варианта.
1) «5»
2) «4»
3) «3»
4) «Неудовлетворительно»
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 30 км/ч. Ответ дайте в метрах.
Сберегательный банк начисляет на срочный вклад 17% годовых. Вкладчик положил на счет 1500 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
Родительский комитет закупил 25 пазлов для подарков детям на окончание года, из них 15 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Толе достанется пазл с машиной.
Объём пирамиды вычисляют по формуле 


2 часть.
Моторная лодка прошла против течения реки 77 км и вернулась в пункт отправления, затратив на обратный путь на 2 часа меньше, чем на путь против течения. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.
В треугольнике АВС углы А и С равны 20° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
4 ВАРИАНТ
«Алгебра»
Найдите значение выражения: 5,4 * 0,8 – 0,88.
На координатной прямой отмечены числа a и b.
Какое из следующих чисел наибольшее?
В ответе укажите номер правильного варианта.
1) a+b; 2) –a; 3) 2b; 4) a−b
Население Канады составляет 2,2·107 человек, а площадь их территории равна 7,7·106 кв. км. Сколько в среднем приходится жителей на 1 кв. км? В ответе укажите номер правильного варианта.
1) примерно 3 человека
2) примерно 3,5 человека
3) примерно 0,29 человека
4) примерно 2,9 человека
Решите уравнение 8x2 − 12x + 4 = 0. Если корней несколько, запишите их через точку с запятой в порядке убывания.
Укажите соответствие между графиками функций и формулами, которые их задают.
1)
2)
3)
4)
Ответ укажите в виде последовательности цифр без пробелов и запятых в указанном порядке
Решите неравенство 9 + 5x < 6 – 4 (x — 3) и определите, на каком рисунке изображено множество его решений. В ответе укажите номер правильного варианта.
«Геометрия»
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные 30° и 50° соответственно.
Центральный угол AOB, равный 60° , опирается на хорду АВ длиной 4. Найдите радиус окружности.
На клетчатой бумаге с размером клетки 1х1 изображён параллелограмм. Найдите его площадь.
Мальчик прошел от дома по направлению на восток 800 м. Затем повернул на север и прошел 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
«Реальная математика»
В таблице приведены нормативы по прыжкам через скакалку за 30 сек. для 9 класса.
|
Мальчики |
Девочки |
|||||
|
Отметка |
«5» |
«4» |
«3» |
«5» |
«4» |
«3» |
|
Количество раз |
58 |
56 |
54 |
66 |
64 |
62 |
Какую оценку получит мальчик, прыгнувший 57 раз за 30 сек.?
В ответе укажите номер правильного варианта.
1) «5»
2) «4»
3) «3»
4) «Неудовлетворительно»
При резком торможении расстояние, пройденное автомобилем до полной остановки (тормозной путь), зависит от скорости, с которой автомобиль двигался. На рисунке показан график этой зависимости. По горизонтальной оси откладывается скорость (в км/ч), по вертикальной – тормозной путь (в метрах). Определите по графику, каким будет тормозной путь автомобиля, который двигается со скоростью 50 км/ч. Ответ дайте в метрах.
Сберегательный банк начисляет на срочный вклад 20% годовых. Вкладчик положил на счет 1100 р. Какая сумма будет на этом счете через год, если никаких операций со счетом проводиться не будет?
Родительский комитет закупил 20 пазлов для подарков детям на окончание года, из них 10 с машинами и 10 с видами городов. Подарки распределяются случайным образом. Найдите вероятность того, что Коле достанется пазл с машиной.
Объём пирамиды вычисляют по формуле 


2 часть
Моторная лодка прошла 36 км по течению реки и вернулась обратно, потратив на весь путь 5 часов. Скорость течения реки равна 3 км/ч. Найдите скорость лодки в неподвижной воде.
В треугольнике АВС углы А и С равны 20° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Используемые ресурсы:
https://oge.sdamgia.ru/


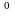 , 45
, 45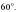
 =90
=90 ,
,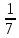 , АС=4
, АС=4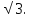 Найдите АВ.
Найдите АВ.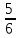 , АС=5
, АС=5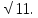 Найдите АВ.
Найдите АВ.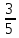 , АВ=5
, АВ=5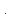 Найдите АС.
Найдите АС.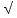 21, АВ=5. Найдите
21, АВ=5. Найдите 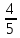 , АВ=25
, АВ=25



























