Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.
Тренировочный вариант №1 ЕГЭ 2023 по математике профильный уровень с ответами и решением по новой демоверсии ЕГЭ 2023 года от ФИПИ для подготовки на 100 баллов в новом формате, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет.
Скачать вариант с ответами
Скачать решение каждого задания
Скачать удобный формат решения
Вариант состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
Решать вариант №1 ЕГЭ 2023 по математике профиль с ответами
егэ2023_математика_профиль_вариант1
Решение каждого задания
решение_вариант1-егэ2023-профиль
1)На окружности отмечены точки 𝐴, 𝐵 и 𝐶. Дуга окружности 𝐴𝐶, не содержащая точку 𝐵, составляет 200°. Дуга окружности 𝐵𝐶, не содержащая точку 𝐴, составляет 80°. Найдите вписанный угол 𝐴𝐶𝐵. Ответ дайте в градусах.
Ответ: 40
2)Найдите объём многогранника, вершинами которого являются вершины 𝐴, 𝐶, 𝐴1, 𝐵1 правильной треугольной призмы 𝐴𝐵𝐶𝐴1𝐵1𝐶1. Площадь основания призмы равна 9, а боковое ребро равно 4.
Ответ: 12
3)В сборнике билетов по математике всего 20 билетов, в 16 из них встречается вопрос по логарифмам. Найдите вероятность того, что в случайно выбранном на экзамене билете школьнику достанется вопрос по логарифмам.
Ответ: 0, 8
4)Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,01. Перед упаковкой каждая батарейка проходит систему контроля качества. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,06. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответ: 0, 069
5)Найдите корень уравнения 3 log9(5𝑥−5) = 5.
Ответ: 6
9)Девять одинаковых рубашек дешевле куртки на 10%. На сколько процентов одиннадцать таких же рубашек дороже куртки?
Ответ: 10
10)На рисунке изображён график функции вида 𝑓(𝑥) = 𝑘𝑥 + 𝑏. Найдите значение 𝑓(7).
Ответ: 13
13)Длина диагонали куба 𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1 равна 3. На луче 𝐴1𝐶 отмечена точка 𝑃 так, что 𝐴1𝑃 = 4. а) Докажите, что 𝑃𝐵𝐷𝐶1 − правильный тетраэдр. б) Найдите длину отрезка 𝐴𝑃.
Ответ: корень из 11
15)В июле 2020 года планируется взять кредит в банке на некоторую сумму. Условия его возврата таковы: – каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года; – с февраля по июнь каждого года необходимо выплатить одним платежом часть долга. Сколько рублей планируется взять в банке, если известно, что кредит будет полностью погашен четырьмя равными платежами (то есть за четыре года) и банку будет выплачено 311 040 рублей?
Ответ: 201300
16)Биссектриса 𝐵𝐵1 и высота 𝐶𝐶1 треугольника 𝐴𝐵𝐶 пересекают описанную окружность в точках 𝑀 и 𝑁. Известно, что угол 𝐵𝐶𝐴 равен 85° и угол 𝐴𝐵𝐶 равен 40°. а) Докажите, что 𝐶𝑁 = 𝐵𝑀. б) Пусть 𝑀𝑁 и 𝐵𝐶 пересекаются в точке 𝐷. Найти площадь треугольника 𝐵𝐷𝑁, если его высота 𝐵𝐻 равна 7.
Ответ: 49
17)Найдите все значения 𝑎, при которых уравнение (𝑎𝑥 2 − 2𝑥) 2 + (𝑎 2 − 𝑎 + 2)(𝑎𝑥 2 − 2𝑥) − 𝑎 2(𝑎 − 2) = 0 имеет ровно два решения.
Ответ: {−2} ∪ {0} ∪ (1; +∞)
18)Последовательность 𝑎1, 𝑎2, …, 𝑎6 состоит из неотрицательных однозначных чисел. Пусть 𝑀𝑘 − среднее арифметическое всех членов этой последовательности, кроме 𝑘 − го. Известно, что 𝑀1 = 1, 𝑀2 = 2. а) Приведите пример такой последовательности, для которой 𝑀3 = 1,6. б) Существует ли такая последовательность, для которой 𝑀3 = 3? в) Найдите наибольшее возможное значение 𝑀3.
Ответ: а) 502111 б) нет в) 2,8
Демоверсия ЕГЭ 2023 математика профильный уровень ФИПИ
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Тренировочные варианты. Первая часть.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Килограмм картошки стоит (20) рублей. Костя купил (2,7, кг) картошки. Сколько рублей сдачи он должен получить со (100) рублей?
(2,7, кг) картошки обойдутся Косте в (20cdot 2,7 = 54) рубля. Таким образом, сдача должна составить (100 — 54 = 46) рублей.
Ответ: 46
На диаграмме показана среднедневная температура воздуха в городе (K) за первые (12) дней февраля (200) года. По вертикали указывается температура в градусах Цельсия, по горизонтали – дни февраля. Определите по диаграмме, сколько было дней, когда среднедневная температура не превышала (3) градуса Цельсия.
Среднедневная температура не превышала (3) градуса Цельсия только первого февраля, таким образом, ответ: (1).
Ответ: 1
В равнобедренном треугольнике один из углов равен (100^circ). Найдите наибольший из внешних углов этого треугольника. Ответ дайте в градусах.
В равнобедренном треугольнике углы при основании равны, а сумма углов треугольника равна (180^circ), следовательно, в треугольнике не может быть двух углов по (100^circ), тогда угол при вершине равен (100^circ), а углы при основании равны по ((180^circ — 100^circ) : 2 = 40^circ).
Внешние углы этого треугольника равны [180^circ — 100^circ = 80^circ,qquad 180^circ — 40^circ = 140^circ,qquad 180^circ — 40^circ = 140^circ,.] Больший из них равен (140^circ).
Ответ: 140
Тимур считает вероятность наступления некоторого события (A) в случае, если он подбросит правильную игральную кость сто раз. У него получилось, что вероятность наступления события (A) равна (0,045). Известно, что Тимур ошибся, но его ошибка наименьшая из возможных при данных условиях. Учитель задумался, насколько ошибся Тимур (учителя интересует ответ, округлённый до десятых). Какой результат должен получить учитель?
Рассмотрим ситуацию, когда (P(A) = 0) (она возможна при данных условиях), тогда ошибка Тимура составит (0,045). Так как ошибка Тимура наименьшая из возможных, то она не превосходит (0,045), но все числа, не превосходящие (0,045), при округлении до десятых дают (0). Таким образом, ответ: (0).
Ответ: 0
Решите уравнение [2^{-x^2} = e^{x^2}]
Так как (2 = e^{ln 2}), то данное уравнение равносильно уравнению [e^{-x^2ln 2} = e^{x^2},,] откуда получаем [-x^2ln 2 = x^2qquadLeftrightarrowqquad x^2(1 + ln 2) = 0qquadLeftrightarrowqquad x = 0,.]
Ответ: 0
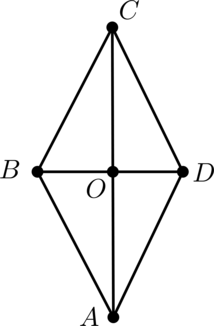
В ромбе (ABCD) одна из диагоналей в (sqrt{3}) раз больше, чем другая диагональ. Найдите больший из углов этого ромба. Ответ дайте в градусах.
Пусть (O) – точка пересечения диагоналей ромба. Пусть (AC : BD = sqrt{3}).
Так как (AO = 0,5AC), а (BO = 0,5BD), то (AO : BO = sqrt{3}), тогда [mathrm{tg}, angle ABO = sqrt{3}, ,] следовательно, (angle ABO = 60^circ), тогда (angle ABC = 2angle ABO = 120^circ).
(angle BCD = 60^circ < angle ABC), таким образом, больший из углов ромба (ABCD) равен (120^circ).
Ответ: 120
Найдите тангенс угла наклона касательной к графику функции (y = 2(ln 2)^{-0,5}cdot e^{x^2}) в точке с абсциссой (x_0 = sqrt{ln 2}).
Тангенс угла наклона касательной к графику функции (y = f(x)) в точке с абсциссой (x_0) равен (f'(x_0)). [y’ = 2(ln 2)^{-0,5}cdot 2xcdot e^{x^2},,] тогда при (x_0 = sqrt{ln 2}) имеем: [y'(sqrt{ln 2}) = 2(ln 2)^{-0,5}cdot 2sqrt{ln 2}cdot e^{ln 2} = 8,.]
Ответ: 8
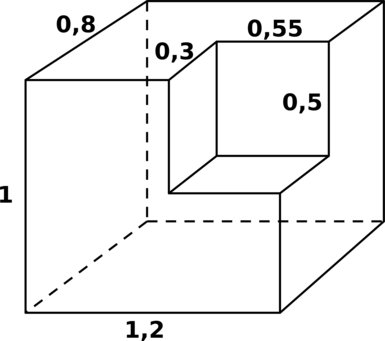
Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.
Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).
Таким образом, искомый объём равен [0,8cdot 1cdot 1,2 — 0,3cdot 0,5cdot 0,55 = 0,8775,.]
Ответ: 0,8775
Найдите (sin^2 2x), если (sin x = 0,3).
[sin^2 2x = (sin 2x)^2 = (2cdotsin xcdotcos x)^2 = 4cdotsin^2xcdotcos^2x,.]
Так как (sin x = 0,3), то (cos^2 x = 1 — sin^2x = 1 — 0,09 = 0,91), следовательно, значение исходного выражения равно [4cdot 0,09cdot 0,91 = 0,3276,.]
Ответ: 0,3276
Путь материальной точки, движущейся по прямой, имеет вид (x(t) = t^3 + 2t^2 — t + 1). Каким оказалось перемещение этой точки из положения, которое она занимала в момент (t = -1), в положение, которое она занимала в момент (t = 1)?
[x(-1) = -1 + 2 + 1 + 1 = 3,qquadqquad x(1) = 1 + 2 — 1 + 1 = 3, ,] следовательно, перемещение составило [|x(-1) — x(1)| = |3 — 3| = 0,.]
Ответ: 0
Два автомобиля выехали с постоянными скоростями из пунктов (A) и (B) навстречу друг другу. Известно, что скорость одного из них в (1,2) раза больше, чем скорость другого. Они встретелись через (t) часов. Известно, что медленному автомобилю понадобилось (T) часов, чтобы добраться до противоположного пункта. Найдите (dfrac{T}{t}).
Пусть (v, км/ч) – скорость медленного автомобиля, тогда (1,2v, км/ч) – скорость быстрого автомобиля, следовательно, скорость сближения автомобилей равна (v + 1,2v = 2,2v, км/ч).
Пусть (S, км) – расстояние между пунктами (A) и (B), тогда (t = dfrac{S}{2,2v}), а (T = dfrac{S}{v}), следовательно, [dfrac{T}{t} = dfrac{S}{v} : dfrac{S}{2,2v} = 2,2,.]
Ответ: 2,2
Найдите точку локального минимума функции (y = x^3 — 3x).
ОДЗ: (x) – произвольный.
1) [y’ = 3x^2 — 3]
Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 — 3 = 0qquadLeftrightarrowqquad x = pm 1,.] Производная существует при любом (x).
2) Найдём промежутки знакопостоянства (y’):
3) Эскиз графика (y):
Таким образом, (x = 1) – точка локального минимума функции (y).
Ответ: 1

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
24 сентября 2018
В закладки
Обсудить
Жалоба
Первый тренировочный вариант по математике от 4ЕГЭ.
Варианты будут выходить каждые 2 недели. Следующий — 8 октября. Ответы публикуются сразу в конце документа.
v1-math-4ege.pdf
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
В сентябре 1 кг винограда стоил 60 рублей, в октябре виноград подорожал на 25%, а в ноябре еще на 20%. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?
Ответ:
2
На рисунке жирными точками показано суточное количество осадков, выпадавших в Мурманске с 7 по 22 ноября 1995 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней из данного периода выпадало менее 3 миллиметров осадков.
Ответ:
3
Найдите корень уравнения
Ответ:
4
5
Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
| Перевозчик | Стоимость перевозки одним автомобилем (руб. на 100 км) |
Грузоподъемность автомобилей (тонн) |
| А | 3200 | 3,5 |
| Б | 4100 | 5 |
| В | 9500 | 12 |
Ответ:
6
Найдите сумму координат вектора
Ответ:
7
Найдите значение выражения
Ответ:
8
На рисунке изображен график производной функции f(x), определенной на интервале (−7; 4). Найдите промежутки возрастания функции f(x). В ответе укажите сумму целых точек, входящих в эти промежутки.
Ответ:
9
Найдите объем V части цилиндра, изображенной на рисунке. В ответе укажите
Ответ:
10
11
Найдите наименьшее значение функции на отрезке [−2,5; 0].
Ответ:
12
Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?
Ответ:
13
а) Решите уравнение
б) Найдите решения уравнения, принадлежащие отрезку [3; 5].
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
В правильной треугольной пирамиде SABC с основанием ABC известны ребра SC = 25. M — середина ребра SA.
а) Докажите, что проекции точек S и M на плоскость основания делят высоту AN треугольника ABC на три равные части.
б) Найдите угол, образованный плоскостью основания и прямой MN.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
Прямая касается окружностей радиусов R и r в точках A и B. Известно, что расстояние между центрами равно a причем r < R и r + R < a. Найдите AB.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
Найдите все значения a при каждом из которых система не имеет решений.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Перед каждым из чисел 14, 15, . . ., 20 и 4, 5, . . ., 8 прозвольным образом ставят знак плюс или минус, после чего от каждого из образовавшихся чисел первого набора отнимают каждое из образовавшихся чисел второго набора, а затем все 35 полученных результатов складывают. Какую наименьшую по модулю и какую наибольшую сумму можно получить в итоге?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Чтобы отправить работу учителю, перейдите на следующую страницу, сверьте ваши решения заданий с развернутым ответом с образцами, оцените ваши решения и сохраните выставленные баллы.
- 11.09.2021
Первый тренировочный вариант ЕГЭ 2022 по математике на основе демоверсии ЕГЭ 2022 базового уровня
В 2022 году произошло МНОГО разнообразных и значимых изменений в ЕГЭ, поэтому обязательно ознакомьтесь со списком изменений, если еще не смотрели.
- Посмотреть демоверсию 2022 по математике + изменения (база)
Вариант создан по кодификатору ФИПИ ЕГЭ 2022 и в полном соответствии со всеми изменениями демоверсии ЕГЭ 2022 база.
Автор-составитель: Проект ЕГЭ 100 БАЛЛОВ https://vk.com/ege100ballov
- Другие тренировочные варианты ЕГЭ по математике базового уровня
Есть вопросы? Пишите в комментариях ниже!
Некоторые задания из тренировочной работы №1
Задание 2
На автозаправке клиент отдал кассиру 1000 рублей и попросил залить бензин до полного бака. Цена бензина 32 рубля за литр. Клиент получил 72 рубля сдачи. Сколько литров бензина было залито в бак?
Задание 8
Площадь поверхности прямоугольного параллелепипеда с рёбрами 𝑎, 𝑏 и 𝑐 вычисляется по формуле 𝑆=2(𝑎𝑏+𝑎𝑐+𝑏𝑐). Найдите площадь поверхности прямоугольного параллелепипеда с рёбрами 5, 6 и 20.
Задание 11
На чемпионате по прыжкам в воду выступают 20 спортсменов, среди них 5 прыгунов из России и 7 прыгунов из Китая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что вторым будет выступать прыгун из Китая.
Задание 19
Найдите четырёхзначное натуральное число, кратное 45, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.

Пробный вариант № 1 ЕГЭ по математике профильного уровня на 2021 год составлен в соответствии с кодификатором ФИПИ и официальными демоверсиями.
Файл в формате pdf содержит задания, решения и ответы.
Скачать вариант в формате pdf — СКАЧАТЬ.
Вариант составлен авторами: Школа Пифагора.
Смотрите также:
- ЕГЭ по математике
- Расписание ЕГЭ 2021
- Шкала перевода баллов ЕГЭ
Одноклассники
Вконтакте
Мой мир