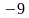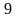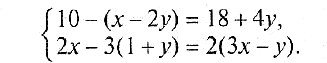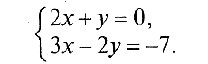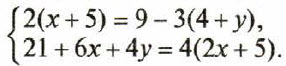Итоговый тест по Алгебре 7 класс
Даны основные примеры итогового теста (не все) 7 класс, Алгебра
Математика 7 класс | Автор: Архиполва НМ | ID: 7821 | Дата: 14.3.2016
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
Упростите выражение -4m + 9n — 7m — 2n.
-3m + 11n
-3m + 7n
11m + 7n
-11m + 7n
Вопрос №
2
Решите уравнение 10у – 13,5 = 2у — 37,5.
6,375
3
-3
4
Вопрос №
3
Упростите выражение с7 : c4 • c.
c в 5 степени
c в 6 степени
c в 4 степени
c в 12 степени
Вопрос №
4
Выполните умножение (3a — b)(2b — 4a).
-12a2 – 10ab – 2b2
-12a2 + 10ab – 2b2
6ab – 2b2
6ab – 4b
Вопрос №
5
Найдите значение выражения (-1)3 – (-2)3 + 52 – 72.
83
33
-16
-17
Вопрос №
6
Выразите у через х в выражении -5х + у = -17.
У = 17 + 5х
У = -5х + 17
У = -17 + 5х
У = 17 — 5х
Вопрос №
7
Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?
-1,8
1,8
7
-7
Вопрос №
8
Составьте выражение по условию задачи: «Турист шел со скоростью b км/ч. Какое расстояние он пройдет за 8 часов?».
8 — b
8 + b
8b
8 : b
Вопрос №
9
В одной системе координат заданы графики функций у = 2х – 4 и у = -3. Определите координаты точки их пересечения.
(1,5; -3)
(1,5; 1)
(0,5; -3)
(-0,5; -3)
Вопрос №
10
Через какую точку проходит график функции у = 3х + 5?
(2; -3)
(1; -2)
(2; 11)
(-2; 11)
Пояснительная записка
Работа содержит 16 заданий курса алгебры и геометрии .
Каждый из двух вариантов содержит две части.
Часть 1 — 12 заданий базового уровня
Часть 2 — 4 задачи высокого уровня, где требуется написать развернутое решение.
Критерии оценивания: За каждый верный ответ 1-й части начисляется 1 балл, за каждое верное решение задачи 2-й части – 2 балла. Максимальное количество баллов – 20. Оценка ставится в зависимости от набранных баллов:
|
Баллы |
Оценка |
|
0-6 |
2 |
|
7-10 |
3 |
|
11-15 |
4 |
|
16-20 |
5 |
Вариант № 1
Часть 1
1. Вычислите (32)4 : (35 × 32)
2. Выполните умножение: (с – 5) (c+1)
3. Решением системы уравнений: является пара чисел:
а) (2; 3); б) (- 2; 3); в) (2; — 3); г) (- 2; — 9); д) (- 2; 9).
4. Решите уравнение 3(5 – 2х) – 4 = 4 – 5х
5. Решите систему линейных уравнений:
6. Постройте график функции у=2х+2.
7. Упростите выражение (х – 2)2 + (х – 1)(х +1 )
8. Два угла треугольника равны 300 и 530. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, АВ=5см. Найдите ВС.
10. Дано: Найдите:
.
C
O
B
11. Выберите верное утверждение:
1. Если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180°,то такие прямые параллельны.
2. Если угол равен 47°, то смежный с ним равен 153°.
3. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
4. Через любые две точки проходит бесконечно много прямых.
12. В треугольнике АВС АВ=ВС, ВЕ – медиана треугольника. АВЕ = 400. Найти ∠ АВС.
Часть 2
13.Решите уравнение: х2 + 4х+3=0
14. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч. Найдите собственную скорость лодки и скорость течения реки.
15. Дано: Найти:
m
n
1
2
3
4
A
C
B
16. В треугольнике СКЕ стороны СЕ и КE равны, биссектрисы СМ и КН пересекаются в точке А. Докажите, что треугольники КАМ и САН равны.
Вариант № 2
Часть 1
1. Вычислите 26 * (22)5 : 213
2. Выполните умножение: (а – 3) (а + 4)
3. Решением системы уравнений: является пара чисел:
а) (5; 2); б) ( 5; — 2); в) (- 5; — 2); г) (- 5; — 7); д) (5; — 7).
4. Решите уравнение 6(4 – х) + 4х = 3+х
5. Решите систему уравнений:
6. Постройте график функции у= -2х-2.
7. Упростите выражение: ( х + 3)2 + (х – 1) (х +1)
8. Два угла треугольника равны 400 и 380. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, ВС=12см. Найдите АВ.
10. Дано: Найдите:
.
C
O
B
A
11. Выберите верное утверждение:
1. Если две прямые параллельны третьей, то они пересекаются.
2. В равнобедренном треугольнике медиана, проведенная к боковой стороне, является высотой и биссектрисой.
3. Если при пересечении двух прямых секущей сумма соответственных углов равна 180°,то такие прямые параллельны.
4. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
12. В треугольнике АВС АВ=ВС, ВК –высота треугольника. АВС = 1300. Найти ∠ КВС.
Часть 2
13.Решите уравнение: х2 – 4х+3=0
14.Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.
15. Дано: Найти:
A
B
C
b
a
1
2
3
4
16. В равнобедренном треугольнике КЕС с основанием СК медианы СМ и КН пересекаются в точке А. Докажите, что треугольник КАС – также равнобедренный.
Итоговый тест по алгебре за 7 класс
Часть 1.
А1. Упростите выражение -4m + 9n — 7m — 2n.
1) -3m + 11n
2) -3m + 7n
3) 11m + 7n
4) -11m + 7n
A2. Решите уравнение 10у – 13,5 = 2у — 37,5.
1) 6,375
2) 3
3) -3
4) 4
A3. Упростите выражение с
7
: c
4
∙ c.
1) c
5
2) c
6
3) c
4
4) c
12
A4. Выполните умножение (3a — b)(2b — 4a).
1) -12a
2
– 10ab – 2b
2
2) -12a
2
+ 10ab – 2b
2
3) 6ab – 2b
2
4) 6ab – 4b
A5. Преобразуйте в многочлен (4х – 5у)
2
.
1) 16х
2
– 20ху + 25у
2
2) 16х
2
— 40ху + 25у
2
3) 4х
2
– 25у
2
4) 16х
2
– 25у
2
A6. Упростите выражение —3а
7
b
2
∙(5a
3
)
2
.
1) 15a
13
b
2
2) -15a
12
b
2
3) 75a
12
b
2
4) -75a
13
b
2
A7. Найдите значение выражения (-1)
3
– (-2)
3
+ 5
2
– 7
2
.
1) 83
2) 33
3) -16
4) -17
А8. Представьте выражение в виде квадрата двучлена 4у
2
— 12у + 9.
1) (4у — 3)
2
2) (2у — 9)
2
3) 2у — 3
2
4) (2у — 3)
2
А9. Выразите у через х в выражении -5х + у = -17.
1) У = 17 + 5х
2) У = -5х + 17
3) У = -17 + 5х
4) У = 17 — 5х
А10. Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?
1) -1,8
2) 1,8
3) 7
А11. Выполните умножение дробей:
Бланк ответов — Алгебра 7 класс
Ключ ответов — Алгебра 7 класс
Итоговая контрольная работа по алгебре за курс 7 класса с ответами и решениями по УМК Макарычев (Просвещение). Поурочное планирование по алгебре для 7 класса. Урок 101. Контрольная работа по теме «Обобщение и систематизация знаний учащихся». Алгебра 7 класс Макарычев Итоговая контрольная работа.
Смотреть Список контрольных по алгебре в 7 классе по УМК Макарычев
Итоговая контрольная работа
Цель: проверить знания, умения и навыки учащихся по теме.
Тип урока: урок контроля, оценки и коррекции знаний.
ХОД УРОКА
I. Сообщение темы и цели урока
II. Контрольная работа в 2 вариантах
ИКР. Вариант 1 (транскрипт)
- Упростите выражение (а + 2b)2 – (а – b)(b + а) и найдите его значение при а = 1 и b = 1/5.
- Решите уравнение (5x+2)/3 + (3x–1)/5 = 5.
- Найдите значение выражения ((З4)2 •211)/(4 • 364).
- Постройте график функции у = 3х – 6 и определите, проходит ли он через точки А (41; 117) и В (53; 152).
- Сумма двух чисел равна 80, а сумма 50% первого числа и 25% второго числа равна 26. Найдите эти числа.
- Решите уравнение (х – 2)(5х + 3) = (х – 2)(3х – 5).
ИКР. Вариант 2 (транскрипт)
- Упростите выражение (2а + b)2 – (2а – 3b)(3b + 2а) и найдите его значение при а = 2 и b = 1/5.
- Решите уравнение (4x + 2)/7 + (3x – 5)/4 = 3.
- Найдите значение выражения ((53)5 • 316)/(9 • 2257).
- Постройте график функции у = 2х – 4 и определите, проходит ли он через точки А (43; 82) и В (56; 106).
- Сумма двух чисел равна 90, а сумма 75% первого числа и 50% второго числа равна 61. Найдите эти числа.
- Решите уравнение (x – 3)(6x + 5) = (х – 3)(2х – 3).
III. Подведение итогов контрольной работы
- Распределение работ по вариантам и результаты решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).
Обозначения:
+ (число решивших задачу правильно или почти правильно);
± (число решивших задачу со значительными погрешностями);
– (число не решивших задачу);
∅ (число не решавших задачу).
- Типичные ошибки, возникшие при решении задач.
- Наиболее трудные задачи и их разбор (учителем или школьниками, решившими их).
- Разбор всей контрольной работы (вывесить на стенде ответы к заданиям и разобрать наиболее трудные варианты).
IV. Разбор задач (ответы и решения)
Ответы на Вариант 1
№ 1. 1.
№ 2. х = 2.
№ 3. 2.
№ 4. проходит через точку А и не проходит через точку В.
№ 5. первое число 24, второе число 56.
№ 6. х = 2 и х = –4.
Нажмите на спойлер ниже, чтобы увидеть РЕШЕНИЯ.
Нажмите, чтобы открыть РЕШЕНИЯ заданий Варианта 1
Ответы на Вариант 2
№ 1. 2.
№ 2. х = 3.
№ 3. 5.
№ 4. проходит через точку А и не проходит через точку В.
№ 5. первое число 64, второе число 26.
№ 6. х = 3 и х = –2.
Нажмите, чтобы открыть РЕШЕНИЯ заданий Варианта 2
Вы смотрели: Итоговая контрольная работа по алгебре за курс 7 класса с ответами и решениями по УМК Макарычев (Просвещение). Поурочное планирование по алгебре для 7 класса. Урок 101. Контрольная работа по теме «Обобщение и систематизация знаний учащихся». Алгебра 7 класс Макарычев Итоговая контрольная работа + ОТВЕТЫ и РЕШЕНИЯ.
Смотреть Список контрольных по алгебре в 7 классе по УМК Макарычев
Представленный материал является итоговой работой учащихся, оканчивающих 8 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.
Представленный материал является итоговой работой учащихся, оканчивающих 7 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.
Просмотр содержимого документа
«Экзаменационная работа по алгебре за курс 7 класса»
Итоговый тест по математике, 7 класс в формате ОГЭ
Работа состоит из двух частей. Первая часть — базовая, в ней содержатся задания, по основным темам 7 класса. Вторая часть – задания продвинутого уровня для учащихся с более высоким уровнем подготовки.
За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Во второй части работы около каждого задания указано количество баллов, которые засчитываются в рейтинговую оценку ученика при верном выполнении этого задания.
Работа состоит из двух частей и содержит 11 заданий.
На выполнение работы даётся 45 мин.
Тест выполняется на бланке ответов.
Для оценивания результатов выполнения работы применяются два количественных показателя: отметки «2», «3», «4», или «5» и рейтинг – сумма баллов за верно выполненные задания.
Оценка «2» выставляется, если ученик набрал менее 6 баллов.
Отметка «3» выставляется за 6 — 8 баллов.
Отметка «4» выставляется, если набрано от 9 до 12 баллов.
Для получения отметки «5» необходимо набрать 13 — 16 баллов.
С критериями оценивания и структурой работы необходимо ознакомить учащихся до проведения итоговой работы.
Инструкция для учащегося
Работа состоит из двух частей и содержит 11 заданий.
В каждом задании первой части только ОДИН верный ответ.
На выполнение работы даётся 45 мин.
Первая часть теста выполняется на бланке ответов. Необходимо указать только ответ.
Вторая часть выполняется на обороте бланка ответов. Нужно записать решение и ответ.
Критерии оценивания
Оценка «2» выставляется, если ученик набрал менее 6 баллов.
Отметка «3» выставляется за 6 — 8 баллов.
Отметка «4» выставляется, если набрано от 9 до 12 баллов.
Для получения отметки «5» необходимо набрать 13 — 16 баллов.
Вариант 1
1. Упростите 5(2а + 1) – 3
|
А |
5а + 2 |
Б |
10а — 2 |
В |
2а +10 |
Г |
10а + 2 |
2. Вынесите общий множитель за скобки 
|
А |
|
Б |
|
В |
|
Г |
|
3. Упростите выражение: 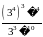
|
А |
81 |
Б |
27 |
В |
-27 |
Г |
9 |
4. Упростите выражение 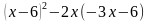
|
А |
|
Б |
|
В |
|
Г |
|
5. Решите уравнение: 
|
А |
3 |
Б |
|
В |
|
Г |
|
6. Боковая сторона равнобедренного треугольника на 8 см меньше основания. Найдите стороны треугольника, если известен периметр треугольника 44 см.
|
А |
20 см, 12 см, 12 см |
Б |
12 см, 20 см, 20 см |
В |
10 см, 6 см, 6 см |
Г |
10 см, 10см, 6 см |
7. Представьте многочлен в виде произведения 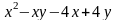
|
А |
(х+ у)(х – 4) |
Б |
(х – у)(х – 4) |
В |
(х – у)(х + 4) |
Г |
(х + у)(х + 4) |
8. Вычислите координаты точки пересечения прямых 2х + 3у = – 12 и 4х – 6у = 0
|
А |
(3; – 2) |
Б |
(– 3; 2) |
В |
(– 3; – 2) |
Г |
( 3; 2) |
Часть 2.
9. (2 балла) Решите уравнение: 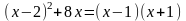
10. (3 балла) Решите систему уравнений: 
11. (3 балла) Решите задачу: Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.
Бланк ответов для 1 части
|
Фамилия |
класс |
вариант |
|
№ задания |
Ответ |
Комментарий (исправление ошибочных ответов) |
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Задания 2 части выполняются на обратной стороне бланка ответов
Ответы
|
Вариант 1 |
|
|
Часть 1 |
|
|
1 |
10а + 2 |
|
2 |
|
|
3 |
27 |
|
4 |
|
|
5 |
|
|
6 |
20 см, 12 см, 12 см |
|
7 |
(х – у)(х – 4) |
|
8 |
(– 3; – 2) |
|
Часть 2 |
|
|
9 |
– 1,25 |
|
10 |
(– 7; 3) |
|
11 |
120⁰ |
Решение второй части:
1 вариант
9. 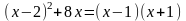



10. 
Если то
Ответ: (– 7; 3)
11. Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.
Пусть градусная мера меньшего из углов равна х, тогда градусная мера большего равна 2х. Сумма смежных углов равна .
х = , Ответ: 120⁰
Рекомендуется вначале прочитать конспекты уроков по алгебре за 7 класс (учебник Макарычева Ю.Н.) В тесте 20 вопросов, из которых четыре — повышенной сложности (ввод ответа с клавиатуры). Нет ограничения по времени. В случае явно плохих результатов (меньше 15% правильных ответов) тестирование по теме «Алгебра 7: ИТОГОВЫЙ ТЕСТ (Макарычев Ю.Н.)» заканчивается досрочно! Неудовлетворительная оценка выставляется, если правильных ответов меньше 50% ! Автор вопросов теста: Л.И.Мартышова. Вернуться на страницу «Алгебра 7 класс».
1. 1-я часть. Первые 16 вопросов с выбором одного правильного ответа из всех предложенных с проверкой правильного ответа сразу.
Решите уравнение 5у – 3,5 = 2у + 5,5.
2.
Даны прямые a, b, с, d, заданные, соответственно, уравнениями
Укажите пару параллельных прямых.
3.
Упростите выражение –За5b2 * (7а3)2.
147а10b2
–21а10b2
–147a11b2
21а11b2
4.
Выполните умножение (За – b)(2b + 4а).
12a2 – 2ab – 2b2
6ab – 4b
12a2 + 2ab – 2b2
баb – 2b2
5.
Преобразуйте в многочлен (4у – 5х)2.
16y2 – 20ху + 25x2
16y2 – 40xу + 25x2
4y2 – 25x2
16y2 – 25x2
6.
Выясните, на сколько медиана ряда 7, 3, 4, 3, 8, 8, 3, 12, 17, 2 больше его моды.
7.
Упростите выражение 3х(3x2 + 1) – (х – 3)(х + 3) – 9(х3 + 1).
3x + x2
x2 – 3
3x – 1
3x – x2
8.
Решите уравнение 7,5 – 2х = 5x – 6,5.
9.
Даны прямые а, b, с, d, заданные, соответственно, уравнениями
Укажите пару параллельных прямых.
10.
Упростите выражение –8x6y * (2x3)5.
–16x14у
–16x21у
256x21у
–256x21у
11.
Выполните умножение (х – 5у)(3у + 2х).
2x2 – 15y2
2x2 – 13xу – 15y2
7 ху
2x2 – 7xу – 15y2
12.
Преобразуйте в многочлен (5b – 7a)2.
25b2 – 49a2
25b2 – 35ab + 49a2
5b2 – 35ab + 7a2
25b2 – 70аb + 49a2
13.
Выясните, на сколько размах ряда 7, 2, 4, 2, 3, 2, 8, –6, 8, –2 больше его медианы.
14.
Упростите выражение (4 – у)(4 + у) – 2у(2y2 – 1) + 4(y3 – 4).
y2 + 2y
y2 – 2y
2y + y2
2y – y2
15.
Решите систему уравнений

29/7; –29/7
–2/7; 2/7
29/7; –2/7
2/7; –29/7
16.
График линейной функции пересекает ось координат в точках (–3; 0) и (0;6). Задайте эту функцию формулой.
17. 2-я часть. Последние 4 вопроса повышенной сложности. Напечатайте свой ответ в пустое поле. Правильный ответ будет показан в конце теста.
Решите систему уравнений
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.
18. Решите уравнение 5y2 – 2у = 0.
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.
19. Найдите два последовательных чётных числа, квадраты которых отличаются на 724.
Ответ: .
Примечание: разделитель между двумя числами — точка с запятой.
20.
Решите систему уравнений

Ответ: .
Примечание: разделитель между двумя числами — точка с запятой; разделитель целой и дробной части числа — запятая.






 3
3