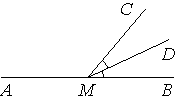
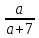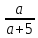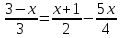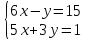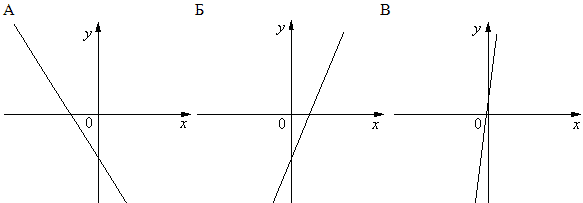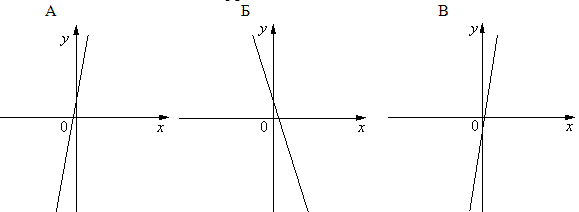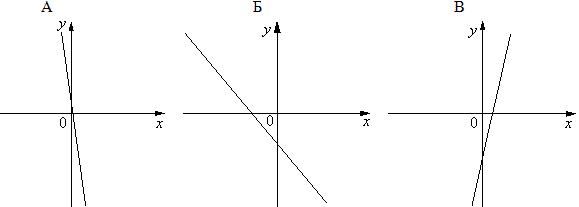Пояснительная записка
Работа содержит 16 заданий курса алгебры и геометрии .
Каждый из двух вариантов содержит две части.
Часть 1 — 12 заданий базового уровня
Часть 2 — 4 задачи высокого уровня, где требуется написать развернутое решение.
Критерии оценивания: За каждый верный ответ 1-й части начисляется 1 балл, за каждое верное решение задачи 2-й части – 2 балла. Максимальное количество баллов – 20. Оценка ставится в зависимости от набранных баллов:
|
Баллы |
Оценка |
|
0-6 |
2 |
|
7-10 |
3 |
|
11-15 |
4 |
|
16-20 |
5 |
Вариант № 1
Часть 1
1. Вычислите (32)4 : (35 × 32)
2. Выполните умножение: (с – 5) (c+1)
3. Решением системы уравнений: является пара чисел:
а) (2; 3); б) (- 2; 3); в) (2; — 3); г) (- 2; — 9); д) (- 2; 9).
4. Решите уравнение 3(5 – 2х) – 4 = 4 – 5х
5. Решите систему линейных уравнений:
6. Постройте график функции у=2х+2.
7. Упростите выражение (х – 2)2 + (х – 1)(х +1 )
8. Два угла треугольника равны 300 и 530. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, АВ=5см. Найдите ВС.
10. Дано: Найдите:
.
C
O
B
11. Выберите верное утверждение:
1. Если при пересечении двух прямых секущей сумма накрест лежащих углов равна 180°,то такие прямые параллельны.
2. Если угол равен 47°, то смежный с ним равен 153°.
3. Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и двум прилежащим углам другого треугольника, то такие треугольники равны.
4. Через любые две точки проходит бесконечно много прямых.
12. В треугольнике АВС АВ=ВС, ВЕ – медиана треугольника. АВЕ = 400. Найти ∠ АВС.
Часть 2
13.Решите уравнение: х2 + 4х+3=0
14. Расстояние между двумя пунктами по реке равно 80 км. Это расстояние лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч. Найдите собственную скорость лодки и скорость течения реки.
15. Дано: Найти:
m
n
1
2
3
4
A
C
B
16. В треугольнике СКЕ стороны СЕ и КE равны, биссектрисы СМ и КН пересекаются в точке А. Докажите, что треугольники КАМ и САН равны.
Вариант № 2
Часть 1
1. Вычислите 26 * (22)5 : 213
2. Выполните умножение: (а – 3) (а + 4)
3. Решением системы уравнений: является пара чисел:
а) (5; 2); б) ( 5; — 2); в) (- 5; — 2); г) (- 5; — 7); д) (5; — 7).
4. Решите уравнение 6(4 – х) + 4х = 3+х
5. Решите систему уравнений:
6. Постройте график функции у= -2х-2.
7. Упростите выражение: ( х + 3)2 + (х – 1) (х +1)
8. Два угла треугольника равны 400 и 380. Найдите градусную меру третьего угла этого треугольника.
9. В треугольнике АВС А=900,
В=600, ВС=12см. Найдите АВ.
10. Дано: Найдите:
.
C
O
B
A
11. Выберите верное утверждение:
1. Если две прямые параллельны третьей, то они пересекаются.
2. В равнобедренном треугольнике медиана, проведенная к боковой стороне, является высотой и биссектрисой.
3. Если при пересечении двух прямых секущей сумма соответственных углов равна 180°,то такие прямые параллельны.
4. Катет прямоугольного треугольника, лежащий против угла в 30°, равен половине гипотенузы.
12. В треугольнике АВС АВ=ВС, ВК –высота треугольника. АВС = 1300. Найти ∠ КВС.
Часть 2
13.Решите уравнение: х2 – 4х+3=0
14.Теплоход 120 км проходит за 5 ч против течения реки и 180 км за 6 ч по течению. Найдите скорость течения реки и собственную скорость теплохода.
15. Дано: Найти:
A
B
C
b
a
1
2
3
4
16. В равнобедренном треугольнике КЕС с основанием СК медианы СМ и КН пересекаются в точке А. Докажите, что треугольник КАС – также равнобедренный.
Экзамен по математике в 7 классе
Данный материал предназначен для проведения итоговой аттестации по
математике(алгебра и геометрия) за курс 7 класса. Составлен на основе примерной
программой общеобразовательных учреждений, составитель: Т.А.Бурмистрова и
учебников «Алгебра 7 класс» авт. Макарычев Ю.Н. др. — Просвещение, 2013 г. и
«Геометрия 7—9» авт. Атанасян Л.С. и др.— Просвещение, 2013 г.
Инструкция по выполнению работы
Работа состоит из двух частей и содержит 16 заданий.
Часть 1 содержит 11 заданий базового уровня сложности(9 заданий по
алгебре и 2 задания по геометрии), предусматривающих следующие формы ответа:
задания с выбором ответа из четырех предложенных (5 заданий), задания с кратким
ответом (5 задания), 1 задание на соответствие.
Часть 2 содержит 5 задания повышенного уровня сложности (3 задания по
алгебре и 2 задания по геометрии), требующих развернутого ответа (с записью
решения). Задания во второй части располагаются по нарастанию сложности.
На проведение экзамена отводится 90 минут.
Справочная литература, калькуляторы, мобильные телефоны на экзамене не
используются. Разрешается использовать таблицу квадратов двузначных чисел.
Оценка выполнения отдельных заданий и работы в целом
За каждое верно выполненное задание первой части учащемуся начисляется 1
балл.
Задания второй части имеют разный вес в зависимости от их относительной
сложности в работе. Задания 12—13 оцениваются по 2 балла каждое, № 14—15 по 3
балла; №16 оценивается в 4 балла. При их оценке используются специально
разработанные критерии, в соответствии с которыми учащийся, демонстрирующий
умение решить ту или иную задачу, получает установленный балл, или балл, на 1
меньше установленного. Общий балл формируется путем суммирования баллов,
полученных за выполнение первой и второй частей работы.
Схема формирования общего балла
Максимальное
количество баллов за
выполнение заданий
части 1
Максимальное количество баллов за
выполнение заданий части 2
Шкала перевода общего балла в школьную отметку
Отметка по
пятибалльной
шкале
Ключи и критерии оценки заданий Части 2
х+12=1,5(х-3)
Ответ: 42 куста
4х—8=2(х+8)
Ответ: 12 м., 48
марок
Ответ: 10 дней
Критерии оценки выполнения задания
Ход решения верный, получен верный ответ.
Ход решения верный, но допущена одна вычислительная ошибка, в
результате которой возможен неверный ответ.
Другие случаи, не соответствующие указанным критериям.
Комментарий: ответ без решения не принимается и оценивается в 0 баллов.
№13
Критерии оценки выполнения задания
Ход решения верный, получен верный ответ.
Ход решения верный, но допущена одна вычислительная ошибка, в
результате которой возможен неверный ответ.
Другие случаи, не соответствующие указанным критериям.
Критерии оценки выполнения задания
Ход доказательства верный. Все его этапы обоснованы с помощью теорем,
свойств, признаков и т.д.
Ход доказательства верный, но не для всех этапов указано его обоснование.
Дано доказательство без ссылок на геометрические утверждения.
Другие случаи, не соответствующие указанным критериям.
Критерии оценки выполнения задания
Ход решения задачи верный. Составлено и верно решено уравнение.
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода решения. В
результате этой ошибки возможен неверный ответ.
Составлено верное уравнение. Решение не выполнено.
Другие случаи, не соответствующие указанным критериям.
Критерии оценки выполнения задания
Ход решения задачи верный. Составлено и верно решено уравнение. Дан
ответ на вопрос задачи.
Уравнение составлено и верно. Ответ на вопрос задачи не найден и не
указан.
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода решения. В
результате этой ошибки возможен неверный ответ.
Составлено верное уравнение. Решение не выполнено.
Другие случаи, не соответствующие указанным критериям.
Экзаменационная работа по математике за курс 7 класса
2014-2015 учебный год
Ученика(цы) 7__ класса_____________________________________
Вариант 1
Часть 1
1. Найдите корень уравнения
Ответ ______________
2. Упростите выражение .
1) 2) 3) 4)
3. Выберите выражение, тождественно равное выражению .
1) 2) 3) 4)
4. Какая из данных функций не является прямой пропорциональностью:
1) 2) 3) 4)
5.Найдите значение выражения .
Ответ _____________________
6.Возведите в степень выражение .
1) 2) 3) 4)
7. Преобразуйте выражение в многочлен.
1) 3)
2) 4)
8. Каждому аргументу функции приведите в соответствие его значение.
А) –5 Б) 6 В)
1) 13 2) –20 3) –4 4) –5
9. Найдите 30% от числа 90.
Ответ____________________
10. В равнобедренном треугольнике АВС с основание АС угол В равен 42°. Найдите два
других угла треугольника АВС.
Ответ __________________
11. Один из смежных углов равен
. Сколько градусов составляет второй угол?
Ответ__________________
Часть 2
12. Упростите выражение (2 балла)
13. Решите систему уравнений . (2 балла)
.)2()2)(8(2)8(
22
−+−+−+ aaaa
14. По данным рисунка докажите, что а||b, если c —секущая . Перечертите рисунок, запишите
дано, доказать, доказательство. (3 балла)
а
b
c
15. Периметр равнобедренного треугольника равен 54 см. его боковая сторона в 2,5 раза
больше основания. Вычислите стороны треугольника.(3 балла)
16. Решите задачу.
На первом участке на 9 кустов смородины больше, чем на втором. Если со второго участка
пересадить на первый участок 3 куста, то на первом участке станет в 1,5 раза больше кустов
смородины, чем на втором. Сколько кустов смородины на первом участке?(4 балла)
Экзаменационная работа по математике за курс 7 класса
2014-2015 учебный год
Ученика(цы) 7__ класса_____________________________________
Вариант 2
Часть 1
1. Найдите корень уравнения .
Ответ ____________________
2. Упростите выражение .
1) 2) 3) 4)
3. Выберите выражение, тождественно равное выражению .
1) 2) 3) 4)
4. Какая из данных функций не является прямой пропорциональностью:
1) 2) 3) 4)
5. Найдите значение выражения .
Ответ______________________
6. Возведите в степень выражение .
1) 2) 3) 4)
7. Преобразуйте выражение в многочлен.
1) 3)
2) 4)
8. Каждому аргументу функции приведите в соответствие его значение.
А) –4 Б) 6 В) 7
1) 0 2) 11 3) –11 4) 1
9. Найдите 50% от числа 76.
Ответ_____________________
10. Два угла треугольника равны
. сколько градусов составляет третий угол
треугольника?
Ответ_____________________
11. Выберите правильное утверждение:
1. Две прямые параллельны, если накрест лежащие углы равны.
2. Две прямые параллельны, если вертикальные углы равны.
3. Две прямые параллельны, если односторонние углы равны.
4. Две прямые параллельны, если сумма соответственных углов равна
Часть 2
12. Упростите выражение (2 балла)
13. Решите систему уравнений (2 балла).
14. По данным рисунка докажите, что а||b, если c —секущая. Перечертите рисунок, запишите
дано, доказать, доказательство. (3 балла)
а
b
с
15. Один острый угол прямоугольного треугольника на 32° больше другого. Найдите больший
острый угол. Ответ дайте в градусах. (3 балла)
16. Решите задачу.
У Миши в 4 раза больше марок, чем у Андрея. Если Миша отдаст Андрею 8 марок, то у
него станет марок вдвое больше. Сколько марок у каждого мальчика? (4 балла)
).2)(53()1)(12()1)(13( −+−−−++− nnnnnn
Экзаменационная работа по математике за курс 7 класса
2014-2015 учебный год
Ученика(цы) 7__ класса_____________________________________
Вариант 3
Часть 1
1. Найдите корень уравнения .
Ответ __________________
2. Упростите выражение .
1) 2) 3) 4)
3. Выберите выражение, тождественно равное выражению .
2) 2) 3) 4)
4. Какая из данных функций не является прямой пропорциональностью:
1) 2) 3) 4)
5. Найдите значение выражения .
Ответ_________________
6. Возведите в степень выражение .
1) 2) 3) 4)
7. Преобразуйте выражение в многочлен.
1) 3)
2) 4)
8. Каждому аргументу функции приведите в соответствие его значение.
А) –4 Б) 5 В)
1) –27 2) –29 3) 34 4) 0
9. Найдите 25% от числа 36.
Ответ _________________
10. В равнобедренном треугольнике АВС с основание АС угол А равен 42°. Найдите два
других угла треугольника АВС.
Ответ __________________
11. Один из смежных углов равен
. Сколько градусов составляет второй угол?
Ответ__________________
Часть 2
12. Упростите выражение (2 балла)
13. Решите систему уравнений .(2 балла)
14. По данным рисунка докажите, что а||b, если c —секущая . Перечертите рисунок,
запишите дано, доказать, доказательство. (3 балла)
а
b
с
15. Найдите углы треугольника АВС, если угол А на
меньше угла В и в 3 раза меньше угла
С. (3 балла)
16. Решите задачу.
Чтобы сдать в срок книгу в библиотеку, ученик должен был читать ежедневно по 40 страниц,
но он читал в день на 15 страниц меньше и сдал книгу на 6 дней позже срока. За сколько дней
ученик должен был прочесть книгу? (4 балла)
.)9()9)(7(2)7(
22
−+−−−− yyyy
Экзаменационная работа по математике за курс 7 класса
2014-2015 учебный год
Ученика(цы) 7__ класса_____________________________________
Вариант 4
Часть 1
1. Найдите корень уравнения .
Ответ __________________
2. Упростите выражение .
1) 2) 3) 4)
3. Выберите выражение, тождественно равное выражению .
3) 2) 3) 4)
4. Какая из данных функций не является прямой пропорциональностью:
1) 2) 3) 4)
5. Найдите значение выражения .
Ответ_______________________
6. Возведите в степень выражение .
1) 2) 3) 4)
7. Преобразуйте выражение в многочлен.
1) 3)
2) 4)
8. Каждому аргументу функции приведите в соответствие его значение.
А) –4 Б) 1 В)
1) –2 2) 2 3)13 4) 11
9.Найдите 30% от числа 60.
Ответ______________________
10. Два угла треугольника равны
. Сколько градусов составляет третий угол
треугольника?
Ответ_____________________
11. Выберите правильное утверждение:
1. Если односторонние углы равны, то две прямые параллельны.
2. Если соответственные углы равны, то две прямые параллельны.
3. Если сумма соответственных углов равна
, то две прямые параллельны.
4. Если сумма накрест лежащих углов равна
, то две прямые параллельны.
Часть 2
12. Упростите выражение (2 балла)
13. Решите систему уравнений .(2 балла)
14. По данным рисунка докажите, что а||b, если c —секущая . Перечертите рисунок, запишите
дано, доказать, доказательство. (3 балла)
а
b
С
15. В равнобедренном треугольнике АВС, с основанием АС, проведена медиана ВD. Найдите
углы треугольника ВDС, если угол АВD=
. (3 балла)
16. Решите задачу.
Если к задуманному числу прибавить 7, полученную сумму умножить на 3 и из произведения
вычесть 47, то получится задуманное число. Какое число задумано?
(4 балла)
).3)(62()1)(43()2)(15( −++−+−−− yyyyyy
Переводной экзамен по математике
7 класс
Вариант 0701
Общее время работы – 90 минут
Характеристика работы:
Всего в работе 15 заданий – базового уровня.
Работа состоит из двух модулей: «Алгебра» и «Геометрия».
Советы и указания по выполнению работы:
Начать советуем с заданий, которые вызывают у Вас меньше затруднений, затем переходит к другим. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы.
Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Ответы на вопросы 4, 7, 8, 9 запишите в виде последовательности букв, без запятых и пробелов.
Оценивание работы:
Задания с 1 по 5 оцениваются по 1 баллу.
Задания с 6 по 9 оцениваются по 2 балла.
Задания с 10 по 15 оцениваются по 3 балла.
Баллы, полученные за верно выполненные задания, суммируются.
Для успешной сдачи переводной работы необходимо набрать не менее 16 баллов.
Часть А
Модуль «Алгебра»
|
Ответы на задания с 1 по 9 впишите в БЛАНК №1 |
-
Укажите все значения переменной a, при которых имеет смысл выражение
-
a – любое число, кроме 0;
-
a – любое число, кроме – 7;
-
a – любое число;
-
a – любое число, кроме 0 и – 7.
-
Укажите уравнение, корень которого – число 1.
-
| x | = — 1;
-
(x – 1)(x + 1) = 1;
-
(x + 1)2 = 0;
-
(x + 3)(x – 4) = — 12.
-
Укажите одночлен стандартного вида.
-
– 5ac2b · 1,6;
-
– 8ac2b;
-
– 7acbc;
-
– 5abc · 1,6c
-
Сопоставьте две части формулы:
|
1) |
(a + b)2 = |
А) |
(a + b)(a2 – ab + b2) |
|
2) |
a3 – b3 = |
Б) |
a2 + 2ab + b2 |
|
3) |
(a – b)3 = |
В) |
(a – b)(a2 + ab + b2) |
|
4) |
a3 + b3 = |
Г) |
a3 – 3a2b + 3ab2 – b3 |
Модуль «Геометрия»
-
Градусная мера одного из смежных углов в три раза больше другого. Найдите градусную меру большего из смежных углов.
-
122º;
-
135º;
-
98°;
-
нет верного ответа.
-
Градусные меры углов треугольника относятся как 2: 3 : 7. Найдите градусную меру меньшего из углов этого треугольника.
-
10°;
-
20º;
-
30º;
-
40º
-
Сопоставьте понятие с верным определением:
|
1) |
Смежные углы — |
А) |
углы, лежащие по одну сторону от секущей внутри этих параллельных прямых |
|
2) |
Соответственные углы — |
Б) |
равные углы, лежащие по одну сторону от секущей параллельные прямые |
|
3) |
Односторонние углы — |
В) |
углы, имеющие общую сторону, их сумма равна 180° |
-
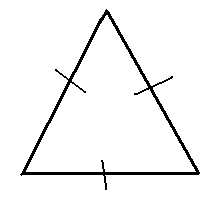
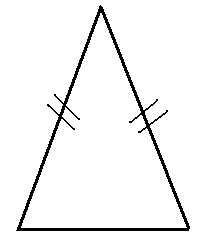
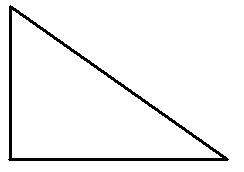
Сопоставьте треугольник с верным названием:
|
1) |
|
А) |
прямоугольный |
|
2) |
|
Б) |
равносторонний |
|
3) |
|
В) |
тупоугольный |
|
4) |
|
Г) |
равнобедренный |
-
Сопоставьте название с верным определением:
|
1) |
Медиана — … |
А) |
отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны |
|
2) |
Высота — … |
Б) |
отрезок, соединяющий вершину треугольника с серединой противоположной стороны |
|
3) |
Биссектриса — … |
В) |
перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону |
Часть Б
|
Ответы с ПОЛНЫМ решением на задания с 10 по 15 впишите в БЛАНК №2 |
Модуль «Алгебра»
-
Разложите на множители
(5х + у)2 – (х – 5у)2
-
Решите уравнение: 4(х + 1) = 15х – 7(2х + 5)
-
Решите уравнение:
-
Решите систему методом подстановки:
Модуль «Геометрия»
-
На боковых сторонах равнобедренного треугольника АВС отложены равные отрезки АМ и АК. Докажите, что ΔABC = ΔABD.
-
В треугольнике АВС с углом С равным 60° проведена биссектриса СМ. Найдите СМ и расстояние от точки М до стороны ВС, если расстояние от точки М до стороны АС = 25 см.
Переводной экзамен по математике
7 класс
Вариант 0702
Общее время работы – 90 минут
Характеристика работы:
Всего в работе 15 заданий – базового уровня.
Работа состоит из двух модулей: «Алгебра» и «Геометрия».
Советы и указания по выполнению работы:
Начать советуем с заданий, которые вызывают у Вас меньше затруднений, затем переходит к другим. Для экономии времени пропускайте задание, которое не удается выполнить сразу, и переходите к следующему. Если у Вас останется время, Вы сможете вернуться к пропущенным заданиям.
Все необходимые вычисления, преобразования и т.д. выполняйте в черновике. Записи в черновике не учитываются при оценивании работы.
Рекомендуем внимательно читать условие и проводить проверку полученного ответа.
Ответы на вопросы 4, 7, 8, 9 запишите в виде последовательности букв, без запятых и пробелов.
Оценивание работы:
Задания с 1 по 5 оцениваются по 1 баллу.
Задания с 6 по 9 оцениваются по 2 балла.
Задания с 10 по 15 оцениваются по 3 балла.
Баллы, полученные за верно выполненные задания, суммируются.
Для успешной сдачи переводной работы необходимо набрать не менее 16 баллов.
Часть А
Модуль «Алгебра»
|
Ответы на задания с 1 по 9 впишите в БЛАНК №1 |
-
Укажите все значения переменной a, при которых имеет смысл выражение
-
a – любое число;
-
a – любое число, кроме 0;
-
a – любое число, кроме – 5;
-
a – любое число, кроме 0 и – 5.
-
Укажите уравнение, корень которого – число 2.
-
(x – 2)(x + 2) = 2;
-
(x + 2)2 = 0;
-
(x + 4)(x – 1) = 6;
-
| x | = 4.
-
Укажите одночлен стандартного вида.
-
– 4abс · 1,5a2b;
-
– 6ab2a2c;
-
– 4b2a3c · 1,5;
-
– 6b2a3c
-
Сопоставьте две части формулы:
|
1) |
(a + b)3 = |
А) |
(a + b)(a – b) |
|
2) |
(a – b)2 = |
Б) |
(a + b)(a2 – ab + b2) |
|
3) |
a2 – b2 = |
В) |
a3 + 3a2b + 3ab2 + b3 |
|
4) |
a3 + b3 = |
Г) |
a2 – 2ab + b2 |
Модуль «Геометрия»
-
Градусная мера одного из смежных углов в семь раз больше другого. Найдите градусную меру большего из смежных углов.
-
122º;
-
135º;
-
157,5°;
-
нет верного ответа.
-
Градусные меры углов треугольника относятся как 3: 5 : 7. Найдите градусную меру большего из углов этого треугольника.
-
84°;
-
90º;
-
70º;
-
75º
-
Сопоставьте понятие с верным определением:
|
1) |
Вертикальные углы — |
А) |
углы, лежащие по одну сторону от секущей внутри этих параллельных прямых |
|
2) |
Накрест лежащие углы — |
Б) |
углы с общей вершиной, образуемые при пересечении двух прямых так, что стороны одного угла являются продолжением сторон другого |
|
3) |
Односторонние углы — |
В) |
углы, которые лежат во внутренней области по разные стороны от секущей |
-
Сопоставьте треугольник с верным названием:
|
1) |
|
А) |
равносторонний |
|
2) |
|
Б) |
прямоугольный |
|
3) |
|
В) |
тупоугольный |
|
4) |
|
Г) |
равносторонний |
-
Сопоставьте понятие с верным определением:
|
1) |
Середина отрезка — … |
А) |
луч, который исходит из вершины угла и делит угол на две равные части |
|
2) |
Угол — … |
Б) |
точка, равноудаленная от концов отрезка |
|
3) |
Биссектриса угла — … |
В) |
геометрическая фигура, образованная двумя лучами, выходящими из одной точки |
Часть Б
|
Ответы с ПОЛНЫМ решением на задания с 10 по 15 впишите в БЛАНК №2 |
Модуль «Алгебра»
-
Разложите на множители
(х + 3у)2 – (3х –у)2
-
Решите уравнение: 5(х – 3) = 14 – 2(7 – 2x)
-
Решите уравнение:
-
Решите систему методом подстановки:
Модуль «Геометрия»
-
Отрезки АВ и BC пересекаются в точке О, которая является серединой отрезка AD, углы BAO и CDO равны. Докажите, что ΔAОB = ΔDОС.
-
В треугольнике АВС с углом С равным 60° проведена биссектриса СМ. Найдите расстояние от точки М до сторон АС и ВС, если СМ = 20 см.
Итоговый тест по Алгебре 7 класс
Даны основные примеры итогового теста (не все) 7 класс, Алгебра
Математика 7 класс | Автор: Архиполва НМ | ID: 7821 | Дата: 14.3.2016
Помещать страницу в закладки могут только зарегистрированные пользователи
Зарегистрироваться
Вопрос №
1
Упростите выражение -4m + 9n — 7m — 2n.
-3m + 11n
-3m + 7n
11m + 7n
-11m + 7n
Вопрос №
2
Решите уравнение 10у – 13,5 = 2у — 37,5.
6,375
3
-3
4
Вопрос №
3
Упростите выражение с7 : c4 • c.
c в 5 степени
c в 6 степени
c в 4 степени
c в 12 степени
Вопрос №
4
Выполните умножение (3a — b)(2b — 4a).
-12a2 – 10ab – 2b2
-12a2 + 10ab – 2b2
6ab – 2b2
6ab – 4b
Вопрос №
5
Найдите значение выражения (-1)3 – (-2)3 + 52 – 72.
83
33
-16
-17
Вопрос №
6
Выразите у через х в выражении -5х + у = -17.
У = 17 + 5х
У = -5х + 17
У = -17 + 5х
У = 17 — 5х
Вопрос №
7
Какое значение принимает сумма х + у, если х = -2,6; y = -4,4?
-1,8
1,8
7
-7
Вопрос №
8
Составьте выражение по условию задачи: «Турист шел со скоростью b км/ч. Какое расстояние он пройдет за 8 часов?».
8 — b
8 + b
8b
8 : b
Вопрос №
9
В одной системе координат заданы графики функций у = 2х – 4 и у = -3. Определите координаты точки их пересечения.
(1,5; -3)
(1,5; 1)
(0,5; -3)
(-0,5; -3)
Вопрос №
10
Через какую точку проходит график функции у = 3х + 5?
(2; -3)
(1; -2)
(2; 11)
(-2; 11)
1 вариант
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа 0,098; –0,02; 0,09; 0,11. Какой точкой
изображается число 0,09? Запишите номер ответа.
1) А; 2) В; 3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,4; 2) 0,5; 3) 0,6; 4) 0,7.
4. Решите уравнение 2 – 3(2х + 2) = 5 – 4х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b<0; 2) k>0, b<0; 3) k>0,
b>0. В ответе укажите последовательность
цифр.
6. Найдите значение выражения при а = 0,2, b = 1,5.
Запишите ответ.
7. Вычислите: .
Модуль Геометрия
8. Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Смежные углы равны.
2) Любые две прямые имеют ровно одну общую точку.
3) Если угол равен 108°, то вертикальный с ним
равен 108°.
4) Если две стороны и угол между ними одного
треугольника равны соответственно двум сторонам
и углу между ними другого треугольника, то такие
треугольники равны.
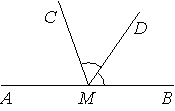
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC=24°.
Найдите угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 68. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. Мотоциклист проехал 19 километров за 15 минут.
Сколько километров он проедет за 18 минут, если
будет ехать с той же скоростью?
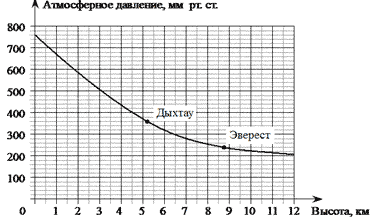
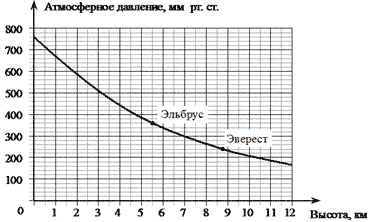
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Дыхтау?
13. На диаграмме показано содержание
питательных веществ в молочном шоколаде.
Определите по диаграмме, содержание каких
веществ превосходит 25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 3 часа,
вернулись обратно через 5 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
3 км/ч, а собственная скорость лодки 6 км/ч?
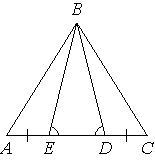
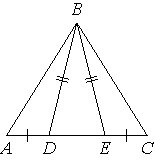
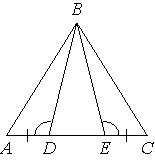
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
углы АDB и BEC равны (см. рисунок).
Оказалось, что отрезки AЕ и CD тоже
равны. Докажите, что
треугольник АВС — равнобедренный.
2 вариант
Часть 1
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа 0,508; 0,85; -0,05; 0,058. Какой точкой
изображается число 0,058? В ответе укажите номер
правильного варианта.
1) А; 2) В;3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,3; 2) 0,4; 3) 0,5; 4) 0,6.
4. Решите уравнение 8 – 5(2х – 3) = 13 – 6х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b>0; 2) k>0, b>0; 3) k>0,
b<0. В ответе укажите последовательность
цифр.
6.Найдите значение выражения при а = 0,3, b =
0,2.Запишите ответ.
7. Вычислите: .
Модуль Геометрия
8.Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Если угол равен 47°, то смежный с ним равен 153°.
2) Если две прямые перпендикулярны третьей
прямой, то эти две прямые параллельны.
3) Через любую точку проходит ровно одна прямая.
4) Если сторона и прилежащие к ней углы одного
треугольника равны соответственно стороне и
прилежащим к ней углам другого треугольника, то
такие треугольники равны.
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC =
48°. Найдите угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 88. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. За 20 минут велосипедист проехал 7 километров.
Сколько километров он проедет за 35 минут, если
будет ехать с той же скоростью?
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Эльбруса?
13. На диаграмме показано содержание
питательных веществ в мороженом. Определите по
диаграмме, содержание каких веществ превосходит
25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 2 часа,
вернулись обратно через 6 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
3 км/ч, а собственная скорость лодки 6 км/ч?
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
отрезки AD и CE равны (см. рисунок).
Оказалось, что отрезки BD и BE тоже
равны. Докажите, что треугольник АВС —
равнобедренный.
3 вариант
Часть 1
Модуль Алгебра
1. Найдите значение выражения .
2. На координатной прямой точками отмечены
числа –0,74; –0,047; 0,07; –0,407. Какой точкой
изображается число ?0,047? В ответе укажите номер
правильного варианта.
1) А; 2) В; 3) С; 4) D.
3. Какое из следующих чисел заключено между
числами и
. Запишите номер
ответа.
1) 0,1; 2) 0,2; 3) 0,3; 4) 0,4.
4. Решите уравнение 11 – 7(х + 2) = 5 – 2х.
5. На рисунке изображены графики функций
вида y = kx+b. Установите соответствие между
графиками функций и знаками коэффициентов k и b.
1) k <0, b<0; 2) k<0, b>0; 3) k>0,
b<0. В ответе укажите последовательность
цифр.
6. Найдите значение выражения при а = 0,5, b =
0,1.Запишите ответ.
7.Вычислите: .
Модуль Геометрия
8. Какие из следующих утверждений верны? Укажите
номера верных утверждений.
1) Если три стороны одного треугольника
соответственно равны трём сторонам другого
треугольника, то такие треугольники равны.
2) Сумма вертикальных углов равна 180о.
3) Через точку, не лежащую на данной прямой,
можно провести прямую, перпендикулярную этой
прямой.
4) Если угол равен 30о, то смежный с ним
равен 60о.
9. На прямой AB взята точка M.
Луч MD — биссектриса угла CMB. Известно,
что DMC=41°. Найдите
угол CMA. Ответ дайте в градусах.
10. Периметр квадрата равен 84. Найдите площадь
этого квадрата.
Модуль Реальная математика
11. Автомобиль проехал 17 километров за 15 минут.
Сколько километров он проедет за 18 минут, если
будет ехать с той же скоростью?
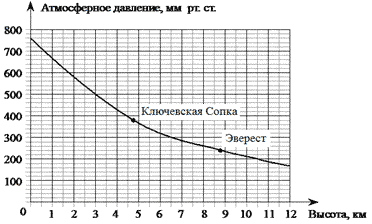
12. На графике изображена зависимость
атмосферного давления от высоты местности над
уровнем моря. По горизонтали указана высота над
уровнем моря в километрах, по
вертикали — атмосферное давление в
миллиметрах ртутного столба. На сколько
миллиметров ртутного столба атмосферное
давление на высоте Эвереста ниже атмосферного
давления на высоте Ключевской Сопки?
13. На диаграмме показано содержание
питательных веществ в сгущённом молоке.
Определите по диаграмме, содержание каких
веществ превосходит 25%.
1. белки
2. жиры
3. углеводы
4. прочее
В ответ запишите номера выбранных вариантов
ответов без пробелов, запятых и других
дополнительных символов.
Часть 2
14. Туристы проплыли на лодке от лагеря
некоторое расстояние вверх по течению реки,
затем причалили к берегу и, погуляв 3 часа,
вернулись обратно через 5 часов от начала
путешествия. На какое расстояние от лагеря они
отплыли, если скорость течения реки равна
2 км/ч, а собственная скорость лодки 8 км/ч?
15. На
стороне АС треугольника АВС выбраны
точки D и E так, что
отрезки AD и CE равны (см. рисунок).
Оказалось, что углы АDB и BEC тоже равны.
Докажите, что треугольник АВС-равнобедренный.
Приложение 1
Приложение 2
Итоговый тест по математике, 7 класс в формате ОГЭ
Работа состоит из двух частей. Первая часть — базовая, в ней содержатся задания, по основным темам 7 класса. Вторая часть – задания продвинутого уровня для учащихся с более высоким уровнем подготовки.
За каждое верно решенное задание первой части учащемуся начисляется 1 балл. Во второй части работы около каждого задания указано количество баллов, которые засчитываются в рейтинговую оценку ученика при верном выполнении этого задания.
Работа состоит из двух частей и содержит 11 заданий.
На выполнение работы даётся 45 мин.
Тест выполняется на бланке ответов.
Для оценивания результатов выполнения работы применяются два количественных показателя: отметки «2», «3», «4», или «5» и рейтинг – сумма баллов за верно выполненные задания.
Оценка «2» выставляется, если ученик набрал менее 6 баллов.
Отметка «3» выставляется за 6 — 8 баллов.
Отметка «4» выставляется, если набрано от 9 до 12 баллов.
Для получения отметки «5» необходимо набрать 13 — 16 баллов.
С критериями оценивания и структурой работы необходимо ознакомить учащихся до проведения итоговой работы.
Инструкция для учащегося
Работа состоит из двух частей и содержит 11 заданий.
В каждом задании первой части только ОДИН верный ответ.
На выполнение работы даётся 45 мин.
Первая часть теста выполняется на бланке ответов. Необходимо указать только ответ.
Вторая часть выполняется на обороте бланка ответов. Нужно записать решение и ответ.
Критерии оценивания
Оценка «2» выставляется, если ученик набрал менее 6 баллов.
Отметка «3» выставляется за 6 — 8 баллов.
Отметка «4» выставляется, если набрано от 9 до 12 баллов.
Для получения отметки «5» необходимо набрать 13 — 16 баллов.
Вариант 1
1. Упростите 5(2а + 1) – 3
|
А |
5а + 2 |
Б |
10а — 2 |
В |
2а +10 |
Г |
10а + 2 |
2. Вынесите общий множитель за скобки
3. Упростите выражение:
4. Упростите выражение 
5. Решите уравнение:
6. Боковая сторона равнобедренного треугольника на 8 см меньше основания. Найдите стороны треугольника, если известен периметр треугольника 44 см.
|
А |
20 см, 12 см, 12 см |
Б |
12 см, 20 см, 20 см |
В |
10 см, 6 см, 6 см |
Г |
10 см, 10см, 6 см |
7. Представьте многочлен в виде произведения
|
А |
(х+ у)(х – 4) |
Б |
(х – у)(х – 4) |
В |
(х – у)(х + 4) |
Г |
(х + у)(х + 4) |
8. Вычислите координаты точки пересечения прямых 2х + 3у = – 12 и 4х – 6у = 0
|
А |
(3; – 2) |
Б |
(– 3; 2) |
В |
(– 3; – 2) |
Г |
( 3; 2) |
Часть 2.
9. (2 балла) Решите уравнение:
10. (3 балла) Решите систему уравнений: 
11. (3 балла) Решите задачу: Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.
Бланк ответов для 1 части
|
Фамилия |
класс |
вариант |
|
№ задания |
Ответ |
Комментарий (исправление ошибочных ответов) |
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
Задания 2 части выполняются на обратной стороне бланка ответов
Ответы
|
Вариант 1 |
|
|
Часть 1 |
|
|
1 |
10а + 2 |
|
2 |
|
|
3 |
27 |
|
4 |
|
|
5 |
|
|
6 |
20 см, 12 см, 12 см |
|
7 |
(х – у)(х – 4) |
|
8 |
(– 3; – 2) |
|
Часть 2 |
|
|
9 |
– 1,25 |
|
10 |
(– 7; 3) |
|
11 |
120⁰ |
Решение второй части:
1 вариант
9.

10. 
Если 

11. Один из смежных углов в 2 раза больше другого. Найдите больший смежный угол.
Пусть градусная мера меньшего из углов равна х, тогда градусная мера большего равна 2х. Сумма смежных углов равна 
х = 
Представленный материал является итоговой работой учащихся, оканчивающих 8 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.
Представленный материал является итоговой работой учащихся, оканчивающих 7 класс о учебнику «Алгебра 8 кл» для общеобразовательных учреждений (Макарычев Ю.Н. и др.: Просвещение, 2013 г)
Назначение итоговой работы – оценить уровень овладения обучающимися программным материалом, учесть полученные результаты при составлении рабочих программ, дифференцируя уровень заданий по содержательным линиям.