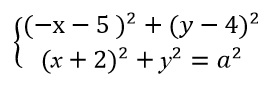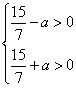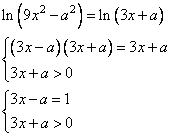Говорят, что задание 18 Профильного ЕГЭ по математике (на числа и их свойства) решить невозможно. Но это не так. Можно научиться! Можно сделать первый шаг – прочитать эту статью и узнать о секретах решения задачи 18.
Еще говорят, что это задача «на смекалку». Но и это не так. Дело не в загадочной «смекалке», а в знании определенных приемов, ключиков, хитрых инструментов. Некоторые из них вы сейчас увидите. Пусть это будет первое знакомство с нестандартными, ни на что не похожими задачами на числа и их свойства.
4. Маша и Наташа делают фотографии. Каждый день каждая девочка делает на одну фотографию больше, чем в предыдущий день. В конце Наташа сделала на 935 фотографий больше, чем Маша.
а) Могло ли это произойти за 5 дней?
б) Могло ли это произойти за 9 дней?
в) Какое максимальное количество фотографий могла сделать Наташа, если Маша в последний день сделала меньше 50 фотографий?
Пусть в первый день Маша делает х фотографий, а Наташа у фотографий.
На второй день: Маша , а Наташа
фотографию.
В n-ный день Маша сделает , а Наташа
фотографию.
По условию, число фотографий, которые ежедневно делает Маша, образует арифметическую прогрессию с разностью 1. Число Наташиных фотографий также образует арифметическую прогрессию. Вспомним формулу суммы арифметической прогрессии:
За n дней Маша сделает , а Наташа
фотографий. Разность этих величин
Мы получили, что .
а) Случай n = 5 возможен. Это значит, что то . Каждый день Наташа делала на 187 фотографий больше, чем Маша.
б) Случай n = 9 невозможен. Уравнение не имеет целых решений, поскольку 935 не делится на 9.
Это один из приемов решения нестандартных задач. Часто мы получаем уравнение с двумя (тремя, четырьмя…) переменными. Помогает то, что эти переменные – натуральные. Мы внимательно смотрим на полученное уравнение. Если его левая часть положительна, то и правая должна быть положительна. Если левая четна, то и правая должна быть четна. Если левая часть кратна 9, то и правая часть должна быть кратна 9.
в) В последний день Маша сделала меньше 50 фотографий.
Еще один лайфхак. В задачах на числа и их свойства строгие неравенства лучше заменять нестрогими:
.
Найдем, какое максимальное количество фотографий могла при этом сделать Наташа.
У нас есть единственное уравнение:
. Поскольку
– целое, n должно быть делителем числа 935. Разложим 935 на множители: 935 = 5∙11∙17.
Числа 1, 5, 11, 17, 55, 85, 187, 935 – делители числа 935.
При этом невозможно, поскольку по условию
.
Составим таблицу для значений n, равных 1, 5, 11 и 17.
| Количество фотографий,сделанных Наташей за |
||||
|---|---|---|---|---|
| 1 | 935 | |||
| 5 | 187 | |||
| 11 | 85 | |||
| 17 | 55 |
Количество фотографий, которые могла сделать Наташа, не превышает 1632. Если , то
.
Ответ: 1632.
Посмотрите, как мы действовали. Сначала сделали «заготовку» для всех трех пунктов. Да, такой прием тоже часто применяется в нестандартных задачах.
Получили уравнение . Из одного этого уравнения (как в сказке про суп из топора) мы получаем всё, что нам нужно. В пункте (в) есть перебор вариантов, но не хаотичный, а умный. Иначе перебирать варианты можно бесконечно.
Вот еще одна задача на числа и их свойства:
2. Группу школьников нужно перевезти из летнего лагеря одним из двух способов: либо двумя автобусами типа A за несколько рейсов, либо тремя автобусами типа В за несколько рейсов, причём в этом случае число рейсов каждого автобуса типа B будет на один меньше, чем рейсов каждого автобуса типа А. В каждом из случаев автобусы заполняются полностью. Какое максимальное количество школьников можно перевезти при указанных условиях, если в автобус типа B входит на 7 человек
меньше, чем в автобус типа A?
Помните, как мы решали текстовые задачи? Мы записывали данные задачи в таблицу. Сделаем так же.
| Тип автобуса | Сколько автобусов | Сколько рейсов | Сколько человек в автобусе |
|---|---|---|---|
По условию, количество школьников, которое надо перевезти, одно и то же.
Оно равно . Отсюда
.
Выразим одну из переменных через другую:
Мы видим, что переменная n и в числителе, и в знаменателе дроби. Оценить m трудно, правда? Чтобы проще было это сделать, выделим в дроби целую часть.
Еще один прием решения нестандартных задач – выделение целой части. Это помогает сделать оценку какой-либо величины.
.
Поскольку m – натуральное число (количество школьников в автобусе типа В), выражение в правой части также должно быть целым положительным. Значит, 42 делится на без остатка.
Выпишем делители числа 42. Это 1; 2; 3; 6: 7; 14; 21; 42.
Заполним таблицу. Значения m вычисляем по формуле , а общее количество школьников – как
.
| Общее количество школьников | |||
|---|---|---|---|
| 1 | 4 | 56 | 504 |
| 2 | 5 | 35 | 420 |
| 3 | 6 | 28 | 420 |
| 6 | 9 | 21 | 504 |
| 7 | 10 | 20 | 540 |
| 14 | 17 | 17 | 816 |
| 21 | 24 | 16 | 1104 |
| 42 | 45 | 15 | 1980 |
Наибольшее количество школьников, которое можно перевезти в условиях задачи, равно 1980.
Конечно, мы выбирали довольно простые задачи. И конечно, есть и другие приемы их решения.
Например, метод «Оценка плюс пример». Мы разбираем множество нестандартных задач на наших интенсивах в ЕГЭ-Студии, а также на Онлайн-курсе.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Профильный ЕГЭ по математике, задание 18. Секреты решения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Мы знаем, что в ЕГЭ по математике вторая часть кажется значительно сложнее первой. Но особенно много вопросов вызывает задание №18. Многие думают, что решить его под силам только олимпиадникам.
Но так ли это?
Давай попробуем разобраться, почему эта задача кажется такой необычной и сложной. А еще разберемся, как ее решать!
Формат задачи
По формату задача абсолютно стандартная. Она состоит из нескольких пунктов, за каждый из которых можно получить баллы. Давай посмотрим подробнее:
Пункт А
В этой части задачи в большинстве случаев надо дать ответ на вопрос о возможности или невозможности какой-то ситуации. Если ты отвечаешь, что ситуация возможна, значит, ты можешь подтвердить ее каким-то примером.
Кстати, чаще всего эта часть решается довольно легко. Найти пример не составит труда.
Главное — не торопиться и внимательно прочитать условие задачи!
Пункт Б
Этот пункт очень схож с пунктом А. Но очень часто решение пункта Б сводится к тому, что ситуация невозможна. И тебе остается только это доказать. Но не забудь, что невозможность ситуации доказывается в общем виде, а не на конкретном примере.
А как доказать? Обычно такое доказывается с помощью рассмотрения оценок, делимостей, ограничений и т.д.
Но это только звучит сложно и страшно. Если немного потренироваться, ты научишься очень быстро решать такие задачи.
Пункт В
Последний пункт чуть-чуть посложнее, но и получить за него можно 2 балла! С наибольшей вероятностью в пункте В нужно будет найти наименьшее или наибольшее значение величины, связанной с условием задачи.
Тебе нужно будет сделать оценку на искомую величину и привести пример, когда эта оценка выполняется. За каждый правильно выполненный шаг ты получишь по 1 баллу.
Алгоритм решения задачи
К сожалению, эту задачу не получится решить, подобрав типовой алгоритм. Тут придется поразмышлять. Но от этого интереснее!
Мы подготовили для тебя подборку тем, которые пригодятся тебе для решения №18.
Разбирая задание №18, ты потренируешь свой мозг и научишься решать нестандартные задачи.
Если ты переживаешь, оставь эту задачку напоследок. Решишь ее, когда останется время.
Ну а раз ты здесь, значит, ты хочешь получить высокие баллы и максимально в этом заинтересован!
И мы знаем, что у тебя все получится!
2022-03-21 17:59
ЕГЭ
Математика
Задание № 18 варианта КИМ ЕГЭ по математике профильного уровня
Задача с параметром – для обычного школьника одна из самых сложных задач варианта КИМ ЕГЭ: в программах по математике для общеобразовательных школ (за исключением профильных и специализированных классов, школ и лицеев) таким задачам либо не уделяется должного внимания, либо они не рассматриваются вовсе. Несмотря на это, знание набора методов и подходов к решению таких задач и определенная практика их решения позволяют продвинуться в решении задачи с параметром достаточно далеко и если уж не решить ее полностью, то хотя бы получить за нее некоторое количество баллов на экзамене.
Ранее, до появления единого государственного экзамена, задачи с параметрами входили в варианты вступительных экзаменов по математике в ведущие вузы, а сегодня входят в вариант КИМ ЕГЭ профильного уровня. Дело в том, что эти задачи обладают высокой диагностической ценностью: они позволяют не только определить, насколько хорошо выпускник знает основные разделы школьного курса математики, но и проверить, насколько высок уровень его математического и логического мышления, насколько сильны первоначальные навыки математической исследовательской деятельности, а главное – насколько успешно он сможет овладеть курсом математики в вузе.
«Научите меня решать задачи с параметром», – такую просьбу я часто слышу от своих учеников. Что ж, эта задача потребует от выпускника немало интеллектуальных усилий. С чего начать изучение? С освоения методов решения задач с параметром. Собственно, если вы внимательно читали наши рекомендации, как подготовиться к решению сложных задач варианта КИМ ЕГЭ, то заметили, что это универсальный совет. Именно так построен наш курс «1С:Репетитор»: изучаем как можно более широкий спектр методов и приемов решения задач и тренируемся в применении этих методов на практике.
Чему нужно научиться, решая задачи с параметром
В первую очередь – правильно применять равносильные преобразования уравнений, неравенств и их систем. То есть понять, при каких ограничениях, накладываемых на параметр, можно выполнять то или иное преобразование. Лучше всего начать с заданий вида: «Для каждого значения параметра решить…» и рассмотреть по возможности все основные элементарные функции, встречающиеся в школьном курсе математики.
Если с несложными задачами такого вида школьник справляется неплохо, то можно переходить к изучению аналитических методов решения задач, содержательно усложняя и классифицируя задачи с точки зрения применения к ним этих методов исследования. Имеется в виду знакомство с подходами к решению задач, содержащих формулировки типа: «При каких значениях параметра уравнение (неравенство, система) имеет одно (два, три, бесконечно много и т.д.) решений», «При каких значениях параметра решением уравнения (неравенства, системы) является некоторое подмножество множества действительных чисел» и т.д.
Следующий шаг, который мы рекомендуем, – тщательно изучить схему исследования квадратичной функции. Поскольку квадратичная функция является одной из самых хорошо изученных в школьном курсе математики, на ее основе можно предложить большое количество исследовательских задач, разнообразных по форме и содержанию, чем и пользуются составители вариантов КИМ ЕГЭ.
Мы рекомендуем подойти к рассмотрению данных задач по следующей схеме:
Следующая тема курса – графические методы решения задач с параметром
Существует два принципиально различных подхода – построение графиков функций или уравнений в плоскости (x; y) или в плоскости (x; a). Кроме того, для графического метода решения задач с параметром в плоскости (x; y) необходимо рассмотреть различные виды преобразования графиков – обычно это параллельный перенос, поворот прямой и гомотетия. Есть класс задач, решение которых основано на аналитических свойствах функций (области определения, области значений, четности, периодичности и т.д.), эти свойства и приемы их использования тоже нужно знать.
На этом перечень методов решения задач с параметрами, разумеется, не заканчивается, но анализ вариантов КИМ ЕГЭ профильного уровня и практика показывают, что в настоящее время этого достаточно для успешного решения задачи № 18 на экзамене.
В заключение отметим, что выстроить подобный курс самостоятельно, без преподавателя, обычный школьник не сможет, даже имея под рукой хорошие учебные пособия по методам решения задач с параметром. Здесь необходима помощь опытного наставника, который сможет подобрать нужные задачи и выстроить траекторию движения школьника по ним.
Заметим, кстати, что весьма эффективным инструментом для изучения именно методов решения задач с параметром являются интерактивные тренажеры с пошаговым разбором решения.

Работая с таким тренажером, школьник одновременно учится выстраивать логику решения задачи с параметром и контролирует правильность выполнения каждого шага решения. Это очень важное умение, так как одна из основных сложностей в решении задачи с параметром состоит в том, что необходимо на каждом шаге решения понимать, что означают уже полученные результаты и что (в зависимости от этих результатов) еще остается сделать, чтобы довести решение до конца.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
Купить доступ к этой задаче в составе
экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Разбор задач с параметрами из ЕГЭ по математике, по теме задачи с параметром ЕГЭ, как решать задание 18 в экзамене ЕГЭ, задачи с параметром ЕГЭ, задания с параметром ЕГЭ, задача 18 ЕГЭ, модуль и окружности, решение параметров ЕГЭ, решение задачи 18, система уравнений с параметром, научиться решать задачи с параметрами, сложных задач варианта КИМ ЕГЭ, начертить графики функций, ЕГЭ по математике профильного уровня, методы решения уравнений и неравенств, выпускникам 11 класса в 2018 году, поступающим в технический вуз.
Задачи с параметром
В 18 задании – предпоследнем задании профильного уровня ЕГЭ по математике – необходимо продемонстрировать умение решать задачи с параметрами. В подавляющем большинстве данное задание представляет собой систему из двух уравнений с параметром а, и необходимо найти такие значения, при которых система будет вести себя заданным образом – иметь два или одно или вообще не иметь решений.
Разбор типовых вариантов заданий №18 ЕГЭ по математике профильного уровня
Первый вариант задания (демонстрационный вариант 2018)
[su_note note_color=”#defae6″]
Найдите все положительные значения a, при каждом из которых система имеет единственное решение:
- (|x|–5)2+(y–4)2=4
- (x–2)2+y2=a2
[/su_note]
Алгоритм решения:
- Рассматриваем второе уравнения, устанавливаем, что является его графиком.
- Определяем условие единственности решения.
- Находим расстояние между центрами, определяем значения параметра.
- Записываем ответ.
Решение:
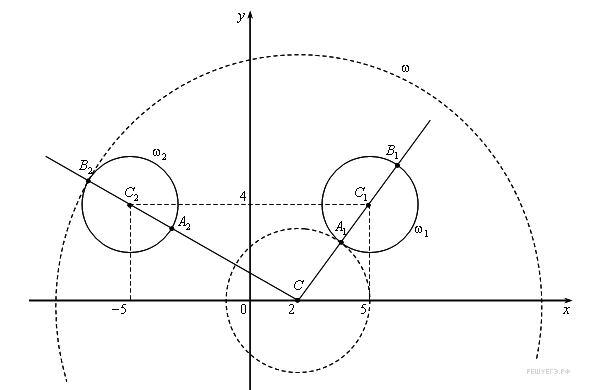
1. Первое уравнение – это две окружности радиусами 3 и координатами центров С 2(5;4) и С2(-5;4). Одну окружность задает данное уравнение при х≥0, а вторую – при х<0. Они не пересекаются и не касаются.
2. Второе уравнение – это одна окружность радиуса “а” с координатами центра: С (-2;0).
3. Наличие единственного решения означает, что одна окружность должна коснуться одной из окружностей в одной точке. Поэтому следует решить попарно две системы.
Первая:
Вторая:
Естественно, в первом и втором случае получается пара корней т. е. координат касания внешним и внутренним образом.
Но стоит заметить что нас будут интересовать только корни определяющие касание внешнее левой окружности и касание внутреннее правой окружности. Т. к. два других уравнения противоречить условию и будут иметь более одного решения. Достаточно взглянуть на прилагаемый рисунок:
4. Воспользуемся приложенным рисунком.
Проведем лучи СС1, и СС2, обозначив точки их пересечения с окружностями А1, В1 и А2, В2.
Тогда
Если a<CA2 или CA2<a<CB2 окружности не пересекаются. А это означает, корней система иметь не может.
5. Имеем: исходная система имеет единственное решение при
Ответ:
Второй вариант (из Ященко, №1)
[su_note note_color=”#defae6″]
Найдите все значения а, при каждом из которых уравнение
имеет ровно один корень.
[/su_note]
Решение:
Данное уравнение равносильно виду:
Рассматриваем случай:
при условии
Получаем .
При этом значении х условие принимает вид:
Отсюда
Имеем в данном случае: при
.
Рассмотрим теперь случай:
,
при этом .
Решаем уравнение. Получаем:
Отсюда .
Условие принимает вид:
Следовательно, получается . То есть
при
.
Корни и
равны между собой, если
.
Таким образом, уравнение имеет только один корень если и
.
Ответ:
Даниил Романович | Просмотров: 5.5k
Блок 1. Введение
| 1.1 | Решите уравнения с параметром а: а) ax = − 5; б) (a−1)x = −3; в) (a−2)x = 2−a г) (a−2)x = (a−2)(a+3) |
Смотреть видеоразбор |
| 1.2 | Определите при каких значениях параметра а: а) уравнение |x| = a−3 имеет один корень; б) уравнение |x| = a2−5 не имеет корней. |
Смотреть видеоразбор |
| 1.3 | Функция задана формулой y=x^2+ax+b. Найдите a и b, если: а) график функции проходит через точки (0;3) и (-1;8); б) наименьшее значение, равное −4, функция принимает при x = 1 |
Смотреть видеоразбор |
Блок 2. Координатно-параметрический метод
| 2.1 | Найдите все значения параметра а, при каждом из которых уравнение frac{|3x|-2x-2-a}{x^2-2x-a}=0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.2 | Найдите все значения а, при каждом из которых система уравнений begin{cases} frac{xy^2-3xy-3y+9}{sqrt{x+3}}=0 \ y=ax end{cases} имеет ровно два различных решения | Смотреть видеоразбор |
| 2.3 | Найдите все значения параметра а, при каждом из которых уравнение frac{x^2-4x+a}{5x^2-6ax+a^2} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.4 | Найти все значения а, при каждом из которых уравнение sqrt{3x-2} cdot ln(x-a) = sqrt{3x-2} cdot ln(2x+a) имеет ровно один корень на отрезке [0; 1] | Смотреть видеоразбор |
| 2.5 | Найти все значения а, при каждом из которых уравнение (4^x-3 cdot 2^x + 3a — a^2)cdotsqrt{2-x} = 0 имеет ровно два различных корня | Смотреть видеоразбор |
| 2.6 | Найти все действительные значения величины h , при которых уравнение x(x+1)(x+h)(x+1+h) = h^2 имеет 4 действительных корня | Смотреть видеоразбор |
Блок 3. Преобразование графиков
| 3.1 | Найдите все значения a, при каждом из которых наименьшее значение функции f(x) = 2ax+|x^2-8x+7| больше 1 | Смотреть видеоразбор |
| 3.2 | Найти все значения параметра a, при каждом из которых уравнение (|x-2|+|x+a|)^2-7(|x-2|+|x+a|)-4a(4a-7) = 0 имеет ровно два корня | Смотреть видеоразбор |
| 3.3 | Максимальное значение выражения x + 2y при условии log_{frac{x^2+y^2}{2}}ay ge 1 равно 4. Чему равно положительное значение параметра a? | Смотреть видеоразбор |
| 3.4 | Найти все значения параметра a, при каждом из которых уравнение f(x) = |a+2|sqrt[3]{x} имеет 4 решения, где f — чётная периодическая функция с периодом T=frac{16}{3}, определённая на всей числовой прямой, причём f(x)=ax^2, если 0 le x le frac{8}{3} | Смотреть видеоразбор |
Блок 4. Системы с параметром
| 4.1 | Найдите все положительные значения a, при каждом из которых система begin{cases} (|x|-5)^2+(y-4)^2=9 \ (x+2)^2+y^2=a^2 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.2 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} frac{(y^2-xy-4y+2x+4)sqrt{x+4}}{sqrt{5-y}} \ a=x+y end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.3 | Найдите все значения параметра a, при каждом из которых система уравнений begin{cases} (x-2a+3)^2+(y-4)^2=2,25 \ (x+3)^2+(y-a)^2=a^2+2a+1 end{cases} имеет единственное решение | Смотреть видеоразбор |
| 4.4 | Найти все значения параметра a, при каждом из которых система begin{cases} ((x-5)^2+(y-3)^2-9)((x-2)^2+(y-1)^2) le 0 \ y=ax+a+3 end{cases} не имеет решений | Смотреть видеоразбор |
Блок 5. Квадратичная функция
| 5.1 | Найти все значения параметра a, при каждом из которых неравенство |frac{x^2+ax+1}{x^2+x+1}| lt 3 выполняется при всех значениях x | Смотреть видеоразбор |
| 5.2 | При каких значениях p вершины парабол y=-x^2+2px+3 и y=x^2-6px+p расположены по разные стороны от оси x? | Смотреть видеоразбор |
| 5.3 | Найти все значения a, при каждом из которых f(x)=x^2-|x-a^2|-5x имеет хотя бы одну точку максимума | Смотреть видеоразбор |
| 5.4 | Найдите все значения параметра a при каждом из которых множество значений функции y=frac{3x+3-2ax}{x^2+2(2a+1)x+4a^2+4a+2} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.5 | Найти все значения параметра a, при каждом из которых множество значений функции y=frac{5a-15x+ax}{x^2-2ax+a^2+25} содержит отрезок [0;1] | Смотреть видеоразбор |
| 5.6 | Найдите все значения параметра a, при каждом из которых неравенство |frac{x^2+x-2a}{x+a}-1| le 2 не имеет решений на интервале (1;2) | Смотреть видеоразбор |
| 5.7 | Найдите все значения параметра a, при каждом из которых уравнение frac{a^3-(x+2)a^2+xa+x^2}{a+x} = 0 имеет ровно один корень | Смотреть видеоразбор |
| 5.8 | Найдите все значения a, при каждом из которых множество значений функции y=frac{cos{x}-a}{cos{2x}-4}содержит число −2 | Смотреть видеоразбор |
| 5.9 | Найти все значения параметра a, при каждом из которых уравнение (4cos{x}-3-a)cos{x}-2,5cos{2x}+1,5=0 имеет хотя бы один корень | Смотреть видеоразбор |
| 5.10 | Найти все значения параметра a, при каждом из которых уравнение 4^{|x|}=frac{7a}{a-5}cdot 2^{|x|}-frac{12a+17}{a-5} имеет ровно два различных корня | Смотреть видеоразбор |
| 5.11 | Найдите все значения а, при каждом из которых множество решений неравенства frac{a-(a^2-2a-3)cos{x}+4}{sin^2{x}+a^2+1} lt 1 содержит отрезок [-frac{pi}{3}; frac{pi}{2}] | Смотреть видеоразбор |
Блок 6. Расположение корней квадратного уравнения
| 6.1 | Найти все значения параметра a, при которых разность между корнями уравнения x^2+3ax+a^4=0 максимальна | Смотреть видеоразбор |
| 6.2 | Найти все значения параметра а, при каждом из которых уравнение log_{1-x}(a-x+2) = 2 имеет хотя бы один корень, принадлежащий промежутку (-1;1] | Смотреть видеоразбор |
Блок 7. Аналитический метод
| 7.1 | При каких значениях а корни уравнения |x-a^2|=-a^2+2a+3 имеют одинаковые знаки? | Смотреть видеоразбор |
| 7.2 | Найти все значения параметра а, при которых неравенство x^2+2|x-a| ge a^2 справедливо для всех действительных x | Смотреть видеоразбор |
| 7.3 | Найти все значения параметра а, при каждом из которых уравнение |sin^2{x}+2cos{x}+a|=sin^2{x}+cos{x}-a имеет на промежутке (frac{pi}{2};pi] единственный корень | Смотреть видеоразбор |
| 7.4 | Найти все значения параметра а, при каждом из которых уравнение (x^2-4ax+a(4a-1))^2-3(x^2-4ax+a(4a-1))-|a|(|a|-3)=0 имеет более двух корней | Смотреть видеоразбор |
Блок 8. Функциональные методы
| 8.1 | Найти все значения параметра a, при каждом из которых уравнение x^2+(a+7)^2=|x-7-a|+|x+a+7| имеет единственный корень | Смотреть видеоразбор |
| 8.2 | Найти все значения параметра a, при каждом из которых система begin{cases} ax^2+4ax-8y+6a+28 le 0 \ ax^2-6ay-8x+11a-12 le 0 end{cases} имеет ровно одно решение | Смотреть видеоразбор |
| 8.3 | Найдите все значения параметра alpha из интервала (0; pi), при каждом из которых система begin{cases} x^2+y^2-4(x+y)sin{alpha}+8sin^2{alpha} = 2sin{alpha}-1 \ frac{x}{y}+frac{y}{x} = 2sin{alpha}+4sin^2{alpha} end{cases} имеет единственное решение | Смотреть видеоразбор |
| 8.4 | Найдите все неотрицательные значения параметра a, при каждом из которых множество решений неравенства 1 le frac{2a+x^2-4log_{frac{1}{3}}(4a^2-4a+9)}{5sqrt{18x^4+7x^2}+2a+4+(log_{frac{1}{3}}(4a^2-4a+9))} состоит из одной точки и найти это решение. | Смотреть видеоразбор |
| 8.5 | Найдите все значения a, для каждого из которых уравнение 8x^6+(a-|x|)^3+2x^2-|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.6 | Найти все значения параметра a, при каждом из которых уравнение x^10+(a-2|x|)^5+x^2-2|x|+a=0 имеет более трёх различных решений. | Смотреть видеоразбор |
| 8.7 | Найти все значения параметра a, при каждом из которых уравнение 64x^6-(a-3x)^3+4x^2+3x=a имеет более одного корня. | Смотреть видеоразбор |
| 8.8 | Найти все значения параметра a, для каждого из которых существует хотя бы одна пара чисел x и y , удовлетворяющих неравенству 5|x-2|+3|x+a| le sqrt{4-y^2}+7 | Смотреть видеоразбор |
| 8.9 | Найти все значения параметра a, при каждом из которых уравнение (log_7(2x+2a)-log_7(2x-2a))^2-8a(log_7(2x+2a)-log_7(2x-2a))+12a^2+8a-4 имеет ровно два корня. | Смотреть видеоразбор |
| 8.10 | Найти все значения параметра a, при каждом из которых уравнение a^2-10a+5sqrt{x^2+25}=4|x-5a|-8|x| имеет хотя бы один корень | Смотреть видеоразбор |
| 8.11 | Найти все значения параметра a, при которых уравнение (a+2)^2 cdot log_3(2x-x^2)+(3x-1)^2 cdot log_{11}(1-frac{x^2}{2})=0 имеет решение | Смотреть видеоразбор |
| 8.12 | При каких значениях параметра a уравнение ax^6=e^x имеет одно положительное решение? | Смотреть видеоразбор |
Блок 9. Разные задачи с параметром
| 9.1 | Найти все значения параметра a, при которых уравнение sqrt{1-(x^2-4x-a^2+2a+3)^6}+sqrt{1+(x^2-4x-a^2+2a+3)^6} = 2 имеет только один положительный корень | Смотреть видеоразбор |
| 9.2 | Найти все положительные значения параметра a, при каждом из которых наименьшее значение f(x)=2x^3-3ax^2+5 на отрезке, заданном неравенством |x-2| le 1, не меньше, чем −3 | Смотреть видеоразбор |
| 9.3 | Найдите все значения параметра b , при каждом из которых для любого a неравенство (x-a-2b)^2+(y-3a-b)^2 lt frac{1}{2} имеет хотя бы одно целочисленное решение (x, y). | Смотреть видеоразбор |
| 9.4 | Найти все a, при каждом из которых уравнение sqrt{a-9cos^4{x}}=sin^2{x} имеет решение | Смотреть видеоразбор |
| 9.5 | Найдите наибольшее целое значение a, при котором уравнение 3x^2-12x+3a+9=4sin{frac{4x-x^2-a-3}{2}} cdot cos{frac{x^2-2x-a-1}{2}} имеет ровно два различных решения | Смотреть видеоразбор |
| 9.6 | Найдите все целые отрицательные значения параметра a, при каждом из которых существует такое действительное число b>a, что неравенство 21b ge 6|a+b|-3|b-2|-|a-b|-9|a^2-b+2|+16 не выполнено | Смотреть видеоразбор |