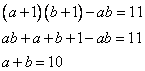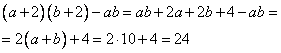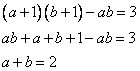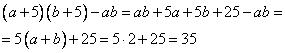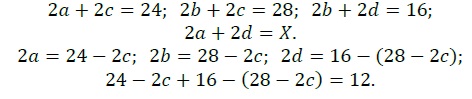Как делать 20 задание в егэ по математике базовый уровень

Задачи на сообразительность

Задание №20 ЕГЭ по математике содержит задачу на сообразительность. Задачи в этом разделе более интуитивно понятно, нежели в 19 задании ЕГЭ, но тем не менее достаточно сложны для обычного школьника. Итак, перейдем к рассмотрению типовых вариантов.

Разбор типовых вариантов заданий №20 ЕГЭ по математике базового уровня

Вариант 20МБ1

[su_note note_color=”#defae6″]

В обменном пункте можно совершить одну из двух операций:

• за 2 золотых монеты получить 3 серебряных и одну медную;
• за 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

[/su_note]

Алгоритм выполнения:

1. Ввести условные обозначения.
2. Записать данные задачи с помощью условных обозначений.
3. Логически рассуждая определить неизвестное.

Решение:

По условию золотых монет не появилось, значит все полученные после осуществления второй операции золотые монеты, Николай обменял с помощью первой операции. Золотые монеты можно менять только по 2 штуки, следовательно, вторых операций было четное число.

Введем обозначение, пусть вторых операций было 2n(число всегда четное).

Если применить вторую операцию получим:

5 · 2n серебряных обменяли на 3 · 2n золотых + 2n медных.

Все золотые монеты были обменяны в ходе первой операции. За одну операцию можно обменять сразу 2 золотые монеты, значит, всего операций будет совершено (3 · 2n)/2 = 3 n. То есть

3 · 2n золотых обменяли на 3· 3n серебряных + 3n медных.

Или после преобразования:

3 · 2n золотых обменяли на 9n серебряных + 3n медных

Сопоставим результаты первой и второй операции:

5 · 2n серебряных обменяли на 3 · 2n золотых + 2n медных.

3 · 2n золотых обменяли на 9n серебряных + 3n медных

Получим

5 · 2n серебряных обменяли на 9n серебряных + 3n медных+2n медных

Или

10 n серебряных обменяли на 9n серебряных + 5n медных

Если, обменяв 10 n серебряных монет, получим 9 n серебряных монет, то количество серебряных монет у Николая уменьшилось на n. Из последнего выражения видно, что Николай получил 5n медных монет, а по условию появилось 50 медных, то есть 5n = 50.

n = 10

Ответ: 10

Вариант 20МБ2

[su_note note_color=”#defae6″]

Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

[/su_note]

Алгоритм выполнения:

1. Определить, кто и во сколько раз дольше ел печенье.
2. Определить, кто и во сколько раз дольше ел варенье.
3. Сопоставить результаты.
4. Найти неизвестное.

Решение:

1. Так как варенье и Маша, и Медведь съели поровну, и при этом Медведь ел варенье в 3 раза быстрее, то Маша ела варенье (свою половину) в 3 раза дольше, чем Медведь (такую же половину).
2. Тогда получается, что Медведь ел печенья в 3 раза дольше Маши и к тому же ел их в 3 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 3∙3=9 печений, съеденных Медведем.
3. В сумме эти печенья составляют 1+9=10 и таких сумм в 100 печеньях ровно 100:10 = 10.
4. Значит, Маша съела 10 печений, а Медведь 9∙10=90.

Ответ: 90

Вариант 20МБ3

[su_note note_color=”#defae6″]

Маша и Медведь съели 51 печенье и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в четыре раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

[/su_note]

Алгоритм выполнения:

1. Определить, кто и во сколько раз дольше ел печенье.
2. Определить, кто и во сколько раз дольше ел варенье.
3. Сопоставить результаты.
4. Найти неизвестное.

Решение:

1. Так как варенье и Маша, и Медведь, съели поровну, и при этом Медведь ел варенье в 4 раза быстрее, то Маша ела варенье (свою половину) в 4 раза дольше, чем Медведь (такую же половину).
2. Тогда получается, что Медведь ел печенья в 4 раза дольше Маши и к тому же ел их в 4 раза быстрее, то есть, на одно съеденное Машей печенье приходилось 4∙4=16 печений, съеденных Медведем.
3. В сумме эти печенья составляют 1+16=17 и таких сумм в 51 печеньях ровно 51:17 = 3.
4. Значит, Маша съела 3 печенья, а Медведь 3∙16=48.

Ответ: 48

Вариант 20МБ4

[su_note note_color=”#defae6″]

Если бы каждый из двух сомножителей увеличили на 1, их произведение увеличилось бы на 11. На самом деле каждый из двух сомножителей увеличили на 2. На сколько увеличилось произведение?

[/su_note]

Алгоритм выполнения:

1. Ввести условные обозначения.
2. Записать первое условие с помощью условных обозначений.
3. Преобразовать полученное выражение.
4. Записать с помощью условных обозначений второе условие.
5. Преобразовать полученное выражение.
6. Найти неизвестное.

Решение:

Пусть первый сомножитель равен a, а второй b, их произведение равно ab.

При увеличении этих сомножителей на 1 их произведение возрастает на 11, то есть,

Перенесем произведение ab в левую часть с противоположным знаком и раскроем скобки перемножив.

Теперь аналогично вычислим, на сколько увеличится произведение, если сомножители увеличить на 2 и подставим уже известное нам a + b = 10 :

Ответ: 24

Вариант 20МБ5

[su_note note_color=”#defae6″]

Если бы каждый из двух сомножителей увеличили на 1, их произведение увеличилось бы на 3. На самом деле каждый из двух сомножителей увеличили на 5. На сколько увеличилось произведение?

[/su_note]

Алгоритм выполнения:

1. Ввести условные обозначения.
2. Записать первое условие с помощью условных обозначений.
3. Преобразовать полученное выражение.
4. Записать с помощью условных обозначений второе условие.
5. Преобразовать полученное выражение.
6. Найти неизвестное.

Решение:

Пусть первый сомножитель равен a, а второй b, их произведение равно ab.

При увеличении этих сомножителей на 1 их произведение возрастает на 3, то есть,

Перенесем произведение ab в левую часть с противоположным знаком и раскроем скобки перемножив.

Теперь аналогично вычислим, на сколько увеличится произведение, если сомножители увеличить на 5 и подставим уже известное нам a + b = 2:

Ответ: 35

Вариант 20МБ6

[su_note note_color=”#defae6″]

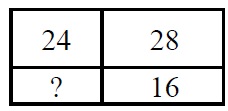
Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными отрезками. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

[/su_note]

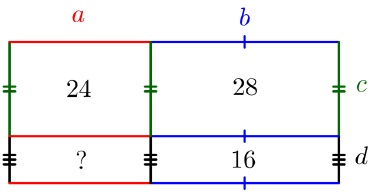
Перерисуем прямоугольник в удобном для нас виде:

Теперь составим уравнения с помощью формулы периметра прямоугольника:

Ответ: 12

Вариант 20МБ7

[su_note note_color=”#defae6″]

Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 10 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 42 очка, если известно, что по крайней мере один раз он ошибся?

[/su_note]

Алгоритм выполнения

1. Составляем комбинации правильных и неправильных ответов и определяем кол-во баллов в них, например: 1) 1 прав+1 неправ=7–10=–3 балла; 2) 2 прав+1неправ=2·7–10=4 балла и т.д.
2. Из баллов за прав.ответы и баллов за их комбинации «набираем» 42 балла. Подсчитываем кол-во вопросов, которые при этом были заданы.
3. Оставшуюся разницу между полученным числом вопросов и данными 25-ю вопросами определяем как те, на которые не было дано ответа.
4. Делаем проверку полученного результата.

Решение:

Введем обозначения: прав.ответ – 1П, неправ.ответ – 1Н.

Задаем комбинации и определяем кол-во баллов, которое при этом будет начислено:

1П=7 баллов

1П+1Н=7–10=–3 б.

2П+1Н=2·7–10=4 б.

3П+1Н=3·7–10=11 б.

Суммируем баллы, которые можно при этом получить: 7+ (–3)+4+11=19. Это явно мало. И гарантированно можно добавить еще 11: 19+11=30. Чтобы «добрать» до 42 баллов, нужно далее добавить 12 баллов, которые набираются тройным вхождением 4-х баллов. В целом получаем:

7+(–3)+4+11+11+3·4=42.

Распишем полученную комбинацию слагаемых в виде ответов:

1П+(1П+1Н)+(2П+1Н)+(3П+1Н)+(3П+1Н)+3·(2П+1Н)=1П+1П+1Н+2П+1Н+3П+1Н+3П+1Н+6П+3Н=16П+7Н (ответов).

16+7=23 ответа. 25–23=2 ответа, за которые было получено по 0 баллов, т.е. это вопросы, оставшиеся без ответов.

Итак, по нашим подсчетам верных ответов было дано 16.

Проверим это:

16 ответов по 7 б. + 7 ответов по (–10) б. + 2 ответа по 0 б. = 16·7–7·10+2·0=112–70+0=42 (балла).

Ответ: 16

Вариант 20МБ8

[su_note note_color=”#defae6″]

В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором – 97, в третьем – 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?

[/su_note]

Алгоритм выполнения

1. Находим общую сумму для всех чисел в таблице (сложив суммы для каждого из 3-х столбцов).
2. Определяем диапазон допустимых значений для сумм чисел в каждой строке.
3. Разделив общую сумму сначала на наименьшую сумму чисел в каждой строке, а затем на наибольшую, получаем искомое кол-во строк.

Решение:

Общая сумма чисел в таблице равна: 103+97+93=293.

Поскольку по условию суммы чисел в каждой строке составляют >21, но <24, то кол-во строк X может быть равным меньше, чем 293:21≈13,95, и больше, чем 293:24≈12,21. Т.е.: 12,21 < X < 13,95. Единственное целое число в полученном диапазоне – 13. Значит, искомое кол-во строк равно 13.

Ответ: 13

Вариант 20МБ9

[su_note note_color=”#defae6″]

В доме всего восемнадцать квартир с номерами от 1 до 18. В каждой квартире живет не менее одного и не более трех человек. В квартирах с 1-й по 13-ю включительно живет суммарно 15 человек, а в квартирах с 11-й по 18-ю включительно живет суммарно 20 человек. Сколько всего человек живет в этом доме?

[/su_note]

Алгоритм выполнения

1. Определяем максимальное кол-во живущих в 11–13-й квартирах, используя данные о том, сколько человек живет в 1–13-й квартирах.
2. Находим минимальное число жильцов 11–13-й квартир, учитывая данные о живущих в 11–18-й квартирах.
3. Сопоставляет данные, полученные в пп.1–2, получаем точное кол-во жильцов этих квартир №№11–13.
4. Находим кол-во живущих в квартирах 1–10-й и 14–18-й.
5. Вычисляем общее число жильцов дома.

Решение:

В первых 13 квартирах (с 1-й по 13-ю) живет 15 человек. Это означает, что в 11-ти квартирах живет по 1 человеку плюс в 2-х квартирах по 2 человека (11·1+2·2=15). Следовательно, в 11–13-й (т.е. в 3-х) квартирах проживает не менее 3-х и не более 5 (1+2+2) человек.

Во вторых 8 квартирах (11-й по 18-ю) проживает 20 человек. При этом с 14-й по 18-ю квартиры (т.е. в 5 квартирах) не может проживать более чем 5·3=15 человек. А следовательно, в 11-13-й квартирах живет не менее, чем 20–15=5 человек.

Т.е. с одной стороны в 11-13-й квартирах должно жить не более 5 человек, а с другой – не менее 5. Вывод: в этих квартирах живет ровно 5 человек, т.к. других допустимых для обоих случаев значений тут нет.

Тогда получаем: в 1–10-й квартирах живет 15–5=10 человек, в 14–18-й – 20–5=15 человек. Всего в доме проживает: 10+5+15=30 человек.

Ответ: 30

Вариант 20МБ10

[su_note note_color=”#defae6″]

В обменном пункте можно совершить одну из двух операций:

• за 4 золотых монеты получить 5 серебряных и одну медную;
• за 7 серебряных монет получить 5 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 45 медных. На сколько уменьшилось количество серебряных монет у Николая?

[/su_note]

Алгоритм выполнения

1. Определяем кол-во серебряных монет, которые необходимы Николаю для совершения двойного обмена так, чтобы у него не появились золотые монеты. Двойной обмен – это обмен сначала серебряных монет на золотые и медные, а затем золотые на серебряные и медные.
2. Определяем кол-во разных монет, которые появятся у Николая в результате 1 двойного обмена.
3. Вычисляем кол-во двойных обменов, которые необходимо совершить, чтобы появилось 45 медных монет.
4. Находим кол-во серебряных монет, которые должен был иметь Николай изначально, чтобы совершить нужное кол-во обменов, и которые получил в результате всех обменов.
5. Определяем искомую разницу.

Решение:

Совершить 1-й обмен Николай должен по 2-й схеме, т.к. у него есть только серебряные монеты. Для того же, чтобы в результате у него не оказалось золотых монет, нужно найти минимальное кратное для 5 золотых, которые он получит, и 4 золотых, которые у него за 1 раз могут принять в полном объеме (без остатка). Это – число 20.

Соответственно, чтобы получить 20 золотых монет, у Николая должно быть 20:5=4 комплекта серебряных монет по 7 штук. Значит, первоначально их у него должно быть 4·7=28. И при этом Николай получает еще и 1·4=4 медных монеты.

Совершая обмен, Николай отдает 20:4=5 комплектов золотых медалей. Взамен он получает 5·5=25 серебряных монет и 1·5=5 медных монет.

Т.о., в результате одного обмена у Николая появится 25 серебряных монет и 4+5=9 медных монет. Поскольку в итоге у Николая оказалось 45 медных монет, значит, было совершено 45:9=5 двойных обменов.

Если в результате 1 двойного обмена у Николая оказалось 25 серебряных монет, то после 5 таких обменов у него их окажется 25·5=125 штук. А первоначально он должен был для этого иметь 28·5=140 серебряных монет. Следовательно, их количество у Николая уменьшилось на 140–125=15 штук.

Ответ: 15

Вариант 20МБ11

[su_note note_color=”#defae6″]

Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нем 357 квартир?

[/su_note]

Алгоритм выполнения

1. Определяем уравнение для определения кол-ва квартир в доме всего через параметры, заявленные в условии (т.е. через кол-во квартир на этаже и т.д.).
2. Раскладываем 357 на множители.
3. Находим соответствие полученных множителей конкретным параметрам, сходя из условия о том, какой из параметров больше или меньше прочих.

Решение:

Т.к. на всех этажах одинаковое кол-во квартир (Х), по всех подъездах одинаковое кол-во этажей (Y), то обозначив кол-во подъездов через Z, можем записать: 357=X·Y·Z.

Разложим 357 на простые множители. Получим: 357=3·7·17·1. Причем это единственный вариант расклада. Т.к. Y>X>Z>1, то единицу в раскладе не учитываем и определяем, что Z=3, X=7, Y=17.

Поскольку кол-во этажей было обозначено через Y, то искомое число – 17.

Ответ: 17

Вариант 20МБ12

[su_note note_color=”#defae6″]

Из десяти стран семь подписали договор о дружбе ровно с тремя странами, а каждая из оставшихся трех – ровно с семью. Сколько всего было подписано договоров?

[/su_note]

Алгоритм выполнения

1. Подсчитываем кол-во договоров, подписанных 7-ю странами.
2. Определяем кол-во договоров, которые подписали 3 оставшиеся страны.
3. Находим общее кол-во подписанных договоров. Делим его на 2, т.к. договоры двусторонние.

Решение:

Первые 7 стран подписали договоры с 3 странами, т.е. на этих договорах поставлено 7·3=21 подпись. Аналогично остальные 3 страны при оформлении договоров с 7-ю странами поставили 3·7=21 подпись. Значит, всего поставлено 21+21=42 подписи.

Т.к. все договоры двусторонние, то это значит, что на каждом из них зафиксировано 2 подписи. Следовательно, договоров вдвое меньше, чем подписей, т.е. 42:2=21 договор.

Ответ: 21

Вариант 20МБ13

[su_note note_color=”#defae6″]

На поверхности глобуса фломастером проведены 13 параллелей и 25 меридианов. На сколько частей проведенные линии разделили поверхность глобуса?

Меридиан – это дуга окружности, соединяющая Северный и Южный полюсы. Параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора.

[/su_note]

Алгоритм выполнения

1. Доказываем, что параллели делят глобус на 13+1 часть.
2. Доказываем, что меридианы делят глобус на 25 частей.
3. Определяем кол-во частей, на которые в целом разделен глобус, как произведение найденных чисел.

Решение:

Если всякая параллель – это окружность, то она является замкнутой линией. А это означает, что 1-я параллель делит глобус на 2 части. Далее 2-я параллель обеспечивает деление на 3 части, 3-я – на 4 и т.д. В итоге 13 параллелей разделят глобус на 13+1=14 частей.

Меридиан является дугой окружности, соединяющей полюса, т.е. замкнутой линией она не является и глобус на части не делит. А вот 2 меридиана уже делят, т.е. 2 меридиана обеспечивают деление на 2 части, далее 3-й меридиан добавляет 3-ю часть, 4-й – 5-ю часть и т.д. Значит, в конечном счете, 25 меридианов создает на глобусе 25 частей.

Всего частей на глобусе получается: 14·25=350 частей.

Ответ: 350

Вариант 20МБ14

[su_note note_color=”#defae6″]

В корзине лежит 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов – хотя бы один груздь. Сколько рыжиков в корзине?

[/su_note]

Алгоритм выполнения

1. Определяем кол-во груздей среди 12 грибов и рыжиков среди 20 грибов.
2. Доказываем, что имеется единственно верное число, отображающее кол-во рыжиков. Фиксируем его в ответе.

Решение:

Если среди 12 грибов есть как минимум 1 рыжик, значит, груздей здесь не более 11. Если среди 20 грибов имеется не менее 1 груздя, то тут не более 19 рыжиков.

Это означает, что если груздей не может быть больше 11, то рыжиков не может быть меньше 30–11=19 штук. Т.е. рыжиков с одной стороны не больше 19, а с другой – не меньше 19. Следовательно, рыжиков может быть только ровно 19.

Ответ: 19

Вариант 20МБ15

[su_note note_color=”#defae6″]

Если бы каждый из двух множителей увеличили на 1, то их произведение увеличилось бы на 3. На сколько увеличится произведение этих множителей, если каждый из них увеличить на 5?

[/su_note]

Алгоритм выполнения

1. Вводим обозначения для множителей. Это позволит выразить и первоначальное произведение (до увеличения множителей).
2. Составляем уравнение для ситуации, когда множители увеличены на 1. Выполняем преобразования. Получаем новое выражение, отображающее связь между первоначальными множителями.
3. Составляем уравнение для ситуации, когда множители увеличены на 5. Выполняем преобразования. Вводим в уравнение выражение, полученное в п.2, находим искомую разницу.

Решение:

Пусть 1-й множитель равен х, 2-й – у. Тогда их произведение – ху.

После того, как множители увеличены на 1, получаем:

(х+1)(у+1)=ху+3

ху+у+х+1=ху+3

х+у=2

После увеличения множителей на 5 имеем:

(х+5)(у+5)=ху+N, где N – искомая разница произведений.

Выполняем преобразования:

ху+5у+5х+25=ху+N

N=ху+5у+5х+25– ху

N=5(х+у)+25

Т.к. выше уже определено, что х+у=2, то получим:

N=5·2+25=35.

Ответ: 35

Вариант 20МБ16

[su_note note_color=”#defae6″]

Саша пригласил Петю в гости, сказав, что живет в седьмом подъезде в квартире № 462, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом семиэтажный. На каком этаже живет Саша? (На всех этажах число квартир одинакова, нумерация квартир в доме начинается с единицы.)

[/su_note]

Алгоритм выполнения

1. Способом подбора определяем кол-во квартир на площадке. Это должно быть такое число, чтобы номер квартиры оказался большим, чем кол-во квартир в 6-ти подъездах, однако меньшим, чем кол-во квартир в 7-ми.
2. Определяем кол-во квартир в 6-ти подъездах. От 462 отнимаем это кол-во и делим на число квартир на площадке. Так узнаем искомый номер этажа. Примечание: 1) если получено целое число, то искомый номер этажа на 1 больше, чем вычисленное значение; 2) если получено дробное число, то номером этажа будет округленный в большую сторону результат.

Решение:

Ищем кол-во квартир на площадке, проверяя число за числом.

Предположим, что это кол-во равно 3. Тогда получим, что в 7 подъездах на 6 этажах имеется 7·6·3=126 квартир,

а в 7 подъездах на 7 этажах 7·7·3=147 квартир.

Квартира №462 точно не попадает в диапазон квартир №№126–147.

Аналогично проверяя числа 4, 5 и т.д., придем к числу 10. Докажем, что именно оно подходит:

в 7 подъездах на 6 этажах находится 7·6·10=420 квартир,

в 7 подъездах на 7 этажах: 7·7·10=490 квартир. Поскольку 420<462<490, то условие задания выполнено.

Для того чтобы попасть в квартиру №462, нужно пройти мимо 462–420=42 квартир. Т.к. на каждой площадке находится 10 квартир, то 42:10=4,2 этажей для этого нужно преодолеть. 4,2 означает, что 4 этажа нужно пройти полностью и подняться на 5-й. Т.о., искомый этаж – 5-й.

Ответ: 5

Даниил Романович | Просмотров: 13.5k

Единый государственный экзамен по математике базового уровня состоит из 20 заданий. В задании 20 проверяются навыки решения логических задач. Школьник должен уметь применять свои знания для решения задач на практике, в том числе на арифметическую и геометрическую прогрессию. Здесь вы можете узнать, как решать задание 20 ЕГЭ по математике базового уровня, а также изучить примеры и способы решения на основе подробно разобранных заданий.

Слайд 1

Задания на смекалку ЕГЭ по математике базового уровня. Задания №20 Мысиковой Юлии Александровны, ученицы 11 «А» социально-экономического класса Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа №45»

Слайд 2

Улитка на дереве Решение. Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Итого, за сутки она продвигается на 3 – 2 = 1 метр. За 7 суток она поднимется на 7 метров. На восьмой день она заползёт вверх еще на 3 метра и впервые окажется на высоте 7 + 3 = 10 (м), т.е. на вершине дерева. Ответ: 8 Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м. За сколько дней улитка доползёт от основания до вершины дерева?

Слайд 3

Бензоколонки Решение. Начертим окружность и расположим точки (бензоколонки)так, чтобы расстояния соответствовали условию. Заметим, что все расстояния между точками А, С и D известны. АС =20, АD=30, СD=20. Отметим точку А. От точки А по часовой стрелке отметим точку С, помним, что АС=20. Теперь будем отмечать точку D, которая лежит от А на расстоянии 30, это расстояние нельзя откладывать от А по часовой стрелке, так как тогда получится расстояние между С и D равно 10, а по условию СD= 2 0 . Значит от А до D надо двигаться против часовой стрелки, отмечаем точку D. Так как СD=20, то длина всей окружности равна 20+30+20=70. Так как АВ=35, то точка В диаметрально противоположна точке А. Расстояние от С до В будет равно 35-20=15. Ответ: 15. На кольцевой дороге расположены четыре бензоколонки: A, B, C и Д. Расстояние между A и B — 35 км, между A и C — 20 км, между C и Д —20 км, между Д и A — 30 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между B и C. Ответ дайте в километрах.

Слайд 4

В кинозале Решение. 1 способ. Просто считаем сколько мест в рядах до восьмого: 1 – 24 2 – 26 3 – 28 4 – 30 5 – 32 6 – 34 7 – 36 8 – 38. Ответ: 38. В пер­вом ряду ки­но­за­ла 24 места, а в каж­дом сле­ду­ю­щем на 2 боль­ше, чем в преды­ду­щем. Сколь­ко мест в вось­мом ряду? 2 способ. Замечаем, что количество мест в рядах составляет арифметическую прогрессию с первым члено в 24 и разность равной 2. По формуле n — го члена прогрессии находим восьмой член а 8 = 24 + (8 – 1)*2 = 38. Ответ: 38.

Слайд 5

Грибы в корзине Решение. Из условия , что среди любых 27 гри­бов име­ет­ся хотя бы один рыжик следует – количество груздей не больше 26. Из второго условия, что среди любых 25 гри­бов хотя бы один груздь, следует — количество рыжиков не больше 24. Так как всего грибов – 50, то рыжиков 24, а груздей – 26. Ответ: 24. В кор­зи­не лежат 50 гри­бов: ры­жи­ки и груз­ди. Из­вест­но, что среди любых 27 гри­бов име­ет­ся хотя бы один рыжик, а среди любых 25 гри­бов хотя бы один груздь. Сколь­ко ры­жи­ков в кор­зи­не?

Слайд 6

Кубики в ряд Решение. Если пронумеровать все кубики числами от одного до шести (не учитывая, что имеются кубики разного цвета), то получим общее число перестановки кубиков: Р(6)=6*5*4*3*2*1=720 Теперь вспомним, что имеются 2 кубика красного цвета и перестановка их местами (Р(2)=2*1=2) не даст нового способа, поэтому полученное произведение надо уменьшить в 2 раза. Аналогично, вспоминаем, что у нас имеются 3 кубика зелёного цвета, поэтому придётся полученное произведение уменьшить ещё и в 6 раз (Р(3)=3*2*1=6) Итак, получим общее число способов расстановки кубиков 60. Ответ: 60. Сколь­ки­ми спо­со­ба­ми можно по­ста­вить в ряд два оди­на­ко­вых крас­ных ку­би­ка, три оди­на­ко­вых зелёных ку­би­ка и один синий кубик?

Слайд 7

На бе­го­вой до­рож­ке Тре­нер по­со­ве­то­вал Ан­дрею в пер­вый день за­ня­тий про­ве­сти на бе­го­вой до­рож­ке 15 минут, а на каж­дом сле­ду­ю­щем за­ня­тии уве­ли­чи­вать время, про­ведённое на бе­го­вой до­рож­ке, на 7 минут. За сколь­ко за­ня­тий Ан­дрей про­ведёт на бе­го­вой до­рож­ке в общей слож­но­сти 2 часа 25 минут, если будет сле­до­вать со­ве­там тре­не­ра? Решение. 1 способ. Замечаем, что надо найти сумму арифметической прогрессии с первым членом 15 и разность равной 7. По формуле суммы n первых членов прогрессии S n =(2a 1 +(n-1)d)*n/2 имеем 145=(2*15+(n–1)*7)*n/2, 290=(30+(n–1)*7)*n, 290=(30+7n–7)*n, 290=(23+7n)*n, 290=23n+7n 2 , 7n 2 +23n-290=0, n=5 . Ответ: 5. 2 способ. Более трудоёмкий. 1-15-15 2-22-37 3-29-66 4-36-102 5-43-145. Ответ: 5.

Слайд 8

Меняем монеты За­да­ние 20. В об­мен­ном пунк­те можно со­вер­шить одну из двух опе­ра­ций: за 2 зо­ло­тые мо­не­ты по­лу­чить 3 се­реб­ря­ные и одну мед­ную; за 5 се­реб­ря­ных монет по­лу­чить 3 зо­ло­тые и одну мед­ную. У Ни­ко­лая были толь­ко се­реб­ря­ные мо­не­ты. После не­сколь­ких по­се­ще­ний об­мен­но­го пунк­та се­реб­ря­ных монет у него стало мень­ше, зо­ло­тых не по­яви­лось, зато по­яви­лось 50 мед­ных. На сколь­ко умень­ши­лось ко­ли­че­ство се­реб­ря­ных монет у Ни­ко­лая? Решение. Пусть Николай сделал сначала х операций второго типа, а затем у операций первого типа. Тогда имеем: Тогда серебряных монет стало на 3у -5х = 90 – 100 = -10 т.е. на 10 меньше . Ответ: 10

Слайд 9

Хозяин договорился Решение. Из условия понятно, что по­сле­до­ва­тель­ность цен за каждый выкопанный метр является ариф­ме­ти­че­ской про­грес­сией с пер­вым чле­ном а 1 = 3700 и раз­но­стью d=1700 . Сумма пер­вых n чле­нов ариф­ме­ти­че­ской про­грес­сии вы­чис­ля­ет­ся по фор­му­ле S n = 0,5(2a 1 + (n – 1)d)n . Подставляя исходные данные, получаем: S 10 = 0,5(2*3700 + (8 – 1)*1700)*8 = 77200 . Таким образом, хо­зя­ин дол­жен будет за­пла­тить ра­бо­чим 77200 руб. Ответ: 77200. Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3700 рублей, а за каждый следующий метр — на 1700 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?

Слайд 10

Вода в котловане В ре­зуль­та­те па­вод­ка кот­ло­ван за­пол­нил­ся водой до уров­ня 2 метра. Стро­и­тель­ная помпа не­пре­рыв­но от­ка­чи­ва­ет воду, по­ни­жая её уро­вень на 20 см в час. Под­поч­вен­ные воды, на­о­бо­рот, по­вы­ша­ют уро­вень воды в кот­ло­ва­не на 5 см в час. За сколь­ко часов ра­бо­ты помпы уро­вень воды в кот­ло­ва­не опу­стит­ся до 80 см? Решение. В результате работы насоса и подтопления почвенными водами уровень воды в котловане понижается на 20-5=15 сантиметров за час. Чтобы уровень снизился на 200-80=120 сантиметров необходимо 120:15=8 часов. Ответ: 8.

Слайд 11

Бак с щелью В бак объёмом 38 литров каждый час, начиная с 12 часов, наливают полное ведро воды объёмом 8 литров. Но в днище бака есть небольшая щель, и из неё за час вытекает 3 литра. В какой момент времени (в часах) бак будет заполнен полностью? Решение. К концу каждого часа объём воды в баке увеличивается на 8 − 3 = 5 литров. Через 6 часов, то есть в 18 часов, в баке будет 30 литров воды. В 19 часов в бак дольют 8 литров воды и объём воды в баке станет равным 38 литров. Ответ: 19.

Слайд 12

Скважина Неф­тя­ная ком­па­ния бурит сква­жи­ну для до­бы­чи нефти, ко­то­рая за­ле­га­ет, по дан­ным гео­ло­го­раз­вед­ки, на глу­би­не 3 км. В те­че­ние ра­бо­че­го дня бу­риль­щи­ки про­хо­дят 300 мет­ров в глу­би­ну, но за ночь сква­жи­на вновь «за­или­ва­ет­ся», то есть за­пол­ня­ет­ся грун­том на 30 мет­ров. За сколь­ко ра­бо­чих дней неф­тя­ни­ки про­бу­рят сква­жи­ну до глу­би­ны за­ле­га­ния нефти? Решение. Учитывая заиливание скважины, в течении суток проходят 300-30=270 метров. Значит за 10 полных суток будет пройдено 2700 метров и за 11-й рабочий день будет пройдено ещё 300 метров. Ответ: 11.

Слайд 13

Глобус На по­верх­но­сти гло­бу­са фло­ма­сте­ром про­ве­де­ны 17 па­рал­ле­лей и 24 ме­ри­ди­а­на. На сколь­ко ча­стей про­ведённые линии раз­де­ли­ли по­верх­ность гло­бу­са? Решение. Одна параллель разбивает поверхность глобуса на 2 части. Две на три части. Три на четыре части и т. д. 17 параллелей разбивают поверхность на 18 частей. Проведём один меридиан, и получим одну целую (не разрезанную) поверхность. Проведём второй меридиан и у нас уже две части, третий меридиан разобьёт поверхность на три части и т. д. 24 меридиана разбили нашу поверхность на 24 части. Получаем 18*24=432. Все линии разделят поверхность глобуса на 432 части. Ответ: 432.

Слайд 14

Кузнечик прыгает Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 8 прыжков, начиная прыгать из начала координат? Решение: Немного подумав, мы можем за­ме­тить, что куз­не­чик может ока­зать­ся толь­ко в точ­ках с чётными ко­ор­ди­на­та­ми, по­сколь­ку число прыж­ков, ко­то­рое он де­ла­ет, чётно. Например, если он сделает пять прыжков в одну сторону, то в обратную сторону он сделает три прыжка и окажется в точках 2 или −2. Мак­си­маль­но куз­не­чик может ока­зать­ся в точ­ках, мо­дуль ко­то­рых не пре­вы­ша­ет восьми. Таким об­ра­зом, куз­не­чик может ока­зать­ся в точ­ках: −8, −6, −4, −2, 0, 2, 4, 6 и 8; всего 9 точек. Ответ: 9 .

Слайд 15

Новые бактерии Каж­дую се­кун­ду бак­те­рия де­лит­ся на две новые бак­те­рии. Из­вест­но, что весь объём од­но­го ста­ка­на бак­те­рии за­пол­ня­ют за 1 час. За сколь­ко се­кунд бак­те­рии за­пол­ня­ют по­ло­ви­ну ста­ка­на? Решение. Вспомним, что 1 час = 3600 секундам. Через каждую секунду бактерий становится в два раза больше. Значит, чтобы из половины стакана бактерий получился полный стакан нужна всего 1 секунда. Поэтому стакан был заполнен на половину за 3600-1=3599 секунд. Ответ: 3599.

Слайд 16

Делим числа Про­из­ве­де­ние де­ся­ти иду­щих под­ряд чисел раз­де­ли­ли на 7. Чему может быть равен оста­ток? Решение. Задача простая, так как среди десяти подряд идущих натуральных чисел хотя бы одно делится на 7. Значит и всё произведение будет делиться на 7 без остатка. То есть остаток равен 0. Ответ: 0.

Слайд 17

Где живёт Петя? Задача 1. В доме, в котором живёт Петя, один подъезд. На каждом этаже по шесть квартир. Петя живёт в квартире № 50. На каком этаже живёт Петя? Решение: Делим 50 на 6, получаем частное 8 и 2 в остатке. Это значит, что Петя живёт на 9 этаже. Ответ: 9. Задача 2. Во всех подъездах дома одинаковое число этажей, и на всех этажах одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 455 квартир? Решение: Решение этой задачи вытекает из разложения числа 455 на простые множители. 455 = 13*7*5. Значит в доме 13 этажей, по 7 квартир на каждом этаже в подъезде, 5 подъездов. Ответ: 13.

Слайд 18

Задача 3. Саша пригласил Петю в гости, сказав, что живёт в восьмом подъезде в квартире № 468, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом двенадцатиэтажный. На каком этаже живёт Саша? (На всех этажах число квартир одинаково, номера квартир в доме начинаются с единицы.) Решение: Петя может подсчитать, что в двенадцатиэтажном доме в первых семи подъездах 12*7=84 площадки. Дальше, перебирая возможное количество квартир на одной площадке, можно увидеть, что их меньше шести, так как 84*6 = 504. Это больше 468. Значит , на каждой из площадок 5 квартир, тогда в первых семи подъездах 84*5 =420 квартир. 468 – 420 = 48, то есть Саша живёт в 48 квартире в 8 подъезде (если бы нумерация была с единицы в каждом подъезде). 48:5 = 9 и 3 в остатке. Таким образом Сашина квартира на 10 этаже. Ответ: 10.

Слайд 19

Меню ресторана В меню ресторана имеется 6 видов салатов, 3 вида первых блюд, 5 видов вторых блюд и 4 вида десерта. Сколько вариантов обеда из салата, первого, второго и десерта могут выбрать посетители этого ресторана? Решение. Если мы пронумеруем каждый салат, первое, второе, десерт, то: с 1 салатом, 1 первым,1 вторым можно подать один из 4-х десертов. 4 варианта. Со вторым вторым тоже 4 варианта и т.д. Всего получим 6*3*5*4=360. Ответ: 360.

Слайд 20

Маша и медведь Медведь съел свою половину банки варенья в 3 раза быстрее, чем Маша, значит, у него еще осталось в 3 раза больше времени на кушанье печенья. Т.к. Медведь ест печенье в 3 раза быстрее, чем Маша и еще у него осталось в 3 раза больше времени (он съел в 3 раза быстрее свою половину банки варенья), то он съедает в 3⋅3=9 раз больше печений, чем Маша (9 печений съедает Медведь, в то время как Маша только 1 печенье). Получается, что в отношении 9:1 едят Медведь и Маша печенье. Всего получается 10 долей, значит, 1 доля равна 160:10=16. В итоге, Медведь съел 16⋅9=144 печений. Ответ: 144 Маша и Медведь съели 160 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенье они съели поровну?

Слайд 21

Палки и линии На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Решение. Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14+4+6=24 линии, следовательно, кусков будет 25. Ответ: 25

Слайд 22

Врач прописал Врач прописал пациенту принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а в каждый следующий день — на 3 капли больше, чем в предыдущий. Приняв 30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет 250 капель )? Решение На первом этапе приёма капель число принимаемых капель в день представляет собой возрастающую арифметическую прогрессию с первым членом, равным 3, разностью, равной 3 и последним членом, равным 30. Следовательно: Тогда 3 + 3( n -1)=30; 3+ 3 n -3=30; 3 n =30; n =10 , т.е. прошло 10 дней по схеме увеличения до 30 капель. Знаем формулу суммы ариф . прогрессии: Вычислим S10 :

Слайд 23

За следующие 3 дня – по 30 капель: 30 · 3 = 90 (капель) На последнем этапе приёма: Т.е. 30 -3( n-1 ) =0; 30 -3n+3=0; -3n=-33; n=11 т.е. 11 дней приём лекарства уменьшался. Найдём сумму арифметич . прогрессии 4) Значит, 165 + 90 + 165 = 420 капель всего 5) Тогда 420 : 250 = 42/25 = 1 (17/25) пузырька Ответ: надо купить 2 пузырька

Слайд 24

Магазин бытовой техники В магазине бытовой техники объём продаж холодильников носит сезонный характер. В январе было продано 10 холодильников, и в три последующих месяца продавали по 10 холодильников. С мая продажи увеличивались на 15 единиц по сравнению с предыдущим месяцем. С сентября объём продаж начал уменьшаться на 15 холодильников каждый месяц относительно предыдущего месяца. Сколько холодильников продал магазин за год? Решение. Последовательно рассчитаем сколько холодильников было продано за каждый месяц и просуммируем результаты: 10 · 4+(10+15)+(25+15)+(40+15 )+( 55+15)+(70-15)+ (55-15 )+( 40-15)+ ( 25-15 )= = 40+25+40+55+70+55+40+25+10=120+110+130=360 Ответ: 360.

Слайд 25

Ящики Ящики двух видов, имеющие одинаковую ширину и высоту, укладывают на складе в один ряд длиной 43м, приставляя друг к другу по ширине. Ящики одного вида имеют длину 2м, а другого-5м. Какое наименьшее число ящиков потребуется для заполнения всего ряда без образования пустых мест? Решение Т.к . надо найти наименьшее число ящиков, то => надо взять наибольшее количество больших ящиков. Значит 5 · 7 = 35; 43 – 35 = 8 и 8:2=4 ; 4+7=11 Значит, ящиков всего 11 . Ответ: 11.

Слайд 26

Таблица В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 119, во втором — 125, в третьем — 133, а сумма чисел в каждой строке больше 15, но меньше 18. Сколько всего строк в столбце? Решение. Общая сумма во всех столбцах = 119 + 125 + 133 = 377 Числа 18 и 15 не включены в предел, значит: 1) если сумма в строке = 17, то, количество строк равно 377 : 17= =22,2 2) если сумма в строке = 16, то, количество строк равно 377 : 16= =23,5 Значит кол-во строк = 23 (т.к. оно должно быть между 22,2 и 23,5 ) Ответ: 23

Слайд 27

Викторина и задания Список заданий викторины состоял из 36 вопросов. За каждый правильный ответ ученик получал 5 очков, за неправильный ответ с него списывали 11 очков, а при отсутствие ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 75 очков, если известно, что по крайней мере один раз он ошибся? Решение. 1 способ: Пусть Х – количество верных ответов у – количество неверных ответов. Тогда составим уравнение 5х -11у = 75, где 0 < х < 36 и 0 < у < 36 . Из уравнения видно, что у делится на 5. Пусть: 1) у=5, тогда 5х = 75 + 11у= 75 + 55=130, тогда х = 130 : 5 = 26 и это меньше 36. 2) у=10, тогда 5х =75 +11у=75+110=185, тогда х = 185 : 5=37, но это больше 36 . Ответ:26 2 способ: 36 вопросов — 11 очков за неправильный ответ + 1 = 26 очков

Слайд 28

Группа туристов Группа туристов преодолела горный перевал. Первый километр подъёма они преодолели за 50 минут, а каждый следующий километр проходили на 15 минут дольше предыдущего. Последний километр перед вершиной был пройден за 95 минут. После десятиминутного отдыха на вершине туристы начали спуск, который был более пологим. Первый километр после вершины был пройден за час, а каждый следующий на 10 минут быстрее предыдущего. Сколько часов группа затратила на весь маршрут, если последний километр спуска был пройден за 10 минут? Решение. На подъём в гору группа затратила 290 минут, на отдых 10 минут, на спуск с горы 210 минут. В сумме туристы затратили на весь маршрут 510 минут. Переведём 510 минут в часы и получим, что за 8,5 часов туристы преодолели весь маршрут . Ответ: 8,5

Слайд 29

Спасибо за внимание!

Единый государственный экзамен является на данный момент единственной

формой итоговой аттестации выпускников средней школы. А получение

аттестата о среднем образовании не возможно без успешной сдачи ЕГЭ по

математике. Математика является не только важным учебным предметом, но

и достаточно сложным. Математическими способностями обладают далеко

не все дети, а от успешной сдачи экзамена зависит их дальнейшая судьба.

Учителя выпускных классов снова и снова задают вопрос: «Как помочь

школьнику при подготовке к ЕГЭ и успешно его сдать?». Для того, чтобы

выпускник получил аттестат достаточно сдать математику базового уровня. А

успешность сдачи экзамена напрямую связана с тем, как учитель владеет

методикой решения различных задач. Вашему вниманию предлагаю примеры

решения задания №20 математика базовый уровень ФИПИ 2018 под

редакцией М.В. Ященко.

1.На ленте по разные стороны от середине отмечены две полосы: синяя и

красная. Если ленту разрезать по красной полосе, то одна часть будет на 5 см

длиннее другой. Если ленту разрезать по синей полосе, то одна часть будет на

15 см длиннее другой. Найдите расстояние между красной и синей

полосами.

Решение:

Пусть а см расстояние от левого конца ленты до синей полосы, в см

расстояние от правого конца ленты до красной полосы, с см расстояние

между полосами. Известно, что если ленту разрезать по красной полосе, то

одна часть на 5 см длиннее другой, то есть а + с – в =5. Если разрезать по

синей полосе, то одна часть будет длиннее другой на 15 см, значит, в +с –

а=15. Сложим два равенство почленно: а+с-в+в+с-а=20, 2с=20, с=10.

Ответ:10.

2. Среднее арифметическое 6 различных натуральных чисел равно 8. На

сколько нужно увеличить наибольшее из этих чисел, чтобы среднее

арифметическое стало на 1 больше.

Решение: Так как среднее арифметическое 6 натуральных чисел равно 8,

значит, сумма этих чисел равна 8*6=48. Среднее арифметическое чисел

увеличилось на 1 и стало равно 9, а количество чисел не изменилось, значит,

сумма чисел стане равной 9*6=54. Чтобы найти на сколько увеличилось одно

из чисел, нужно найти разность 54-48=6.

Ответ:6.

3. Клетки таблицы 6х5 раскрашены в черные и белые цвета. Пар соседних

клеток разного цвета 26, пар соседних клеток черного цвета 6. Сколько пар

соседних клеток белого цвета.

Решение:

В каждой горизонтали образуется 5 пар соседних клеток, значит, по

горизонтали всего будет 5*5=25 пар соседних клеток. По вертикали

образуется 4 пары соседних клеток, то есть всего пар соседних клеток по

вертикали будет 4*6=24. Всего образуется 24+25=49 пар соседних клеток. Из

них разного цвета 26 пар, черного 6 пар, следовательно белых пар будет 49-

26-6 = 17 пар.

Ответ: 17 .

4.На прилавке цветочного магазина стоят три вазы с розами: белая, синяя и

красная. Слева от красной вазы находится 15 роз, справа от синей вазы 12

роз. Всего в вазах 22 розы. Сколько роз в белой вазе?

Решение: Пусть х роз находится в белой вазе, у роз – в синей, z роз – в

красной. По условию задачи в вазах 22 розы, то есть х+у+ z=22. Известно,

что слева от красной вазы, то есть в синей и белой 15 роз, значит, х+у=15. А

справа от синей вазы, то есть в белой и красной вазах 12 роз, значит х+ z= 12.

Получили:

х+у+ z=22;

х+у=15;

х+ z= 12.

Прибавим почленно 2-ое и 3-ье равенства: х+у+х+ z=27 или 22 +х=27, х=5.

Ответ: 5.

5.Маша и Медведь съели 160 печений и банку варенья, начав и закончив

одновременно. Сначала Маша ела варенье, а Медведь печенья, но в какой-то

момент они поменялись. Медведь и то и другое ест в 3 раза быстрее Маши.

Сколько печений съел Медведь, если варенья они съели поровну.

Решение: Так как Маша и Медведь начали есть печенья и варенье

одновременно и закончили одновременно, причем ели один продукт, а затем

другой, и по условию задачи Медведь ест и то и другое в 3 раза быстрее, чем

Маша, значит Медведь поглощал еду в 9 раз быстрее Маши. Тогда пусть х

печений съела Маша, а Медведь 9х печений. Известно, что всего они съели

160 печений. Получим: х+9х=160, 10х=160, х=16, значит, медведь съел

16*9=144 печенья.

Ответ:144.

6.Из книги выпало несколько идущих подряд листов. Номер последней

страницы перед выпавшими листами 352. Номер первой страницы после

выпавших листов записывается теми же цифрами, но в другом порядке.

Сколько листов выпало?

Решение: Пусть х листов выпало, тогда количество выпавших страниц 2х, то

есть четное число. Номер первой выпавшей страницы 353. Разность между

номером первой выпавшей страницы и первой страницы после выпавших

должно быть четным числом, значит, номер после выпавших листов будет

523. Тогда количество выпавших листов будет равно (523-353):2=85.

Ответ: 85.

7. Про натуральные числа А,В,С известно, что каждое из них больше 5, но

меньше 9. Загадали натуральное число, затем умножили на А, прибавили В и

вычли С. Получили 164. Какое число было задумано?

Решение: Пусть х загаданное натуральное число, тогда Ах+В-С=164, Ах=

164 – (В-С), так как числа А,В,С больше 5, но меньше 9, то -2≤В-С≤2,

значит, Ах= 166; 165; 164;163;162. Из чисел 6,7,8 только 6 является

делителем 162. Следовательно, х=162:6=27.

Ответ:27

Предлагаем вашему вниманию разбор 20 задания по математике (базовый уровень) к ЕГЭ 2019 с комментариями

01 октября 2018

Демонстрационная версия ЕГЭ (базовый уровень) – 2019 год

Задание 20

В обменном пункте можно совершить одну из двух операций:

1. За 2 золотых монеты получить 3 серебряных и одну медную
2. За 5 серебряных монет получить 3 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 50 медных. На сколько уменьшилось количество серебряных монет у Николая?

Решение:

Т.к. у Николая нет золотых монет, значит он может начинать со второй операции, пусть таких операций он совершил b,

Тогда количество первых операций будет a.

Составим уравнение для золотых монет:

2a = 3b

a = 1,5b

Общее количество операций: a + b = 50

1,5b + b = 50

2,5b = 50

b = 20

Первая операция была проделана: a = 20 · 1,5 = 30 раз

Получено: 3 · 30 = 90 серебряных монет

Вторая операция проделана 20 раз (b = 20) 

Получено: 5 · 20 = 100 серебряных монет

Количество серебряных монет у Николая уменьшилось на 10 монет:

100 – 90 = 10 монет.

Ответ: 10

Или

Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трех из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвертого прямоугольника.

Решение:

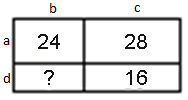
Выразим периметры прямоугольников:

2 · (a + b) = 24

2 · (a + c) = 28

2 · (d + c) = 16

2 · (d + b) = ?

d + b = 8 – 2

d + b = 6

2 · (d + b) = 2 · 6 = 12

Ответ: 12.

#ADVERTISING_INSERT#