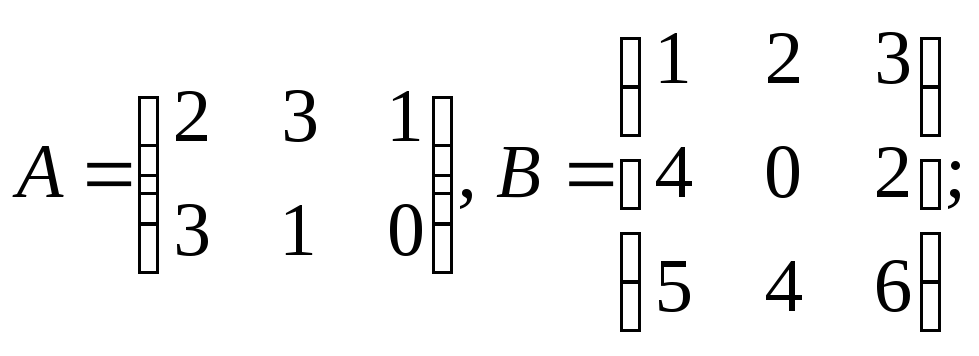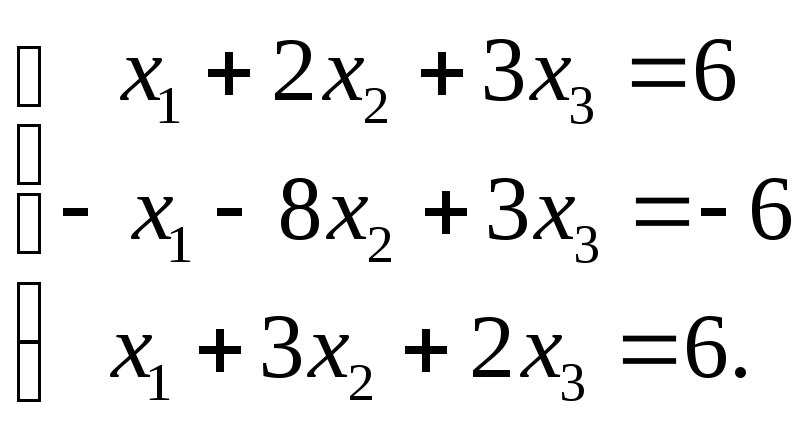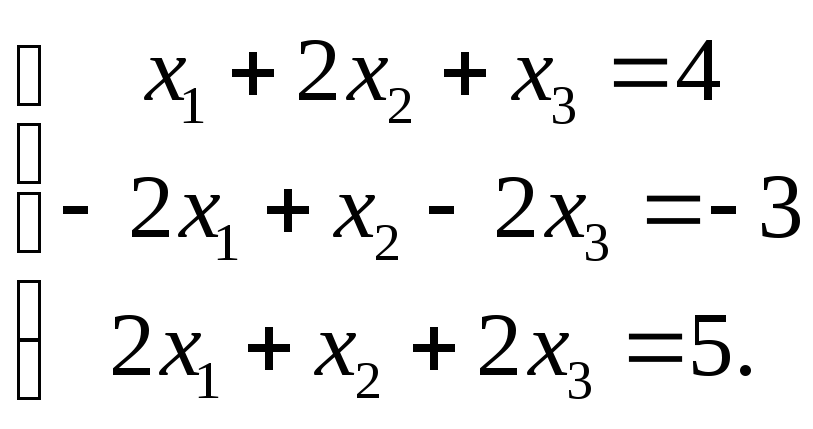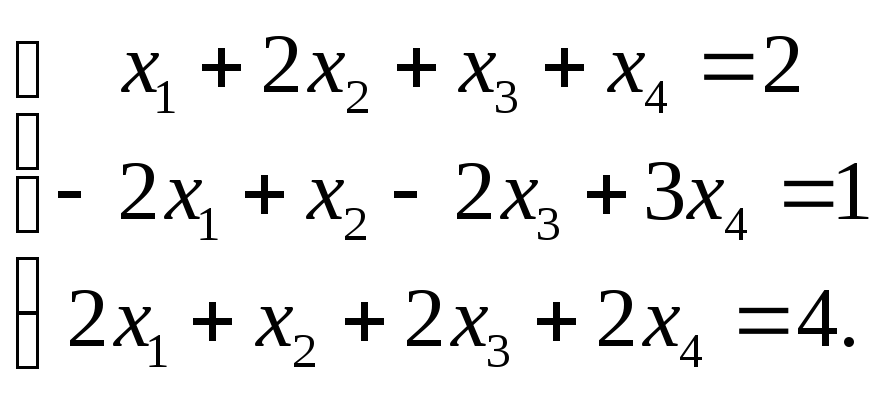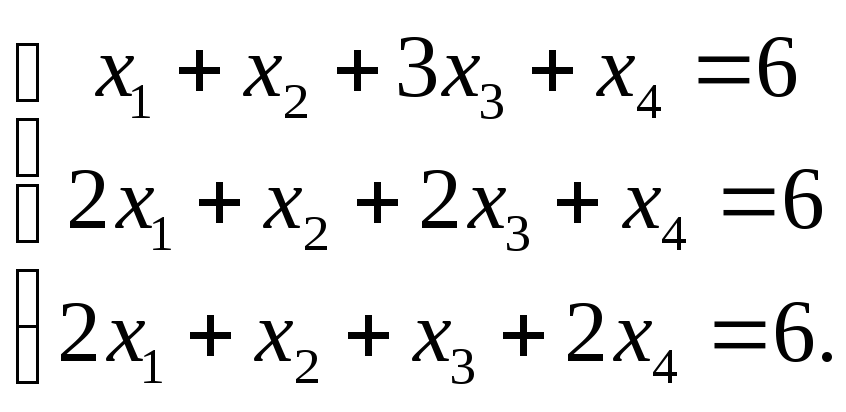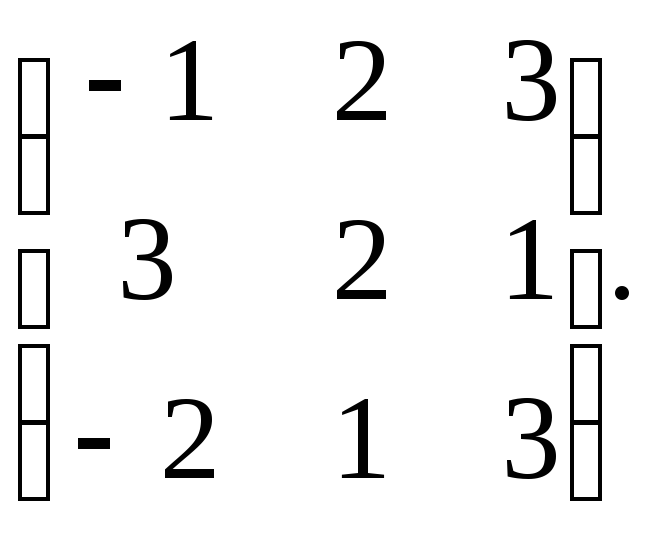Как сдать линейную алгебру
Самая начальная и одна из самых непростых математических дисциплин имеет весьма много подвохов. Но сдать экзамен по ней не так уж и сложно: нужно освежить в памяти знания, полученные в течение семестра.

Инструкция
Линейная алгебра, как правило, это «вводная дисциплина» в дальнейшее изучение математических наук. С нее начинается изучение самых простых понятий, но в то же время и самых важных. В связи с этим начать подготовку к экзамену стоит с повторения темы «Матрицы и операции над ними». Важно вспомнить свойства сложения и умножения. Они во многом упрощают жизнь при решении определенных задач.
Повторите все, что связано с определителем матрицы. Здесь особое внимание нужно обратить на свойства, так как именно с их помощью вы сможете найти определитель абсолютно любой матрицы. Но это вам понадобится при решении практического задания. К экзамену вам обязательно нужно будет знать метод Гаусса. Он является основным в применении к решению задач. Суть его в том, чтобы быстро найти определитель какой-либо матрицы.
Далее нужно восстановить в памяти такие понятия, как минор и его алгебраические дополнения. Они приводят к рангу матрицы, который является максимально возможным порядком всех отличных от нуля миноров.
Данную теорию нужно повторить, потому что в заданиях к билетам часто нужно не только посчитать определитель матрицы, но и найти ее ранг. По определению находить его чаще всего не рационально. Поэтому матрицу с помощью метода Гаусса обычно приводят к «ступенчатому» виду. Причем все миноры, которые отличны от нуля, так и остаются ненулевыми, а те, что равны нулю, остаются нулевыми.
Следующий раздел для повторения — это тема «Обратная матрица». Найти обратную к исходной — любое задание каждого преподавателя. В этом случае нужно вспомнить теорему о существовании таковой: если определитель матрицы не равен нулю, то обратная к ней существует.
И последнее, что нужно знать к экзамену, чтобы его сдать на положительную оценку, это система линейных уравнений. Изученные сведения о матрицах и действий над ними помогут вам освоиться и здесь. Все преобразования, которые нужно провести с линейными уравнениями, так или иначе подчиняются законам матричных операций.
Обратите внимание
1) Перемножение двух матриц порою вызывает трудности, тем более если долго с данной операцией не работал. Поэтому обязательно повторите и вспомните, как правильно умножаются две матрицы.
2) Все теоремы, которые были изучены в процессе прохождения курса линейной алгебры, нужно знать с доказательствами. В большинстве случаев на экзаменах преподаватели спрашивают не саму теорию, которой не так уж и много, а именно доказательства и понимание теорем.
Полезный совет
1) Постарайтесь не забывать, что при транспозиции четность перестановки меняется.
2) Помните, что транспонированная матрица — это преобразование, при котором каждая строка становится столбцом.
3) Определитель матрицы не изменится, если из какой-либо ее строки вычесть любую другую, домноженную на произвольное действительное число.
4) Определитель матрицы равен сумме всех элементов произвольной строки, домноженных на их алгебраические дополнения.
5) Все элементарные преобразования преобразуют систему линейных уравнений в систему ей равносильную.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вопросы
для подготовки к экзамену по линейной
алгебре и аналитической геометрии
Элементы
линейной алгебры
1. Матрицы, виды матриц (квадратная,
диагональная, единичная, нулевая).
2. Действия с матрицами (сложение,
умножение на число, умножение матриц),
их свойства; перестановочные матрицы,
необходимое условие перестановочности
матриц.
3. Определитель матрицы n–го
порядка, свойства определителей.
4. Миноры и алгебраические дополнения.
Разложение определителя по элементам
произвольной строки или столбца.
5. Ранг матрицы. Ступенчатая матрица.
Элементарные преобразования строк
(столбцов) матрицы, определение. Теорема
о ранге ступенчатой матрицы.
6. Обратная матрица, теорема о единственности
обратной матрицы в случае ее существования.
Способы нахождения обратной матрицы:
с помощью элементарных преобразований,
алгебраических дополнений.
7. Системы линейных уравнений, основная
и расширенная матрицы системы, матричная
форма записи системы линейных уравнений.
8. Системы линейных уравнений и методы
их решения: с помощью обратной матрицы
(обоснование), метод Крамера (обоснование),
метод Гаусса (описание алгоритма).
Элементы векторной алгебры и
аналитической геометрии
1.
Вектор. Операции
с векторами (сложение, умножение на
число, скалярное произведение). Свойства
скалярного произведения векторов.
Коллинеарные векторы, определение.
Необходимое и достаточное условия
коллинеарности двух векторов.
2.
Теорема о разложении вектора по двум
неколлинеарным векторам.
3.
Координаты вектора. Необходимое и
достаточное условие коллинеарности
двух векторов в координатной форме.
4.
Скалярное произведение двух векторов,
заданных координатами. Необходимое и
достаточное условие перпендикулярности
двух векторов, заданных координатами.
5.
Линейная
зависимость и линейная независимость
векторов, определение. Основные теоремы
о линейной зависимости: линейная
зависимость системы векторов, содержащей
нулевой вектор; содержащей два
пропорциональных вектора. Связь между
линейной зависимостью и коллинеарностью
двух векторов. Связь между линейной
зависимостью и компланарностью трех
векторов.
6. Деление отрезка
в данном отношении.
7.
Уравнение линии на плоскости. Вывод
уравнения окружности.
8.
Уравнение прямой линии на плоскости.
Направляющий и нормальный векторы
прямой, определения. Уравнение прямой,
заданной: точкой и направляющим вектором;
точкой и нормальным вектором; точкой и
угловым коэффициентом; двумя точками.
9.
Взаимное расположение прямых на
плоскости: угол между двумя прямыми;
необходимые и достаточные условия
параллельности и перпендикулярности
двух прямых.
10.
Общее уравнение прямой. Теорема о том,
что любое уравнение первой степени
относительно переменных x,
y
определяет прямую линию на плоскости.
11.
Расстояние от точки до прямой.
12.
Геометрический смысл линейных неравенств
с двумя переменными.
13.
Кривые второго порядка: эллипс (вывод
канонического уравнения эллипса),
гипербола (вывод канонического уравнения
гиперболы), парабола (вывод канонического
уравнения параболы).
14.
Уравнение плоскости, заданной: точкой
и нормальным вектором; тремя точками.
Условия параллельности и перпендикулярности
плоскостей. Угол между двумя плоскостями.
Расстояние от точки до плоскости.
Уравнение плоскости, проходящей через
заданную точку параллельно заданной
плоскости.
15.
Уравнение прямой, заданной точкой и
направляющим вектором; параметрические
уравнения прямой. Угол между прямой и
плоскостью. Условия параллельности и
перпендикулярности прямой и плоскости.
16.
Уравнение прямой, проходящей через
заданную точку перпендикулярно заданной
плоскости. Уравнение плоскости, проходящей
через заданную точку перпендикулярно
заданной прямой.
Задания для
подготовки к экзамену по линейной
алгебре и аналитической геометрии
1.
Даны матрицы
и
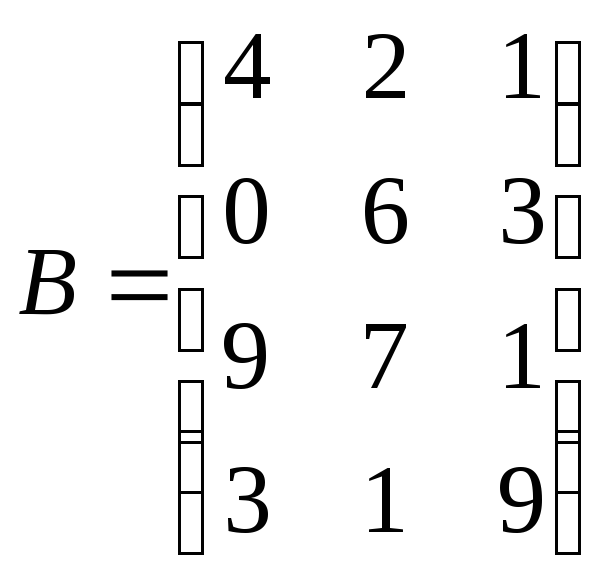
Найдите сумму этих матриц и разность
А
– В.
2.
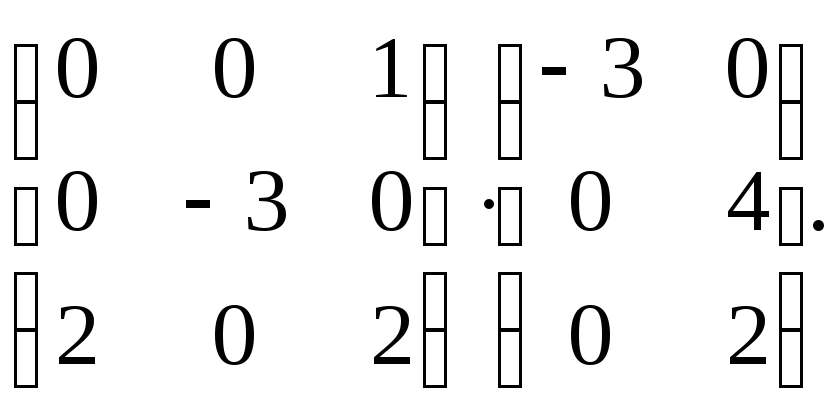
Найдите произведение матриц: а)
б)
3.
Найдите элемент с21
матрицы С = АВ,
если
4.
Решите уравнение
.
5.
Вычислите определитель: а)

б)
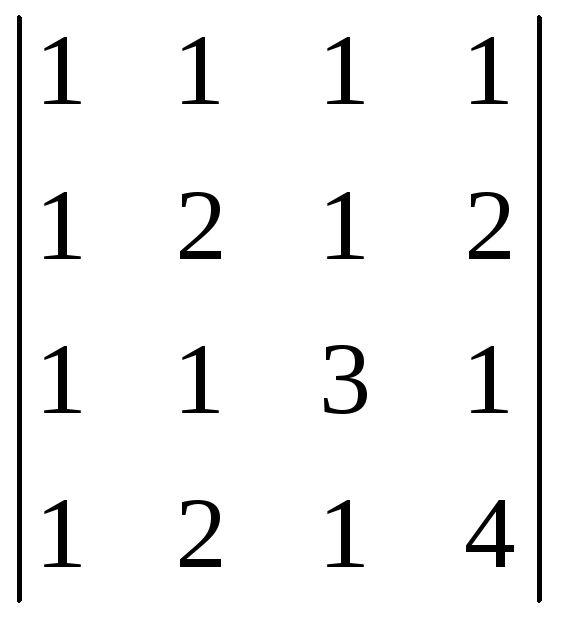
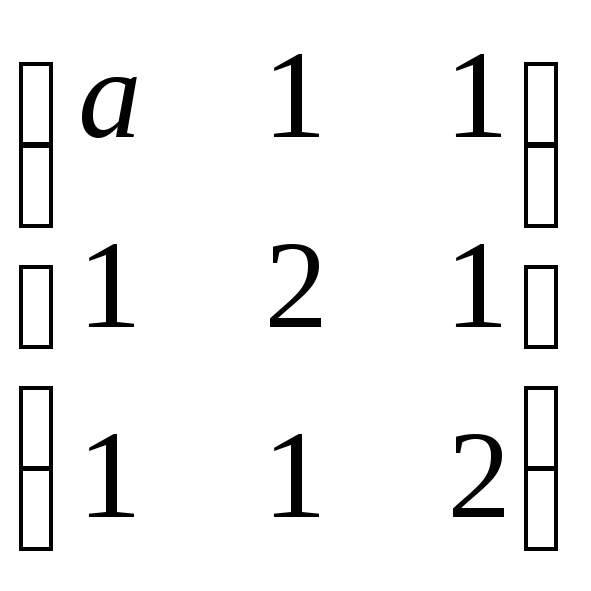
6.
При каких значениях параметра а
матрица
не имеет обратной?
7. Решите систему
уравнений:
а)
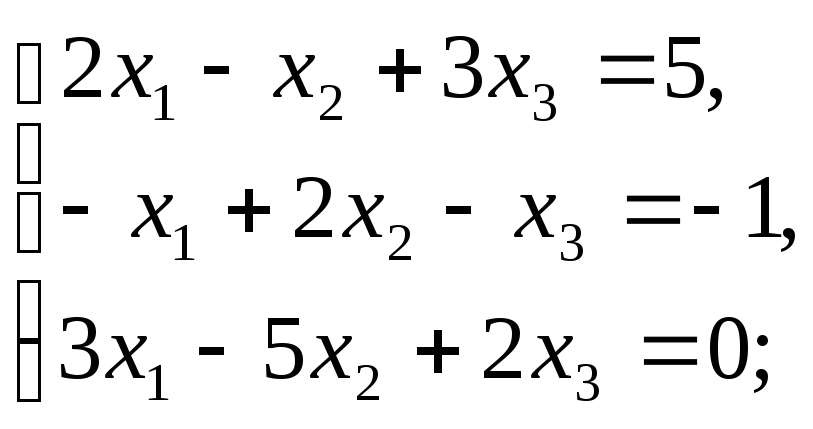
в)
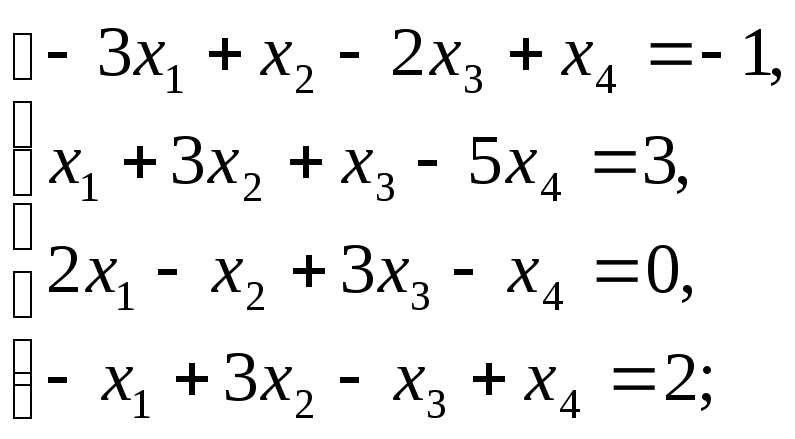
8.
Даны векторы
и
.
Найдите: а)
;
б)
.
9.
Даны векторы
.
Найдите угол между векторами:
а)
и
;
б)
и
;
в)
и
.
10.
Найдите угол между векторами
и
,
если А(2;5;0),
Р(−2;4;8),
М(0;−1;5).
11.
Найдите х,
при котором векторы
и
перпендикулярны.
12.
Даны векторы
и
.
При каком значении m
эти векторы коллинеарны?
13.
На векторах
и
построен параллелограмм. Найдите длины
диагоналей этого параллелограмма и
косинус острого угла между ними, если
.
14.
Найдите вектор
,
cонаправленный
с вектором
,
если известно, что
.
15.
Найдите вектор
,
коллинеарный вектору
,
если известно, что
.
16. Исследуйте на
линейную зависимость векторы:
1)
;
2)
.
17.
Разложите вектор
по векторам
,
если это возможно.
18.
Напишите уравнение прямой, проходящей
через точку М(0;−2)
перпендикулярно прямой x + 2y – 1 = 0.
19.
Прямая проходит через середину отрезка,
соединяющего точки А(−2;−2)
и В(4;0),
перпендикулярно этому отрезку. Составьте
уравнение этой прямой.
20.
Найдите расстояния от точек А(1;−2),
В(0;−1)
и С(2;−2)
до прямой 2x + y
− 2 = 0.
21. Даны вершины
треугольника: А(−2;−4), В(−5;2), С(3;6).
1)
Напишите уравнения прямых, содержащих
стороны треугольника АВС.
2)
Напишите уравнение прямой, содержащей
медиану АМ
и найдите ее длину.
3)
Напишите уравнение прямой, содержащей
высоту ВН
и найдите ее длину.
4)
Напишите уравнение прямой, содержащей
среднюю линию MN
(точка N –
середина стороны СА),
найдите ее длину.
5)
Найдите расстояние от точки В
до медианы АМ.
22.
Изобразите на плоскости множество
точек, координаты которых удовлетворяют
системе линейных неравенств:
1)
2)
23.
Что представляют собой геометрические
места точек плоскости, заданные следующими
уравнениями? Изобразите эти геометрические
места точек.
1)
25x2
+ 9y2
= 225; 2) 36y2
− 9x2=
324;
3)
x2
+ y2
= 25; 4) x2
− 16y2
= 16;
5)
у2
= 5х; 6)
16x2
+ 25y2
+ 64x
− 50y
− 311 = 0.
24.
Напишите уравнение плоскости, проходящей
через точки М1(−2;3;−5),
М2(1;2;−4)
и М3(5;0;−3).
25.
Даны точки М1(1;−3;5)
и М2(3;2;0).
Напишите уравнение плоскости, проходящей
через точку М1
и перпендикулярной вектору
.
26.
Напишите уравнение прямой, проходящей
через точку
М(1;3;−2)
и
параллельной вектору
.
27.
Напишите уравнение прямой, проходящей
через точки
М1(5;–3;2)
и
М2(3;1;–2).
28.
Определите взаимное расположение
плоскостей: а) 2x
– 3y
– 4z
+ 11 = 0, –4x
+ 6y
+ 8z
+ 36 = 0;
б)
2x
– 3z
– 12 = 0, 4x
+ 4y
– 6z
+ 7 = 0; в) 3x
– 2y
– 2z
+ 7 = 0, 2x
+ 2y
+ z
+ 4 = 0.
29.
Найдите угол между плоскостями
и
.
30.
Напишите уравнение плоскости, проходящей
через точку М(2;–1;6) параллельно плоскости
x
+ y
– 2z
+ 5 = 0.
31.
Найдите расстояние от точки А(3;9;1)
до плоскости x
– 2y
+ 2z
– 3 = 0.
32. Напишите
уравнение плоскости, проходящей через
точку М(–1;–5;8)
перпендикулярно прямой
.
33. Напишите
уравнение прямой, проходящей через
начало координат перпендикулярно
плоскости, заданной уравнением
3x + 5z – 5 = 0.
Задания для
самостоятельной работы
Вариант 1.1
1) Найдите
произведения (если они существуют) АВ
и ВА, где
2) Решите систему
уравнений
3) Найдите косинус
угла между векторами
и
,
если известно, что
4) Напишите
уравнение прямой, проходящей через
точку М(–3;2)
параллельно прямой 3x + y – 1 = 0.
5) Какую линию
на плоскости задает уравнение x2
+ 4y2 = 36? Постройте
эту линию в прямоугольной системе
координат.
Вариант 1.2
1) Найдите произведения
(если они существуют) АВ и ВА,
где
2) Решите систему
уравнений
3) При каком
значении параметра а векторы
и
будут коллинеарны?
4) Напишите
уравнение прямой, проходящей через
точку М(–2;–1)
параллельно прямой 3x – 2y + 7 = 0.
5) Какую линию
на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.
Вариант 2.1
1) Найдите матрицу
C = 2AВ
− 3B, если
2) Решите систему
уравнений
3) Найдите длину
вектора
,
если известно, что
4) Напишите
уравнение прямой, проходящей через
точку М(0;–2)
перпендикулярно прямой x – 2y + 5 = 0.
5) Какую линию
на плоскости задает уравнение 6x2
− 4y2 = 36? Постройте
эту линию в прямоугольной системе
координат.
Вариант 2.2
1) Найдите матрицу
C = 3AВ
− 2А, если
2) Решите систему
уравнений
3) Найдите длину
вектора
,
если известно, что А(1;0;2), В(–1;0;3),
С(–2;–3;5).
4) Напишите
уравнение прямой, проходящей через
точку М(–1;3)
перпендикулярно прямой x – 2y + 7 = 0.
5) Какую линию
на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.
БИЛЕТ
(образец)
1. а) Алгебраическое
дополнение элемента матрицы. Разложение
определителя матрицы по элементам
любого столбца.
б) Вычислите
сумму А13 – А32,
где Aij − алгебраическое
дополнение соответствующего элемента
матрицы
2. а) Теорема
о том, что координаты точек, лежащих в
одной полуплоскости относительно
прямой, заданной уравнением Ax
+ By
+ C
= 0, удовлетворяют одному из неравенств
Ax
+ By
+ C
> 0, Ax
+ By
+ C
< 0.
б) Не
выполняя построение, выясните, пересекает
ли прямая 3x
– y
+ 5 = 0 отрезок АВ,
где А(5;–1),
В(–3;2).
3. 1)
Найдите матрицу C
= 3AВ
− 2А,
если
2) Решите
систему уравнений
3) Найдите
длину вектора
,
если известно, что А(1;0;2),
В(–1;0;3),
С(–2;–3;5).
4) Напишите
уравнение прямой, проходящей через
точку М(–1;3)
перпендикулярно прямой
x – 2y + 7 = 0.
5) Какую
линию на плоскости задает уравнение
?
Постройте эту линию в прямоугольной
системе координат.
Образование
Подготовится к экзамену по линейной алгебре
В июне у меня намечается сессия и особую сложность из всех предметов,которые предстоит сдавать на ней представляет линейная алгебра , так как ,у меня с ней возникли некоторые проблемы, да и преподаватель очень строгий. К тому же у нас с ним не сложились отношения , так как он любит поиздеваться, а я не любитель терпеть подобное и говорю всё ,что лежит на душе.В последний раз,когда он отнёсся по-хамски , я сказал, что он мой лучший преподаватель), думаю не стоило так,но тогда я был очень взбешён .Так или иначе мне придётся попотеть, чтобы сдать нормально экзамен.
Критерий завершения
Я сдал экзамен по линейной алгебре (при этом выполнив весь план действий описанный ниже).
Личные ресурсы
Интернет(форумы,учебные порталы,онлайн калькуляторы),Учебники, одногруппники,друзья,прошлый преподаватель, мозги.
Экологичность цели
Я хочу достигнуть этой цели для того,чтобы не вылететь из универа и не попасть в армию).
Как сдать экзамен по линейной алгебре?
Предстоит экзамен по линейной алгебре, а вы знаете как найти обратную матрицу, что такое собственный вектор и как отличаются способы Гаусса и Крамера для решения СЛАУ? Мы знаем выход.
Подробно решим и объясним задачи из билета в режиме реального времени.
Схема работы
Оформляете заявку на сайте
Оплачиваете заказ прямо из дома
Автор в указанное время консультирует онлайн
Экзамен сдан!
Почему МатБюро?
- Быстро: первое решение в течение 2-5 минут после отсылки задания, оперативное последующее выполнение задач (как оказывается онлайн помощь).
- Подробно и понятно: сможете разобраться в решении, ответить на вопросы преподавателя, защитить работу (ниже примеры решений).
- Удобно: передаем решение подходящим для вас способом: e-mail, ВКонтакте, WhatsApp, Viber, Telegram.
- Качественно: гарантируем высокое качество решений от специалистов с многолетним опытом решения задач по математике (гарантии)
- Выгодно: цена помощи на экзамене по алгебре — от 1000 рублей. Это не выше, чем у частных лиц, плюс качество и надежность от компании МатБюро (отзывы студентов).
Проконсультируем по темам линейной алгебры: векторы и матрицы, системы уравнений, линейные функции, пространства и операторы, собственные векторы и значения, квадратичные формы; и аналитической геометрии: на плоскости и в пространстве, кривые второго порядка и т.д.
Сдайте экзамен и получите отлично!
Отзывы студентов
- Помогли сделать расчетку и сдать экзамен, за что очень благодарен! Решение как и просил было подробное, так что трудностей с тем, чтобы разобраться в материале и понять, что там написано, практически не возникало. На экзамене помогли оперативно, отдельное спасибо Сергею.
Антон (2013)
- Огромное спасибо за онлайн помощь! Работа выполнена идеально! Отдельная благодарность Анне!)
Даниил (2014)
- Заказывал Online помощь на экзамен по высшей математике, спасибо очень выручили. Всё очень быстро и качественно
Дмитрий (2015)
- Действительно хороший сайт! Не подвели, все выполнили вовремя и даже больше, чем я указывала в заказе. Еще не раз к вам обращусь)
Мария (2015)
- Спасибо Matburo! Буквально спасли от отчисления.
Андрей (2016)
- Молодцы!!! Быстро и оперативно отозвались, специалиста дали отличного, все в срок и по времени сделал! Спасибо!
Вячеслав (2017)
- Узнал о матбюро от одногруппников. Очень советовали вас. Все советуют. Недорого быстро и правильно
Павел (2017)
- Работа выполнена очень оперативно и подробно,очень быстрый и грамотный специалист,жду теперь ,когда скажут результаты,но думаю,что все хорошо)Огромная благодарность МатБюро и исполнителю Анне)
Ольга (2017)
- Просто огромное СПАСИБО МатБюро и автору (выполнения заказа). Все прошло просто отлично, работа выполнена замечательно, без вашей помощи я бы не сдала экзамен. Уже не первый раз пользуюсь вашими услугами и буду рекомендовать вас друзьям.
Юлия (2018)
- Заказывали онлайн-помощь по высшей математике. Работа была выполнена быстро, правильно, все понятно и доступно расписано. Спасибо большое.
Светлана (2018)
Все отзывы о МатБюро
Примеры решений
Полезная информация
- Как оказывается онлайн помощь на экзамене или контрольной
- Гарантии выполнения, риски, условия возврата оплаты
Скоро сложный экзамен? Дадим консультацию.
Курс лекций для студентов 1 курса по высшей математике любых форм обучения. Я собрала теорию и примеры с решениями к каждой теме, чтобы вы смогли подготовиться к экзамену или освежить память перед контрольной работой!
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Высшая математика
Высшая математика — это курс обучения в высших учебных заведениях, включающий высшую алгебру и математический анализ для 1 курса.
Высшая математика включает обычно аналитическую геометрию, элементы высшей и линейной алгебры, дифференциальное и интегральное исчисления, дифференциальные уравнения, теорию множеств, теорию вероятностей и элементы математической статистики.
Часто используется в экономике и технике. Является обязательным предметом в российских высших учебных заведениях, за исключением специальностей, в которых различные разделы математики разнесены по разным дисциплинам.
Линейная алгебра
Линейная алгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.
Курс лекций на темы:
- Матрицы, частные виды матриц: определение и примеры
- Операции с матрицами: определения и пример с решением
- Определители 2 и 3 порядков, вычисление, свойства
- Минор, алгебраическое дополнение, разложение определителя по элементам ряда
- Обратная матрица, её вычисление
- Решение определенных систем с помощью обратной матрицы
- Решение определенных систем с помощью правила Крамера
- Решение систем с помощью метода Гаусса
- Ранг матрицы. Критерий совместности систем линейных алгебраических уравнений
Векторная алгебра
Векторная алгебра в математике расположена по разделам:
- раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства;
- часть линейной алгебры, занимающаяся векторными пространствами;
- различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Курс лекций на темы:
- Векторы. Линейные операции над векторами
- Разложение вектора по базису: определение и пример с решением
- Скалярное произведение векторов: определение и пример с решением
- Векторное произведение векторов: определение и пример с решением
- Смешанное произведение трёх векторов: определение и пример с решением
Аналитическая геометрия
Аналитическая геометрия — раздел геометрии, в котором геометрические фигуры и их свойства исследуются средствами алгебры. В основе этого метода лежит так называемый метод координат, впервые применённый Декартом в 1637 году. Каждому геометрическому соотношению этот метод ставит в соответствие некоторое уравнение, связывающее координаты фигуры или тела. Такой метод «алгебраизации» геометрических свойств доказал свою универсальность и плодотворно применяется во многих естественных науках и в технике. В математике аналитическая геометрия является также основой для других разделов геометрии — например, дифференциальной, алгебраической, комбинаторной и вычислительной геометрии.
Курс лекций на темы:
- Уравнения прямой линии на плоскости
- Уравнения плоскости в пространстве
- Эллипс, гипербола, парабола
Пределы, непрерывность функций
Понятие предела бесконечной числовой последовательности и предела функции лежит в основе всей теории дифференциального и интегрального исчисления.
Непрерывность функции. Функция f(x) называется непрерывной в точке a, если: 1)эта функция определена в некоторой окрестности точки a; 2)существует предел lim f(x) ; →ax.
Курс лекций на темы:
- Предел бесконечной числовой последовательности
- Предел функции при x>a
- Предел функции при x>∞
- Свойства бесконечно малых и бесконечно больших величин
- Свойства пределов в высшей математике
- Кратко о двух замечательных пределов
- Сравнение бесконечно малых функций
- Эквивалентные бесконечно малые величины: теоремы и таблица
- Непрерывность функции
Производная функции
Производная функции — понятие дифференциального исчисления, характеризующее скорость изменения функции в данной точке. Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Курс лекций на темы:
- Производная. Геометрический смысл производной
- Правила дифференцирования и таблица производных основных функций
- Дифференцирование логарифмических, параметрических и неявно заданных функций
- Производные высших порядков: определение и пример с решением
- Дифференциал функции, его свойства и применение
- Применение 1-й и 2-й производной для исследования функций
Неопределенный интеграл
Неопределённый интеграл для функции f(x) — это совокупность всех первообразных данной функции.
Курс лекций на темы:
- Первообразная. Неопределённый интеграл и его свойства
- Таблица интегралов и табличное интегрирование
- Интегрирование по частям
- Интегрирование подстановкой
- Интегрирование простейших рациональных дробей
- Разложение многочлена на множители
- Разложение рациональной дроби на сумму элементарных дробей
- Интегралы от иррациональных функций
- Интегрирование тригонометрических функций
- Интегрирование иррациональных функций с помощью тригонометрических подстановок
Определенный интеграл
Определённый интеграл — одно из основных понятий математического анализа, один из видов интеграла. Определённый интеграл является числом, равным пределу сумм особого вида (интегральных сумм)[⇨]. Геометрически определённый интеграл выражает площадь «криволинейной трапеции», ограниченной графиком функции[⇨]. В терминах функционального анализа, определённый интеграл — аддитивный монотонный функционал, заданный на множестве пар, первая компонента которых есть интегрируемая функция или функционал, а вторая — область в множестве задания этой функции (функционала).
Курс лекций на темы:
- Задача о площади криволинейной трапеции, определение определенного интеграла
- Все свойства определённого интеграла
- Формула Ньютона — Лейбница
- Способы вычисления определённого интеграла
- Несобственные интегралы: определение и пример с решением
Дифференциальное исчисление функций нескольких переменных
Курс лекций на темы:
- Функции нескольких переменных. Область определения, граница. Линии и поверхности уровня. Предел и непрерывность
- Частные приращения и частные производные. Теорема о равенстве частных смешанных производных
- Полное приращение и полный дифференциал
- Производная по направлению
- Градиент и его свойства
- Экстремум функции двух переменных. Необходимые и достаточные условия экстремума
Обыкновенные дифференциальные уравнения
Курс лекций на темы:
- Основные определения о дифференциальных уравнениях
- Дифференциальные уравнения первого порядка
- Уравнения с разделяющимися переменными
- Линейные уравнения первого порядка
- Задача Коши для уравнения 1-го порядка
- Линейные дифференциальные уравнения высших порядков
- Структура общего решения линейного неоднородного дифференциального уравнения
Двойные интегралы
Курс лекций на темы:
- Двойной интеграл. Объём цилиндрического тела
- Основные свойства и приложения двойного интеграла
- Вычисление двойного интеграла в декартовых координатах
Возможно эти страницы вам будут полезны:
- Предмет высшая математика
- Решение задач по высшей математике
- Помощь по высшей математике
- Заказать контрольную работу по высшей математике
- Решение высшей математики на заказ
- Готовые контрольные работы по высшей математике
- Готовые курсовые работы по высшей математике
- Высшая математика для заочников