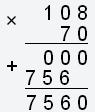Как находить проценты егэ - ExamHelp.top - все самое полезное для учащихся

Задачи на проценты

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №3 ЕГЭ по математике нам предстоит решить простую задачу на проценты или часть от целого. Данные задачи в большинстве случаев интуитивно понятны, так как взяты из реальных жизненных ситуаций, тем не менее необходимо быть внимательным при их выполнении.

Тематика заданий: часть от целого, доли, проценты

Бал: 1 из 20

Сложность задания: ♦♦◊

Примерное время выполнения: 3 мин.

[/su_box]

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

Вариант 3МБ1

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 8% годовых. Вкладчик положил на счёт 7000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

Вариант 1.

Сложить 100% и процент годовых.
Найти 1% от суммы, для этого сумму разделить на 100.
Умножить стоимость 1% на искомое количество процентов.

Вариант 2.

Сложить 100% и процент годовых.
Полученные проценты перевести в десятичную дробь (разделить на сто).
Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

Вариант 1.

Вклад 8 % годовых означает, что начальная сумма 7000 рублей через год увеличится на 8%, то есть составит 100+8=108% от исходной суммы.

Способ нахождения процента от числа №1. Для того, чтобы найти процент от числа нужно данное число разделить на 100(узнать сколько составляет 1 %), а затем умножить на искомое количество процентов.

Вычислим 108% от 7000, получим:

7000 : 100 = 70(рублей) – составит 1 %.
70 · 108 = 7560(рублей) – составит вклад через год.

Вариант 2.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь(разделить на сто), затем умножит число на полученную десятичную дробь.

108% = 108 : 100 = 1,08

7000 · 1,08 или

Выполнив умножение столбиком, имеем:

Ответ: 7560.

Вариант 3МБ2

[su_note note_color=”#defae6″]

Банк начисляет на срочный вклад 7 % годовых. Вкладчик положил на счёт 3000 рублей. Сколько рублей будет на этом счёте через год, если никаких операций, кроме начисления процентов, со счётом проводиться не будет?

[/su_note]

Алгоритм выполнения:

Вариант 1.

Сложить 100% и процент годовых.
Найти 1% от суммы, для этого сумму разделить на 100.
Умножить стоимость 1% на искомое количество процентов.

Вариант 2.

Сложить 100% и процент годовых.
Полученные проценты перевести в десятичную дробь (разделить на сто).
Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

Вариант 1.

Вклад 7 % годовых означает, что начальная сумма 3000 рублей через год увеличится на 7%, то есть составит 100+7=107% от исходной суммы.

Вычислим 107% от 3000, получим:

3000 : 100 = 30(рублей) – составит 1 %.
30 · 107 = 3210(рублей) – составит вклад через год.

Вариант 2.

Способ нахождения процента от числа №2. Для того, чтобы найти процент от числа, нужно перевести искомый процент в десятичную дробь (разделить на сто), затем умножит число на полученную десятичную дробь.

107% = 107 : 100 = 1,07

3000 · 1,07 или

Ответ: 3210.

Вариант 3МБ3

[su_note note_color=”#defae6″]

В сентябре 1 кг слив стоил 40 рублей, в октябре сливы подорожали на 40%, а в ноябре ещё на 15%. Сколько рублей стоил 1 кг слив после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

Найти сколько составляет один процент от начальной стоимости.
Сложить 100% и на сколько процентов произошло подорожание впервые.
Умножить стоимость одного процента на полученное количество процентов.
Найти стоимость 1% от новой стоимости.
Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
Умножить стоимость одного процента на полученное количество процентов.

Решение с пояснениями:

Найдем сколько составляет один процент от начальной стоимости:

40 : 100 = 0,4 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 40 = 140 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

140 · 0,4 = 56 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

56 : 100 = 0,56 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 15 = 115 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

115 · 0,56 = 64,4 (рубля) – конечная стоимость.

Решение в общем виде:

Подорожание на 40% означает увеличение стоимости на 140%, то есть, 40 рублей становятся равными

рублей.

Затем, в ноябре стоимость слив увеличилась еще на 15%, что составило

рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 40+15=55% и вычислять 155% от 40 рублей! Это будет приводить к неверным решениям.

Ответ: 64,4.

Вариант 3МБ4

[su_note note_color=”#defae6″]

В сентябре 1 кг винограда стоил 90 рублей, в октябре виноград подорожал на 20 %, а в ноябре ещё на 25 %. Сколько рублей стоил 1 кг винограда после подорожания в ноябре?

[/su_note]

Алгоритм выполнения:

Найти сколько составляет один процент от начальной стоимости.
Сложить 100% и на сколько процентов произошло подорожание впервые.
Умножить стоимость одного процента на полученное количество процентов.
Найти стоимость 1% от новой стоимости.
Сложить 100 % и количество процентов, на которое подорожал товар во второй раз.
Умножить стоимость одного процента на полученное количество процентов.

Подробный разбор:

Найдем сколько составляет один процент от начальной стоимости:

90 : 100 = 0,9 (рублей) – составляет 1 % от начальной стоимости.

Сложим 100% и на сколько процентов произошло подорожание впервые.

100 + 20 = 120 (%) – составила стоимость от начальной цены после первого подорожания.

Умножим стоимость одного процента на полученное количество процентов.

120 · 0,9 = 108 (рублей) – стали стоить сливы в октябре.

Найдем стоимость 1% от новой стоимости.

108 : 100 = 1,08 (рубля) – 1% от новой стоимости.

Сложим 100 % и количество процентов, на которое подорожал товар во второй раз.

100 + 25 = 125 (%) – составила стоимость в ноябре от цены в октябре.

Умножим стоимость одного процента на полученное количество процентов.

125 · 1,08 = 135 (рублей) – конечная стоимость.

Решение в общем виде:

Подорожание на 20% означает увеличение стоимости на 120%, то есть, для 90 рублей имеем:

рублей.

Затем, в ноябре стоимость слив увеличилась еще на 25%, что составило

рублей.

Замечание: обратите внимание, что в данной задаче нельзя просто складывать проценты 20+25=45% и вычислять 145% от 90 рублей! Это будет приводить к неверным решениям.

Ответ: 135.

Вариант 3МБ5

[su_note note_color=”#defae6″]

Ивану Кузьмичу начислена заработная плата 20000 рублей. Из этой суммы вычитается налог на доход физических лиц в размере 13 %. Сколько рублей он получит после уплаты подоходного налога?

[/su_note]

Алгоритм выполнения:

Вариант 1.

Вычесть из 100% налог в процентах.
Найти 1% от начальной суммы, для этого сумму разделить на 100.
Умножить стоимость 1% на искомое количество процентов.

Вариант 2.

Вычесть из 100% налог в процентах.
Полученные проценты перевести в десятичную дробь (разделить на сто).
Найти процент от числа (число умножить на полученную десятичную дробь).

Решение:

Вариант 1.

Вычтем из 100% налог в процентах.

100 – 13 = 87 (%) – получит Иван Кузьмич после вычета налога.

Найдем 1 % от начальной суммы.

20000 : 100 = 200 (рублей) – составит 1%.

Найдем 87% от 20000.

87 · 200 = 17400 (рублей) – получит Иван Кузьмич.

Вариант 2.

Вычтем из 100% налог в процентах. 100 – 13 = 87 (%)

Полученные проценты переведем в десятичную дробь (разделить на сто). 87 : 100 = 0,87

Найдем процент от числа (число умножить на полученную десятичную дробь).

20000 · 0,87 = 17400 (рублей)

Ответ: 17400 рублей получит Иван Кузьмич.

Вариант 3МБ6

[su_note note_color=”#defae6″]

ЕГЭ по физике сдавали 25 выпускников школы, что составляет треть от общего числа выпускников. Сколько выпускников этой школы не сдавали экзамен по физике?

[/su_note]

Решение:

Нам известно, что количество учеников, сдававших ЕГЭ по физике равно 25, и это составляет 1/3 от общего числа выпускников. Значит 25 – это 1/3, тогда общее число учеников:

25 • 3 = 75

Количество учеников, не сдававших ЕГЭ по физике, равно:

75 – 25 = 50

Ответ: 50

Вариант 3МБ7

[su_note note_color=”#defae6″]

Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена стоимость футболки?

[/su_note]

Алгоритм выполнения

От 800 отнимаем 680. Узнаем, сколько рублей составило снижение.
Делим результат вычитания на 800. Это даст нам долю, которую составляет скидка от первоначальной стоимости.
Полученное число умножаем на 100. Получаем снижение в процентах.

Решение:

800 – 680 = 120 (руб.) – составляет снижение

120 : 800 = 0,15 – доля скидки

0,15 ·100 = 15 %

Ответ: 15

Вариант 3МБ8

[su_note note_color=”#defae6″]

В магазине вся мебель продается в разобранном виде. Покупатель может заказать сборку мебели на дому, стоимость которой составляет 5% от стоимости купленной мебели. Шкаф стоит 3500 рублей (наверное, это было очень давно – прим. ред. 🙂 ) Во сколько рублей обойдется покупка этого шкафа вместе со сборкой?

[/su_note]

Алгоритм выполнения

Определяем, сколько составляет 5% от стоимости мебели. Для этого 3500 делит на 100 и умножаем на 5.
К 3500 прибавляем полученное число.

Решение:

3500 : 100 · 5 = 175 (руб.) – стоимость сборки мебели

3500 + 175 = 3675 (руб.) стоит мебель со сборкой

Ответ: 3675

Вариант 3МБ9

[su_note note_color=”#defae6″]

Товар на распродаже уценили на 40%, при этом он стал стоить 840 рублей. Сколько рублей стоит товар до распродажи?

[/su_note]

Алгоритм выполнения

От 100 % вычитаем 40%, чтобы найти, сколько процентов составляет уцененная стоимость. Получим 60 %.
Воспользуемся правилом нахождения целого по его части. Для этого 840 разделим на 60 и умножим на 100.

Решение:

100 – 40 = 60 % – составляет цена товара после его уценки.

840 : 60 · 100 = 1400 (руб.)

1400

Вариант 3МБ10

[su_note note_color=”#defae6″]

Магазин делает пенсионерам скидку. Батон хлеба стоит в магазине 15 рублей, а пенсионер заплатил за него 14 рублей 40 копеек (грандиозная скидка – прим. ред. 😉 ) Сколько процентов составила скидка для пенсионера?

[/su_note]

Алгоритм выполнения

От 15 руб. отнимаем 14 руб.40 коп. Так найдем сумму скидки. Выразим эту сумму в рублях.
Полученное число разделим на 15 и умножим на 100 %.

Решение:

15 руб. – 14 руб.40 коп. = 60 коп. = 0,6 руб.

0,6 : 15 ·100 % = 4 %.

Ответ: 4

Вариант 3МБ11

[su_note note_color=”#defae6″]

Число хвойных деревьев в парке относится к числу лиственных как 93:7. Других деревьев в парке нет. Сколько процентов деревьев в парке составляют лиственные?

[/su_note]

Алгоритм выполнения

Суммируем 93 и 7, чтобы найти общее кол-во деревьев в парке.
Кол-во лиственных деревьев (7) делим на общее кол-во деревьев и умножаем на 100 %.

Решение:

93 + 7 = 100 (шт.) – деревьев всего в парке.

7 : 100 ·100 = 7 %

Ответ: 7

Вариант 3МБ12

[su_note note_color=”#defae6″]

Городской бюджет составляет 48 млн. рублей, а расходы на одну из его статей составили 40%. Сколько миллионов рублей потрачены на эту статью бюджета?

[/su_note]

Алгоритм выполнения

Нужно применить правило нахождения части от целого по ее проценту. Для этого целое делится на 100 и умножается на кол-во процентов.

Решение:

48 : 100 · 40 = 19,2 (млн.руб.)

Ответ: 19,2

Вариант 3МБ13

[su_note note_color=”#defae6″]

Поступивший в продажу в феврале мобильный телефон стоил 1800 рублей. В июне он стал стоить 1530 рублей. На сколько процентов снизилась цена мобильного телефона в период с февраля по июнь?

[/su_note]

Алгоритм выполнения

Из 1800 вычитаем 1530. Определяем, сколько рублей составила скидка.
Полученное число делим на первоначальную цену и умножаем на 100 %.

Решение:

1800 – 1530 = 270 (руб.) – скидка

270 : 1800 · 100 = 15 %

Ответ: 15

Вариант 3МБ14

[su_note note_color=”#defae6″]

В период распродажи магазин снижал цены дважды: в первый раз на 10%, во второй – на 25%. Сколько рублей стал стоить чайник после второго снижения цен, если до начала распродажи он стоил 1600 рублей?

[/su_note]

Алгоритм выполнения

Определяем, сколько (в руб.) составляет 10 % от стоимости чайника. Для этого 1600 делим на 100 и умножаем на 10.
От первоначальной стоимости отнимаем сумму скидки, составляющей 10 %.
Полученную цену со скидкой делим на 100 и умножаем на 25. Так найдем величину скидки (в руб.) после второго снижения цены.
От числа, полученного в п.2 отнимаем число, полученное в п.3.

Решение:

1600 : 100 · 10 = 160 (руб.) – составляет скидка в 10 %

1600 – 160 = 1440 (руб.) – стал стоить чайник после понижения цены на 10 %

1440 : 100 · 25 = 360 (руб.) составляет скидка в 25 %

1440 – 360 = 1080 (руб.)

Ответ: 1080

Вариант 3МБ15

[su_note note_color=”#defae6″]

Магазин детских товаров закупает погремушки по оптовой цене 110 рублей за одну штуку и продает с наценкой 30%. Сколько рублей будут стоить 4 такие погремушки, купленные в этом магазине?

[/su_note]

Алгоритм выполнения

Определяем, сколько рублей составляет наценка в 30 %. Для этого закупочную стоимость делим на 100 и умножаем на 30.
К закупочной стоимости прибавляет сумму наценки.
Полученное число умножаем на 4.

Решение:

110 : 100 · 30 = 33 (руб.) – равна наценка

110 + 33 = 143 (руб.) – стоит погремушка в магазине

143 · 4 = 572 (руб.) – стоят 4 погремушки

Ответ: 572

Вариант 3МБ16

[su_note note_color=”#defae6″]

Число больных гриппом в школе уменьшилось за месяц в два раза. На сколько процентов уменьшилось число больных гриппом?

[/su_note]

Алгоритм выполнения

Обозначим число больных через х. Тогда кол-во больных через месяц станет равным х/2.
х/2 делим на х и умножаем на 100 %. Так найдем кол-во процентов, которое составит число больных через месяц по отношению к первоначальному их кол-ву. В процессе вычисления х сократится.

Решение:

х / 2 : х · 100 % = х / 2· 1 / х· 100 % =1 / 2 · 100 % = 0,5 · 100 % = 50 %

Ответ: 50

Даниил Романович | Просмотров: 14.5k

Источник

Задачи на проценты из вариантов ЕГЭ по математике

Смотри также видео «Текстовые задачи на ЕГЭ по математике».
Текстовая задача — это не только задача на движение и работу. Есть еще задания на проценты, на растворы, сплавы и смеси, на движение по окружности и нахождение средней скорости. О них мы и расскажем.

Начнем с задач на проценты. Если эта тема сложна для тебя — посмотри материал простейшие текстовые задачи. В частности, в нем мы сформулировали важное правило: за 100% мы принимаем ту величину, с которой сравниваем.

Мы также вывели полезные формулы:

если величину увеличить на процентов, получим $xcdot left( 1+ genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right);$
если величину уменьшить на процентов, получим $xcdot left( 1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right);$
если величину увеличить на процентов, а затем уменьшить на , получим $xcdot left( 1+ genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right)left( 1- genfrac{}{}{}{0}{displaystyle q}{displaystyle 100} right);$

если величину дважды увеличить на процентов, получим $xcdot left( 1+ genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right)^2;$
если величину дважды уменьшить на процентов, получим $xcdot left( 1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right)^2.$

Воспользуемся ими для решения задач.

. В 2008 году в городском квартале проживало 40000 человек. В 2009 году в результате строительства новых домов число жителей выросло на , а в 2010 году — на по сравнению с 2009 годом. Сколько человек стало проживать в квартале в 2010 году?

По условию, в 2009 году число жителей выросло на , то есть стало равно человек.

А в 2010 году число жителей выросло на , теперь уже по сравнению с 2009 годом. Получаем, что в 2010 году в квартале стало проживать жителей.

Следующая задача предлагалась на пробном ЕГЭ по математике в декабре 2010 года. Она проста, но справились с ней немногие.

. В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

На первый взгляд кажется, что в условии ошибка и цена акций вообще не должна измениться. Ведь они подорожали и подешевели на одно и то же число процентов! Но не будем спешить. Пусть при открытии торгов в понедельник акции стоили рублей. К вечеру понедельника они подорожали на и стали стоить $xcdot left(1+ genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right)$ . Теперь уже эта величина принимается за 100% , и к вечеру вторника акции подешевели на по сравнению этой величиной. Соберем данные в таблицу:

По условию, акции в итоге подешевели на 4%.

Получаем, что
$xcdot left(1+ genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right) left(1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right)=xcdot left(1- genfrac{}{}{}{0}{displaystyle 4}{displaystyle 100} right).$

Поделим обе части уравнения на (ведь он не равен нулю) и применим в левой части формулу сокращенного умножения:

$1- genfrac{}{}{}{0}{displaystyle p^2}{displaystyle 100^2}=1- genfrac{}{}{}{0}{displaystyle 4}{displaystyle 100};$
$genfrac{}{}{}{0}{displaystyle p^2}{displaystyle 100^2}=genfrac{}{}{}{0}{displaystyle 4}{displaystyle 100}.$

По смыслу задачи, величина положительна.
Получаем, что p=20 .

. Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 2000 рублей, через два года был продан за 15842 рублей.

Эта задача тоже решается по одной из формул, приведенных в начале статьи. Холодильник стоил 20000 рублей. Его цена два раза уменьшилась на , и теперь она равна:

$20000cdot left(1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right) ^2=15842;$

$left(1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right) ^2=genfrac{}{}{}{0}{displaystyle 15842}{displaystyle 20000};$

$left(1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100} right) ^2=genfrac{}{}{}{0}{displaystyle 7921}{displaystyle 10000};$

$1- genfrac{}{}{}{0}{displaystyle p}{displaystyle 100}=genfrac{}{}{}{0}{displaystyle 89}{displaystyle 100};$

p=11.

. Четыре рубашки дешевле куртки на . На сколько процентов пять рубашек дороже куртки?

Пусть стоимость рубашки равна , стоимость куртки . Как всегда, принимаем за сто процентов ту величину, с которой сравниваем, то есть цену куртки. Тогда стоимость четырех рубашек составляет 92% от цены куртки, то есть .

Стоимость одной рубашки — в раза меньше:

А стоимость пяти рубашек:

$5x=1,15y=genfrac{}{}{}{0}{displaystyle 115}{displaystyle 100}y=115%y.$

Получили, что пять рубашек на 15% дороже куртки.

Ответ: .

. Семья состоит из мужа, жены и их дочери-студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67% . Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?

Нарисуем таблицу. Ситуации, о которых говорится в задаче («если бы зарплата мужа увеличилась, если бы стипендия дочки уменьшилась…») назовем «ситуация » и «ситуация ».

	муж	жена	дочь	Общий доход
В реальности
Ситуация
Ситуация			$genfrac{}{}{}{0}{displaystyle 1}{displaystyle 3}z$

Осталось записать систему уравнений:

$left{begin{matrix}2x+y+z=1,67left( x+y+z right)\ x+y+genfrac{}{}{}{0}{displaystyle 1}{displaystyle 3}z=0,96left( x+y+z right)end{matrix}right. .$

Но что же мы видим? Два уравнения и три неизвестных! Мы не сможем найти , и по отдельности. Правда, нам это и не нужно. Лучше возьмем первое уравнение и из обеих его частей вычтем сумму x+y+z .

Получим:

Это значит, что зарплата мужа составляет 67% от общего дохода семьи.

Во втором уравнении мы тоже вычтем из обеих частей выражение x+y+z , упростим и получим, что

Значит, стипендия дочки составляет от общего дохода семьи. Тогда зарплата жены составляет 27% общего дохода.

Ответ: 27.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Задачи на проценты из вариантов ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В понедельник акции компании подорожали на некоторое количество процентов, а во вторник подешевели на то же самое количество процентов. В результате они стали стоить на 4 % дешевле, чем при открытии торгов в понедельник. На сколько процентов подорожали акции компании в понедельник?

Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.

Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?

Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?

Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника, если, выставленный на продажу за 20 000 рублей, через два года был продан за 15 842 рублей.

Пройти тестирование по этим заданиям

Источник

Павел Бердов
уроки математики

§ 1.: Задача B1 — время, числа и проценты
§ 2.: Решение задач B1: № 1—16
§ 3.: Решение задач B1: №17—32
Глава 1.: Округление с избытком и недостатком
§ 1.: Наибольшее и наименьшее значение
§ 2.: Задача B2: лекарство и таблетки
§ 3.: Тест к уроку «Округление с избытком и недостатком» (1 вариант)
§ 4.: Проценты в задачах на наибольшее-наименьшее значение: используем формулы процентов
§ 5.: Проценты в задачах на наибольшее-наименьшее значение используем пропорции
Глава 2.: Задачи на проценты
§ 1.: Задачи на проценты считаем проценты с помощью формулы
§ 2.: Формула простого процента: неизвестно конечное значение
§ 3.: Формула простого процента: как найти исходное значение
§ 4.: Процент: неизвестно начальное значение (метод пропорции)
§ 5.: Задачи на проценты: считаем проценты с помощью пропорции
§ 6.: Задачи на проценты: стандартный расчет с помощью пропорций
§ 7.: Процент: налоги и зарплата. Считаем с помощью коэффициентов
§ 8.: Задачи B2 на проценты: налоги и зарплата
§ 9.: Задача B2 на проценты: вычисление полной стоимости покупки
§ 10.: Задача B2 на проценты: железнодорожные билеты
Глава 3.: Сложный процент
§ 1.: Сложные задачи на проценты
§ 2.: Задача B2: Сложный процент и метод коэффициентов
§ 3.: Задача B2: Сложный процент и стандартная формула
§ 4.: Сложные задачи B2 на проценты: вычисление полной стоимости
Глава 4.: Сложные и нестандартные задачи
§ 1.: Нестандартные задачи B2: кредит в банке
§ 2.: Нестандартная задача B2: студенты, гонорары и налоги
§ 3.: Задача B2 про комиссию в терминале

Источник

1. Прикладные задачи (задачи из повседневной жизни)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Решение задач на проценты

Основные моменты:

(blacktriangleright) Процент – это число, равное (frac{1}{100}) части от данного числа.

(blacktriangleright) Пример: (13%) от числа (N) равно:

Способ 1: (dfrac{N}{100}cdot 13) (где (frac{N}{100}) – сотая часть числа (N), а значит (frac{N}{100}cdot 13) – тринадцать таких частей.)

Способ 2: (0,13N) (то есть перевести процент в так называемый “десятичный вид”: (frac{13}{100}=0,13))

(blacktriangleright) Чтобы найти, сколько процентов составляет число (A) от числа (B), нужно найти (dfrac{A}{B}cdot 100
%).

(blacktriangleright) Чтобы найти, на сколько процентов число (A) больше (меньше) числа (B), нужно найти, сколько процентов составляет число (A) от числа (B), а затем из этого количества процентов отнять (100%) (из (100%) отнять найденное количество процентов).

Задание
1

#1477

Уровень задания: Равен ЕГЭ

Авиабилет стоит 12000 рублей. Двум пассажирам из группы в десять человек была сделана скидка в 6(%). Сколько в сумме отдали эти 10 пассажиров за перелёт?

Билет со скидкой стоит (12000 cdot (1 — 0,06) = 11280) рублей. Из группы в десять человек двое летели со скидкой, остальные восемь платили по 12000 рублей за билет. В сумме эти 10 пассажиров отдали (12000 cdot 8 + 11280 cdot 2 = 118560) рублей.

Ответ: 118560

Задание
2

#2814

Уровень задания: Равен ЕГЭ

Артём считает ворон. Он пришёл к выводу, что в данный момент около его окна кружит (55) ворон. Известно, что Артём ошибся и на самом деле количество этих самых ворон на (20%) больше, чем насчитал Артём. Сколько ворон кружит около окна Артёма в данный момент?

На самом деле искомое количество ворон равно (55cdot (1 + 0,2) = 66).

Ответ: 66

Задание
3

#2978

Уровень задания: Равен ЕГЭ

Аня купила 10 яблок и несколько груш, причем яблоки составляют 40(%) от всех фруктов. Сколько груш купила Аня?

Пусть всего было (x) груш, тогда всего фруктов (10+x). Так как яблоки составляют (40%) от всех фруктов, то получаем следующее уравнение [(10+x)cdot 0,4=10quadRightarrowquad x=15.]

Ответ: 15

Задание
4

#1483

Уровень задания: Равен ЕГЭ

Масса топлива ракеты до старта составляла 280 тонн. Через некоторое время часть топлива сгорела и масса оставшегося топлива стала 238 тонн. На сколько процентов уменьшилась масса топлива?

Сгорело (280 — 238 = 42) тонны топлива. Чтобы найти, сколько процентов от 280 составляет 42, надо разделить 42 на 280 и умножить на 100(%): (42 : 280 cdot 100% = 15%).

Ответ: 15

Задание
5

#1484

Уровень задания: Равен ЕГЭ

Масса палки колбасы до того, как её заметил Артем Я., составляла 1,2 килограмма. Артем Я. кое-что сделал с колбасой, после чего масса оставшейся части палки колбасы стала 0,75 килограмма. На сколько процентов уменьшилась масса палки колбасы?

Артем Я. куда-то дел (1,2 — 0,75 = 0,45) килограмма колбасы. Чтобы найти, сколько процентов от 1,2 составляет 0,45, надо разделить 0,45 на 1,2 и умножить на 100(%): (0,45 : 1,2 cdot 100 % = 37,5%).

Ответ: 37,5

Задание
6

#1485

Уровень задания: Равен ЕГЭ

Объем воды в графине до того, как его заметил Коля, составлял 2 литра. Коля выпил часть воды так, что оставшийся объем составил 1,3 литра. На сколько процентов уменьшился объем воды в графине?

Коля выпил (2 — 1,3 = 0,7) литра воды. Чтобы найти, сколько процентов от 2 составляет 0,7, надо разделить 0,7 на 2 и умножить на 100(%): (0,7 : 2 cdot 100% = 35%).

Ответ: 35

Задание
7

#1479

Уровень задания: Равен ЕГЭ

Билет в кино стоит 500 рублей. Двум киноманам из группы в пять человек была сделана скидка в 1(%). Сколько в сумме отдали эти 5 киноманов за сеанс в кино?

Билет со скидкой стоит (500 cdot (1 — 0,01) = 495) рублей. Из группы в пять человек двое шли со скидкой, остальные трое платили по 500 рублей за билет. В сумме эти 5 киноманов отдали (500 cdot 3 + 495 cdot 2 = 2490) рублей.

Ответ: 2490

Уметь правильно и быстро решать текстовые задачи на проценты необходимо не только учащимся, которым предстоит сдача ЕГЭ по математике базового или профильного уровня, но и всем взрослым, поскольку подобные задания постоянно встречаются в повседневной жизни. Повышение цен, планирование семейного бюджета, выгодное вложение финансовых средств и множество других вопросов невозможно уладить без данных навыков. При подготовке к сдаче аттестационного испытания обязательно нужно повторить, как решать задачи на проценты: в ЕГЭ по математике они встречаются как в базовом, так и в профильном уровне.

Необходимо запомнить

Процент — это (frac{1}{100}) часть от какого-либо числа. Обозначает долю чего-либо по отношению к целому. Письменный символ — (%). При подготовке к ЕГЭ по теме «Проценты» школьникам как в Москве, так и в других точках РФ необходимо запомнить следующую формулу:

[1%= frac{1}{100}=0.01]

Как ее применить?

Для того чтобы решить простое задание с процентами в ЕГЭ по математике, нужно:

Разделить имеющееся число на (100).
Умножить полученное значение на то количество (%), которое нужно найти.

Например, для того чтобы вычислить (10%) от числа (300), нужно найти (1) процент, разделив (300:100=3). И полученное от предыдущего действия число (3cdot10=30). Ответ: (30).

Это простейшие задания. Учащиеся 11 класса в ЕГЭ сталкиваются с необходимостью выполнить решение сложных задач на проценты. Как правило, речь в них идет о банковских вкладах или платежах. Ознакомиться с формулами и правилами их применения вы можете, перейдя в раздел «Теоретическая справка». Здесь вы сможете не только повторить основные определения, но и познакомиться с вариантами решения сложных задач на проценты по банковскому кредиту, а также с упражнениями из других разделов алгебры, например, задачами на перевод единиц измерения, которые встречаются в ЕГЭ.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задачи на проценты

Разбор типовых вариантов заданий №3 ЕГЭ по математике базового уровня

Вариант 3МБ1

Алгоритм выполнения:

Решение:

Вариант 3МБ2

Алгоритм выполнения:

Решение:

Вариант 3МБ3

Алгоритм выполнения:

Решение с пояснениями:

Решение в общем виде:

Вариант 3МБ4

Алгоритм выполнения:

Подробный разбор:

Решение в общем виде:

Вариант 3МБ5

Алгоритм выполнения:

Решение:

Вариант 3МБ6

Решение:

Вариант 3МБ7

Алгоритм выполнения

Решение:

Вариант 3МБ8

Алгоритм выполнения

Решение:

Вариант 3МБ9

Алгоритм выполнения

Решение:

Вариант 3МБ10

Алгоритм выполнения

Решение:

Вариант 3МБ11

Алгоритм выполнения

Решение:

Вариант 3МБ12

Алгоритм выполнения

Решение:

Вариант 3МБ13

Алгоритм выполнения

Решение:

Вариант 3МБ14

Алгоритм выполнения

Решение:

Вариант 3МБ15

Алгоритм выполнения

Решение:

Вариант 3МБ16

Алгоритм выполнения

Решение:

Задачи на проценты из вариантов ЕГЭ по математике

Решение задач на проценты

Необходимо запомнить

Новое и интересное на сайте: