Как находить точку минимума функции егэ 11 задание - ExamHelp.top

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Найдите точку минимума функции

Найдите точку минимума функции принадлежащую промежутку

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 1.

Найдите точку минимума функции

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Сибирь

Найдите точку минимума функции

Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье

Найдите точку минимума функции

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

Найдите точку минимума функции

Всего: 219 1–20 | 21–40 | 41–60 | 61–80 …

Источник

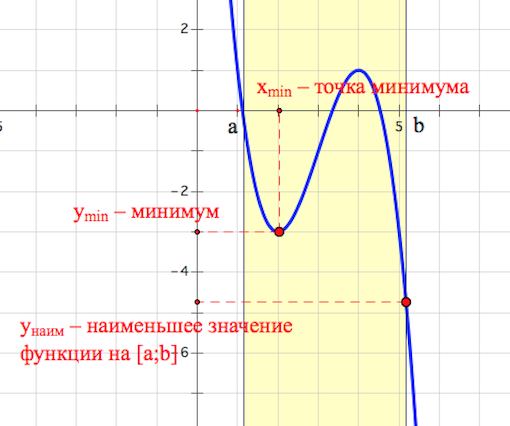
В (11) задании ЕГЭ нужно уметь находить точки минимума и максимума функции, определять наибольшее и наименьшее значения функции на отрезке.

За правильное выполнение задания даётся (1) первичный балл.

Пример:

найди точку минимума функции

y=(x+5)2(x−1)+7

Алгоритм выполнения задания

1. Определи тип задания:

найди точку максимума (минимума);
найди точку максимума (минимума) на отрезке;
найди максимальное (минимальное) значение функции;
найди максимальное (минимальное) значение функции на отрезке.

2. Вычисли производную (f’(x)).

3. Реши уравнение (f’(x)=0).

4. Выполни действия в соответствии с типом задания, сделай вывод.

5. Запиши в ответе значение, которое требуется найти.

Как решить задание из примера?

1. В задании нужно найти точку максимума.

2. Производная функции:

y′=2(x+5)(x−1)+x+52=(x+5)(2x−2+x+5)=3(x+5)(x+1).

3. Приравняем производную к нулю и найдём корни уравнения:

4. Найдём промежутки возрастания и убывания функции (рис. (1)). В точке (-1) функция меняет знак с минуса на плюс, значит, это точка минимума.

Рис. (1). Промежутки возрастания и убывания функции

5. Запишем ответ (непосредственно в самом задании — без точки в конце).

Ответ: (-1).

Обрати внимание!

В заданиях «Как на ЕГЭ» ответы записывай в виде целого числа или десятичной дроби без пробелов и точки в конце.

Если получилась обыкновенная дробь и её нельзя перевести в конечную десятичную дробь — ищи ошибку в решении!

Источники:

Рис. 1. Промежутки возрастания и убывания функции. © ЯКласс.

Источник

Выпускники, прошедшие через ЕГЭ по математике, отмечают, что задание под номером 11 – самое сложное в первой части профильного варианта. Весь сыр-бор из-за производной.

Переживать из-за производной не стоит, пользуясь всего лишь двумя алгоритмами, можно решить абсолютно любое задание с ней, эта статья посвящена им. Также в материале будут представлены интересные хитрости, позволяющие быстро решать задачи из ЕГЭ на производную, без каких-либо алгоритмов.

В этом материале:

Почему только 40 процентов сдающих успешно справляются с производной в ЕГЭ
Как выглядят два прототипа 11 задания из первой части профильной математики ЕГЭ
Как найти две точки экстремума функции
Как найти наибольшее или наименьшее значение функции
Хитрость, помогающая быстро разобраться с производной в ЕГЭ

Все, кто хоть немного знаком с темой выпускного госэкзамена (например, те, кто ходят на онлайн занятия по математике к репетитору), в курсе, что профильный вариант математики содержит две части: с кратким ответом и подробным ответом. Краткая часть содержит 11 заданий, последнее связано с производной, вот на нем следует остановиться подробнее.

Задача задания: выяснить, знают ли сдающие школьники понятие производной и умеют ли они вычислять ее. Статистика показывает, что 60% из них не в состоянии успешно выполнить это задание, это большая цифра.

В оправдание сдающих можно сказать то, что тема производной впервые рассматривается на уроках математики в выпускном классе, в середине года, у школьников просто не хватает времени хорошо проработать тему.

Как выглядят два прототипа 11 задания из первой части профильной математики ЕГЭ?

Для упрощения задачи выпускникам составители придумали сделать два вида задания, каждое из них решается по одному и тому же алгоритму, отличаются только числа и буквы. Чтобы успешно справиться с одним из прототипов, требуется только запомнить таблицу производных, также стоит походить на онлайн занятия математикой.

Прежде чем приступить к решению, стоит разобраться в сути задания. Существует небольшая хитрость для этого. Выпускники плохо ориентируются в понятиях, они не могут отличить «точку максимума» от «точки минимума», «наибольшее» или «наименьшее значение» функции.

Точку экстремума (максимума или минимума) функции принято обозначать буквой x, а наибольшее или наименьшее значение принято обозначать буквой y. Здесь легко растеряться и ошибиться. Чтобы этого избежать, нужно обратить внимание на слово «точка экстремума». Слово «точка» – маркер, если оно есть в задании, значит требуется найти x, в противном случае – y.

Для работы в Учи.Дома мы тщательно отбираем онлайн репетиторов по математике, которые зажигают в детях интерес к предмету. Их профессионализм и энергичность дают потрясающий результат: ученики с нетерпением ждут новых занятий и без напоминаний выполняют домашние задания.

Как найти две точки экстремума функции?

Если ученик понял разницу между x и y, нужно перейти к следующей части – поиску точек экстремума. Математическая функция содержит две точки, в которых производная равняется нулю. Чтобы понять, где точка минимума, а где максимума – нужно обратить внимание на то, какой знак у производной до и после точки. Если до знак был «+», а стал «-», то это точка максимума, и наоборот, если знак до точки был «-» – это точка минимума. Алгоритм работает следующим образом:

Он универсален для каждого прототипа 11 задания, где требуется найти точки максимума или минимума. Такой метод часто репетиторы разбирают на онлайн занятиях математикой.

Как найти наибольшее или наименьшее значение функции?

Второй тип задания отличается от первого даже своим видом, а не только формулировкой. Сдающему представляется не только сама функция, но и ее отдельный промежуток вида [a, b]. Изначально про точки этого промежутка нет никакой информации, но на них следует обратить внимание.

Начало алгоритма похоже на предыдущий: нужно найти точки максимума и минимума, определить изменение функций в этих точках. После этого нужно приступить к данному в задании промежутку – определить поведение функции в его точках.

Хитрость, помогающая быстро разобраться с производной в ЕГЭ

Для части заданий можно проигнорировать указанные выше алгоритмы, сделать все проще и быстрее с помощью маленькой хитрости. Стоит быть внимательным при ее использовании чтобы не ошибиться, она не работает для всех заданий.

Хитрость относится к формату ЕГЭ, задание номер 11 требует краткого ответа. Это значит, что в бланк ответов нельзя вписать бесконечную дробь, некоторые математические знаки, обозначающие числа (например, число Пи или число Е), знаки для синуса, логарифма и т.д. Для подкованного выпускника – это упрощение решения.

Хотите, чтобы ваш ребенок полюбил математику с младших классов? Запишите его на бесплатный вводный урок, где мы покажем, каким увлекательным может быть этот «сложный» предмет.

Пример использования хитрости

Для успешного выполнения ученик должен наизусть помнить таблицу производных, далее – простая логика.

Другие хитрости можно изучить на онлайн занятиях по математике в онлайн-школе Учи.Дома

В задании есть число Е, значит, придется брать производную от него, причем ответ будет тем же самым числом. Поскольку в бланке ответов число Е вписать нельзя, становится понятно, что основная задача – это избавиться от него. Но возможно ли это сделать? Да, если вспомнить свойства степеней и одну хитрость.

В указанном примере нужно превратить число в единицу, поскольку Е – это основание степени, нужно, чтобы его показатель был равен нулю. Получается – (x — 9) = 0. При таком раскладе даже второклассник сможет найти икс, он равен 9.

Можно по-другому избавиться от числа. Скобки в примере – тоже своего рода множитель. Если представить, что результат действий в скобках равен нулю, то получается, что 10 – x = 0. Икс находится так же просто, он равен уменьшаемому – десяти.

На этом решение не заканчивается. В задании потребовалось найти наименьшее значение функции – нужно подставить икс в данную функцию.

В первом примере, когда икс равен 9 – значение функции игрек равно 1, в другом примере, где икс равен 10, игрек равен 0. Второе значение меньше первого, значит нужно именно его вписать в ответ.

Чтобы вписать правильный ответ, нужно применить оба метода для того, чтобы найти именно наименьшее или наибольшее значение.

Применяя оба метода, довольно легко можно решить любое 11 задание в ЕГЭ. Не стоит забывать и про хитрости формата, для упрощения задачи. Но лучше все же ходить и на онлайн занятия математикой к репетиторам, чтобы быть уверенным в успешной сдаче экзамена.

Что следует запомнить:

Нужно учить таблицы производных;
Алгоритмы – удобный и верный способ решения;
При использовании хитростей нужно обращать внимание на производную.

Источник

Решение заданий ЕГЭ по теме: «Наибольшее и наименьшее значения функции» Задание 11 ЕГЭ 2022 по математике профильного уровня.

→ скачать презентацию

Для выполнения задания 11 необходимо уметь выполнять действия с функциями

Примеры заданий:

Задание №1. Найдите точку минимума функции y=x³-9x²+12.

Задание №2. Найдите наибольшее значение функции 𝑦 =𝑥³/4− 27𝑥 + 11 на отрезке −[8; 0].

Задание № 3. Найдите наибольшее значение функции 𝑦 = (𝑥 + 9)² ⋅ (𝑥 − 5) − 5 на отрезке [−19; −5] .

Основные понятия

Точка минимума — такая точка x₀, если у неё существует окрестность, для всех точек которой выполняется неравенство f(x)>f(x₀)

Минимум функции — значение функции в точке минимума x₀

Точка максимума — такая точка x₀ , если у неё существует окрестность, для всех точек которой выполняется неравенство f(x)<f(x₀)

Максимум функции — значение функции в точке максимума x₀

Точки минимума и точки максимума называются точками экстремума.
Точки, в которых производная функции равна нулю или не существует, называются критическими точками.

Экстремумы могут существовать только в критических точках. Однако, не все критические точки являются экстремумами.

Теорема (достаточный признак существования экстремума функции).

Критическая точка x₀ является точкой экстремума функции f(x), если при переходе через эту точку производная функции меняет знак, причём, если знак меняется с «плюса» на «минус», то точкой максимума, а если с «минуса» на «плюс», то точкой минимума.

Связанные страницы:

Источник

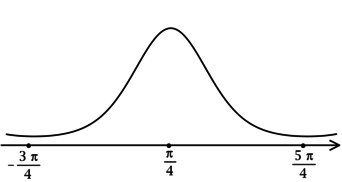
Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Также можно сказать, что в этих точках меняется направление движения функции: если функция перестает падать и начинает расти – это точка минимума, наоборот – максимума.

Минимумы и максимумы вместе именуют экстремумами функции.

Иными словами, все пять точек, выделенных на графике выше, являются экстремумами.

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

Благодаря этому найти эти точки не составляет проблем, даже если у вас нет графика функции.

Внимание! Когда пишут экстремумы или максимумы/минимумы имеют в виду значение функции т.е. (y). Когда пишут точки экстремумов или точки максимумов/минимумов имеют в виду иксы в которых достигаются максимумы/минимумы. Например, на рисунке выше, (-5) точка минимума (или точка экстремума), а (1) – минимум (или экстремум).

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

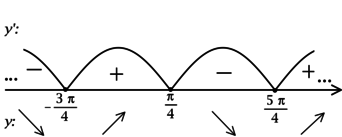
Давайте вместе найдем количество точек экстремума функции по графику производной на примере:

У нас дан график производная — значит ищем в каких точках на графике производная равна нулю. Очевидно, это точки (-13), (-11), (-9),(-7) и (3). Количество точек экстремума функции – (5).

Внимание! Если дан график производной функции, а нужно найти точки экстремумов функции, мы не считаем максимумы и минимумы производной! Мы считаем точки, в которых производная функции обращается в ноль (т.е. пересекает ось (x)).

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно вспомнить еще два важных правил:

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.

С помощью этих правил давайте найдем на графике производной точки минимума и максимума функции.

Понятно, что минимумы и максимумы надо искать среди точек экстремумов, т.е. среди (-13), (-11), (-9),(-7) и (3).

Чтобы проще было решать задачу расставим на рисунке сначала знаки плюс и минус, обозначающие знак производной. Потом стрелки – обозначающие возрастание, убывания функции.

Начнем с (-13): до (-13) производная положительна т.е. функция растет, после — производная отрицательна т.е. функция падает. Если это представить, то становится ясно, что (-13) – точка максимума.

(-11): производная сначала положительна, а потом отрицательна, значит функция возрастает, а потом убывает. Опять попробуйте это мысленно нарисовать и вам станет очевидно, что (-11) – это минимум.

(- 9): функция возрастает, а потом убывает – максимум.

(-7): минимум.

(3): максимум.

Все вышесказанное можно обобщить следующими выводами:

— Функция имеет максимум там, где производная равна нулю и меняет знак с плюса на минус.
— Функция имеет минимум там, где производная равна нулю и меняет знак с минуса на плюс.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

Чтобы ответить на этот вопрос, нужно делать все то же, что и в предыдущем пункте: находить где производная положительна, где отрицательна и где равна нулю. Чтобы было понятнее напишу алгоритм с примером решения:

Найдите производную функции (f'(x)).
Найдите корни уравнения (f'(x)=0).
Нарисуйте ось (x) и отметьте на ней точки полученные в пункте 2, изобразите дугами промежутки, на которые разбивается ось. Подпишите над осью (f'(x)), а под осью (f(x)).
Определите знак производной в каждом промежутке (методом интервалов).
Поставьте знак производной в каждом промежутке (над осью), а стрелкой укажите возрастание (↗) или убывание (↘) функции (под осью).
Определите, как изменился знак производной при переходе через точки, полученные в пункте 2:
— если (f’(x)) изменила знак с «(+)» на «(-)», то (x_1) – точка максимума;
— если (f’(x)) изменила знак с «(-)» на «(+)», то (x_3) – точка минимума;
— если (f’(x)) не изменила знак, то (x_2) – может быть точкой перегиба.

Всё! Точки максимумов и минимумов найдены.

Изображая на оси точки в которых производная равна нулю – масштаб можно не учитывать. Поведение функции можно показать так, как это сделано на рисунке ниже. Так будет очевиднее где максимум, а где минимум.

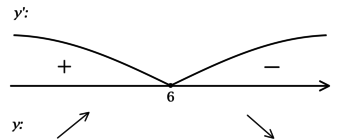
Пример(ЕГЭ). Найдите точку максимума функции (y=3x^5-20x^3-54).
Решение:
1. Найдем производную функции: (y’=15x^4-60x^2).
2. Приравняем её к нулю и решим уравнение:

(15x^4-60x^2=0) (|:15)
(x^4-4x^2=0)
(x^2 (x^2-4)=0)
(x=0) (x^2-4=0)
(x=±2)

3. – 6. Нанесем точки на числовую ось и определим, как меняется знак производной и как движется функция:

Теперь очевидно, что точкой максимума является (-2).

Ответ. (-2).

Смотрите также:
Связь функции и её производной | 7 задача ЕГЭ
Разбор задач на поиск экстремумов, минимумов и максимумов

Скачать статью

Источник

Задача 1. Найдите точку максимума функции

Решение: + показать

Задача 2. Найдите точку минимума функции

Решение: + показать

Задача 3. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 4. Найдите наибольшее значение функции $y=2+9x-frac{x^3}{3}$ на отрезке

Решение: + показать

Задача 5. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 6. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 7. Найдите точку максимума функции $y=6+12x-2x^{frac{3}{2}}.$

Решение: + показать

Задача 8. Найдите наибольшее значение функции $y=-frac{2}{3}xsqrt x+3x+8$ на отрезке

Решение: + показать

Задача 9. Найдите точку минимума функции $y=-frac{x^2+25}{x}$ .

Решение: + показать

Задача 10. Найдите наименьшее значение функции $y=frac{x^2+900}{x}$ на

Решение: + показать

Задача 11. Найдите точку максимума функции $y=frac{441}{x}+x+18.$

Решение: + показать

Задача 12. Найдите точку минимума функции $y=(3x^2-15x+15)e^{x-15}.$

Решение: + показать

Задача 13. Найдите точку максимума функции $y=(x+11)^2cdot e^{3-x}.$

Решение: + показать

Задача 14. Найдите наименьшее значение функции на отрезке .

Решение: + показать

Задача 15. Найдите наибольшее значение функции на отрезке

Решение: + показать

Задача 16. Найдите наименьшее значение функции на отрезке $[frac{1}{12};frac{5}{12}].$

Решение: + показать

Задача 17. Найдите наименьшее значение функции на отрезке $[frac{3}{4};frac{5}{4}].$

Решение: + показать

Задача 18. Найдите наименьшее значение функции $y=e^{2x}-11e^x-1$ на отрезке .

Решение: + показать

Задача 19. Найдите наибольшее значение функции на отрезке $[0;frac{pi}{2}].$

Решение: + показать

Задача 20. Найдите наименьшее значение функции на отрезке $[-frac{pi}{3};frac{pi}{3}].$

Решение: + показать

Задача 21. Найдите наибольшее значение функции на отрезке $[-frac{3pi}{2};0]$ .

Решение: + показать

Задача 22. Найдите наименьшее значение функции $y=4cosx+frac{15}{pi}x+9$ на отрезке $[-frac{2pi}{3};0].$

Решение: + показать

Задача 23. Найдите наименьшее значение функции на отрезке $[0;frac{pi}{4}].$

Решение: + показать

Задача 24. Найдите точку минимума функции принадлежащую промежутку $(0;frac{pi}{2})$ .

Решение: + показать

* Замечание. Важно!

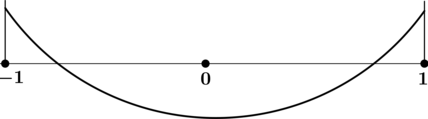
Не следует считать (могло сложиться такое мнение при разборе примеров выше), что наименьшее (наибольшее) значение функции на отрезке совпадает с минимумом (максимумом) на отрезке!

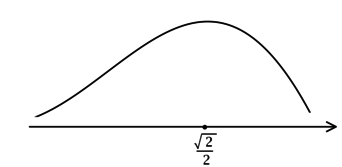
Например, на рисунке ниже наименьшее значение функции на отрезке достигается на конце отрезка , а именно, в точке .

То есть, вообще говоря, при нахождении наименьшего значения функции на отрезке следует выбрать наименьшую из величин:

1) $y(x_{min})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

При нахождении наибольшего значения функции на отрезке следует выбрать большую из величин:

1) $y(x_{max})$ (их может быть несколько) из рассматриваемого отрезка

2) ,

Но, если, например, на рассматриваемом отрезке функция имеет только один экстремум – минимум и мы ищем наименьшее значение, то отпадает необходимость находить значения функции на концах отрезка.

Аналогично в случае с нахождением наибольшего значения функции на отрезке, на котором содержится только один экстремум – максимум.

В случае же, когда на отрезке рассматриваемом функция не имеет экстремумов, то для нахождения наибольшего/наименьшего значений требуется лишь сравнить эти самые значения функции на концах отрезка и взять наибольшее/наименьшее из них.

Вы можете пройти тест “Исследование функции при помощи производной”

Источник

Тема 11.

Исследование функций с помощью производной

Поиск наибольшего/наименьшего значения у сложных функций

Вспоминай формулы по каждой теме

Решай новые задачи каждый день

Вдумчиво разбирай решения

ШКОЛКОВО.

Готовиться с нами — ЛЕГКО!

Подтемы раздела

исследование функций с помощью производной

11.01Поиск точек экстремума у элементарных функций

11.02Поиск точек экстремума у сложных функций

11.03Поиск точек экстремума у произведения

11.04Поиск точек экстремума у частного

11.05Поиск точек экстремума у функций с тригонометрией

11.06Поиск точек экстремума у смешанных функций

11.07Поиск наибольшего/наименьшего значения у элементарных функций

11.08Поиск наибольшего/наименьшего значения у сложных функций

11.09Поиск наибольшего/наименьшего значения у произведения

11.10Поиск наибольшего/наименьшего значения у частного

11.11Поиск наибольшего/наименьшего значения у функций с тригонометрией

11.12Поиск наибольшего/наименьшего значения у смешанных функций

11.13Нетипичные задачи

Решаем задачи

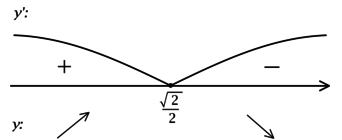
Найдите наименьшее значение функции

2
y =log3(x + 8x+ 19)

Показать ответ и решение

Выпишем ОДЗ:

1) Обозначим тогда

Найдем производную функции по

Найдём критические точки, то есть внутренние точки области определения
функции, в которых её производная равна 0 или не существует:

1--⋅--2x-+8---= 0 ⇔ 2x+ 8= 0
ln3 x2+ 8x+ 19

Отсюда При этом производная существует всюду на ОДЗ.

Для того, чтобы найти наибольшее/наименьшее значение функции, нужно
понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства и промежутки монотонности y :

3) Эскиз графика y :

Таким образом, наименьшее значение функции достигается в точке
минимума

Найдите наименьшее значение функции

на
отрезке .

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна 0 или не существует):

x2− 4
2x ⋅ e = 0 ⇔ x = 0

Таким образом, при x = 0 . Производная существует при любом .

2) Найдём промежутки знакопостоянства и промежутки монотонности :

3) Найдём промежутки знакопостоянства y ′ и промежутки монотонности на отрезке
:

4) Эскиз графика на отрезке :

Таким образом, наименьшего на отрезке значения функция достигает в точке
.

Тогда — наименьшее значение функции на отрезке .

Найдите наименьшее значение функции

на отрезке [0;π].

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

′
y = −2⋅sin2x

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:

πn
− 2⋅sin2x =0 ⇔ 2x = πn, n ∈ℤ ⇔ x= -2-, n ∈ℤ

Производная существует при любом

2) Найдём промежутки знакопостоянства ′
y и промежутки монотонности y :

Здесь бесконечное число промежутков, в которых чередуются знаки производной.

3) Найдём промежутки знакопостоянства и промежутки монотонности на отрезке [0;π]:

4) Эскиз графика на отрезке [0;π]:

Таким образом, наименьшего на отрезке [0;π] значения функция достигает в точке минимума x = π-:
2

( π)
y 2 = cosπ =− 1

Найдите наименьшее значение функции

Показать ответ и решение

Способ 1.

Функцию можно переписать в виде

(x− 7)2+1
y = 4

Эта функция является композицией двух функций: возрастающей y = 4x
1 и
возрастающей при x> 7 и убывающей при x< 7 функции 2
y2 =(x − 7) + 1:

Следовательно, исходная функция возрастает при x > 7 и убывает при x < 7,
то есть x= 7 является точкой минимума.

Следовательно, в этой точке достигается наименьшее значение функции:

P.S. Композиция двух возрастающих или двух убывающих функций —
возрастающая, а возрастающей и убывающей — убывающая.

Способ 2.

Функция определена при всех Исследуем функцию и найдем ее
промежутки возрастания и убывания, для этого найдем ее производную:

Найдем нули производной:

Нули производной и точки, в которых она не существует, разбивают область
определения производной на промежутки, на каждом из которых она непрерывна и
принимает значения одного знака. Найдем знаки производной на каждом из таких
промежутков:

PICT

При производная отрицательна, то есть функция
убывает; при производная положительна, то есть функция
возрастает. Следовательно, x= 7 является точкой минимума и наименьшего
значения функция достигает в этой точке:

72−14⋅7+50 1
y(7)= 4 = 4 = 4

Найдите наименьшее значение функции

∘ -----------
f (x)= x4− 4x2+ 13

Показать ответ и решение

Преобразуем исходную функцию:

Заметим, что (2 )2
x − 2 ≥ 0. Значит,

( )2 ∘ -----------
x2− 2 + 9≥ 9 ⇒ (x2− 2)2 +9 ≥ 3 ⇔ f(x) ≥3

Мы доказали, что Значит, если мы докажем, что существует такая точка x = x0, что то 3 будет
наименьшим значением функции f(x).

Для этого найдем точку, в которой

Пусть x =√2,
0 тогда

Значит, наименьшее значение функции равно 3.

Найдите наименьшее значение функции

2x x
y = e − 8e +9

на отрезке [0;2].

Показать ответ и решение

Найдем критические точки функции 2x x
f(x) =e − 8e + 9. Для этого посчитаем производную:

′ 2x x x x
f (x)= 2 ⋅e − 8e = 2e (e − 4)

Теперь найдем нули производной:

x x x
2e (e − 4)= 0 ⇔ e = 4 ⇔ x = ln4

При этом 2
0 <ln4< lne = 2, то есть данная точка лежит на отрезке [0;2].

Наименьшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:

pict

Таким образом, наименьшее значение функции на отрезке [0;2] равно -7.

Найдите наибольшее значение функции

√ - ∘ -----
y = 2⋅ x2+ 1

на отрезке

Показать ответ и решение

Найдем ОДЗ: — любое число.

1) Найдем производную:

√- 2x √ - x
y′ = 2 ⋅-√-2----= 2⋅√--2---
2 x + 1 x + 1

Найдём критические точки, то есть внутренние точки области определения функции, в которых её производная равна 0 или не
существует:

√2-⋅√--x---= 0 ⇔ x = 0
x2 +1

Производная существует при любом

2) Найдём промежутки знакопостоянства и промежутки монотонности y :

3) Найдём промежутки знакопостоянства и промежутки монотонности на отрезке

4) Эскиз графика на отрезке

Таким образом, наибольшего на отрезке значения функция достигает в точке или в точке x = 1. Сравним
значения функции в этих точках:

√ - √---- √ - √-
y(−1)= 2⋅ 1+ 1 = 2⋅ 2 = 2

√ - √---- √- √ -
y(1)= 2⋅ 1 +1 = 2⋅ 2= 2

Тогда наибольшее значение функции на отрезке равно 2.

Найдите наибольшее значение функции

Показать ответ и решение

1) Обозначим , тогда .

Найдём критические точки (то есть внутренние точки области определения функции, в которых её
производная равна или не существует):

(так
как , но et > 0 при любом ), откуда находим корень x = 6 . Для того, чтобы
найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.

2) Найдём промежутки знакопостоянства ′
y :

3) Эскиз графика:

Таким образом, x = 6 – точка максимума функции и наибольшее значение достигается в
ней:

Итого: − 4 – наибольшее значение функции .

Найдите наибольшее значение функции

2 √ -
y = − log17(2x − 2 2x+ 2)

Показать ответ и решение

Найдем ОДЗ: 2 √ -
2x − 2 2x+ 2 > 0 .

1) Обозначим 2 √-
2x − 2 2x + 2 = t(x) , тогда .

Найдем производную:

′ ′ ′ ′ 2 √ - ′
y = yt ⋅tx = (− log17t) ⋅(2x − 2 2x+ 2) =

√ -
1 1 √ - 1 4x − 2 2
= − ln-17 ⋅-t ⋅(4x− 2 2) = − ln17 ⋅2x2-−-2√2x-+-2

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна
или не существует):

√ -
-1-- ---4x−√2--2--- √ -
− ln17 ⋅2x2 − 2 2x+ 2 = 0 ⇔ 4x− 2 2 = 0

— на ОДЗ, откуда находим корень √ -
x = --2
2 .

Производная функции не существует при 2 √-
2x − 2 2x +2 = 0 , но у данного уравнения отрицательный
дискриминант, следовательно, у него нет решений.

Для того, чтобы найти наибольшее/наименьшее значение функции, нужно понять, как схематично выглядит её
график.

2) Найдём промежутки знакопостоянства ′
y и промежутки монотонности :

3) Эскиз графика :

Таким образом, наибольшего значение функция достигает в точке √ -
x = --2
2 :

( √-)
y -2- = − log171 = 0
2

Найдите наибольшее значение функции

2x x
y =− e +4e + 3

на отрезке [0;1].

Показать ответ и решение

Найдем критические точки функции 2x x
f(x) =− e +4e + 3. Для этого посчитаем производную:

′ ( 2x) x x x
f(x)= 2⋅ −e + 4e =2e (2− e )

Теперь найдем нули производной:

x x x
2e (2 − e )= 0 ⇔ e = 2 ⇔ x = ln2

При этом то есть данная точка лежит на отрезке [0;1].

Наибольшее значение функции на отрезке достигается в точке экстремума или на концах отрезка. Сравним значения
функции во всех таких точках:

pict

Таким образом, наибольшее значение функции на отрезке [0;1] равно 7.

Найдите наибольшее значение функции

√-
y = ecosx+sinx− 2 .

Показать ответ и решение

1) Обозначим √ --
cos x + sin x − 2 = t(x) , тогда .

√ -- √-
y′ = y′t ⋅ t′x = (et)′ ⋅ (cosx + sin x − 2)′ = et ⋅ (− sin x + cosx ) = ecosx+sin x− 2 ⋅ (− sin x + cosx).

√-
ecosx+sinx− 2 ⋅ (− sin x + cosx ) = 0 ⇔ − sinx + cos x = 0

(так
как √-
ecosx+sinx− 2 = et , но et > 0 при любом ), что равносильно tgx = 1 при , откуда
находим корни x = π-+ πk, k ∈ − ℤ
4 . Для того, чтобы найти наибольшее/наименьшее значение функции,
нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства : (их бесконечно много, но они чередуются)

3) Эскиз графика:

Таким образом, π
x = 4-+ 2πk, k ∈ ℤ – точки локальных максимумов функции и наибольшее значение
достигается в одной из них:

Итого: – наибольшее значение функции .

Источник

Как выглядят два прототипа 11 задания из первой части профильной математики ЕГЭ?

Как найти две точки экстремума функции?

Как найти наибольшее или наименьшее значение функции?

Хитрость, помогающая быстро разобраться с производной в ЕГЭ

Пример использования хитрости

Минимумом называют точку на функции, в которой значение функции меньше, чем в соседних точках.

Максимумом называют точку на функции, в которой значение функции больше, чем в соседних точках.

Минимумы и максимумы вместе именуют экстремумами функции.

В точках экстремумов (т.е. максимумов и минимумов) производная равна нулю.

Как найти точки экстремумов функции по графику производной (7 задание ЕГЭ)?

Как найти точки максимумов или минимумов функции по графику производной (7 задание ЕГЭ)?

— Производная положительна там, где функция возрастает. — Производная отрицательна там, где функция убывает.

Как найти точки максимумов и минимумов если известна формула функции (12 задание ЕГЭ)?

* Замечание. Важно!

Новое и интересное на сайте:

В точках экстремумов (т.е. максимумов и минимумов) производная
равна нулю.

— Производная положительна там, где функция возрастает.
— Производная отрицательна там, где функция убывает.