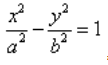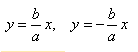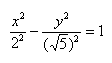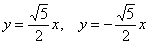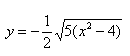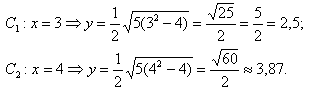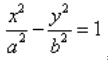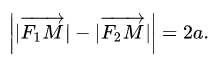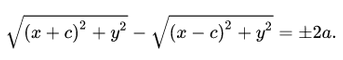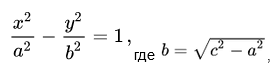09
Янв 2022
Категория: 10 Графики функций
2022-01-09
2022-09-11
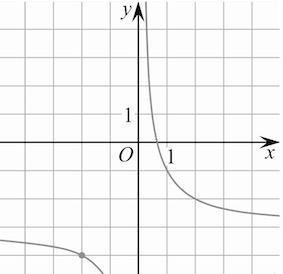
Задача 1. На рисунке изображён график функции Найдите
Решение: + показать
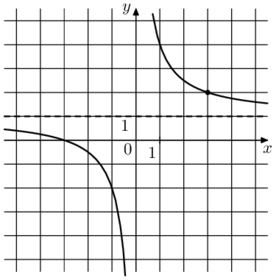
Задача 2. На рисунке изображён график функции вида где числа
и
— целые. Найдите значение
, при котором
Решение: + показать
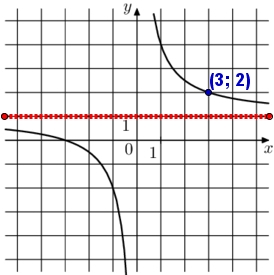
Задача 3. На рисунке изображён график функции вида где
– целые числа. Найдите
Решение: + показать
Задача 4. На рисунке изображён график функции Найдите
Решение: + показать
Задача 5. На рисунке изображены графики функций и
и которые пересекаются в точках
и
. Найдите ординату точки
Решение: + показать
Вы можете пройти тест “Гиперболы”
Автор: egeMax |
Нет комментариев
ЕГЭ Профиль №10. Гипербола
Скачать файл в формате pdf.
ЕГЭ Профиль №10. Гипербола
| Задача 1. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( { — 12} right).)
Ответ
ОТВЕТ: 0,75. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (fleft( { — 12} right) = frac{3}{{ — 12}} + 1 = 0,75.) Ответ: 0,75. |
|
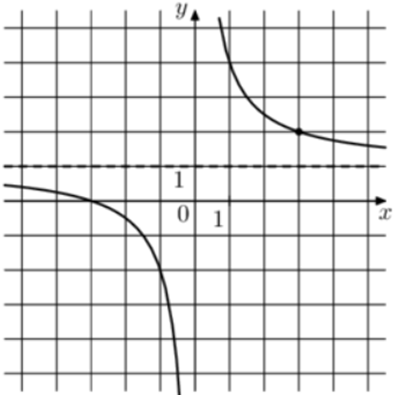
| Задача 2. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {50} right).)
Ответ
ОТВЕТ: — 2,96. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {2; — 2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{ — 2 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: ( — 1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 3). Следовательно, (a = — 3). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} — 3,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 3) и (fleft( {50} right) = frac{2}{{50}} — 3 = — 2,96.) Ответ: – 2,96. |
|
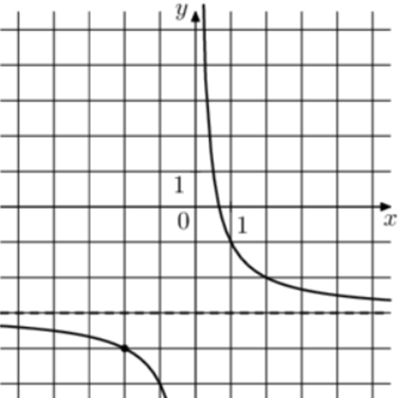
| Задача 3. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {7,5} right).)
Ответ
ОТВЕТ: 1,6. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 1} right)) и (left( {3;1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{1} + a}\{1 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 1 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 2). Следовательно, (a = 2). График проходит через точку (left( {1; — 1} right)), поэтому: ( — 1 = frac{k}{1} + 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} + 2) и (fleft( {7,5} right) = — frac{3}{{7,5}} + 2 = 1,6.) Ответ: 1,6. |
|
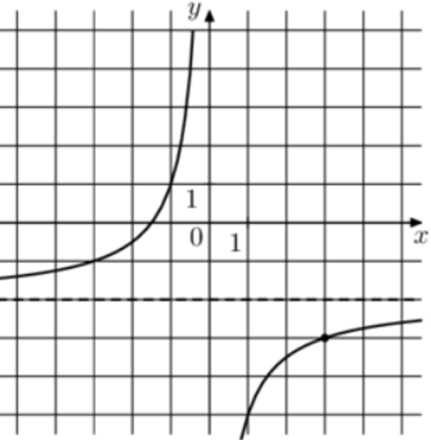
| Задача 4. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите (fleft( {0,25} right).)
Ответ
ОТВЕТ: — 14. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и (fleft( {0,25} right) = — frac{3}{{0,25}} — 2 = — 14.) Ответ: – 14. |
|
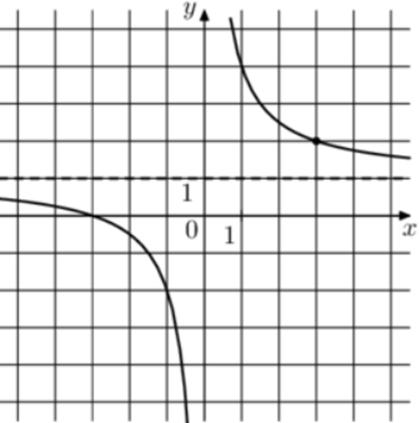
| Задача 5. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,8.
Ответ
ОТВЕТ: — 15. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;4} right)) и (left( {3;2} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{4 = frac{k}{1} + a}\{2 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: (2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Тогда: (4 = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,x = — 15.) Ответ: – 15. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1;4} right)), поэтому: (4 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{x} + 1) и (frac{3}{x} + 1 = 0,8,,,,,,,, Leftrightarrow ,,,,,,,,frac{3}{x} = — frac{1}{5},,,,,,,,, Leftrightarrow ,,,,,,,,,,x = — 15.) Ответ: – 15. |
|
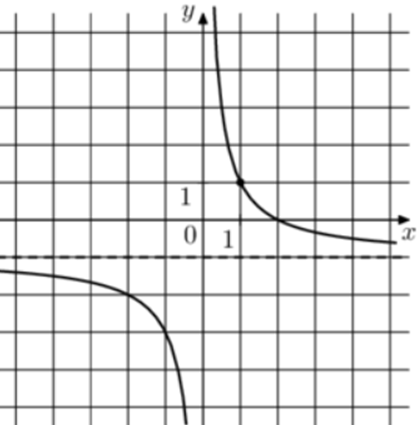
| Задача 6. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 19.
Ответ
ОТВЕТ: 0,1. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1;1} right)) и (left( {2;0} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = frac{k}{1} + a}\{0 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: (1 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Тогда: (1 = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,,, Leftrightarrow ,,,,,,,,,x = 0,1.) Ответ: 0,1. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 1). Следовательно, (a = — 1). График проходит через точку (left( {1;1} right)), поэтому: (1 = frac{k}{1} — 1,,,,,,,, Leftrightarrow ,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{x} — 1) и (frac{2}{x} — 1 = 19,,,,,,, Leftrightarrow ,,,,,,,,,frac{2}{x} = 20,,,,,,,, Leftrightarrow ,,,,,,,,x = 0,1.) Ответ: 0,1. |
|
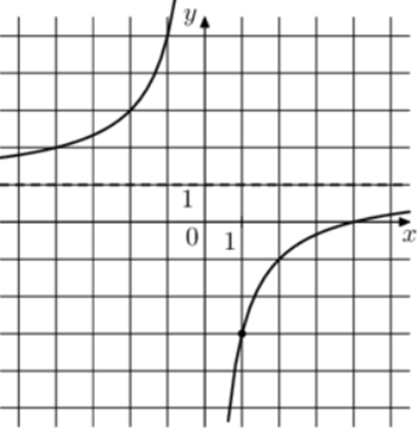
| Задача 7. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно 0,75.
Ответ
ОТВЕТ: 16. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 3} right)) и (left( {2; — 1} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 3 = frac{k}{1} + a}\{ — 1 = frac{k}{2} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{2},,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Тогда: ( — 3 = — 4 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,,, Leftrightarrow ,,,,,,,,x = 16.) Ответ: 16. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = 1). Следовательно, (a = 1). График проходит через точку (left( {1; — 3} right)), поэтому: ( — 3 = frac{k}{1} + 1,,,,,,,, Leftrightarrow ,,,,,,,k = — 4.) Таким образом, (fleft( x right) = — frac{4}{x} + 1) и ( — frac{4}{x} + 1 = 0,75,,,,,,, Leftrightarrow ,,,,,, — frac{4}{x} = — frac{1}{4},,,,,,, Leftrightarrow ,,,,,,x = 16.) Ответ: 16. |
|
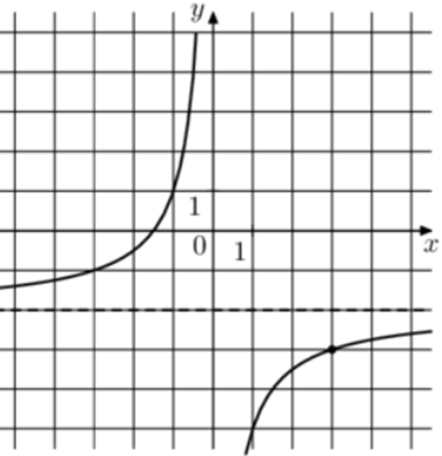
| Задача 8. На рисунке изображён график функции (fleft( x right) = frac{k}{x} + a.) Найдите, при каком значении x значение функции равно ( — 9,5.)
Ответ
ОТВЕТ: 0,4. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{x} + a) проходит через точки (left( {1; — 5} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = frac{k}{1} + a}\{ — 3 = frac{k}{3} + a}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = k — frac{k}{3},,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Тогда: ( — 5 = — 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,,, Leftrightarrow ,,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,,,, Leftrightarrow ,,,,,,,,x = 0,4.) Ответ: 0,4. 2 Способ Заметим, что график имеет горизонтальную асимптоту (y = — 2). Следовательно, (a = — 2). График проходит через точку (left( {1; — 5} right)), поэтому: ( — 5 = frac{k}{1} — 2,,,,,,,, Leftrightarrow ,,,,,,,k = — 3.) Таким образом, (fleft( x right) = — frac{3}{x} — 2) и ( — frac{3}{x} — 2 = — 9,5,,,,,,, Leftrightarrow ,,,,,,, — frac{3}{x} = — frac{{15}}{2},,,,,, Leftrightarrow ,,,,,,x = 0,4.) Ответ: 0,4. |
|
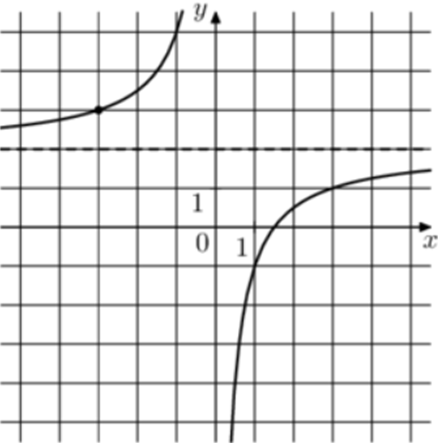
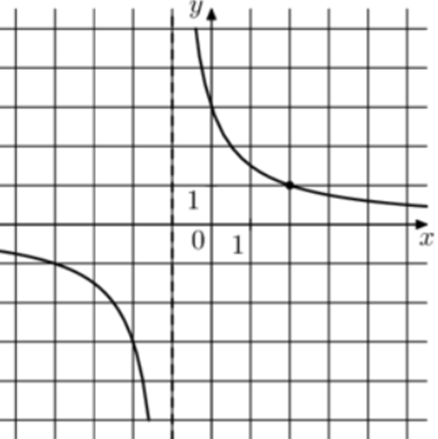
| Задача 9. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {19} right).)
Ответ
ОТВЕТ: 0,15. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{*{20}{c}}{3 = frac{k}{{0 + a}}}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3a,,,,,}\{k = 2 + a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15.) Ответ: 0,15. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (fleft( {19} right) = frac{3}{{19 + 1}} = 0,15). Ответ: 0,15. |
|
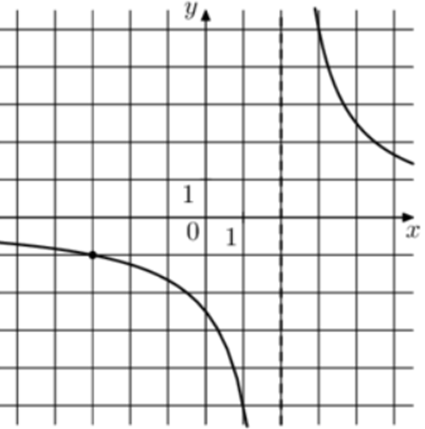
| Задача 10. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( { — 4frac{2}{3}} right).)
Ответ
ОТВЕТ: — 0,75. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 3; — 1} right)) и (left( {1; — 5} right)). (left{ {begin{array}{*{20}{c}}{ — 1 = frac{k}{{ — 3 + a}}}\{ — 5 = frac{k}{{1 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3 — a,,,,,}\{k = — 5 — 5a}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3 — a = — 5 — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 2,,,,k = 5.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{5}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{5}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 2). Следовательно, (a = — 2). График проходит через точку (left( { — 3; — 1} right)), поэтому: ( — 1 = frac{k}{{ — 2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x — 2}}) и (fleft( { — 4frac{2}{3}} right) = frac{3}{{ — 4frac{2}{3} — 2}} = frac{5}{{ — frac{{20}}{3}}} = — 0,75.) Ответ: – 0,75. |
|
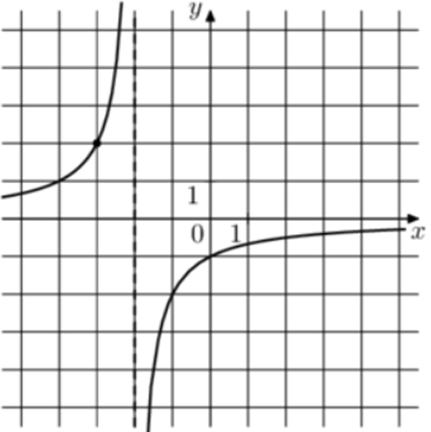
| Задача 11. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {18} right).)
Ответ
ОТВЕТ: — 0,1. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {18} right) = frac{{ — 2}}{{18 + 2}} = — 0,1.) Ответ: – 0,1. |
|
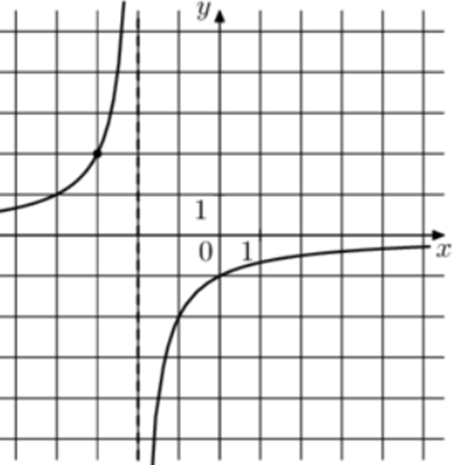
| Задача 12. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите (fleft( {6frac{1}{3}} right).)
Ответ
ОТВЕТ: — 0,24. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}}}\{2 = frac{k}{{ — 3 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a,,,,,}\{k = 2a — 6,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (fleft( {6frac{1}{3}} right) = frac{{ — 2}}{{6frac{1}{3} + 2}} = frac{{ — 2}}{{frac{{25}}{3}}} = — 0,24.) Ответ: – 0,24. |
|
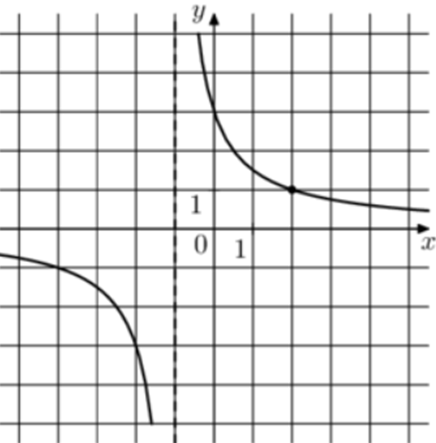
| Задача 13. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: 14. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {0;3} right)) и (left( {2;1} right)). (left{ {begin{array}{*{20}{c}}{3 = frac{k}{a},,,,,,}\{1 = frac{k}{{2 + a}}}end{array}} right.,,,,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 3a,,,,,,,,,,,}\{k = 2 + a,,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,,3a = 2 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1,,,,k = 3.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 1). Следовательно, (a = 1). График проходит через точку (left( {0;3} right)), поэтому: (3 = frac{k}{{0 + 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, (fleft( x right) = frac{3}{{x + 1}}) и (frac{3}{{x + 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x + 1 = 15,,,,,,, Leftrightarrow ,,,,,,,x = 14.) Ответ: 14. |
|
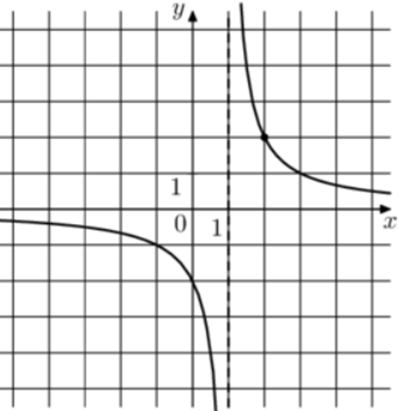
| Задача 14. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,08.)
Ответ
ОТВЕТ: — 24. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {2;2} right)) и (left( {3;1} right)). (left{ {begin{array}{*{20}{c}}{2 = frac{k}{{2 + a}},,,,,,}\{1 = frac{k}{{3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 4 + 2a,,,,,,,,,,,}\{k = 3 + a,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,4 + ,2a = 3 + a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {2;2} right)), поэтому: (2 = frac{k}{{2 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 2.) Таким образом, (fleft( x right) = frac{2}{{x — 1}}) и (frac{2}{{x — 1}} = — 0,08,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 25,,,,,,, Leftrightarrow ,,,,,,,x = — 24.) Ответ: – 24. |
|
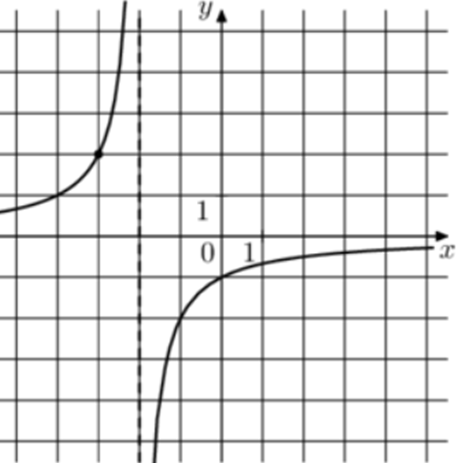
| Задача 15. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = — 0,04.)
Ответ
ОТВЕТ: 48. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( { — 1; — 2} right)) и (left( { — 3;2} right)). (left{ {begin{array}{*{20}{c}}{ — 2 = frac{k}{{ — 1 + a}},,,,,,}\{2 = frac{k}{{ — 3 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = 2 — 2a}\{k = 2a — 6}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,2a — 6 = 2 — 2a,,,,,,,,, Leftrightarrow ,,,,,,,,a = 2,,,,k = — 2.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = — 2). Следовательно, (a = 2). График проходит через точку (left( { — 1; — 2} right)), поэтому: ( — 2 = frac{k}{{ — 1 + 2}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 2.) Таким образом, (fleft( x right) = frac{{ — 2}}{{x + 2}}) и (frac{{ — 2}}{{x + 2}} = — 0,04,,,,,,,, Leftrightarrow ,,,,,,,x + 2 = 50,,,,,,, Leftrightarrow ,,,,,,,x = 48.) Ответ: 48. |
|
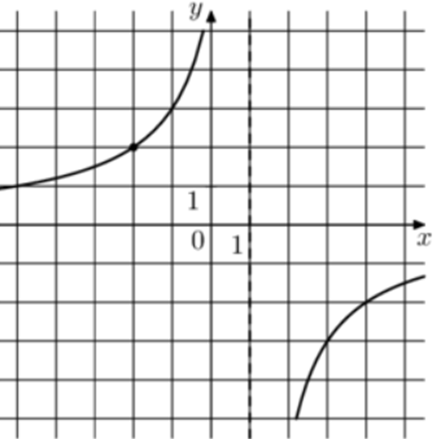
| Задача 16. На рисунке изображён график функции (fleft( x right) = frac{k}{{x + a}}.) Найдите значение x, при котором (fleft( x right) = 0,2.)
Ответ
ОТВЕТ: — 29. |
 |
|
Решение
1 Способ График гиперболы (fleft( x right) = frac{k}{{x + a}}) проходит через точки (left( {3; — 3} right)) и (left( { — 1;3} right)). (left{ {begin{array}{*{20}{c}}{ — 3 = frac{k}{{3 + a}},,,,,,}\{3 = frac{k}{{ — 1 + a}},,,,,}end{array}} right.,,,,,,, Leftrightarrow ,,,,,,,left{ {begin{array}{*{20}{c}}{k = — 9 — 3a,,,,,,,,,,,}\{k = 3a — 3,,,,,,,,,,,,,,}end{array}} right., Leftrightarrow ,,,,,,,3a — 3 = — 9 — 3a,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 1,,,,k = — 6.) Следовательно, уравнение гиперболы: (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29. 2 Способ Заметим, что график имеет вертикальную асимптоту (x = 1). Следовательно, (a = — 1). График проходит через точку (left( {3; — 3} right)), поэтому: ( — 3 = frac{k}{{3 — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 6.) Таким образом, (fleft( x right) = frac{{ — 6}}{{x — 1}}) и (frac{{ — 6}}{{x — 1}} = 0,2,,,,,,,, Leftrightarrow ,,,,,,,x — 1 = — 30,,,,,,, Leftrightarrow ,,,,,,,x = — 29.) Ответ: – 29. |
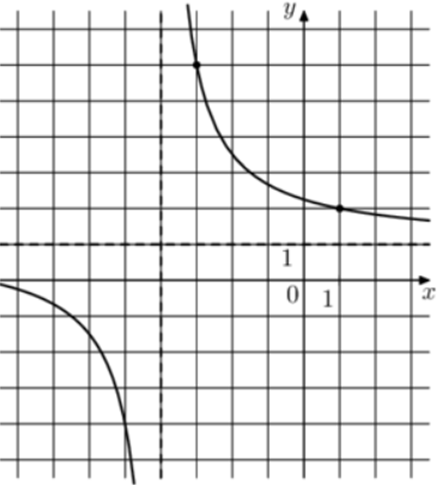
| Задача 17. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 1. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Ответ: 1. |
|
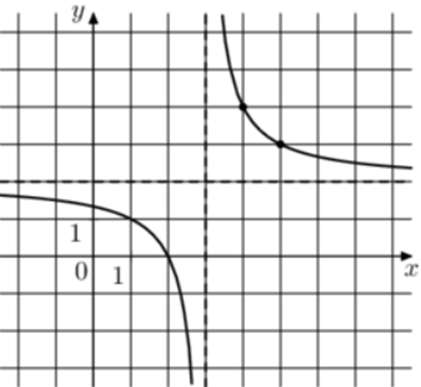
| Задача 18. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2. |
|
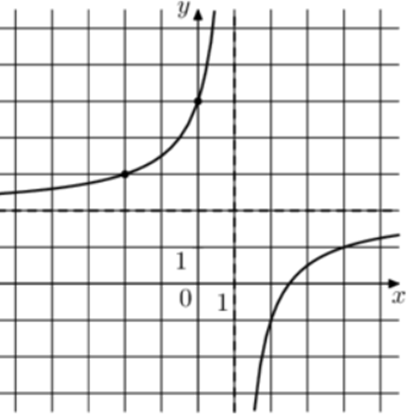
| Задача 19. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Ответ: 2. |
|
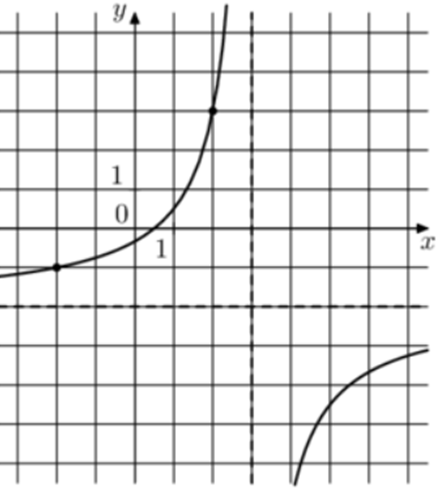
| Задача 20. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите k.
Ответ
ОТВЕТ: — 2. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = -2), то (k = -2). Ответ: -2. |
|
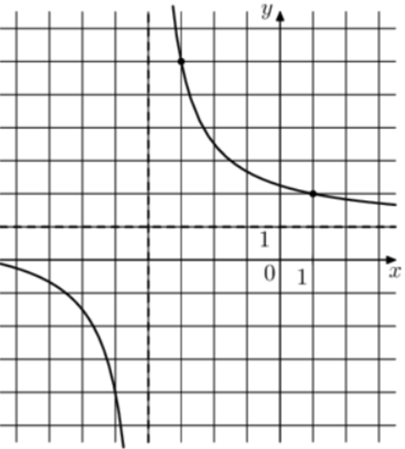
| Задача 21. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 9. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 1), то (k = 1). Так как график функции имеет вертикальную асимптоту (x = — 4), то (b = 4). Следовательно: (fleft( x right) = 1 + frac{{a — 4}}{{x + 4}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 3;6} right)). Тогда: (6 = 1 + frac{{a — 4}}{{ — 3 + 4}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 4}}{1} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 9.,,,) Ответ: 9. |
|
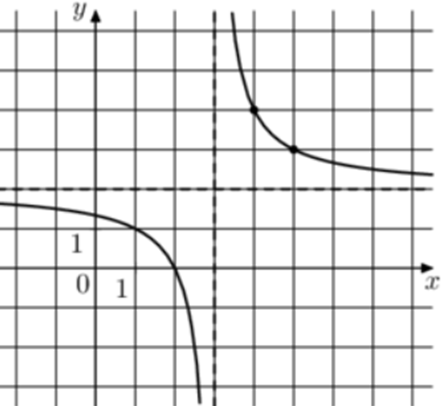
| Задача 22. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 4. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = 2), то (k = 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = 2 + frac{{a + 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {5;3} right)). Тогда: (3 = 2 + frac{{a + 6}}{{5 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a + 6}}{2} = 1,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 4.,,,) Ответ: – 4. |
|
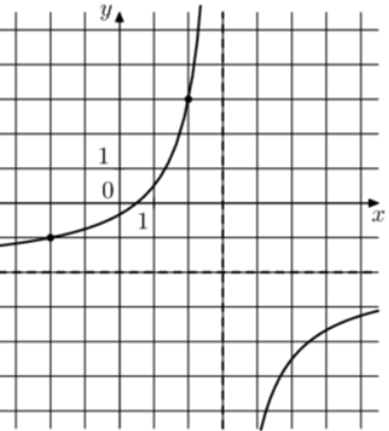
| Задача 23. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: 1. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 2), то (k = — 2). Так как график функции имеет вертикальную асимптоту (x = 3), то (b = — 3). Следовательно: (fleft( x right) = — 2 + frac{{a — 6}}{{x — 3}}.) Воспользуемся тем, что график функции проходит через точку (left( {2;3} right)). Тогда: (3 = — 2 + frac{{a — 6}}{{2 — 3}},,,,,,,, Leftrightarrow ,,,,,,,,frac{{a — 6}}{{ — 1}} = 5,,,,,,,,, Leftrightarrow ,,,,,,,,a = 1.,,,) Ответ: 1. |
|
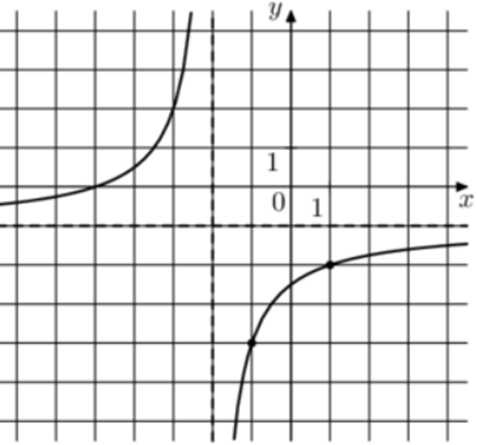
| Задача 24. На рисунке изображён график функции (fleft( x right) = frac{{k,x + a}}{{x + b}}.) Найдите a.
Ответ
ОТВЕТ: — 5. |
 |
|
Решение
Преобразуем данную функцию (fleft( x right) = frac{{kx + a}}{{x + b}}) следующим образом: (fleft( x right) = frac{{kx + a}}{{x + b}} = frac{{kx + kb + a — kb}}{{x + b}} = frac{{kleft( {x + b} right)}}{{x + b}} + frac{{a — kb}}{{x + b}} = k + frac{{a — kb}}{{x + b}}) Так как график функции имеет горизонтальную асимптоту (y = — 1), то (k = — 1). Так как график функции имеет вертикальную асимптоту (x = — 2), то (b = 2). Следовательно: (fleft( x right) = — 1 + frac{{a + 2}}{{x + 2}}.) Воспользуемся тем, что график функции проходит через точку (left( { — 1; — 4} right)). Тогда: ( — 4 = — 1 + frac{{a + 2}}{{ — 1 + 2}},,,,,,,, Leftrightarrow ,,,,,,,,a + 2 = — 3,,,,,,,,, Leftrightarrow ,,,,,,,,a = — 5.,,,) Ответ: – 5. |
|
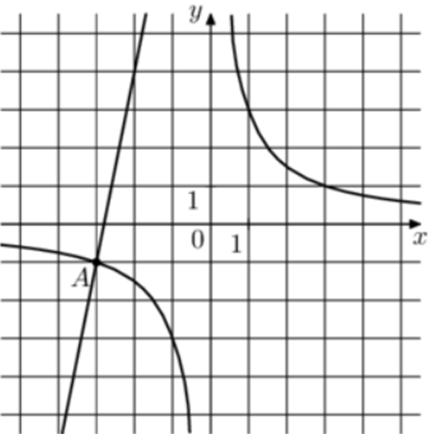
| Задача 25. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 0,2. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;3} right)). Следовательно: (3 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 3 cdot 5 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,5x + 14 = frac{3}{x},,,,,,,,, Leftrightarrow ,,,,,,,5{x^2} + 14x — 3 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 0,2,,,,{x_2} = — 3.) Значение (x = — 3) является абсциссой точки А. Следовательно, абсцисса точки В равна 0,2. Ответ: 0,2. |
|
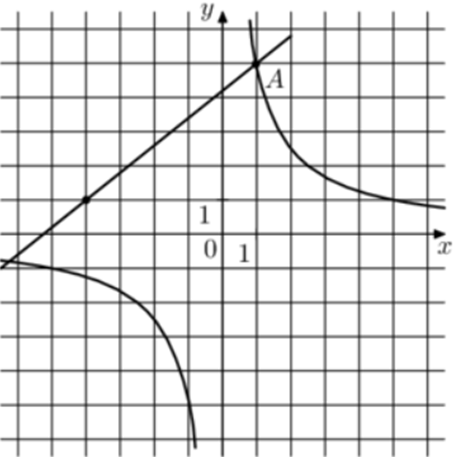
| Задача 26. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: — 6,25. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1;5} right)). Следовательно: (5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 4;1} right)) и (left( {1;5} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = — 4a + b}\{5 = a + b,,,,,}end{array}} right.) Вычтем из первого уравнения второе: ( — 4 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{4}{5}.) Тогда: (1 = — 4 cdot frac{4}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{21}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{4}{5}x + frac{{21}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{4}{5}x + frac{{21}}{5}}\{y = frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{4}{5}x + frac{{21}}{5} = frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} + 21x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = — 6,25.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна – 6,25. Ответ: – 6,25. |
|
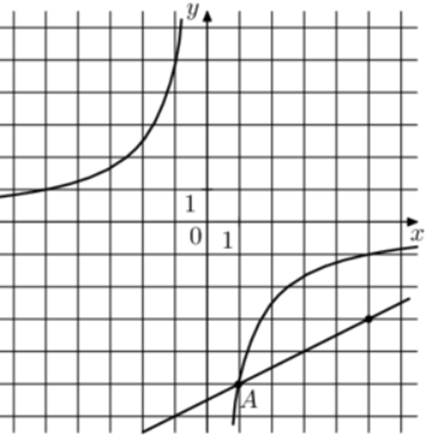
| Задача 27. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 10. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10.) Значение (x = 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 10. Ответ: 10. |
|
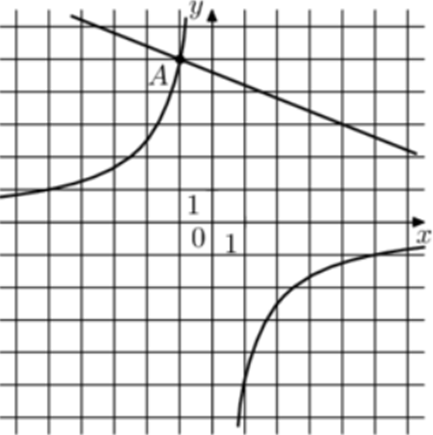
| Задача 28. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите абсциссу точки B.
Ответ
ОТВЕТ: 12,5. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{5 = — a + b}\{3 = 4a + b}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,, Leftrightarrow ,,,,,,2{x^2} — 23x — 25 = 0,,,,,, Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = 12,5.) Значение (x = — 1) является абсциссой точки А. Следовательно, абсцисса точки В равна 12,5. Ответ: 12,5. |
|
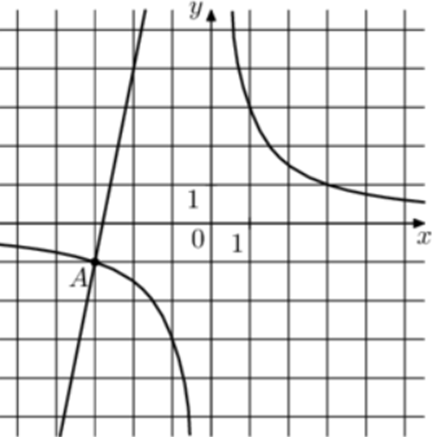
| Задача 29. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: 15. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 3; — 1} right)). Следовательно: ( — 1 = frac{k}{{ — 3}},,,,,, Leftrightarrow ,,,,,,,k = 3.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{3}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 3; — 1} right)) и (left( { — 2;4} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 1 = — 3a + b}\{4 = — 2a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 5 = — a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 5.) Тогда: ( — 1 = — 15 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = 14.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 5x + 14.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 5x + 14}\{y = frac{3}{x},,,,,,,,,,,,,}end{array}} right.,,,,,, Leftrightarrow ,,,,,,5x + 14 = frac{3}{x},,,,,, Leftrightarrow ,,,,,5{x^2} + 14x — 3 = 0,,,,,, Leftrightarrow ) ( Leftrightarrow ,,,,,{x_1} = — 3,,,,{x_2} = frac{1}{5},,,,{y_1} = — 1,,,,,{y_2} = 15.) Следовательно, (Aleft( { — 3; — 1} right)) и (Bleft( {frac{1}{5};15} right)). Таким образом, ордината точки В равна 15. Ответ: 15. |
|
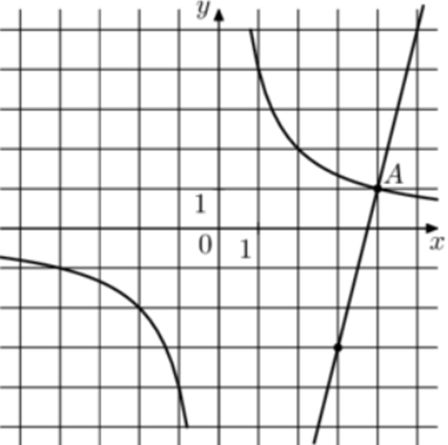
| Задача 30. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 16. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {4;1} right)). Следовательно: (1 = frac{k}{4},,,,,,,,, Leftrightarrow ,,,,,,,,,k = 4.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = frac{4}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {4;1} right)) и (left( {3; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{1 = 4a + b,,}\{ — 3 = 3a + b}end{array}} right.) Вычтем из первого уравнения второе: (4 = a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = 4.) Тогда: (1 = 16 + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — 15.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = 4x — 15.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = 4x — 15}\{y = frac{4}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,4x — 15 = frac{4}{x},,,,,,,,, Leftrightarrow ,,,,,,,4{x^2} — 15x — 4 = 0,,,,,,, Leftrightarrow )( Leftrightarrow ,,,,,{x_1} = 4,,,,{x_2} = — frac{1}{4},,,,{y_1} = 1,,,,,{y_2} = — 16.) Следовательно, (Aleft( {4;1} right)) и (Bleft( { — frac{1}{4}; — 16} right)). Таким образом, ордината точки В равна – 16. Ответ: – 16. |
|
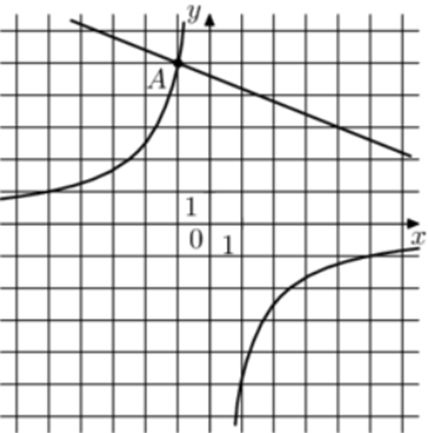
| Задача 31. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,4. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( { — 1;5} right)). Следовательно: (5 = frac{k}{{ — 1}},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( { — 1;5} right)) и (left( {4;3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{5 = — a + b,,}\{3 = 4a + b,,}end{array}} right.) Вычтем из первого уравнения второе: (2 = — 5a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = — frac{2}{5}.) Тогда: (5 = frac{2}{5} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = frac{{23}}{5}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = — frac{2}{5}x + frac{{23}}{5}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = — frac{2}{5}x + frac{{23}}{5}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,, — frac{2}{5}x + frac{{23}}{5} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,2{x^2} — 23x — 25 = 0,,,,,,, Leftrightarrow ,,,,,,,,,,,) ( Leftrightarrow ,,,,,,{x_1} = — 1,,,,{x_2} = frac{{25}}{2},,,,,,,,,,{y_1} = 5,,,,{y_2} = — 0,4.) Следовательно, (Aleft( { — 1;5} right)) и (Bleft( {frac{{25}}{2}; — 0,4} right)). Таким образом, ордината точки В равна – 0,4. Ответ: – 0,4. |
|
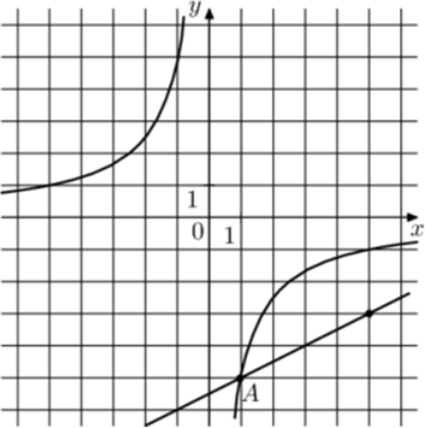
| Задача 32. На рисунке изображены графики функций (fleft( x right) = frac{k}{x}) и (gleft( x right) = a,x + b,,) которые пересекаются в точках A и B. Найдите ординату точки B.
Ответ
ОТВЕТ: — 0,5. |
 |
|
Решение
График гиперболы (fleft( x right) = frac{k}{x}) проходит через точку (left( {1; — 5} right)). Следовательно: ( — 5 = frac{k}{1},,,,,,,,, Leftrightarrow ,,,,,,,,,k = — 5.) Таким образом, уравнение гиперболы имеет вид: (fleft( x right) = — frac{5}{x}.) График прямой (gleft( x right) = ax + b) проходит через точки (left( {1; — 5} right)) и (left( {5; — 3} right)). Следовательно: (left{ {begin{array}{*{20}{c}}{ — 5 = a + b,,,}\{ — 3 = 5a + b}end{array}} right.) Вычтем из первого уравнения второе: ( — 2 = — 4a,,,,,,,,, Leftrightarrow ,,,,,,,,,a = frac{1}{2}.) Тогда: ( — 5 = frac{1}{2} + b,,,,,,,,, Leftrightarrow ,,,,,,,,,b = — frac{{11}}{2}.) Таким образом, уравнение прямой имеет вид: (gleft( x right) = frac{1}{2}x — frac{{11}}{2}.) Чтобы найти координаты точек пересечения прямой и гиперболы необходимо решить систему уравнений: (left{ {begin{array}{*{20}{c}}{y = frac{1}{2}x — frac{{11}}{2}}\{y = — frac{5}{x},,,,,,,,,,,,,}end{array}} right.,,,,,,,, Leftrightarrow ,,,,,,,,frac{1}{2}x — frac{{11}}{2} = — frac{5}{x},,,,,,,,, Leftrightarrow ,,,,,,,{x^2} — 11x + 10 = 0,,,,,,, Leftrightarrow ,,,,,,,,) ( Leftrightarrow ,,,,,,,,{x_1} = 1,,,,{x_2} = 10,,,,,,,,,,,{y_1} = — 5,,,,{y_2} = — 0,5.) Следовательно, (Aleft( {1; — 5} right)) и (Bleft( {10; — 0,5} right)). Таким образом, ордината точки В равна – 0,5. Ответ: – 0,5. |
В ЕГЭ 2022 года добавили новую задачу на графики функций. Для решения этой задачи нужно сначала определить формулу функции, а затем вычислить ответ на вопрос задачи. И если вычисление ответа по известной формуле обычно не составляет труда, то вот определение самой формулы часто ставит школьников в тупик. Поэтому мы разберем три разных подхода к этому вопросу.
Замечание. Про то как определяется формула у прямой и параболы я написала в этой и этой статьях. Поэтому здесь в примерах я буду использовать другие функции – дробные, иррациональные, показательные и логарифмические, но все три описанных здесь способа работают и для линейных, и для квадратичных функций в том числе.
1 способ – находим формулу по точкам
Этот способ подходит вообще для любой девятой задачи, но занимает достаточно много времени и требует хорошего навыка решения систем уравнений.
Давайте разберем алгоритм на примере конкретной 9-ой задачи ЕГЭ:

Алгоритм:
1. Находим 2 точки с целыми координатами. Обычно они выделены жирно, но если это не так, то не проблема найти их самому.
Пример:
2. Подставляем эти координаты в «полуфабрикат» функции. Вместо (f(x))– координату игрек, вместо (x) – икс. Получается система.

3. Решаем эту систему и получаем готовую формулу.

4. Готово, функция найдена, можно переходить ко второму этапу – вычислению (f(-8)). Если вы вдруг не знаете, что это значит – в конце статьи я рассматриваю этот момент более подробно.

Давайте посмотрим метод еще раз на примере с логарифмической функцией.
Пример:

2 способ – преобразование графиков функций
Этот способ сильно быстрее первого, но требует больше знаний. Для использования преобразований функций нужно знать, как выглядят функции без изменения и как преобразования их меняют. Наиболее удобно использовать этот способ для иррациональной функции ((y=sqrt{x}) ) и функции обратной пропорциональности ((y=frac{1}{x})).
Вот как выглядит применение этого способа:

Для использования этого способа надо знать, как выглядят изначальные функции:

И понимать, как меняются функции от преобразований:




Часто даже по «полуфабрикату» функции понятно, какие преобразования сделали с функцией:

Пример:

3 способ – гибридный
Идеально подходит для логарифмических и показательных функций, так как обычно у таких функций неизвестно основание и с помощью преобразований его не найти. С другой стороны, независимо от оснований любая показательная функция должна проходить через точку ((0;1)), а любая логарифмическая — через точку ((1;0)).

По смещению этих точек легко понять, как именно двигали функцию, но только если ее не растягивали, а лишь перемещали вверх-вниз, влево-вправо (как обычно и бывает в задачах на ЕГЭ).
Основание же лучше находить уже следующим действием, используя подстановку координат точки в «полуфабрикат» функции.


Как отвечать на вопросы в задаче, когда уже определили функцию
— Если просят найти (f)(любое число), то нужно это число подставить в готовую функцию вместо икса.
Пример:
— Если просят найти «при каком значении x значение функции равно *любому числу*», то надо решить уравнение, в одной части которого будет функция, а в другой — то самое число. Аналогично надо поступить, если просят «найти корень уравнения (f(x)=) *любое число*».
Пример:
— Если просят найти абсциссу точки пересечения – надо приравнять 2 функции и решить получившееся уравнение. Корень уравнения и будет искомой абсциссой. Аналогично надо делать в задачах, где даны две точки пересечения (A)(*любое число*;*другое число*) и (B(x_0;y_0)) и просят найти (x_0).
Пример:

— Если просят найти ординату точки пересечения – надо приравнять 2 функции, найти иксы и подставить подходящий икс в любую функцию. Точно также решаем если просят найти (y_0) точки пересечения двух функций.
Пример:

— Иногда просят найти просто какой-либо из коэффициентов функции. Тогда надо просто восстановить функцию и записать в ответ то, о чем спросили:
Пример:

9 задание егэ математика профиль 2022 гипербола
Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Как решать 9 задание ЕГЭ 2022 математика профиль видео теория:
1)На рисунке изображён график функции вида f(x)= a3x+b x+c, где числа a, b и c — целые. Найдите a.
2)На рисунке изображён график функции вида f(x)= 2ax+b x+c, где числа a, b и c — целые. Найдите a.
3)На рисунке изображён график функции вида f(x)= ax+b x+c, где числа a, b и c — целые. Найдите a.
4)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(−22).
5)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.
6)На рисунке изображён график функции вида f(x)= 2ax+b x+c, где числа a, b и c — целые. Найдите a.
7)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(15).
8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.
9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.
10)На рисунке изображён график функции вида f(x)=log1.4(x−a)+b, где числа a, b — целые. Найдите ab.
11)На рисунке изображён график функции вида f(x)=2ax+b, где числа a, b — целые. Найдите сумму коэффициентов a+b, если f(1)=10.
12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b — целые. Найдите сумму коэффициентов a+b.
13)На рисунке изображён график функции вида f(x)=ln(a+x)+b, где числа a, b — целые. Найдите сумму коэффициентов a+b, если A(0;ln2e).
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Повышенный.
Средний процент выполнения: 74.8%
Ответом к заданию 9 по математике (профильной) может быть Целое число или конечная десятичная дробь.
Задание №9 с ответами решу ЕГЭ 2022 профиль математика 11 класс
Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
1)На рисунке изображён график функции вида f(x)= a3x+b x+c, где числа a, b и c — целые. Найдите a.
2)На рисунке изображён график функции вида f(x)= 2ax+b x+c, где числа a, b и c — целые. Найдите a.
3)На рисунке изображён график функции вида f(x)= ax+b x+c, где числа a, b и c — целые. Найдите a.
4)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(−22).
5)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите решение уравнения f(x)=18.
6)На рисунке изображён график функции вида f(x)= 2ax+b x+c, где числа a, b и c — целые. Найдите a.
7)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите f(15).
8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.
9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.
10)На рисунке изображён график функции вида f(x)=log1.4(x−a)+b, где числа a, b — целые. Найдите ab.
11)На рисунке изображён график функции вида f(x)=2ax+b, где числа a, b — целые. Найдите сумму коэффициентов a+b, если f(1)=10.
12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b — целые. Найдите сумму коэффициентов a+b.
13)На рисунке изображён график функции вида f(x)=ln(a+x)+b, где числа a, b — целые. Найдите сумму коэффициентов a+b, если A(0;ln2e).
ЕГЭ — ПРОФИЛЬ. Тригонометрия. • Тригонометрические формулы • Преобразование тригонометрических выражений • Тригонометрические уравнения • Задания 4. Показать полностью.
Вычисления и преобразования — готовимся к ЕГЭ по Математике вместе с Александром Антипиным. Со мной вы сможете сдать экзамены на 90-100 баллов! Задание 9. Вычисления и преобразования. Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11.
Например, задание № 4 (9) Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических.
Задачи для практики
5 На рисунке изображён график функции вида f x a x b c, где числа a, b и c целые.
100ballnik. com
12.11.2017 10:33:27
2017-11-12 10:33:27
9 задание егэ математика профиль 2022 гипербола
ЕГЭ — ПРОФИЛЬ. Тригонометрия. • Тригонометрические формулы • Преобразование тригонометрических выражений • Тригонометрические уравнения • Задания 4. Показать полностью.
Вычисления и преобразования — готовимся к ЕГЭ по Математике вместе с Александром Антипиным. Со мной вы сможете сдать экзамены на 90-100 баллов! Задание 9. Вычисления и преобразования. Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11.
Например, задание № 4 (9) Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических.
9)На рисунке изображён график функции вида f(x)=log5(ax+b)+c, где числа a, b, c — целые. Найдите наибольшее значение функции g(x)=−x2+ax+b.
8)На рисунке изображён график функции вида f(x)= a x+b +c, где числа a, b и c — целые. Найдите x, при котором f(x)=21.
Как решать 9 задание ЕГЭ 2022 математика профиль видео теория:
4 x a b, где числа a, b целые.
M. vk. com
20.08.2018 21:30:39
2018-08-20 21:30:39
Задание 9. Графики функций. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Повышенный.
Средний процент выполнения: 74.8%
Ответом к заданию 9 по математике (профильной) может быть Целое число или конечная десятичная дробь.
Задачи для практики
Необходимо зарегистрироваться
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
12)На рисунке изображён график функции вида f(x)=log2(ax+b)+2, где числа a, b — целые. Найдите сумму коэффициентов a+b.
Задание 9. Графики функций. ЕГЭ 2022 по математике профильного уровня
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Повышенный.
Средний процент выполнения: 74.8%
Ответом к заданию 9 по математике (профильной) может быть Целое число или конечная десятичная дробь.
Необходимо зарегистрироваться
Для доступа к решениям необходимо включить уведомления от группы Турбо в вк — это займет буквально 10 секунд. Никакого спама, только самое важное и полезное для тебя. Ты всегда можешь запретить уведомления.
Как формулируется новое задание 9 ЕГЭ 2022 по математике? По графику функции, который дается в условии, вам нужно определить неизвестные параметры в ее формуле. Возможно — найти значение функции в некоторой точке или координаты точки пересечения графиков функций.
Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических.
Egeturbo. ru
20.01.2020 7:02:07
2020-01-20 07:02:07
Источники:
Https://100ballnik. com/%D0%B7%D0%B0%D0%B4%D0%B0%D0%BD%D0%B8%D0%B5-%E2%84%969-%D1%81-%D0%BE%D1%82%D0%B2%D0%B5%D1%82%D0%B0%D0%BC%D0%B8-%D1%80%D0%B5%D1%88%D1%83-%D0%B5%D0%B3%D1%8D-2022-%D0%BF%D1%80%D0%BE%D1%84%D0%B8%D0%BB/
Https://m. vk. com/video300967651_456240737
Https://egeturbo. ru/ege/math/tasks/9
Задание 9 ЕГЭ по литературе 2022: теория и практика » /> » /> .keyword { color: red; } 9 задание егэ математика профиль 2022 гипербола
Задание 9. Анализ средств выразительности. ЕГЭ 2022 по литературе
9 задание егэ математика профиль 2022 гипербола
ЕГЭ — ПРОФИЛЬ. Тригонометрия. • Тригонометрические формулы • Преобразование тригонометрических выражений • Тригонометрические уравнения • Задания 4. Показать полностью.
Вычисления и преобразования — готовимся к ЕГЭ по Математике вместе с Александром Антипиным. Со мной вы сможете сдать экзамены на 90-100 баллов! Задание 9. Вычисления и преобразования. Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11.
Например, задание № 4 (9) Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических.
Инверсия — «я не люблю иронии твоей», «свидание продлить желаешь ты» и др.
Метафора — «кипят во мне мятежно ревнивые тревоги и мечты» и др.
Эпитет — «отжившие», «нежившие», «ревнивые тревоги» и др.
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
Задача 6
Риторический вопрос.
M. vk. com
21.09.2018 11:11:50
2018-09-21 11:11:50
Задание 9. Анализ средств выразительности. ЕГЭ 2022 по литературе
За это задание ты можешь получить 1 балл. На решение дается около 5 минут. Уровень сложности: Базовый.
Средний процент выполнения: 66.4%
Ответом к заданию 9 по литературе может быть Последовательность цифр, чисел или слов. Порядок записи имеет значение.
Задачи для практики
Задача 1
Ещё он не сшит, твой наряд подвенечный,
И хор в нашу честь не споёт…
А время торопит — возница беспечный, —
И просятся кони в полёт.
Ах, только бы тройка не сбилась бы с круга,
Не смолк бубенец под дугой…
Две вечных подруги — любовь и разлука —
Не ходят одна без другой.
Мы сами раскрыли ворота, мы сами
Счастливую тройку впрягли,
И вот уже что-то сияет пред нами,
Но что-то погасло вдали.
Святая наука — расслышать друг друга
Сквозь ветер, на все времена…
Две странницы вечных — любовь и разлука —
Поделятся с нами сполна.
Чем дольше живём мы, тем годы короче,
Тем слаще друзей голоса.
Ах, только б не смолк под дугой колокольчик,
Глаза бы глядели в глаза.
То берег — то море, то солнце — то вьюга,
То ангелы — то вороньё…
Две вечных дороги — любовь и разлука —
Проходят сквозь сердце моё.
(Б. Ш. Окуджава, 1982)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в шестой строфе данного стихотворения.
метафора антонимы анафора гротеск ирония
Решение
Ищем ответ в ШЕСТОЙ строфе (это последняя)
Метафора: «проходят сквозь сердце»
Антонимы: «любовь и разлука»
Анафора: «то» в первой и второй строчках
Задача 2
Здесь лапы у елей дрожат на весу,
Здесь птицы щебечут тревожно —
Живёшь в заколдованном диком лесу,
Откуда уйти невозможно.
Пусть черёмухи сохнут бельём на ветру,
Пусть дождём опадают сирени —
Всё равно я отсюда тебя заберу
Во дворец, где играют свирели.
Твой мир колдунами на тысячи лет
Укрыт от меня и от света.
И думаешь ты, что прекраснее нет,
Чем лес заколдованный этот!
Пусть на листьях не будет росы поутру,
Пусть луна с небом пасмурным в ссоре, —
Всё равно я отсюда тебя заберу
В светлый терем с балконом на море.
В какой день недели, в котором часу
Ты выйдешь ко мне осторожно?
Когда я тебя на руках унесу
Туда, где найти невозможно?
Украду, если кража тебе по душе, —
Зря ли я столько сил разбазарил?!
Соглашайся хотя бы на рай в шалаше,
Если терем с дворцом кто-то занял!
(В. С. Высоцкий, 1970)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в первых двух строфах.
анафора литота антитеза эпитет сравнение
Решение
Анафора — «Здесь»
Эпитет — «заколдованный лес»
Сравнение — «черёмухи сохнут бельём на ветру», «дождём опадают сирени»
Задача 3
Мне выпало счастье быть русским поэтом.
Мне выпала честь прикасаться к победам.
Мне выпало горе родиться в двадцатом,
В проклятом году и в столетье проклятом.
Мне выпало всё. И при этом я выпал,
Как пьяный из фуры, в походе великом.
Как валенок мёрзлый, валяюсь в кювете.
Добро на Руси ничего не имети.
(Д. С. Самойлов, 1981)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в данном произведении.
сравнение литота антитеза лексический повтор гротеск
Решение
Сравнение — «как пьяный», «как валенок»
Антитеза — счастье и горе
Лексический повтор — «проклятое»
Задача 4
Геннадию Шпаликову
Всего-то — чтоб была свеча,
Свеча простая, восковая,
И старомодность вековая
Так станет в памяти свежа.
И поспешит твоё перо
К той грамоте витиеватой,
Разумной и замысловатой,
И ляжет на душу добро.
Уже ты мыслишь о друзьях
Всё чаще, способом старинным,
И сталактитом стеаринным
Займёшься с нежностью в глазах.
И Пушкин ласково глядит,
И ночь прошла, и гаснут свечи,
И нежный вкус родимой речи
Так чисто губы холодит.
(Б. А. Ахмадулина, 1960)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в данном произведении.
гипербола олицетворение ирония инверсия эпитет
Решение
Олицетворение — «перо поспешит»
Инверсия — «поспешит твоё перо», «уже ты мыслишь о друзьях»
Эпитет — «вековая старомодность», «витиеватая грамотность» и проч.
Задача 5
Печально я гляжу на наше поколенье!
Его грядущее — иль пусто, иль темно,
Меж тем, под бременем познанья и сомненья,
В бездействии состарится оно.
Богаты мы, едва из колыбели,
Ошибками отцов и поздним их умом,
И жизнь уж нас томит, как ровный путь без цели,
Как пир на празднике чужом.
К добру и злу постыдно равнодушны,
В начале поприща мы вянем без борьбы;
Перед опасностью позорно-малодушны,
И перед властию — презренные рабы.
Так тощий плод, до времени созрелый,
Ни вкуса нашего не радуя, ни глаз,
Висит между цветов, пришлец осиротелый,
И час их красоты — его паденья час!
Мы иссушили ум наукою бесплодной,
Тая завистливо от ближних и друзей
Надежды лучшие и голос благородный
Неверием осмеянных страстей.
Едва касались мы до чаши наслажденья,
Но юных сил мы тем не сберегли;
Из каждой радости, бояся пресыщенья,
Мы лучший сок навеки извлекли.
Мечты поэзии, создания искусства
Восторгом сладостным наш ум не шевелят;
Мы жадно бережём в груди остаток чувства –
Зарытый скупостью и бесполезный клад.
И ненавидим мы, и любим мы случайно,
Ничем не жертвуя ни злобе, ни любви,
И царствует в душе какой-то холод тайный,
Когда огонь кипит в крови.
И предков скучны нам роскошные забавы,
Их добросовестный, ребяческий разврат;
И к гробу мы спешим без счастья и без славы,
Глядя насмешливо назад.
Толпой угрюмою и скоро позабытой
Над миром мы пройдём без шума и следа,
Не бросивши векам ни мысли плодовитой,
Ни гением начатого труда.
И прах наш, с строгостью судьи и гражданина,
Потомок оскорбит презрительным стихом,
Насмешкой горькою обманутого сына
Над промотавшимся отцом.
(М. Ю. Лермонтов, 1838)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
гипербола метонимия метафора эпитет перифраза
Решение
Метонимия — «богаты мы едва из колыбели», «и к гробу мы спешим»
Метафора — «В начале поприща мы вянем без борьбы», «Тощий плод», «Чаша наслаждения»
Эпитет — «презренные рабы», «наукою бесплодной», «пришлец осиротелый»
Задача 6
Я не люблю иронии твоей,
Оставь её отжившим и нежившим,
А нам с тобой, так горячо любившим,
Ещё остаток чувства сохранившим,
Нам рано предаваться ей!
Пока ещё застенчиво и нежно
Свидание продлить желаешь ты, —
Пока ещё кипят во мне мятежно
Ревнивые тревоги и мечты –
Не торопи развязки неизбежной!
И без того она недалека:
Кипим сильней, последней жаждой полны,
Но в сердце тайный холод и тоска…
Так осенью бурливее река,
Но холодней бушующие волны…
(Н. А. Некрасов, 1850)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
гипербола инверсия метафора эпитет риторический вопрос
Решение
Инверсия — «я не люблю иронии твоей», «свидание продлить желаешь ты» и др.
Метафора — «кипят во мне мятежно ревнивые тревоги и мечты» и др.
Эпитет — «отжившие», «нежившие», «ревнивые тревоги» и др.
Задача 7
Тебе не наскучило каждому сниться,
Кто с князем твоим горевал на войне,
О чём же ты плачешь, княгиня зегзица,
О чём ты поёшь на кремлёвской стене?
Твой Игорь не умер в плену от печали,
Погоне назло доконал он коня,
А как мы рубились на тёмной Каяле —
Твой князь на Каяле оставил меня.
И впору бы мне тетивой удавиться,
У каменной бабы воды попросить.
О том ли в Путивле кукуешь, зегзица,
Что некому раны мои остудить?
Так долго я спал, что по русские очи
С калёным железом пришла татарва,
А смерть твоего кукованья короче,
От крови моей почернела трава.
Спасибо тебе, что стонала и пела.
Я ветром иду по горячей золе,
А ты разнеси моё смертное тело
На сизом крыле по родимой земле.
(А. А. Тарковский, 1945–1946)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
гипербола метафора анафора оксюморон риторический вопрос
Решение
Метафора — «у каменной бабы воды попросить», «кукуешь в Путивле» и др.
Анафора — «о чём же»
Риторический вопрос — «О чём ты поёшь на кремлёвской стене?» и др.
Задача 8
В соседнем доме окна жёлты.
По вечерам — по вечерам
Скрипят задумчивые болты,
Подходят люди к воротам.
И глухо заперты ворота,
А на стене — а на стене
Недвижный кто-то, чёрный кто-то
Людей считает в тишине.
Я слышу всё с моей вершины:
Он медным голосом зовёт
Согнуть измученные спины
Внизу собравшийся народ.
Они войдут и разбредутся,
Навалят на спины кули.
И в жёлтых окнах засмеются,
Что этих нищих провели.
(А. А. Блок, 1903)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
повтор метафора эпитет оксюморон гипербола
Решение
1. повтор — «По вечерам — по вечерам», «А на стене — а на стене».
2. метафора — «черный кто-то».
3. эпитет — «медный голос», «задумчивые болты», «измученные спины».
Задача 9
Изыде сеятель сеяти семена своя
Свободы сеятель пустынный,
Я вышел рано, до звезды;
Рукою чистой и безвинной
В порабощенные бразды
Бросал живительное семя —
Но потерял я только время,
Благие мысли и труды…
Паситесь, мирные народы!
Вас не разбудит чести клич.
К чему стадам дары свободы?
Их должно резать или стричь.
Наследство их из рода в роды
Ярмо с гремушками да бич.
(А. С. Пушкин, 1823)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в данном стихотворении.
аллитерация эпитет гротеск градация риторический вопрос
Решение
Аллитерация — «с», «р»
Эпитет — «пустынный сеятель», «чистая и безвинная рука», «мирные народы» и др.
Риторический вопрос — «к чему стадам дары свободы?»
Задача 10
О, как убийственно мы любим,
Как в буйной слепоте страстей
Мы то всего вернее губим,
Что сердцу нашему милей!
Давно ль, гордясь своей победой,
Ты говорил: она моя…
Год не прошёл — спроси и сведай,
Что уцелело от нея?
Куда ланит девались розы,
Улыбка уст и блеск очей?
Всё опалили, выжгли слёзы
Горячей влагою своей.
Ты помнишь ли, при вашей встрече,
При первой встрече роковой,
Её волшебный взор, и речи,
И смех младенчески-живой?
И что ж теперь? И где всё это?
И долговечен ли был сон?
Увы, как северное лето,
Был мимолётным гостем он!
Судьбы ужасным приговором
Твоя любовь для ней была,
И незаслуженным позором
На жизнь её она легла!
Жизнь отреченья, жизнь страданья!
В её душевной глубине
Ей оставались вспоминанья…
Но изменили и оне.
И на земле ей дико стало,
Очарование ушло…
Толпа, нахлынув, в грязь втоптала
То, что в душе её цвело.
И что ж от долгого мученья,
Как пепл, сберечь ей удалось?
Боль, злую боль ожесточенья,
Боль без отрады и без слёз!
О, как убийственно мы любим!
Как в буйной слепоте страстей
Мы то всего вернее губим,
Что сердцу нашему милей.
(Ф. И. Тютчев, 1851)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в данном стихотворении. Запишите цифры, под которыми они указаны.
метафора гипербола архаизм риторический вопрос ирония
Решение
1. Метафора: «куда ланит девались розы», «толпа, нахлынув, в грязь втоптала то, что в душе ее цвело»
3. Архаизм: сведай, ланит, уст, очей
4. Риторический вопрос: «Что уцелело от нея?», «Куда ланит девались розы, // Улыбка уст и блеск очей?», «И что ж теперь? И где всё это? // И долговечен ли был сон?» и др.
Задача 11
У врат обители святой
Стоял просящий подаянья
Бедняк иссохший, чуть живой
От глада, жажды и страданья.
Куска лишь хлеба он просил,
И взор являл живую муку,
И кто-то камень положил
В его протянутую руку.
Так я молил твоей любви
С слезами горькими, с тоскою;
Так чувства лучшие мои
Обмануты навек тобою!
(М. Ю. Лермонтов, 1830)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, используемых поэтом в данном стихотворении. Запишите цифры, под которыми они указаны.
инверсия градация антитеза эпитет литота
Решение
Инверсия: «у врат обители святой», чувства лучшие мои обмануты навек тобою»
Антитеза: хлеб-камень
Эпитет: «святая обитель», «иссохший бедняк», «живая мука» и проч.
Задача 12
Снег идёт, снег идёт.
К белым звёздочкам в буране
Тянутся цветы герани
За оконный переплёт.
Снег идёт, и всё в смятеньи,
Всё пускается в полёт, —
Чёрной лестницы ступени,
Перекрёстка поворот.
Снег идёт, снег идёт,
Словно падают не хлопья,
А в заплатанном салопе
Сходит наземь небосвод.
Словно с видом чудака,
С верхней лестничной площадки,
Крадучись, играя в прятки,
Сходит небо с чердака.
Потому что жизнь не ждёт.
Не оглянешься — и святки.
Только промежуток краткий,
Смотришь, там и новый год.
Снег идёт, густой-густой.
В ногу с ним, стопами теми,
В том же темпе, с ленью той
Или с той же быстротой,
Может быть, проходит время?
Может быть, за годом год
Следуют, как снег идёт,
Или как слова в поэме?
Снег идёт, снег идёт,
Снег идёт, и всё в смятеньи:
Убелённый пешеход,
Удивлённые растенья,
Перекрёстка поворот.
(Б. Л. Пастернак, 1957)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в первых трёх строфах данного стихотворения. Запишите цифры, под которыми они указаны.
повтор метафора метонимия эпитет гипербола
Решение
1. повтор — «Снег идет, снег идет».
2. метафора — «Снег идет, снег идет, // Словно падают не хлопья, // А в заплатанном салопе // Сходит наземь небосвод».
4. эпитет — «заплатанном салопе».
Задача 13
Интеллигенция была моим народом,
Была моей, какой бы ни была,
А также классом, племенем и родом –
Избой! Четыре все её угла.
Я радостно читал и конспектировал,
Я верил больше сложным, чем простым,
Я каждый свой поступок корректировал
Львом чувства — Николаичем Толстым.
Работа чтения и труд писания
Была святей Священного Писания,
А день, когда я книги не прочёл,
Как тень от дыму, попусту прошёл.
Я чтил усилья токаря и пекаря,
Шлифующих металл и минерал,
Но уровень свободы измерял
Зарплатою библиотекаря.
Те земли для поэта хороши,
Где — пусть экономически нелепо –
Но книги продаются за гроши,
Дешевле табака и хлеба.
А если я в разоре и распыле
Не сник, а в подлинную правду вник,
Я эту правду вычитал из книг:
И, видно, книги правильные были!
(Б. А. Слуцкий)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в шестой строфе данного стихотворения.
ЕГЭ — ПРОФИЛЬ. Тригонометрия. • Тригонометрические формулы • Преобразование тригонометрических выражений • Тригонометрические уравнения • Задания 4. Показать полностью.
Вычисления и преобразования — готовимся к ЕГЭ по Математике вместе с Александром Антипиным. Со мной вы сможете сдать экзамены на 90-100 баллов! Задание 9. Вычисления и преобразования. Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых можно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11.
Например, задание № 4 (9) Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических.
На решение отводится примерно 5 минут.
Чтобы решить задание 9 по математике профильного уровня необходимо знать:
Ты помнишь ли, при вашей встрече, При первой встрече роковой, Её волшебный взор, и речи, И смех младенчески-живой.
Egeturbo. ru
27.02.2018 11:35:03
2018-02-27 11:35:03
Задание 9. Вычисления и преобразования
Если задание решено правильно, то получишь 1 балл.
На решение отводится примерно 5 минут.
Чтобы решить задание 9 по математике профильного уровня необходимо знать:
Задания подразделяются на несколько видов:
- преобразования числовых рациональных выражений; преобразования алгебраических выражений и дробей; преобразования числовых/буквенных иррациональных выражений; действия со степенями; преобразование логарифмических выражений; преобразования числовых/буквенных тригонометрических выражений.
. . .
Формулы сокращенного умножения
1) (a + b)^2 = a^2 + 2ab + b^2
2) (a — b)^2 = a^2 — 2ab + b^2
3) a^2 — b^2 =(a + b)(a — b)
Я не люблю иронии твоей,
Оставь её отжившим и нежившим,
А нам с тобой, так горячо любившим,
Ещё остаток чувства сохранившим,
Нам рано предаваться ей!
(Н. А. Некрасов, 1850)
Из приведённого ниже перечня выберите три названия художественных средств и приёмов, использованных поэтом в стихотворении.
Bingoschool. ru
02.03.2017 19:00:56
2017-03-02 19:00:56
Источники:
Https://m. vk. com/video300967651_456240737
Https://egeturbo. ru/ege/lit/tasks/9
Https://bingoschool. ru/ege/maths-profile/tasks/9/
МАТЕМАТИЧЕСКИЙ КОМПОТ: ГИА: ОГЭ и ЕГЭ » /> » /> .keyword { color: red; } 9 задание егэ математика профиль 2022 гипербола
МАТЕМАТИЧЕСКИЙ КОМПОТ
МАТЕМАТИЧЕСКИЙ КОМПОТ
Сайты:
1. РешуОГЭ Математика — популярный российский онлайн-портал, посвящённый подготовке к ОГЭ (по конкретным разделам можно составить тест по всем или определенным вопросам из кодификатора экзамена, можно ввести ответ и проверить его).
2. АлексЛарин — основной целью создания этого сайта было оказание информационной поддержки студентам и абитуриентам при подготовке к ГИА (ОГЭ и ЕГЭ) по математике, поступлении в ВУЗы, решении задач и изучении различных разделов высшей математики.
4. Лучшее время — время для математики — «Распечатай и реши» карточки по типам заданий ОГЭ из открытого банка заданий.
6. Сайт Павла Бердова содержит разборы задач по темам, тесты и рекомендации по подготовке к ЕГЭ и ОГЭ.
А = 1
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
Найдите, при каком значении х значение функции равно 0,8.
Mathscompot. blogspot. com
20.07.2020 19:24:09
2020-07-20 19:24:09
9 задание егэ математика профиль 2022 гипербола
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 9 № 508951
На рисунке изображён график функции Найдите
График функции имеет горизонтальную асимптоту Y = 1, значит, A = 1. По графику F(3) = 2, тогда Таким образом,
Задание 9 № 508961
На рисунке изображён график функции Найдите, при каком значении X значение функции равно 0,8.
График функции имеет горизонтальную асимптоту Y = 1, значит, A = 1. По графику F(3) = 2, тогда Таким образом,
Задание 9 № 509167
На рисунке изображены графики функций и которые пересекаются в точках A и B. Найдите абсциссу точки B.
По графику, F(2) = 1, тогда Значит, гипербола имеет вид
Заметим, что A — тангенс угла наклона прямой по отношению к оси абсцисс, тогда По графику, G(2) = 1, тогда Значит, функция прямой имеет вид
2. АлексЛарин — основной целью создания этого сайта было оказание информационной поддержки студентам и абитуриентам при подготовке к ГИА (ОГЭ и ЕГЭ) по математике, поступлении в ВУЗы, решении задач и изучении различных разделов высшей математики.
Решение:
АлексЛарин — основной целью создания этого сайта было оказание информационной поддержки студентам и абитуриентам при подготовке к ГИА ОГЭ и ЕГЭ по математике, поступлении в ВУЗы, решении задач и изучении различных разделов высшей математики.
Ege. sdamgia. ru
17.05.2017 6:21:22
2017-05-17 06:21:22
Решение №2126 На рисунке изображён график функции f(x)=k/x+a. Найдите, при каком значении х значение функции равно 0,8.
На рисунке изображён график функции f(x) = frac + a. Найдите, при каком значении х значение функции равно 0,8.
Решение:
Коэффициент а прибавленный к функции влияет на Сдвиг гиперболы по оси у, гипербола сдвинута На 1 вверх:
А = 1
Подставим координаты Точки (3; 2) принадлежащей Гиперболе и найдём K:
Функция имеет Вид:
Найдём, При каком значении Х значение F(x) = 0,8:
На рисунке изображён график функции Найдите, при каком значении X значение функции равно 0,8.
6. Сайт Павла Бердова содержит разборы задач по темам, тесты и рекомендации по подготовке к ЕГЭ и ОГЭ.
Задание 9 508961.
Ege314.ru
16.10.2018 15:52:49
2018-10-16 15:52:49
Источники:
Https://mathscompot. blogspot. com/p/blog-page_73.html
Https://ege. sdamgia. ru/test? theme=125
-
Решение
-
Видеорешение
Воспользуемся правилом
Правило
Для гиперболы, записанной в общем виде:
(displaystyle y=frac{k}{x+color{blue}{b}}+color{green}{c}{small,}) где (displaystyle k,cancel{=},0{ small ,})
горизонтальная асимптота задается уравнением прямой
(displaystyle y=color{green}{c}{small,})
а вертикальная асимптота задается уравнением прямой
(displaystyle x=color{blue}{-b}{small.})
На рисунке изображены
- горизонтальная асимптота гиперболы – прямая (displaystyle y=color{green}{1}{small;})
- вертикальная асимптота гиперболы – прямая (displaystyle x=color{blue}{3}{small.})
Значит, (displaystyle color{green}{c}=color{green}{1}) и (displaystyle color{blue}{b}=color{blue}{-3}{small.})
Тогда уравнение гиперболы имеет вид (displaystyle y=frac{1}{xcolor{blue}{-3}}+color{green}{1}{small.})
Ответ: (displaystyle {b}={-3}) и (displaystyle {c}={1}{small.})
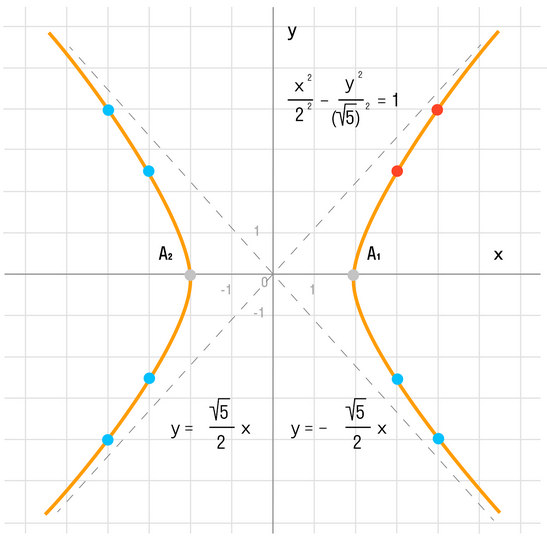
Гипербола
Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).
Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.
Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.
Пример №2:
$$y=frac<1>-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота
Находим вторую асимптоту.
Дробь (color <frac<1>>) отбрасываем
Остается y≠ -1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠1 это вторая асимптота.
Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):
3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:
Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.
4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:
Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.
Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.
6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:
а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.
Находим вторую асимптоту.
Остается y≠ -1 это вторая асимптота.
б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.
в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5
г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).
д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).
е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).
7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment
Гипербола: формулы, примеры решения задач
Определение гиперболы, решаем задачи вместе
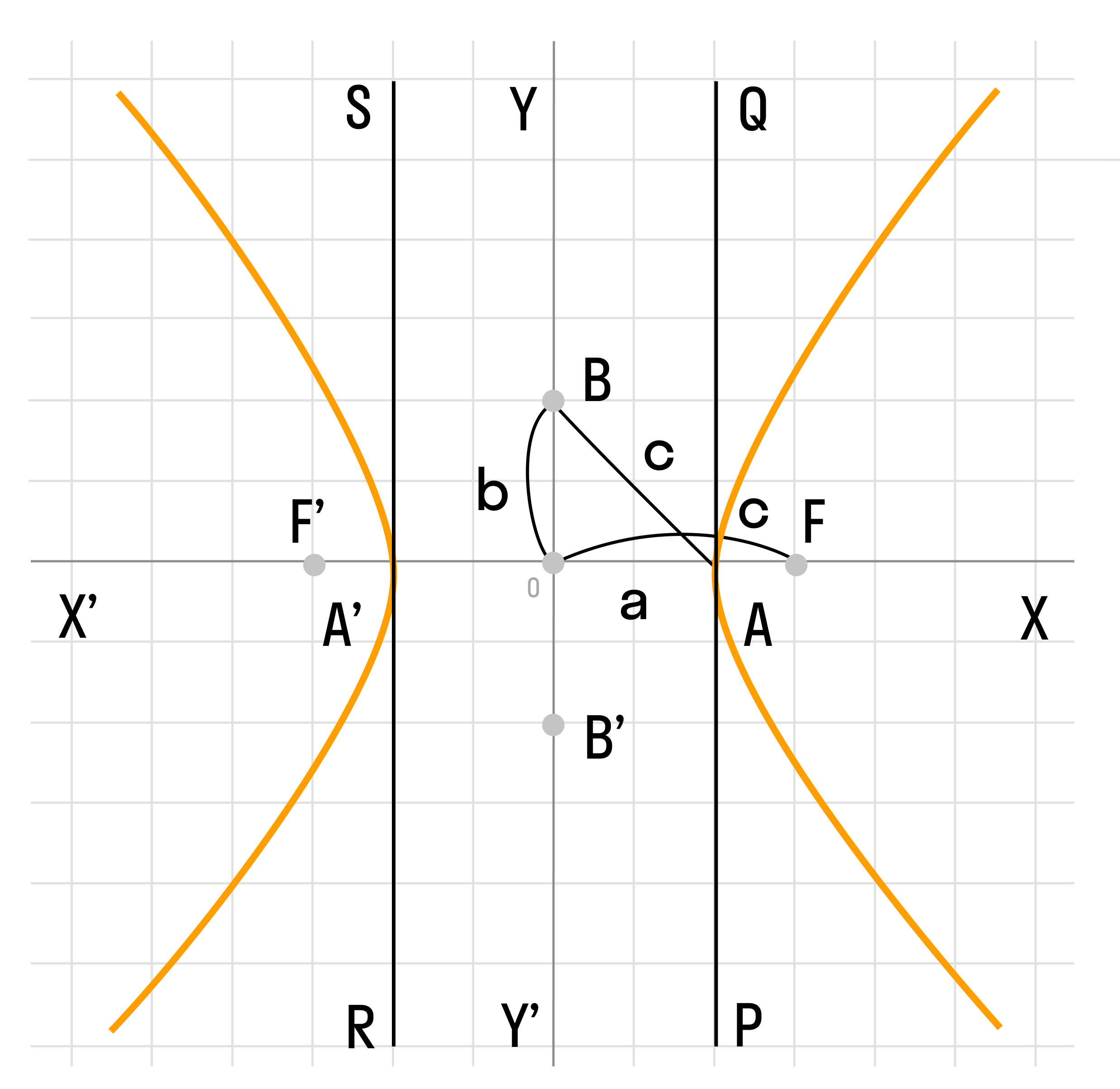
Определение гиперболы. Гиперболой называется множество всех точек плоскости, таких, для которых модуль разности расстояний от двух точек, называемых фокусами, есть величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы имеет вид:

где a и b — длины полуосей, действительной и мнимой.
На чертеже ниже фокусы обозначены как 

На чертеже ветви гиперболы — бордового цвета.
При a = b гипербола называется равносторонней.
Пример 1. Составить каноническое уравнение гиперболы, если его действительная полуось a = 5 и мнимая = 3.
Решение. Подставляем значения полуосей в формулу канонического уравения гиперболы и получаем:

Точки пересечения гиперболы с её действительной осью (т. е. с осью Ox) называются вершинами. Это точки (a, 0) (- a, 0), они обозначены и надписаны на рисунке чёрным.
Точки 


называются фокусами гиперболы (на чертеже обозначены зелёным, слева и справа от ветвей гиперболы).
называется эксцентриситетом гиперболы.
Гипербола состоит из двух ветвей, лежащих в разных полуплоскостях относительно оси ординат.
Пример 2. Составить каноническое уравнение гиперболы, если расстояние между фокусами равно 10 и действительная ось равна 8.
Если действительная полуось равна 8, то её половина, т. е. полуось a = 4 ,
Если расстояние между фокусами равно 10, то число c из координат фокусов равно 5.
То есть, для того, чтобы составить уравнение гиперболы, потребуется вычислить квадрат мнимой полуоси b.
Подставляем и вычисляем:
Получаем требуемое в условии задачи каноническое уравнение гиперболы:

Пример 3. Составить каноническое уравнение гиперболы, если её действительная ось равна 48 и эксцентриситет 
Решение. Как следует из условия, действительная полуось a = 24 . А эксцентриситет — это пропорция и так как a = 24 , то коэффициент пропорциональности отношения с и a равен 2. Следовательно, c = 26 . Из формулы числа c выражаем квадрат мнимой полуоси и вычисляем:

Результат — каноническое уравнение гиперболы:
Если 




Если 




На чертеже расстояния обозначены оранжевыми линиями.
Для каждой точки, находящейся на гиперболе, сумма расстояний от фокусов есть величина постоянная, равная 2a.
Прямые, определяемые уравнениями

называются директрисами гиперболы (на чертеже — прямые ярко-красного цвета).
Из трёх вышеприведённых уравнений следует, что для любой точки гиперболы

где 





Пример 4. Дана гипербола 
Решение. Смотрим в уравнение директрис и обнаруживаем, что требуется найти эксцентриситет гиперболы, т. е. 

Получаем уравнение директрис гиперболы:
Многие задачи на директрисы гиперболы аналогичны задачам на директрисы эллипса. В уроке «Эллипс» это пример 7.
Характерной особенностью гиперболы является наличие асимптот — прямых, к которым приближаются точки гиперболы при удалении от центра.
Асимптоты гиперболы определяются уравнениями

На чертеже асимптоты — прямые серого цвета, проходящие через начало координат O.
Уравнение гиперболы, отнесённой к асимптотам, имеет вид:


В том случае, когда угол между асимптотами — прямой, гипербола называется равнобочной, и если асимптоты равнобочной гиперболы выбрать за оси координат, то её уравнение запишется в виде y = k/x , то есть в виде уравения обратной пропорциональной зависимости.
Пример 5. Даны уравнения асимптот гиперболы 

Решение. Дробь в уравнении асимптот гиперболы — это пропорция, следовательно, нужно сначала найти коэффициент пропорциональности отношения 

Теперь имеем все данные, чтобы получить каноническое уравнение гиперболы. Получаем:
Гипербола обладает оптическим свойством, которое описывается следующим образом: луч, исходящий из источника света, находящегося в одном из фокусов гиперболы, после отражения движется так, как будто он исходит из другого фокуса.
Решить задачи на гиперболу самостоятельно, а затем посмотреть решения
Пример 6. Фокусы эллипса расположены на оси Ox симметрично относительно начала координат. Составить каноническое уравнение эллипса, если:
1) b = 4 , а один из фокусов в точке (5; 0)
2) действительная ось 6, расстояние между фокусами 8
3) один из фокусов в точке (-10; 0), уравнения асимптот гиперболы
Что такое гипербола
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие гиперболы
Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.
Каноническое уравнение гиперболы в алгебре выглядит так:
, где a и b — положительные действительные числа.
Кстати, канонический значит принятый за образец.
В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.
Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.
Вспомним особенности математической гиперболы:
- Две симметричные ветви.
- Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.
Если гипербола задана каноническим уравнением, то асимптоты можно найти так:
Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.
Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.
Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:
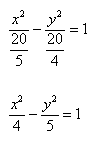
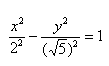
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.
Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.
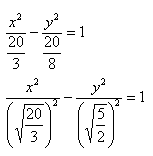
- Произведем сокращение при помощи трехэтажной дроби:
- Воспользуемся каноническим уравнением
- Найдем асимптоты гиперболы. Вот так:
Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты. - Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).
- Найдем асимптоты гиперболы. Вот так:
Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.
Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).
Найдем дополнительные точки — хватит двух-трех.
В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.
Способ такой же, как при построении эллипса. Из полученного канонического уравнения
на черновике выражаем:
Уравнение распадается на две функции:
— определяет верхние дуги гиперболы (то, что ищем);
— определяет нижние дуги гиперболы.
Далее найдем точки с абсциссами x = 3, x = 4:
Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.
Действительная ось гиперболы — отрезок А1А2.
Расстояние между вершинами — длина |A1A2| = 2a.
Действительная полуось гиперболы — число a = |OA1| = |OA2|.
Мнимая полуось гиперболы — число b.
В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.
Форма гиперболы
Повторим основные термины и узнаем, какие у гиперболы бывают формы.
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.
Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.
Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.
Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.
Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.
Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.
Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Фокальное свойство гиперболы
Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).
Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.
Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .
Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:
Рассмотрим, как это выглядит на прямоугольной системе координат:
- пусть центр O гиперболы будет началом системы координат;
- прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
- прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).
Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:
Запишем это уравнение в координатной форме:
Избавимся от иррациональности и придем к каноническому уравнению гиперболы:
, т.е. выбранная система координат является канонической.
Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.
Директориальное свойство гиперболы
Директрисы гиперболы — это две прямые, которые проходят параллельно оси.
ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.
Директориальное свойство гиперболы звучит так:
Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.
Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.
На самом деле для фокуса F2 и директрисы d2 условие
можно записать в координатной форме так:
Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:
Построение гиперболы
Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.
Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.
В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:
Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:
Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.
По определению эксцентриситет гиперболы равен
Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.
Так как b^2 = c^2 — a^2, то величина b изменится.
При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.
Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.
Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2
Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.
источники:
http://function-x.ru/curves_hyperbola.html
http://skysmart.ru/articles/mathematic/chto-takoe-giperbola