Как найти объем фигуры егэ - ExamHelp.top

Каталог заданий
Задания 2. Стереометрия. Объем составного многогранника

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 2 № 27044

Найдите объем многогранника, изображенного на рисунке (все двугранные углы многогранника прямые).

Аналоги к заданию № 27044: 4893 4903 4895 4897 4899 4901 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 2 № 27117

Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

1 комментарий · Сообщить об ошибке · Помощь

Тип 2 № 27187

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27187: 25531 25539 25533 25535 25537 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27188

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27188: 25551 25559 25553 25555 25557 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 2 № 27189

Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Аналоги к заданию № 27189: 25571 25579 25573 25575 25577 Все

Кодификатор ФИПИ/Решу ЕГЭ: 5.5.7 Объём куба, прямоугольного параллелепипеда, пирамиды, призмы

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Объем правильной треугольной пирамиды

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b). Нужно найти ( displaystyle {{S}_{осн}}) и ( displaystyle H).

( displaystyle {{S}_{осн}}) – это площадь правильного треугольника ( displaystyle ABC).

Вспомним, как искать эту площадь. Используем формулу площади:

( displaystyle S=frac{1}{2}abcdot sin gamma ).

У нас «( displaystyle a)» – это ( displaystyle a), а «( displaystyle b)» – это тоже ( displaystyle a), а ( displaystyle sin gamma =sin 60{}^circ =frac{sqrt{3}}{2}).

Значит, ( displaystyle {{S}_{ABC}}=frac{1}{2}{{a}^{2}}frac{sqrt{3}}{2}=frac{{{a}^{2}}sqrt{3}}{4}).

Теперь найдем ( displaystyle H).

По теореме Пифагора для ( displaystyle Delta SOC)

( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}).

Чему же равно ( displaystyle OC)? Это радиус описанной окружности в ( displaystyle Delta ABC), потому что пирамидаправильная и, значит, ( displaystyle O) – центр ( displaystyle Delta ABC).

Найдем ( displaystyle OC) (Подробнее смотри в теме «Правильный треугольник»).

ravnostoronnij treugolnik piramida najti obyom

( displaystyle OC=frac{2}{3}CK), так как ( displaystyle O) – точка пересечения и медиан тоже.

( displaystyle C{{K}^{2}}=A{{C}^{2}}-A{{K}^{2}}) (теорема Пифагора для ( displaystyle Delta ACK))

( displaystyle C{{K}^{2}}-{{a}^{2}}-frac{{{a}^{2}}}{4}=frac{3{{a}^{2}}}{4}); ( displaystyle CK=frac{asqrt{3}}{2})

Значит, ( displaystyle OC=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})

Подставим ( displaystyle OC) в формулу для ( displaystyle H).

( displaystyle {{H}^{2}}={{b}^{2}}-O{{C}^{2}}={{b}^{2}}-{{left( frac{asqrt{3}}{3} right)}^{2}}={{b}^{2}}-frac{{{a}^{2}}}{3})

И подставим все в формулу объема:

( displaystyle V=frac{1}{3}{{S}_{ABC}}cdot H=frac{1}{3}cdot frac{{{a}^{2}}sqrt{3}}{4}cdot sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}})

( displaystyle V=frac{{{a}^{2}}sqrt{3}}{12}sqrt{{{b}^{2}}-frac{{{a}^{2}}}{3}}).

Внимание: если у тебя правильный тетраэдр (т.е. ( displaystyle b=a)), то формула получается такой:

( displaystyle V=frac{{{a}^{3}}}{6sqrt{2}}).

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Вычисление объемов фигур

Задание
1

#3043

Уровень задания: Равен ЕГЭ

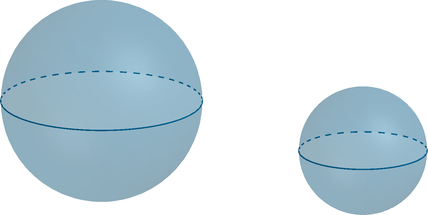
Радиус первого шара в (5) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса (R) ищется по формуле (S=4pi R^2). Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как [dfrac{S_1}{S_2}=dfrac{4pi , R_1^2}{4pi , R_2^2}] Так как радиус первого шара больше радиуса второго шара в 5 раз, то (R_1=5R_2). Следовательно, [dfrac{S_1}{S_2}=dfrac{(5R_2)^2}{R_2^2}=25.] Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Ответ: 25

Задание
2

#3046

Уровень задания: Равен ЕГЭ

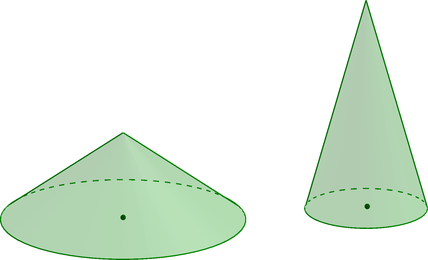
Даны два конуса. Радиус второго конуса в (3) раза больше радиуса первого конуса, а высота второго конуса в (6) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен (18).

Объем конуса с высотой (h) и радиусом основания (R) вычисляется по формуле (V=frac13pi R^2h). Следовательно, объем первого конуса относится к объему второго конуса как [dfrac{V_1}{18}=dfrac{V_1}{V_2}=
dfrac{frac13pi ,R_1^2,h_1}{frac13 pi
,R_2^2,h_2}=left(dfrac{R_1}{R_2}right)^2cdot
dfrac{h_1}{h_2}] Так как радиус второго в 3 раза больше радиуса первого, то (R_2=3R_1). Так как высота второго в 6 раз меньше высоты первого, то (h_1=6h_2). Следовательно, [dfrac{V_1}{18}=left(dfrac{R_1}{3R_1}right)^2cdot dfrac{6h_2}{h_2}=
dfrac19cdot 6=dfrac23 quadRightarrowquad V_1=dfrac23cdot
18=12.]

Ответ: 12

Задание
3

#3048

Уровень задания: Равен ЕГЭ

Даны два конуса: (K_1) и (K_2). Площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как (4:1). Известно, что радиус (K_1) в 4 раза больше образующей (K_1) и в 2 раза больше радиуса (K_2). Найдите отношение образующей (K_2) к образующей (K_1).

Площадь полной поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi R (R+l)). Тогда площадь полной поверхности (K_1) относится к площади полной поверхности (K_2) как [dfrac41=dfrac{pi ,R_1cdot (R_1+l_1)}{pi , R_2cdot (R_2+l_2)}] Из условия следует, что (R_1=4l_1), (R_2=frac12R_1=2l_1), следовательно, [dfrac41=dfrac{4l_1cdot (4l_1+l_1)}{2l_1cdot (2l_1+l_2)}
quadRightarrowquad dfrac{l_2}{l_1}=dfrac12=0,5]

Ответ: 0,5

Задание
4

#3044

Уровень задания: Равен ЕГЭ

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в (343) раза больше объема второго шара?

Объем шара радиуса (R) ищется по формуле (V=dfrac43 pi R^3). Следовательно, объем первого шара относится к объему второго как [dfrac{343}1=dfrac{V_1}{V_2}=dfrac{frac43 pi , R_1^3}{frac43 pi , R_2^3}=
left(dfrac{R_1}{R_2}right)^3 quadRightarrowquad
dfrac{R_1}{R_2}=sqrt[3]{343}=7.] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Ответ: 7

Задание
5

#3051

Уровень задания: Равен ЕГЭ

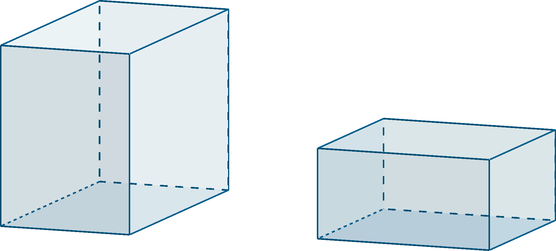
Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы (a), (b) и (c) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле (V=abc). Следовательно, объем первого параллелепипеда относится к объему второго как [dfrac{105}{V_2}=dfrac{V_1}{V_2}=dfrac{a_1b_1c_1}{a_2b_2c_2}] Из условия следует, что (a_1=7a_2), (b_2=2b_1), (c_1=3c_2). Тогда [dfrac{105}{V_2}=dfrac{7a_2cdot b_1cdot 3c_2}{a_2cdot 2b_1cdot c_2}=
dfrac{7cdot 3}2 quadRightarrowquad V_2=dfrac{105cdot
2}{21}=10.]

Ответ: 10

Задание
6

#3049

Уровень задания: Равен ЕГЭ

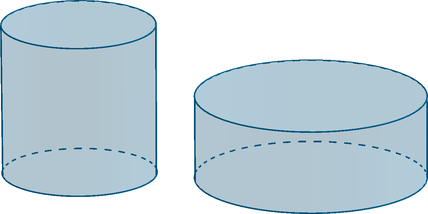
Площадь боковой поверхности первого цилиндра равна (16). Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой (H) и радиусом основания (R) ищется по формуле (S=2pi RH). Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как [dfrac{16}{S_2}=dfrac{S_1}{S_2}=dfrac{2pi ,R_1,H_1}{2pi ,R_2,H_2}=
dfrac{R_1}{R_2}cdot dfrac{H_1}{H_2}] Из условия следует, что (R_2=4R_1), (H_1=5H_2), значит, [dfrac{16}{S_2}=dfrac{R_1}{4R_1}cdot dfrac{5H_2}{H_2}=
dfrac14cdot 5=dfrac54] Следовательно, [S_2=dfrac{16cdot 4}5=12,8.]

Ответ: 12,8

Задание
7

#3047

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как (3:7). Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как (15:7).

Площадь боковой поверхности конуса с образующей (l) и радиусом основания (R) ищется по формуле (S=pi Rl). Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как [dfrac 37=dfrac{S_1}{S_2}=dfrac{pi R_1,l_1}{pi R_2,l_2}] Так как радиус первого конуса относится к радиусу второго как (15:7), то есть (frac{R_1}{R_2}=frac{15}7), то [dfrac37=dfrac {15}7cdot dfrac{l_1}{l_2} quadRightarrowquad
dfrac{l_1}{l_2}=dfrac37cdot dfrac7{15}=dfrac15=0,2.]

Ответ: 0,2

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Базовая информация

Объем геометрической фигуры — это количественная характеристика пространства, которое занимает тело. Она определяется его формой и размерами.
Чтобы задачи на вычисление объемов геометрических фигур не вызывали затруднений, рекомендуем освежить в памяти основные формулы.

Объем куба равняется кубу длины его грани.

Для его расчета используется формула: V = a³, где V — объем куба,
a — длина его грани.

Объем призмы равняется произведению площади основания фигуры на высоту.
Чтобы его рассчитать, воспользуйтесь следующий формулой: V = S_o h, где V — объем призмы, So — площадь ее основания, h — ее высота.
Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты.
Формула для его расчета: V = a · b · h, где a — длина,
b — ширина, h — высота.
Объем пирамиды равняется трети от произведения площади ее основания на высоту.

Рассчитать его можно по формуле:

V =
1/3
S_o· h ,

где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.

Объем цилиндра равняется произведению площади его основания на высоту.
Формулы для его расчета:

V =

π R² h

V =

S_o h

Где V — объем цилиндра, So — площадь основания цилиндра, R — радиус цилиндра, h — высота цилиндра, π = 3.141592.

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Многогранники

Многогранник – это поверхность, составленная из многоугольников, ограничивающая некоторое геометрическое тело.

В данной теме мы рассмотрим составные многогранники (многогранники, состоящие обычно из нескольких параллелепипедов).

Объемы различных многогранников:

Призма $V=S_{осн}·h$
Пирамида $V={1}/{3}S_{осн}·h$
Параллелепипед $V=a·b·c$, где $a, b$ и $c$ — длина, ширина и высота.
Куб $V=а^3$, где $а$ — сторона куба

Задачи на нахождение объема составного многогранника:

Первый способ.

Составной многогранник надо достроить до полного параллелепипеда или куба.
Найти объем параллелепипеда.
Найти объем лишней части фигуры.
Вычесть из объема параллелепипеда объем лишней части.

Пример:

Найдите объём многогранника, изображённого на рисунке (все двугранные углы прямые).

Решение:

1. Достроим составной многогранник до параллелепипеда.

Найдем его объем. Для этого перемножим все три измерения параллелепипеда:

$V=10·9·4=360$

2. Найдем объем лишнего маленького параллелепипеда:

Его длина равна $9-4=5$

Ширина равна $4$

Высота равна $7$

$V=7·4·5=140$

3. Вычтем из объема параллелепипеда объем лишней части и получим объем заданной фигуры:

$V=360-140=220$

Ответ: $220$

Второй способ

Разделить составной многогранник на несколько параллелепипедов.
Найти объем каждого параллелепипеда.
Сложить объемы.

Задачи на нахождение площади поверхности составного многогранника.

— Если можно составной многогранник представить в виде прямой призмы, то находим площадь поверхности по формуле:

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

Чтобы найти площадь основания призмы, надо разделить его на прямоугольники и найти площадь каждого.

Пример:

Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы прямые).

Представим данный многогранник как прямую призму с высотой равной $12$.

$S_{полн.пов.}=P_{осн}·h+2S_{осн}$

$P_{осн}=8+6+6+2+2+4=28$

Чтобы найти площадь основания, разделим его на два прямоугольника и найдем площадь каждого:

$S_1=6·6=36$

$S_2=2·4=8$

$S_осн=36+8=44$

Далее подставим все данные в формулу и найдем площадь поверхности многогранника

$S_{полн.пов.}=28·12+2·44=336+88=424$

Ответ: $424$

— Если составной многогранник нельзя представить в виде призмы, то площадь полной поверхности можно найти как сумму площадей всех граней, ограничивающих поверхность.

Задачи на нахождение расстояния между точками составного многогранника.

В данных задачах приведены составные многогранники, у которых двугранные углы прямые. Надо соединить расстояние между заданными точками и достроить его до прямоугольного треугольника. Далее остается воспользоваться теоремой Пифагора для нахождения нужной стороны.

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$АС^2+ВС^2=АВ^2$

Задачи на нахождение угла или значения одной из тригонометрических функций обозначенного в условии угла составного многогранника.

Так как в данных задачах приведены составные многогранники, у которых все двугранные углы прямые, то достроим угол до прямоугольного треугольника и найдем его значение по тригонометрическим значениям.

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$:

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

Синусом ($sin$) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
Косинусом ($cos$) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Тангенсом ($tg$) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету.

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Задачи на рассмотрение подобия фигур.

При увеличении всех линейных размеров многогранника в $k$ раз, площадь его поверхности увеличится в $k^2$ раз.

При увеличении всех линейных размеров многогранника в $k$ раз, его объём увеличится в $k^3$ раз.

Источник

Объем правильной треугольной пирамиды

Вычисление объемов фигур

Базовая информация

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Многогранники

Объемы различных многогранников:

Задачи на нахождение объема составного многогранника:

Теорема Пифагора

Новое и интересное на сайте: