B этой статье:
Kак научиться решать задачи ЕГЭ по планиметрии? Пошаговая методика.
Полезные факты и классические схемы для решения задач по планиметрии.
Приемы и секреты решения задач по планиметрии.
«B учебнике нет, а на экзамене есть». На какие теоремы стоит обратить внимание.
Решения заданий № 16 Профильного ЕГЭ по математике.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
И сейчас — самое главное о задаче 16 (Планиметрия).
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Bсе это вы найдете в нашем ЕГЭ-Cправочнике. Ничего лишнего там нет. Учите наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
Bот список из 32 полезных фактов — и их доказательства. Да, это первый этап освоения планиметрии. Доказав все эти полезные факты, вы обнаружите, что пункт (а) задачи 16 перестал быть для вас проблемой.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем. Учите их наизусть! И конечно, доказывайте! Лучше всего начинать именно с задач на доказательство.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы. A вы их знаете? Если нет — выучите.
5) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится. Только то, что есть в нашем ЕГЭ-Cправочнике. Зато знать это надо наизусть.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур, — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б). Так, например, было на Досрочном ЕГЭ. Простейший пункт (а), и в нем «спрятана» идея: в пункте (б) ищите вписанные в окружность четырехугольники.
Перейдем к практике. Разберем несколько реальных задач Профильного ЕГЭ под номером 16. Больше планиметрии — на интенсивах ЕГЭ-Cтудии и на Oнлайн-курсе.
Начнем с интересного приема. Бывает, что в задаче значимые отрезки пересекаются вот такой буквой Ж. Или вот такой буквой Х. Хорошо, если мы можем перестроить это Ж или Х в треугольник. Например, провести какие-нибудь отрезки, параллельные и равные (или пропорциональные) нашим.
1. (ЕГЭ — 2017)
Oснования трапеции равны 4 и 9, а её диагонали равны 5 и 12.
а) Докажите, что диагонали трапеции перпендикулярны.
б) Найдите высоту трапеции.
Посмотреть решение
Следующая задача — на применение одной из наших классических схем
2. B остроугольном треугольнике KMN проведены высоты KB и NA.
а) Докажите, что угол ABK равен углу ANK.
б) Найдите радиус окружности, описанной около треугольника ABM, если известно, что и
.
Посмотреть решение
3. (ЕГЭ-2020, Демовариант).
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
а) Докажите, что прямые AD и BC параллельны.
б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Посмотреть решение
B следующей задаче больше алгебры, чем геометрии. Действительно, бывает так, что планиметрическая задача быстро сводится к уравнению или системе уравнений.
4. Параллелограмм ABCD и окружность расположены так, что сторона AB касается окружности, CD является хордой, а стороны DA и BC пересекают окружность в точках P и Q соответственно.
а) Докажите, что около четырехугольника ABQP можно описать окружность.
б) Найдите длину отрезка DQ, если известно, что AP = a, BC = b, BQ = c.
Посмотреть решение
5. B прямоугольном треугольнике ABC точки M и N — середины гипотенузы AB и катета BC соответственно. Биссектриса угла BAC пересекает прямую MN в точке L.
а) Докажите, что треугольники AML и BLC подобны.
б) Найдите отношение площадей этих треугольников, если
Посмотреть решение
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 2, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 4, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 6, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 16
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 12, задача 16
Планиметрия. Стрим 10 марта. Разбор домашнего задания
Надеемся, что статья была для вас полезной. Что вы возьметесь за планиметрию и получите на экзамене необходимые баллы. Удачи вам!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 16. Планиметрия u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Как подготовиться к решению заданий ЕГЭ № 16 по планиметрии | 1С:Репетитор
Задача № 16 по планиметрии, которую включает вариант КИМ ЕГЭ по математике профильного уровня, – объективно одна из самых трудных, если не самая сложная для абитуриентов. Дело в том, что в обычной (не профильной или специализированной) школе планиметрию изучают только в 7–9-х классах, на эту дисциплину отводится два урока в неделю, что совершенно недостаточно для того, чтобы хорошо изучить свойства фигур планиметрии и научиться применять их при решении задач. Кроме того, каждая задача по геометрии уникальна по своему содержанию, поэтому для решения таких задач практически неприменим алгоритмический подход, который является весьма успешным при решении задач по алгебре, в результате многие школьники даже не пытаются решать геометрические задачи. Все это приводит к тому, что и сравнительно несложная задача по планиметрии становится непосильной для выпускников школ.
Ситуацию можно исправить, но потребуется немало сил и времени и, конечно, хорошая методика подготовки. Наша методика основана на концепции известного отечественного методолога и методиста, специалиста по преподаванию геометрии И.Ф. Шарыгина. Суть концепции, которую сам автор называл «геометрией фигуры», заключается в том, что в учебных материалах последовательно разбираются свойства геометрических фигур и их элементов (замечательных линий и точек), начиная от прямоугольного треугольника и заканчивая комбинациями многоугольников и окружностей, причем внимание акцентируется именно на решении задач.
Конечно, для решения геометрических задач большое значение имеет хорошее знание теории, поэтому в наших материалах много кратких видеолекций, суммирующих необходимые теоретические знания . Обучая теории, мы сразу же разбираем опорные задачи, в которых она применяется, осваиваем специальные приемы решения задач – например метод проекций, метод площадей, метод вспомогательной окружности и т. д.
После изучения теории нужно браться за самостоятельное решение задач. При этом можно выбрать приемлемую траекторию продвижения по системе задач. Для менее подготовленных школьников мы рекомендуем решать задачи «по фигурам», то есть в следующем порядке.
Сначала – прямоугольный треугольник, медиана в прямоугольном треугольнике, биссектриса в прямоугольном треугольнике, высота в прямоугольном треугольнике . Затем переходим к равнобедренному и произвольному треугольникам, параллелограмму, трапеции и т. д.
Для более сильных школьников предлагается другой путь – систематизация и обобщение свойств геометрических фигур и их элементов.
Прямоугольный треугольник, произвольный треугольник (теорема синусов, теорема косинусов, площади), медиана в прямоугольном треугольнике, медиана в равнобедренном и произвольном треугольнике и т. д.
Описанный подход позволяет нашим ученикам актуализировать свои школьные знания, обобщить и углубить их, систематически сочетая изучение теории с практикой ее применения. Большую помощь в решении задач оказывают пошаговые тренажеры: в геометрической задаче, ход решения которой может быть неочевиден с самого начала, тренажер позволяет сориентироваться в шагах решения, проверить промежуточные вычисления на каждом шаге и обосновать сами шаги нужной теоремой или свойством.
После такой подготовки задачи по планиметрии варианта КИМ ЕГЭ покажутся и не такими уж сложными. Посмотрим, например, как можно «раскусить» следующую довольно непростую, но в то же время изящную задачу, предлагавшуюся на экзамене в 2016–2017 годах.
Пример задачи № 16 по планиметрии:
Точка O — центр окружности, описанной около остроугольного треугольника ABC, I — центр вписанной в него окружности, H — точка пересечения высот. Известно, что ∠BAC =∠OBC +∠OCB.
Чертеж 1
- Докажите, что точка I лежит на окружности, описанной около треугольника BOC.
- Найдите угол OIH, если ∠ABC =55°.
Ответ: 175°.
Решение:
- Посмотрим на чертеж. Если нам предлагают доказать, что четыре точки лежат на одной окружности, то согласно теореме об угле, вписанном в окружность, и следствиям из нее, нужно либо поискать на чертеже 1 равные углы, опирающиеся на один и тот же отрезок (хорду) и расположенные по одну сторону от него, либо углы, сумма которых равна 180° и которые также опираются на один и тот же отрезок, но расположены по разные стороны от него. В нашем случае подходит первый вариант.
- Итак, во-первых, по теореме об угле, вписанном в окружность, ∠BAC =∠OBC +∠OCB=12∠BOC,
но ∠OBC +∠OCB+∠BOC=180°,
то есть ∠BOC+12∠BOC=180°⇔∠BOC=120°⇒∠BAC=60°
- Во-вторых, находим угол между двумя биссектрисами. В нашем случае ∠BIC=90°+12∠BAC=120°.
Этот факт мы доказываем в своем курсе, чтобы на экзамене вы могли без труда им воспользоваться. - Прежде всего найдем все углы треугольника ABC: ∠BAC =60°, ∠ABC =55°, ∠ACB =65°.
- Затем подумаем вот о чем: а не лежит ли точка H на окружности, описанной около треугольника BOC? И это действительно так: обсуждая в нашем курсе свойства высот треугольника, мы обращаем внимание учащихся на тот факт, что угол между высотами – в данном случае ∠BHC =180°-∠BAC=120°, то есть наша догадка верна.
- Теперь осталось правильно расположить точки B, H, I,O, C на окружности (чертеж 2) и вычислить угол OIH. Например, так:
∠OIH=180°-∠HCO,
∠HBO=∠HCB-∠OCB,
∠HCB=90°-∠ABC=35°,
∠OCB=30° ⇒ ∠HBO= ∠HCB — ∠OCB =5° ⇒ ∠OIH=175° — Вот и ответ.
Итого, ∠BOC=∠BIC=120°, следовательно точка I лежит на окружности, описанной около треугольника BOC.
Оценить свои стартовые знания по планиметрии вы можете с помощью заданий с кратким ответом: №3 и №6 . Если возникнут затруднения, воспользуйтесь подсказками: они помогут справиться с решением. Если же эти задачи вы решаете легко, то приступайте к более сложным (и более увлекательным) задачам по планиметрии.
Регулярно тренируйтесь в решении задач
Чтобы начать заниматься на портале «1С:Репетитор», достаточно зарегистрироваться.
Вы можете:
- Начать заниматься бесплатно.
- Получить доступ ко всей теории и тренажерам задачи №16. Это стоит всего 990 рублей.
- Купить доступ к этой задаче в составе экспресс-курса «Геометрия» и научиться решать задачи №14 и №16 на максимальный балл.
Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.
Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.
Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 16 на экзамене ЕГЭ, задачи по планиметрии, решение задач, по планиметрии, методы решения задач, теория по теме «Планиметрия, часть С», пробники ЕГЭ, а основе экзаменов прошлых лет просмотреть, подготовка к ЕГЭ 2018, учимся решать задачи по планиметрии, Планиметрические задачи профильного ЕГЭ, Решение задач по планиметрии, тесты по планиметрии, примеры и решения заданий по теме планиметрии, задачи сопровождаются подробными пояснениями и чертежами, задачи на нахождение углов и радиусов, треугольник, трапеция, параллелограмм, квадрат, ромб, прямоугольник, примеры решения задач ЕГЭ по геометрии, Видеокурс по решению задач по планиметрии, какого радиуса должна быть окружность, тесты для подготовки и самоподготовки к ЕГЭ, КИМ ЕГЭ 2017, подготовка к ЕГЭ, профиль математика, математика профильного уровня, задачи ЕГЭ 2017 по стереометрии, подготовка к ЕГЭ, выпускникам 11 класса, в 2018 году, поступающим в технический вуз, материал для подготовки к ЕГЭ.
Мотивация
Если вы откроете список всех задач по Планиметрии №16, которые встречались на ЕГЭ по Профилю за всё время его существования, вы удивитесь тому, как сильно она усложнилась, и на сегодняшний день на этой позиции стоит достаточно содержательная геометрическая задача с действительно порой навороченными конструкциями, которые вводят в ступор, начинающих её решать школьников. Всё это еще приправлено тем, что из года в год, на фоне эволюции этой задачи, или из-за этого, процент учеников школ решающих геометрию в ЕГЭ весьма низкий:
Хуже решается только задача по Стереометрии №13. Отсюда комом накатывается мнение, что «№16 решать дано не всем», «лучше меньше баллов, зато точно решу №12», «я нарисовал треугольник, а что делать не вижу дальше» и куча других деструктивных мыслей, которые точно не помогают вам в подготовке к ЕГЭ. По факту, из моего личного опыта, задачи по Геометрии что в ЕГЭ, что в ОГЭ, очень плохо решаются в силу отсутствия какого-то четкого алгоритма действий(как это есть в параметрах, уравнениях и неравенствах, финансовой математике), которые бы точно приводили к конкретным результатам — делай раз, делай два…
Всё правда, нам нужен не просто набор теории и формул с фактами, этого недостаточно. Нам нужна практика, опыт решения задач и стараться чувствовать эту логику при решении задач. И тут я не открою странных лайфхаков, секретных методик, будистких тайн и введьминых приколов. Будем честны, нужно время, конкретная структура и понятный набор ресурсов.
В рамках этой статьи я вложу весь свой преподавательский опыт и свои знания, как человека, который не перестаёт учиться и осваивать новые знания, чтобы помочь вам забрать на экзамене баллы за одну из самых сложных задач.
Начинаем с азов
Давайте представим, что ваша задача поднять с нуля ваши знания по геометрии на приемлемый для ЕГЭ и выше уровень. Нам не обойтись без основ и фундамента, с которым вы встречались со времен 7 класса. Что делаем? Берем учебник Атанасяна, и тут у многих расширятся зрачки и волна ужаса пройдет ледяной лавиной от бровей до мизинцев. На самом деле прошу не пугаться, нам нужен какой-то подробный школьный учебник, в котором будет изложена вся структурированная теория, необходимая и та, что мы можем применять для решения задач. Если у вас есть альтернативный — без проблем, используйте его.
Схема работы следующая: открываем со второй главы и для каждого параграфа нас будут интересовать все доказанные теоремы, а вернее не просто сухой факт, а то откуда он берется и как его доказать. Сначала пробуем сами как-то к этому придти, если не получается, то смотрим на то, какое доказательство приводит автор.
Важно! Мы не сидим тупо перед книжкой, развивая геморрой, мы берем ручку и листочек, и сидим выписываем, конспектируем и пробуем доказывать все указанные теоремы. А после просматриваем задачи в конце, решать все не нужно, только те, которые вам покажутся реально сложными и с наскока не понятными как решать.
Что нам это даст? Мы учимся воспринимать конструкции, понимать логику построения доказательства в геометрии того или иного утверждения, а также мы сами того не подозревая запоминаем всю нужную информацию, которую мы будем применять позже для решения задач №16 на ЕГЭ!
Подумайте сами, математика — это про структуру, логику, и сколько вам нужно времени чтобы зазубрить строчку предложения? 5 ? 10 минут? А на сколько вас хватит держать это всё в голове? Вы забудете при первой же возможности. Нам нужна логика доказательства этого факта, благодаря которой наш мозг будет обучаться новому подходу в мышлении и все что связанно с геометрическими фактами вы запомните намного лучше, если будете реально пытаться доказать простейшие факты из учебника. А также на самом экзамене, уровень стресса которого пробивает все возможные значения, вы будете 100% уверены, что используемый вами факт при решении задачи не вымысел возбужденного воображения.
Сколько нужно на это времени? Если идти со скоростью две главы в день, то около недели.
Как закрепить полученный результат на практике?
Теперь, друг, ты — мощь и сила! Но без практики нам не обойтись поэтому все полученные навыки начинаем применять для решения конкретных задач. Тут нам поможет книга Гордина «Планиметрия».
Схема работы с ней следующая: можете кратко просмотреть задачи данные в качестве разобранных в начале каждой главы, попробовать решить самостоятельно и потом сравнить с данным решением. Далее, переходим на отработку задач первого уровня, тут прям всё решать нет большого смысла, хоть и страшно полезно, но в режиме ограниченного времени сразу смотрим на задачи второго уровня и пытаемся прорешать максимальное количество в каждом разделе. После того как разобрались со вторым уровнем стараемся решить задачи из третьего, но тут уже можно прыгать с задачи на задачу, так как местами именно в третий уровень уже включены задачи чуть сложнее ЕГЭ. И ещё: главы про симметрии, вектора, координаты и повороты можете пропускать, если чувствуете нехватку сил, времени и вдохновения.
Кабанеем
Если со всем предыдущими пунктами справились — Glückwünsch! Поздравляю! У нас как раз есть время чтобы порешать сложные задачи и разобрать другие методы для планиметрии Прасолова. Это поможет вам разобраться с самыми разнообразными методами, которые могут повстречаться вам при решении геометрических задач. Плюс, будет реально посмотреть эту книгу и книгу Ткачука при подготовке уже к ДВИ МГУ, но это совсем другая история))
Уровень: Убийца планиметрии
На этом мы выходим на финальный этап и раз наша цель именно ЕГЭ, то дальше делаем следующее:
Открываем все задачи ЕГЭ с 2014 года и планомерно их прорешиваем. Такая процедура даст нам понимание того, что такое реальные ЕГЭшные задачи, а не Статград, от которого порой хочется сбежать. Плюс нарабатывается навык решения задачи за ограниченное время и правильное оформление всего что вы нарешали.
На этом всё?
На этом этапе я всегда даю себе время на подумать, потому что хочется что-то ещё добавить и впихнуть максимальное количество пользы. Но в данном случае, я в одной статье уместил годы опыта и сотни учеников. Схема рабочая, пользуйтесь.
Всегда рад отзывам и комментариям!
С Пламенной любовью,
Никита Салливан из Умскул.
Планиметрия – профильный ЕГЭ по математике (оглавление)
Планиметрия плохо дается многим ученикам. На ЕГЭ эта задача №16 – одна из самых сложных задач и многие даже не пытаются за нее браться.
Весь секрет в том, что понимание планиметрии приходит не постепенно, а сразу. Вчера не получалось, а сегодня уже все понятно. Большинству просто не хватает терпения дойти до этого момента.
Надеемся, что ты не такой и не бросишь занятия на полпути. И вот тебе в помощь все, что нужно знать по планиметрии + несколько вебинаров для отработки навыков!
Планиметрия – часть 1. ЕГЭ №3 (бывшая №6)
Если вы плохо знаете планиметрию, начинайте с этой части и смотрите вебинар за вебинаром, ставьте на паузу и решайте задачи вместе с ведущим вебинаров Алексеем Шевчуком.
Помните, планиметрия требует нарешенности. Чтобы научиться решать любую задачу по планиметрии, нужно решать много задач.
Начните с самого начала.
Планиметрия – прямоугольный треугольник
Итак, прямоугольный треугольник, его свойства, площадь и углы прямоугольного треугольника, теорема Пифагора, тригонометрический функции острых углов, медиана и высота.
Планиметрия – равнобедренный треугольник и произвольный треугольник
В этом видео мы вспомним все свойства равнобедренных треугольников и научимся их применять в задачах из ЕГЭ.
Очень часто все “проблемы” с решением задач на равнобедренный треугольник решаются построением высоты. Также мы научимся решать и “обычные” треугольники.
Убедимся в достоверности утверждении из прошлого урока о прямоугольных треугольниках – очень часто решение задач сводится к нескольким прямоугольным треугольникам.
Вписанная окружность
В этом видео мы узнаем, что такое вписанная окружность, где находится её центр, и другие ее свойства. В какие фигуры можно, а в какие нельзя вписать окружность.
Научимся решать задачи на вписанную окружность – очень важный навык в понимании планиметрии.
Описанная окружность. Многоугольники
Вы этом видео вы узнаете, что такое описанная окружность, где находится её центр, и другие свойства. Около каких фигур можно, а вокруг каких нельзя описать окружность.
Также мы узнаем, что такое правильные многоугольники, и какие у них свойства; как они связаны с описанной окружностью.
Научимся решать задачи из ЕГЭ на описанную окружность и правильные многоугольники.
Что приблизит нас к умению решать любые задачи по планиметрии.
Теорема косинусов и синусов
Универсальный инструмент при решении треугольников – это теоремы косинусов и синусов.
Они подходят для любых треугольников, а не только для прямых (как теорема Пифагора).
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
На этом уроке мы выучим сами теоремы и научимся применять их при решении задач первой части.
Планиметрия – часть 2. ЕГЭ №16
Эта часть планиметрии – для продвинутых, для тех, кто уже хорошо усвоил планиметрию из первой части.
Принцип тот же – смотрите вебинар за вебинаром и, самое главное, ставьте на паузу и решайте задачи.
Планиметрия. Подобие треугольников. Задачи на доказательство. ЕГЭ №16
Подобие треугольников. Это одна из самых сложных задачи планиметрии в профильном ЕГЭ. Полные 3 балла за эту задачу получают менее 1% выпускников!
Основная сложность – построение доказательств. Баллы здесь снимают за любой пропущенный шаг доказательства.
Например, нам часто кажется очевидным, что треугольники на рисунке подобны и мы забываем указать, по какому признаку. И за это нам снимут баллы.
В этом видео вы научитесь применять подобие треугольников для доказательств, указывать признаки подобия и доказывать каждое умозаключение.
Вы научитесь правильно записывать решение задачи, сокращать записи чтобы не тратить время на выписывание всех своих мыслей или полных названий теорем.
Вы научитесь также применять подобие треугольников не только для доказательств, а и для расчётных задач.
Метод вспомогательной окружности. Из реального ЕГЭ 2016 года
Метод вспомогательной окружности – это очень классный метод, используемый в планиметрии но, к сожалению, он не всегда очевиден. Иногда в задаче нет даже намёка ни на какие окружности, но тем не менее, если догадаться её на рисунке достроить, решение становится в разы проще!
Как минимум, сразу же становятся равными друг другу очень неочевидные углы – те, которые опираются на одну дугу, но без окружности увидеть это было бы нереально сложно. Либо произведения отрезков хорд равны друг другу.
Это очень крутой и удобный метод – но нужно понимать, в каких ситуациях он применяется, ведь далеко не всегда нужно на и без того сложный рисунок лепить ещё и окружность.
Теорема Менелая и Чевы. “Секретный” метод решения самой сложной задачи ЕГЭ по математике
Задача №16. Планиметрия. Одна из самых сложных задач на ЕГЭ. Редко кто (менее 1% учеников!) набирает полные баллы по ней и поэтому грех не воспользоваться шорткатами и лайфхаками, если они есть.
Теорема Менелая и Чевы – один из таких шорткатов. Эти теоремы не входят в стандартную школьную программу, но они невероятно мощный инструмент! Они могут очень-очень упростить решение и сами по себе они красивые и легко запоминаются.
Итак, смотрите видео, учите теорему Менелая и Чевы, используйте ее на ЕГЭ.
Теорема Менелая и Чевы — её уже запретили, наконец, или нет?
Каждый год начинают ходить слухи, что теоремами Менелая и Чевы В ЭТОМ ГОДУ НЕЛЬЗЯ будет пользоваться на ЕГЭ. Правда ли это? Чтобы понять это, достаточно заглянуть в обычный…
Впрочем, смотрите это видео и узнаете, как понять, какими теоремами можно, а какими нельзя пользоваться. А также, на этом вебе мы разберём, что это за теоремы такие, и как ими пользоваться.
Вы узнаете, насколько они крутые и мощные, и насколько экономят нам время в некоторых задачах.
Планиметрия Статград март 2021
Задача №16 из мартовского статграда на планиметрию ничем не удивляет: снова окружность и пропорциональные отрезки в ней, прямоугольные треугольники, вот это всё.
Скучно… Раз-два, и ответ готов!
Но погодите-ка, а почему у нас с вами ответ получился разный? И вроде бы оба делаем всё правильно…
На уроках нашего курса я рассказывал о таких задачах, но их уже давненько не попадалось на ЕГЭ, и все уж думали, что ушла эпоха. Конечно, никакого парадокса в этой задаче нет, нужно всего лишь (ха-ха) быть очень внимательными:)
Смотрите видео, и узнаете, в чём же особенность этой задачи, как её правильно решать и оформлять, а также – как ничего не упустить на экзамене и не потерять баллы!
Планиметрия. Окружности. Задача из олимпиады Физтеха 2020
Планиметрия и окружности! Куда же деться от них в 16 задаче на ЕГЭ?
Те, кто ходил на наш курс подготовки, посвященный 16 задаче, знают, что окружности в задачах на планиметрию попадаются чаще всего.
Иногда вписанные. Иногда описанные. С разными вписанными или описанными фигурами. Иногда одна окружность . Иногда две. Они касаются друг друга или пересекаются друг с другом. Никуда не деться от окружностей – остается только научится их решать и получать удовольствие от красивых задач!
В этом видео мы разберём, что бы вы думали? Задачу 16 из ЕГЭ?
Нет! Пойдём дальше – разберём задачу из олимпиады Физтеха прошлого года.
Стойте, не разбегайтесь! Олимпиады далеко не всегда бывают сложными (особенно, если вы прошли наш курс по 16-й задаче). Эта задача вполне себе ЕГЭ-шного уровня. Про окружности и прямоугольные треугольники.
Готовьтесь и “разминайте” свои теоремы Пифагора, теорему синусов и прочих косинусов.
Разбор задачи №16 (б) из реального варианта ЕГЭ 2021 по профильной математике
Продолжение предыдущего видео. Разбор части (б):
Теперь слово вам…
Как вам наш гид по планиметрии? Что нового вы узнали? Что еще хотите узнать?
Как вам теорема Менелая и Чевы? Один из моих знакомых сказал: “В школе ее от нас утаивали!”. Шутка, в которой есть доля… шутки.
Готовьтесь к планиметрии и забирайте свои 3 балла на ЕГЭ.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Планиметрия
Подобие треугольников
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.
Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)
- Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
- Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Признаки подобия треугольников:
- Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
- Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между ними равны, то такие треугольники подобны.
- Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.
Площади фигур
Площадь треугольника
- $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
- $S={a·b·sinα}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
- Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
- $S=p·r$, где $r$ — радиус вписанной окружности
- $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
- Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.
- Для равностороннего треугольника $S={a^2 √3}/{4}$, где $а$ — длина стороны.
Площади четырехугольников
Прямоугольник
$S=a·b$, где $а$ и $b$ — смежные стороны.
Ромб
$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба
$S=a^2·sinα$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.
Трапеция
$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.
Квадрат
$S=a^2$, где $а$ — сторона квадрата.
Параллелограмм
$S=a·b·sinα$, где $а$ и $b$ — длины сторон параллелограмма, а $α$ — угол между этими сторонами.
Пропорциональные отрезки в прямоугольном треугольнике
В прямоугольном треугольнике с прямым углом $С$ и высотой $СD$:
Квадрат высоты, проведенной к гипотенузе, равен произведению отрезков, на которые высота поделила гипотенузу.
$CD^2=DB·AD$
В прямоугольном треугольнике : квадрат катета равен произведению гипотенузы на проекцию этого катета на гипотенузу.
$CB^2=AB·DB$
$AC^2=AB·AD$
Произведение катетов прямоугольного треугольника равно произведению его гипотенузы на высоту, проведенную к гипотенузе.
$AC·CB=AB·CD$
Метрические соотношения в окружности
1. Две касательные, проведенные к окружности из одной точки, равны, и центр окружности лежит на биссектрисе угла между ними.
2. Если хорды $АС$ и $BD$ пересекаются в некоторой точке $N$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AN·NC=BN·ND$
Пример:
Хорды $АВ$ и $CD$ пересекаются в точке $Е$. Найдите $ЕD$, если $АЕ=16, ВЕ=9, СЕ=ED$.
Решение:
Если хорды $АВ$ и $СD$ пересекаются в некоторой точке $Е$, то произведение отрезков одной хорды равно произведению отрезков другой хорды.
$AЕ·ЕВ=СЕ·ЕD$
Так как $СЕ=ED$, данное выражение можно записать в виде:
$ЕD^2=AЕ·ЕВ$
Подставим числовые значения
$ЕD^2=16·9$
$ЕD=√{16·9}=4·3=12$
Ответ: $12$
3. Если из одной точки к одной окружности проведены две секущие, то произведение первой секущей на ее внешнюю часть равно произведению второй секущей на свою внешнюю часть.
$АС·ВС=EC·DC$
4. Если из одной точки к окружности проведены секущая и касательная, то произведение секущей на ее внешнюю часть равно квадрату длины касательной.
$BD·СB=AB^2$
Вписанные и описанные окружности для четырехугольников.
1. Если суммы противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
$АВ+CD=BC+AD$
2. Если сумма противоположных углов четырехугольника равна $180°$, то только тогда около него можно описать окружность.
$∠В+∠D=180°$
$∠A+∠C=180°$
Вневписанные окружности
Вневписанной окружностью треугольника называется окружность, касающаяся одной из его сторон и продолжений двух других.
Для каждого треугольника существует три вневписанных окружности, которые расположены вне треугольника, центрами вневписанных окружностей являются точки пересечения биссектрис внешних углов треугольника.
Точки $О_1, О_2$ и $О_3$ – центры вневписанных окружностей.
Связь площади треугольника с радиусами вневписанных окружностей.
Введем обозначения:
$S$ — площадь треугольника;
$p$ — полупериметр треугольника;
$a, b, c$ — стороны треугольника;
$r_a, r_b, r_c$ — радиусы вневписанных окружностей касающиеся соответственно сторон $a, b$ и $c$;
Для данных обозначений справедливы равенства:
$r_a={S}/{p-a};$
$r_b={S}/{p-b};$
$r_c={S}/{p-c}.$
Пример:
В прямоугольном треугольнике $АВС$ угол $С=90°, АС=6, ВС=8$. Найдите радиус вневписанной окружности, касающейся гипотенузы.
Решение:
Радиус вневписанной окружности, касающейся стороны $АВ$ равен:
$r_{АВ}={S}/{p-АВ}$, где $S$ — площадь треугольника, $р$ — полупериметр треугольника.
Чтобы подставить в формулу данные, найдем сначала площадь треугольника и его полупериметр.
Площадь прямоугольного треугольника равна половине произведения катетов:
$S={АС·АВ}/{2}={6·8}/{2}=24$
Нам неизвестна гипотенуза, найдем ее по теореме Пифагора:
$АВ=√{АС^2+СВ^2}=√{6^2+8^2}=√{100}=10$
Зная все стороны, вычислим полупериметр:
$р={6+8+10}/{2}=12$
Теперь можем все данные подставить в формулу нахождения радиуса вневписанной окружности:
$r_{АВ}={S}/{p-АВ}={24}/{12-10}={24}/{2}=12$
Ответ: $12$
Биссектриса
Биссектриса – это линия, которая делит угол пополам.
Свойства биссектрисы:
1. В равнобедренном треугольнике биссектриса, проведённая из вершины к основанию, является также и медианой, и высотой.
2. Если точка лежит на биссектрисе, то расстояния от неё до сторон угла равны.
$AD=DC$
3. Три биссектрисы в треугольнике пересекаются в одной точке, эта точка является центром вписанной в треугольник окружности.
4. Биссектриса угла в параллелограмме отсекает равнобедренный треугольник.
5. Биссектрисы смежных углов перпендикулярны.
6. В треугольнике биссектриса угла делит противоположную сторону на отрезки, отношение которых такое же, как отношение сторон треугольника, между которыми эта биссектриса прошла.
${AB}/{AC}={BA_1}/{A_1C}$
7. Для нахождения длины биссектрисы справедлива формула:
$АА_1=√{АВ·АС-ВА_1·А_1 С}$
Медиана
Медиана — это линия, проведенная из вершины треугольника к середине противоположной стороны.
Свойства медиан:
1. Медиана делит треугольник на два равновеликих треугольника, т.е. на два треугольника, у которых площади равны.
$S_1=S_2$
2. Медианы пересекаются в одной точке и этой точкой делятся в отношении два к одному, считая от вершины.
3. В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы и радиусу описанной около этого треугольника окружности.
4. Для нахождения длины медианы, проведенной к стороне «с», справедлива формула:
$М_с={√{2(а^2+b^2)-c^2}}/{2}$
Высота
Высота в треугольнике — это линия, проведенная из вершины треугольника к противоположной стороне под углом в 90 градусов.
$BB_1$ — высота
Свойства высот:
1. Три высоты (или их продолжения) пересекаются в одной точке.
2. При пересечении двух высот получаются подобные треугольники:
$∆АА_1 В~∆СС_1В;$
$∆АС_1 М~∆СМА1$
3. Угол между высотами в остроугольном треугольнике равен углу между сторонами, к которым эти высоты проведены.
4. Высоты треугольника обратно пропорциональны его сторонам:
$h_a:h_b:h_c={1}/{a}:{1}/{b}:{1}/{c}$
Теорема синусов
Во всяком треугольнике стороны относятся как синусы противолежащих углов:
${a}/{sinα}={b}/{sinβ} ={c}/{sinγ} =2R$, где $R$ — радиус описанной около треугольника окружности.
Пример:
В треугольнике $АВС ВС=16, sin∠A={4}/{5}$. Найдите радиус окружности, описанной вокруг треугольника $АВС$.
Решение:
Воспользуемся теоремой синусов:
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной окружности
${ВС}/{sinA} =2R$
Далее подставим числовые данные и найдем $R$
${16·5}/{4}=2R$
$R={16·5}/{4·2}=10$
Ответ: $10$
Теорема косинусов
Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
$a^2=b^2+c^2-2·b·c·cosα.$
«
Методика решения задач повышенного уровня сложности по планиметрии
(на
примере №18 — С4 ЕГЭ)»
Симакина
Елена Анатольевна,
учитель
математики МБОУ «Лицей»
Новомосковск
февраль 2015
Цели
и задачи:
1) оказание
практической помощи учителям математики в решении геометрических задач
повышенного уровня сложности;
2) создание
банка методических материалов, которые могут быть использованы учителями в
практической деятельности;
3) повышение
педагогического и методического мастерства, развитие и поддержка новых
технологий в организации образовательного процесса;
4) обмен
педагогическим опытом.
Структура теста ЕГЭ по математике профильный
уровень
В 2015 году тест ЕГЭ по математике состоит из 21
задания, из них: заданий по алгебре и началам анализа — 15, по геометрии
— 6.
Заданий базового уровня сложности 9, повышенного — 10, высокого —
2.
Работа рассчитана на 235 минут.
Минимальный порог –
27 баллов.
Экзаменационная
работа состоит из двух частей, которые различаются по содержанию,
сложности и числу заданий.
Определяющим
признаком каждой части работы является форма заданий:
·
часть 1 содержит 9 заданий (задания 1–9) с кратким ответом;
·
часть 2 содержит пять заданий (задания 10–14) с кратким ответом
и семь заданий (задания 15- 21) с развёрнутым ответом.
Изменения
в ЕГЭ 2014/15 по математике в большей мере относятся к изменению
типа задачи С4
(в новой версии задание 18). Если в вариантах 2010-2013 задача С4
была
многовариантной, т.е. содержала в условии некоторую неопределенность,
позволявшую
трактовать условие неоднозначно, что приводило к возможности построения
нескольких чертежей, удовлетворяющих условию задачи. Перебор возникающих
вариантов являлся частью решения задач такого типа.
В
подготовительный период и на самом экзамене ЕГЭ 2014 предлагались задачи
на доказательство и вычисление, решение которых состояло из двух
частей. В первой части решения было необходимо проанализировать имеющуюся
в условии задачи геометрическую конфигурацию и доказать, что она обладает
определенным свойством. Во второй части решения, опираясь на доказанное
свойство или возможно и без него, было необходимо решить задачу на
нахождение величин (линейных, угловых, отношений отрезков, площадей фигур).
Соответствующая структура задания сохраняется и в задании 18 ЕГЭ 2015.
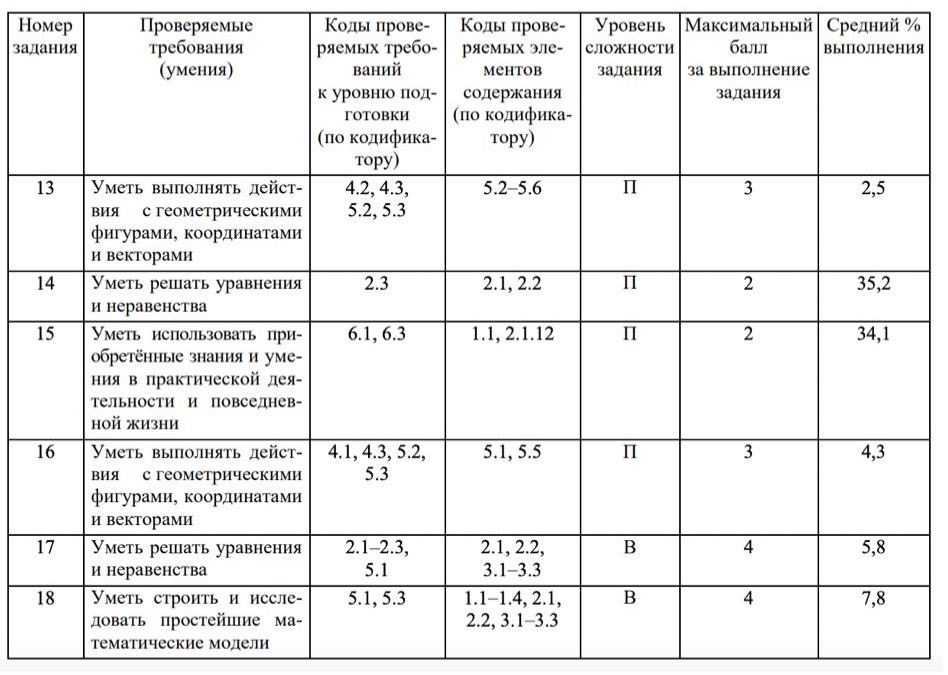
|
Проверяемые элементы содержания и виды деятельности |
Уровень сложности задания |
Максимальный балл за выполнение задания |
Примерное время выполнения задания (мин.) |
|
Задание |
П |
3 |
25 |
По фактическим
данным выполнения, задание 18 является границей, разделяющий высокий и
повышенный уровень подготовки участников ЕГЭ.
Критерии оценивания в 2014
году приведены в таблице.
|
Содержание критерия |
Баллы |
|
Имеется верное доказательство |
3 |
|
Получен обоснованный ответ в пункте |
2 |
|
Имеется верное доказательство |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных |
0 |
|
Максимальный балл |
3 |
При
подготовке к сдаче ЕГЭ и обучении решению задач С4 следует отметить, что
для выполнения первого пункта задачи нужно помнить основные определения,
теоремы и следствия из них, а также признаки и свойства геометрических
фигур. В основном первая часть решения сводится к доказательству одного
из следующих свойств приведенной в условии геометрической конфигурации:
а) подобия
указанных треугольников;
б)
параллельность или перпендикулярность указанных прямых;
в) равенство
указанных углов, отрезков, площадей или их заданное отношение;
г)
принадлежность указанной фигуры к определенному типу:
·
треугольник
является прямоугольным, равнобедренным и т.д.;
·
четырехугольник
является описанным или вписанным;
·
четырехугольник
обладает признаками параллелограмма, ромба, трапеции и т.д.;
·
точка
равноудалена от вершин или сторон многоугольника, то есть является
центром вписанной или описанной окружностей;
·
прямая
содержит указанные точку или отрезок.
Для
успешной сдачи ЕГЭ необходимо разобрать с учащимися достаточное количество
задач подобного типа. Желательно
на уроках повторения давать учащимся задачи блоками, напомнив основные
теоретические факты, которые могут оказаться полезными для решения
предложенных задач. Причем их набор должен быть шире, чем требуется
для решения каждой отдельной задачи из предложенного блока. Для выполнения второго пункта задачи
на нахождение требуемых величин в заданной геометрической фигурации нужно
помнить основные формулы для вычисления соответствующих элементов:
а)
для линейных – это теоремы: Пифагора, косинусов, синусов, о секущих и
касательных, о хордах; формулы: длины медианы, биссектрисы и т.д.;
б)
для угловых – это теоремы: косинусов, синусов, об измерении углов,
связанных с окружностью (центральных, вписанных, не вписанных, между хордой
и касательной) и т.д.;
в)
для площадей – это теоремы: об отношении площадей подобных фигур; об
отношении площадей фигур, имеющих равные элементы; формулы вычисления площадей
треугольника и многоугольников, круга и его частей и т.д.
г)
отношений отрезков или площадей фигур – это теоремы: Фалеса, о
пропорциональных отрезках, о метрических соотношениях в треугольнике и
круге, об отношении соответствующих элементов подобных фигур и т.д.
Будет
целесообразным записать учащимися памятку решения геометрических задач по
пунктам и пользоваться ею.
Памятка
решения геометрических задач.
1) Чтение
условия задачи.
2) Выполнение
чертежа с буквенными обозначениями.
3) Краткая
запись условия (база знаний)
4) Деталировка
– вычерчивания отдельных деталей на дополнительных чертежах; исходная сложная
задача разбивается на несколько простых
5) Составление
цепочки действий
6) Реализация
алгоритма решения
7) Проверка
правильности решения (логику доказательства, найденные величины имеют
геометрический смысл)

Задача
1
(медианы
в треугольнике).
Медианы АМ и BN
треугольника АВС перпендикулярны и пересекаются в точке Р.
а) Докажите, что
СР=АВ.
б) Найдите S ΔАВС, если известно, что АС=6 и ВС=7.
Повторить.
1) медианы треугольника пересекаются в одной точке и точкой пересечения делятся
в отношении 2:1; 2) медиана прямоугольного треугольника, проведенная к
гипотенузе, равна ее половине; 3) каждая медиана делит треугольник на два, равных
по площади.

1) Так
как медианы треугольника пересекаются в одной точке, то СР – это отрезок
медианы. Пусть СР пересекается с АВ в точке К, тогда СК – медиана треугольника
и СР= СК=2РК (свойство медиан)
2) РК
– медиана прямоугольного треугольника АВР, поэтому РК=0,5АВ.
3) Из
1) и 2)=>АВ=2PK =СР.
Пункт
а) доказан.
б) 1) Пусть ВР=2х,
PN=х,
АР=2у, РМ=у. Применяя теорему Пифагора для треугольников ВМР и АРN,
получим систему
2) АМ – медиана
треугольника АВC, поэтому площадь
треугольника АВМ равна
Значит, площадь
треугольника АВС равна
Ответ: S ΔАВС =
Задача
2 (метод площадей).
Окружность с
центром О, вписанная в S ΔАВС касается стороны ВС в точке Р и пересекает отрезок ВО в точке Q.
Отрезки OC II QP
а) Доказать: S ΔАВС – равнобедренный
б) Найти S ΔBPQ,
если точка О делит высоту ВН в отношении ВО: ОН=3:1, АС =2а.
Повторить.
Для доказательства пункта a)
необходимо вcпомнить признаки
равнобедренного треугольника: если высота и биссектриса, проведенная к одной
стороне, совпадают, то такой треугольник является равнобедренным.
Решение
а) 1) ΔАВС –
описанный около окружности, поэтому О – точка пересечения биссектрис.

2) OPBC (радиус,
проведенный в точку касания), значит ΔВРО – прямоугольный.
3) Пусть углы АСО
и ВСО равны α, тогда угол СОР равен 90-α и равен углу ОРQ,
так как ОС II QP,
углы OPQ
и COP
– накрест лежащие.
ΔQOP
— равнобедренный, так как OQ=OP (радиусы).
QOP
=-2
4) Пусть ВО
пересекается с АС в точке Н. Рассмотрим треугольники ВОР и ВСН. У них угол при
вершине В общий, ВОР=
ВСН=2α. Значит, ΔВОР
подобен ΔВСН по двум углам. Следовательно, ВНС=
ВРО=90°
5) Рассмотрим
треугольник АВС. У него ВН является биссектрисой и высотой. Поэтому по признаку
равнобедренного треугольника ΔАВС – равнобедренный. Пункт а) доказан.
б) При нахождении S ΔBQP
будем использовать «метод площадей»: если два треугольника имеют общий угол, то
их площади относятся как произведения сторон, содержащих этот угол, то есть если
= k
и = m,
то = km
.
1) ΔАВС –
равнобедренный (см. пункт а), ВН – высота, => ВН – медиана. Если АС = 2а по
условию, то НС = а.
2) НС = СР = а (свойство
отрезков касательных)
3) СО –
биссектриса ΔВНС. По свойству биссектрисы треугольника =
= 3:1(по условию).
Поэтому ВС=3а, тогда ВР = ВС – РС = 3а — а = 2а. С другой стороны = 3,
S ΔBHC=0,5∙
ВН∙ НС =0,5∙ НС=0,5
∙а
=
а2
4)
BQ : BH=1 : 2; BP : BC=2 : 3. Поэтому SBQP =
0,5 ∙ =
.
Задача в пункте б)
может быть решена другими способами. Например, ΔОНС и ΔВНС имеют общую высоту HС.
=
. SOPC =
SOHC.
Поэтому SBPO=0,5
S BHC.
Аналогично, SBQP =
SBPO.
Значит, SBQP =
Возможно и третье
решение. Из треугольника ВНС найти синус угла НВС, далее, вычислив стороны BQ
и BP
треугольника BQP, найти его площадь
SBQP
=
Ответ:
Задача
3 (вписанный четырехугольник).
На гипотенузу АВ
прямоугольного ΔАВС опустили высоту СН. Из точки Н на катеты опустили
перпендикуляры НК и НЕ
а) Доказать, что
точки А, В, К и Е лежат на одной окружности,
б) Найти радиус
этой окружности, если АВ=12, СН=5.
Повторить.
Свойство вписанного четырехугольника: сумма противоположных углов равна 180°,
справедливо и обратное.
Решение

а) Если точки А,
В, К и Е лежат на одной окружности, то четырехугольник АВКЕ – вписанный.
1) Пусть угол А равен α, угол В равен β, тогда
α+β=90°. Используя свойство прямоугольного треугольника (сумма острых углов
равна 90°) и далее в ΔАСН, ΔКСН, ΔСНВ и ΔСНЕ, получим
2)
Четырехугольник КСЕН – прямоугольник, поэтому его диагонали равны и точкой
пересечения делятся пополам. Значит, ΔОНЕ и ΔОНК равнобедренные ∠ОКН=∠ОНК=α,
∠ОНЕ=∠ОЕН=β
(как углы при основании).
3) В
четырехугольнике АКЕВ: ∠А+∠КЕВ=α+90°+β=180°,
∠B+∠АКЕ=
α+90°+β=180°. Значит, около АКЕВ можно описать окружность. Пункт а) доказан.
б) 1) Нарисуем
окружность. Проведем АR перпендикулярно
АВ, точка R принадлежит окружности.
Угол RAB
равен 90° — вписанный, поэтому опирается на диаметр окружности RB.

Угол НЕВ равен
90°, поэтому точки R, H
и Е лежат на одной прямой
2) АСHR
– параллелограмм, противоположные стороны его равны. AR=CH=5
3) По теореме
Пифагора из ΔARB получим, что BR==
=13. Значит Rокр=0,5
ВК=6,5
Другой способ
нахождения радиуса окружности: из ΔАСВ найти угол α, его катеты и АЕ. В ΔАКЕ ∠АКЕ=90°+α.
Треугольник АКЕ вписанный в данную окружность. По следствию из теоремы синусов
=2R
Ответ:
6,5.
Задача
4 (описанный четырехугольник).
В равнобедренную
трапецию АВСD с основаниями AD
и ВС вписана окружность, СН – высота трапеции.
а) Доказать, что
центр окружности, вписанной в трапецию, лежит на отрезке ВН.
б)
Найдите диагональ АС, если известно, что средняя линия трапеции равна , а угол AOD
равен 135°, где О – центр окружности, вписанной в трапецию, AD
– большее основание.
Решение.

а) 1) Пусть точки K
и L
– точки касания окружности оснований трапеции, тогда
ОК = ОL = rвпис
2) ΔBOK=ΔHOL
по катету(см. пункт 1) и острому углу (углы OBK
и LHO
равны как накрест лежащие при BC II AD
и секущей BH. Поэтому ВО = ОН.
3) Центр
вписанной в трапецию окружности лежит на пересечении биссектрис внутренних
углов трапеции. Данная трапеция ABCD
– равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и
ΔСОК равны (по катету и острому углу)
4) Из 2) и 3)
следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного
треугольника ΔВСН. О – центр описанной около треугольника окружности.
Следовательно О принадлежит ВН (его середина). Пункт а) доказан.
б) Для
доказательства пункта б) сделаем дополнительный чертеж

1) Пусть
MN
– средняя линия трапеции. Точка О принадлежит MN
и О – её середина, поэтому МО =
2) АО
– биссектриса, углы МАО и RAO
равны, углы RAO и МОА раны как накрест
лежащие. ΔАМО – равнобедренный, АМ=МО=. Тогда АВ = 2АМ=
3)
∠AOD=135°
(по условию), ∠OAD+∠ODA=45°.
Значит, ∠BAD=∠CDA=45°.
Пусть BR
перпендикулярен AD. BR = AR=
4) Пусть
CD1
II BD
и точка D1
лежит на прямой AD. Четырехугольник
ВСD1D
– параллелограмм. CD1=BD
(противоположные стороны), BD=AC(диагонали
равнобедренной трапеции). Тогда СD1=BD=AC.
5) 1
– равнобедренный, AD1
– основание. АD1=AD+DD1=AD+BC=2MN=2. CH=BR=
. По теореме Пифагора из
ΔCHА:
AC==
2=
= 3
Ответ:
АС = 3.
Задача
5
В треугольнике АВС угол ВАС равен 60°,
угол АВС равен 45°. Продолжения высот треугольника АВС пересекают
описанную около него окружность в точках M,
N,
P.
а) Докажите, что треугольник MNP
прямоугольный.
б) Найдите площадь треугольника MNP,
если ВС=12.
Повторить.
Свойство вписанных углов; теорему синусов.
Решение.

АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность
в точках M, N
и P
соответственно.
Тогда вписанные углы PNB
и PCB
опираются на одну и ту же дугу, поэтому
Аналогично,
Значит,
Следовательно, треугольник MNP
прямоугольный. Пункт а) доказан.
б) Угол MNA
равен углу NBA , угол APM
равен углу ACP (вписанные углы,
опирающиеся на одну дугу).
Тогда
Следовательно, = 30°.
Пусть R
– радиус описанной окружности треугольника АВС. По теореме синусов
Тогда
=
Следовательно,
Ответ:
Заключение.
Выше разобранные задачи естественно не
исчерпывают все возможные типы задач №18, которые могут быть предложены на
экзамене. Показаны отдельные методические приемы решения планиметрических задач
повышенной сложности, которые могут быть использованы учителями математики при
подготовке учащихся к успешной сдачи ЕГЭ.
Источники:
1. Учебно-методические
материалы для председателей и членов региональных предметных комиссий по
проверке выполнения заданий с развернутым ответом экзаменационных работ ЕГЭ
2014 года. ФИПИ.
2. Гордин
Р.К. ЕГЭ 2014. Математика. Решение задачи С4. — 3-е
изд. доп. – М.: МЦНМО, 2014. – 448 с.
3. Прокофьев
А.А., Корянов А.Г. Математика. Подготовка к ЕГЭ: решение планиметрических
задач (С4). – Ростов-на-Дону, Легион, 2014. – 208 с. – (Готовимся к
ЕГЭ.).
4. Прокофьев
А.А., Корянов А.Г. Готовим к ЕГЭ хорошистов и отличников. Лекции 5–8
- http://4ege.ru/metamatika-teoriya/3797-zadanie-s4.html
- http://www.egetrener.ru/treningC4.php
Тема 1. Методы решения планиметрических задач
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ФАКТЫ
1. Треугольники
По соотношению сторон треугольники разделяются на разносторонние и равнобедренные (в том числе и равносторонние).
По величине наибольшего угла треугольники разделяются на остроугольные, прямоугольные и тупоугольные.
Признаки равенства треугольников:
1. По двум сторонам и углу между ними:
2. По стороне и двум прилежащим к ней углам:
3. По трем сторонам:
Признаки подобия треугольников:
1. , если
.
2. , если
.
3. , если
.
Средняя линия — отрезок, соединяющий середины двух сторон треугольника.
Медиана — отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса — отрезок, выходящий из вершины треугольника и делящий угол пополам.
Биссектриса угла треугольника делит его противолежащую сторону на отрезки, пропорциональные прилежащим сторонам.
Высота — отрезок, выходящий из вершины треугольника и перпендикулярный противоположной стороне.
Срединный перпендикуляр — прямая, проведенная через середину стороны треугольника, перпендикулярная к этой стороне.
Четыре замечательные точки треугольника:
1. Точка пересечения медиан (медианы пересекаются в одной точке).
2. Точка пересечения биссектрис — центр вписанной окружности (биссектрисы пересекаются в одной точке).
3. Точка пересечения высот (высоты пересекаются в одной точке).
4. Точка пересечения срединных перпендикуляров — центр описанной окружности (срединные перпендикуляры пересекаются в одной точке).
Две прямые на плоскости называются параллельными, если они не пересекаются.
Аксиома параллельных прямых: через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны, соответственные углы равны, а сумма односторонних углов равна .
2. Четырехугольники
Четырехугольники могут быть выпуклыми и невыпуклыми.
Выпуклые четырехугольники по наличию параллельных сторон делятся на параллелограммы (2 пары параллельных сторон), трапеции (1 пара параллельных сторон) и общего вида (нет параллельных сторон).
К частным видам параллелограммов относятся прямоугольники (4 угла прямые), ромбы (4 стороны равны), квадраты (обладают свойствами как прямоугольников, так и ромбов).
Свойства параллелограммов:
— В любом параллелограмме противоположные стороны равны, противоположные углы равны, диагонали в точке пересечения делятся пополам.
— В прямоугольнике диагонали равны.
— В ромбе диагонали перпендикулярны.
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник — параллелограмм.
К частным видам трапеций относятся равнобедренные (боковые стороны равны) и прямоугольные (одна из боковых сторон перпендикулярна основаниям).
Свойства трапеций:
— Средняя линия трапеции (отрезок, соединяющий середины боковых сторон) параллельна основаниям трапеции, а длина ее равна полусумме длин оснований.
— В равнобедренной трапеции диагонали равны, углы при одном и том же основании равны.
3. Окружность и круг
Окружность — геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Окружность является замкнутой плоской линией.
Круг — часть плоскости, ограниченная окружностью.
Радиус — отрезок, соединяющий центр окружности с точкой на окружности.
Хорда — отрезок, соединяющий две произвольные точки окружности.
Диаметр — хорда, проходящая через центр окружности.
Центральный угол — угол между двумя радиусами, его величина совпадает с градусной мерой дуги, на которую он опирается.
Вписанный угол — угол между двумя хордами, с вершиной на окружности; измеряется половиной градусной меры дуги, на которую он опирается.
Если проведены две хорды AB и CD окружности, пересекающиеся в точке Р, то выполняется равенство .
Если две хорды окружности параллельны, то градусные меры дуг, заключенных между ними, равны.
Касательная к окружности — прямая, имеющая с окружностью одну общую точку. Радиус, проведенный в точку касания, перпендикулярен касательной.
Угол между касательной и хордой, проведенными через точку окружности, измеряется половиной градусной меры дуги, заключенной между касательной и хордой.
Теорема Птолемея для вписанных четырехугольников: Произведение длин диагоналей вписанного четырехугольника ABCD равно сумме произведений длин пар противоположных сторон:
AC ВD = AB
CD + BС
АD.
Если четырехугольник вписан в окружность, то суммы его противолежащих углов равны .
Если четырехугольник ABCD описан около окружности, то суммы длин его противоположных сторон равны.
ОСНОВНЫЕ ФОРМУЛЫ
1. Произвольный треугольник ( — стороны;
,
,
—
ротиволежащие им углы;
— полупериметр;
— радиус описанной окружности;
— радиус вписанной окружности;
— площадь;
— высота, проведенная к стороне
:
(теорема косинусов);
(теорема синусов).
2. Прямоугольный треугольник ( — катеты;
— гипотенуза;
— проекции катетов на гипотенузу;
— высота, проведенная к гипотенузе):
(теорема Пифагора);
3. Равносторонний треугольник:
4. Произвольный выпуклый четырехугольник ( и
— диагонали;
— угол между ними;
— площадь):
5. Параллелограмм (и
— смежные стороны;
— угол между ними;
— высота, проведенная к стороне
;
— площадь):
6. Ромб: .
7. Прямоугольник: .
8. Квадрат ( — диагональ):
.
9. Трапеция ( и
— основания;
— расстояние между ними;
— средняя линия;
— площадь):
10. Описанный многоугольник ( — полупериметр;
— радиус вписанной окружности;
— площадь):
.
11. Правильный многоугольник ( — сторона правильного
-угольника;
— радиус описанной окружности;
— радиус вписанной окружности;
— площадь):
12. Окружность, круг ( — радиус;
— длина окружности;
— площадь круга):
13. Сектор ( — длина дуги, ограничивающей сектор;
— градусная мера центрального угла;
— радианная мера центрального угла;
— радиус;
— площадь):
ОБРАЗЦЫ РЕШЕНИЯ ЗАДАЧ
Задача 1. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки 5 см и 12 см. Найти катеты треугольника.
Решение:
АМ = 5; ВМ = 12. Пусть радиус вписанной окружности равен см.
По свойствам отрезков касательных, проведенных к окружности из внешней точки: BM = BN, AM = AP.
Тогда BC = BN + NC = 12 + ,
AC = AP + PC = 5 + , AB = BM + MA = 12 + 5 = 17.
По теореме Пифагора АВ = АС
+ ВС
.
( + 12)
+ (
+ 5)
= 17
.
Упростив уравнение, получим + 17
— 6 = .
Его корни = — 2 (посторонний) и
= 3.
Тогда АС = 5 + 3 = 8; ВС = 12 + 3 = 15.
Ответ: 8 см, 15 см.
Задача 2. В параллелограмме ABCD со стороной AD = 25 проведена биссектриса угла А, проходящая через точку Р на стороне ВС. Найдите периметр трапеции APCD, если ее средняя линия равна 15, а диагональ .
Решение:
1) , так как АР — биссектриса; тогда
АВР — равнобедренный (АВ = ВР);
2) MN — средняя линия трапеции APCD: 2MN = AD + PC; AD + PC = 30; PC = 5; BP = 20; AB = 20.
По теореме косинусов:
3) В АВР: AP
= AB
+BP
— 2AB
BP
cos
AВР.
4) В АВC: AC
= AB
+ BC
— 2AB
BC
cos
AВР.
Из 4) находим cosAВР =
; подставив найденное значение в 3), получим АР
= 900, АР = 30.
5) = AP + РС + CD + DА = 30 + 5 + 20 + 25 = 80.
Ответ: 80.
Задача 3. Сторона правильного шестиугольника ABCDEF равна . Найдите радиус окружности, вписанной в треугольник МРК, где точки М, Р, К — середины сторон шестиугольника ABCDEF соответственно.
Решение: Для наглядности изобразим правильный шестиугольник как вписанный в окружность.
1) По свойствам правильного шестиугольника BE = 2 AF = .
2) ABEF — равнобедренная трапеция, в которой МК — средняя линия: МК = .
3) РК — равносторонний. Радиус искомой вписанной окружности
PN, PN =
МК.
PN = = 72, следовательно,
= 24.
Ответ: 24.
Задача 4. Углы при одном из оснований трапеции равны и
, а разность квадратов длин ее оснований равна 8. Найти площадь трапеции.
Решение:
В трапеции ,
.
Продолжим боковые стороны AD и ВС до пресечения их в точке Р. CРD — прямоугольный, так как
.
S = S
— S
Пусть AB = , CD =
; по условию
—
= 8, AB
CD.
S CP
DP; S
=
PB
PA.
;
;
;
.
.
.
S —
=
—
8 = 1.
Ответ: 1.
-
Домашнее задание № 1
Домашнее задание № 1
1. В треугольнике АВС медианы АЕ и СD пересекаются в точке О. АЕ = 9; СD = 12; АС = 10. Найдите площадь треугольника АВС. Ответ: 72.
2. В равнобедренном треугольнике основание равно 16, а боковая сторона 10. Найдите расстояние между центрами его вписанной и описанной окружностей. Ответ: 5.
3. Высоты, проведенные из вершины тупого угла параллелограмма, составляют угол . Одна из высот делит сторону, к которой проведена, на отрезки 2 и 8, считая от вершины острого угла. Найдите площадь параллелограмма. Ответ: 20.
4. В четырехугольнике ABCD длина стороны АВ составляет 12 см; sinBAC =0,33; sin
ADB =,44. Сумма углов
BAD и
BCD составляет
. Найдите длину стороны ВС. Ответ: 9.
5. Один из углов трапеции равен , а боковые стороны перпендикулярны. Найдите меньшую боковую сторону трапеции, если средняя линия трапеции равна 10 см, а одно из оснований 8 см. Ответ: 2.
6. Найдите периметр правильного восьмиугольника ABCDEFGH, если площадь четырехугольника ABEG = 8(3 + 2
. Ответ: 32.
3