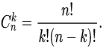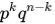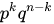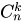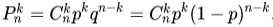Как наугад сдать егэ

Основные термины (генерируются автоматически): теория вероятностей, правильный ответ, вероятность сдачи ЕГЭ, ЕГЭ, единый государственный экзамен, вероятность, задание, исход, ответ, событие.

Похожие статьи

Муниципальное бюджетное образовательное учреждение

«Средняя общеобразовательная школа № 17»

Рузаевского муниципального района

Научно-исследовательская работа по математике на тему:

«Вероятность успешной сдачи ЕГЭ

путем угадывания верных ответов»

Автор: 

Никашкин Артем,  10 «А»  класс

Руководитель: 

Курганова Юлия Александровна,

учитель математики

Рузаевка, 2015 г.

Содержание работы:

Введение

По окончании 11 класса школы все старшеклассники  столкнутся с достаточно серьезным испытанием своих знаний — сдачей ЕГЭ, единого государственного экзамена.  Участники ЕГЭ этого года должны будут сдавать два обязательных предмета: русский язык и математика и предметы по выбору:

• обществознание,
• физика,
• химия,
• история,
• география,
• биология,
• литература,
• иностранный язык,
• информатика.

  ЕГЭ – это серьёзный шаг в жизни каждого выпускника. Успешно сдать все экзамены мечтает каждый ученик, но кто-то предпочитает регулярное посещение занятий, выполнение домашних заданий, активную работу на уроке, а кому-то остается надеяться только на шпаргалки и на удачу. Среди нерадивых учеников возникает вопрос: «Нельзя ли выбрать наугад ответы и при этом успешно сдать ЕГЭ?». Меня заинтересовал ответ на этот вопрос.

Успешная сдача ЕГЭ – это дело случая?

Случай, случайность – с ними мы встречаемся повседневно: случайная встреча, случайная поломка, случайная ошибка, угадал или не угадал правильный ответ в тесте.…Этот ряд можно продолжить и дальше. Казалось бы, тут нет места для математики, – какие уж законы в царстве Случая! Но и здесь вездесущая царица наук – математика – может обнаружить интересные закономерности и спрогнозировать результат.

Учитывая актуальность данной темы, нами проведена исследовательская работа, которую мы назвали «Вероятность успешной сдачи ЕГЭ путем угадывания верных ответов».

Цель исследования – определение вероятности успешной сдачи ЕГЭ путем угадывания правильного ответа.

Предмет исследования — результаты тестовых заданий по русскому языку и обществознанию (как одного из часто выбираемых выпускниками предметов).

Мы выдвинули следующую гипотезу: выбор ответов наугад не может обеспечить успешной сдачи ЕГЭ.

Цель и предмет исследования обусловили выдвижение и решение следующих задач исследования:

1. Найти и изучить теоретический материал по данной теме, используя справочную литературу и ресурсы Интернета.

2. Провести статистический эксперимент (тесты по русскому языку и обществознанию в 10 «А» классе)

3. Проанализировать результаты тестовых работ средствами теории вероятностей.

В курсе математики я изучал элементы теории вероятности, основные понятия и приемы обработки данных. Но для решения данной проблемы мне понадобилось изучить дополнительную литературу, я познакомился с историей развития теории вероятности и подобрал для обработки результатов повторных независимых испытаний формулу Бернулли. Вычислил вероятность успешной сдачи ЕГЭ работы путем угадывания правильного ответа с помощью этой формулы.

1. Теоретическая часть

1.1. Испытание, событие, случайная величина.

Под испытанием (опытом) в теории вероятностей принято понимать наблюдение какого-либо явления при соблюдении определенного комплекса условий, который должен каждый раз строго выполняться при повторении данного испытания. Если то же самое явление наблюдается при другом комплексе условий, то это уже другое испытание.

Когда речь идет о соблюдении комплекса условий данного испытания, имеется в виду постоянство значений всех факторов, контролируемых в данном испытании. Но при этом, как правило, имеет место большое число неконтролируемых факторов, которые трудно или невозможно учесть.

Результаты испытаний можно охарактеризовать качественно и количественно.

Качественная характеристика заключается в регистрации какого-либо явления, которое может наблюдаться или не наблюдаться при данном испытании. Любое из этих явлений называется в теории вероятностей событием.

События делятся на:

Теория вероятностей рассматривает именно случайные события. При этом предполагается, что испытание может быть повторено неограниченное (по крайней мере, теоретически) число раз. Например, выполнение штрафного броска в баскетболе есть испытание, а попадание в кольцо — событие.

Другим примером события, часто приводимым в учебниках по теории вероятностей, является выпадение определенного числа очков (от 1 до 6) при бросании игральной кости.

События в теории вероятностей принято обозначать начальными прописными латинскими буквами А, В, С, …

Случайные события называются несовместными если появление одного исключает появление другого. В противном случае они называются совместными.

Если в результате опыта произойдет хоть одно из некой группы событий, то они образуют полную группу. Появление хотя бы одного события из полной группы – достоверное событие.

Если, по условиям испытания нет никаких оснований предполагать, что один из исходов появляется чаще других, то все исходы являются равновозможными.

Два события называются независимыми, если появление одного из них не изменяет вероятности другого.

Количественная характеристика испытания состоит в определении значений некоторых величин, которыми интересуются при данном испытании (например, число подтягиваний на перекладине или время на беговой дистанции). В силу действия большого числа неконтролируемых факторов эти величины могут принимать различные значения в результате испытания. Причем до испытания невозможно предсказать значение величины, поэтому она называется случайной величиной.

1.2. Вероятность событий.

Вероятность какого либо события – численное выражение возможности его наступления.

В некоторых простейших случаях вероятности событий могут быть легко определены непосредственно исходя из условий испытаний.

Представим себе общую схему таких испытаний.

Пусть испытание имеет n возможных несовместных исходов, т. е. отдельных событий, которые могут появиться в результате данного испытания; причем при каждом повторении испытания возможен один и только один из этих исходов. Кроме того, пусть по условиям испытания, нет никаких оснований предполагать, что один из исходов появляется чаще других, т. е. все исходы являются равновозможными.

Допустим теперь, что при n равновозможных несовместных исходах интерес представляет некоторое событие А, появляющееcя при каждом из m исходов и не появляющееся при остальных n–т исходах. Тогда принято говорить, что в данном испытании имеется п случаев, из которых т благоприятствуют появлению события А.

Вероятность события А равна отношению числа исходов, благоприятствующих событию А, к общему числу всех равновозможных несовместных исходов опыта:

Данная формула представляет собой так называемое классическое определение вероятности по Лапласу, пришедшее из области азартных игр, где теория вероятностей применялась для определения перспективы выигрыша.

Статистическое определение вероятности.

Будем фиксировать число испытаний, в результате которых появилось некоторое событие А. Пусть было проведено N испытаний, в результате которых событие А появилось ровно nN раз. Тогда число nN называется частотой события, а отношение  — частостью (относительной частотой) события.

Замечательным экспериментальным фактом является то, что частость события при большом числе повторений испытания начинает мало изменяться и стабилизируется около некоторого определенного значения, в то время как при малом числе повторений она принимает различные, совершенно случайные значения. Поэтому интуитивно ясно, что если при неограниченном повторении испытания частость события будет стремиться к вполне определенному числовому значению, то это значение можно принять и качестве объективной характеристики события А. Такое число Р(А), связанное с событием А, называется вероятностью события А.

Математически неограниченное число повторений испытания записывается в виде предела (lim) при N, стремящемся к бесконечности ():

Поскольку nN никогда не может превзойти N, то вероятность оказывается заключенной в интервале 

Следует отметить, что приведенное определение вероятности является абстрактным, оно не может быть экспериментально проверено, так как на практике нельзя реализовать бесконечно большое число повторений испытания.

Пусть проводятся независимые испытания, при каждом из которых вероятность события А неизменна. Справедливо утверждение, называемое законом больших чисел или теоремой Бернулли: если N достаточно велико, то с вероятностью сколь угодно близкой к единице, отличие  от Р(А) меньше любого наперед заданного положительного числа или, в символьной записи, . Т.е. много раз бросая монету, мы “почти наверняка” будем получать примерно равные частоты выпадения герба и цифры.

1.3. Теория вероятностей в жизни.

 Игры в кости

Кости — одна из древнейших игр. Инструментом для игры являются кубики (кости) в количестве от одного до пяти в зависимости от вида игры. Суть игры состоит в выбрасывании кубиков и дальнейшем подсчёте очков, количество которых и определяет победителя. Разновидности игры предполагают разный подсчёт очков.

Коды на ….

— сейфах

— телефонные номера

— пароль в социальных сетях (агент, одноклассники и т.д.)

Лотереи

Лотерея — организованная игра, при которой распределение выгод и убытков зависит от случайного извлечения того или иного билета или номера (жребия, лота). Кто из нас не мечтал выиграть в лотерею миллион! Но все мы реалисты, и понимаем, что вероятность такого выигрыша очень мала. Ведь игра в лотерею — это игра с судьбой, попытка поймать удачу; и чем больше выигрыш стоит на кону — тем сильнее ощущения!

Карточные игры

Карточная игра — игра с применением игральных карт, характеризуется случайным начальным состоянием, для определения которого используется набор (колода).

Важным принципом практически всех карточных игр является случайность порядка карт в колоде. Перед использовании той же колоды в следующей игре карты в ней перемешиваются (перетасовываются).

Игровые автоматы

Известно, что в игровых автоматах скорость вращения барабанов зависит от работы микропроцессора, повлиять на который нельзя. Но можно вычислить вероятность выигрыша на игровом автомате, в зависимости от количества символов на нем, числа барабанов и других условий. Однако выиграть это знание вряд ли поможет. Тут все решает Её величество фортуна.

1.4. История  возникновения  и  развития  теории  вероятности.

Замечательно, что эта наука, началом которой были рассуждения об азартных играх, должна стать одним из важнейших предметов человеческого знания.

П.Лаплас [11]

       Развитие теории вероятности как самостоятельной науки началось с писем Паскаля к Ферма в 1654 году.

        В это время шевалье де Мере задал Паскалю два вопроса, касающихся азартных игр. Этим вопросам и посвящены письма Паскаля к Ферма.

         Первая задача де Мере состояла в состояла в следующем: сколько раз надо бросить две игральные кости, чтобы вероятность выпадения двух шестёрок была больше половины? С этой задачей де Мере справился,  Паскаль, обсудив его решение, признал его правильным. Вторая задача оказалась более сложной. Два игрока играют в азартную игру до n выигрышей. Как следует разделить между ними ставку, если игра прервана, когда первый игрок выиграл a партий, а второй b партий, a, b < n?

         Для решения этой задачи Паскаль ввёл основные понятия теории вероятностей. Он отчётливо сознавал, что открыл новую область науки. Это видно из письма Паскаля в Парижскую академию, где он, в частности, писал: “Это учение, объединяющее точность математических доказательств с неопределённостью случая и примиряющее эти, казалось бы, противоречивые элементы, с полным правом может претендовать на титул – математика случайного.”

          Первая книга, посвящённая теории вероятностей, была написана в 1656 году Христианом  Гюйгенсом, знатным голландским дворянином, красавцем, пренебрегавшим развлечениями света ради физики и математики. Она представляла из себя “ рассуждение о приложении теории вероятностей к азартным играм “ и содержала множество изящных и точных расчётов.

В дальнейшем теорию вероятностей развивали: Якоб  Бернулли, английский математик Абрахам де Муавр (1667 — 1754);  в 1764 году были посмертно опубликованы работы малоизвестного английского священника Томаса Байеса, увековечившие его имя. Бюффон, автор знаменитой 36-томной “ Естественной истории ”, расширил область применения теории, построив пример геометрической вероятности (“Игла Бюффона”). Но только в 19 веке теория вероятностей вновь привлекает внимание крупнейших современных математиков, первым из которых следует назвать Лапласа.

          Дальнейшее развитие теории вероятностей связано с великим именем Карла Фридриха Гаусса (1777 — 1855) и Симеона Дени Пуассона (1781 — 1840).

Во второй половине 19 века появилась блестящая плеяда русских математиков. Ведущим среди них были П.Л.Чебышев, А.А.Марков, А.М.Ляпунов. Исследования П.Л.Чебышева продолжили его ученики А.А.Марков и А.М.Ляпунов. Их трудами теория вероятностей стала достаточно строгой и разработанной областью науки.

           Но ещё в ХХ веке большинство учёных не признавало её равноправной ветвью математики. По выражению одного из них, теория вероятностей нечто среднее между математикой, физикой и шаманством. Причиной этого было отсутствие аксиоматического обоснования. В 1900 году на Международном съезде математиков Гильберт составил список важнейших нерешённых проблем математики. Это было своеобразное завещание ХХ веку. В этот список он включил проблему аксиоматического обоснования теории вероятностей.

          Наиболее интересные попытки решить эту задачу предпринимались русским математиком Бернштейном(1917) и эмигрантом из Германии Мизесом, а удалось это сделать в 1933 году советскому математику Андрею Николаевичу Колмогорову.

          Система аксиоматического обоснования А.Н.Колмогорова стала общепринятой и служит твёрдой основой для дальнейшего развития теории вероятностей.    

1.5. О математике Якобе Бернулли

Я́коб Берну́лли (нем. Jakob Bernoulli, 27 декабря 1654, Базель, — 16 августа 1705, там же) — швейцарский математик, старший брат Иоганна Бернулли; профессор математики Базельского университета (с 1687 года). Якоб родился в семье преуспевающего фармацевта Николая Бернулли. Вначале учился богословию, но увлёкся математикой, которую изучил самостоятельно. В 1677 году совершил поездку во Францию для изучения идей Декарта, затем в Нидерланды и Англию, где познакомился с Гуком и Бойлем.

Вернувшись в Базель, некоторое время работал частным учителем. В 1684 году женился на Юдит Штупанус (Judith Stupanus), у них родились сын и дочь.

С 1687 года — профессор физики (позже — математики) в Базельском университете.

1684: штудирует первый мемуар Лейбница по анализу и становится восторженным адептом нового исчисления. Пишет письмо Лейбницу с просьбой разъяснить несколько тёмных мест. Ответ он получил только спустя три года (Лейбниц тогда был в командировке в Париже); за это время Якоб Бернулли самостоятельно освоил дифференциальное и интегральное исчисление, а заодно приобщил к нему брата Иоганна. По возвращении Лейбниц вступает в активную и взаимно-полезную переписку с обоими. Сложившийся триумвират — Лейбниц и братья Бернулли — 20 лет возглавлял европейских математиков и чрезвычайно обогатил новый анализ.

1699: оба брата Бернулли избраны иностранными членами Парижской Академии наук.

В честь Якоба и Иоганна Бернулли назван кратер Bernoulli на Луне.

Научная деятельность

Первое триумфальное выступление молодого математика относится к 1690 году. Якоб решает задачу Лейбница о форме кривой, по которой тяжелая точка опускается за равные промежутки времени на равные вертикальные отрезки. Лейбниц и Гюйгенс уже установили, что это полукубическая парабола, но лишь Якоб Бернулли опубликовал доказательство средствами нового анализа, выведя и проинтегрировав дифференциальное уравнение. При этом впервые появился в печати термин «интеграл».

Якоб Бернулли внёс огромный вклад в развитие аналитической геометрии и зарождение вариационного исчисления. Его именем названа лемниската Бернулли. Он исследовал также циклоиду, цепную линию, и особенно логарифмическую спираль. Последнюю из перечисленных кривых Якоб завещал нарисовать на своей могиле; по невежеству там изобразили спираль Архимеда, см. фотографию справа. Согласно завещанию, вокруг спирали выгравирована надпись на латыни, «EADEM MUTATA RESURGO» («изменённая, я вновь воскресаю»), которая отражает свойство логарифмической спирали восстанавливать свою форму после различных преобразований.

Якобу Бернулли принадлежат значительные достижения в теории рядов, дифференциальном исчислении, теории вероятностей и теории чисел, где его именем названы «числа Бернулли».

«Искусство предположений»

Он изучил теорию вероятностей по книге Гюйгенса «О расчётах в азартной игре», в которой ещё не было определения и понятия вероятности (её заменяет количество благоприятных случаев). Якоб Бернулли ввёл значительную часть современных понятий теории вероятностей и сформулировал первый вариант закона больших чисел. Якоб Бернулли подготовил монографию в этой области, однако издать её не успел. Она была напечатана посмертно, в 1713 году, его братом Николаем, под названием «Искусство предположений». Это содержательный трактат по теории вероятностей, статистике и их практическому применении, итог комбинаторики и теории вероятностей XVII века. Имя Якоба носит важное в комбинаторике распределение Бернулли.

Якоб Бернулли издал также работы по различным вопросам арифметики, алгебры, геометрии и физики.

1.6. Формула Бернулли

     Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А. Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рn(m) того, что в результате n испытаний событие А наступило ровно m раз. Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей.  Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. Пусть в результате n  независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие  с вероятностью q . Обозначим Ai – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны. Если в результате  опытов событие А наступает ровно m   раз, то остальные n — m раз это событие не наступает. Событие А может появиться m  раз в n  испытаниях в различных комбинациях, число которых равно количеству сочетаний из n  элементов по m . Это количество сочетаний находится по формуле:  

     Вероятность каждой комбинации равна произведению вероятностей:  pmqn-m

 Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли: Рn(m)=Сnmpmqn-m

 Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.

При решении вероятностных задач часто приходиться сталкиваться с ситуациями, в которых одно и тоже испытание повторяется многократно и исход каждого испытания независим от исходов других. Такой эксперимент называется схемой повторных независимых испытаний или схемой Бернулли. Пусть в результате испытания возможны два исхода: либо появится событие А, либо противоположное ему событие. Проведем n испытаний Бернулли. Это означает, что все n испытания независимы; вероятность появления события A в каждом отдельно взятом или единичном испытании постоянна и от испытания к испытанию не изменяется (т.е. испытания проводятся в одинаковых условиях). Обозначим вероятность появления события A в единичном испытании буквой p, т.е , а вероятность противоположного события (событие А не наступило) — буквой. Тогда вероятность того, что событие А появится в этих n испытаниях ровно k раз, выражается формулой Бернулли

Определить вероятность получения положительной отметки за тестовую работы можно по формуле Бернулли. «Наше представление… было бы только иллюзией, если бы данные опыта не подтверждали правоту сделанных предположений…»(А.Н. Колмогоров).

2. Экспериментальная часть.

Экзаменационные работы по различным предметам имеют свои особенности и во многих из них, в том числе по русскому языку и обществознанию в части А даны задания с выбором ответа. Мы намеренно взяли для исследования именно эти предметы русский язык как один из обязательных (вы конечно же спросите: «почему я не выбрал математику?» Да потому, что с 2010 года часть А то есть та часть в которой нужно было выбрать вариант правильного ответа отменили) и предмет по выбору — обществознание (как наиболее часто выбираемый выпускниками предмет). Среди нерадивых учеников возникает вопрос: «А нельзя ли выбрать наугад ответ и тем самым преодолеть так называемый порог на экзамене?»

Я провел  опрос среди обучающихся 10 класса: можно ли практически угадать 17 заданий из 30, т.е. сдать ЕГЭ по русскому языку без подготовки. Результаты такие: 53,2% респондентов считают, что смогут сдать экзамен указанным выше способом.

Я решил проверить, правы ли они? Ответить на этот вопрос можно путем использования элементов теории вероятностей.

Русский язык.

По данному предмету тест включает 39 заданий типа А, В и С, из которых 30 заданий типа А с выбором ответа из 4-х предложенных. Для того, чтобы пройти порок на экзамене в 2014 году достаточно было в  части А правильно выполнить 17 заданий. Каждое задание имело 4 варианта ответов, один из которых правильный. Определить вероятность получения положительной оценки на экзамене можно по формуле Бернулли:

Схема Бернулли описывает эксперименты со случайным исходом, заключающиеся в следующем.[5,]Проводятся n последовательных независимых одинаковых экспериментов, в каждом из которых выделяется одно и тоже событие А, которое может наступить или не наступить в ходе эксперимента. Так как испытания одинаковы, то в любом из них событие А наступает с одинаковой вероятностью. Обозначим ее р = Р(А). Вероятность дополнительного события обозначим q. Тогда q = P(Ā) = 1-p

Пусть событие А – это правильно выбранный ответ из четырех предложенных в одном задании первой части. Вероятность события А определена как отношение числа случаев, благоприятствующих этому событию (т.е. правильно угаданный ответ, а таких случаев 1), к числу всех случаев (таких случаев 4). Тогда p=P(A)= и  q=P(Ā)=1-p=.

Вероятность получения положительной оценки:

=  =119759850

0,00163*100%0,163%        

Таким образом, вероятность благополучного исхода примерно равна 0,163%!

На примере варианта теста  ЕГЭ 2014 года я предложил обучающимся 10 «А» класса выбрать ответы путем угадывания. И вот, что у меня получилось.

Результаты статистического эксперимента по русскому языку

Средний балл по классу составил 8,7. Наибольшее количество баллов набрала Чудаева Диана — 16, наименьшее – Сапожников Эдуард(3 балла). 

Обществознание

Первая часть варианта ЕГЭ 2014 года по обществознанию содержит 20 заданий с выбором ответа, из которых только один верный. Определим вероятность получения положительной оценки. Рособрнадзором установлен  минимальный первичный балл по обществознанию – 15.

Вероятность получения положительной оценки:

=  =15504

0,000003*100%=0,0003%        

Таким образом, вероятность благополучного исхода примерно равна 0,0003%!

Я попросил обучающихся 10 «А» класса угадать ответы по обществознанию.

Результаты статистического эксперимента по обществознанию

 Средний балл составил 4,76 балла. Самый высокий балл — 9, самый низкий — 2. Таким образом, ни один обучающийся не смог набрать нужное количество баллов.

Выводы

Результаты практических экспериментов и их теоретическое обоснование подтверждают правильность выдвинутой гипотезы. Ни один из учащихся не смог угадать количество правильных ответов, необходимых для успешной сдачи ЕГЭ.

Данные исследования позволяют сделать вывод, что только планомерная, вдумчивая и добросовестная учеба в школе позволит учащимся успешно сдавать экзамены в форме ЕГЭ.

Заключение

Я учусь в 10 классе, и наследующий год мне тоже предстоит сдача экзаменов в форме ЕГЭ. Я думаю, что цель моей работы – математически  доказать, что вероятность угадать верные ответы на ЕГЭ очень мала,  — достигнута. Опытным путём подтверждена гипотеза: выбор ответов наугад не может обеспечить успешной сдачи ЕГЭ. А значит к экзаменам надо готовиться, а не рассчитывать на авось. Некоторые думают: наудачу сдам. Моя работа совершенно разбивает их надежды полученными мною результатами. Надеюсь, что не только я, но и мои одноклассники, друзья и сидящие здесь в зале  более ответственно отнесутся к предстоящим экзаменам в форме тестирования.  

Рекомендации

Результаты данного исследования можно рекомендовать для сообщения обучающимся старших классов.

Литература

1. АлимовШ.А.Алгебра и начала математического анализа.10-11 классы:учеб.для общеобразовательных учреждений: базовый уровень. М.:Просвещение,2010.
2. Бродский Я.С. «Статистика. Вероятность. Комбинаторика»-М.: Оникс; Мир и Образование, 2008 г.
3. Бунимович Е.А., Суворова С.Б. Методические указания к теме «Статистические исследования»//Математика в школе.-2003.-№3.
4. Гусев В.А. Внеклассная работа по математике в 6-8 классах.-М.:Просвещение,1984.
5. Лютикас В.С. Факультативный курс по математике: Теория вероятностей.-М.:Просвещение 1990.
6. Макарычев Ю.Н. Алгебра: элементы статистики и теории вероятностей: учеб. пособие для учащихся 7-9 кл. общеобразоват. учреждений-М.:Просвещение,2007.
7. Ожегов С.И. Словарь русского языка:.М.:Рус.яз.,1989.
8. Панов Э. Введение в статистику//Математика(приложение к газете «Первое сентября»),2004,№25-26.
9. Семеновых А. Комбинаторика//Математика(приложение к газете «Первое сентября»),2004,№16,17.
10. Федосеев В.Н .Элементы теории вероятностей для VII-IX классов средней школы.//Математика в школе.-2002.-№4,5.
11. Что такое. Кто такой: В 3 т.Т.1 – 4-е изд. перераб.и доп.-М.:Педагогика-Пресс,1997.

Ресурсы:

1. http://www.blagodeteleva-vovk.com/theory/never.htm
2. http://habrahabr.ru/blogs/gtd/101695
3. http://www.prosto.ws/2010/03/02/ot-teorii-veroyatnosti-k-teorii-vsego
4. http://www.mathematics.ru/courses/algebra/content/chapter4/section3/paragraph1/theory.html
5. http://ru.wikipedia.org/wiki
6. www.fipi.ru

Вообще не думать об экзаменах до 9-го класса, а после ОГЭ обнаружить себя с тройками по всем предметам? Нормально. И даже не смертельно. А вот как сдать ЕГЭ, если ты тупой? От этого экзамена зависит куда больше, чем от не самой лучшей оценки по ОГЭ. Итак, ситуация: 10-11 класс, а вы не знаете ничего. Что делать? Изучать нашу стратегию подготовки к ЕГЭ, конечно же!

Как сдать ЕГЭ, если ничего не знаешь, и на что надеяться

Прежде чем начать полноценную подготовку к экзаменам, разберитесь, с какой точки вы начинаете и на что хотите претендовать в конце. Сначала выберите два предмета, которые вы точно будете сдавать на ЕГЭ: русский, который считается обязательным, и второй предмет, необходимый для поступления на конкретное направление.

Важно: в 2021 году ЕГЭ по математике не был обязательным из-за коронавируса. Но в 2022 его, скорее всего, снова придется сдавать, чтобы получить аттестат. Следите за обновлениями!

Вы начинаете с минимума, но помните, что предметов может быть больше. Обычно вузы требуют от абитуриентов баллы по трем предметам.

Попробуйте написать варианты ЕГЭ прошлого года по каждому из выбранных предметов. Найти их можно, например, на этом сайте. Когда вы прорешаете задания, сверьтесь с ответами (только не делайте этого заранее!) и переведите первичные баллы во вторичные. Суммируйте, а потом воспользуйтесь любым калькулятором ЕГЭ (у многих вузов есть свои), чтобы понять, на какие программы вы уже проходите даже после первой попытки.

Еще один отличный вариант понять, как сдать ЕГЭ, если ничего не знаешь, – прийти на наш бесплатный пробный урок. Наши преподаватели расскажут тебе о лайфхаках, с помощью которых ты сможешь решать задания автоматически. И не надо ничего зубрить! А еще ты разберешься в особенностях экзамена и сможешь составить свою стратегию подготовки к ЕГЭ. Записывайся!

Определитесь с вузом

Узнав баллы, позвольте себе помечтать. На каком направлении вам было бы интересно учиться? В каком городе? Не обязательно думать только о Москве и Санкт-Петербурге. Отличные вузы есть в Казани, Владивостоке, Новосибирске и других крупных городах России. А проходные баллы в них значительно ниже!

Ориентируясь на результат калькулятора ЕГЭ, выберите вуз, к поступлению в который вы находитесь ближе всего. Его проходной балл станет вашей первой планкой. Установите и следующую цель – проходной балл вуза покруче, который будет вас мотивировать.

Разберитесь, что такое ЕГЭ

Не так страшен черт, как его малюют. ЕГЭ – экзамен, к которому реально подготовиться. Гарантию успешной сдачи вы получите, изучив кодификатор и структуру КИМа. Варианты делятся на две части – тестовую и письменную. К первой подготовиться проще: главное знать, какие типы заданий вообще могут быть по каждому из номеров. Тогда на экзамене любой из тестовых вопросов не станет для вас неожиданностью.

Выберите стратегию подготовки к ЕГЭ

Набрав максимальные 34 первичных балла за первую часть по русскому языку, вы получите 59 вторичных. Еще 3 за вторую часть – у вас уже «четвёрка» в переводе на традиционную систему оценок. Поэтому сдать ЕГЭ, сфокусировавшись только на первой части, более чем реально. Попробуйте довести ее до автоматизма, постоянно отрабатывая материал на специальных порталах:

•  «Решу ЕГЭ»;
• официального сайта ФИПИ;
• «Незнайка».

Благодаря этому у вас появится отличная и действенная стратегия подготовки к ЕГЭ.

Обращайтесь за помощью

Подготовиться к экзамену в одиночку непросто. А уж сдать ЕГЭ, если ничего не знаешь, тем более. Поэтому не стесняйтесь обращаться за помощью к другим людям.

Во-первых, найдите того, кто будет также заинтересован в подготовке. Это может быть друг или подруга, которым тоже будет нужно подтянуть знания к ЕГЭ. Вместе вы сможете делиться успехами, мотивируя друг друга, и повторять материал.

Во-вторых, можно попросить помощи у одноклассников-отличников или школьных учителей. Что-то непонятно? Спрашивайте у тех, кто знает наверняка.

Найдите курсы

Попробуйте отслеживать свой прогресс с помощью дневника: помечайте, какие задания вы стали решать, а с чем до сих пор есть трудности. Если за два месяца подготовки положительных изменений будет не очень много, подумайте, не пора ли искать курсы для подготовки к ЕГЭ.

А если все-таки пора, то обязательно заглядывайте к нам на бесплатный пробный урок. На занятии тебе объяснят, как решать самые непонятные задания. А еще ты узнаешь, как не попадаться в ловушки экзаменаторов. Проще говоря, мы расскажем тебе, как сдать ЕГЭ, если ты тупой (а все потому, что мы не верим, что ты тупой) 🙃

Помните, ЕГЭ – не единственный вариант

Онлайн-образование 

Можно оплатить учебу в онлайн-университете, куда опять же принимают без всяких экзаменов и даже аттестатов. Правда, за качество образования в таких заведениях никто не ручается, а реальных дипломов они почти не выдают. Максимум – о дополнительном образовании.

Колледж 

Если подготовка к ЕГЭ все-таки кажется слишком трудной, не стоит забывать, что получить профессиональное образование, а затем и поступить в вуз – кстати, в обход ГИА, – можно через колледж или училище. Главное, чтобы у вас на руках был аттестат, который позволит участвовать в конкурсе на поступление. И все, никакие отдельные экзамены не потребуются. (И не надо думать о том, как сдать ЕГЭ, если ты тупой 😉)

Пойти работать

Наконец, можно научиться чему-то на реальной работе. Отправляйтесь во взрослую жизнь с низкого старта и принимайтесь за трудоустройство уже после 9 класса. Пожалуй, это самый радикальный и ненадежный путь, который, впрочем, может стать спасительным для тех, кто просто не хочет учиться в стандартной образовательной системе.

10 класс позади. Наступило лето и последние школьные каникулы. Давайте посмотрим на истории тех, кто успешно сдал ЕГЭ — уже летом они действовали не так, как большинство честно отдыхающих школьников. Чем отличалась их подготовка? Какие ошибки совершают 99% школьников? Я задала вопросы школьникам, которые сдали ЕГЭ на 100 баллов. Их советы и рекомендации собраны в этой статье.

В прошлом году ЕГЭ сдавали более 700 тысяч человек, но среди них всего 6729 сдали хотя бы один из экзаменов на 100 баллов.

Что значит «всего», скажет обычный школьник? Разве сдать ЕГЭ на высокие баллы так легко? Конечно же, нет – придётся приложить усилия. Но давайте разберёмся, так ли страшен ЕГЭ, как его малюют. ЕГЭ – это набор типовых заданий. Так говорят и эксперты, и выпускники, успешно его сдавшие. Основная проблема кроется в том, что многие школьники допускают одни и те же ошибки в подготовке. Но что же это за ошибки и как их избежать?

1. Что сдавать будем

До начала подготовки нужно, конечно же, определиться с предметами, которые вы собираетесь сдавать. Большинство успешно сдавших ЕГЭ делают это не летом, а еще в 9 – 10 классах.
После того как вы определились с предметами, определите свой уровень знаний — для этого достаточно пройти тест на сайте “Решу ЕГЭ”.

2. В каких случаях брать репетитора

Теперь когда вы осознаете весь объем работы, определитесь, нужен ли вам репетитор. Кто-то говорит, что невозможно подготовиться к ЕГЭ без репетитора, но примеры выпускников, которых я опросила, доказывают обратное.

Причины из-за которых обращаются к репетитору в каждом случае свои. Для некоторых репетитор выполняет роль наставника — он поможет правильно рассчитать время подготовки, подбодрит в моменты стресса, не даст расслабиться. Кому-то он нужен, только чтобы подтянуть слабые места. Так что вы должны решить, справитесь вы самостоятельно или нет, и какие функции в вашем случае будет выполнять репетитор.

Как выбрать репетитора — материал для отдельной статьи. Буду рада, если вы в комментариях поделитесь своими примерами.

3. Деньги на ветер

Неочевидный тезис, но по утверждению школьников подготовительные курсы в университетах, если это касается ЕГЭ – пустая трата денег.

Существует ошибочное мнение, что подобные курсы обеспечат вам высокие баллы на экзамене. Однако преподаватели вузов не имеют отношения к школьной программе, и материал, который там дают, вряд ли встретится на ЕГЭ. Заниматься подготовкой со школьным учителем или репетитором, который уже набил руку в этом деле, гораздо продуктивнее.

4. Стерпится — слюбится

Некоторые ребята боятся менять репетиторов, даже если кажется, что они не подходят – неудобно как-то перед человеком, а вдруг новый будет ещё хуже. Вот, что по этому поводу говорит Анна Панасян, 100 баллов по химии и по русскому:

«Начала я свою подготовку еще в далеком 9 классе, тогда я ходила к репетитору 1 раз в неделю, но через год я поменяла учителя, потому что мне совершенно не нравился тот подход, которым она пыталась научить меня биологии, так как через неделю я забывала абсолютно все, что мы с ней проходили. Итак в 10 классе я пошла к другому репетитору, и ни капли не пожалела.

Совет одиннадцатиклассникам: не бойтесь менять учителей, в этом нет ничего страшного».

5. На ощупь в темноте или всё под контролем

Знаете, что может убить к чертям всю подготовку? Отсутствие плана. Сегодня вам хочется готовиться, завтра нет, потом вы забросили все на неделю… А перед экзаменом вдруг вспомнили, что ещё кучу всего нужно повторить. Чтобы успешно подготовиться к экзамену, Катя Рябинина, 100 баллов по английскому за олимпиаду (без олимпиады 95), распределяла время таким образом:

«У меня немножко бзик с тем, чтобы правильно распределять время, и в какой-то момент я поняла, что по обществознанию мне надо очень много запомнить. Я делала такую табличку в Google Sheets, там у меня были записаны темы, а напротив темы в каждой ячейке я писала дату, в которую я эту тему буду повторять. Ячейку я закрашивала цветом в зависимости от того, насколько хорошо я знаю материал. В моём случае повторить тему это было полностью от руки переписать конспект по память, не открывая учебник. Ближе к делу я понимала, где у меня остаются проблемные места и тратила время на то, что действительно проседает».

6. Барьеры для прокрастинации

Когда речь заходит об откладывании дел на потом, любят приплетать отсутствие мотивации. Но мотивация – очень абстрактная вещь. Возможно, дело в том, что нам всем сложно концентрироваться на чём-то одном в течение долгого времени. И тут на помощь приходит… наблюдение за собой. Например, некоторым людям сложно заставить себя что-то делать в домашней обстановке. Решение этой проблемы от Анны Панасян:

«Я поняла, что мне проще делать всё в школе. Там именно рабочая обстановка. А дома мне тяжело заставить себя что-то делать. Поэтому в школе я прорешивала как можно больше заданий».

Еще две рекомендации от Ирины Чебесовой, 91 балл по информатике:

«Когда ты занимаешься, каждый час-полчаса надо делать перерывы — как минимум, зарядка для глаз, разминка для тела, чтобы снять напряжение. Также надо переключаться между предметами, иначе голова становится тяжёлой и воспринимать информацию тяжелее».

Ирина на вручении золотой медали.

7. Не количество, а качество

Один из самых распространённых советов при подготовке – нарешивайте тесты. И чем больше, тем лучше. А что, если я скажу, что это не работает?

Не работает, когда вы делаете это бездумно или решаете непонятные задания наугад: «Ну, вроде, ответ совпал, вдруг пронесёт…» На экзамене может так не повезти.

«ЕГЭ — набор типовых заданий. Надо не думать, как решается каждая конкретная задача, а вырабатывать общие модели решения. Если ты не уверен, какой здесь ответ, не надо тыкать наугад — пожалуйста, разберись, как решается задание, посмотри теорию, потому что на экзамене может так не повезти».

— говорит Ирина Чебесова.

8. Разбираем ошибки, а не лезем в бутылку

Бывает так: сегодня решаешь вариант, и всё получается, задания щёлкаешь, как орешки, и уже грезишь мыслями о поступлении. А на следующий день вообще не идёт — ошибки в простейших заданиях.

Не обращать внимание на эти ошибки — будет самой большой ошибкой. Чтобы слабых пробников не было, собирайте статистику ваших ошибок. Разбирайте задания, в которых вы допустили ошибки, даже если они кажутся элементарными. А чтобы узнать, как вы усвоили материал, сравните эту работу со следующей.

9. Облом на финишной прямой

Весь год вы упорно трудились. Занимались с репетитором, разбирали непонятные задания, вели конспекты. Даже прохожих распугивали, крича по ночам в окно “Халява, приди!” Но даже отличники совершают эту досадную ошибку — не учатся правильно оформлять задания.

Если вы не вписываетесь в формат и записываете решение так, как сердцем навеяло, то есть шанс не сдать экзамен. Оставьте творческие порывы на потом — организаторы ЕГЭ ценят, когда всё делается по образцу.

«На экзамене по биологии в последней задаче я допустила дурацкую ошибку. Её решение и все вычисления нужно было ещё раз переписать в ответ. Я этого не сделала. И хоть я решила задачу правильно, мне её не засчитали — из-за этого у меня минус два первичных балла, а во вторичных около пяти. Это очень много!»

— говорит Эстер Киреева, 87 баллов по русскому.

10. “Я каменщик, работаю три дня без зарплаты…”

Решай больше. Засиживайся допоздна. Жертвуй сном и приёмами пищи. Если ты, конечно, хочешь отбросить коньки под конец учебного года.

Ни в коем случае не стоит пренебрегать отдыхом. Простые физические упражнения и зарядка для глаз поможет снять напряжение и дольше сохранять концентрацию. Полноценный сон также важен — каждый, наверняка, слышал про это.

Если вы чувствуете, что сил больше нет, не бойтесь уйти в отрыв — на неделю, например, во время каникул, выбросьте из головы мысли о подготовке. Запланировать подобный перерыв вы можете уже сейчас.

Эстер Киреева говорит:

«У нас некоторые ребята улетали на отдых в середине учебного года и на неделю забывали про учёбу и подготовку. Это хорошо разгружает голову».

Такая перезагрузка поможет ринуться в бой с новыми силами. Главное, не растянуть этот отдых на месяц.

Подводя итоги

Итак, как же сдать ЕГЭ и не сойти с ума во время подготовки?

1. После выбора предметов для сдачи определяем уровень подготовки и решаем, нужен ли репетитор. Не стоит бояться менять репетитора, если что-то не срослось.
2. Затем составляем план подготовки в специальном документе. Там же можно вести статистику ошибок.
3. Наблюдаем за собой — в какое время и где работа идёт наиболее продуктивно, а где и в каких ситуациях случаются завалы.
4. Не забываем про регулярный отдых, полноценный сон и питание. В середине учебного года делаем недельный перерыв, во время которого можно полностью забыть про экзамены. Это поможет набраться сил для дальнейшей подготовки.
5. Непонятные задания прорабатываем. Решаем не интуитивно, а вырабатываем общие модели решения. Помним, что ЕГЭ — набор типовых заданий. И набиваем руку в правильном оформлении ответов на бумаге.

Не стоит паниковать из-за сдачи ЕГЭ. Да, это не просто очередное испытание, как говорят многие — от этого во многом зависит то, как сложится ваша профессиональная карьера. Но справиться с этим испытанием в ваших силах.

Удачи, выпускник!

Как сдать ЕГЭ по математике? Наверняка этим вопросом задавались многие ученики 11 класса и их родители. Чтобы дать ответ на этот вопрос, нужно понять для чего нужен ЕГЭ по математике, и что от него зависит. Как правило, этого достаточно.

Прежде всего, ученик, который сдает этот экзамен, показывает знания, приобретенные им к концу обучения в школе. Кроме того, вне зависимости от конкретной школы или ее месторасположения, это позволяет всем поступающим в вузы иметь равные условия при приеме. Помимо этого, на ЕГЭ по математике осуществляется строгое наблюдение за учениками, чтобы они не могли списать решение или воспользоваться другими недобросовестными методами сдачи экзамена. Как правило, при входе в аудиторию перед экзаменом проводится проверка на наличие шпаргалок и прочих инструментов, позволяющих «нечестно» сдать экзамен, а также ведется жесткий контроль во время самой сдачи. Иначе говоря, главной задачей ЕГЭ является определение действительного уровня знаний ученика.

Теперь давайте попробуем представить себе ситуацию в будущем, после того, как будут сданы все экзамены. Вы получаете то, что так хотели — свои заветные высокие баллы за ЕГЭ по математике, ради которых вы так много работали. Вы подаете документы в приемную комиссию вуза вашей мечты. И вам не нужно сомневаться в том, что вы поступите туда без проблем, так как ваших баллов вполне достаточно для зачисления. Правда, может оказаться так, что это вуз, где нужно сдавать дополнительное вступительное испытание, но и его вы сдадите без проблем, ведь в вашем запасе огромный багаж знаний. И вскоре начинается веселая студенческая жизнь, интересные лекции, зачеты и экзамены, ну и, разумеется, праздники, да много чего. И жизнь можно считать вполне удавшейся, ведь вы выбрали свою любимую специальность.

Помечтали? А теперь давайте вернемся на землю и хорошо подумаем о том, как этого можно достичь. Как сдать ЕГЭ и при этом получить хорошую оценку? Не стоит раньше времени вешать нос, так как у этой задачи существует решение! На самом деле, вариантов не так уж много, и все они просты и понятны. Если у вас есть какие-нибудь свои, то, пожалуйста, поделитесь, был бы вам очень благодарен. Ну что же, посмотрим на каждый вариант в отдельности.

Расставить ответы наугад

Существует легенда о том, что одному мальчику удалось сдать ЕГЭ, расставив ответы в бланках (КИМах) наугад. При этом он был таким счастливчиком, что сдал экзамен на отлично! Представьте себе, что такие фантастические истории, как это ни странно, можно услышать из уст не только учеников, но также и их родителей! Однако, как показывает практика, эти истории не являются ничем другим, как выдумкой тех, кто их рассказывает.

Предположим даже на секундочку, что эти рассказы — чистая правда. Счастливчик-абитуриент поступает в вуз, он совершенно уверен в том, что все сложится как надо. Но что, если все пойдет не так гладко, как он планировал, и его результаты решат перепроверить? Скорее всего, все его результаты будут аннулированы, поэтому от поступления в вуз придется отказаться. В общем, мягко говоря, нельзя назвать этот способ очень надежным.

Сдать ЕГЭ по математике, используя шпаргалку или телефон

Это может сработать, но далеко не всегда. Можно попробовать списать или использовать заранее заготовленные шпаргалки. Это классический вариант сдачи экзаменов некоторыми учениками, с которым все мы хорошо знакомы. Шпаргалки для сдачи контрольных и экзаменов писали и пишут многие, и по разным предметам. А при сдаче ЕГЭ по математике в последнее время начинают применяться самые разные и неожиданные методы: это и обычные шпаргалки записанные на простой бумаге, мобильные телефоны, известные теперь уже всем невидимые наушники и т. п.

Но использовать все эти средства удается далеко не всегда, из-за того, что в последнее время ужесточился контроль процедуры сдачи экзаменов их организаторами. Разумеется, полагаться на эти методы не стоит. При этом также важно учитывать возможность отстранения от сдачи экзаменов. А после того, как вас заметят за использованием этих средств, хорошие результаты вы уже навряд ли когда-нибудь получите.

Выучить математику, чтобы сдать ЕГЭ

А вот это действительно работает. Это самый надежный метод, который позволяет сдать ЕГЭ по математике! Да, да, все очень просто! Нужно как следует изучить материал! Хотя для этого придется хорошо постараться. Придется полистать учебники, запастись терпением и начать изучать теорию, решать разного рода задачи. Как репетитор по математике и физике заявляю, что это очень сильно поможет вам на экзамене, ведь у вас в запасе будут реальные знания.

В первую очередь нужно обратиться к учебникам по математике. Но при этом нужно помнить, что учебник должен соответствовать экзамену. Есть множество прекрасных классических пособий («Математика абитуриенту», В. В. Ткачук; «Математика. Задачи с ответами и решениями», И. Н. Сергеев), но есть и подделки, с которыми лучше не иметь дела. При подготовке также могут помочь сайты и тематические форумы в интернете, популярность которых растет с каждым днем.

Кроме этого, существуют всевозможные курсы для подготовки к экзаменам. Также вы можете нанять репетитора по математике и физике. Это обычно дает более действенный результат, так как опытный педагог знает все детали и нюансы подготовки к экзаменам. Индивидуальные занятия с репетитором очень важны, так как на них вы можете задавать вопросы преподавателю лично и сразу же получать ответы, выявить свои слабые места и устранить пробелы в знаниях. Но и занятия в школе бывают полезны, так как именно на них дается тот материал, который будет использован при сдаче экзамена. Не стесняйтесь задавать своему учителю любые интересующие вас вопросы, просить помощи в том, в чем вы не уверены.

Как видите, есть множество способов, позволяющих подготовиться к экзаменам, но ни один из них не подействует, если сам ученик не проявит желания заниматься. Можно сколько угодно ходить по репетиторам или сидеть в интернете, но если вы сами не проявите интерес, не будете стараться уложить в голове эти знания, никакой из этих методов не поможет. Поэтому главное – это ваше желание получить знания, ведь репетитор не ответит за вас на экзамене. А качественное образование позволит получить хорошую профессию и станет залогом успешной жизни.

Репетитор по математике и физике
Сергей Валерьевич

Советы стобалльников

Выпускники, которым удалось сдать ЕГЭ на сто баллов, составили список ценных советов. Эти рекомендации помогли им и будут эффективны для многих старшеклассников:

1. Не стоит слепо полагаться на популярные пособия для подготовки к экзамену. Многие школьники скупают все учебники с многообещающими названиями и начинают делать все задания подряд. Если на подготовку не выделен год, стоит начать с выполнения самых сложных заданий и прорабатывать то, что дается тяжелее всего.
2. Следует разобраться с критериями оценки ЕГЭ и понять верную структуру ответов.
3. Очень полезно создать свой «банк аргументов» для сочинений. Это особенно пригодится тем, кому сложно дается писать сочинения. Нужно выделить темы, которые будут встречаться на экзамене, например: природа, семья, любовь. По каждой из них можно найти анализ проблем и запомнить основные моменты и клише.
4. Стоит максимально рационально использовать оставшееся время и полностью посвятить его подготовке к ЕГЭ. Лучше временно игнорировать соблазны и отвлечения, своими делами можно будет со спокойной душой заняться после сдачи экзамена. Но и забывать об отдыхе тоже не стоит, не нужно пренебрегать полноценным сном. Мозг работает гораздо продуктивнее, когда голова свежая, а тело отдохнувшее.

Перед самым экзаменом необходимо быть максимально расслабленным.

Многие ребята сдают ЕГЭ гораздо хуже, чем могли бы на самом деле, именно из-за волнения. Чтобы набрать хороший балл, перед сдачей лучше вообще не думать о ЕГЭ. Войдя в кабинет, можно посмотреть в окно, послушать, как поют птички, и подумать о том, что все события в жизни происходят только к лучшему.

Экстренные рекомендации

Но бывают ситуации, когда до экзамена осталось всего пару недель, а старшеклассник сидит и думает: «как сдать ЕГЭ, если ты тупой». Школьнику кажется, что он абсолютно ничего не знает и времени на подготовку слишком мало. Однако даже за такой короткий срок можно многое сделать, например:

1. Чтобы сдать математику, нужно выполнить всего 5 базовых заданий, и это вполне реально, если потратить на отработку заданий каждого типа по 1−2 дня. Школьнику стоит помнить, что он учился целых 11 лет, делал уроки, писал контрольные работы и далеко не всегда получал за это двойки, иначе ему бы не удалось добраться до ЕГЭ.
2. При подготовке к экзамену по русскому языку не нужно игнорировать определенные типы заданий, например, сочинение. За письменную работу можно набрать нормальный балл, если просто корректно выразить свою позицию, написать нужное количество слов и не допускать фактических ошибок. В 9 классе школьники уже пережили итоговую аттестацию и ничего страшного не произошло, так что не стоит себя недооценивать.

Главное, что нужно понимать при подготовке к экзамену по любому предмету, будь то алгебра, биология, обществознание, история, информатика или химия — нужно избавиться от волнения и поверить в себя. Стоит взять себя в руки и начать готовиться как можно раньше. Да, никто не говорил, что будет легко, любая серьезная работа протекает трудно, но это того стоит.

Ответы на популярные вопросы

Существует ряд вопросов, с которыми стоит разобраться до экзамена. Список того, что следует знать выпускникам:

1. Бывает, старшеклассник решает сдавать определенные предметы и указывает их в своем заявлении, но потом решает остановиться на других дисциплинах. Выбирать дополнительные экзамены можно только до 1 февраля, но разрешено поменять предметы по уважительной причине, если до экзамена осталось минимум 2 недели и с позволения комиссии. Например, уважительная причина в такой ситуации — это когда выбранный университет меняет дисциплины в списке вступительных экзаменов. Если в феврале ученик выбрал несколько предметов про запас, он имеет право не идти на те экзамены, которые ему не нужны.
2. Не прийти на ЕГЭ можно только по уважительной причине, например ввиду болезни. Тогда экзамен позволят сдать в резервный день. Уважительную причину необходимо документально подтвердить, иначе посетить экзамен в резервное время не позволят.
3. Если школьник вообще не сможет сдать русский и базу по математике, ему не дадут школьный аттестат, но позволят пересдать эти предметы на следующий год. Экзамен по выбору, пропущенный по неуважительной причине, тоже можно сдать через год.
4. Проверка результатов обычно занимает не более 2 недель. Их можно узнать в онлайн-режиме по регистрационному коду, например, на портале «Госуслуги». Проверкой каждой работы занимается несколько специалистов. Тестовую часть проверяет компьютер. Эксперты просматривают обезличенные бланки, которые распределяются между специалистами автоматически. Никто не знает, чью именно работу он проверяет.
5. Пытаться договориться с членами комиссии и давать взятки — очень рискованно и противозаконно. Никто не гарантирует, что подобные действия дадут желаемый эффект, проверка результатов ЕГЭ происходит под жестким контролем. Если кто-то узнает об этой ситуации, все ее участники будут наказаны, а экзамен не засчитают.
6. Если ученик несогласен с поставленными баллами, можно подать апелляцию. Это возможно сделать в течение двух дней после того, как стали известны результаты. Апелляцию разумно требовать, если школьник уверен, что, например, сочинение было написано просто безупречно. Подавать апелляцию на тест не стоит. Максимум, чего можно добиться — узнать, что компьютер не так прочитал знак, но такой шанс минимален. Бывает, что после апелляции баллы уменьшают, так что лучше хорошо подумать перед тем, как привлекать внимание к выполненной работе.

Незнание правил не освобождает от ответственности. Перед экзаменом стоит убедиться, что старшекласснику известны все подробности и нюансы проведения ЕГЭ.

Важные предостережения

Мошенники нередко предлагают купить ответы экзамена, но это ложные обещания. Утечка результатов полностью исключена. Никто не знает, какие вопросы будут на ЕГЭ, до начала выполнения работы. Встречались случаи, когда родители школьников приобретали ответы за 50 тыс. р. и больше, но не находили ни единого соответствия.

На экзамен нельзя брать телефон. На входе в место проведения экзамена будет стоять металлоискатель.

Даже если школьнику удастся пронести телефон, воспользоваться им вряд ли удастся. При этом старшеклассник рискует, что его выгонят с экзамена, результаты не засчитают, на пересдачу не пустят, а вдобавок еще и выпишут штраф.

Не следует рассчитывать и на помощь комиссии. Допустимо задавать вопросы только касаемо заполнения бланка. Школьнику громко и четко ответят, подозвать к себе специалиста и шепотом попросить помочь не удастся, да и смысла в этом мало, в комиссии сидят административные работники или преподаватели по другим предметам.

Во время написания работ идет видеотрансляция. За экспертами следят общественные наблюдатели, прокуратура и Рособрнадзор. Если кто-то решится оказать помощь ученику, то будет оштрафован. Все максимально строго.

Крайние меры

Не стоит брать с собой шпаргалки и телефон. Вероятность, что удастся списать или написать сообщение знакомому преподавателю, минимальна, а вот риск огромный. Но некоторые выпускники твердо решили сдать ЕГЭ любой ценой, поэтому чтобы операция не обернулась полным провалом, стоит прочитать и список рекомендаций на самый крайний случай. Если ученик твердо решил взять на экзамен шпаргалки, телефон и наушники, ему не совсем ясно, куда это прятать. Возможны следующие варианты:

1. Одежда. Парням лучше всего надеть пиджак с внутренними глубокими карманами. Если члены комиссии попросят его снять, стоит послушаться, чтобы у них не возникло никаких подозрений. Потом можно надеть пиджак опять, сославшись на холод, например. Девушка может надеть опять же жакет похожего типа и юбку со скрытыми карманами.
2. Шпаргалки лучше всего писать в маленьком компактном блокноте. Если в магазине такого не будет, можно вырезать середину простой тетради на 24 или 48 листов. В блокнот полезно выписать самые важные формулы. Лучше всего вкладывать шпаргалки в носовой платок. Эта вещь не вызывает подозрений.
3. Если выпускник решил пронести телефон, следует отключить звук и вибрацию, а также узнать, как передавать ммс. Пользоваться соцсетями для передачи сообщений не нужно, подойдет ммс и обычная электронная почта.
4. Даже если ученику удалось обзавестись надежным помощником на ЕГЭ, не стоит ждать, пока тот все решит, следует выполнить задания своими силами, а потом сверить с полученными ответами.
5. На экзамене нужно всеми силами стараться быть незаметным, не привлекать к себе внимания. Ни в коем случае нельзя хамить членам комиссии, не стоит переговариваться с другими выпускниками. Задания группы С следует писать максимально разборчиво, при необходимости нужно просить дополнительные листы.

Самое лучшее, что можно предпринять, чтобы успешно сдать ЕГЭ — хорошо подготовиться.

Если до экзамена осталось совсем немного времени, не стоит пренебрегать этой возможностью. Следует провести с пользой каждую свободную минуту. Даже за неделю можно многое сделать. Главное — осознать свои слабые места и постараться восполнить пробелы.

Читайте также:

• что такое ОГЭ;
• хитрые способы, как списать на ЕГЭ.