1. Метод доказательства от противного заключается:
а) в предположении противоположного +
б) в том, что этот метод противный
в) в перестановке условия и заключения
2. Если при пересечении двух прямых секущей смежные углы равны, то прямые параллельны, так ли это:
а) да
б) нет +
в) зависит от условий задачи
3. Теоремой, обратной данной называется:
а) аксиома, требующая доказательства
б) обычная теорема, где есть условие и заключение
в) теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы +
4. Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны, так ли это:
а) нет +
б) да
в) зависит от условий задачи
5. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны:
а) накрест лежащие, соответственные и односторонние углы равны
б) накрест лежащие и соответственные углы равны
в) накрест лежащие или соответственные углы равны +
6. Если при пересечении двух прямых секущей односторонние углы равны, то прямые параллельны, так ли это:
а) да
б) нет +
в) зависит от условий задачи
7. Если прямая перпендикулярна к одной из двух параллельных прямых, то:
а) она параллельна к другой
б) она не перпендикулярна к другой
в) она перпендикулярна и к другой +
8. Если при пересечении двух прямых секущей … yглы равны, то прямые параллельны:
а) горизонтальные +
б) односторонние
в) соответственные
9. Если две параллельные прямые пересечены секущей, то:
а) накрест лежащие углы не равны
б) односторонние углы равны
в) накрест лежащие углы равны +
10. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны. Верно ли утверждение:
а) нет
б) да +
в) зависит от условий задачи
11. Если две прямые параллельны третьей, то они:
а) параллельны +
б) пересекаются
в) совпадают
12. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна:
а) 90°
б) 180° +
в) 120°
13. Если прямая пересекает одну из двух параллельных прямых, то:
а) она пересекает и другую +
б) они все параллельны
в) она не пересекает другую
14. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы:
а) не равны
б) зависит от условий задачи
в) равны +
15. Какой учёный использовал подход, основанный на аксиомах, изложенный в сочинении «Начала»:
а) Евклид +
б) Пифагор
в) Лобачевский
16. Используя данные, отмеченные на рисунке, выберите параллельные стороны четырехугольника ABCD:
а) CB
б) CD +
в) AD
17. Аксиома:
а) утверждение (высказывание), требующее доказательства
б) свойства геометрических фигур
в) утверждение (высказывание), которое принимается без доказательства +
18. Используя данные, отмеченные на рисунке, выберите параллельные стороны четырехугольника ABCD:
а) AD
б) AB +
в) CB
19. Две прямые на плоскости называются параллельными, если они:
а) совпадают
б) пересекаются под прямым углом
в) не пересекаются +
20. Используя данные, отмеченные на рисунке, выберите параллельные прямые:
а) AB
б) DE +
в) FC
21. Прямые ОВ и СК параллельные, а ОА и СК — скрещивающиеся. Найти угол между прямыми ОА и СК если угол АОВ=37 градусов:
а) 37 +
б) 73
в) 19
22. Используя данные, отмеченные на рисунке, выберите параллельные прямые:
а) FC
б) BC +
в) AB
23. Плоскости пересекаются по прямой, так ли это:
а) нет
б) зависит от задачи
в) да +
24. Параллельны ли прямые на рисунке:
а) нет
б) да +
в) отчасти
25. Если две прямые в пространстве не имеют общих точек, то они параллельны, так ли это:
а) да
б) зависит от условия задачи
в) нет +
26. Используя данные, отмеченные на рисунке, выберите параллельные стороны четырехугольника ABCD:
а) AD
б) AB +
в) BC
27. Две прямые в пространстве называются … если они лежат в одной плоскости и не пересекаются:
а) параллельные +
б) скрещивающиеся
в) перпендикулярные
28. Используя данные, отмеченные на рисунке, выберите параллельные стороны четырехугольника ABCD:
а) AD
б) BC
в) DC +
29. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые:
а) параллельны +
б) перпендикулярны
в) скрещивающиеся
30. Используя данные, отмеченные на рисунке, укажите параллельные стороны четырехугольника ABCD. Выберите правильный вариант:
а) AB, BC
б) BC, DA +
в) DA, CD
Геометрия, 7 класс
Фамилия имя ____________________________
Тест по теме “Параллельные прямые»
Вопрос 1. Две прямые на плоскости называются параллельными, если они
А) пересекаются
Б) совпадают
В) не пересекаются
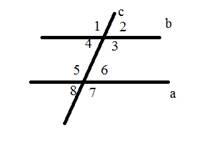
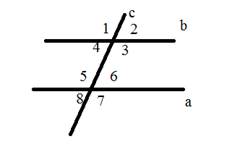
Вопрос 2. Какие углы являются соответственными?
А) 1 и 5, 3 и 6
Б) 1 и 5, 4 и 8, 2 и 6, 3 и 7
В) 1 и 8, 2 и 7, 4 и 5, 3 и 6
Вопрос 3. Какие углы накрест лежащие?
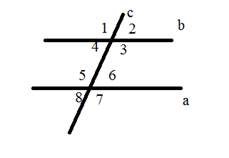
А) 1 и 3, 2 и 4, 5 и 7, 6 и 8
Б) 2 и 5, 1 и 6
В) 3 и 5, 4 и 6
Вопрос 4. Какие углы односторонние?
А) 4 и 5, 3 и 6
Б) 1 и 5, 2 и 6, 4 и 8, 3 и 7
В) 1 и 4, 2 и 3, 5 и 8, 6 и 7
Вопрос 5. Секущая двух прямых — это
А) любая прямая из трёх
Б) прямая, которая пересекает две прямые в двух точках
В) прямая, которая пересекает хотя бы одну прямую из двух
Вопрос 6. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны.
А) накрест лежащие или соответственные углы равны
Б) накрест лежащие и соответственные углы равны
В) накрест лежащие, соответственные и односторонние углы равны
Вопрос 7. Вставьте правильное слово.
Если при пересечении двух прямых секущей ……………… односторонних углов равна 1800, то прямые параллельны
А) частное
Б) сумма
В) разность
Вопрос 8. Аксиома — это
А) утверждение, требующее доказательства
Б) исходное положение, на основе которых доказываются далее теоремы
В) свойства геометрических фигур
Вопрос 9. Какой учёный использует подход, основанный на аксиомах, изложенный в сочинении «Начала»?
А) Евклид
Б) Лобачевский
В) Пифагор
Подборка по базе: Дана функция y=2(arctgx−9arcctgx) Найдите y′′(x). В ответ введит, ОТВЕТЫ НА ВОПРОСЫ (30ВОПРОСОВ).docx, Бух учет вопросы.docx, Контрольные вопросы к зачету.docx, 5 вопрос по налоговому праву.docx, тестовые вопросы к разделу 5 экономика.docx, Физическая культура (ДО, ПНК, ПДО, 4 часть) тестовые вопросы к р, 1-30 вопросы диф зачета.docx, 1-30 вопросы диф зачета.docx, Ответы на вопросы. Педагогика.docx
Вопрос 1. Две прямые на плоскости называются параллельными, если они
А) пересекаются
Б) совпадают
В) не пересекаются
Вопрос 2. Какие углы являются соответственными?
А) 1 и 5, 3 и 6
Б) 1 и 5, 4 и 8, 2 и 6, 3 и 7
В) 1 и 8, 2 и 7, 4 и 5, 3 и 6
Вопрос 3. Какие углы накрест лежащие?
А) 1 и 3, 2 и 4, 5 и 7, 6 и 8
Б) 2 и 5, 1 и 6
В) 3 и 5, 4 и 6
Вопрос 4. Какие углы односторонние?
А) 4 и 5, 3 и 6
Б) 1 и 5, 2 и 6, 4 и 8, 3 и 7
В) 1 и 4, 2 и 3, 5 и 8, 6 и 7
Вопрос 5. Секущая двух прямых — это
А) любая прямая из трёх
Б) прямая, которая пересекает две прямые в двух точках
В) прямая, которая пересекает хотя бы одну прямую из двух
Вопрос 6. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны.
А) накрест лежащие или соотвественные углы равны
Б) накрест лежащие и соотвественные углы равны
В) накрест лежащие, соотвественные и односторонние углы равны
Вопрос 7. Вставьте правильное слово.
Если при пересечении двух прямых секущей ……………… односторонних углов равна 180, то прямые параллельны
А) частное
Б) сумма
В) разность
Вопрос 8. Аксиома — это
А) утверждение, требующее доказательства
Б) исходное положение, на основе которых доказываются далее теоремы
В) свойства геометрических фигур
Вопрос 9. Какой учёный использует подход, основанный на аксиомах, изложенный в сочинении «Начала»?
А) Евклид
Б) Лобачевский
В) Пифагор
Вопрос 10. Как звучит аксиома параллельных прямых?
А) Через точку, не лежащую на данной прямой, проходит бесконечное множество прямых, параллельных данной
Б) Через точку, не лежащую на данной прямой, нельзя провести ни одной прямой, параллельной данной
В) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
Вопрос 11. Если прямая пересекает одну из двух параллельных прямых, то
А) она пересекает и другую
Б) она не пересекает другую
В) они все параллельны
Вопрос 12. Если две прямые параллельны третьей, то они
А) совпадают
Б) параллельны
В) одинаковые
Вопрос 13. Если две параллельные прямые пересечены секущей, то
А) накрест лежащие углы отсутствуют
Б) односторонние углы равны
В) накрест лежащие углы равны
Вопрос 14. Если прямая перпендикулярна к одной из двух параллельных прямых, то
А) она перпендикулярна и к другой
Б) она параллельна к другой
В) она не является перпендикуляром другой
Результаты авторизованых пользователей
| Название теста | Дата | Результат | Пользователь |
|---|---|---|---|
| История / Тест с ответами: “Древняя Греция” | 03-10-2023 06:43:18 pm | 8/20 | Даня Зуев |
| Литература / Тест с ответами: “Какие бывают дожди” К.Паустовский | 03-10-2023 07:28:01 am | 0/20 | Ирина Никифорова |
| Физика / Тест с ответами: “Преломление света” | 03-10-2023 05:21:03 am | 0/20 | Елизавета Каплан |
| История / Тест с ответами: “Экономическое развитие России при Екатерине II” | 03-09-2023 04:45:50 pm | 13/20 | Дима |
| География / Тест с ответами: “Форма, размеры, движение Земли” | 03-09-2023 03:08:20 pm | 3/3 | Emmy Bakharu |
Результаты
#1. Если при пересечении двух прямых секущей … yглы равны, то прямые параллельны
A. горизонтальные
A. горизонтальные
B. односторонние
B. односторонние
C. соответственные
C. соответственные
#2. При пересечении двух параллельных прямых третьей прямой, образованные ими накрест лежащие углы
A. не равны
A. не равны
B. зависит от условий задачи
B. зависит от условий задачи
C. равны
C. равны
#3. Если сумма внутренних односторонних углов равна 180°, то прямые параллельны. Верно ли утверждение
A. нет
A. нет
B. да
B. да
C. зависит от условий задачи
C. зависит от условий задачи
#4. Аксиома
A. утверждение (высказывание), требующее доказательства
A. утверждение (высказывание), требующее доказательства
B. свойства геометрических фигур
B. свойства геометрических фигур
C. утверждение (высказывание), которое принимается без доказательства
C. утверждение (высказывание), которое принимается без доказательства
#5. Две прямые на плоскости называются параллельными, если они
A. совпадают
A. совпадают
B. пересекаются под прямым углом
B. пересекаются под прямым углом
C. не пересекаются
C. не пересекаются
#6. Теоремой, обратной данной называется
A. аксиома, требующая доказательства
A. аксиома, требующая доказательства
B. обычная теорема, где есть условие и заключение
B. обычная теорема, где есть условие и заключение
C. теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы
C. теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы
#7. Если две параллельные прямые пересечены секущей, то
A. накрест лежащие углы не равны
A. накрест лежащие углы не равны
B. односторонние углы равны
B. односторонние углы равны
C. накрест лежащие углы равны
C. накрест лежащие углы равны
#8. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны
A. накрест лежащие, соответственные и односторонние углы равны
A. накрест лежащие, соответственные и односторонние углы равны
B. накрест лежащие и соответственные углы равны
B. накрест лежащие и соответственные углы равны
C. накрест лежащие или соответственные углы равны
C. накрест лежащие или соответственные углы равны
#9. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны
A. накрест лежащие, соответственные и односторонние углы равны
A. накрест лежащие, соответственные и односторонние углы равны
B. накрест лежащие и соответственные углы равны
B. накрест лежащие и соответственные углы равны
C. накрест лежащие или соответственные углы равны
C. накрест лежащие или соответственные углы равны
#10. Если прямая пересекает одну из двух параллельных прямых, то
A. она пересекает и другую
A. она пересекает и другую
B. они все параллельны
B. они все параллельны
C. она не пересекает другую
C. она не пересекает другую
#11. Теоремой, обратной данной называется
A. аксиома, требующая доказательства
A. аксиома, требующая доказательства
B. обычная теорема, где есть условие и заключение
B. обычная теорема, где есть условие и заключение
C. теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы
C. теорема, в которой условием является заключение данной теоремы, а заключением – условие данной теоремы
#12. При пересечении двух параллельных прямых третьей прямой, сумма образованных ими внутренних односторонних углов равна
A. 90°
A. 90°
B. 180°
B. 180°
C. 120°
C. 120°
#13. Используя данные, отмеченные на рисунке, выберите параллельные стороны четырехугольника ABCD
A. AD
A. AD
B. AB
B. AB
C. BC
C. BC
#14. Если две прямые параллельны третьей, то они
A. параллельны
A. параллельны
B. пересекаются
B. пересекаются
C. совпадают
C. совпадают
#15. Используя данные, отмеченные на рисунке, выберите параллельные прямые
A. AB
A. AB
B. DE
B. DE
C. FC
C. FC
#16. Какой учёный использовал подход, основанный на аксиомах, изложенный в сочинении “Начала”
A. Евклид
A. Евклид
B. Пифагор
B. Пифагор
C. Лобачевский
C. Лобачевский
#17. Плоскости пересекаются по прямой, так ли это
A. нет
A. нет
B. зависит от задачи
B. зависит от задачи
C. да
C. да
#18. Если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны, так ли это
A. нет
A. нет
B. да
B. да
C. зависит от условий задачи
C. зависит от условий задачи
#19. Если прямая перпендикулярна к одной из двух параллельных прямых, то
A. она параллельна к другой
A. она параллельна к другой
B. она не перпендикулярна к другой
B. она не перпендикулярна к другой
C. она перпендикулярна и к другой
C. она перпендикулярна и к другой
#20. Если две параллельные прямые пересечены секущей, то
A. накрест лежащие углы не равны
A. накрест лежащие углы не равны
B. односторонние углы равны
B. односторонние углы равны
C. накрест лежащие углы равны
C. накрест лежащие углы равны
7 « . » класс ____________________________( Ф.И.)
Параллельные прямые. Геометрия, 7 класс. К учебнику: Геометрия. 7-9 класс Атанасян Л.С.,
Бутузов В.Ф., Кадомцев С.Б. 2021г
1. Две прямые на плоскости называются параллельными, если они
А) пересекаются Б) совпадают В) не пересекаются
2. Какие углы являются соответственными?
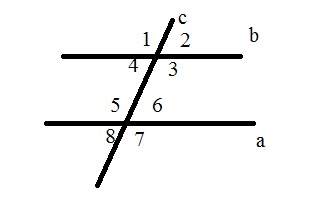
А) 1 и 5, 3 и 6
Б) 1 и 5, 4 и 8, 2 и 6, 3 и 7
В) 1 и 8, 2 и 7, 4 и 5, 3 и 6
3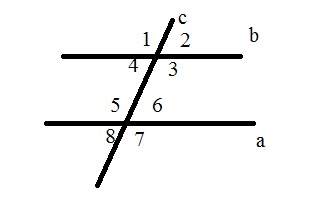 . Какие углы накрест лежащие?
А) 1 и 3, 2 и 4, 5 и 7, 6 и 8
Б) 2 и 5, 1 и 6
В) 3 и 5, 4 и 6
4. Какие углы односторонние?
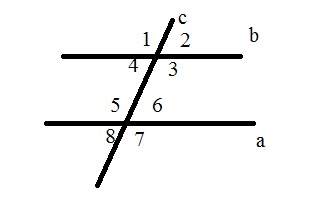
А) 4 и 5, 3 и 6
Б) 1 и 5, 2 и 6, 4 и 8, 3 и 7
В) 1 и 4, 2 и 3, 5 и 8, 6 и 7
5. Секущая двух прямых — это
А) любая прямая из трёх Б) прямая, которая пересекает две прямые в двух точках В) прямая, которая пересекает хотя бы одну прямую из двух
6. Какого условия достаточно, чтобы две прямые пересечённые секущей были параллельны.
А) накрест лежащие или соответственные углы равны
Б) накрест лежащие и соответственные углы равны
В) накрест лежащие, соответственные и односторонние углы равны
7. Вставьте правильное слово.
Если при пересечении двух прямых секущей ……………… односторонних углов равна 180градусов, то прямые параллельны
А) частное Б) сумма В) разность
8. Аксиома — это
А) утверждение, требующее доказательства
Б) исходное положение, на основе которых доказываются далее теоремы
В) свойства геометрических фигур
9. Какой учёный использует подход, основанный на аксиомах, изложенный в сочинении «Начала»?
А) Евклид Б) Лобачевский В) Пифагор
10. Как звучит аксиома параллельных прямых?
А) Через точку, не лежащую на данной прямой, проходит бесконечное множество прямых, параллельных данной
Б) Через точку, не лежащую на данной прямой, нельзя провести ни одной прямой, параллельной данной
В) Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
11. Если прямая пересекает одну из двух параллельных прямых, то
А) она пересекает и другую Б) она не пересекает другую
В) они все параллельны
12. Если две прямые параллельны третьей, то они
А) совпадают Б) параллельны В) одинаковые
13. Если две параллельные прямые пересечены секущей, то
А) накрест лежащие углы отсутствуют Б) односторонние углы равны
В) накрест лежащие углы равны
14. Если прямая перпендикулярна к одной из двух параллельных прямых, то
А) она перпендикулярна и к другой Б) она параллельна к другой
В) она не является перпендикуляром другой
15. Метод доказательства от противного заключается
А) в перестановке условия и заключения Б) в предположении противоположного В) в том, что этот метод противный
16. Какие части различают в теореме?
А) дано и решение Б) условие и заключение В) решение и доказательство
17. Теоремой, обратной данной называется
А) аксиома, требующая доказательства
Б) обычная теорема, где условие и заключение
В) теорема, в которой условием является заключение данной теоремы, а заключением — условие данной теоремы
Метод Бэкона — индуктивный метод познания, представленный Ф. Бэконом в сочинении «Новый Органон» (1620).
Недовольный состоянием наук своего времени, Бэкон предпринял попытку обновить способ исследования природы, который бы не только сделал более надёжными имеющиеся науки и искусства, но сверх того дал возможность открывать новые, ещё неизвестные человечеству.
«Новый Органон» стал второй частью обширного труда «Великое восстановление наук», которое, по задумке Бэкона, должно состоять из шести частей. Однако, автор закончил лишь две первые части.
Многие исследователи отмечали смутность и незавершённость в изложении Бэкона своей индукции. Распространено заблуждение, что индукция «Нового Органона» есть просто путь познания от конкретного опыта к общезначимым основоположениям. Такая индукция широко использовалась в науке и до него, и Бэкон неоднократно отмечал ошибочность общепринятого опытного познания[1]:
Два пути могут существовать для отыскания и открытия истины. Один воспаряет от ощущений и частностей к наиболее общим аксиомам и, идя от этих оснований и их непоколебимой истинности, обсуждает и открывает средние аксиомы. Этим путём и пользуются ныне. Другой же путь выводит аксиомы из ощущений и частностей, поднимаясь непрерывно и постепенно, пока наконец не приходит к наиболее общим аксиомам. Это путь истинный, но не испытанный. Оба эти пути исходят из ощущений и частностей и завершаются в высших общностях. Но различие их неизмеримо. Ибо один лишь бегло касается опыта и частностей, другой надлежащим образом задерживается на них.
Ошибочность прежней индукции
Для того чтобы проникнуть в глубину природы, необходимо верным и осторожным путём отвлекать от вещей понятия и аксиомы, «и вообще необходима более надёжная работа разума»[2].
Силлогизм не приложим к принципам знаний, так как состоит из предложений, предложения из слов, а слова суть знаки понятий. Поэтому если сами понятия спутаны и необдуманно отвлечены от вещей, то нет ничего прочного в том, что построено на них. Поэтому единственная надежда — в истинной индукции[1]:
Чтобы хорошо и правильно строить эту индукцию нужно применить много такого, что до сих пор не приходило на ум ни одному из смертных, и затратить больше работы, чем до сих пор было затрачено на силлогизм. До сих пор в недрах природы таится много весьма полезного, что не имеет родства или соответствия с уже изобретённым и целиком расположено за пределами воображения.
Согласно Бэкону, самым лучшим из всех доказательств является опыт, если только он коренится в эксперименте. Однако, «опытное познание, которое обычно применяют люди, слепо и имеет четыре недостатка»[2]:
- ненадёжность впечатлений самих чувств;
- неопределённость и плохое отвлечение понятий от впечатлений чувств;
- заключение об основах наук посредством простого перечисления;
- открытие и проверка, когда сначала строятся самые общие основания, а потом посредством их проверяются средние аксиомы.
Открытие аксиом
Правильно открытые и установленные аксиомы влекут за собой многочисленные ряды практических приложений. Эти аксиомы открывают исследователю формы или истинные отличия вещей, которые в действительности суть законы чистого действия.
Для построения аксиом должна быть придумана иная форма индукции, чем та, которой пользовались до сих пор. Настоящая индукция, которая будет полезна для открытия новых и доказательства уже известных наук и искусств, должна разделять природу посредством должных разграничении и исключений. И затем после достаточного количества отрицательных суждений она должна заключать о положительном.
Для наук следует ожидать пользы тогда, когда исследование восходит по непрерывным ступеням — от частностей к меньшим аксиомам и затем к средним, одна выше другой, и наконец к самым общим. Самые низшие аксиомы мало отличаются от голого опыта. Высшие и самые общие аксиомы умозрительны и абстрактны. Средние же аксиомы «истинны, тверды и жизненны, от них зависят человеческие дела»[1].
В Новом Органоне Бэкон указывает два рода аксиом превращения тел.
Первый рассматривает тело как соединение простых природ. Так, в золоте, например, соединяется то, что оно желто, тяжело, ковко, тягуче и т. д. Аксиома этого рода выводит вещь из форм простых природ.
Так, тот, кто знает формы и способы наведения желтизны, тяжести, ковкости, прочности и т. п., а также их степени и меры, тот может соединить их в каком-либо теле, откуда последует превращение в золото.
Этот род работы относится к первичному действию и исходит из того, что постоянно, вечно и всеобще в природе, и открывает человеческому могуществу широкие дороги, которые едва может охватить и представить себе человеческая мысль[3].
Второй род аксиом зависит от открытия скрытого процесса и направлен не на простые природы, а на конкретные тела (например, при рождении животных от совокупления до родов).
Выявление форм
По Бэкону, в природе не существует ничего действительного, помимо единичных тел, осуществляющих сообразно с законом отдельные чистые действия. Формами Бэкон называет этот закон и его подразделения.
Дело и цель человеческого знания в том, чтобы открывать форму данной природы, или истинное отличие, или производящую природу, или источник происхождения (ибо таковы имеющиеся у нас слова, более всего приближающиеся к обозначению этой цели.
Бэкон неоднократно предупреждает, что никто успешно не отыщет природу вещи в самой вещи — исследование должно быть расширено до более общего, поскольку то, что в одних вещах считается скрытым, в других имеет явную и обычную природу. Кроме того, Бэкон утверждает, что знание причины какой-либо природы (например, белизны или теплоты) только в некоторых предметах, несовершенно. Знание же формы охватывает единство природы в несходных материях.
Чем больше исследование склоняется к простым природам, тем более все будет ясно и очевидно, так как переходит от многообразного к простому, от бесконечного и смутного к конечному и определённому. Естественное исследование лучше всего подвигается вперед, когда физическое завершается в математическом.
Исследование форм (у Бэкона — на примере теплоты) происходит следующим образом:
- Сначала нужно для каждой данной природы представить в таблице все известные примеры, сходящиеся в этой природе, хотя бы и посредством самых различных материй. Эта таблица называется таблицей присутствия (Примеры, сходящиеся в природе тепла).
- Во-вторых, должно представить разуму примеры, которые лишены данной природы (в предметах наиболее родственных тем, в которых данная природа присутствует), так как форма так же должна отсутствовать там, где отсутствует природа, как и присутствовать там, где она присутствует. Это таблица отсутствия в ближайшем (Примеры ближайшего, лишённого природы тепла).
- В-третьих, должно представить разуму примеры, в которых исследуемая природа присутствует в большей и в меньшей степени. Это возможно или посредством сопоставления роста и уменьшения этого свойства в одном и том же предмете, или посредством сравнения его в различных предметах. Это таблица степеней (Таблица степеней для тепла).
Эти три таблицы представляют исследователю примеры. За этим следует сама индукция:
Первое дело истинной индукции есть отбрасывание отдельных природ, которые не встречаются в каком-либо примере, где присутствует данная природа, или встречаются в каком-либо примере, где отсутствует данная природа, или встречаются растущими в каком-либо примере, где данная природа убывает, или убывают, когда данная природа растёт. После сделанного должным образом исключения останется положительная и хорошо определённая форма. Сказать это просто, но путь к этому извилист и труден[1].
Представив в «Новом Органоне» таблицы исследования природы тепла, Бэкон показывает пример предварительного выведения формы теплоты[1]:
Из всех примеров и из каждого из них видно, что природа, частным случаем которой является тепло, есть движение. Истинными отличиям, которые делают определённым движение и приводят его к форме тепла являются следующие:
- тепло есть движение, при котором тело стремится к расширению, при том такое, что тело одновременно стремится вверх;
- тепло не есть движение равномерного расширения всей массы, но расширения в малейших частицах тела;
- это движение прокалывания и проникновения довольно быстрое, а не медленное.
Эти отличия позволяют сделать начальное истолкование природы тепла. После этого нужно перейти к дальнейшим вспомогательным средствам и истинной и совершенной индукции.
Однако, назвав вспомогательные средства, Бэкон так и не написал о последних этапах индукции, которые должны представить аксиомы и показать переход от них к новым опытам и открытиям.
Известно, что вторая часть его «Нового Органона» осталась незаконченной. Именно в этой части он намеревался в дополнение к теории индукции развивать новую теорию дедукции, как это видно из следующих строк его сочинения[3]: «Указания относительно истолкования природы распадаются на два отдела. В первом дело идёт об образовании положений из опыта, а во втором — о дедукции, или о выводе новых экспериментов из положений (de ducendis auf denvandis experimentis novis ab axiomatibus)». Отсюда видно, что Бэкон не успел развить это положение. Но и изложенный в «Новом Органоне» индуктивный метод Бэкон не рассматривал, как законченный; учёный надеялся на то, что метод будет развит будущими поколениями.
Литература
- Бэкон Ф. Сочинения. В 2-х томах. Т. I. — М.: Мысль (Философское наследие), 1971. — 590 с.
- Бэкон Ф. Сочинения. В 2-х томах. Т. II. — М.: Мысль (Философское наследие), 1972. — 582 с.
- Городенский Н. Франциск Бэкон, его учение о методе и энциклопедия наук. Сергиев Посад, 1915.
- Субботин А. Л. Фрэнсис Бэкон. М.: Мысль, 1974.-175 с.
- Ф. Бэкон Новый Органон, или Истинные указания для истолкования природы. — М., 1978. — 575 с.
- Ф. Бэкон О достоинстве и приумножении наук. — М., 1977. — 567 с.
Примечания
- ↑ 1 2 3 4 5 Ф. Бэкон Новый Органон, или Истинные указания для истолкования природы. — М., 1978. — 575 с.
- ↑ 1 2 Ф. Бэкон О достоинстве и приумножении наук. — М., 1977. — 567 с.
- ↑ 1 2 Бэкон Ф. Сочинения. В 2-х томах. Т. II. — М.: Мысль (Философское наследие), 1972. — 582 с.
См. также
- Метод
- Форма
- Научное исследование
Эта страница в последний раз была отредактирована 12 апреля 2020 в 11:06.
Как только страница обновилась в Википедии она обновляется в Вики 2.
Обычно почти сразу, изредка в течении часа.
«Начала» (греч. Στοιχεῖα, лат. Elementa) — главный труд Евклида, написанный около 300 г. до н. э. и посвящённый систематическому построению геометрии. Считается вершиной античной геометрии и античной математики вообще, итогом её трёхсотлетнего развития и основой для последующих исследований. «Начала», наряду с двумя трудами Автолика из Питаны — древнейшее из дошедших до современности античных математических сочинений; все труды предшественников Евклида известны только по упоминаниям и цитатам позднейших комментаторов.
Прокл сообщает (ссылаясь на Евдема), что подобные сочинения создавались и до Евклида: «Начала» были написаны Гиппократом Хиосским, а также платониками Леонтом и Февдием. Но эти сочинения, по-видимому, были утрачены ещё в античности.
Текст «Начал» на протяжении веков были предметом дискуссий, к ним написаны многочисленные комментарии. Из античных комментариев сохранился текст Прокла, являющийся важнейшим источником по истории и методологии греческой математики. В нём Прокл даёт краткое изложение истории греческой математики (так называемый «Евдемов каталог геометров»), обсуждает взаимосвязь метода Евклида и логики Аристотеля, роль воображения в доказательствах. Среди древних комментаторов — Папп Александрийский; основные комментаторы эпохи Возрождения — Пьер де ла Рамэ, Федериго Коммандино, Христоф Шлюссель (Клавиуса) и Генри Савиль.
«Начала» оказали огромное влияние на развитие математики вплоть до Новейшего времени, высокий интеллектуальный уровень произведения и его фундаментальная значимость для науки в целом отмечается ключевыми учёными современности. Книга переведена на множество языков мира, по количеству переизданий «Начала» не имеют себе равных среди светских книг.
В «Началах» излагаются планиметрия, стереометрия, арифметика, отношения по Евдоксу. В классической реконструкции Гейберга весь труд состоит из 13 книг. К ним традиционно присоединяют две книги о пяти правильных многогранниках, приписываемые Гипсиклу Александрийскому и школе Исидора Милетского.
Изложение в «Началах» ведётся строго дедуктивно. Каждая книга начинается с определений. В первой книге за определениями идут аксиомы и постулаты. Затем следуют предложения, которые делятся на задачи (в которых нужно что-то построить) и теоремы (в которых нужно что-то доказать). Определения, аксиомы, постулаты и предложения пронумерованы, например, ссылка «I, Определения, 2» — второе определение первой книги.
Первая книга
Первая книга начинается определениями, из которых первые семь (I, Определения, 1—7) гласят:
- Точка есть то, что не имеет частей. (Σημεῖόν ἐστιν, οὗ μέρος οὐθέν— букв. «Точка есть то, часть чего ничто»)
- Линия — длина без ширины.
- Края же линии — точки.
- Прямая линия есть та, которая равно лежит на всех своих точках. (Εὐθεῖα γραμμή ἐστιν, ἥτις ἐξ ἴσου τοῖς ἐφ’ ἑαυτῆς σημείοις κεῖται)
- Поверхность есть то, что имеет только длину и ширину.
- Края же поверхности — линии.
- Плоская поверхность есть та, которая равно лежит на всех своих линиях.
Комментаторы эпохи Возрождения предпочитали говорить, что точка есть место без протяжения. Современные авторы, напротив, признают невозможность определения основных понятий, в частности, таков подход в «Основаниях геометрии» Гильберта.
Постулаты Евклида
Наиболее интересен в аксиоматике Евклида последний, знаменитый пятый постулат. Среди других, интуитивно очевидных постулатов, он нарочито чужероден, его громоздкая формулировка закономерно вызывает некоторое чувство протеста и желание отыскать для него доказательство. Такие доказательства уже в древности пытались построить Птолемей и Прокл; а в Новое время из этих попыток развилась неевклидова геометрия. Следует отметить, что первые 28 теорем I книги относятся к абсолютной геометрии, то есть не опираются на V постулат.
Прокл (V в. н. э.)
За постулатами следуют аксиомы (I, Аксиомы, 1—9), которые имеют характер общих утверждений, относящихся в равной мере как к числам, так и к непрерывным величинам:
- Равные одному и тому же равны и между собой.
- И если к равным прибавляются равные, то и целые будут равны.
- И если от равных отнимаются равные, то остатки будут равны.
- (И если к неравным прибавляются равные, то целые будут не равны.)
- (И удвоенные одного и того же равны между собой.)
- (И половины одного и того же равны между собой.)
- И совмещающиеся друг с другом равны между собой.
- И целое больше части.
- (И две прямые не содержат пространства.)
В скобки взяты аксиомы, принадлежность которых Евклиду Гейберг, автор классической реконструкции текста «Начал», счёл сомнительной. Постулаты 4—5 (I, Постулаты, 4—5) в ряде списков выступают как аксиомы (I, Аксиомы, 10—11).
За аксиомами следуют три теоремы, представляющие собой задачи на построение, давно вызывающие споры. Так, вторая из них (I, Предложения, 2) предлагается «от данной точки отложить прямую, равную данной прямой». Нетривиальность этой задачи состоит в том, что Евклид не переносит отрезок на прямую соответствующим раствором циркуля, полагая такую операцию недозволенной, и использует третий постулат (I, Постулаты, 3) в неожиданно узком смысле.
При доказательстве четвёртой теоремы (I, Предложения, 4), выражающей признак равенства треугольников, Евклид использует метод наложения, никак не описанный в постулатах и аксиомах.
Затем рассматриваются различные случаи равенства и неравенства треугольников; теоремы о параллельных прямых и параллелограммах; так называемые «местные» теоремы о равенстве площадей треугольников и параллелограммов на одном основании и под одной высотой. Заканчивается I книга теоремой Пифагора.
Книги II—XIII
II книга — теоремы так называемой «геометрической алгебры».
III книга — предложения об окружностях, их касательных и хордах, центральных и вписанных углах.
IV книга — предложения о вписанных и описанных многоугольниках, о построении правильных многоугольников.
V книга — общая теория отношений, разработанная Евдоксом Книдским.
VI книга — учение о подобии геометрических фигур. Эта книга завершает евклидову планиметрию.
VII, VIII и IX книги посвящены теоретической арифметике. Евклид в качестве чисел рассматривает исключительно натуральные числа; для него «Число есть совокупность единиц». Здесь излагаются теория делимости и пропорций, доказывается бесконечность множества простых чисел, приводится алгоритм Евклида для нахождения наибольшего общего делителя двух чисел, строятся чётные совершенные числа. Евклид доказывает также формулу для суммы геометрической прогрессии.
X книга — классификация несоизмеримых величин. Это самая объёмная из книг «Начал».
XI книга — начала стереометрии: теоремы о взаимном расположении прямых и плоскостей; теоремы о телесных углах, объём параллелепипеда и призмы, теоремы о равенстве и подобии параллелепипедов.
XII книга — теоремы о пирамидах и конусах, доказываемые с помощью метода исчерпывания. Здесь доказывается, например, теорема о том, что объём конуса составляет одну треть от объёма цилиндра с теми же основанием и высотой.
XIII книга — построение правильных многогранников; доказательство того, что существует ровно пять правильных многогранников.
Евклид нигде в книге не ссылается на других греческих математиков, хотя несомненно опирается на их результаты. Историки науки показали, что прототипом для труда Евклида послужили более ранние сочинения античных математиков:
- Книги I—IV и XI — «Начала» Гиппократа Хиосского.
- Книги V—VI и XII — труды Евдокса Книдского.
- Книги VII—IX — сочинения Архита Тарентского и других пифагорейцев. По мнению Ван дер Вардена, это самая древняя по содержанию часть «Начал», восходящая к V веку до н. э.
- Книги X и XIII — труды Теэтета Афинского.
Вопрос о том, содержат ли «Начала» какие-либо результаты самого Евклида или автор занимался только систематизацией и унификацией накопленных знаний, является предметом дискуссий. Есть предположение, что алгоритм построения правильного 15-угольника разработан Евклидом; вероятно, он же произвёл отбор и окончательную формулировку аксиом и постулатов.
В целом содержание «Начал» покрывает значительную часть античной теоретической математики. Однако некоторая часть известного древнегреческим математикам материала осталась вне этого труда — например, конические сечения (Евклид посвятил им отдельный труд, который не сохранился), длина окружности, теория приближённых вычислений.
Манускрипты и издания
Греческий текст «Начал»
При раскопках античных городов найдено несколько папирусов, содержащих небольшие фрагменты «Начал» Евклида. Самый известный был найден в «городе папирусов» Оксиринхе в 1896—1897 и содержит формулировку одного из утверждений второй книги с рисунком (II, Предложения, 5).
Папирус из Оксиринха
Греческий текст «Начал» Евклида известен по византийским манускриптам, два самых известных из них хранятся Бодлианской библиотеке и Ватиканской апостольской библиотеке (двухтомный Ватиканский манускрипт).
На их основе, а также с учётом арабских переводов «Начал» (датируемых IX веком и позднее) оригинальный текст был реконструирован датским историком науки Гейбергом в конце XIX века, его методы подробно описаны Хизом (англ. Thomas Little Heath)). Гейберг использовал в своей реконструкции 8 греческих манускриптов, датируемых современными исследователями IX—XI веками. Из этих манускриптов семь в своем заглавии имеют пометку «из издания Теона» или «из лекций Теона» и поэтому называются Теоновскими. Ватиканский манускрипт такой пометки не имеет и считается неподверженным редакции Теона. Теоновские манускрипты разнятся между собой, и общих признаков, отличающих их от ватиканского манускрипта, немного (наиболее существенный — концовка IV книги). На полях манускриптов имеются многочисленные комментарии, взятые частично из комментариев Прокла, которые вписывают «Начала» в контекст греческой культуры, например, сообщается о том, что Пифагор, открыв свою теорему, принёс в жертву быков.
История обретения византийских манускриптов темна. Вероятно, они попали в Европу ещё в XVI веке, но не были опубликованы. В первом издание греческого текста, осуществленном Йоханом Хервагеном (Johann Herwagen) между 1533 и 1558 годами под редакцией Симона Гринера (Simon Gryner, он же Grynaeus, профессор греческого языка в базельском университете), использованы манускрипты, которые, по мнению Гейберга, представляют собой весьма плохие копии XVI века. Лишь в 1808 году Пейрар (фр. François Peyrard) во время наполеоновских экспроприаций нашёл три манускрипта в Риме и среди них важнейший — двухтомный ватиканский манускрипт.
Латинский текст «Начал»
Манускрипт из Люнебурга, ок. 1200 года, передающий геометрию Боэция
В Европе «Начала» Евклида на латинском языке были хорошо известны и в Средние века, и в эпоху Возрождения, однако далеко не в привычном теперь виде. Средневековые латинские трактаты, содержащие фрагменты «Начал» Евклида, каталогизированы мюнхенским учёным Фолькертсом (нем. Menso Folkerts), разделившим манускрипты на следующие группы:
- Так называемая «Геометрия Боэция» (в действительности трактат Боэцию не принадлежит). Трактаты этой группы начинаются словами «Incipit Geometriae Boetii», имеют ряд общих признаков, хотя их тексты значительно расходятся. Текст занимает пять-шесть рукописных листов. Доказательства предложений отсутствуют, однако имеются иллюстрации с дополнительными построениями. Иногда доказательствами снабжаются только первые три теоремы. Первым определением предшествует утверждение о том, что основа геометрии в измерении длин, высот и ширин, после этого евклидовы определения приобретают другой смысл, например, линия — объект, длину которого измеряют, а ширину нет и т. д. Язык не испытал влияния арабского, поэтому считается, что геометрия Боэция — прямой перевод с греческого на латинский. Опубликован манускрипт из Люнибурга.
- «Геометрия» Аделарда составляет большой класс манускриптов, написанных разными авторами в разное время. Наибольшая подгруппа, названная как «Adelard II», содержит все 15 книг «Начал» Евклида, впрочем, сохранность манускриптов такова, что говорить об этом нужно с осторожностью. Характерная черта — наличие доказательств, причём в лучших манускриптах доказательства предшествуют изложению (enucatio); некоторые доказательства даны подробно, другие лишь намечены. Некоторые изложения (enunciatio) в Adelard II буквально воспроизводят Боэция, другие имеют иную формулировку часто с арабскими эквивалентами вместо латинских терминов. Текст значительно разнится от манускрипта к манускрипту (в книгах VII—IX и XI—XIII доказательства особенно разнятся), так, что в средние века не было канонического текста для Adelard II, который все время дополнялся и улучшался. Стоит подчеркнуть, что доказательства отличаются способом выражения, но не математической сутью. В течение всего XII века шла работа по улучшению доказательств.
- «Геометрия» Кампануса— комплекс рукописей XIII—XV веков. В этой версии «Начала» весьма схожи с византийскими манускриптами и вполне могут рассматриваться как довольно точный перевод, в котором, однако присутствуют арабские термины (например, параллелепипед назван «belmaui»).
Это издание представляет собой 15 книг, формулировки предложений близки к Adelard II, но доказательства следует за изложением. В заглавии манускриптов обычно отождествлены Евклид, автор «Начал», и ученик Сократа философ Евклид Мегарский. Печатные издания «Начал» Евклида каталогизированы Томасом-Стэнфордом (англ. Charles Thomas—Stanford). Первое печатное издание «Начал» было осуществлено Эрхардом Ратдольтом в Венеции в 1482 году и воспроизводило «Начала» в обработке Кампано. Следующее издание не копировало первое, было осуществлено Бартоломео Дзамберти в 1505 году. Из предисловия известно, что Дзамберти переводил греческий манускрипт, передающий «Начала» в обработке Теона, однако, Гейбергу не удалось его идентифицировать.
В XVI веке считалось, что Евклиду принадлежат лишь формулировки теорем, доказательства же были придуманы позже; были распространены издания «Начал» без доказательств и издания, сравнивающие доказательства Кампана и Дзамберти. Этот взгляд имел вполне твёрдую основу: в начале XVI века была издана геометрия Боэция, которая тоже являлась переводом «Начал» Евклида, но доказательств в этом издании не содержалось. Считалось также, что использование в доказательствах буквенных обозначений подразумевает знакомство с буквенной алгеброй. Это мнение было отвергнуто в XVII веке.
Русские переводы
Первое издание «Начал» на русском языке издано в 1739 году; книга вышла в Петербурге под названием «Евклидовы элементы из двенадцати нефтоновых книг выбранныя и в осмь книг через профессора мафематики Андрея Фархварсона сокращенныя, с латинского на российский язык хирургусом Иваном Сатаровым преложенныя». Перевод выполнил Иван Сатаров под руководством шотландского математика Генри Фарварсона. Имя Ньютона («Нефтона») в названии упомянуто, возможно, в рекламных целях, к содержанию книги он никакого отношения не имеет. Перевод был сделан с сокращённого французского издания «Начал» Такэ (фр. André Tacquet). Немного позднее вышли ещё 2 перевода, также сокращённые до 8 книг:
- 1769 год: перевод Курганова «Евклидовы Елементы Геометрии, то есть первыя основания науки о измерении протяжения»;
- 1784 год: перевод Прохора Суворова и Василия Никитина «Евклидовых стихий осьмь книг, а именно: первая, вторая, третья, четвёртая, пятая, шестая, одиннадцатая и двенадцатая; к сим прилагаются книги тринадцатая и четырнадцатая. Переведены с греческого и поправлены. В Санкт-Петербурге, в типографии Морского шляхетного Кадетского Корпуса» (переизданы в 1789 году).
Практически полностью (кроме X книги) «Начала» на русском языке вышли в переводе Фомы Петрушевского: книги 1—6 и 11—13 в 1819 году, книги 7—9 в 1835 году. В 1880 году вышел перевод Ващенко-Захарченко. Ещё один сокращённый перевод был издан в Кременчуге (1877 год) под названием «Восемь книг геометрии Эвклида»; перевод под руководством А. А. Соковича (1840—1886), директора местного реального училища, выполнили два воспитанника этого училища.
Последнее по времени полное академическое издание было опубликовано в 1949—1951 годах, перевод с греческого и комментарии — Дмитрия Мордухай-Болтовско́го.
Всемирное распространение
На китайском языке первые 6 книг «Начал» издал Маттео Риччи во время своей миссии в Китае (1583‑1610 годы). Полный перевод, выполненный британским миссионером Уайли (англ. Alexander Wylie), вышел с хвалебным предисловием Цзэн Гофаня, написанным в 1865 году.