Вопросы по курсу «Линейная
алгебра» 1 курс 1 семестр
-
Матрицы,
определение, виды матриц -
Операции
над матрицами, свойства операций -
Определители
второго и третьего порядка. Способы
вычисления. -
Свойства
определителей. -
Обратная
матрица. Существование, единственность.
Нахождение обратной матрицы. -
Ранг
матрицы. Вычисление ранга различными
способами -
Системы
линейных уравнений. Матричная запись
системы. -
Применение
обратной матрицы к решению линейных
систем. -
Метод
Крамера решения линейных систем. -
Решение
систем линейных уравнений методом
Гаусса. -
Теорема
Кронекера–Капелли. Решение неопределенных
систем линейных уравнений. -
Решение
систем линейных уравнений методом
Жордана-Гаусса. -
Математическая
модель Леонтьева межотраслевого
баланса. -
Однородные
системы линейных уравнений. Структура
общего решения ЛОС -
Фундаментальная
система решений. -
Векторы.
Основные операции над векторами. -
Скалярное
произведение 2-х векторов и его свойства. -
Векторное
произведение векторов и его свойства. -
Смешанное
произведение векторов и его свойства -
Простейшие
задачи на плоскости. -
Различные
уравнения прямой. -
Угол
между прямыми. Условия перпендикулярности
и параллельности прямых. -
Общее
уравнение кривой. Кривые второго
порядка. -
Эллипс.
-
Гипербола.
-
Парабола.
-
Уравнение
плоскости. -
Угол
между плоскостями. Условия параллельности
и перпендикулярности плоскостей -
Уравнения
прямой в пространстве. -
Угол
между прямыми. Условия параллельности
и перпендикулярности прямых. -
Угол
между прямой и плоскостью. Условия
параллельности и перпендикулярности
прямой и плоскости -
n
–мерное векторное линейное пространство.
Аксиомы. Примеры. -
Линейно
зависимые и линейно независимые системы
векторов. -
Базис
линейного пространства. Разложение
вектора по произвольному базису. -
Линейные
преобразования. Изменение матрицы
линейного преобразования при изменении
базиса. -
Линейные
операторы. Основные понятия. Действия
над линейными операторами. -
Собственные
значение и собственные векторы матрицы. -
Линейная
модель торговли. -
Квадратичные
формы. Приведение квадратичной формы
к каноническому виду -
Канонический
вид квадратичной формы. Метод Лагранжа.
метод собственных векторов -
Определение
положительной и отрицательной
квадратичной формы. -
Понятие
комплексного числа. Геометрическая
интерпретация комплексного числа. -
Алгебраическая
и тригонометрическая форма записи
комплексного числа. -
Основные
свойства комплексных чисел. -
Возведение
в степень извлечение из степени
комплексного числа.
1. Матрицы, определение,
виды матриц
Матрица –
это таблица из m строк и n столбцов.
Произведение m×n называют размером
матрицы.
Виды:
-
Квадратной
матрицей называется матрица, у которой
количество строк равно количеству
столбцов (размера n×n), число n называется
порядком матрицы. -
Нулевой
матрицей называется матрица, все
элементы которой равны нулю. -
Вектор-строкой
называется матрица, состоящая из одной
строки. -
Вектор-столбцом
называется матрица, состоящая из одного
столбца. -
Диагональной
матрицей называется квадратная матрица,
все элементы которой, стоящие вне
главной диагонали, равны нулю.
-
Единичной
матрицей (E) называется
диагональная матрица, диагональные
элементы которой равны 1
-
Верхней
треугольной матрицей называется
матрица, все элементы которой ниже
главной диагонали равны нулю.
-
Нижней
треугольной матрицей называется
матрица, все элементы которой выше
главной диагонали равны нулю. -
Ступенчатой
матрицей называется матрица,
удовлетворяющая следующим условиям:-
если
матрица содержит нулевую строку, то
все строки, расположенные под нею,
также нулевые; -
если
первый ненулевой элемент некоторой
строки расположен в столбце с номером
i, и следующая строка не нулевая, то
первый ненулевой элемент следующей
строки должен находиться в столбце с
номером большим, чем i.
-
2. Операции над матрицами,
свойства операций
Операции
над матрицами:
-
Сложение
матриц. -
Вычитание
матриц. -
Умножение
матрицы на число. -
Умножение
матриц. -
Транспонирование.
-
Элементарные
преобразования:
-
перестановка
любых двух строк матрицы; -
умножение
любой строки на произвольное, отличное
от нуля, число; -
сложение
любой строки с другой строкой ,
умноженной на произвольное число;
Свойства
операции сложения.
-
Сочетательный:
для матриц А, В и С одного порядка
характерно свойство ассоциативности
сложения А+(В+С)=(А+В)+С. -
Для
матриц данного порядка существует
нейтральный элемент по сложению,
которым является нулевая матрица. То
есть, справедливо свойство А+О=А. -
Для
ненулевой матрицы А данного порядка
существует матрица (–А), их суммой
является нулевая матрица: А+(-А)=О. -
Для
матриц А и В данного порядка справедливо
свойство коммутативности сложения
А+В=В+А.
Свойства
операции умножения матрицы на число.
-
Для
матриц одного порядка А и В,
а также произвольного действительного
(или комплексного) числасправедливо
свойство дистрибутивности умножения
относительно сложения.
-
Для
произвольной матрицы А и
любых действительных (или комплексных)
чисели
справедливо
свойство ассоциативности умножения.
-
Нейтральным
числом по умножению на произвольную
матрицу А является единица,
то есть,.
-
0 * A
= 0
Свойства операции умножения
матриц.
-
Свойство ассоциативности
умножения матриц.
-
Два свойства дистрибутивности
.
-
В общем случае операция
умножения матриц некоммутативна.
-
Для произвольной
матрицы А порядка p на n справедливо
равенство,
а для произвольной матрицы А порядка n на p —
равенство.
3. Определители второго и
третьего порядка. Способы вычисления.
Вычисление
определителя второго порядка.
Чтобы
вычислить определитель матрицы второго
порядка, надо от произведения элементов
главной диагонали отнять
произведение элементов побочной
диагонали:
Вычисление
определителя третьего порядка.
-
Правило
треугольника
Схематически это правило можно изобразить
следующим образом:
Произведение элементов в первом
определителе, которые соединены прямыми,
берется со знаком «плюс»; аналогично,
для второго определителя — соответствующие
произведения берутся со знаком «минус»,
т.е.
-
Правило
Саррюса
Справа от определителя дописывают
первых два столбца и произведения
элементов на главной диагонали и на
диагоналях, ей параллельных, берут со
знаком «плюс»; а произведения
элементов побочной диагонали и
диагоналей, ей параллельных, со знаком
«минус»:
4. Свойства определителей.
-
Определитель
транспонированной матрицы равен
определителю исходной матрицы. -
Умножение
всех элементов строки или столбца
определителя на некоторое число λ
равносильно умножению определителя
на это число. -
Если
в определителе переставить местами
любые две строки или два столбца, то
определитель изменяет свой знак на
противоположный. -
Если
матрица содержит нулевую строку
(столбец), то определитель этой матрицы
равен нулю. -
Если
две строки (столбца) матрицы равны
между собой, то определитель этой
матрицы равен нулю. -
Если
две строки (столбца) матрицы пропорциональны
друг другу, то определитель этой матрицы
равен нулю. -
Определитель
матрицы треугольного вида равен
произведению элементов, стоящих на
главной диагонали. -
Если
все элементы k-ой строки (столбца)
определителя представлены в виде сумм
ak j + bk j, то определитель можно представить
в виде суммы соответствующих
определителей. -
Определитель
не изменится, если к элементам любой
его строки (или столбца) прибавить
соответствующие элементы другой строки
(или соответствующего столбца),
умноженные на одно и тоже число.
5. Обратная матрица.
Существование, единственность. Нахождение
обратной матрицы.
Вопросы к
экзамену и билеты
1. Матрицы: понятие
матрицы, частные виды матриц
2. Элементарная
алгебра матриц (основные операции матричной алгебры).
3. Определители:
понятие определителя, вычисление определителей второго и третьего порядков.
4. Понятия минора, алгебраического
дополнения. Разложение определителя по строке, столбцу.
5. Свойства
определителей.
6. Системы линейных
уравнений: определение mxn системы линейных уравнений, понятия однородной и
неоднородной, совместной и несовместной, определенной и неопределенной систем
линейных уравнений.
7. Матричная запись
системы линейных уравнений. Решение системы линейных уравнений с помощью
обратной матрицы.
8. Формулы Крамера
для решения системы линейных уравнений.
9. Обратная матрица:
определение, вычисление обратной матрицы.
10. Условие
существования
обратной матрицы.
11. Ранг матрицы.
Элементарные преобразования матриц. Вычисле-ние ранга матрицы.
12. Критерий
совместности системы линейных уравнений (теорема Кронекера-Капелли).
13.
Метод
Гаусса решения системы линейных урвнений. Общее решение системы линейных
уравнений.
14. Модель
многоотраслевой экономики Леонтьева.
15. Векторы. Линейные
операции с векторами: определение, свойства.
16. Проекция вектора
на ось. Координаты вектора. Разложение вектора в декартовой прямоугольной
системе координат. Модуль и направляющие косинусы вектора.
17. Линейные операции
с векторами в координатной форме. Условие коллинеарности векторов.
18. Скалярное
произведение векторов: определение, свойства, координатная форма, приложения.
19. Векторное
произведение векторов: определение, свойства, координатная форма, приложения.
20. Смешанное
произведение векторов: определение, свойства, координатная форма, приложения.
21. Уравнение линии на
плоскости. Уравнение первой степени и линии первого порядка.
22. Нормальное
уравнение прямой на плоскости. Уравнение прямой в отрезках.
23. Уравнение прямой с
угловым коэффициентом. Уравнение пучка прямых.
24. Уранения прямой,
проходящей через заданную точку параллельно/перпендикулярно данной прямой.
25. Уравнение прямой,
проходящей через две заданные точки.
26. Угол между двумя
прямыми. Условия параллельности/ перпендикулярности двух прямых. Расстояние от
точки до прямой. Координаты точки пересечения двух прямых.
27. Кривые второго
порядка. Общее уравнение линии второго порядка.
28. Парабола:
каноническое уравнение; фокус, директриса паболы, их геометричесий смысл.
29. Эллипс:
каноническое уравнение; фокусы, директрисы, эксцентриситет эллипса, их
геометричесий смысл.
30. Гипербола:
каноническое уравнение; фокусы, директрисы, эксцентриситет гиперболы, их геометрический
смысл.
31. Уравнения
плоскости: общее, “в отрезках”; уравнение плоскости, проходящей через заданную
точку перпендикулярно данному вектору.
32. Угол между двумя
плоскостями, условие параллельности/ перпендикулярности двух плоскостей.
33. Уравнения прямой в
пространстве: канонические, парамет-рические, общие уравнения.
34. Угол между двумя
прямыми, заданными каноническими уравнениями. Условие
параллельности/перпендикулярности двух прямых.
35. Угол между прямой
и плоскостью.
ПРИМЕРНЫЕ
ЭКЗАМЕНАЦИОННЫЕ
БИЛЕТЫ
Экзаменационный
билет № 1
1.
Системы
линейных уравнений: определение mxn системы линейных уравнений, понятия
однородной и неоднородной, совместной и несовместной, определенной и
неопределенной систем линейных уравнений.
2.
Вычислить
ранг матрицы 
3.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок AB в
отношении 1:3, параллельно прямой , если А (2; 1), В (12,–6).
Экзаменационный
билет № 2
1.
Матрицы:
понятие матрицы, частные виды матриц, линейные операции матричной алгебры.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Найти
косинус угла между векторами и
, если даны координаты точек: А (3; – 2;
1); В (2; 1; 6); С (1; 3; – 2).
Экзаменационный
билет № 3
1.
Гипербола:
каноническое уравнение; фокусы, директрисы, эксцентриситет гиперболы, их
геометрический смысл.
2.
Вычислить
произведение матриц: .
3.
В
треугольнике с вершинами А (4; 1), В (–1; 5) и С (3; –1) найти уравнение
стороны АС и высоты ВD.
Экзаменационный
билет № 4
1.
Элементарная
алгебра матриц (основные операции матричной алгебры).
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок AB в
отношении 2:1, параллельно прямой , если А (2; 1), В (12,–6).
Экзаменационный
билет № 5
1.
Эллипс:
каноническое уравнение; фокусы, директрисы, эксцентриситет эллипса, их
геометрический смысл.
2.
Вычислить
ранг матрицы 
3.
Дан
эллипс . Найти:
1) его полуоси; 2) фокусы; 3) эксцентриситет; 4) уравнения директрис.
Экзаменационный
билет № 6
1.
Определители:
понятие определителя, вычисление определителей второго и третьего порядков.
2.
Вычислить
произведение матриц: 
3.
Найти
косинус угла между векторами и
, если даны координаты точек: А (1; –3;
4); В (–3; 1; 2); С (2; 4; –5).
Экзаменационный
билет № 7
1.
Парабола:
каноническое уравнение; фокус, директриса параболы, их геометрический смысл.
2.
Вычислить
ранг матрицы 
3.
Вычислить
площадь параллелограмма, построенного на векторах
и
, если:
Экзаменационный
билет № 8
1.
Понятия
минора, алгебраического дополнения. Теорема о разложении определителя.
2.
Вычислить
линейную комбинацию матриц А и В:
Дано:

3.
В
треугольнике с вершинами А (4; 1), В (–1; 5) и С (3; –1) найти уравнение стороны
АС и медианы ВЕ.
Экзаменационный
билет № 9
1.
Кривые
второго порядка. Общее уравнение линии второго порядка.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Составить
уравнение стороны АС треугольника, если точки А (2; 3) и В (–1, 4) – его
вершины, а М (2, 2) –точка пересечения его высот.
Экзаменационный
билет № 10
1.
Свойства
определителей.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
В
треугольнике с вершинами А (4; 1), В (–1; 5) и С (3; –1) найти уравнение
стороны АС и высоты ВD.
Экзаменационный
билет № 11
1.
Обратная
матрица: определение, вычисление обратной матрицы. Условие существования
обратной матрицы.
2.
Вычислить
произведение матриц: 
3.
Вычислить
площадь параллелограмма, построенного на векторах
и
, если:
.
Экзаменационный
билет № 12
1.
Системы
линейных уравнений: определение mxn системы линейных уравнений, понятия
однородной и неоднородной, совместной и несовместной, определенной и
неопределенной систем линейных уравнений.
2.
Вычислить
ранг матрицы 
3.
Найти
косинус угла между векторами и
, если даны координаты точек: А (3; – 2;
1); В (2; 1; 6); С (1; 3; – 2).
Экзаменационный
билет № 13
1.
Угол
между двумя прямыми. Условия параллельности/ перпендикулярности двух прямых.
2.
Вычислить
произведение матриц: .
3.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок МК в
отношении 1:2, параллельно прямой , если М (6; –2), К (2,– 2).
Экзаменационный
билет № 14
1.
Матричная
запись системы линейных уравнений. Решение системы линейных уравнений с помощью
обратной матрицы.
Найти
матрицу, обратную данной: A=.
2.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок AB в
отношении 1:2, параллельно прямой , если
А (2; 1), В (12,–6).
Экзаменационный
билет № 15
1.
Уравнения
прямой, проходящей через заданную точку параллельно/ перпендикулярно данной
прямой.
2.
Вычислить
ранг матрицы 
3.
В
треугольнике с вершинами А (10; –2), В (–1; 4) и С (3; 
стороны АВ и медианы СЕ.
Экзаменационный
билет № 16
1.
Формулы
Крамера для решения системы линейных уравнений.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок AB в
отношении 1:2, параллельно прямой , если А (2; 1), В
(12,–6).
Экзаменационный
билет № 17
1.
Уравнение
прямой, проходящей через заданную точку параллельно/ перпендикулярно данной
прямой.
2.
Найти
матрицу, обратную данной: A=.
3.
По
данному уравнению определить: 1) тип кривой,
2) координаты фокусов 3) эксцентриситет. Сделать чертеж.
Экзаменационный
билет № 18
1.
Ранг
матрицы: понятие о ранге матрицы, свойства ранга. Способы вычисления ранга
матрицы.
2.
Вычислить
произведение матриц:
3.
Найти
косинус угла между векторами и
, если даны координаты точек: А (10; 2;
–5); В (3; –1; 2); С (0; 5; – 2).
Экзаменационный
билет № 19
1.
Уравнение
прямой с угловым коэффициентом. Уравнение прямой в отрезках.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Проверить
коллинеарность векторов и
, построенных на векторах
и
, если:
Экзаменационный
билет № 20
1.
Критерий
совместности системы линейных уравнений (теорема Кронекера-Капелли).
2.
Вычислить
линейную комбинацию матриц А и В:
Дано:

–А +2В.
3.
В
треугольнике с вершинами А (4; 1), В (–1; 5) и С (3; –1) найти уравнение
стороны АС и медианы ВЕ.
Экзаменационный
билет № 21
1.
Общее
уравнение прямой на плоскости. Нормальное уравнение прямой.
2.
Вычислить
произведение матриц: .
3.
Вычислить
площадь параллелограмма, построенного на векторах и
, если:
.
Экзаменационный
билет № 22
1.
Уравнение
прямой, проходящей через данную точку в заданном направлении. Уравнение пучка
прямых.
2.
Найти
матрицу, обратную данной: A=.
3.
Составить
уравнение стороны АС треугольника, если точки
А (1; 3) и В (1, – 4) – его вершины, а М (2; 2) –точка пересечения его высот.
Экзаменационный
билет № 23
1.
Уравнение
прямой, проходящей через две заданные точки.
2.
Вычислить
ранг матрицы 
3.
Вычислить
площадь параллелограмма, построенного на векторах и
, если:
;
Экзаменационный
билет № 24
1.
Уравнение
линии на плоскости. Уравнение первой степени и линии первого порядка.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
Найти
косинус угла между векторами и
, если даны координаты точек: А (5; 3 ; – 2); В
(–5; 8; 6); С (0; –12; 12).
Экзаменационный
билет № 25
1.
Метод
Гаусса решения системы линейных урвнений. Общее решение системы линейных
уравнений
2.
Вычислить
произведение матриц: 
3.
В
треугольнике с вершинами А (10; –2), В (–1; 4) и С (3; 
стороны АВ и высоты СD.
Экзаменационный
билет № 26
1.
Проекция
вектора на ось. Координаты вектора. Разложение вектора в декартовой
прямоугольной системе координат. Модуль и направляющие косинусы вектора.
2.
Вычислить
определитель, используя подходящее разложение по строке или столбцу

3.
По
данному уравнению определить тип кривой, найти координаты фокусов,
эксцентриситет, построить кривую: .
Экзаменационный
билет № 27.
1.
Линейные
операции с векторами в координатной форме. Условие коллинеарности векторов.
2.
Вычислить
ранг матрицы 
3.
Составить
уравнение прямой, проходящей через точку С, которая делит отрезок МК в
отношении 2:1, параллельно прямой , если М (6; 2), К ( –1,2).
Экзаменационный
билет № 28
1. Скалярное
произведение векторов: определение, свойства, координатная форма, приложения.
2. Вычислить
произведение матриц: 
3. В треугольнике с
вершинами А (4; 1), В (1; 6) и С (– 3; 1) найти уравнение стороны АС и высоты
ВD.
Экзаменационный
билет № 29
1.
Модель
многоотраслевой экономики Леонтьева.
2.
Найти
матрицу, обратную данной: A=.
3.
По
данному уравнению определить тип кривой, построить кривую, найти координаты
фокусов, эксцентриситет: .
Экзаменационный
билет № 30
1.
Смешанное
произведение векторов: определение, свойства, координатная форма, приложения.
2.
Вычислить
произведение матриц: .
3.
Составить
уравнение стороны АВ треугольника, если точки А (–5; 2) и С ( 2, – 4) – его
вершины, а М (1, 2) –точка пересечения его высот.
Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
|
Единственный в мире Музей Смайликов |
|
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ
по курсу «Линейная алгебра и аналитическая геометрия»(1 семестр)
1-й поток, 2009 год
ЧАСТЬ 1.
ЛИНЕЙНАЯ АЛГЕБРА
1. Операции над матрицами и их свойства.
2. Линейная зависимость и независимость. Базис и размерность линейной оболочки.
3. Перестановки и подстановки, транспозиции, четность.
4. Определитель и его свойства как функции столбцов (строк).
5. Определитель транспонированной матрицы.
6. Определитель произведения матриц.
7. Невырожденные матрицы. Обратные матрицы. Критерий обратимости матрицы.
8. Миноры и их алгебраические дополнения. Теорема Лапласа.
9. Явный вид обратной матрицы.
10. Ранг матрицы и линейная зависимость строк и столбцов. Теорема о базисном миноре.
11. Ранг суммы и произведения матриц. Ранг матрицы и элементарные преобразования.
12. Приведение матрицы к ступенчатому виду. Приведение к диагональному виду.
13. Эквивалентные матрицы. Критерий эквивалентности.
14. Системы линейных алгебраических уравнений. Эквивалентность систем. Элементарные преобра- зования уравнений и умножение на невырожденные матрицы.
15. Системы с невырожденной матрицей. Правило Крамера.
16. Критерий совместности системы линейных алгебраических уравнений. Критерий единственности решения.
17. Метод Гаусса исследования и решения систем линейных алгебраических уравнений. Число ариф- метических операций в методе Гаусса.
18. Геометрические свойства множества решений однородной системы линейных алгебраических уравнений. Фундаментальная система решений.
19. Геометрические свойства множества решений неоднородной системы линейных алгебраических уравнений. Общее решение.
20. Линейное пространство. Базис и размерность. Переход к другому базису, матрица перехода.
21. Линейные подпространства и многообразия. Сумма и пересечение подпространств. Прямая сумма подпространств.
1
ЧАСТЬ 2.
ЭЛЕМЕНТЫ ОБЩЕЙ АЛГЕБРЫ
1. Декартово произведение множеств и бинарные отношения. Отношение эквивалентности. Отно- шение частичного порядка.
2. Алгебраические операции. Ассоциативность и скобки.
3. Группы и подгруппы. Симметрическая и знакопеременная группы.
4. Группа невырожденных матриц. Группа невырожденных треугольных матриц. Группа ортого- нальных матриц.
5. Степени элемента. Циклические группы. Подгруппы циклической группы. Абелевы группы.
6. Подгруппы, смежные классы, нормальные подгруппы (нормальные делители).
7. Конечные группы. Теорема Лагранжа.
8. Изоморфизм и гомоморфизм групп. Фактор-группа по нормальной подгруппе. Свободная группа.
9. Поле комплексных чисел. Комплексная плоскость. Тригонометрическая форма комплексного числа. Модуль и аргумент произведения комплексных чисел.
10. Формула Муавра. Корни из единицы. Группа корней n-й степени из единицы. Первообразные корни.
11. Кольца, поля, линейные пространства над полем.
12. Кольцо вычетов. Поле вычетов по простому модулю.
13. Характеристика поля. Необходимое и достаточное условие существования поля из n элементов.
14. Многочлены как формальные выражения и как функции. Условие эквивалентности двух опре- делений многочлена.
15. Кольцо многочленов. Идеал. Деление с остатком. Наибольший общий делитель. Алгоритм Ев- клида.
16. Целостное кольцо и поле частных.
17. Гауссовы кольца. Разложение на неприводимые множители в кольце многочленов от n перемен- ных.
18. Значения многочлена и корни. Теорема Безу. Алгебраическое расширение поля. Размерность расширения.
19. Основная теорема алгебры. Разложение многочленов на линейные множители.
20. Каноническое разложение комплексных и вещественных многочленов. Кратность корня.
21. Формулы Виета. Общие и элементарные симметрические многочлены.
2
ЧАСТЬ 3.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
1. Аффинная система координат. Преобразование координат.
2. Направленные отрезки. Свободный вектор.
3. Линейные операции над векторами. Кооординаты вектора. Проекции вектора.
4. Линейная зависимость векторов. Коллинеарные и компланарные векторы.
5. Параметрические уравнения прямой и плоскости.
6. Общее уравнение прямой в аффинной системе координат на плоскости. Критерий параллельности вектора прямой.
7. Общее уравнение плоскости в аффинной системе координат в пространстве. Критерий парал- лельности вектора плоскости.
8. Скалярное произведение геометрических векторов, его вычисление в прямоугольных декартовых координатах.
9. Векторное и смешанное произведения векторов, их вычисление в прямоугольных декартовых координатах.
10. Нормали к прямой и плоскости. Расстояние от точки до прямой и до плоскости.
11. Алгебраические линии и поверхности. Инвариантность порядка. Матричная запись общего урав- нения второго порядка на плоскости и в пространстве.
12. Приведенные уравнения линии второго порядка на плоскости. Метод вращений.
13. Эллипс. Фокусы и директрисы.
14. Гипербола. Фокусы и директрисы.
15. Парабола. Фокус и директриса.
16. Преобразования прямоугольных декартовых систем координат и ортогональные матрицы.
17. Приведенные уравнения поверхности второго порядка. Метод вращений.
18. Эллипсоид, гиперболоиды, параболоиды, конус и цилиндрические поверхности.
19. Прямолинейные образующие однополостного гиперболоида и гиперболического параболоида.
3
- Пространства R и
.
- Понятие вектора и линейные операции над векторами.
- Скалярное произведение и его свойства.
- Понятие угла между векторами.
- Условие коллинеарности и ортогональности векторов.
- Линейная зависимость векторов.
- Векторное произведение векторов и его свойства.
- Смешанное произведение векторов и его свойства.
- Евклидово пространство. Неравенство Коши-Буняковского.
- Ортогональный базис. Разложение вектора по ортобазису.
- Виды матриц.
- Действия над матрицами.
- Определители второго и третьего порядков, их свойства.
- Алгебраические дополнения и миноры.
- Определители n-го порядка.
- Вычисление определителя разложением по строке (столбцу).
- Понятие обратной матрицы.
- Построение обратной матрицы элементарными преобразованиями.
- Ранг матрицы.
- Системы двух и трех линейных уравнений. Правило Крамера.
- Система m линейных уравнений с n неизвестными.
- Решение системы линейных уравнений методом Гаусса.
- Решение однородных систем линейных уравнений.
- Решение систем линейных уравнений со ступенчатой матрицей.
- Общее решение систем линейных уравнений. Главные и свободные неизвестные.
- Геометрическая интерпретация систем линейных уравнений в случае двух или трех неизвестных.
- Ненулевые решения однородной системы линейных уравнений.
- Преобразование координат при замене базиса.
- Критерий линейной независимости строк (столбцов).
- Матрица линейного оператора.
- Преобразование матрицы линейного оператора при замене базиса.
- Приведение матриц линейного оператора к диагональному виду.
- Свойства собственных векторов с одинаковыми и различными собственными значениями.
- Формула линейного функционала.
- Матрица билинейной формы.
- Матрица симметричной билинейной формы.
- Преобразование матрицы билинейной формы при замене базиса.
- Единственность симметричной билинейной формы, порождающей квадратичную форму.
- Критерий Сильвестра положительной определенности квадратичной формы.









 Скачать 38.9 Kb.
Скачать 38.9 Kb.
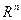 .
.