На этой странице вы узнаете
- Почему неизвестное обозначают через x?
- Откуда у квадратного уравнения растут корни и сколько их?
- Как находить корни квадратного уравнения, не считая их?
С задачами мы сталкиваемся постоянно. Например, когда ведем ежедневник. И каждый раз возникает вопрос: как успеть решить все-все за день? Неужели нет какого-то понятного и простого алгоритма, который всегда будет работать?
В жизни такой алгоритм вряд ли существует. Но математика здесь преуспела! Главный секрет математики в том, что любую задачу можно решить уравнением. А решить уравнение — значит найти все его корни или доказать, что их нет.
Давай разберемся, как это сделать.
Понятие уравнения
Вспомним, что:
Уравнение — это равенство, содержащее неизвестное, обозначенное буквой.

Представим, что перед нами лежит две коробки: закрытая и открытая. Мы видим, что лежит в открытой. И тут нам говорят: коробки одинаковые! Тогда мы можем сделать вывод, что в первой коробке точно такая же «начинка», как и в открытой.
По такой же логике решаются и уравнения: мы знаем, что с обеих сторон от знака «равно» лежит что-то равнозначное.
Корнем уравнения называется такое значение неизвестного, при котором уравнение становится верным равенством.
Например, число 8 будет корнем уравнения (2x-3=5+x), потому что равенство (2*8-3=5+8) верное.
Арабские математики в IX веке для записи формул использовали слова. Неизвестную величину они называли «шей», что буквально означает «нечто». Выглядело это примерно так:
Позднее испанские ученые переводили записи на свой язык. Они записывали неизвестное как xei, поскольку в их языке отсутствовал звук [ш]. С появлением формул слово сократилось до одной буквы x.
Линейные уравнения
Линейное уравнение — это уравнение, в котором неизвестная находится в степени 1.
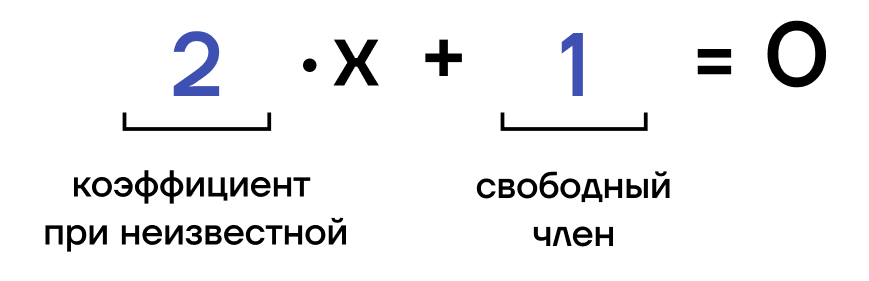
Вид линейного уравнения:
(х) — неизвестная;
(а) — коэффициент при неизвестной;
(b) — свободный член.
Стоит отметить, что а и b в таком уравнение известны, также оба этих числа можно называть коэффициентами.
Линейные уравнения — самые простые, ведь в них нет ни степеней, ни корней. Только переменная, обозначаемая буквой, и несколько цифр.
Предположим, что мы играли с собакой пятью игрушками. Вдруг она убежала и вернулась с еще несколькими вещами. Мы удивились: откуда она их только достала? Но в итоге продолжили играть уже 8 игрушками. Так сколько вещей принесла собака?
Если было пять вещей, а стало восемь, ответ очевиден: 3 игрушки. В виде уравнения это можно записать так:
(5+x=8 => x=3)
Алгоритм решения линейных уравнений
1. Первым делом нужно выразить х. Иными словами, все буквы должны быть в одной стороне, а все цифры в другой.
2. После распределения букв и цифр по разным сторонам от знака равно нужно посчитать, чему равны левая и правая части уравнения.
3. Найти неизвестную.
А какие инструменты у нас есть, чтобы выражать и находить значения переменных? Преобразования, которые можно совершать:
- Переносить слагаемое в другую часть уравнения с противоположным знаком.
(x-5=0
x=0+5
x=5)
Вспомним: цифры и буквы должны быть по разным сторонам от равно, именно поэтому мы перенесли 5. Почему мы поменяли знак? Все просто: значение уравнения не должно поменяться. Иными словами, если мы отнимаем что-то от левой части, то должны отнять и у правой.
- Умножать или делить обе части уравнение на одно и то же число или выражение, которое не равно нулю.
(3x=12 |: 3)
(frac{3x}{3}=frac{12}{3})
(x=4)
Здесь работает такое же правило, как и в предыдущем пункте. Чтобы все было «по-честному», если мы что-то делаем с одной стороной уравнения, то же действие производится и со второй стороной.
Давайте рассмотрим решение линейного уравнения на следующем примере
(2x+5-4x+2=0)
- Сначала раскроем скобки. Для этого умножим каждое слагаемое в скобке на число перед ней.
(2*x+2*5-4x+2=0)
(2x+10-4x+2=0)
- Для упрощения сложим подобные слагаемые, то есть слагаемые, у которых совершенно одинаковые переменные. Если у нас просто числа без переменных, то они тоже будут подобными слагаемыми: их сближает отсутствие буквы.
((2x-4x)+(10+2)=0)
(-2x+12=0)
- А теперь уже известное нам действие: буквы влево, цифры вправо. Поэтому мы переносим число 12 на другую сторону, не забывая поменять знак.
(-2x=-12)
Чтобы найти значение х, нужно, чтобы слева переменная была «чистой», то есть без коэффициентов. Поэтому мы делим все уравнение на (-2).
(frac{-2x}{-2}=frac{-12}{-2})
(x=6)
Значение неизвестной найдено, то есть единственное решение данного уравнения 6.
С линейными уравнениями можно столкнуться и в жизни. Допустим, нам нужно приготовить 570 грамм теста на пирожки.
Обозначим вес одной части за x. Составим и решим уравнение для получения этого количества теста:
(12x+6x+x=570)
(19x=570)
(x=30)
Мы узнали, что одна часть — это 30 грамм. Теперь посчитаем, сколько грамм продуктов нам потребуется.
Мука: 12*30=360 грамм.
Вода: 6*30=180 грамм.
Растительное масло: 1*30=30 грамм.
Квадратные уравнения
Мы уже знаем, что такое линейное уравнение. Но как выглядит квадратное? Неужели геометрия пробралась и сюда?
На самом деле все проще: название этого вида уравнения вовсе не связано с геометрическими фигурами: оно происходит от степени.
Квадратное уравнение — это уравнение, в котором неизвестная находится в степени 2.
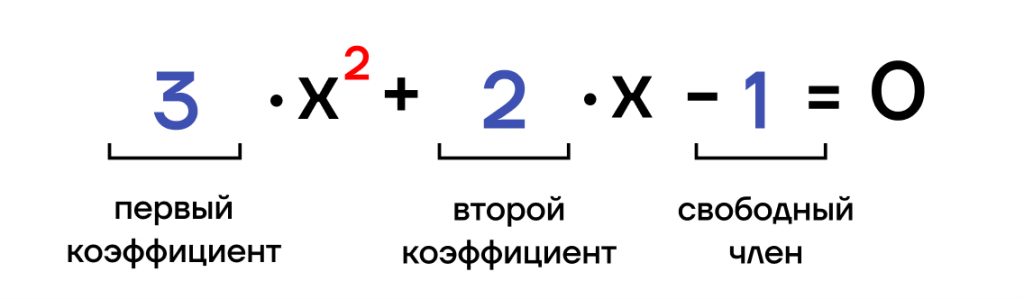
Вид квадратного уравнения:
(х) — неизвестная;
(а) и (b) — коэффициенты при неизвестной;
(с) — свободный член.
Стоит отметить, что а, b и с — известные числа.
Какими бывают квадратные уравнения?
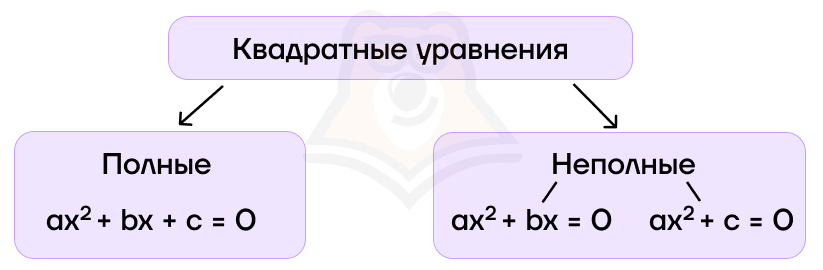
Эти виды квадратных уравнений отличаются тем, что у полного квадратного уравнения есть оба коэффициента и свободный член, а у неполного может отсутствовать или второй коэффициент, или свободный член.
Рассмотрим решение несколько неполных квадратных уравнений на примере:
- (x^2+2x=0).
Вспомним, что (x^2) — это (x*x), а (2x) — это (2*x). Тогда наше уравнение примет следующий вид:
(x*x+2*x=0).
Мы видим общий множитель х, а значит, его можно вынести за скобку:
(x(x+2)=0).
Если произведение двух множителей равно 0, то каждый множитель равен 0.
Отсюда мы получаем два уравнения: (x=0) и (x+2=0), следовательно,
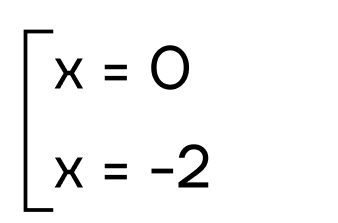
Ответ: 0 и -2.
- (x^2-4=0).
Снова воспользуемся простым правилом: буквы влево, цифры вправо:
(x^2=4).
А теперь, чтобы найти значение переменной, достаточно будет извлечь квадратный корень:
(x=±2).
Почему у нас получилось два числа? Все просто: если возвести в квадрат число 2, то получится 4, также будет и с числом ((-2): (-2)^2=(-2)*(-2)=4).
Ответ: 2 и -2.
Теперь переходим к другому виду уравнений — полное квадратное уравнение. Оно может иметь 2 корня, 1 корень или не иметь корней. Количество корней зависит от дискриминанта.
Что такое дискриминант?
Дискриминант в квадратном уравнении — это выражение, которое ищется по следующей формуле, где а, b и с берутся из уравнения:
(D=b^2-4⋅a⋅c)
Ответ может быть разным, и зависеть он будет именно от дискриминанта. Достаточно запомнить три факта:
— Если D > 0, то уравнение имеет 2 корня.
— Если D = 0, то уравнение имеет 1 корень.
— Если D < 0, то уравнение не имеет корней.
Неужели мы должны тратить свои силы, чтобы просто узнать, какое количество корней у уравнения? Неужели нельзя сразу решить и узнать ответ? Но дискриминант нас обхитрил: он нужен не только для того, чтобы узнать количество корней, но и для решения уравнения.
Способов решения квадратных уравнений очень много. Рассмотрим самые популярные среди них.
Способы решения квадратных уравнений
- Решение через дискриминант.
Корни квадратного уравнения находятся по этим формулам, где а и b берутся из уравнения, а D — это дискриминант:
(x_1=frac{-b+sqrt{D}}{2⋅a}
x_2=frac{-b-sqrt{D}}{2⋅a})
Заметим, что у нас появляются (x_1) и (x_2). Это связано с тем, что в квадратном уравнении ищется 2 корня.
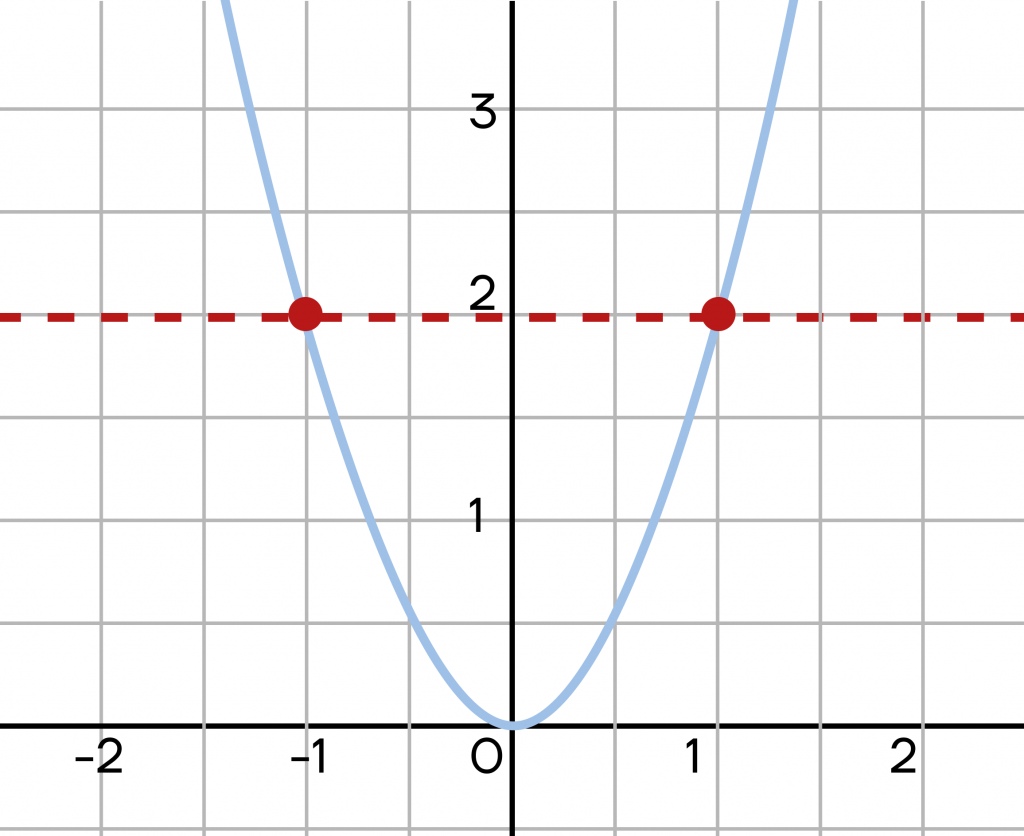
Теперь присмотримся к формулам: они отличаются только тем, что перед корнем из дискриминанта стоит разный знак. Почему так происходит? На самом деле, квадратное уравнение описывает параболу, и если провести в любом ее месте горизонтальную линию, то получим две точки на ветвях. Поэтому мы делаем шаги «в разные стороны». А подробнее про параболы и чтение графиков можно узнать в статье «Основные элементарные функции».
А какой формулой пользоваться в случае, если дискриминант равен 0? Если мы подставим D=0 в данные формулы, то получим:
(x_1=frac{-b+sqrt{D}}{2⋅a}=frac{-b+sqrt{0}}{2a}=frac{-b}{2a}) и (x_2=frac{-b-sqrt{D}}{2⋅a}=frac{-b-sqrt{0}}{2a}=frac{-b}{2a}).
Следовательно, (x_1=x_2) и можно воспользоваться одной формулой:
(x_1=frac{-b}{2⋅a})
Алгоритм решения квадратного уравнения через дискриминант
1. Определить, чему равны коэффициенты при каждом члене уравнения. Иными словами, необходимо найти a, b, c.
2. Найти дискриминант по формуле и определить, какое количество корней будет у уравнения. Это поможет не ошибиться в дальнейшем решении.
3. Подставить коэффициенты и дискриминант в формулы и посчитать корни.
- По теореме Виета.
По теореме Виета корни нужно подбирать, то есть искать их не вычисляя, а просто подставляя нужное число. Поэтому она удобна для нахождения рациональных корней (чисел, которые можно представить в виде обыкновенной дроби).
В чем заключается теорема Виета? Это система из двух формул, в которую подставляются коэффициенты при переменных. Такую систему нужно лишь запомнить и немного потренироваться ее использовать.
А вот что применять: решение через дискриминант или теорему Виета — это дело вкуса. Тем и прекрасна математика: решить один и тот же пример можно несколькими способами, причем ответ всегда будет одинаковым.
Франсуа Виет выявил интересную связь между коэффициентами квадратного уравнения и корнями этого же уравнения. Эта связь формулируется так:
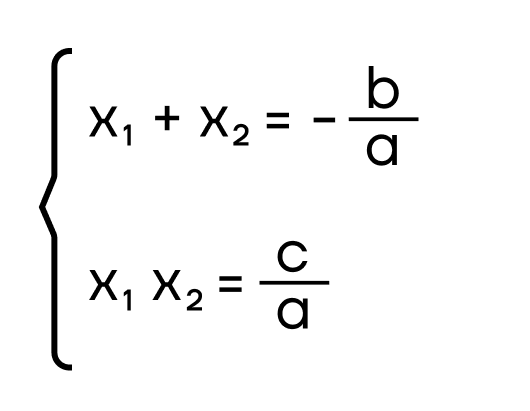
(а, b) и (с) — коэффициенты квадратного уравнения;
(x_1) и (x_2) — корни квадратного уравнения.
Алгоритм решения квадратного уравнения с помощью теоремы Виета
1. Определить, чему равны коэффициенты при каждом члене уравнения.
2. Подставить в формулы известные числа.
3. Найти корни уравнения.
Давайте рассмотрим решение квадратного уравнения на следующем примере
(2x^2-5x-3=0).
Коэффициенты нам уже известны: (a=2, b=-5, c=-3).
1 способ:
- Найдем дискриминант:
(D=b^2-4ac=(-5)^2-4⋅2⋅-3=25+24=49).
- Дискриминант больше нуля, следовательно, у уравнения 2 корня, найдем их:
(x_1=frac{-b+sqrt{D}}{2a}=frac{-(-5)+sqrt{49}}{2⋅2}=frac{5+7}{4}=frac{12}{4}=3.)
(x_2=frac{-b-sqrt{D}}{2a}=frac{-(-5)-sqrt{49}}{2⋅2}=frac{5-7}{4}=frac{-2}{4}=-frac{1}{2}.)
Решениями уравнения являются числа (3) и (-frac{1}{2}).
2 способ:
- Запишем систему по теореме Виета:
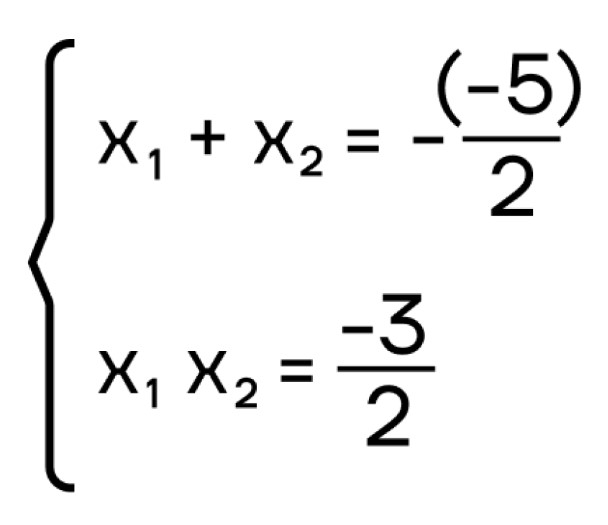
- Теперь подберем такие два числа, чтобы их сумма была (frac{5}{2}), а произведение ((-frac{3}{2})), это будут числа (3) и (-frac{1}{2}).
Значит, решениями уравнения являются числа (3) и (-frac{1}{2}).
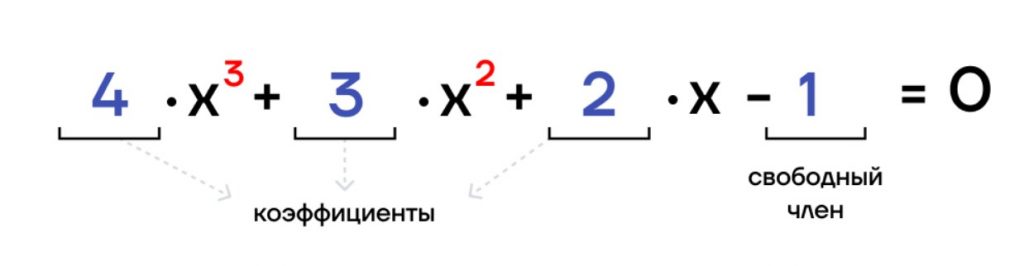
Кубические уравнения
Перейдем к последнему виду уравнений. Их название тоже связано не со стереометрией, а со степенью.
Кубическое уравнение — это уравнение, в котором неизвестная находится в степени 3.
Вид кубического уравнения:
(х) — неизвестная;
(а, b) и (с) — коэффициенты при неизвестной;
(d) — свободный член.
Стоит отметить, что а, b, с и d — известные числа.
Преобразования, которые можно совершать в кубических уравнениях:
- Вынесение общего множителя за скобки.
Предположим, у нас есть две тарелки с фруктами, но вот беда: мы любим только апельсины. В каждой тарелке лежит по два апельсина, следовательно, мы можем переложить их в одну тарелку, а все остальные фрукты в другую. После чего довольными пойти кушать апельсины и смотреть сериалы. Таким образом, само содержание тарелок у нас не поменяется, но расположение фруктов в них изменится.
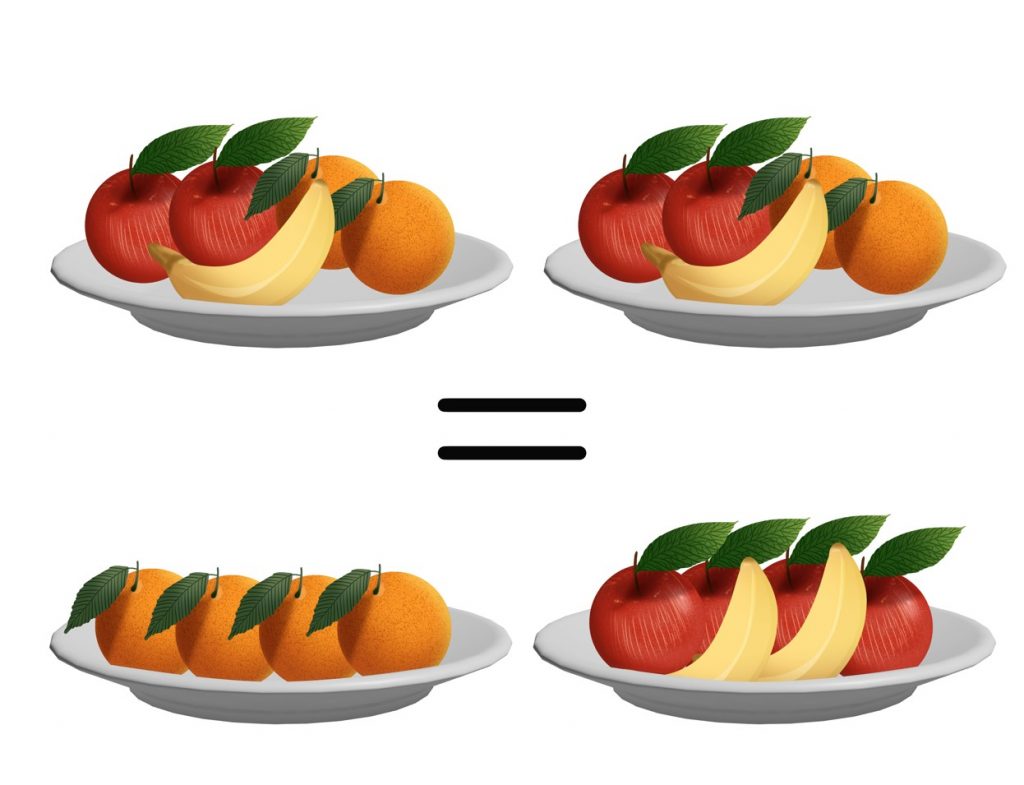
Алгоритм решения кубического уравнения методом вынесения общего множителя за скобку
1. Разложить каждое слагаемое на множители.
2. Вынести за скобку множители, которые есть в обоих слагаемых.
3. Вынести скобку, как общий множитель.
Пример:
(x^3-2x^2-3x=x*x*x-2*x*x-3*x=x(x^2-2x-3)).
- Группировка.
В этом случае мы действуем аналогично, но переменная, которую мы выносим за скобку, усложняется: мы перекладываем в другую тарелку не только апельсины, но и бананы.
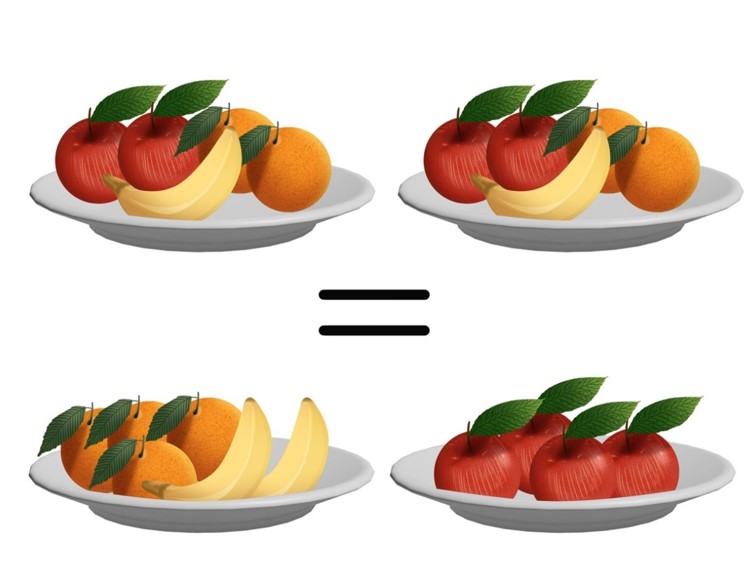
Алгоритм решения кубического уравнения методом группировки
Объединить слагаемые в пары.Вынести общий множитель из каждой скобки, чтобы получились одинаковые скобки.Еще раз вынести общий множитель так, чтобы получилось произведение.
Пример: (6x^3+9x^2+8x+12=6x^3+9x^2+8x+12=)
(=(3x^2*2x+3x^2*3)+(4*2x+4*3)= 3x^2(2x+3)+4(2x+3)=
=(3x^2+4)(2x+3).)
Рассмотрим решение кубического уравнения.
(4x+x^3=x^2+4)
- Перенесем все слагаемые в левую часть, чтобы дальнейшие преобразования было удобнее совершать.
(4x+x^3-x^2-4=0.)
- Заметим, что повторяются четверки, значит, они должны быть в разных группах. При этом у нас есть две переменные, степени которых отличаются не так сильно, тогда их тоже можно развести в разные группы. Получается, что удобнее группировать 1-е и 2-е слагаемые и 3-е и 4-е слагаемые.
((4x+x^3)-(x^2+4)=0.)
- Вынесем общий множитель х из первой скобки:
(x(4+x^2)-(x^2+4)=0.)
- Вынесем еще один общий множитель (x^2+4) за скобки:
((x-1)(4+x^2)=0.)
Почему в первой скобке получилось (х – 1)? Заметим, что до вынесения общего множителя за скобку, перед вторым слагаемым стоял просто минус. В этом случае запись можно заменить на аналогичную:
(x(4+x^2)-1*(x^2+4)=0)
((x-1)(4+x^2)=0)
- Чтобы произведение было равно 0, один из множителей должен быть равен 0. Запишем совокупность:
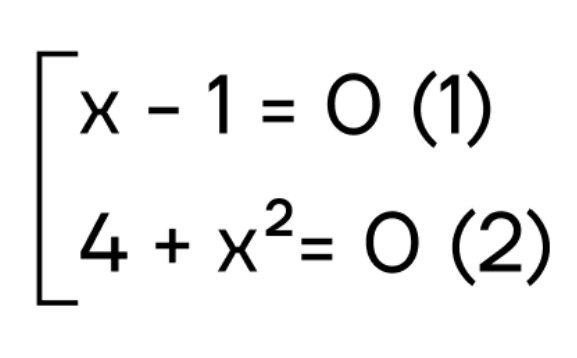
- Решим каждое уравнение отдельно:
| (x-1=0) (x=1) |
(4+x^2=0) (x^2=-4) Нет решений, так как (x^2 ≥ 0) верно для любого х. |
Из этого следует, что у данного уравнения есть только одно решение x=1.
Почему важно уметь решать уравнения? Они могут встретиться во всех заданиях на ОГЭ и ЕГЭ. Уравнения — это основа любой задачи, а значит, их нужно уметь решать, чтобы справляться с более сложными заданиями.
Теперь, когда вы разобрались в линейных, квадратных и кубических уравнениях мы предлагаем вам усложнить задачу и познакомиться с целыми рациональными, дробно-рациональными и иррациональными уравнениями.
Термины
Обыкновенная дробь — это запись вида m/n, где m и n любые натуральные числа (числа, используемые при счете). Например, (frac{1}{2}).
Система уравнений — это два и более равенства, объединенных фигурной скобкой, имеющих несколько решений, которые одновременно являются решениями для всей системы.
Фактчек
- В линейном уравнении неизвестная находится в степени 1. Для решения такого уравнения в одной части уравнения нужно оставить только неизвестную, а в другой собрать все остальное.
- В квадратном уравнении неизвестная в квадрате, то есть в степени 2. Решать такое уравнение можно, например, через дискриминант:
(D=b^2-4⋅a⋅c)
(x_1=frac{-b+sqrt{D}}{2⋅a})
(x_2=frac{-b-sqrt{D}}{2⋅a})
Второй способ решения квадратного уравнения: теорема Виета:
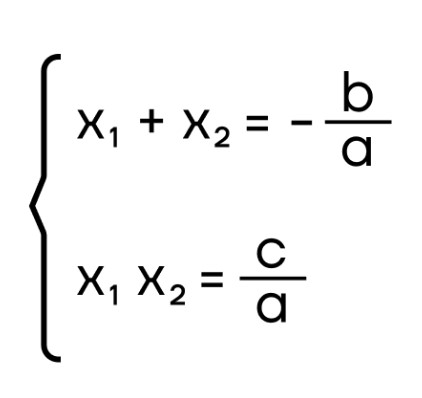
- В кубическом уравнении неизвестная находится в кубе, то есть в степени 3. Для решения такого уравнения используется вынесение общего множителя за скобки и способ группировки.
Проверь себя
Задание 1.
Найдите корень уравнения (2x+4⋅3-2x=0).
- 3
- 2
- -2
- -3
Задание 2.
Сколько корней будет у уравнения (x^2+x-2=0)?
- нет корней
- один корень
- два корня
- три корня
Задание 3.
Найдите корни уравнения (x^2+4x-5=0).
- 1 и 5
- 1 и -5
- 1 и 2
- -1 и 2
Задание 4.
Найдите корни уравнения (x^2-5x=0).
- 0 и 5
- 2 и 5
- 25 и 5
- 0 и 4
Задание 5.
Найдите корни уравнения (12x+4-12x^3-4x^2=0).
- (frac{-1}{3})
- (-1) и (1)
- (-1, -frac{1}{3}) и (1)
- (-1, frac{1}{3}) и (1)
Ответы: 1. — 4; 2. — 3; 3. — 2; 4. — 1; 5. — 3.
Задание 745
Найдите корень уравнения: $$frac{4}{7}x=7frac{3}{7}$$
Ответ: 13
Скрыть
$$frac{4}{7}x=7frac{3}{7}Leftrightarrow$$ $$frac{4}{7}x=frac{52}{7}Leftrightarrow$$$$x=frac{52}{7}*frac{7}{4}Leftrightarrow$$$$x=13$$
Задание 749
Найдите корень уравнения: $$(x-6)^{2}=-24x$$
Ответ: -6
Скрыть
$$(x6)^{2}=-24xLeftrightarrow$$$$x^{2}-12x+36=-24xLeftrightarrow$$$$x^{2}+12x+36=0Leftrightarrow$$$$(x+6)^{2}=0Leftrightarrow$$$$x=-6$$
Задание 1486
Найдите корень уравнения $$8(6+x)+2x=8$$.
Ответ: -4
Задание 1723
Найдите корни уравнения $$25x^2-1=0$$.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: -0,2; 0,2
Скрыть
$$25x^2-1=0 Leftrightarrow$$$$25x^{2}=1 Leftrightarrow $$$$x^{2}=frac{1}{25} Leftrightarrow $$$$x=pm sqrt{frac{1}{25}}=$$$$pmfrac{1}{5}=pm 0,2$$
Задание 1724
Найдите корни уравнения $$2x^2-10x=0$$.
Если корней несколько, запишите их через точку с запятой в порядке возрастания.
Ответ: 0; 5
Скрыть
$$2x^2-10x=0 Leftrightarrow$$$$2x(x-5)=0 Leftrightarrow$$$$x=0 ; x=5$$
Задание 1727
На рисунке изображены графики функций $$y=3-x^2$$ и $$y=-2x$$. Вычислите координаты точки B.
Ответ: 3; -6
Скрыть
Приравняем функции, и найдем координаты точки, абсцисса которой будет положительна:
$$3-x^{2}=-2x$$
$$x^{2}-2x-3=0$$
По теореме Виета:
$$left{begin{matrix}x_{1}+x_{2}=2\x_{1}*x_{2}=-3 end{matrix}right.Leftrightarrow$$$$left{begin{matrix}x_{1}=3\x_{2}=-1end{matrix}right.$$
То есть рассматривать мы будем точку с абсциссой 3. Подставим ее в любую из функций:
$$y(3)=3-3^{2}=-6$$
То есть координаты точки B $$(3;-6)$$
Задание 1728
Уравнение $$x^2+px+q=0$$ имеет корни −6; 4. Найдите p.
Ответ: 2
Скрыть
По теореме Виета: $$x_{1}+x_{2}=-p$$, тогда $$p=-(-6+4)=2$$
Задание 1729
Квадратный трёхчлен разложен на множители: $$x^2+6x-27=(x+9)(x-a)$$. Найдите a.
Ответ: 3
Скрыть
Для этого воспользуемся формулой : $$ax^{2}+bx+c=a(x-x_{1})(x-x_{2})$$, где $$x_{1}$$ и $$x_{2}$$ — корни уравнения $$ax^{2}+bx+c=0$$
$$x^2+6x-27=0$$
По теореме Виета:
$$left{begin{matrix} x_{1}+x_{2}=-6\x_{1}*x_{2}=27end{matrix}right.Leftrightarrow$$$$left{begin{matrix} x_{1}=-9\x_{2}=3end{matrix}right.$$
Тогда $$ax^{2}+bx+c=(x+9)(x-3)$$
Задание 1730
Решите уравнение $$(x-4)^{2}+(x+9)^{2}=2x^{2}$$.
Ответ: -9,7
Скрыть
$$(x-4)^{2}+(x+9)^{2}=2x^{2}$$
$$x^{2}-8x+16+x^{2}+18x+81-2x^{2}=0$$
$$10x+97=0$$
$$10x=-97| :10$$
$$x=-9,7$$
Задание 1747
Решите уравнение: $$(-5x+3)(-x+6)=0$$.
Если корней несколько, запишите их в ответ в порядке возрастания, через точку с запятой.
Ответ: 0,6; 6
Скрыть
$$(-5x+3)(-x+6)=0 Leftrightarrow $$произведение равно нулю, когда один из множителей равен нулю $$left [ begin{matrix}-5x+3=0\ -x+6=0end{matrix}right.Leftrightarrow $$$$left [ begin{matrix}-5x=-3|:(-5)\ -x=-6|:(-1)end{matrix}right.Leftrightarrow $$$$left [ begin{matrix}x=0,6\ x=6end{matrix}right.$$
Задание 4660
Решите уравнение $$x^{12}=(4x-3)^{6}$$. Если уравнение имеет более одного корня, в ответе укажите наибольший из них.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Извлекаем корень шестой степени. Следует учитывать, что если извлекается корень четной степени из выражения в этой же степени, то остается в итоге модуль выражения, то есть $$sqrt[2n]{(y)^{2n}}=|y|$$. Получаем: $$x^{2}=|4x-3|$$
Решаем с учетом раскрытия модуля: Если $$xgeq frac{3}{4}$$, то: $$x^{2}=4x-3$$, и корни это уравнения 1 и 3
Если $$x< frac{3}{4}$$, то: $$x^{2}=-4x+3$$. Получим иррациональные корни $$-2pm sqrt{7}$$, каждый из которых меньше 3.
Задание 8883
Найдите корень уравнения: $$3frac{5}{9}x=5frac{1}{3}$$
Ответ: 1,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10043
Найдите корень уравнения $$(2x-1,4)^{3}=-512$$
Ответ: -3,3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10851
Найдите корень уравнения $${left(6x-13right)}^2={left(6x-11right)}^2$$.
Ответ: 2
Скрыть
Возведем в квадрат левую и правую части уравнения: $$36x^2-156x+169=36x^2-132x+121$$.
Упростим выражение, получим: $$-156x+132x=121-169to x=2$$
Задание 10991
Решите уравнение $${left(x+3right)}^2={left(x+3right)}^4$$. В ответе укажите меньший корень.
Ответ: -4
Скрыть
$${left(x+3right)}^2={left(x+3right)}^4; $$пусть $${left(x+3right)}^2=yge 0:$$
<div class=»respons-table-block»>$$y=y^2to yleft(y-1right)=0leftrightarrow left[ begin{array}{c} {left(x+3right)}^2=0 \ {left(x+3right)}^2=1 end{array} right.leftrightarrow left[ begin{array}{c} x=-3 \ x=-2 \ x=-4 end{array} right.to $$</div>
Ответ: -4
Линейные, квадратные, кубические уравнения
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = /$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
2. Решаем получившиеся уравнения каждое отдельно.
Вынесем х как общий множитель за скобки:
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
При решении последнего уравнения возможны два случая:
2. $D = 0$. В данном случае решение даёт два двукратных корня:
Извлечем кубический корень из обеих частей
Соберем известные слагаемые в правой части
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x · x + 1 · x — <3·x>/ = 0$
3. решаем полученное уравнение
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = <3>/<4>$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = <3>/<4>$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
Воспользуемся основным свойством пропорции
Раскроем скобки и соберем все слагаемые в левой части уравнения
Решим данное квадратное уравнение первым устным способом, т.к.
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
Линейные, квадратные и простейшие кубические уравнения. Примеры
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). [f(x)=g(x) qquad qquad (1)] Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой (x) .
Замечание
Заметим, что (x) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида ((1)) будем называть множество значений переменной (x) , при которых определены (то есть не теряют смысла) функции (f(x)) и (g(x)) .
Пример
Уравнение (dfrac <10>=5) определено при всех значениях переменной (x) , кроме (x=1) , потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения (xin (-infty;1)cup(1;+infty)) .
Определение
Корнем уравнения называется то числовое значение (x) , при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число (x=3) , потому как тогда уравнение принимает вид (dfrac<10><3-1>=5) или, что то же самое, (5=5) , что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение (dfrac 1x=0) ни при каких значениях (x) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель (1ne 0) .
2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.
Определение
Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения.
Например, уравнения (x=3) и (3x=6+x) эквивалентны, т.к. оба имеют единственное решение (x=3) .
Эквивалентность уравнений обозначается так: (x=3 quad Leftrightarrow quad 3x=6+x) .
Свойства уравнений
1. В любом уравнении можно переносить слагаемые из одной части равенства в другую, при этом меняя их знак на противоположный. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+4=2x^2) можно переписать в виде (x+4-2x^2=0) .
2. В любом уравнении можно правую и левую части умножать или делить на одно и то же число, не равное нулю. При этом полученное уравнение равносильно исходному.
Например, уравнение (0,5x=-2) равносильно уравнению (x=-4) , которое получено из исходного путем умножения обеих частей на (2) .
3. В любом уравнении можно к правой и левой частям прибавлять одно и то же число. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+2=5x^2) после прибавления к обеим частям (-2) примет вид (x=5x^2-2) .
[<Large<text<Линейные уравнения>>>] Линейное уравнение – это уравнение вида [ax + b = 0qquad qquad (2)] где (ane 0,b) – числа, или уравнение, к нему сводящееся.
ОДЗ линейного уравнения ((2)) — все (x inmathbb) .
Линейное уравнение (ax+b=0) преобразуется в (ax=-b) и всегда имеет единственное решение (x=-dfrac ba) .
Например, (2x-4=0) имеет корень (x=2) . Замечание: при переносе слагаемых из одной части равенства в другую знак слагаемого меняется на противоположный. Например, выражение (x-5=8) преобразуется в выражение (x=8+5) .
Знак, стоящий перед слагаемым – это и есть его знак, то есть в выражении (x-5) два слагаемых: (x) и (-5) . Если перед слагаемым не стоит никакого знака, то подразумевается, что перед ним стоит знак “ (+) ”.
[<Large<text<Квадратные уравнения>>>] Квадратное уравнение – это уравнение вида [ax^2+bx+c=0 qquad qquad (3)] где (a, b, c) – числа, причем (ane 0) , или уравнение, к нему сводящееся.
Число (a) называется старшим (первым) коэффициентом, число (b) – вторым коэффициентом, число (c) – свободным членом.
Замечание
1) Заметим, что если (a=0) , то уравнение ((3)) становится линейным; именно поэтому в определении (ane 0) .
2) Выражение (ax^2+bx+c) называется квадратичным (квадратным) трехчленом.
ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене (7-x^2+2x) коэффициент (a=-1) , (b=2) и (c=7) ! Так как (7-x^2+2x=-x^2+2x+7) , а по определению (a) – коэффициент перед (x^2) , (b) – коэффициент перед (x) , (c) – свободный член.
Определение
Дискриминантом квадратного уравнения ((3)) называется выражение (D=b^2-4ac) .
Корни квадратного уравнения
1) Если дискриминант квадратного уравнения больше нуля ( (D>0) ), то оно имеет два различных корня [x_1=dfrac<-b-sqrt D> <2a>qquad text <и>qquad x_2=dfrac<-b+sqrt D><2a>]
2) Если дискриминант квадратного уравнения равен нулю ( (D=0) ), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) [x=-dfrac b<2a>]
3) Если дискриминант квадратного уравнения меньше нуля ( (D ), то оно не имеет корней.
Пример:
Решите уравнение [3x^2 — 33x + 90 = 0.]
Решение.
Найдём дискриминант данного уравнения: [D = 33^2 — 4cdot 3cdot 90 = 9] Следовательно, уравнение имеет два различных корня, равных [x_1=dfrac<33 + 3> <6>= 6 qquad text <и>qquad x_2=dfrac<33 — 3> <6>= 5]
Теорема Виета
Пусть квадратное уравнение (ax^2 + bx + c = 0) , (aneq 0) , имеет два корня (x_1) и (x_2) (возможно, совпадающих), то есть (Dgeqslant 0) . Тогда их сумма равна [x_1+x_2=-dfrac] а их произведение равно [x_1cdot x_2=dfrac]
Доказательство
Определение
Квадратное уравнение называется приведенным, если старший коэффициент (a=1) .
Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на (a) .
Следствие
Для приведенного квадратного уравнения (x^2+px+q=0) теорема Виета выглядит следующим образом: [x_1+x_2=-p, qquad qquad x_1cdot x_2=q]
Теорема: разложение на множители квадратного трехчлена
Пусть уравнение (ax^2 + bx + c = 0) , (aneq 0) , имеет два корня (возможно, совпадающих), то есть (Dgeqslant 0) . Тогда при любом значении (x) выполнено [ax^2 + bx + c = a(x — x_1)(x — x_2),] где (x_1) и (x_2) – корни уравнения (ax^2 + bx + c = 0) (возможно, совпадающие).
Доказательство
Сделаем преобразования: [begin &a(x-x_1)(x-x_2)=aleft(x — dfrac<-b + sqrt><2a>right)left(x — dfrac<-b — sqrt><2a>right) =aleft(x^2 — xleft(dfrac<-b + sqrt> <2a>+ dfrac<-b — sqrt><2a>right) + dfrac<4a^2>right)=\[2ex] &=aleft(x^2-xcdot left(-dfrac baright)+dfrac<4a^2>right) =a(x^2+dfrac ba x+dfrac ca)=ax^2+bx+c end]
Пример
Разложить на множители квадратный трехчлен (3x^2-2x-1) .
Решение.
Рассмотрим уравнение (3x^2-2x-1=0) и найдем его корни.
(D=(-2)^2-4cdot 3cdot (-1)=16) , значит
Таким образом, (3x^2-2x-1=3(x-1)(x+frac13)=(x-1)(3x+1)) .
[<Large<text<Простейшие кубические уравнения>>>] (bullet) Кубический корень из числа (a) – это такое число (b) , которое при возведении в куб равно (a) : [sqrt[3] a=bquad text<то же самое, что >quad a=b^3] (bullet) Таблица кубов чисел от 1 до 10: [begin <|ll|>hline 1^3=1 & quad6^3=216 \ 2^3=8 & quad7^3=343\ 3^3=27 & quad8^3=512\ 4^3=64 & quad9^3=729\ 5^3=125 & quad10^3=1000\ hline end] (bullet) Простейшие кубические уравнения – уравнения, сводящиеся к виду [x^3=a] Для любого числа (a) такие уравнения имеют единственный корень [x=sqrt[3]a] Пример:
1) решением уравнения (x^3=-8) является (x=sqrt[3]<-8>=-2) .
2) решением уравнения (x^3=64) является (x=4) .
Теория линейных и квадратных уравнений традиционно изучается школьниками Москвы и других городов в 8 классе. И хотя данная тема рассматривается в рамках образовательного курса достаточно подробно, и ей отводится немало времени, с заданиями из этого раздела выпускники не всегда справляются с легкостью. Именно поэтому, готовясь к сдаче ЕГЭ, учащимся непременно стоит освежить в памяти теорию и разобраться в решении задач с линейными и квадратными уравнениями.
Сделать это легко, оперативно и эффективно вам позволит образовательный портал «Школково». Всю необходимую теорию по теме «Квадратные и линейные уравнения» для подготовки к ЕГЭ вы можете найти в соответствующем разделе. Весь базовый материал составлен нашими специалистами на основе многолетнего опыта и представлен в максимально доступной форме. Изучив определения, формулы и основные свойства линейных и квадратных уравнений, учащиеся смогут не только вспомнить всею необходимую теорию, но и грамотно объяснить принцип решения задач ЕГЭ. Закрепить усвоенный материал вам помогут упражнения в разделе «Каталог». Здесь вы можете найти как простые, так и более сложные задачи по данной теме. Для каждого задания на сайте наши специалисты прописали подробный алгоритм решения и правильный ответ.
Изучить теорию по теме «Линейные и квадратные уравнения» и попрактиковаться в выполнении упражнений можно в режиме онлайн. При необходимости любое задание можно сохранить в «Избранное», чтобы в дальнейшем можно было к нему вернуться или обсудить с преподавателем.
источники:
http://mathlesson.ru/node/8077
http://shkolkovo.net/theory/109
Каталог заданий.
Линейные, квадратные, кубические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 5 № 26662
Найдите корень уравнения:
Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 5 № 26663
Найдите корень уравнения:
Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
3
Тип 5 № 77368
Решите уравнение
Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 5 № 77369
Решите уравнение
Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
5
Тип 5 № 77371
Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.
Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения
Решение
·
·
Курс Д. Д. Гущина
·
3 комментария · Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
Поверните устройство
- Классы
- ЕГЭ (профиль)
- 01. Простейшие уравнения
- Теория: 01. Линейные уравнения и раскрытие скобок (целые коэффициенты)
Решите линейное уравнение:
Решим линейное уравнение
Для его решения нужно сначала раскрыть скобки в обеих частях этого уравнения, а затем решить полученное линейное уравнение.
1. Раскроем скобки:
2. Решим полученное линейное уравнение:
Перенеся (displaystyle color< 7x>) в левую часть, а (displaystyle color< -2>) в правую часть с противоположными знаками, получаем:
Разделив обе части уравнения на (displaystyle 12<small ,>) получаем:
Линейные, квадратные, кубические уравнения
Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.
Линейные уравнения
Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$
Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.
$5 (5 + 3х) — 10х = 8$
$25 + 15х — 10х = 8$
Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.
$15х — 10х = 8 — 25$
Приведем подобные слагаемые.
$5х = -17$ — это конечный результат преобразований.
После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = /$
Квадратные уравнения
Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.
Числа $a, b, c$ называются коэффициентами квадратного уравнения.
- $a$ — старший коэффициент;
- $b$ — средний коэффициент;
- $c$ — свободный член.
Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.
Решение неполных квадратных уравнений
Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.
1. Вынесем общий множитель $x$ за скобки.
Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:
2. Решаем получившиеся уравнения каждое отдельно.
Вынесем х как общий множитель за скобки:
Приравняем каждый множитель к нулю и найдем корни уравнения.
$x = 0$ или $4х — 5 = 0$
$х_1 = 0 х_2 = 1,25$
Ответ: $х_1 = 0; х_2 = 1,25$
Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$
Для решения данного неполного квадратного уравнения выразим $x^2$.
При решении последнего уравнения возможны два случая:
2. $D = 0$. В данном случае решение даёт два двукратных корня:
Извлечем кубический корень из обеих частей
Соберем известные слагаемые в правой части
Дробно рациональные уравнения
Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.
Чтобы решить дробное уравнение, необходимо:
- найти общий знаменатель дробей, входящих в уравнение;
- умножить обе части уравнения на общий знаменатель;
- решить получившееся целое уравнение;
- исключить из его корней те, которые обращают в ноль общий знаменатель.
1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
2. находим общий знаменатель дробей и умножаем на него обе части уравнения
$4x · x + 1 · x — <3·x>/ = 0$
3. решаем полученное уравнение
Решим вторым устным способом, т.к. $а + с = b$
Тогда $х_1 = — 1, х_2 = <3>/<4>$
4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Ответ: $х_1 = — 1, х_2 = <3>/<4>$
При решении уравнения с двумя дробями можно использовать основное свойство пропорции.
Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)
Воспользуемся основным свойством пропорции
Раскроем скобки и соберем все слагаемые в левой части уравнения
Решим данное квадратное уравнение первым устным способом, т.к.
В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.
Репетитор по математике
Меня зовут Виктор Андреевич, — я репетитор по математике . Последние десять лет я занимаюсь только преподаванием. Я не «натаскиваю» своих учеников. Моя цель — помочь ребенку понять предмет, научить его мыслить, а не применять шаблоны, передать свои знания, а не просто «добиться результата».
Предусмотрен дистанционный формат занятий (через Skype или Zoom). На первом же уроке оцениваем уровень подготовки ребенка. Если ребенка устраивает моя подача материала, то принимаем решение о дальнейшем сотрудничестве — составляем расписание и индивидуальный план работы. После каждого занятия дается домашнее задание — оно всегда обязательно для выполнения. [в личном кабинете родители могут контролировать успеваемость ребенка]
Стоимость занятий
Набор на 2020/2021 учебный год открыт. Предусмотрен дистанционный формат.
Видеокурсы подготовки к ЕГЭ-2021
Решения авторские, то есть мои (автор ютуб-канала mrMathlesson — Виктор Осипов). На видео подробно разобраны все задания.
Теория представлена в виде лекционного курса, для понимания методик, которые используются при решении заданий.
Группа Вконтакте
В группу выкладываются самые свежие решения и разборы задач. Подпишитесь, чтобы быть в курсе и получать помощь от других участников.
Преимущества
Педагогический стаж
Сейчас существует много сайтов, где вам подберут репетитора по цене/опыту/возрасту, в зависимости от желаний. Но большинство анкет там принадлежат либо студентам, либо школьным учителям. Для них репетиторство — дополнительный временный заработок, из этого формируется отношение к деятельности. У студентов нет опыта и желания совершенствоваться, у школьных учителей — нет времени и сил после основной деятельности. Я занимаюсь только репетиторством с 2010 года. Все свои силы и знания трачу на совершенствование только в этой области.
Собственная методика
За время работы я накопил огромное количество материала для подготовки к итоговым экзаменам. Ребенку не будет даваться неадаптированная школьная программа. С каждым я разберу поэтапно специфичные примеры, темы, способы решений, необходимые для успешной сдачи ЕГЭ и ОГЭ. При этом это не будет «натаскиванием» на решение конкретных задач, но полноценная структурированная подготовка. Естественно, если таковые найдутся, устраню «пробелы» и в школьной программе.
Гарантированный результат
За время моей работы не было ни одного случая, где не прослеживалась бы четкая тенденция к улучшению знаний у ученика. Ни один откровенно не «завалил» экзамен. Каждый вырос в «понимании» математики в сравнении со своим первоначальным уровнем. Естественно, я не могу гарантировать, что двоечник за полгода подготовится на твердую «пять». Но могу с уверенностью сказать, что я подготовлю ребенка на его максимально возможный уровень за то время, что осталось до экзамена.
Индивидуальная работа
Все дети разные, поэтому способ и форма объяснения корректируются в зависимости от уровня понимания ребенком предмета. Индивидуальная работа с каждым учеником — каждому даются отдельные задания, теоретический материал.
источники:
http://examer.ru/ege_po_matematike/teoriya/kvadratnye_uravneniya
http://mathlesson.ru/node/7967
Тема урока: «Подготовка к ЕГЭ. 1 задание.Простейшие
уравнения. Профиль.»
Цель: подготовить к успешной сдаче экзамена по
профильной математике
Структура №1
задания профиль математика простейшие уравнения
1. Линейные,
квадратные, кубические уравнения
2.
Рациональные уравнения
3. Иррациональные
уравнения
4.
Показательные уравнения
5. Логарифмические
уравнения
6. Тригонометрические уравнения
1.Линейные,
квадратные, кубические уравнения
|
Карточка №1 Линейные |
|
1. Найдите корень уравнения: Решение. Последовательно получаем: Ответ: 13. Решить самостоятельно 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. |
|
Карточка №2 Квадратные уравнения |
|
Найдите корень уравнения Решение. Выполним преобразования, используя формулы
Ответ: 3. Приведём другое решение: Выполним преобразования,
Ответ: 3. Решить задания 1. Решите уравнение 2. Решите уравнение 3. Найдите корень уравнения 4. Найдите корень уравнения: 5. Решите уравнение 6. Решите уравнение 7. Решите уравнение 8. Решите уравнение 9. Решите уравнение 10. Решите уравнение |
|
Карточка №3 Кубические уравнения |
|
Найдите корень Решение. Извлекая кубический корень из обеих частей Ответ: −1. Решить самостоятельно 1. Найдите корень уравнения 2. Найдите корень уравнения 3. Найдите корень уравнения 4. Найдите корень уравнения 5. Найдите корень уравнения |
2. Рациональные
уравнения
|
Карточка №4 |
|
Найдите корень уравнения: Решение. Избавимся от знаменателя:
Ответ: 14. Решить самостоятельно 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. |
3. Иррациональные
уравнения
|
Карточка №5 Иррациональные уравнения |
|
Найдите корень уравнения Решение. Возведем в квадрат: Ответ: 3. Решить самостоятельно 1.Найдите корень уравнения 2.Найдите корень уравнения 3.Найдите корень уравнения: 4.Найдите корень уравнения 5.Найдите корень уравнения 6. Решите уравнение 7. Решите уравнение 8. Решите уравнение 9. Решите 10. Найдите корень уравнения |
4.Показательные
уравнения
|
Карточка №6 Показательные уравнения |
|
Найдите корень Решение. Перейдем к одному основанию степени: Ответ: −1. Решить самостоятельно 1. Найдите корень уравнения 2. Найдите корень уравнения 3.Найдите корень уравнения 4.Найдите корень уравнения 5.Найдите корень уравнения 6.Найдите корень уравнения: 7.Найдите решение уравнения: 8. Найдите корень уравнения: 9.Решите уравнение 10.Решите уравнение 11.Найдите корень 12.Найдите корень уравнения |
5.Логарифмические
уравнения
|
Карточка №7 Логарифмические |
|
1. Найдите корень уравнения Решение. Последовательно получаем: Ответ: −124. Решить самостоятельно 1.Найдите корень 2.Найдите корень уравнения 3.Найдите корень 4.Найдите корень уравнения 5.Найдите корень уравнения 6.Решите уравнение 7.Решите уравнение 8.Решите 9.Найдите корень уравнения 10.Найдите корень 11.Решите уравнение |
6.Тригонометрические
уравнения
|
Карточка №8 Тригонометрические уравнения |
|
1. Найдите корни уравнения: Решение. Последовательно получаем:
Значениям Если Если Значениям Следовательно, наибольшим Ответ: −4. Решить самостоятельно 1. Решите уравнение 2. Решите 3. Решите уравнение |
Домашнее
задание на сайте Решу ЕГЭ профиль до 25.02.22
№44022425
Определение
Уравнение (с одной переменной) — это некоторое равенство двух выражений, содержащее неизвестную (переменную). [f(x)=g(x) qquad qquad (1)]Пусть для определенности все дальнейшие уравнения содержат переменную, обозначенную буквой (x).
Замечание
Заметим, что (x) — это просто некоторое число, значение которого неизвестно.
Определение
Областью определения (или областью допустимых значений, сокращенно ОДЗ) любого уравнения вида ((1)) будем называть множество значений переменной (x), при которых определены (то есть не теряют смысла) функции (f(x)) и (g(x)).
Пример
Уравнение (dfrac {10}{x-1}=5) определено при всех значениях переменной (x), кроме (x=1), потому что в этом случае знаменатель дроби в левой части равенства обращается в ноль. Значит, ОДЗ уравнения (xin
(-infty;1)cup(1;+infty)).
Определение
Корнем уравнения называется то числовое значение (x), при котором уравнение обращается в верное равенство.
Иногда корни уравнения называют решением этого уравнения.
Например, корнем уравнения из предыдущего примера является число (x=3), потому как тогда уравнение принимает вид (dfrac{10}{3-1}=5) или, что то же самое, (5=5), что является верным равенством.
Замечание
1) Заметим, что уравнение может как иметь корни, так и не иметь корней. Например, уравнение (dfrac 1x=0) ни при каких значениях (x) не может быть верным, потому что дробь равна нулю, когда ее числитель равен нулю, а знаменатель при этом не теряет смысла. У нашей дроби числитель (1ne 0).
2) Фраза “решить уравнение” означает найти все корни данного уравнения или доказать, что корней нет.
Определение
Два уравнения равносильны (или эквивалентны), если они имеют одинаковые решения.
Например, уравнения (x=3) и (3x=6+x) эквивалентны, т.к. оба имеют единственное решение (x=3).
Эквивалентность уравнений обозначается так: (x=3 quad
Leftrightarrow quad
3x=6+x).
Свойства уравнений
1. В любом уравнении можно переносить слагаемые из одной части равенства в другую, при этом меняя их знак на противоположный. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+4=2x^2) можно переписать в виде (x+4-2x^2=0).
2. В любом уравнении можно правую и левую части умножать или делить на одно и то же число, не равное нулю. При этом полученное уравнение равносильно исходному.
Например, уравнение (0,5x=-2) равносильно уравнению (x=-4), которое получено из исходного путем умножения обеих частей на (2).
3. В любом уравнении можно к правой и левой частям прибавлять одно и то же число. При этом полученное уравнение равносильно исходному.
Например, уравнение (x+2=5x^2) после прибавления к обеим частям (-2) примет вид (x=5x^2-2).
[{Large{text{Линейные уравнения}}}] Линейное уравнение – это уравнение вида [ax + b = 0qquad qquad (2)] где (ane 0,b) – числа, или уравнение, к нему сводящееся.
ОДЗ линейного уравнения ((2)) — все (x inmathbb{R}).
Линейное уравнение (ax+b=0) преобразуется в (ax=-b) и всегда имеет единственное решение (x=-dfrac ba).
Например, (2x-4=0) имеет корень (x=2).
Замечание: при переносе слагаемых из одной части равенства в другую знак слагаемого меняется на противоположный. Например, выражение (x-5=8) преобразуется в выражение (x=8+5).
Знак, стоящий перед слагаемым – это и есть его знак, то есть в выражении (x-5) два слагаемых: (x) и (-5). Если перед слагаемым не стоит никакого знака, то подразумевается, что перед ним стоит знак “(+)”.
[{Large{text{Квадратные уравнения}}}] Квадратное уравнение – это уравнение вида [ax^2+bx+c=0 qquad qquad (3)] где (a, b, c) – числа, причем (ane 0), или уравнение, к нему сводящееся.
Число (a) называется старшим (первым) коэффициентом, число (b) – вторым коэффициентом, число (c) – свободным членом.
Замечание
1) Заметим, что если (a=0), то уравнение ((3)) становится линейным; именно поэтому в определении (ane 0).
2) Выражение (ax^2+bx+c) называется квадратичным (квадратным) трехчленом.
ВАЖНО! Обращаем ваше внимание на то, что, например, в квадратном трехчлене (7-x^2+2x) коэффициент (a=-1), (b=2) и (c=7)! Так как (7-x^2+2x=-x^2+2x+7), а по определению (a) – коэффициент перед (x^2), (b) – коэффициент перед (x), (c) – свободный член.
Определение
Дискриминантом квадратного уравнения ((3)) называется выражение (D=b^2-4ac).
Корни квадратного уравнения
1) Если дискриминант квадратного уравнения больше нуля ((D>0)), то оно имеет два различных корня [x_1=dfrac{-b-sqrt D}{2a} qquad text{и} qquad
x_2=dfrac{-b+sqrt D}{2a}]
2) Если дискриминант квадратного уравнения равен нулю ((D=0)), то оно имеет два совпадающих корня (часто говорят, что оно имеет один корень) [x=-dfrac b{2a}]
3) Если дискриминант квадратного уравнения меньше нуля ((D<0)), то оно не имеет корней.
Пример:
Решите уравнение [3x^2 — 33x + 90 = 0.]
Решение.
Найдём дискриминант данного уравнения: [D = 33^2 — 4cdot 3cdot 90 = 9] Следовательно, уравнение имеет два различных корня, равных [x_1=dfrac{33 + 3}{6} = 6 qquad text{и} qquad x_2=dfrac{33 —
3}{6} = 5]
Теорема Виета
Пусть квадратное уравнение (ax^2 + bx + c = 0), (aneq 0), имеет два корня (x_1) и (x_2) (возможно, совпадающих), то есть (Dgeqslant 0). Тогда их сумма равна [x_1+x_2=-dfrac{b}{a}] а их произведение равно [x_1cdot x_2=dfrac{c}{a}]
Доказательство
Сумма корней этого уравнения равна [dfrac{-b + sqrt{D}}{2a} +
dfrac{-b — sqrt{D}}{2a} = -dfrac{2b}{2a} = -dfrac{b}{a}] Произведение корней этого уравнения равно [dfrac{-b + sqrt{D}}{2a} cdot dfrac{-b — sqrt{D}}{2a} =
dfrac{(-b + sqrt{D})(-b — sqrt{D})}{4a^2} = dfrac{b^2 — D}{4a^2}
= dfrac{4ac}{4a^2} = dfrac{c}{a}]
Определение
Квадратное уравнение называется приведенным, если старший коэффициент (a=1).
Любое квадратное уравнение можно сделать приведенным: для этого необходимо разделить уравнение на (a).
Следствие
Для приведенного квадратного уравнения (x^2+px+q=0) теорема Виета выглядит следующим образом: [x_1+x_2=-p, qquad qquad x_1cdot x_2=q]
Теорема: разложение на множители квадратного трехчлена
Пусть уравнение (ax^2 + bx + c = 0), (aneq 0), имеет два корня (возможно, совпадающих), то есть (Dgeqslant 0). Тогда при любом значении (x) выполнено [ax^2 + bx + c = a(x — x_1)(x — x_2),] где (x_1) и (x_2) – корни уравнения (ax^2 + bx + c = 0) (возможно, совпадающие).
Доказательство
Сделаем преобразования: [begin{aligned}
&a(x-x_1)(x-x_2)=aleft(x — dfrac{-b + sqrt{D}}{2a}right)left(x
— dfrac{-b — sqrt{D}}{2a}right) =aleft(x^2 — xleft(dfrac{-b +
sqrt{D}}{2a} + dfrac{-b — sqrt{D}}{2a}right) + dfrac{b^2 —
D}{4a^2}right)=\[2ex]
&=aleft(x^2-xcdot left(-dfrac
baright)+dfrac{b^2-(b^2-4ac)}{4a^2}right) =a(x^2+dfrac ba
x+dfrac ca)=ax^2+bx+c
end{aligned}]
Пример
Разложить на множители квадратный трехчлен (3x^2-2x-1).
Решение.
Рассмотрим уравнение (3x^2-2x-1=0) и найдем его корни.
(D=(-2)^2-4cdot 3cdot (-1)=16), значит
[x_1=dfrac{2-4}{2cdot 3}=-dfrac 13 qquad qquad x_2=dfrac{2+4}{2cdot 3}
=1]
Таким образом, (3x^2-2x-1=3(x-1)(x+frac13)=(x-1)(3x+1)).
[{Large{text{Простейшие кубические уравнения}}}] (bullet) Кубический корень из числа (a) – это такое число (b), которое при возведении в куб равно (a): [sqrt[3] a=bquad text{то же самое, что }quad a=b^3] (bullet) Таблица кубов чисел от 1 до 10: [begin{array}{|ll|}
hline
1^3=1 & quad6^3=216 \
2^3=8 & quad7^3=343\
3^3=27 & quad8^3=512\
4^3=64 & quad9^3=729\
5^3=125 & quad10^3=1000\
hline end{array}] (bullet) Простейшие кубические уравнения – уравнения, сводящиеся к виду [x^3=a] Для любого числа (a) такие уравнения имеют единственный корень [x=sqrt[3]a] Пример:
1) решением уравнения (x^3=-8) является (x=sqrt[3]{-8}=-2).
2) решением уравнения (x^3=64) является (x=4).