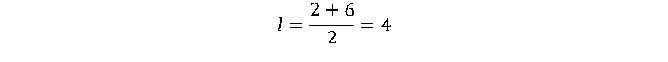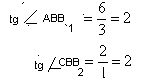На клетчатой бумаге с размером 1х1 изображен треугольник найдите его площадь решу егэ

Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

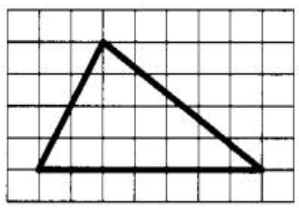
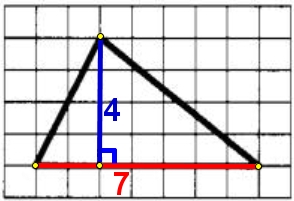
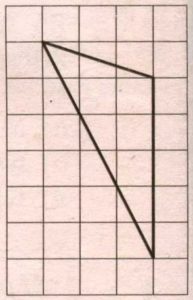
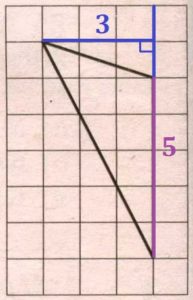
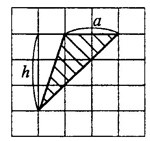
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см times 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

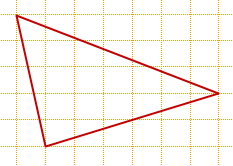
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.

Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2

Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402

Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.

Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.

Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …

Источник

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Источник: ОГЭ Ященко 2022 (36 вар)

Решение:

Находим площадь треугольника по формуле:

Ответ: 14.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.5 / 5. Количество оценок: 26

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время!

В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.

Запись опубликована:13.10.2021
Рубрика записи18. Фигуры на квадратной решётке
Автор записи:Andrei Maniakin

Источник

Рассмотрим задачи,в которых требуется найти площадь треугольника изображённого на клетчатой бумаге.

Начнем с прямоугольных треугольников.

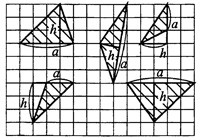
Задача 1

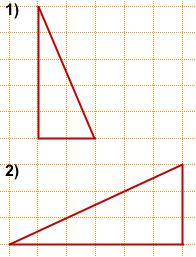
На клетчатой бумаге с размером клетки 1×1 изображен прямоугольный треугольник.

Найти его площадь.

Решение:

Площадь прямоугольного треугольника будем искать с помощью формулы

$[S = frac{1}{2}ab,]$

где a и b — катеты.

Длину катетов считаем по клеточкам.

1) a=2, b=5,

$[ S = frac{1}{2} cdot 2 cdot 5 = 5. ]$

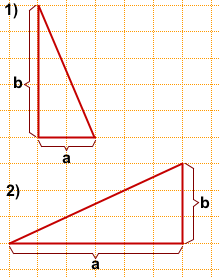
2) a=6, b=3,

$[ S = frac{1}{2} cdot 6 cdot 3 = 9. ]$

Задача 2

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найти его площадь.

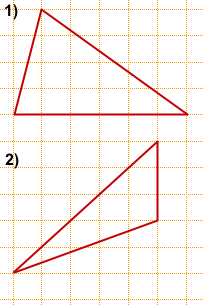
Решение:

Чаще всего площадь произвольного треугольника, изображённого на клетчатой бумаге, ищут по формуле

$[S = frac{1}{2}ah_a ,]$

где a — сторона треугольника, h_a — высота, проведённая к этой стороне.

a и h_a вычисляем по клеточкам (одна из этих величин должна лежать на горизонтальной линии, другая — на вертикальной).

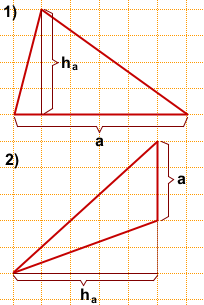
1) a=6, h_a=4,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 6 cdot 4 = 12. ]$

2) a=3, h_a=5,

$[ S = frac{1}{2}ah_a = frac{1}{2} cdot 3 cdot 5 = 7,5. ]$

А как найти площадь, если ни одна из сторон треугольника не лежит на горизонтальной или вертикальной линии клеток?

Иногда площадь треугольника можно найти как разность площадей других фигур.

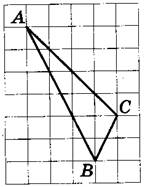
Задача 3

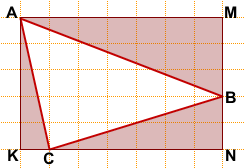
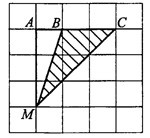
На клетчатой бумаге с размером клетки 1×1 изображён треугольник.

Найдите его площадь.

Решение:

Обозначим вершины треугольника, площадь которого мы ищем, через A, B и C.

Площадь треугольника ABC можно найти как разность площадей прямоугольника AMNK и треугольников AKC, AMB и CBN:

$[S_{Delta ABC} = S_{AMNK} - S_{Delta AKC} - S_{Delta AMB} - S_{Delta CBN} .]$

Площадь прямоугольника найдём по формуле S=ab.

$[ S_{AMNK} = AM cdot AK = 7 cdot 5 = 35. ]$

Площади прямоугольных треугольников найдём по формуле

$[ S = frac{1}{2}ab, ]$

где a и b — катеты.

$[S_{Delta AKC} = frac{1}{2}AK cdot KC = frac{1}{2} cdot 5 cdot 1 = 2,5;]$

$[S_{Delta AMB} = frac{1}{2}AM cdot MB = frac{1}{2} cdot 7 cdot 3 = 10,5;]$

$[S_{Delta CBN} = frac{1}{2}CN cdot BN = frac{1}{2} cdot 6 cdot 2 = 6.]$

Отсюда

$[S_{Delta ABC} = 35 - 2,5 - 10,5 - 6 = 16.]$

Источник

Задания

Версия для печати и копирования в MS Word

Задание 18 № 349113

На клетчатой бумаге с размером клетки 1х1 изображён треугольник. Найдите его площадь.

Спрятать решение

Решение.

Площадь треугольника равна половине произведения основания на высоту, проведенную к данному основанию. Таким образом:

Ответ: 36

Аналоги к заданию № 348403: 348641 348678 349113 350279 350360 350458 350653 351131 351257 352262 … Все

Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.

Спрятать решение

Прототип задания

Сообщить об ошибке · Помощь

Задание:

На клетчатой бумаге с клетками размером 1 см х 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.

Решение:

* Нужно найти площадь треугольника ECB.

* Дорисуем нашу фигуру до прямоугольника и найдем площадь ECB, отняв от площади прямоугольника площадь треугольника ACE и площадь треугольника CBD.

Площадь ABCD = AC * CD (длину умножаем на ширину, так как ABCD — прямоугольник)

AC = 3 клетки = 3 см (так как одна клетка размером 1 см x 1 см)

CD = 4 клетки = 4 см

Площадь ABCD = 3 * 4 = 12 см²

Площадь треугольника = 1/2 * основание * высоту.

* Площадь ACE = 1/2 * AE * AC

AE = 1 клетка = 1 см.

AC = 3 см

Площадь ACE = 1/2 * 1 * 3 = 1.5 см²

* Площадь CBD = 1/2 * CD * BD

CD = 4 клетки = 4 см

BD = 3 клетки = 3 см

Площадь CBD = 1/2 * 4 * 3 = 6 см²

* Итого: площадь ECB = 12 — 1.5 — 6 = 4.5 см²

Ответ: 4.5

Задать свой вопрос

*более 50 000 пользователей получили ответ на «Решим всё»

Условие

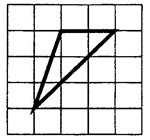
На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

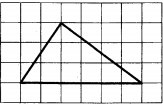
математика 8-9 класс
4682

Решение

S = 1/2*a*h
S = 1/2*6*3 = 9

Ответ: 9

Ошибки в решение (1)

Вопросы к решению (1)

Написать комментарий

Присоединяйся в ВК

На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

Источник задания: ЕГЭ 2021 Математика, И.В. Ященко. 36 вариантов.

Решение:

Найдём площадь треугольника:

Ответ: 7,5.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 0 / 5. Количество оценок: 0

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

Площадь треугольника (задачи на клетчатой бумаге). Готовимся к егэ по математике. Геометрия. Урок 2

Площадь произвольного треугольника равна половине произведения длины его стороны () на высоту (), проведённую к этой стороне: $displaystyle S=frac{ah}{2}$
На рисунке 1 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон и высота, проведённая к этой стороне .
Как правило, удобно брать ту сторону, которая проходит по линиям клетчатой бумаги (или же проходит параллельно осям координат).

Рис. 1.

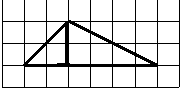
Задача 1. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 2). Найдите его площадь в квадратных сантиметрах.
Решение.
1-й способ.

Рис. 2.

Площадь произвольного треугольника равна половине произведения длины его стороны () на высоту (), проведённую к этой стороне. Проведём высоту . Треугольник тупоугольный, поэтому высота проводится вне треугольника.

Рис. 3.

На рисунке 3 сторона = 2 см, высота = 3 см.
$displaystyle S=frac{ah}{2}=frac{2cdot 3}{2}=3$ см².
Ответ: 3.
Заметим, что так как клетки имеют размер 1 см х 1 см, то площадь в квадратных сантиметрах получится, если мы будем по рисунку считать размер отрезков в клетках. Поэтому единицы длины в этих задачах можно и не писать.
2-й способ.
Достроим треугольник BCM до прямоугольного треугольника MCA (см. рис. 4).

Рис. 4.

Тогда искомую площадь треугольника BCM можно найти как разность площадей двух прямоугольных треугольников MAC и MAB .
Катеты первого из них равны 3 см и 3 см, катеты второго — Зсм и 1 см.
Площадь прямоугольного треугольника равна половине произведения его катетов, следовательно,
$displaystyle S_{MAC}=frac{3cdot 3}{2}=4,5;; S_{MAB}=frac{1cdot 3}{2}=1,5;$
$displaystyle S_{MBC}=S_{MAC}-S_{MAB}=4,5-1,5=3.$
Ответ: 3.

Источник

Квадратная решетка и координатная плоскость

В задании №3 профильного уровня ЕГЭ по математике мы будем работать с фигурами на квадратных решетках – вычислять параметры фигур – стороны или площади, а также расстояния между точками. Приступим непосредственно к разбору типовых вариантов.

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1х1 изображен треугольник. Найдите площадь.

[/su_note]

Алгоритм решения:

Подсчитываем длину основания и высоты.
Записываем формулу вычисления площади.
Вычисляем площадь.
Записываем ответ.

Решение:

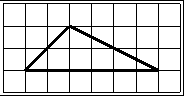
1. Подсчитываем длины основания и высоты:

основание = 6,

высота = 2.

2. Записываем формулу площади треугольника: S= ah|2.

3. Вычисляем площадь: S= 6∙2/2=6

Ответ: 6.

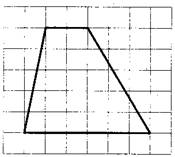
Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 3, большее – 4.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 3,5.

Ответ: 3,5.

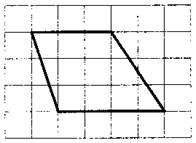
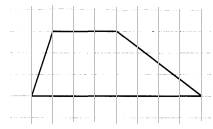
Третий вариант задания (из Ященко, №2)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите длину средней линии этой трапеции.

[/su_note]

Алгоритм решения:

Подсчитываем длину каждого основания и высоты трапеции.
Записываем формулу длины средней линии трапеции.
Вычисляем среднюю линию.
Записываем ответ.

Решение:

1. По условию задачи каждая клетка представляет одну единицу длины. Тогда меньшее основание равно 2, большее – 6.

2. Длина средней линии трапеции находится по формуле

, где a и b – длина верхнего и нижнего оснований трапеции.

3. Имеем:

4. Значит, средняя линия равна 4.

Ответ: 4.

Четвертый вариант задания (из Ященко, №4)

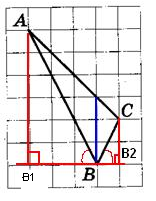
[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его биссектрисы, проведённой из вершины В.

[/su_note]

Алгоритм решения:

Проведем перпендикуряры из вершин Аи С.
Построим биссектрису угла В.
Покажем, что биссектриса параллельна высотам.
Измерим длину биссектрисы.
Запишем ответ.

Решение:

1. Проведем из вершин А и С отрезки АВ₁иСВ₂, перпендикулярные прямой, содержащей вершину В на рисунке.

2. Построим биссектрису угла B.

3. Рассмотрим треугольники АВВ₁ иВВ₂С. Они прямоугольные, тогда из соотношений в прямоугольных треугольниках

Это означает, что углы АВB₁ и СВB₂ равны, так как равны тангенсы этих углов.

Раз равны углы, то стороны AB и BC расположены под одним углом относительно вертикали (На рисунке она проведена синим). Эта вертикаль является биссектрисой. Длина биссектрисы по рисунку равна 3.

Ответ: 3.

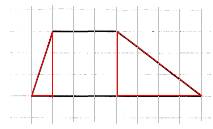
Пятый вариант задания (из Ященко, №7)

[su_note note_color=”#defae6″]

На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.

[/su_note]

Алгоритм решения:

Рассмотрим рисунок и измерим основания.
Проведем высоту.
Запишем формулу площади трапеции.
Вычислим площадь по формуле.

Решение:

1. На рисунке основания равны 3 и 8.

2. Опустим высоту. Она рана 3.

3. Формула трапеции: S=h(a+b)/2, где a,b – основания, h – высота.

4. Вычислим площадь, подставив значения: S=3∙(3+8)/2=16,5

Следовательно, площадь данной трапеции равна 16,5.

Ответ: 16,5.

Даниил Романович | Просмотров: 12.1k

Источник

Условие

Решение

Написать комментарий

Меню

Присоединяйся в ВК

Информация

Квадратная решетка и координатная плоскость

Разбор типовых вариантов заданий №3 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

Алгоритм решения:

Решение:

Второй вариант задания (из Ященко, №1)

Алгоритм решения:

Решение:

Третий вариант задания (из Ященко, №2)

Алгоритм решения:

Решение:

Четвертый вариант задания (из Ященко, №4)

Алгоритм решения:

Решение:

Пятый вариант задания (из Ященко, №7)

Алгоритм решения:

Решение:

Новое и интересное на сайте: