Задание 17 Профильного ЕГЭ по математике — это уравнение, система уравнений или неравенство с параметром. Или несколькими параметрами.
Конечно, за один день научиться решать такие задачи невозможно. И все-таки мы немного расскажем о том, как научиться решать задачи с параметрами. С чего начать. И какие вообще есть методы решения задач с параметрами.
Начнем с хорошей новости. Задача 17 (с параметром) оценивается в целых 4 первичных балла ЕГЭ, которые отлично пересчитываются в тестовые.
Если вы полны решимости получить на ЕГЭ заветные 4 первичных балла за задачу 17 (с параметром), не стоит начинать с реальных экзаменационных задач. Ведь мы хотим получить результат, а не разочарование! Поэтому сначала необходимо повторить следующие темы:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
2. Преобразование графиков функций.
3. Построение графиков функций.
4. Базовые элементы для решения задач с параметрами. Да, мы будем рисовать не только привычные функции. Но еще и окружности, ромбики, полуплоскости и всевозможные их комбинации.
5. Что такое параметр. Простые задачи с параметрами.
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому.
Читайте статью, смотрите видеокурс. И помните, что графический метод — хороший, но не единственный.
Потому что, кроме него, есть и другие:
— Квадратные уравнения и неравенства с параметрами.
— Задачи с параметрами. Условия касания.
— Метод оценки в задачах с параметрами.
— Использование четности функций в задачах с параметрами.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 1, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 5, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 11, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 26, задача 17.
Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 17.
И не думайте, что это все возможные методы решения задач с параметрами. Их намного больше! Мы дали ссылки на те, которые встречаются чаще всего в задачах ЕГЭ.
Несколько мудрых советов о том, как и зачем решать задачи с параметрами.
1. Чтобы на ЕГЭ уверенно справиться с заданием 17, нужно решить не менее 50 задач с параметрами.
2. Настанет момент, когда вы увидите, что задача с параметром похожи на конструктор, где вы собираете решение из знакомых элементов.
3. Два самых главных секрета решения задач с параметрами. Готовы узнать? Вот они:
— Если в задаче с параметром можно сделать замену переменной — сделайте замену.
— Если задачу с параметром можно решить графически — решите графически.
4. Сколько бы вы ни занимались задачами с параметрами, каким бы отличником ни стали — всегда найдется задача, над которой вы задумаетесь. Вот такая, например:
Задача 1. При каких значениях a системы и
равносильны?
Две системы уравнений с двумя переменными называются равносильными, если они имеют одни и те же решения, или обе системы не имеют решений.
1) При — системы равносильны, так как обе не имеют решений.
2) При — второе уравнение имеет решение
которое является решением первой системы.
3) При
Система уравнений
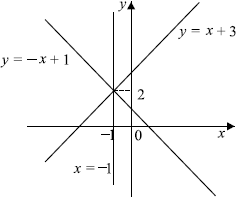
Уравнение задает окружность с центром в начале координат и радиусом
Решениями системы:
являются две точки, в которых прямая пересекает окружность, заданную уравнением
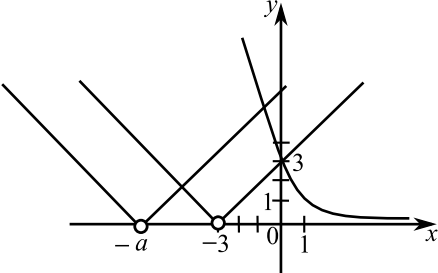
А вот уравнение задает семейство параллельных прямых
Мы хотим, чтобы две системы были равносильны, то есть чтобы окружность, заданная уравнением , пересекала только одну из этого семейства прямых, а именно прямую
, и не имела общих точек с другими прямыми из этого семейства.
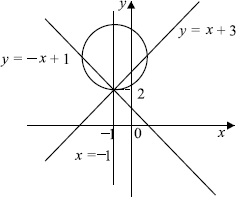
Меняя параметр а, мы можем менять радиус окружности. Мы хотим, чтобы окружность радиуса не имела общих точек с прямыми, параллельными прямой
, то есть лежала ниже прямой, проходящей через точку А на рисунке, и выше прямой, проходящей через точку В.
Когда же происходит касание в точках A и B?
В случае касания радиус окружности Мы легко находим это из прямоугольного треугольника СОА, где О — начало координат.
Значит, в случае касания , а если
— касания не происходит.
Объединяя случаи, получим, что системы равносильны, если
Легко? Если справились — вот еще одна интересная задача:
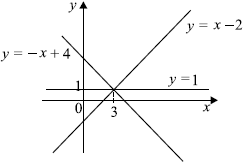
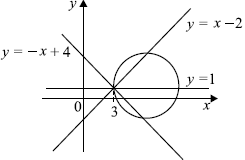
Задача 2. При каких значениях параметра a найдется такое значение параметра , что система уравнений
имеет ровно три различных решения?
Вот решение этой задачи.
Лучше всего осваивать эту непростую тему на нашем Онлайн-курсе подготовки к ЕГЭ на 100 баллов. Или на интенсивах ЕГЭ-Студии в Москве. Удачи, друзья!
Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 17. Задача с параметрами u0026#8212; профильный ЕГЭ по математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Найдите все значения параметра k, при каждом из которых уравнение имеет хотя бы одно решение на интервале
2
Найдите все значения k, при каждом из которых уравнение
имеет хотя бы одно решение на отрезке
Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2017. Вариант 4. (Часть C).
3
Определите, при каких значениях параметра a уравнение
имеет ровно два решения.
Источник: РЕШУ ЕГЭ — Предэкзаменационная работа 2014 по математике.
4
Найдите все значения параметра a, при каждом из которых уравнение
имеет корни, но ни один из них не принадлежит интервалу (4; 19).
5
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы один корень на отрезке [5; 23].
Пройти тестирование по этим заданиям
| 3644 | При каких значениях параметра a уравнение (a^2-6a+8)x^2+. (a^2-4)x+10-3a-a^2=0. имеет более двух корней |
При каких значениях параметра a уравнение (a2-6a+8)x2 +(a2-4)x + 10-3a-a2 =0 имеет более двух корней | |
| 3591 | Найдите все значения a при каждом из которых уравнение a(a+3)x^2+(2a+6)x-3a-9=0 имеет более одного корня |
Найдите все значения a при каждом из которых уравнение a(a+3)x2 +(2a+6)x -3a -9 =0 имеет более одного корня | |
| 3585 | Найдите все значения a при каждом из которых уравнение 2sqrt(x^4+(a-3)^4)=abs(x+a-3)+abs(x-a+3) имеет единственное решение |
Найдите все значения a при каждом из которых уравнение 2sqrt(x4 +(a-3)4) = abs(x+a-3) +abs(x-a+3) имеет единственное решение ! Тренировочная работа по математике №2 СтатГрад 11 класс 13.12.2022 Задание 17 Вариант МА2210209 #Задачи — аналоги 621 104 | |
| 3544 | Найдите все значения a, при которых система уравнений {(abs(y+x^3)-abs(y+3x)=2y+x^3+3x), (abs(-y-3x+1)-abs(y+x^3-a)=), (= -3y-6x-x^3+a+2) :} имеет единственное решение |
Найдите все значения a, при которых система уравнений {|y+x^3|-|y+3x| = 2y+x^3+3x), |-y-3x+1| -|y+x^3-a| =-3y-6x-x3+a+2 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 6 Задание 17 |
|
| 3434 | Найдите все значения параметра a, b при которых неравенство a^3x^4+2ax^3+b <= 2bx^2+b^3x+a выполняется для всех x из отрезка [0; 1] |
Найдите все значения параметра a, b при которых неравенство выполняется для всех x из отрезка [0; 1] ! ДВИ в МГУ 2022 — 5 поток, Вариант 225 Задание 6 # Решение Натальи Яковлевны Захаровой youtube видео разбор | |
| 3405 | Найдите все значения a, при которых система уравнений {(abs(y+1/2x^3)-abs(y+3/2x)=2y+1/2x^3+3/2x), (abs(-y-3/2x+1)-abs(y+1/2x^3-a)=), (-4 y-9/2x-1/2x^3+a+3) :}. имеет единственное решение |
Найдите все значения a, при которых система уравнений { |y+1/2×3| -|y+3/2x| = 2y + 1/2×3 +3/2x |-y-3/2x+1| — |y+1/2×3 -a| = -4y -9/2x -1/2×3 +a +3 имеет единственное решение ! математика 50 вариантов ЕГЭ 2022 профильный уровень Ященко Вариант 8 Задание 17 # Ошибка в ответе пособия у Ященко ? : color{red}{a > -1 ?} |
|
| 3404 | Найдите все значения параметра a, при которых уравнение x^2+(1-a+root(4)(abs(x)))^2=a^2/4. имеет ровно три решения |
Найдите все значения параметра a, при которых уравнение x2 + (1-a+ корень 4 степени из |x|) 2 = a 2/4 имеет ровно три решения ! ДВИ в МГУ 2022 — 1 поток, Вариант 1 Задание 6 | |
| 3391 | Найдите все значения параметра a, при каждом из которых уравнение sqrt(15x^2+6ax+9)=x^2+ax+3 имеет три различных решения |
Найдите все значения параметра a, при каждом из которых уравнение корень из 15×2 +6ax+9 =x2 +ax+3 имеет три различных решения ! ЕГЭ 2022 по математике 27.06.2022 резервный день Задание 17 | |
| 3379 | Найдите все значения параметра a, при каждом из которых уравнение x^2+a^2+2x-4a=abs(4x+2a). имеет более двух различных корней |
Найдите все значения параметра a, при каждом из которых уравнение x2 +a2 +2x -4a = |4x+2a| имеет более двух различных корней ! ЕГЭ 2022 по математике 02.06.2022 основная волна Задание 17 Санкт-Петербург | |
| 3368 | Оценки экспертов решений задания 17 ЕГЭ по математике профильного уровня. Задание № 17 — это уравнение, неравенство или их системы с параметром. Задачи с параметром допускают весьма разнообразные способы решения. Наиболее распространёнными из них являются: – чисто алгебраический способ решения; – способ решения, основанный на построении и исследовании геометрической модели данной задачи; – функциональный способ, в котором могут быть и алгебраические, и геометрические элементы, но базовым является исследование некоторой функции. Зачастую (но далеко не всегда) графический метод более ясно ведёт к цели. Кроме того, в конкретном тексте решения вполне могут встречаться элементы каждого из трёх перечисленных способов |
Критерии оценивания решений задания 17 ЕГЭ по математике профильного уровня ! Примеры оценивания реальных работ 2016-2021 гг # Приведены типы заданий с развёрнутым ответом, используемые в КИМ ЕГЭ по математике и критерии оценки выполнения заданий с развёрнутым ответом, приводятся примеры оценивания выполнения заданий и даются комментарии, объясняющие выставленную оценку | |

Показана страница 1 из 55
За это задание ты можешь получить 4 балла. На решение дается около 35 минут. Уровень сложности: высокий.
Средний процент выполнения: 4.2%
Ответом к заданию 17 по математике (профильной) может быть развернутый ответ (полная запись решения с обоснованием выполненных действий).
Что нужно знать, чтобы решить задание 17:
Для того, чтобы решить задачу необходимо составить математическую модель (уравнение, неравенство или функцию, которую нужно исследовать).
Для решения задач на кредиты, необходимо разобраться в основных схемах кредитования с дифференцированными и аннуитетными платежами. Часто для преобразования уравнения нужно знать формулы алгебраической и геометрической прогрессий.
В задачах на оптимизацию нужно уметь работать с функциями: брать производную, находить точки экстремумов.
Разбор сложных заданий в тг-канале
Задачи для практики
Задача 1
При каком значении $a$ множеством решений неравенства
${1+3^x} / {1+3^{-x}}>{3} / {|x+a|}$ является множество всех положительных чисел?
Решение
Сократив левую часть неравенства на $1 + 3^x$, получим равносильное неравенство $3^x > {3}/{|x + a|}$ или $3^{x-1} > {1}/{|x + a|}$. Так как обе части неравенства положительны, то ${1}/{3^{x-1}} < |x + a| (x ≠ -a)$ или $({1}/{3})^{x-1} < |x + a|$.
Графиком функции $y = ({1}/{3})^{x-1}$ является график функции $y = ({1}/{3})^x$ сдвинутый на $1$ единицу вправо вдоль оси $Ox$. Графиком функции $y = |x + a|$ является график функции $y = |x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x ≠ -a$, точка $(-a; 0)$ на графиках функций $y = |x + a|$ выколота.
Множество положительных чисел будет решением этого неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдет при $a = 3$. Графическая иллюстрация приведена на рисунке.
Ответ: 3
Задача 2
При каком значении $a$ множеством решений неравенства
${1+2^{-x}} / {1+2^x}>{4} / {√ {x^2+2ax+a^2}}$ является множество всех отрицательных чисел?
Решение
Сократив левую часть неравенства на $1+2^x$ и применив свойство квадратного корня $√ {m^2}=|m|$, получим равносильное неравенство ${1} / {2^x}>{4} / {|x+a|}$ или ${1} / {2^{x+2}}>{1} / {|x+a|}$. Так как обе части неравенства положительны, то $2^{x+2}<|x+a|$, при условии $x≠ -a$. Графиком функции $y=2^{x+2}$ является график функции $y=2^x$, сдвинутый на $2$ единицы влево вдоль оси $Ox$. Графиком функции $y=|x+a|$ является график функции $y=|x|$, сдвинутый вдоль оси $Ox$ в зависимости от величины и знака числа $a$. Учитывая, что $x≠ -a$, точка $(-a;0)$ на графиках функций $y=|x+a|$ является выколотой (см. рис.). Множество отрицательных чисел будет решением неравенства, если точка пересечения обоих графиков лежит на оси $Oy$. Это произойдёт при $a=-4$. Графическая иллюстрация приведена на рисунке.
Ответ: -4
Задача 3
Найдите все значения параметра $a$, при каждом из которых система уравнений ${{table {y=a-x{,}}; {|x-2|(y+5x-10)=(x-2)^3};}$ имеет ровно четыре различных решения.
Решение
При замене $y + x = t$ получим систему уравнений ${{table t=a; {|x — 2|(t + 4x — 10) = (x — 2)^3};}$ которая имеет, столько же решений, что и заданная система.
График первого уравнения системы $t = a$ представляет собой прямую, параллельную оси абсцисс.
Построим график второго уравнения.
1) При $x ≥ 2$ получим $(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 — (x — 2)^2) = 0$,
$(x — 2)(t — x^2 + 8x — 14) = 0$,
$x — 2 = 0$ или $t — x^2 + 8x — 14 = 0$.
$x = 2$ — вертикальная прямая.
$t = x^2 — 8x + 14$ — парабола с вершиной $(4; -2), t(2) = 2$.
2) При $x < 2$ получим $-(x — 2)(t + 4x — 10) = (x — 2)^3$,
$(x — 2)(t + 4x — 10 + (x — 2)^2) = 0$.
$x — 2 = 0$ не выполняется при $x < 2$.
$t + 4x — 10 + (x — 2)^2 = 0, t = -x^2 + 6$ — парабола с вершиной $(0; 6), t(2) = 2$.
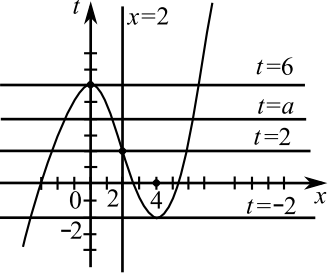
На рисунке изображен график второго уравнения полученной системы.
График прямой $t = a$ и уравнения $|x — 2|(t + 4x — 10) = (x — 2)^3$ имеют ровно $4$ общие точки при $-2 < a < 2, 2 < a < 6$.
Ответ: (-2;2);(2;6)
Задача 4
Найдите все значения параметра $a$, при каждом из которых уравнение ${x-4a} / {x+4}+{x-1} / {x-a}=1$ имеет единственный корень.
Решение
Преобразуем данное уравнение.
${(x — 4a)(x — a) + (x + 4)(x — 1) — (x + 4)(x — a)}/{(x + 4)(x — a)} = 0$,
${x^2 — ax — 4ax + 4a^2 + x^2 + 3x — 4 — x^2 + ax — 4x + 4a}/{(x + 4)(x — a)} = 0$,
${x^2 — x(4a + 1) + 4a^2 + 4a — 4}/{(x + 4)(x — a)} = 0$,
${tablex^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0; (x + 4)(x — a) ≠ 0;$.
Решим уравнение $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
$x = {(4a + 1) ±√{-8a + 17}}/{2}$
1. При $D < 0$ уравнение корней не имеет.
2. При $D = 0, -8a + 17 = 0, a = {17}/{8}$. Уравнение имеет единственный корень $x = {4a + 1}/{2}$ при $a = {17}/{8}. x = {4 · {17}/{8} + 1}/{2} = 4.75$.
Выполнено условие $x ≠ -4, x ≠ a$.
Значит, $a = {17}/{8} = 2.125$ удовлетворяет условию задачи.
3. При $D > 0$ уравнение имеет два корня.
$x = {(4a + 1) ±√{17 — 8a}/{2}$.
Проверим при каких значениях $a$ значения $x = -4$ и $x = a$ являются корнями уравнения $x^2 — x(4a + 1) + 4a^2 + 4a — 4 = 0$.
При $x = -4$ должно выполняться равенство $16 + 4(4a + 1) + 4a^2 + 4a — 4 = 0, a^2 + 5a + 4 = 0, a = -4, a = -1$.
При $x = a$ должно выполняться равенство $a^2 — 4a^2 — a + 4a^2 + 4a — 4 = 0, a^2 + 3a — 4 = 0, a = 1, a = -4$.
При $a = -1, a = 1$ исходное уравнение имеет единственный корень.
При $а=-4$, $D>0$ и корни $х=-4$ и $х=а$ совпадают, поэтому это значение параметра также подходит
Ответ: -4$;$-1$;$1$;$2.125
Задача 5
Найдите все значения параметра $p$, при каждом из которых система неравенств ${{table {px⩾ 5,}; {p<√ {x-1},}; {3x⩾ p+2};}$ имеет хотя бы одно решение на отрезке $[4; 5]$.
Решение
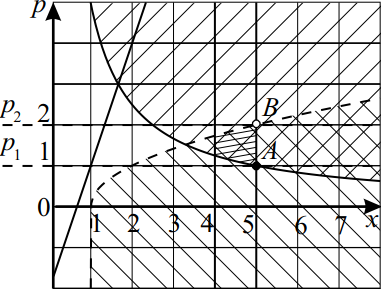
ОДЗ: $x ≥ 1$. Построим следующие графики $px = 5, p = √{x — 1}$ и $3x = p + 2$ в системе координат $Opx$ при $x > 0$ и изобразим решение системы
${tablep ≥ {5}/{x}; p < √{x — 1}; p ≤ 3x — 2;$
Из рисунка видно, что искомые значения $p$ удовлетворяют условию $p_1 ≤ p < p_2$.
Ординату точки $A$ можно найти, подставив $x = 5$ в уравнение $p = {5}/{x}; p_1 = {5}/{5} = 1$.
Ординату точки $B$ можно найти, подставив $x = 5$ в уравнение $p = √{x — 1}: p_2 = √{5 — 1} = √4 = 2$. Отсюда $p ∈ [1; 2)$.
Ответ: [1;2)
Задача 6
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2x+3)(4x^6-19x^4-x^2(5+4a)-a-17)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2x+3 = 0$; при $x = 0$ получим $3=0$, это не верно.
При $x ≠ 0, a = {2x — 3}/{x}, a = 2 — {3}/{x}$.
По условию числа $a$ и $x$ целые, поэтому число ${3}/{x}$ тоже целое, что возможно при $x = ±1, x = ±3$.
При $x = 1$ получим $a = -1$,
при $x = -1$ получим $a = 5$,
при $x = 3$ получим $a = 1$,
при $x = -3$ получим $a = 3$.
2) $4x^6 — 19x^4 — 5x^2 — 4ax^2 — a — 17 = 0$,
$a(4x^2 + 1) = 4x^6 — 19x^4 — 5x^2 — 17$,
$a = {4x^6 — 19x^4 — 5x^2 — 17}/{4x^2 + 1}$.
$a = x^4 -5x^2 — {17}/{4x^2 + 1}$. Так как $a$ и $x$ — целые числа, то ${17}/{4x^2 + 1}$ тоже целое число. Это возможно при $4x^2 + 1 = 1$ или $4x^2 + 1 = 17$.
$x^2 = 0, x = 0, a = 0 — 0 — 17 = -17$;
$x^2 = 4, x = ±2, a = 2^4 — 5·2^2 — {17}/{4·2^2 + 1} = -5$.
Уравнение имеет хотя бы один целый корень при значениях $a$, равных $-17; -5; -1; 1; 3; 5$.
Ответ:
Задача 7
Найдите все целые значения параметра $a$, при каждом из которых уравнение $(ax-2-x)(3x^5+7x^3+2x+4-3x^2a-a)=0$ имеет хотя бы один целый корень.
Решение
Рассмотрим два случая:
1) $ax — 2 — x = 0$; при $x ≠ 0$ получим $a = {2 + x}/{x} = 1 + {2}/{x}$.
Так как по условию $a$ и $x$ целые числа, то ${2}/{x}$ тоже целое число. Это возможно, если $x = ±1$ или $x = ±2$.
$x = 1; a — 2 — 1 = 0; a = 3;$
$x = -1; -a — 2 — (-1) = 0; a = -1;$
$x = 2; 2a — 2 — 2 = 0; a = 2;$
$x = -2; -2a — 2 — (-2); a = 0.$
Если $x = 0$, то $0 — 2 — 0 = 0$ не выполняется.
2) $3x^5 + 7x^3 + 2x + 4 — 3x^2a — a = 0,$
$a(3x^2 + 1) = 3x^5 + 7x^3 + 2x + 4,$
$a = {3x^5 + 7x^3 + 2x + 4}/{3x^2 + 1}$
$a = x^3 + 2x + {4}/{3x^2 + 1}$. Поскольку $a$ и $x$ — целые числа, то ${4}/{3x^2 + 1}$ также целое число. Это возможно, если $3x^2 + 1 = 4$, или $3x^2 + 1 = 2$, или $3x^2 + 1 = 1$.
Получаем $x^2 = 1$ или $3x^2 = 1$ или $x^2 = 0$.
Целые корни:
$x = 1$, тогда $a = 1^3 + 2·1 + {4}/{3·1^2 + 1} = 4$;
$x = -1$, тогда $a = (-1)^3 + 2·(-1) + {4}/{3·(-1)^2 + 1} = -2$;
$x = 0$, тогда $a = 0 + 0 + 4 = 4$.
Целые корни есть при значениях $a: -2; -1; 0; 2; 3; 4$.
Ответ: -2$;$-1$;$0$;$2$;$3$;$4
Задача 8
Найдите все значения $a > 0$, при каждом из которых система
${table(x — 4)^2 + (|y| — 4)^2 = 9; x^2 + (y — 4)^2 = a^2;$
имеет ровно $2$ решения.
Решение
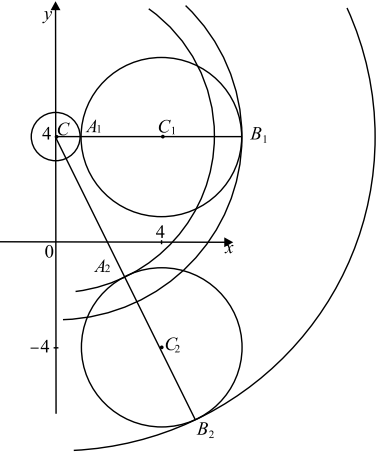
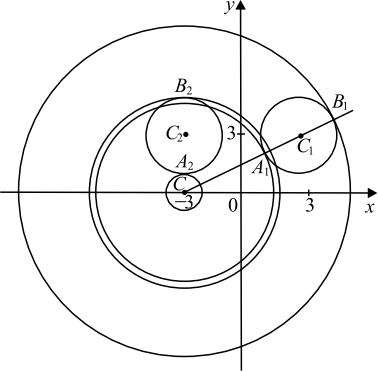
Если $y ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(4; 4)$ радиуса $3$, а если $y < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(4; -4)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (0; 4)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет ровно две общие точки с объединением окружностей $∅_1$ и $∅_2$.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_1(1; 4)$ и $B_1(7; 4)$. То есть при $a = CA_1=1$ и $a = CB_1=7$ окружности $∅$ и $∅_2$ касаются. При $a > 7$ и $a < 1$ окружности $∅$ и $∅_1$ не пересекаются, при $1 < a < 7$ окружности $∅$ и $∅_2$ имеют $2$ общие точки.
Из точки $C$ проведём луч $CC_2$ и обозначим $A_2$ и $B_2$ точки его пересечения с окружностью $∅_2$, где $A_2$ лежит между $C$ и $C_2$. Заметим, что длина отрезка $CC_2 = √{4^2 + (4-(-4))^2} = √{80} = 4√5$.
При $a < CA_2$ или $a > CB_2$ окружности $∅$ и $∅_2$ не пересекаются. При $CA_2 < a < CB_2$ окружности $∅$ и $∅_2$ имеют $2$ общие точки. При $a = CA_2 = 4√5 − 3$ или $a = CB_2 = 4√5 + 3$, окружности $∅$ и $∅_2$ касаются.
Исходная система имеет ровно 2 решения тогда и только тогда, когда окружность $∅$ с одной из окружностей $∅_1$ и $∅_2$ имеет $2$ общие точки, а с другой не пересекается, либо касается одновременно двух окружностей.
Так как $1 < 4√5 − 3 < 7 < 4√5 + 3$, то условию задачи удовлетворяют значения $a ∈ (1; 4√5 − 3) ∪ (7; 4√5 + 3).$.
Ответ: $(1;4√5-3)∪(7;4√5+3)$
Задача 9
Найдите все значения $a > 0$, при каждом из которых система
${table(|x| — 3)^2 + (y — 3)^2 = 4; (x + 3)^2 + y^2 = a^2;$
имеет единственное решение.
Решение
Если $x ≥ 0$, то первое уравнение задаёт окружность $∅_1$ с центром в точке $C_1(3; 3)$ радиуса $2$, а если $x < 0$, то оно задаёт окружность $∅_2$ с центром в точке $C_2(−3; 3)$ того же радиуса.
При $a > 0$ второе уравнение задаёт окружность $∅$ с центром в точке $C (−3; 0)$ радиуса $a$. Поэтому задача состоит в том, чтобы найти все значения параметра $a$, при каждом из которых окружность $∅$ имеет единственную общую точку с объединением окружностей $∅_1$ и $∅_2$.
Из точки $C$ проведём луч $CC_1$ и обозначим $A_1$ и $B_1$ точки его пересечения с окружностью $∅_1$, где $A_1$ лежит между $C$ и $C_1$.
Так как $CC_1 = √{6^2 + 3^2} = √{45} = 3√5$, то $CA_1 = 3√5 − 2, CB_1 = 3√5 + 2$.
При $a < CA_1$ или $a > CB_1$ окружности $∅$ и $∅_1$ не пересекаются. При $CA_1 < a < CB_1$ окружности $∅$ и $∅_1$ имеют $2$ общие точки. При $a = CA_1 = 3√5 − 2$ или $a = CB_1 = 3√5 + 2$, окружности $∅$ и $∅_1$ касаются.
Координаты точки касания окружностей $∅$ и $∅_2$ явно видны на чертеже: это точки $A_2(−3; 1)$ и $B_2(−3; 5)$. То есть при $a = 1$ и $a = 5$ окружности $∅$ и $∅_2$ касаются. При остальных значениях параметра $a$ окружности $∅$ и $∅_2$ либо имеют $2$ общие точки, либо не имеют общих точек.
Исходная система имеет единственное решение тогда и только тогда, когда окружность $∅$ касается ровно одной из двух окружностей $∅_1$ и $∅_2$ и не пересекается с другой.
Так как $1 < 3√5 − 2 < 5 < 3√5 + 2$, то условию задачи удовлетворяют только числа $a = 1$ и $a = 3√5 + 2$.
Ответ: $1;3√5+2$
Задача 10
Найдите все значения параметра $a$, при каждом из которых решение неравенства ${(2√x — a)(a — x)}/ {√{3 — a^2 — x^2}}≥ 0$ содержит отрезок длины не менее $0.5$.
Решение
${(2√x — a)(a — x)}/{√{3 — a^2 — x^2}} ≥ 0$. Попробуем преобразовать неравенство к более простому виду. Заметим, что знаменатель влияет только на ОДЗ. Поэтому неравенство равносильно системе ${table (2√x — a)(a — x) ≥ 0; 3 — a^2 — x^2 > 0;$. Второе неравенство системы преобразуем так, чтобы получить неравенство для внутренней части круга. Первое неравенство преобразуем так, чтобы скобки выглядели симметрично ${table (2√x — a)(a — x) ≤ 0; a^2+x^2 < 3;$
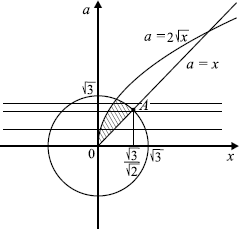
Изобразим множество решений системы в системе координат $Oxa$. Решению соответствует заштрихованная область. При этом каждому фиксированному значению $a$ соответствует горизонтальная прямая. При фиксированном значении a решениями системы будут $x$, равные абсциссам тех точек горизонтальной прямой, которые лежат в заштрихованной области.
Прямая $a = x$ пересекает окружность $x^2 + a^2 = 3$ при $a = x = {√3}/{√2}$.
1) Из рисунка видно, что если горизонтальная прямая $a = a_0$ лежит ниже (не выше) точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до графика $a = x$.
2) Если же горизонтальная прямая $a = a_0$ лежит выше точки $A$, то отрезок этой прямой в заштрихованной области идёт от графика $a = 2√x$ до окружности $a^2 + x^2 = 3$, при этом точки самой окружности в заштрихованную область не входят.
Таким образом, в первом случае (то есть при $a ≤ {√3}/{√2}$) выполняется $a ≤ 2√x, a ≥ x$, следовательно, $x ∈ [{a^2}/{4}; a]$.
При $a > {√3}/{√2}$ решением является промежуток $[{a^2}/{4}; √{3 — a^2})$.
Отсюда решение содержит отрезок длиной не менее ${1}/{2}$, если
$[table{{table a ≤ {√3}/{√2}; a-{1}/{4}a^2 ≥ 0.5}; {{table a > {√3}/{√2}; √{3-a^2}-{a^2}/{4} > 0.5};$
$[table{{table a ≤ {√3}/{√2}; a^2-4a+2 ≤ 0}; {{table a > {√3}/{√2}; 3-a^2 > ({a^2}/{4}+{1}/{2})^2};$
Решив системы, получим: $a ∈[2-√2; {√3}/{√2}]$ или $a ∈ ({√3}/{√2}; √2)$, отсюда $a ∈ [2 — √2; √2)$.
Замечание. Задачу можно решить и другими способами, например аналитически. Получив систему, можно заметить, что первое неравенство системы при $a < 0$ не имеет решений, а при $a ≥ 0$ имеет решением промежуток $[{1}/{4}a^2; a]$ (если $a ≤ 4$) или промежуток $[a; {1}/{4}a^2]$ (если $a > 4$). Решением второго неравенства будут $x$, удовлетворяющие неравенству $x < √{3 — a^2}$. Отсюда, в частности, $a ≤ √3$, то есть случай $a > 4$ не возможен.
Несложно убедиться, что при ограничениях $0 ≤ a ≤ √3$ для решения задачи достаточно решить систему ${table a-{1}/{4}a^2 ≥ 0.5; √{3-a^2}-{a^2}/{4} > 0.5;$
Ответ: $[2-√2;√2)$
Задача 11
Найдите все значения параметра a, при каждом из которых система уравнений ${tabley=√{-8-6x-x^2}; y+ax=a+1;$ имеет единственное решение.
Решение
Построим график уравнения $y = √{−8−6x−x^2}$.
Преобразовав подкоренное выражение, получим: $y = √{1−(x^2 + 6x + 9)}, y =√{1−(x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 1−(x + 3)^2, (x + 3)^2 + y^2 = 1$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность радиусом $1$ с центром в точке $(−3;0)$, лежащая в верхней полуплоскости.
Уравнение $y + ax = a + 1$ запишем в виде $y = −a(x−1) + 1$ — семейство прямых с угловым коэффициентом $−a$, проходящих через точку $M(1;1)$.
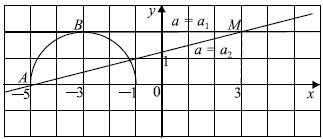
Рассмотрим рисунок. Видно, что система имеет единственное решение, если:
1) прямая $MC$ касается полуокружности, поэтому $−a = a_1 = 0$,
2) прямая и полуокружность имеют единственную общую точку, при этом $a_2 < −a ≤ a_3$.
Найдём $a_2$ из условия, что прямая $y = a_2(x−1) + 1$ проходит через точку $A(−4;0)$.
$a_2(−4−1) + 1 = 0, a_2 ={1}/{5}$.
Найдём $a_3$ из условия, что прямая $y = a_3(x−1) + 1$ проходит через точку $B(−2;0)$.
$a_3(−2−1) + 1 = 0, a_3 ={1}/{3}$.
Имеем ${1}/{5} < −a ≤ {1}/{3}$, значит, $−{1}/{3} ≤ a < −{1}/{5}$.
Следовательно, система имеет единственное решение, если $−{1}/{3} ≤ a < −{1}/{5}$ и $a = 0$.
Ответ: $[-{1}/{3};-{1}/{5});0$
Задача 12
Найдите все значения $a$, при которых система уравнений
${tabley=√{-5-6x-x^2}; y-ax=2-3a;$
имеет ровно два решения.
Решение
Построим график уравнения $y = √{-5 — 6x — x^2}$,
Преобразовав подкоренное выражение, получим $y = √{4 — (x^2 + 6x + 9)}, y = √{2^2 — (x + 3)^2}$.
Если $y ≥ 0$, то $y^2 = 2^2 — (x + 3)^2, (x + 3)^2 + y^2 = 2^2$.
Если $y < 0$, точек, удовлетворяющих уравнению, нет.
Получилась полуокружность с центром в точке $(-3; 0)$ радиусом $2$, лежащая в верхней полуплоскости.
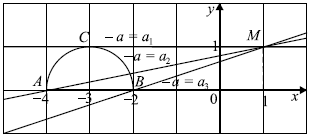
Уравнение $y-ax = 2-3a$ запишем в виде $y = a(x-3)+2$ — семейство прямых с угловым коэффициентом $a$, проходящих через точку $M (3; 2)$.
Рассмотрим рисунок. Видно, что прямая и полуокружность имеют две общие точки, если $a_1 < a ≤ a_2$. Прямая $BM$ касается окружности и является горизонтальной, поэтому её угловой коэффициент равен $0$, значит, $a_1 = 0$. Найдём $a_2$ из условия, что прямая $AM$ $y = a(x — 3) + 2$ проходит через точку $A(-5; 0)$.
$a(-5 — 3) + 2 = 0, a = {1}/{4}$, значит, $a_2 = {1}/{4}$.
Следовательно, система имеет ровно два решения при $0 < a ≤ {1}/{4}$.
Ответ: $(0;{1}/{4}]$
Задача 13
Найдите все значения $a$, при которых система уравнений
${table(x+1)^2=(y-2)^2; (x+1)^2+(y-a)^2=3a^2-2a+4;$
имеет ровно три решения.
Решение
Уравнение $(x + 1)^2 = (y — 2)^2$ равносильно совокупности двух уравнений
$[table x+1=y-2; x+1=-y+2;$ $[table y=x+3; y=-x+1;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x + 3$ и $y = -x + 1$. Заметим, что эти прямые проходят через точку $(-1; 2)$, так как система ${table y = x + 3; y = -x + 1;$ имеет единственное решение $(-1; 2)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x +1)^2 + (y — a)^2 = 3a^2 — 2a + 4$ будет множество всех точек окружности с центром в точке $(-1; a)$, лежащей на прямой $x = -1$, и радиусом $√{3a^2 — 2a + 4}$ (заметим, что $3a^2 — 2a + 4 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(-1; 2)$ лежит на окружности, значит, верно равенство $(-1 + 1)^2 + (2 — a)^2 = 3a^2 — 2a + 4$.
Отсюда получаем: $4 — 4a + a^2 = 3a^2 — 2a + 4; 2a^2 + 2a = 0; 2a ·(a + 1) = 0; $
$a = 0$ или $a = -1$.
Ответ:
Задача 14
Найдите все значения $a$, при которых система уравнений
${table(x-3)^2=(y-1)^2; (x-a)^2+(y-1)^2=3a^2-8a+9;$
имеет ровно три решения.
Решение
Уравнение $(x — 3)^2 = (y — 1)^2$ равносильно совокупности двух уравнений
$[table x-3=y-1; x-3=-y+1;$ $[table y=x-2; y=-x+4;$
Множество решений этой совокупности совпадает с множеством всех точек, лежащих на двух прямых: $y = x — 2$ и $y = -x + 4$. Заметим, что эти прямые проходят через точку $(3; 1)$, так как система ${table y = x — 2; y = -x + 4;$ имеет единственное решение $(3; 1)$.
При каждом значении $a$ множеством решений второго уравнения системы $(x — a)^2 + (y — 1)^2 = 3a^2 — 8a + 9$ будет множество всех точек окружности с центром в точке $(a; 1)$, лежащей на прямой $y = 1$, и радиусом $√{3a^2 — 8a + 9}$ (заметим, что $3a^2 — 8a + 9 > 0$ для любого $a$).
Указанные окружности будут иметь ровно три общие точки с парой указанных выше пересекающихся прямых в том и только том случае, когда окружность проходит через точку пересечения этих прямых.
В таком случае точка $(3; 1)$ лежит на окружности, значит, верно равенство $(3 — a)^2 + (1 — 1)^2 = 3a^2 — 8a + 9$.
Отсюда получаем: $9 — 6a + a^2 = 3a^2 — 8a + 9; 2a^2 — 2a = 0; 2a ·(a — 1) = 0; a = 0$ или $a = 1$.
Ответ: $0;1$
Задача 15
Найдите все значения $a$, при каждом из которых уравнение ${3x + a — x^2 + 4a^2x — x^3}/{4a^2x — x^3} = 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${3x + a — x^2 + 4a^{2}x — x^3}/{4a^{2}x — x^3} = {4a^{2}x — x^3}/{4a^{2}x — x^3} + {-x^2 + 3x + a}/{4a^{2}x — x^3} = 1 + {-x^2 + 3x + a}/{4a^{2}x — x^3}$.
Тогда уравнение примет вид ${-x^2 + 3x + a}/{4a^{2}x — x^3} = 0$. Оно равносильно системе
${table -x^2 + 3x + a = 0; 4a^{2}x — x^3 ≠ 0;$ ${table a = x^2 — 3x; x ≠ 0, x ≠ ±2a;$
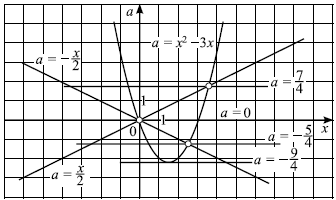
Решим систему графически в системе координат $xOa$. Для этого строим графики функций $a = x^2 — 3x$ и $a = ±{x}/{2}$.
Графиком функции $a = x^2 — 3x$ является парабола, ветви которой направлены вверх. Вершина параболы — точка $({3}/{2}; -{9}/{4})$, точки $(0; 0)$ и $(3; 0)$ принадлежат параболе. Графиками функций $a = ±{x}/{2}$ являются прямые.
Решая уравнение $x^2 — 3x = {x}/{2}$, находим точки пересечения прямой $a = {x}/{2}$ и параболы $a = x^2 — 3x: x = 0, x = {7}/{2}$, откуда $a = 0, a = {7}/{4}$. Аналогично, решая уравнение $x^2 — 3x = — {x}/{2}$, находим $x = 0, x = {5}/{2}$. Тогда $a = 0, a = — {5}/{4}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых при $a = — {9}/{4}, a = — {5}/{4}, a = 0, a = {7}/{4}$.
Ответ: $-{9}/{4};-{5}/{4};0;{7}/{4}$
Задача 16
Найдите все значения $a$, при каждом из которых уравнение ${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x}= 1$ имеет единственный корень.
Решение
В левой части уравнения выделим целую часть
${x^3 + x^2 — 16a^2x — 5x + a}/{x^3 — 16a^2x} = {x^3 — 16a^2x}/{x^3 — 16a^2x} + {x^2 — 5x + a}/{x^3 — 16a^2x} = 1 + {x^2 — 5x + a}/{x^3 — 16a^2x}$.
Тогда уравнение примет вид ${x^2 — 5x + a}/{x^3 — 16a^2x} = 0$.
Оно равносильно системе
${tablex^2 — 5x + a = 0; x^3 — 16a^2x ≠ 0;$ ${tablea = -x^2 + 5x; x ≠ 0, x ≠±4a;$
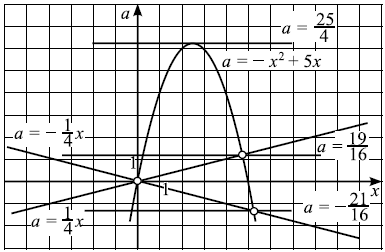
Решим систему графически в системе координат $xOa$. Для этого построим графики функций $a = -x^2 + 5x$ и $a =±{x}/{4}$.
Графиком функции $a = -x^2+5x$ является парабола, ветви которой направлены вниз. Вершина параболы — точка $({5}/{2}; {25}/{4})$, точки (0; 0) и (5; 0) принадлежат параболе. Графиками функций $a =±{x}/{4}$ являются прямые.
Решая уравнение $-x^2 + 5x = {x}/{4}$, находим точки пересечения прямой $a ={x}/{4}$ и параболы $a = -x^2 + 5x: x = 0, x = {19}/{4}$, откуда $a = 0, a = {19}/{16}$. Аналогично, решая уравнение $-x^2 + 5x = -{x}/{4}$, находим $a = 0, a = -{21}/{16}$. Выкалываем эти точки.
По рисунку видим, что ровно одна точка пересечения параболы с каждой из прямых будет при $a = -{21}/{16}, a = 0, a = {19}/{16}; a = {25}/{4}$.
Ответ: $-{21}/{16};0;{19}/{16};{25}/{4}$
Задача 17
Найдите все значения параметра $а$, при которых уравнение $√{3^x-a}+{a-1}/{√{3^x-a}}=1$ имеет ровно два различных корня.
Решение
После приведения к общему знаменателю уравнение примет вид ${3x — a + a — 1}/{√{3^x — a}} = 1$ или ${3^x — 1}/{√{3^x — a}} = 1$. Пусть $3^x = t, t > 0$. Заметим, что после замены каждому положительному корню уравнения ${t — 1}/{√{t — a}} = 1$ соответствует единственный корень исходного уравнения (это следует из монотонности функции $3^x = t$). Уравнение ${t — 1}/{√{t — a}} = 1$ равносильно системе
${tablet — 1=√{t — a}; t>a;$
Возведём в квадрат обе части первого уравнения, учитывая, что $t ≥ 1$.
${tablea=-t^2+3t-1; t>a; t ≥ 1;$
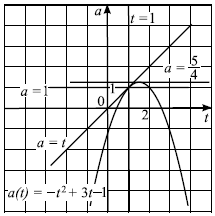
Решим систему графически в системе координат $tOa$.
Вершина параболы $a = -t^2 + 3t — 1$ — точка с координатами $({3}/{2};{5}/{4})$.
Графики функций $a = -t^2 + 3t — 1$ и $a = t$ имеют единственную общую точку $t = 1$. Множество точек, удовлетворяющих неравенству $a < t$, представляет собой полуплоскость, лежащую ниже прямой $a = t$. $-t^2 + 3t — 1 = t, t^2 — 2t + 1 = 0, t = 1$.
По графику видно, что парабола $a = -t^2 +3t-1$ и прямая $a = const$ имеют ровно две общие точки при условии $t ≥ 1$, если $1 < a < {5}/{4}$, значит, исходное уравнение имеет ровно два корня при этих же значениях $a$.
Ответ: $(1;{5}/{4})$
Задача 18
Найдите все значения параметра $a$, при каждом из которых уравнение ${x^2+ax+2}/{2}=√{4x^2+ax+1}$ имеет ровно три различных корня.
Решение
Уравнение ${x^2 + ax + 2}/{2} = √{4x^2 + ax + 1}$ при ${x^2 + ax + 2}/{2} < 0$ не имеет корней. При $x^2 + ax + 2 ≥ 0$ обе части уравнения можно возвести в квадрат.
$(x^2 + ax + 2)^2 = 4(4x^2 + ax + 1)$,
$x^4 + ax^3 + 2x^2 + ax^3 + a^2x^2 + 2ax + 2x^2 + 2ax + 4 = 16x^2 + 4ax + 4$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо, чтобы числа $x_1, x_2, x_3$ были различными и для каждого из этих чисел выполнялось условие $x^2+ax+2 ≥ 0$.
$x_2≠0$ и $x_3≠0$, если $a≠√{12}=2√3$ и $a≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 2. g(0) = 2 > 0$. Числа $x_2 = -a + 2√3$ и $x_3 = -a — 2√3$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + 2√3)^2 + a(-a + 2√3) + 2 ≥ 0; (-a — 2√3)^2 + a(-a — 2√3) + 2 ≥ 0;$
${table-2a√3 + 14 ≥ 0; 2a√3 + 14 ≥ 0;$ ${tablea≤{7}/{√3}; a≥-{7}/{√3};$
Таким образом, $a∊[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$.
Ответ: $[-{7}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{7}/{√3}]$
Задача 19
Найдите все значения параметра a, при каждом из которых уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ имеет ровно три различных корня.
Решение
Уравнение $x^2 + ax + 4 = √{20x^2 + 8ax + 16}$ при $x^2 + ax + 4 <0$ не имеет корней. При $x^2+ax+4≥0$ (1) можно обе части уравнения возвести в квадрат.
$(x^2 + ax + 4)^2 = 20x^2 + 8ax + 16$,
$x^4 +ax^3+4x^2+ax^3+a^2x^2 +4ax+4x^2+4ax+16 = 20x^2+8ax+16$,
$x^4 + 2ax^3 + x^2(a^2 — 12) = 0$,
$x^2(x^2 + 2ax + a^2 — 12) = 0$,
$x^2((x + a)^2 — 12) = 0$,
$x_1 = 0, (x + a — √{12})(x + a + √{12}) = 0$,
$x_2 = -a + √{12}, x_3 = -a — √{12}$.
Чтобы исходное уравнение имело три различных корня, необходимо выполнение условия (1) для чисел $x_1, x_2, x_3$ и выполнение условия, что эти числа различны.
$x_2≠ 0$ и $x_3≠0$, если $a ≠√{12} = 2√3$ и $a ≠-√{12} = -2√3$.
Обозначим $g(x) = x^2 + ax + 4. g(x_1) = g(0) = 4 > 0$. Числа $x_2 = -a + √{12}$ и $x_3 = -a — √{12}$ будут корнями исходного уравнения, если выполняются условия:
${tableg(x_2) ≥ 0; g(x_3) ≥ 0;$ ${table(-a + √{12})^2 + a(-a + √{12}) + 4 ≥ 0; (-a — √{12})^2 + a(-a — √{12}) + 4 ≥ 0;$
${table-a√{12}+16 ≥ 0; a√{12}+16 ≥ 0;$ ${tablea≤{8}/{√3}; a≥-{8}/{√3};$
Таким образом, $a∈[-{8}/{√3}; -2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Ответ: $[-{8}/{√3};-2√3)∪(-2√3;2√3)∪(2√3;{8}/{√3}]$
Задача 20
Найдите все значения $a$, при каждом из которых система уравнений ${table(xy^2-5xy-5y+25)/{√{x+5}}=0; y=ax;$ имеет ровно два различных решения.
Решение
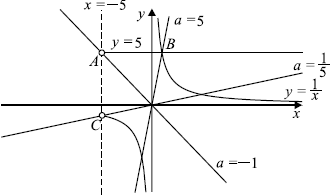
Решим задачу графически. Построим графики первого и второго уравнения и определим, сколько точек пересечения они имеют при различных значениях параметра.
Первое уравнение ${xy^2 — 5xy — 5y + 25}/{√{x + 5}}= 0$ параметра не содержит и представляет собой равенство дроби нулю. Это выполняется, если числитель равен нулю, а знаменатель не равен нулю, при этом оба выражения имеют смысл.
Запишем уравнение в виде ${(y — 5)(xy — 5)}/{√{x + 5}} = 0$, разложив числитель на множители.
При $x ≤ -5$ первое уравнение системы не имеет смысла. При $x > -5$ уравнение задаёт прямую $y = 5$ и гиперболу $y ={5}/{x}$.
Число решений исходной системы равно числу точек пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ с прямой $y = ax$ при условии $x>-5$.
Найдём координаты точек $A, B$ и $C$.
$B$ — точка пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$, чтобы найти её координаты, нужно решить систему уравнений ${tabley = 5; y ={5}/{x};$
Получаем $B(1; 5)$.
У точек $A$ и $C$ абсцисса равна $-5$, ординаты находим из уравнений прямой и гиперболы. $A(-5; 5)$ и $C(-5;-1)$.
При каждом значении $a$ уравнение $y = ax$ задаёт прямую с угловым коэффициентом $a$, проходящую через начало координат. Чтобы найти значение $a$, при котором такая прямая проходит через точку с указанными координатами, нужно подставить координаты в уравнение прямой.
Например, для точки $A(-5; 5)$ получаем $x = -5; y = 5; 5 = a·(-5); a = -1$. Аналогично для $B(1; 5)$ получим $a = 5$. Для $C(-5;-1)$ получим $a ={1}/{5}$.
При $x>-5$ прямая $y = ax$ пересекает прямую $y = 5$ при $a<-1$ и $a>0$, пересекает правую ветвь гиперболы $y ={5}/{x}$ при $a>0$, пересекает левую ветвь гиперболы $y ={5}/{x}$ при $a>{1}/{5}$. При этом прямая $y = ax$ проходит через точку пересечения прямой $y = 5$ и гиперболы $y ={5}/{x}$ при $a = 5$.
Таким образом, исходная система имеет ровно два решения при $0< a ≤0.2; a = 5$.
Ответ: $(0;0.2]∪${5}
Рекомендуемые курсы подготовки
ЕГЭ по математике — Профиль 2023. Открытый банк заданий с ответами.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи с параметром
Задание
1
#1220
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+3=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-3). Рассмотрим два случая:
1) (a=0). В этом случае левая часть равна (0), а правая – нет, следовательно, уравнение не имеет корней.
2) (ane 0). Тогда (x=-dfrac{3}{a}).
Ответ:
(a=0 Rightarrow xin varnothing; \
ane 0 Rightarrow
x=-dfrac{3}{a}).
Задание
2
#1221
Уровень задания: Легче ЕГЭ
Решите уравнение (ax+a^2=0) при всех значениях параметра (a).
Уравнение можно переписать в виде (ax=-a^2). Рассмотрим два случая:
1) (a=0). В этом случае левая и правая части равны (0), следовательно, уравнение верно при любых значениях переменной (x).
2) (ane 0). Тогда (x=-a).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
ane 0 Rightarrow x=-a).
Задание
3
#1222
Уровень задания: Легче ЕГЭ
Решите неравенство (2ax+5cosdfrac{pi}{3}geqslant 0) при всех значениях параметра (a).
Неравенство можно переписать в виде (axgeqslant -dfrac{5}{4}). Рассмотрим три случая:
1) (a=0). Тогда неравенство принимает вид (0geqslant
-dfrac{5}{4}), что верно при любых значениях переменной (x).
2) (a>0). Тогда при делении на (a) обеих частей неравенства знак неравенства не изменится, следовательно, (xgeqslant
-dfrac{5}{4a}).
3) (a<0). Тогда при делении на (a) обеих частей неравенства знак неравенства изменится, следовательно, (xleqslant -dfrac{5}{4a}).
Ответ:
(a=0 Rightarrow xin mathbb{R}; \
a>0 Rightarrow xgeqslant -dfrac{5}{4a}; \
a<0 Rightarrow xleqslant -dfrac{5}{4a}).
Задание
4
#1223
Уровень задания: Легче ЕГЭ
Решите неравенство (a(x^2-6) geqslant (2-3a^2)x) при всех значениях параметра (a).
Преобразуем неравенство к виду: (ax^2+(3a^2-2)x-6a geqslant 0). Рассмотрим два случая:
1) (a=0). В этом случае неравенство становится линейным и принимает вид: (-2x geqslant 0 Rightarrow xleqslant 0).
2) (ane 0). Тогда неравенство является квадратичным. Найдем дискриминант:
(D=9a^4-12a^2+4+24a^2=(3a^2+2)^2).
Т.к. (a^2 geqslant 0 Rightarrow D>0) при любых значениях параметра.
Следовательно, уравнение (ax^2+(3a^2-2)x-6a = 0) всегда имеет два корня (x_1=-3a, x_2=dfrac{2}{a}). Таким образом, неравенство примет вид:
[(ax-2)(x+3a) geqslant 0]
Если (a>0), то (x_1<x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вверх, значит, решением являются (xin (-infty; -3a]cup
big[dfrac{2}{a}; +infty)).
Если (a<0), то (x_1>x_2) и ветви параболы (y=(ax-2)(x+3a)) направлены вниз, значит, решением являются (xin big[dfrac{2}{a};
-3a]).
Ответ:
(a=0 Rightarrow xleqslant 0; \
a>0 Rightarrow xin (-infty; -3a]cup big[dfrac{2}{a}; +infty);
\
a<0 Rightarrow xin big[dfrac{2}{a}; -3abig]).
Задание
5
#1851
Уровень задания: Легче ЕГЭ
При каких (a) множество решений неравенства ((a^2-3a+2)x
-a+2geqslant 0) содержит полуинтервал ([2;3)) ?
Преобразуем неравенство: ((a-1)(a-2)x geqslant a-2). Получили линейное неравенство. Рассмотрим случаи:
1) (a=2). Тогда неравенство примет вид (0 geqslant 0), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
2) (a=1). Тогда неравенство примет вид (0 geqslant -1), что верно при любых значениях (x), следовательно, множество решений содержит полуинтервал ([2;3)).
3) ((a-1)(a-2)>0 Leftrightarrow ain (-infty;1)cup (2;+infty)). Тогда:
(xgeqslant dfrac{1}{a-1}). Для того, чтобы множество решений содержало полуинтервал ([2;3)), необходимо, чтобы
(dfrac{1}{a-1} leqslant 2 Leftrightarrow dfrac{3-2a}{a-1}
leqslant 0
Rightarrow ain (-infty; 1)cup [1,5; +infty)).
Учитывая условие (ain (-infty;1)cup (2;+infty)), получаем (ain
(-infty;1)cup (2;+infty)).
4) ((a-1)(a-2)<0 Leftrightarrow ain (1;2)). Тогда:
(xleqslant dfrac{1}{a-1} Rightarrow dfrac{1}{a-1} geqslant 3).
Действуя аналогично случаю 3), получаем (ain (1;
dfrac{4}{3}big]).
Ответ:
(ain (-infty;dfrac{4}{3}big]cup [2;+infty)).
Задание
6
#1361
Уровень задания: Легче ЕГЭ
Определить количество корней уравнения (ax^2+(3a+1)x+2=0) при всех значениях параметра (a).
Рассмотрим два случая:
1) (a=0). Тогда уравнение является линейным: (x+2=0 Rightarrow
x=-2). То есть уравнение имеет один корень.
2) (ane 0). Тогда уравнение является квадратным. Найдем дискриминант: (D=9a^2-2a+1).
Рассмотрим уравнение (9a^2-2a+1=0): (D’=4-36<0), следовательно, уравнение (9a^2-2a+1=0) не имеет корней. Значит, выражение ((9a^2-2a+1)) принимает значения строго одного знака: либо всегда положительно, либо отрицательно. В данном случае оно положительно при любых (a) (в этом можно убедиться, подставив вместо (a) любое число).
Таким образом, (D=9a^2-2a+1>0) при всех (ane 0). Значит, уравнение (ax^2+(3a+1)x+2=0) всегда имеет два корня: (x_{1,2}=dfrac{-3a-1pm
sqrt D}{2a})
Ответ:
(a=0Rightarrow) один корень
(ane 0 Rightarrow) два корня.
Задание
7
#1363
Уровень задания: Легче ЕГЭ
Решить уравнение (sqrt{x+2a}cdot (3-ax-x)=0) при всех значениях параметра (a).
Данное уравнение равносильно системе:
[begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x=-2a \
&3-(a+1)x=0 qquad (*)
end{aligned} end{gathered} right.
end{cases}]
Рассмотрим два случая:
1) (a+1=0 Rightarrow a=-1). В этом случае уравнение ((*)) равносильно (3=0), то есть не имеет решений.
Тогда вся система равносильна (
begin{cases}
xgeqslant 2\
x=2
end{cases} Leftrightarrow x=2)
2) (a+1ne 0 Rightarrow ane -1). В этом случае система равносильна: [begin{cases}
xgeqslant -2a\
left[ begin{gathered} begin{aligned}
&x_1=-2a \
&x_2=dfrac3{a+1}
end{aligned} end{gathered} right.
end{cases}]
Данная система будет иметь одно решение, если (x_2leqslant -2a), и два решения, если (x_2>-2a):
2.1) (dfrac3{a+1}leqslant -2a Rightarrow a<-1 Rightarrow ) имеем один корень (x=-2a).
2.2) (dfrac3{a+1}>-2a Rightarrow a>-1 Rightarrow ) имеем два корня (x_1=-2a, x_2=dfrac3{a+1}).
Ответ:
(ain(-infty;-1) Rightarrow x=-2a\
a=-1 Rightarrow x=2\
ain(-1;+infty) Rightarrow xin{-2a;frac3{a+1}})

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Параметрические уравнения
Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим. Эта дополнительная величина в уравнении называется параметр. На самом деле с каждым параметрическим уравнением может быть написано множество уравнений.
Способ решения параметрических уравнений
- Находим область определения уравнения.
- Выражаем a как функцию от $х$.
- В системе координат $хОа$ строим график функции, $а=f(х)$ для тех значений $х$, которые входят в область определения данного уравнения.
- Находим точки пересечения прямой, $а=с$, где $с∈(-∞;+∞)$ с графиком функции $а=f(х)$. Если прямая, а=с пересекает график, $а=f(х)$, то определяем абсциссы точек пересечения. Для этого достаточно решить уравнение вида, $а=f(х)$ относительно $х$.
- Записываем ответ.
Общий вид уравнения с одним параметром таков:
$F(x, a) = 0$
При различных значениях, а уравнение $F(x, a) = 0$ может иметь различные множества корней, задача состоит в том, чтобы изучить все случаи, выяснить, что будет при любом значении параметра. При решении уравнений с параметром обычно приходится рассматривать много различных вариантов. Своевременное обнаружение хотя бы части невозможных вариантов имеет большое значение, так как освобождает от лишней работы.
Поэтому при решении уравнения $F(x, a) = 0$ целесообразно под ОДЗ понимать область допустимых значений неизвестного и параметра, то есть множество всех пар чисел ($х, а$), при которых определена (имеет смысл) функция двух переменных $F(x, а)$. Отсюда естественная геометрическая иллюстрация ОДЗ в виде некоторой области плоскости $хОа$.
ОДЗ различных выражений (под выражением будем понимать буквенно — числовую запись):
1. Выражение, стоящее в знаменателе, не должно равняться нулю.
${f(x)}/{g(x)}; g(x)≠0$
2. Подкоренное выражение должно быть неотрицательным.
$√{g(x)}; g(x)≥0$.
3. Подкоренное выражение, стоящее в знаменателе, должно быть положительным.
${f(x)}/{√{g(x)}}; g(x) > 0$
4. У логарифма: подлогарифмическое выражение должно быть положительным; основание должно быть положительным; основание не может равняться единице.
$log_{f(x)}g(x) {tableg(x) > 0; f(x) > 0; f(x)≠1;$
Алгебраический способ решения квадратных уравнений с параметром $ax^2+bx+c=0$
Квадратное уравнение $ax^2+bx+c=0, а≠0$ не имеет решений, если $D < 0$;
Квадратное уравнение имеет два различных корня, когда $D > 0$;
Квадратное уравнение имеет один корень, если $D=0$
Тригонометрические тождества
1. $tgα={sinα}/{cosα}$
2. $ctgα={cosα}/{sinα}$
3. $sin^{2}α+cos^{2}α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^{2}α}$
$cosα=±√{1-sin^{2}α$
4. $tgα·ctgα=1$
5. $1+tg^{2}α={1}/{cos^{2}α}$
6. $1+ctg^{2}α={1}/{sin^{2}α}$
Формулы двойного угла
1. $sin2α=2sinα·cosα$
2. $cos2α=cos^{2}α-sin^{2}α=2cos^{2}α-1=1-2sin^{2}α$
3. $tg2α={2tgα}/{1-tg^{2}α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos{α-β}+cos{α+β}}/{2}$
$sinα·sinβ={cos{α-β}-cos{α+β}}/{2}$
$sinα·cosβ={sin{α+β}+sin{α-β}}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Решение тригонометрического уравнения с параметром рассмотрим на примере.
Пример:
Найдите все значения параметра с, при каждом из которых уравнение $3cos2x-2sin2x=c$ имеет решение.
Решение:
Преобразуем данное уравнение к виду
$√{3^2+(-2)^2}(cos2xcosφ-sin2xsinφ)=c$
Воспользуемся тригонометрической формулой и свернем второй множитель как косинус суммы
$√{13}cos(2x+φ)=c$, где $φ=arccos{3}/{√{13}}$
Уравнение $√{13}cos(2x+φ)=c$ имеет решения тогда и только тогда, когда $-1≤ {c}/{√{13}} ≤ 1$, домножим полученное неравенство на $√{13}$ и получим
$-√{13} ≤ c ≤ √{13}$
Ответ: $-√{13} ≤ c ≤ √{13}$
Неравенства с параметром
Если имеется неравенство вида $F(a,x) ≤ G(a,x)$ то оно будет иметь одно решение, если $F'(a, x)=G'(a, x)$.
Системы уравнений:
Выделяют четыре основных метода решения систем уравнений:
- Метод подстановки: из какого-либо уравнения системы выражаем одно неизвестное через другое и подставляем во второе уравнение системы.
- Метод алгебраического сложения: путем сложения двух уравнений получить уравнение с одной переменной.
- Метод введения новых переменных: ищем в системе некоторые повторяющиеся выражения, которые обозначим новыми переменными, тем самым упрощая вид системы.
- Графический метод решения: из каждого уравнения выражается $«у»$, получаются функции, графики которых необходимо построить и посмотреть координаты точек пересечения.
Логарифмические уравнения и системы уравнений
Основное логарифмическое тождество:
$a^{log_{a}b}=b$
Это равенство справедливо при $b> 0, a> 0, a≠1$
Свойства логарифмов:
Все свойства логарифмов мы будем рассматривать для $a> 0, a≠ 1, b> 0, c> 0, m$ – любое действительное число.
1. Для любых действительных чисел $m$ и $n$ справедливы равенства:
$log_{а}b^m=mlog_{a}b$;
$log_{a^m}b={1}/{m}log_{a}b$.
$log_{a^n}b^m={m}/{n}log_{a}b$
2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.
$log_a(bc)=log_{a}b+log_{a}c$
3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию
$log_a{b}/{c}=log_{a}b-log_{a}c$
4. При умножении двух логарифмов можно поменять местами их основания
$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a, b, c, d >0, a≠1, b≠1$.
5. $c^{log_{a}b}=b^{log_{a}b}$, где $а, b, c > 0, a≠1$
6. Формула перехода к новому основанию
$log_{a}b={log_{c}b}/{log_{c}a}$
7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение
$log_{a}b={1}/{log_{b}a}$
При решении систем, содержащих логарифмические уравнения, часто удается, избавившись от логарифма, заменить одно или оба уравнения системы рациональными уравнениями. После этого надо выразить одну переменную через другую и после постановки получить уравнение с одной переменной. Кроме того, часто встречаются задачи на замену переменной в пределах одного или обоих уравнений системы и системы, требующие отбора решений.
Логарифмические неравенства:
1. Определить ОДЗ неравенства.
2. По свойствам логарифма преобразовать неравенство к простому виду, желательно получить с двух сторон логарифмы по одинаковому основанию.
3. Перейти к подлогарифмическим выражениям, при этом надо помнить, что:
а) если основание больше единицы, то при переходе к подлогарифмическим выражениям знак неравенства остается прежним;
b) если основание меньше единицы, то при переходе к подлогарифмическим выражениям знак неравенства меняется на противоположный;
с) если в основании находится переменная, надо рассмотреть оба варианта.
4. Решить неравенство.
5. Выбрать решения с учетом ОДЗ из п.1
При решении логарифмических неравенств с переменной в основании легче всего воспользоваться тождественными преобразованиями:
$log_{a}f > b ↔ {table (f-a^b)(a-1) > 0; f > 0; a > 0;$
$log_{a}f+log_{a}g > 0 ↔ {table(fg-1)(a-1)> 0; f > 0,g > 0; a > 0;$
$log_{a}f+b > 0 ↔ {table(fa^b-1)(a-1) > 0; f > 0; a > 0;$
Системы, содержащие показательные уравнения
Свойства степеней
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n·a^m=a^{n+m}$
2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются
$a^n:a^m=a^{n-m}$
3. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n·m}$
4. При возведении в степень произведения в эту степень возводится каждый множитель
$(a·b)^n=a^n·b^n$
5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
6. При возведении любого основания в нулевой показатель степени результат равен единице
$a^0=1$
Основные методы решения систем, содержащих показательные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – положительность выражения $a^{f(x)}$, которую полезно учитывать, вводя соответствующее ограничение при замене переменной.
Показательные неравенства, сводящиеся к виду $a^{f(x)} ≥ a^{g(x)}$:
1. Преобразовать показательное уравнение к виду $a^{f(x)} ≥ a^{g(x)}$
2. Перейти показателям степеней, при этом если основание степени меньше единицы, то знак неравенства меняется на противоположный, если основание больше единицы – знак неравенства остается прежним.
3. Решить полученное неравенство.
4. Записать результат.
Показательные неравенства, которые можно разложить на множители или сделать замену переменной.
1. Для данного метода во всем неравенстве по свойству степеней надо преобразовать степени к одному виду $a^{f(x)}$.
2. Сделать замену переменной $a^{f(x)}=t, t>0$.
3. Получаем рациональное неравенство, которое можно решить методом интервалов путем разложения на множители выражения.
4. Делаем обратную замену с учетом того, что $t>0$. Получаем простейшее показательное неравенство $a^{f(x)}=t$, решаем его и результат записываем в ответ.
Уравнения с многочленами
Многочлен может обозначаться записью $Р(х)$ — это означает, что многочлен зависит от «х», если записать $Р(х+1)$ — это означает, что в многочлене вместо «х» надо сделать замену на скобку $(х+1)$
Пример:
Найдите значение выражения: $4(p(2x)−2p(x+3))$, если $p(x)=x−6$
Решение:
В данном условии задан многочлен, зависящий от «х», как $p(x)=x−6$.
Чтобы было понятнее, назовем исходный многочлен основной формулой, тогда, чтобы записать $p(2x)$, в основной формуле заменим «х» на «2х».
$p(2x)=2х-6$
Аналогично $p(x+3)=(х+3)-6=х+3-6=х-3$
Соберем все выражение: $4(p(2x)−2p(x+3))=4((2х-6)-2(х-3))$
Далее осталось раскрыть скобки и привести подобные слагаемые
$4((2х-6)-2(х-3))=4(2х-6-2х+6)=4·0=0$
Ответ: $0$
Системы иррациональных уравнений
Основные методы решения систем, содержащих иррациональные уравнения, ничем принципиально не отличаются от методов решения других систем: это метод алгебраического сложения, замена переменной в пределах одного уравнения или всей системы, подстановка. Единственная особенность – надо расписать ОДЗ каждого уравнения, а в конце решения выбрать решение системы с учетом ОДЗ.
Чтобы решить иррациональное уравнение, необходимо:
1. Преобразовать заданное иррациональное уравнение к виду
$√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
2. Обе части уравнение возвести в квадрат
$√{f(x)}^2={g(x)}^2$ или $√{f(x)}^2=√{g(x)}^2$
3. Решить полученное рациональное уравнение.
4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)