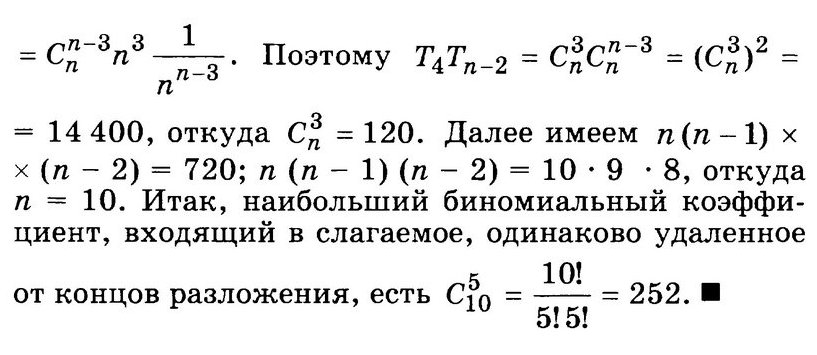Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Без метода (8 шт.)
Категория:
Версия для печати и копирования в MS Word
1
На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
2
За круглый стол на 9 стульев в случайном порядке рассаживаются 7 мальчиков и 2 девочки. Найдите вероятность того, что обе девочки будут сидеть рядом.
3
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки будут сидеть рядом.
4
За круглый стол на 5 стульев в случайном порядке рассаживаются 3 мальчика и 2 девочки. Найдите вероятность того, что девочки не будут сидеть рядом.
5
За круглый стол на 201 стул в случайном порядке рассаживаются 199 мальчиков и 2 девочки. Найдите вероятность того, что между девочками будет сидеть один мальчик.
Пройти тестирование по этим заданиям
Подготовка к ЕГЭ по математике (В4) Решение комбинаторных задач
Зарьянцева В.П.
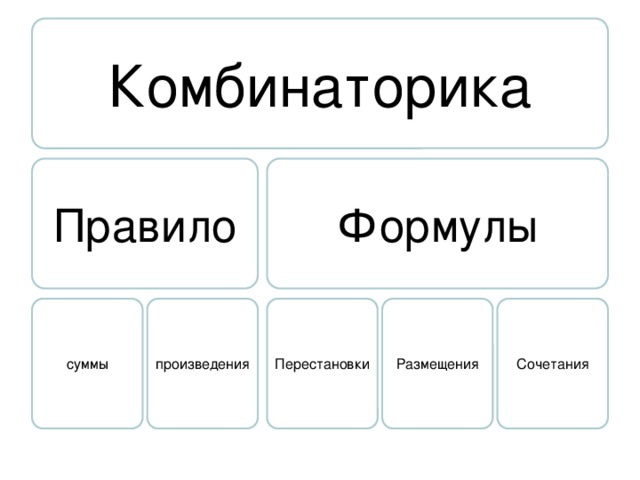
Комбинаторика
Правило
Формулы
суммы
произведения
Перестановки
Размещения
Сочетания
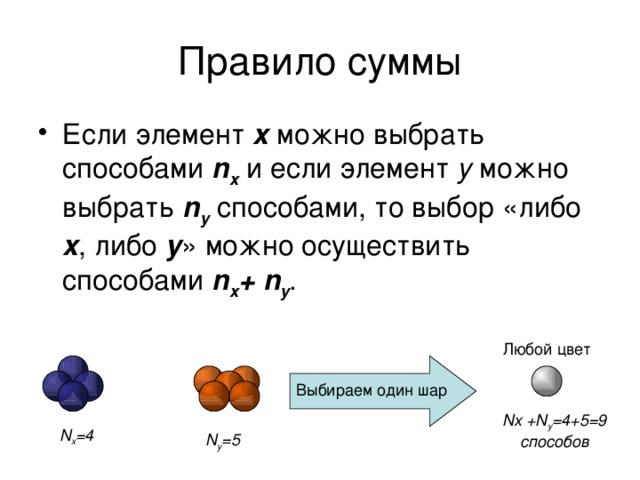
Правило суммы
- Если элемент x можно выбрать способами n x и если элемент y можно выбрать n y способами, то выбор «либо x , либо y » можно осуществить способами n x + n y .
Любой цвет
Выбираем один шар
Nx +N y =4+5=9 способов
N x =4
N y =5
Пример 1
- В коробке 10 тетрадей в клетку и 5 тетрадей в линию. Сколькими способами можно выбрать одну тетрадь?
- Решение: или – логическая сумма
- 10+5=15 (выбор неважен)
- Пример1. Сколько существует способов выбрать кратное двум или трем число из множества чисел : 2,3,4,15,16,20,21, 75,28 ?
- Решение:
- к1=5 –кратное 2 (2,4,16,20,28),
к2=4 – кратное 3 (3,15,21,75)
- к1+к2 = 5+4 = 9
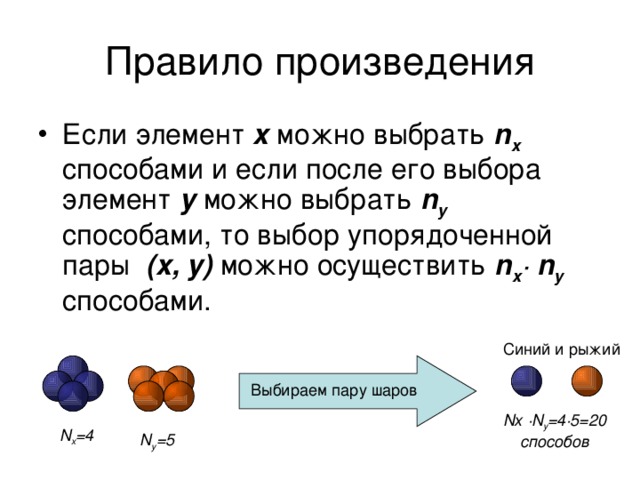
Правило произведения
- Если элемент x можно выбрать n x способами и если после его выбора элемент y можно выбрать n y способами, то выбор упорядоченной пары (x, y) можно осуществить n x ∙ n y способами.
Синий и рыжий
Выбираем пару шаров
Nx ∙N y =4∙5=20 способов
N x =4
N y =5
Пример 2
- В магазине «Все для чая» есть 5 разных чашек и 3 разных блюдца. Сколькими способами можно купить чашку с блюдцем?
- 5*3=15
Пример 2. а) Сколько различных двузначных чисел можно составить из цифр 1,3,5,7,9?
Решение: N= 5х5 = 25 ( Если не сказано, что элемент не повторяется, то выборка с повторениями)
б) Сколько среди них чисел, кратных 5?
Решение: Число кратно 5, если оканчивается цифрой 5 или 0. В нашем случае – 5.
На первой позиции фиксируем одну из пяти цифр, на второй – 5.
N= 5 х1 =5
- Пример5 . Несколько стран в качестве символа своего государства решили использовать флаг в виде четырех горизонтальных полос, одинаковых по ширине, но разных по цвету: белый, синий, красный, зеленый. У каждой страны свой, отличный от других, флаг.
- а ) Сколько всего стран могут использовать такую символику?
- Решение : Цвет верхней полосы можно выбрать одним из 4 способов, второй полосы – одним из трех оставшихся, цвет 3 полосы – одним из 2 оставшихся, а 4 – одним способом. По правилу произведения N= 4х3х2х1=24
- б ) Сколько стран могут использовать такую символику с синей и красной полосами, расположенными рядом?
- Решение : Две полосы, всегда расположенные рядом, можно рассматривать как одну полосу, тогда полос останется 3, из них можно составить 3х2х1=6 разных флагов. Но две полосы (синюю и красную) можно «склеить» по-разному: синяя, а под ней красная, или красная, а под ней синяя. Поэтому общее количество вариантов по правилу суммы равно 6+6=12
- Пример7 . Сколькими способами можно посадить шестерых школьников на скамейку так, чтобы Коля и Оля оказались рядом?
- Решение : Будем считать, что на скамейке 6 пустых мест. Посадить Колю можно шестью способами, после чего Олю посадить рядом с ним одним или двумя способами. Это зависит от того, куда мы посадили Колю – на крайнее место или нет.
- Пусть Коля сидит на краю. Место на краю можно выбрать 2 способами, после чего Олю можно посадить одним способом, после чего оставшиеся 4 места можно занять 4х3х2х1 способами, значит, всего 2х1х4х3х2х2=48 способов
Коля сидит где-то в середине. Место для Коли можно выбрать 4 способами, Олю можно посадить 2 способами, значит, всего
4х2х4х3х2х1=192 способами.
- По правилу сложения 48+192= 240 способов
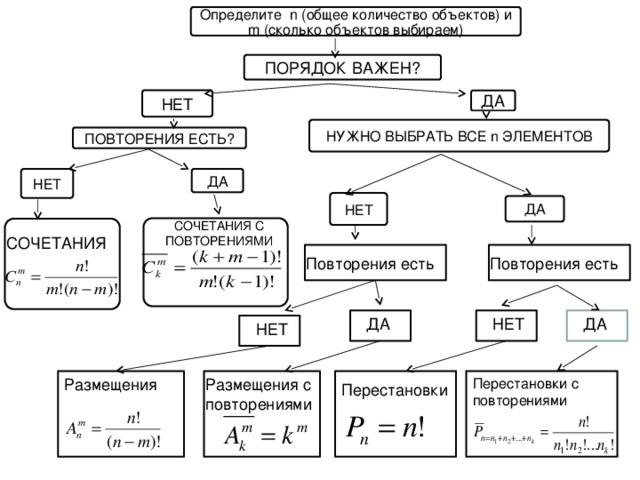
Определите n (общее количество объектов) и m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
НУЖНО ВЫБРАТЬ ВСЕ n ЭЛЕМЕНТОВ
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
НЕТ
ДА
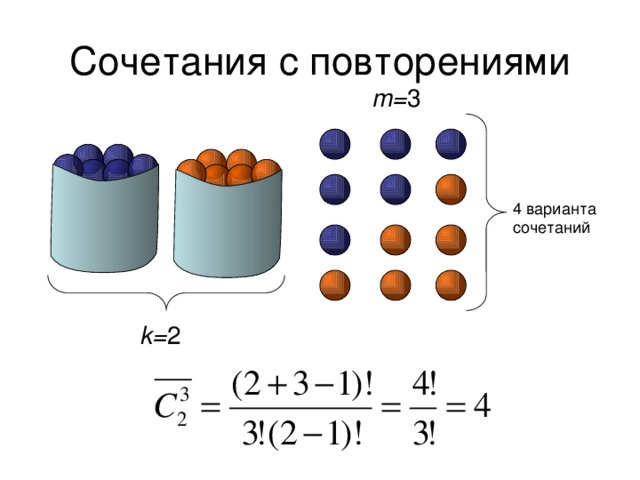
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ
СОЧЕТАНИЯ
Повторения есть
Повторения есть
ДА
ДА
НЕТ
НЕТ
Перестановки с повторениями
Размещения с повторениями
Размещения
Перестановки
13
Перестановки
Перестановки без повторений
- Перестановками без повторений из n различных элементов называются все возможные последовательности этих n элементов. Число перестановок без повторений из n элементов равняется
по определению
Перестановки без повторений
6 различных перестановок
Сколькими способами 4 человека могут разместиться в четырехместном купе?
Задача 19 . Даны цифр: 1,2,3,4,5,6,7. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1234567, 2354167, 7546321 .
Перестановка-упорядоченное множество.
Число перестановок из n элементов вычисляют по формуле P n =n! .
По условию n=7
Так из 7 цифр можно 7!=1*2*3*4*5*6*7=5040 различных чисел.
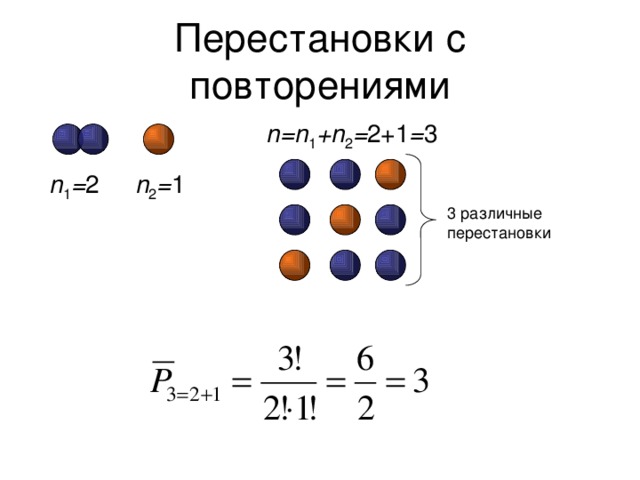
Перестановки с повторениями
- Перестановки с повторением из n элементов k типов
- число элементов 1-го типа n 1 ; число элементов 2-го типа n 2 ; …; число элементов k -го типа n k ,
- все возможные последовательности исходных n элементов. Число перестановок с повторениями обозначают
- подсчитывают так:
Перестановки с повторениями
n=n 1 +n 2 = 2+1 = 3
n 2 = 1
n 1 = 2
3 различные перестановки
Пример 4
- Дворовая футбольная команда выбирает капитана и его заместителя. Сколькими способами это можно сделать, если в команде 11 человек?
Пример 5
- Сколько различных гирлянд можно сделать, если у нас 5 красных, 7 синих и 4 желтых светодиода?
Пример Даны цифр: 1,2,2,3,3,3,4,. Сколько различных чисел можно составить из этих цифр? Каждое число является перестановкой из 7 элементов.
Примеры: 1223334, 4232331,2233314.
Некоторые числа при перестановке одинаковых цифр не меняются.
По условию n = 7, n1=2 , n2 =3
- Сколькими способами можно поселить 7 студентов в три комнаты: одноместную, двухместную и четырехместную?
- Сколько различных гирлянд получится, если замкнуть гирлянду из предыдущей задачи в кольцо?
Размещения
(выборки)
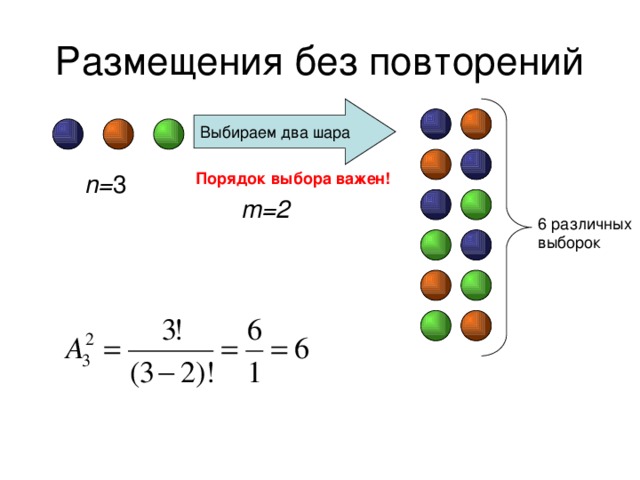
Размещения без повторений
- Размещениями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга или порядком следования элементов, или составом элементов.
- Число размещений без повторений из n элементов по m обозначается символом
Размещения без повторений
Выбираем два шара
n= 3
Порядок выбора важен!
m=2
6 различных выборок
Расписание одного дня состоит из 5 уроков. Определить число вариантов расписания при выборе из 11 дисциплин .
Пример
- Из группы в 15 человек выбирается 4 участника эстафеты 800+400+200+100. Сколькими способами можно расставить спортсменов по этапам эстафеты?
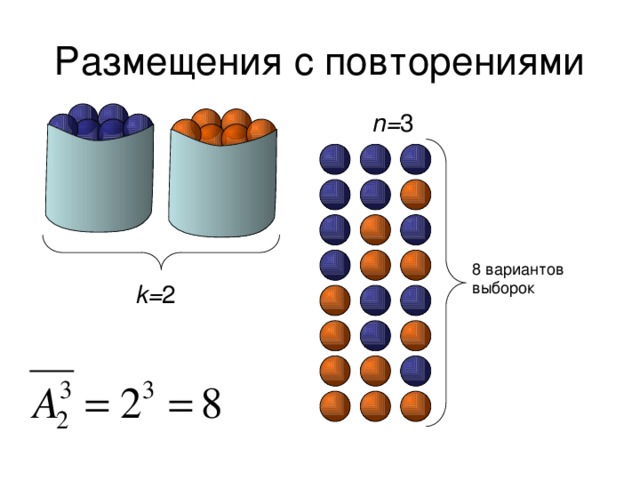
Размещения с повторениями
- Размещения с повторениями из элементов k типов по m элементов ( k и m могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличаются друг от друга или порядком следования элементов, или составом элементов.
Размещения с повторениями
n= 3
8 вариантов выборок
k= 2
Пример 8
- Назовем натуральное число «симпатичным», если в его записи встречаются только нечетные цифры. Сколько существует четырехзначных «симпатичных» чисел?
- k=5 порядок важен
Шифр сейфа состоит из 6 цифр, которые должны набираться последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Сочетания
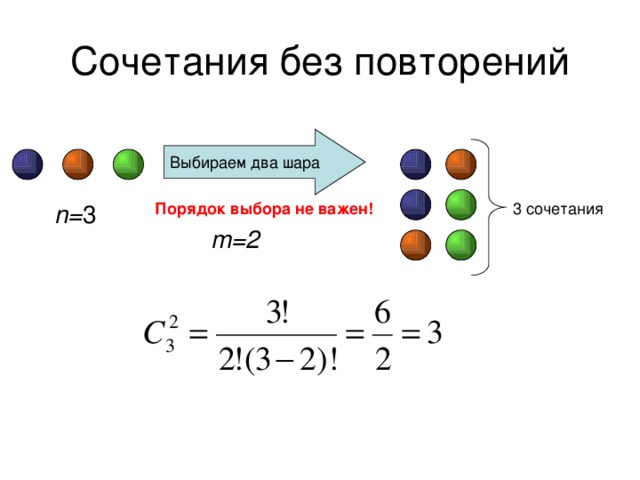
Сочетания без повторений
- Сочетаниями без повторений из n различных элементов по m элементов называются все такие последовательности m различных элементов, выбранных из исходных n , которые отличаются друг от друга составом элементов.
Сочетания без повторений
Выбираем два шара
Порядок выбора не важен!
n= 3
3 сочетания
m=2
Пример 9
- Сколькими способами можно выбрать трех дежурных из группы в 20 человек?
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков.
Сочетания с повторениями
- Сочетаниями с повторениями из элементов k типов по m элементов ( m и k могут быть в любых соотношениях) называются все такие последовательности m элементов, принадлежащих исходным типам, которые отличают друг от друга составом элементов.
Сочетания с повторениями
m= 3
4 варианта сочетаний
k= 2
Пример 10
В вазе стоят 10 красных и 4 розовых гвоздики. Все цветы на внешний вид одинаковы. Сколькими способами можно выбрать 3 цветка из вазы?
Решение Так как по условию задачи все цветы на внешний вид одинаковы, то мы получаем формулу без повторений. Вы выбираем цветы в букет, порядок выбора не важен, следовательно, мы получаем формулу сочетаний без повторений: два типа цветов, выбираем три цветка.
В почтовом отделении продаются открытки 10 видов. Сколькими способами можно купить 12 открыток для поздравлений?
- Один выбор (анализ) элементов или несколько? Если один, то см. п.3
- Каким союзом варианты выбора (анализа) соединяются? «И» – правило произведения, «или» – правило суммы.
Для каждого выбора задаются следующие вопросы:
- Все элементы используются? Если «да», то это перестановки. Переходим к п. 5.
- Порядок выбора элементов важен? Если «да», то это размещения, «нет» – сочетания.
- Есть ли одинаковые элементы? Если «да» – то формула с повторениями, «нет» – без повторений.
Сколько различных гирлянд можно сделать из 10 светодиодов разного цвета?
При замыкании линии в кольцо перестановки, являющиеся циклическими сдвигами относительно друг друга, становятся одинаковыми. Возьмем, например, следующую перестановку и посмотрим, сколько других перестановок явлюяются ее циклическим сдвигом: 1. ккккксссссссжжжж 2. кккксссссссжжжжк 3. ккксссссссжжжжкк … 15. жжккккксссссссжж 16. жккккксссссссжжж Следовательно, все перестановки разбиваются на группы по 16 цепочек в группе. Итак, число кольцевых гирлянд будет
13
Пример 11
- Световое табло состоит из лампочек. Каждая лампочка может находиться в одном из трех состояний («включено», «выключено» или «мигает»). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 18 различных сигналов?
- У людоеда в подвале томятся 25 пленников.
- а) Сколькими способами он может выбрать трех из них себе на завтрак, обед и ужин?
- б) А сколько есть способов выбрать троих, чтобы отпустить на свободу?
Решение 25*24*23 = 13800 способов.
Заметим, что в предыдущем пункте каждую тройку пленников мы посчитали 3·2·1 = 6 раз. Поскольку теперь их порядок нам неважен, то ответом будет число 13800 : 6 = 2300.
Волонтеры разделились на две равные группы для розыска заблудившегося ребенка. Среди них только 4 знакомы с местностью. Каким числом способов они могут разделиться так, чтобы в каждую группу вошло 2 человека, знающих местность, если всего их 16 человек?
Решение Мы делим всех волонтеров на две равные группы, то есть выбираем участников первой группы, а все остальные переходят в другую группу. Один выбор. Теперь рассмотрим этот выбор первой группы. Выбор состоит из выбора волонтеров, знающих местность, и выбора волонтеров, незнающих местность. Следовательно, будем соединять эти два числа правилом произведения . Найдем число выборов волонтеров, знающих местность. Всего таких волонтеров 4 человека. Нам нужно 2. Порядок выбора не важен. Сочетания без повторений.
Найдем число выборов волонтеров, незнающих местность. Всего их 16-4=12 , выбираем шесть человек (ровно половину). Общее число выборов:
- Сколько существует натуральных чисел, меньших 256 10 , таких, что в записи каждого числа в двоичной системе счисления будет равное количество единиц и значащих нулей. В ответе укажите целое число.
Решение Переведем данное число из десятичной системы счисления в двоичную. 256 10 =100000000 2 Следовательно, числа меньше данного состоят из восьми, семи, шести, пяти, четырех, трех, двух и одного разряда.
1) Рассмотрим восьмиразрядные числа. 1ХХХХХХХ. Так как мы точно знаем сколько нулей и единиц, то мы используем формулу перестановки с повторениями.
2) Рассмотрим семиразрядные числа. Очевидно, что такие числа не удовлетворяют условию задачи, так как не могут состоять из одинакового числа единиц и нулей. Аналогичный вывод можно сделать о пятиразрядных, трехразрядных и одноразрядных числах.
3) Рассмотрим шестиразрядные числа. Рассуждая аналогично п.1 получаем:
4) Четырехразрядные числа.
5) Двухразрядное число только одно 10 2
Итак, у нас может быть или восьмиразрядное число, или шестиразрядное число, или четырехразрядное число, или двухразрядное число. Правило суммы.
Пример 15
- В коробке находятся 16 шариков – 4 красных, 4 синих и 8 черных. Из коробки наугад вынули два шарика. Какое из перечисленных сообщений несет в себе наибольший объем информации?
- Один из вынутых шариков – красного цвета, а другой – синего;
- Один из вынутых шариков – синего цвета, а другой – черного;
- Оба вынутых шарика красного цвета;
- Оба вынутых шарика черного цвета;
- Цвета вынутых шариков отличаются друг от друга;
- Вынуты шарики одного и того же цвета.
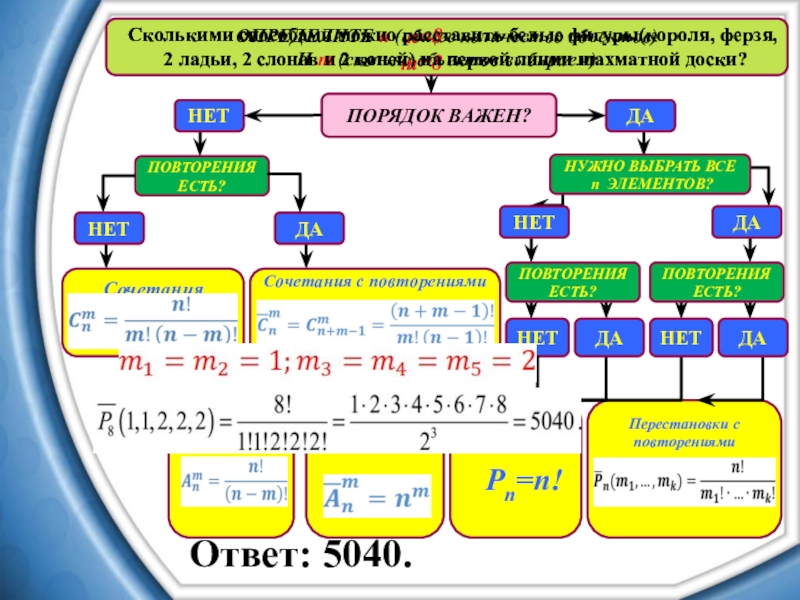
Сколькими способами можно расставить белые фигуры (короля, ферзя, 2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Определить количество чисел, в которых есть цифры 2, 4 и 5 одновременно.
Решение
В этой задаче нам обязательно нужно использовать цифры 2, 4 и 5. Но они могут стоять на разных местах и в разном порядке. У нас три «важные» и две «неважные» цифры в числе — два типа цифр. Это перестановки с повторениями.
Теперь посчитаем сколько различных перестановок «важных» цифр между собой. Это перестановки без повторений
Итак у нас 60 различных перестановок. Теперь посчитаем, сколько различных «неважных» цифр может быть в каждой из этих перестановок. Мы выбираем две «неважные» цифры из шести. Порядок выбора важен . Это размещения без повторений .
В стране 20 городов, каждые два из которых соединены авиалинией. Сколько авиалиний в этой стране?
- Решение:
- Каждая авиалиния соединяет два города. В качестве первого города можно взять любой из 20 городов (город А), а в качестве второго – любой из 19 оставшихся (город В). Перемножив эти числа, получаем 20 • 19 = 380.
- Однако при этом подсчете каждая авиалиния учтена дважды (первый раз, когда в качестве первого города был выбран город А, а второго – город В, а второй раз – наоборот). Таким образом, число авиалиний равно 380:2 = 190.
Материалы для подготовки к ЕГЭ. Онлайн-Справочник по математике.
Раздел 6 «Элементы комбинаторики» (§§ 19-20): Размещения, перестановки, сочетания. Формула бинома Ньютона.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Раздел VI. Элементы комбинаторики
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
§ 19. Размещения, перестановки, сочетания.
200. Размещения.
201. Перестановки.
202. Сочетания и их свойства. Треугольник Паскаля.
§ 20. Формула бинома Ньютона.
203. Бином Ньютона.
204. Свойства формулы бинома Ньютона.
ВСЕ РАЗДЕЛЫ СПРАВОЧНИКА
Материалы для подготовки к ЕГЭ. Онлайн справочник по математике.
Раздел 6 «Элементы комбинаторики» (§§ 19-20): Размещения, перестановки, сочетания. Формула бинома Ньютона.
Просмотров:
2 205
Слайд 5КОМБИНАТОРИКА
Непосредственные подсчеты
Правило умножения
Правило сложения
Перестановки
Размещения
Сочетания

Слайд 6НЕПОСРЕДСТВЕННЫЕ ПОДСЧЕТЫ
Логический перебор
Таблица вариантов
Полный граф
Граф-дерево

Слайд 7В случайном эксперименте симметричную монету бросают:
а)дважды; б)трижды.
Определите все возможные комбинации выпадения
орла и решки.
ОО
ОР
РО
РР
Решение.
Ответ: 4
Логический перебор

Слайд 8
В случайном эксперименте
симметричную
монету бросают:
а)дважды; б)трижды.
Определите все возможные
комбинации
выпадения
орла и решки.
Решение.
Ответ: 8
Логический перебор

Слайд 9Таблица вариантов
Сколько четных двузначных чисел можно составить из цифр 0,
1,2, 5, 8, 9?
Ответ: 15.
Решение.

Слайд 10Полный граф
Андрей, Борис, Виктор и Григорий играли в шахматы. Каждый
сыграл с каждым по одной партии. Сколько партий было сыграно?
Ответ: 6.
Решение.

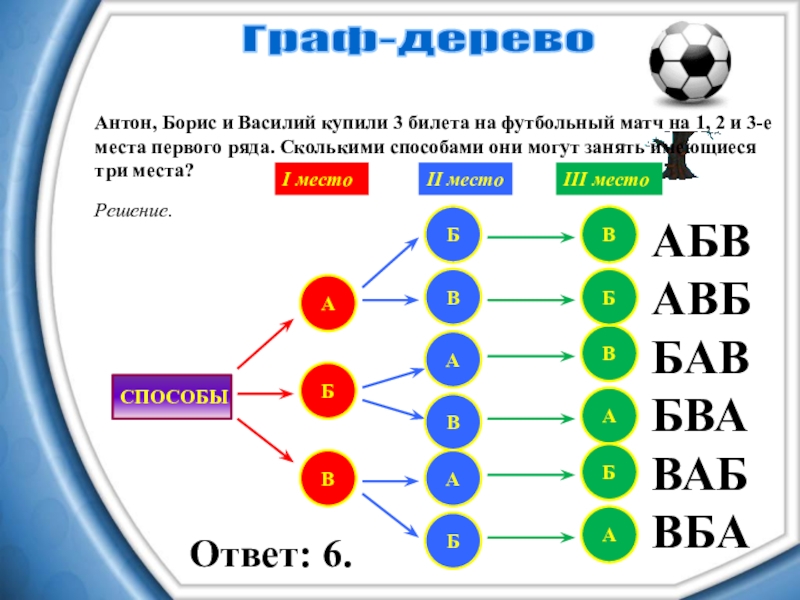
Слайд 11Антон, Борис и Василий купили 3 билета на футбольный матч на
1, 2 и 3-е места первого ряда. Сколькими способами они могут занять имеющиеся три места?
Граф-дерево
Решение.
СПОСОБЫ
А
Б
В
Б
В
А
В
А
Б
В
В
Б
Ответ: 6.
А
Б
А
I место
II место
III место
АБВ
АВБ
БАВ
БВА
ВАБ
ВБА
Слайд 12ПРАВИЛО УМНОЖЕНИЯ
Если элемент множества А может быть выбран m способами, а
элемент множества B – n способами, то упорядоченная пара (A, B) может быть составлена m ∙ n способами.
N= m ∙ n

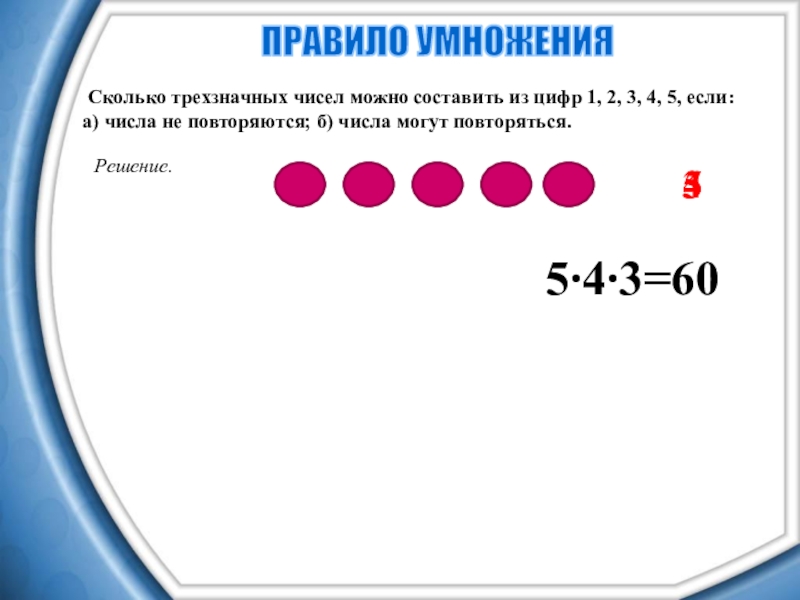
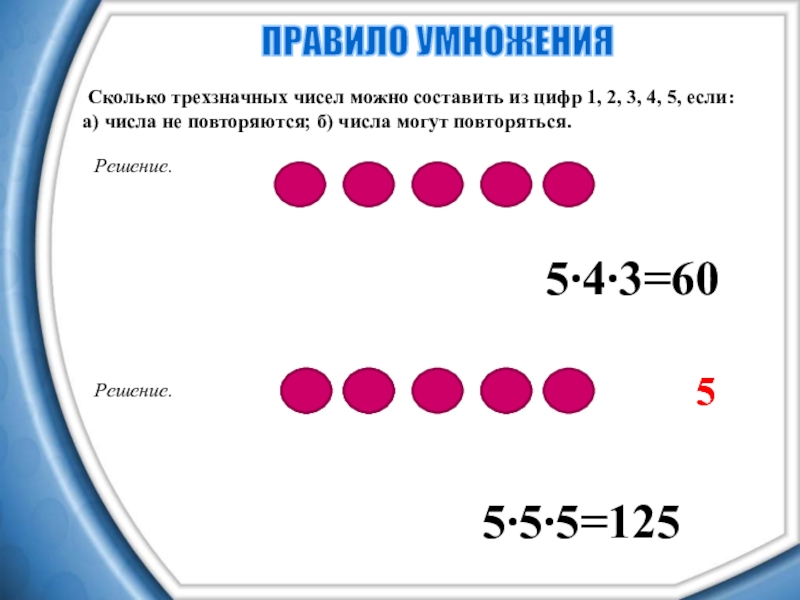
Слайд 13 Сколько трехзначных чисел можно составить из цифр 1, 2, 3,
4, 5, если:
а) числа не повторяются; б) числа могут повторяться.
ПРАВИЛО УМНОЖЕНИЯ
Решение.
5
4
3
5∙4∙3=60
Слайд 14 Сколько трехзначных чисел можно составить из цифр 1, 2, 3,
4, 5, если:
а) числа не повторяются; б) числа могут повторяться.
ПРАВИЛО УМНОЖЕНИЯ
Решение.
5
5∙5∙5=125
5
5
Решение.
5∙4∙3=60
Слайд 15ПРАВИЛО СЛОЖЕНИЯ
Если элемент множества A можно выбрать m способами, элемент множества
B можно выбрать n способами, и множества A и B не имеют общих элементов, то выбор одного из элементов множеств A или B осуществляется m+n способами.
N=m+n

Слайд 16На блюдце лежит 8 яблок и 6 груш. Сколькими способами можно
взять плод с блюдца?
ПРАВИЛО СЛОЖЕНИЯ
Решение.
m=8
n=6
N=8+6=14
Ответ: 14.

Слайд 17Пусть имеется n различных объектов.
Будем переставлять их всеми возможными способами (число объектов остается
неизменными, меняется только их порядок). Получившиеся комбинации называются перестановками,
а их число равно
ПЕРЕСТАНОВКИ
Pn=n!
ПЕРЕСТАНОВКИ С ПОВТОРЕНИЯМИ

Слайд 18ПЕРЕСТАНОВКИ
Сколько перестановок можно получить из букв, составляющих слово «апельсин»?
Решение.
P8 = 8!
= 1 ∙ 2 ∙ 3 ∙ 4 ∙ 5 ∙ 6 ∙ 7 ∙ 8 = 40320
Ответ: 40320.
СПАНИЕЛЬ

Слайд 19Пусть имеется n различных объектов.
Будем выбирать из них m объектов и переставлять всеми возможными способами
между собой (то есть меняется и состав выбранных объектов, и их порядок). Получившиеся комбинации называются размещениями из n объектов по m, а их число равно
РАЗМЕЩЕНИЯ
РАЗМЕЩЕНИЯ С ПОВТОРЕНИЯМИ

Слайд 20Сколько можно составить сигналов из 6 флажков различного цвета, взятых по
2?
РАЗМЕЩЕНИЯ
Решение.
Ответ: 30.

Слайд 21Пусть имеется n различных объектов.
Будем выбирать из них m объектов всевозможными способами (то есть меняется
состав выбранных объектов, но порядок не важен). Получившиеся комбинации называются сочетаниями из n объектов по m, а их число равно
СОЧЕТАНИЯ
СОЧЕТАНИЯ С ПОВТОРЕНИЯМИ

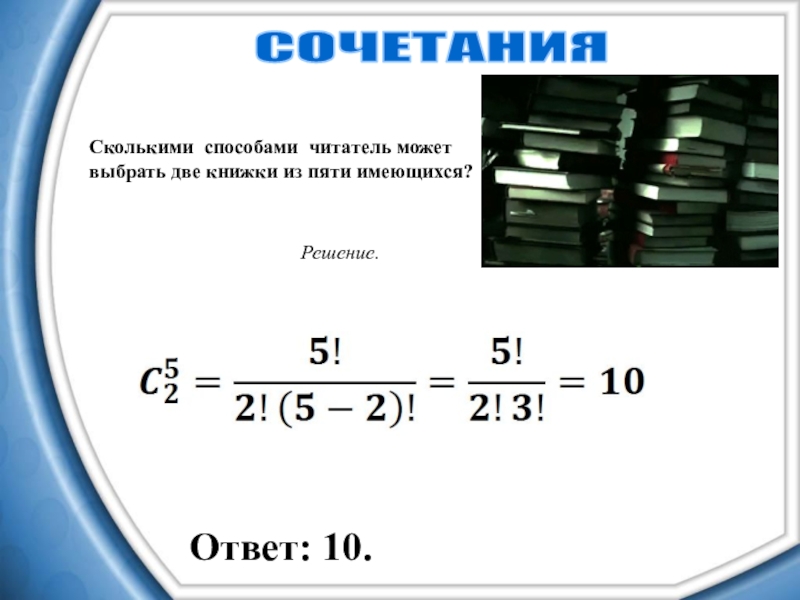
Слайд 22Сколькими способами читатель может выбрать две книжки из пяти имеющихся?
СОЧЕТАНИЯ
Решение.
Ответ: 10.
Слайд 23ПОРЯДОК ВАЖЕН?
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
НЕТ
ДА
ПОВТОРЕНИЯ
ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
НЕТ
ДА
Перестановки с повторениями
Размещения с повторениями
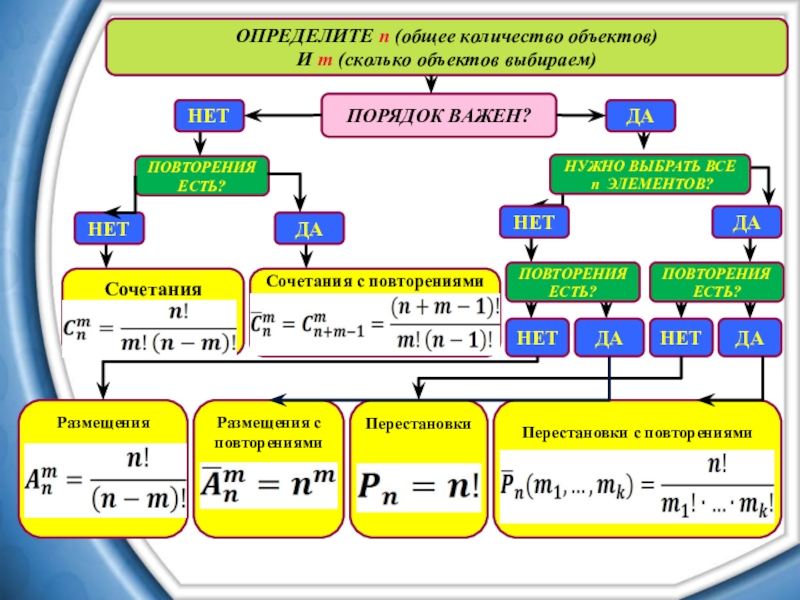
Слайд 24ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ
ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
ДА
Перестановки с повторениями
Размещения с повторениями
Pn=n!
n=10 m=6
НЕТ
Ответ: 1000000.
Шифр сейфа состоит только из 6 цифр, которые должны набираться
последовательно и могут повторяться. Чему в этом случае равно общее число всех возможных комбинаций шифра?
Шифр сейфа состоит только из 6 цифр, которые должны набираться
последовательно и могут повторяться. Чему в этом случае равно общее
число всех возможных комбинаций шифра?
ДА
НЕТ
ДА
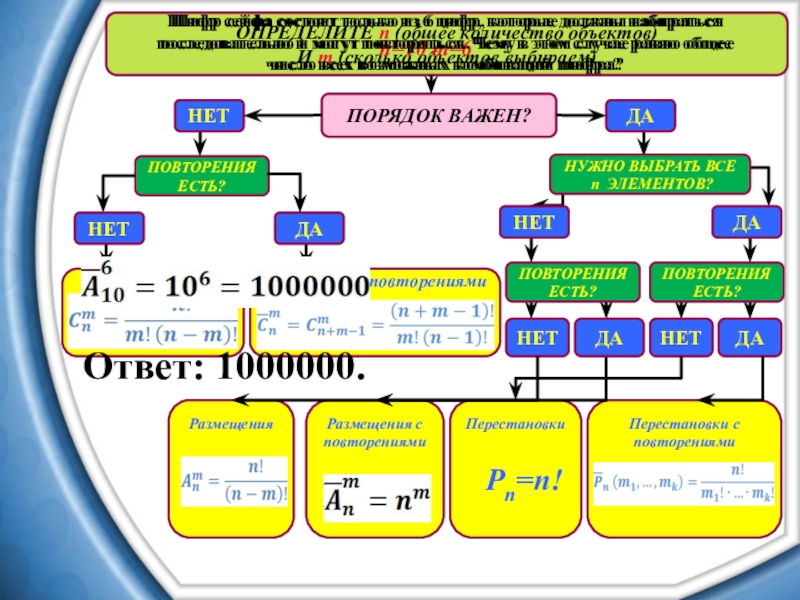
Слайд 25ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
ПОВТОРЕНИЯ
ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
ДА
Перестановки с повторениями
Размещения с повторениями
Pn=n!
n=10 m=5
НЕТ
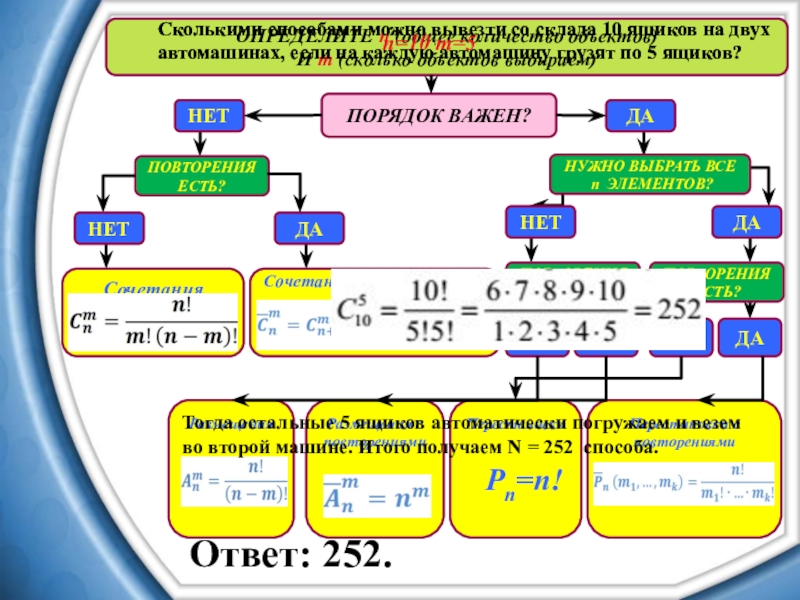
Тогда остальные 5 ящиков автоматически погружаем и везем во второй машине. Итого получаем N = 252 способа.
Ответ: 252.
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
Сколькими способами можно вывезти со склада 10 ящиков на двух автомашинах, если на каждую автомашину грузят по 5 ящиков?
Слайд 26ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ ЕСТЬ?
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
НЕТ
ДА
ДА
Перестановки
с повторениями
Размещения с повторениями
Pn=n!
n=11 m=5
НЕТ
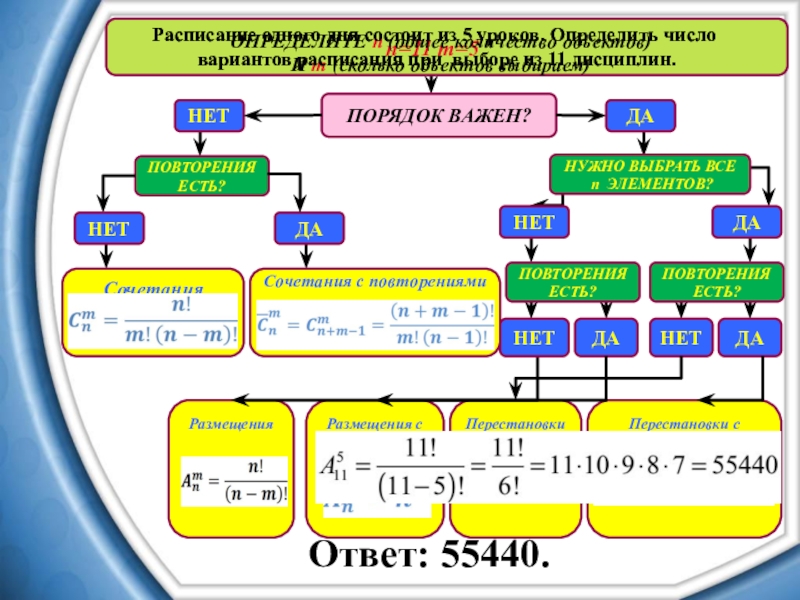
Ответ: 55440.
ДА
НЕТ
НЕТ
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
Расписание одного дня состоит из 5 уроков. Определить число
вариантов расписания при выборе из 11 дисциплин.
Расписание одного дня состоит из 5 уроков. Определить число
вариантов расписания при выборе из 11 дисциплин.
Слайд 27ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
Сочетания
Сочетания с повторениями
ДА
ДА
Перестановки
с повторениями
Размещения с повторениями
Pn=n!
n=4 m=4
НЕТ
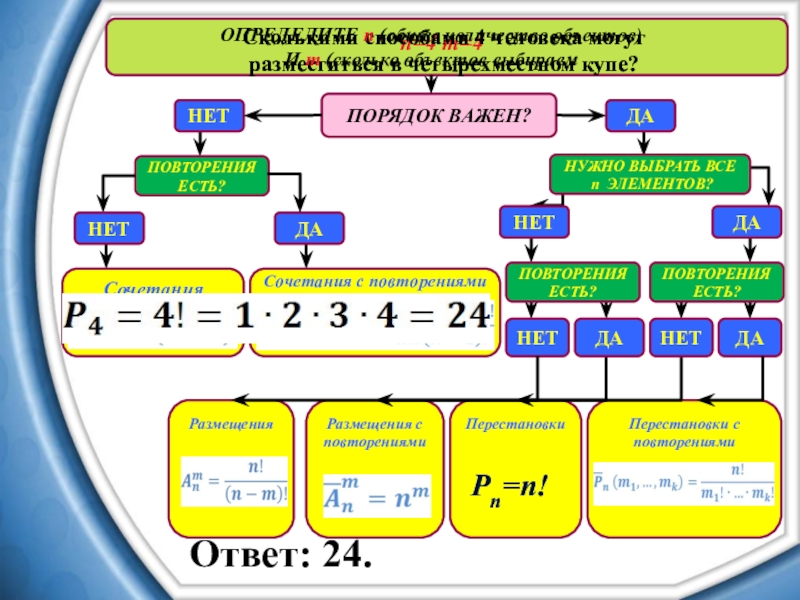
Ответ: 24.
Сколькими способами 4 человека могут разместиться в четырехместном купе?
НЕТ
ДА
Сколькими способами 4 человека могут разместиться в четырехместном купе?
ДА
ДА
НЕТ
ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем
Pn=n!
Слайд 28ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ДА
ПОВТОРЕНИЯ
ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ДА
НЕТ
ДА
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
НЕТ
ДА
Перестановки с повторениями
Размещения с повторениями
Pn=n!
n=10 m=12
НЕТ
ДА
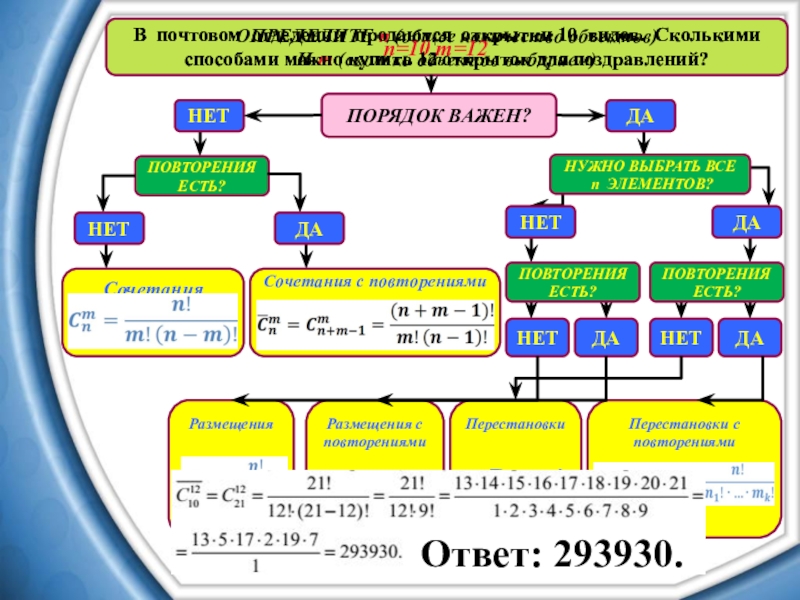
Ответ: 293930.
В почтовом отделении продаются открытки 10 видов. Сколькими
способами можно купить 12 открыток для поздравлений?
В почтовом отделении продаются открытки 10 видов. Сколькими
способами можно купить 12 открыток для поздравлений?
Слайд 29ОПРЕДЕЛИТЕ n (общее количество объектов)
И m (сколько объектов выбираем)
ПОРЯДОК ВАЖЕН?
НЕТ
ПОВТОРЕНИЯ
ЕСТЬ?
НЕТ
НУЖНО ВЫБРАТЬ ВСЕ
n ЭЛЕМЕНТОВ?
ПОВТОРЕНИЯ ЕСТЬ?
ПОВТОРЕНИЯ ЕСТЬ?
ДА
Перестановки с повторениями
Размещения с повторениями
Pn=n!
n=8
m=8
НЕТ
Ответ: 5040.
НЕТ
ДА
НЕТ
Сколькими способами можно расставить белые фигуры(короля, ферзя,
2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
Сколькими способами можно расставить белые фигуры(короля, ферзя,
2 ладьи, 2 слонов и 2 коней) на первой линии шахматной доски?
ДА
ДА
ДА
Что такое комбинаторика и зачем оно нам надо на ЕГЭ по информатике?
Комбинаторика — область математики, в которой изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из элементов заданного множества.
Рассмотрим элементы комбинаторики: бывают перестановки, размещения и сочетания.
◾ПЕРЕСТАНОВКИ
Перестановками называются такие выборки элементов, которые отличаются только порядком расположения элементов.
Представь, что у тебя есть 10 книжек и тебе необходимо их расставить на полке в каком-то порядке, так сколько способов это сделать у тебя есть?
Формула подсчета перестановок:
📍Pn = n·(n−1)·(n−2)…3·2·1 = n!, где n- количество элементов данного множества.
! — это факториал числа — произведение натуральных чисел от 1 до самого числа (включая данное число.
То есть, решением поставленной задачей будет: P(10) = 10·(10−1)·(10−2)…3·2··1 = 3628800
◾РАЗМЕЩЕНИЯ
Размещениями из n элементов по m (мест) называются такие выборки, которые имея по m элементов, выбранных из числа данных n элементов, отличаются одна от другой либо составом элементов, либо порядком их расположения.
Например, тебе уже надо не все 10 книжек расставить по порядку, а только 5 из них,так вот сколько будет способов это сделать?
Число размещений из n по m обозначается A(n;m) и определяется по формуле
📍A(n;m) = n·(n − 1)·(n − 2)·…·(n − m + 1) = n!/(n − m)!
Так вот количество способов подсчитать такое расположение пяти книжек из 10 на полке и будет число размещений из 10 по 5. То есть: A(10;5) = 10!/(10 − 5)! =10!/5!=30240
◾СОЧЕТАНИЯ
Неупорядоченные выборки называются сочетаниями из n элементов по m и обозначаются С(n;m)
Ключевое слово здесь неупорядоченные, то есть нам не важно, какая книжка будет стоять на первом месте, а какая на втором, мы хотим посчитать любые варианты расстановки. Можно интерпретировать как: у нас все также есть 10 книжек, пять из которых нужно расставить в любом порядке, сколько существует возможных вариантов?
📍Число сочетаний определяется по формуле С(n;m) = n!/((n − m)!*m!)
То есть в нашей задаче получится: С(10;5) = 10!/((10 − 5)!*5!)= 252
ВАЖНО: далеко не всегда в ЕГЭ применяются формулы комбинаторики (иногда задачу проще решить перебором), но в любом случае знать основы необходимо.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Рассмотрим теорию, которая относится к разделу комбинаторики. Обрати внимание, что в формулах для нахождения количества перестановок, размещений и сочетаний используется факториал.
Pn=n!
Это упорядоченные совокупности, которые отличаются друг от друга только порядком элементов. Примером является размещение нескольких книг на одной полке.
Это упорядоченные совокупности, которые отличаются друг от друга составом или порядком элементов. Примером является выбор директора и заместителя директора из некоторого числа кандидатов.
Это неупорядоченные совокупности, которые отличаются друг от друга хотя бы одним элементом. Примером будет выбор двух вопросов из списка вопросов к экзамену.