Площадь криволинейной трапеции егэ профиль - ExamHelp.top

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

Алгебра 10-11 класс. Площадь криволинейной трапеции

Алгебра 10-11 класс. Площадь криволинейной трапецииadmin2022-11-04T14:15:40+03:00

Скачать файл в формате pdf.

Алгебра 10-11 класс. Площадь криволинейной трапеции

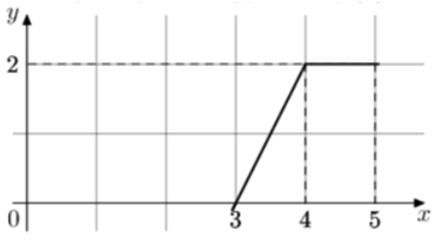
Задача 1. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 5 right) — Fleft( 3 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)). Ответ ОТВЕТ: 3.
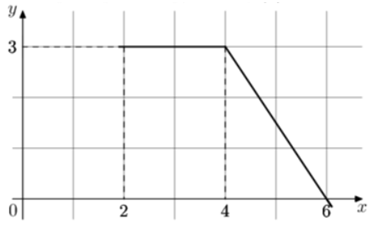
Задача 2. На рисунке изображён график некоторой функции (y = fleft( x right)) (два луча с общей начальной точкой). Пользуясь рисунком, вычислите (Fleft( 6 right) — Fleft( 2 right)), где (Fleft( x right))— одна из первообразных функции (fleft( x right)). Ответ ОТВЕТ: 9.
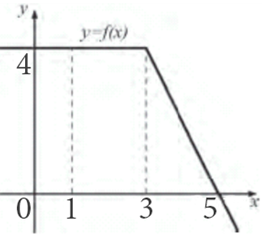
Задача 3. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_1^5 {fleft( x right)} ,dx) Ответ ОТВЕТ: 12.
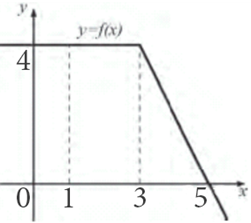
Задача 4. На рисунке изображен график некоторой функции (y = fleft( x right)). Пользуясь рисунком, вычислите определенный интеграл (intlimits_2^5 {fleft( x right)} ,dx) Ответ ОТВЕТ: 8.
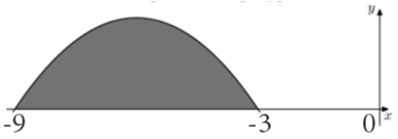
Задача 5. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = frac{2}{3}{x^3} + 20{x^2} + 201x — frac{6}{{13}}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 9.
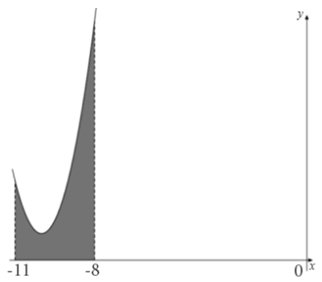Задача 6. На рисунке изображён график некоторой функции (y = fleft( x right)). Функция (Fleft( x right) = — frac{1}{{12}}{x^3} — frac{3}{2}{x^2} — frac{{27}}{4}x — frac{3}{4}) — одна из первообразных функции (fleft( x right)). Найдите площадь закрашенной фигуры. Ответ ОТВЕТ: 9.
Задача 7. Вычислите площадь фигуры ограниченной линиями (y = {x^3},,,y = 0,,,x = 2) Ответ ОТВЕТ: 4.
Задача 8. Вычислите площадь фигуры ограниченной линиями (y = {x^3} + 2,,,y = 0,,,x = 2,,,x = 3) Ответ ОТВЕТ: 18,25.
Задача 9. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 9x — 18,,,y = 0) Ответ ОТВЕТ: 4,5.
Задача 10. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 9,,,y = 0) Ответ ОТВЕТ: 36.

Задача 11. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{{{x^2}}},,,y = 0,,,x = — 4,,,x = — 2)

Ответ

ОТВЕТ: 0,25.

Задача 12. Вычислите площадь фигуры ограниченной линиями (y = — sqrt x ,,,y = 0,,,x = 9,,,x = 36)

Ответ

ОТВЕТ: 126.

Задача 13. Вычислите площадь фигуры ограниченной линиями (y = sin 2x,,,y = 0,,,x = 0,,,x = frac{pi }{2})

Ответ

ОТВЕТ: 1.

Задача 14. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{{{{cos }^2}x}} + frac{2}{pi },,,,y = 0,,,,x = 0,,,,x = frac{pi }{4})

Ответ

ОТВЕТ: 1,5.

Задача 15. Вычислите площадь фигуры ограниченной линиями (y = sqrt x ,,,y = — 2x,,,x = 9)

Ответ

ОТВЕТ: 99.

Задача 16. Вычислите площадь фигуры ограниченной линиями (y = — sqrt x ,,,y = {x^2},,,x = 9)

Ответ

ОТВЕТ: 261.

Задача 17. Вычислите площадь фигуры ограниченной линиями (y = {e^{2x}},,,y = 0,,,,x = ln 2,,,,x = ln 6)

Ответ

ОТВЕТ: 16.

Задача 18. Вычислите площадь фигуры ограниченной линиями (y = frac{1}{x},,,y = 0,,,,x = e,,,,x = {e^3})

Ответ

ОТВЕТ: 2.

Задача 19. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 2x + 3,,,y = 3 — x)

Ответ

ОТВЕТ: 4,5.

Задача 20. Вычислите площадь фигуры ограниченной линиями (y = 1 — {x^2},,,y = — x — 1)

Ответ

ОТВЕТ: 4,5.

Задача 21. Вычислите площадь фигуры ограниченной линиями (y = — {x^2} + 2,,,y = {x^2} — 2x — 2)

Ответ

ОТВЕТ: 9.

Задача 22. Вычислите площадь фигуры ограниченной линиями (y = {x^2} — 4x + 3,,,y = — {x^2} + 6x — 5)

Ответ

ОТВЕТ: 9.

Задача 23. Найдите площадь фигуры, ограниченной графиком функции (y = {x^3}) и касательной, проведенной к ней в точке (left( { — 1;, — 1} right))

Ответ

ОТВЕТ: 6,75.

Задача 24. Найдите площадь фигуры, ограниченной графиком функции (y = {x^3} — 3x) и касательной, проведенной к ней в точке (left( { — 1;,2} right))

Ответ

ОТВЕТ: 6,75.

Задача 25. Вычислите (frac{1}{pi }intlimits_0^4 {sqrt {4x — {x^2}} dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2.

Задача 26. Вычислите (frac{1}{pi }intlimits_{ — 1}^0 {sqrt { — 2x — {x^2}} dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 0,25.

Задача 27. Вычислите (intlimits_0^3 {left| {,x — 2,} right|dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2,5.

Задача 28. Вычислите (intlimits_0^4 {left| {,left| {,x — 2,} right| — 1,} right|dx} ), используя геометрический смысл определенного интеграла

Ответ

ОТВЕТ: 2.

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Первообразная функции»

Открытый банк заданий по теме первообразная функции. Задания B7 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры на плоскости: вычисление величин с использованием углов

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №1164

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(9)-F(5), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(9)-F(5), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=9 и x=5. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 4 и 3 и высотой 3.

Её площадь равна frac{4+3}{2}cdot 3=10,5.

Ответ

10,5

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1158

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 5). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-3; 4].

Показать решение

Решение

Согласно определению первообразной выполняется равенство: F'(x)=f(x). Поэтому уравнение f(x)=0 можно записать в виде F'(x)=0. Так как на рисунке изображён график функции y=F(x), то надо найти те точки промежутка [-3; 4], в которых производная функции F(x) равна нулю. Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 7 (четыре точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1155

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=f(x) (являющийся ломаной линией, составленной из трёх прямолинейных отрезков). Пользуясь рисунком, вычислите F(5)-F(0), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

По формуле Ньютона-Лейбница разность F(5)-F(0), где F(x) — одна из первообразных функции f(x), равна площади криволинейной трапеции, ограниченной графиком функции y=f(x), прямыми y=0, x=5 и x=0. По графику определяем, что указанная криволинейная трапеция является трапецией с основаниями, равными 5 и 3 и высотой 3.

Её площадь равна frac{5+3}{2}cdot 3=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1149

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график функции y=F(x) — одной из первообразных некоторой функции f(x), определённой на интервале (-5; 4). Пользуясь рисунком, определите количество решений уравнения f (x)=0 на отрезке (-3; 3].

Показать решение

Решение

Из рисунка видно, что это будут абсциссы экстремальных точек (максимума или минимума) графика F(x). Их на указанном промежутке ровно 5 (две точки минимума и три точки максимума).

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №1146

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=-x^3+4,5x^2-7 — одна из первообразных функции f(x).

Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной сверху графиком функции y=f(x), прямыми y=0, x=1 и x=3. По формуле Ньютона-Лейбница её площадь S равна разности F(3)-F(1), где F(x) — указанная в условии первообразная функции f(x). Поэтому S= F(3)-F(1)= -3^3 +(4,5)cdot 3^2 -7-(-1^3 +(4,5)cdot 1^2 -7)= 6,5-(-3,5)= 10.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №907

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображён график некоторой функции y=f(x). Функция F(x)=x^3+6x^2+13x-5 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

Заштрихованная фигура является криволинейной трапецией, ограниченной графиком функции y=f(x) и прямыми y=0, x=-4 и x=-1. По формуле Ньютона-Лейбница её площадь S равна разности F(-1)-F(-4), где F(x) — указанная в условии первообразная функции f(x).

Поэтому S= F(-1)-F(-4)= (-1)^3+6(-1)^2+13(-1)-5-((-4)^3+6(-4)^2+13(-4)-5)= -13-(-25)=12.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №307

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x). Функция F(x)=x^3+18x^2+221x-frac12 — одна из первообразных функции f(x). Найдите площадь заштрихованной фигуры.

Показать решение

Решение

По формуле Ньютона-Лейбница S=F(-1)-F(-5).

F(-1)= (-1)^3+18cdot(-1)^2+221cdot(-1)-frac12= -204-frac12.

F(-5)= (-5)^3+18cdot(-5)^2+221cdot(-5)-frac12= -125+450-1105-frac12= -780-frac12.

F(-1)-F(-5)= -204-frac12-left (-780-frac12right)= 576.

Ответ

576

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №306

Тип задания: 7
Тема:
Первообразная функции

Условие

На рисунке изображен график некоторой функции y=f(x).Пользуясь рисунком, вычислите F(9)-F(3), где F(x) — одна из первообразных функции f(x).

Показать решение

Решение

F(9)-F(3)=S, где S — площадь фигуры, ограниченной графиком функции y=f(x), прямыми y=0 и x=3,:x=9. Рассмотрим рисунок ниже.

Данная фигура — трапеция с основаниями 6 и 1 и высотой 2. Ее площадь равна frac{6+1}{2}cdot2=7.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2016. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №104

Тип задания: 7
Тема:
Первообразная функции

Условие

На координатной плоскости изображен график функции y=f(x). Одна из первообразных этой функции имеет вид: F(x)=-frac13x^3-frac52x^2-4x+2. Найдите площадь заштрихованной фигуры.

Показать решение

Решение

На рисунке видно, что заштрихованная фигура ограничена по оси абсцисс точками −4, −1, а по оси ординат графиком функции: f(x). Значит площадь фигуры мы можем найти с помощью разности значений первообразных в точках −4 и −1, по формуле определенного интеграла:

intlimits_{-4}^{-1}f(x)dx=F(-1)-F(-4)

Подставим значение первообразной из условия и получим площадь фигуры:

F(-1)-F(-4)=

=frac13-frac52+4+2-frac{64}{3}+frac{80}{2}-16-2=

=-frac{63}{3}+frac{75}{2}-12=-21+37,5-12=4,5

Ответ

4,5

Задание №103

Тип задания: 7
Тема:
Первообразная функции

Условие

Первообразная y=F(x) некоторой функции y=f(x) определена на интервале (−16; −2). Определите сколько решений имеет уравнение f(x) = 0 на отрезке [−10; −5].

Показать решение

Решение

Формула первообразной имеет следующий вид:

f(x) = F'(x)

По условию задачи нужно найти точки, в которых функция f(x) равна нулю. Принимая во внимание формулу первообразной, это значит, что, нужно найти точки, в которых F'(x) = 0, то есть те точки, в которых производная от первообразной равна нулю.

Мы знаем, что производная равна нулю в точках локального экстремума, т.е. функция имеет решения в тех точках, в которых возрастание F(x) сменяется убыванием и наоборот.

На отрезке [−10; −5] видно что это точки: −9; −7; −6. Значит уравнение f(x) = 0 имеет 3 решения.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Алгебра и начала математического анализа, 11 класс

Урок №23.Площадь криволинейной трапеции. Интеграл и его свойства.

Перечень вопросов, рассматриваемых в теме

1) Нахождение определенного интеграла

2) Нахождение площади криволинейной трапеции с помощью формулы Ньютона – Лейбница

3) Решение задач, с помощью формулы Ньютона – Лейбница

Формула Ньютона – Лейбница

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.

Дополнительная литература:

ОрловаЕ. А., СеврюковП. Ф., СидельниковВ. И., СмоляковА.Н.Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.

Теоретический материал для самостоятельного изучения

Криволинейной трапецией называется фигура, ограниченная графиком непрерывной и не меняющей на отрезке [а;b] знака функции f(х), прямыми х=а, x=b и отрезком [а;b].

Отрезок [a;b] называют основанием этой криволинейной трапеции

формула Ньютона – Лейбница

Если в задаче требуется вычислить площадь криволинейной трапеции, то ответ всегда будет положительный. Если требуется, используя чертеж, вычислить интеграл, то его значение может быть любым(зависит от расположения криволинейной трапеции).

Примеры и разбор решения заданий тренировочного модуля

№1.Найти площадь криволинейной трапеции, изображенной на рисунке

Решение

Для вычисления площади криволинейной трапеции воспользуемся формулой Ньютона – Лейбница.

Ответ:

№2. Вычислить определенный интеграл:

Решение: Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x) . Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) — F(а), это и будет ответ.

№3. Найти площадь криволинейной трапеции (х-1)², ограниченной линиями х=2 и х=1, осью 0х

Решение:

Воспользуемся формулой Ньютона-Лейбница.

Сначала находим первообразную функцию F(x). Далее подставляем значение верхнего предела в первообразную функцию: F(b) .

Затем подставляем значение нижнего предела в первообразную функцию: F(а).

Рассчитываем разность F(b) — F(а), это и будет ответ.

Источник

Канал видеоролика: Мой ЕГЭ профиль и физика

Смотреть видео:

#физика #егэфизика #огэфизика #термодинамика #репетиторпофизике #фтф #мифи #мфти #физтех

Свежая информация для ЕГЭ и ОГЭ по Физике (листай):

С этим видео ученики смотрят следующие ролики:

Геометрия Найти площадь равнобедренной трапеции, если ее высота равна h, а боковая сторона видна

Решение задач Математика и Физика

Геометрия В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон

Решение задач Математика и Физика

Геометрия Основания равнобедренной трапеции равны 8 и 18, а периметр равен 56. Найдите площадь

Решение задач Математика и Физика

Геометрия Площадь трапеции равна произведению полусуммы ее оснований на высоту

Решение задач Математика и Физика

Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):

14.02.2022

Комментарии

RSS

Написать комментарий

Нет комментариев. Ваш будет первым!

Ваше имя:

Загрузка…

Источник

Задания по теме «Площадь криволинейной трапеции»

Учитель математики

высшей квалификационной категории

МОУ Левобережной СОШ г.Тутаева

Борисова Елена Леонидовна

Пример 1

Найти площадь плоской фигуры, ограниченной линиями , .

Решение: Сначала нужно выполнить чертеж. Вообще говоря, при построении

чертежа в задачах на площадь нас больше всего интересуют точки

пересечения линий. Найдем точки пересечения параболы и прямой

. Это можно сделать двумя способами. Первый способ – аналитический.

Решаем уравнение:

Значит, нижний предел интегрирования , верхний предел интегрирования

Гораздо выгоднее и быстрее построить линии поточечно, при этом пределы

интегрирования выясняются как бы «сами собой». Возвращаемся к нашей

задаче: рациональнее сначала построить прямую и только потом параболу.

Выполним чертеж:

А теперь рабочая формула: Если на отрезке некоторая непрерывная

функция больше либо равна некоторой непрерывной функции , то

площадь фигуры, ограниченной графиками данных функций и прямыми ,

, можно найти по формуле:

В рассматриваемом примере очевидно, что на отрезке парабола

располагается выше прямой, а поэтому из необходимо вычесть

Завершение решения может выглядеть так:

Искомая фигура ограничена параболой сверху и прямой

снизу.

На отрезке , по соответствующей формуле:

Ответ:

Пример 2

Вычислить площадь фигуры, ограниченной линиями , , ,

Решение: Сначала выполним чертеж:

Фигура, площадь которой нам нужно найти, заштрихована синим цветом

(внимательно смотрите на условие – чем ограничена фигура!). Но на практике

по невнимательности нередко возникает «глюк», что нужно найти площадь

фигуры, которая заштрихована зеленым цветом!

Этот пример еще полезен и тем, что в нём площадь фигуры считается с

помощью двух определенных интегралов. Действительно:

1) На отрезке над осью расположен график прямой ;

2) На отрезке над осью расположен график гиперболы .

Совершенно очевидно, что площади можно (и нужно) приплюсовать, поэтому:

Ответ:

Пример 3

Вычислить площадь фигуры, ограниченной

линиями: у = 4х – х

, у = 5, х = 3.

Решение:

= 2, у

= 4

= S

ОАВД

– S

ОСД

прям.

ОСД

= F(3) – F(0), где F(x) первообразная для

функции f(х) = 4х – х

F(х)= ; S

ОСД

= 15 – 9 = 6.

Ответ: 6.

Пример 4

Вычислить площадь фигуры, ограниченной линиями ,

Решение:

Представим уравнения в «школьном» виде , и выполним

поточечный чертеж:

Из чертежа видно, что верхний предел у нас «хороший»: .

Но чему равен нижний предел?! Понятно, что это не целое число, но какое?

Может быть ? Но где гарантия, что чертеж выполнен с идеальной

точностью, вполне может оказаться что . Или корень. А если мы вообще

неправильно построили график?

В таких случаях приходиться тратить дополнительное время и уточнять

пределы интегрирования аналитически.

Найдем точки пересечения прямой и параболы .

Для этого решаем уравнение:

Действительно, .

Дальнейшее решение тривиально, главное, не запутаться в подстановках и

знаках, вычисления здесь не самые простые.

На отрезке , по соответствующей формуле:

Ответ:

Пример 5

Вычислить S фигуры, ограниченной линиями у = (х + 2)

, х = 0, у = 0.

Решение:

АОВ – криволинейный треугольник или криволинейная трапеция. (рис 10.)

S = F(0) – F(-2) =

F(x) = x

+4x+4; F(x) =

S =

Ответ:

Пример 6

Найти S фигуры, ограниченной параболой у = х

+ 1 и прямой у = х + 3.

Решение:

Построим в одной системе координат графики данных функций.

1) у = х

+ 1, х

= 0, у

= 0.

2) у = х + 3

3) х

+ 1 = х + 3

= 1, х

=2.

= S

1АВСД

– S

2АВmСД

тр.АВСД

АВmСД

= F(2) – F(-1), F(x) = , S = 6

= S

– S

= 4,5.

II способ.

АВСД

= F(2) – F(-1), F(x) = .

Ответ: S

= 4,5.

Пример 7:

Найдите 3 четверти площади фигуры,

ограниченной параболой, заданной уравнением

у = – х

+4х—3 и осью абсцисс.

Решение:

1) х

=2, у

2) – х

+4х—3=0 х

=3, х

Функция неотрицательна на [1;3]

F(x) = S

= F(3) – F(1) =

3) Умножим S

на . S

иск.

Ответ: 1

Пример 8

Найти S фигуры, ограниченной линиями f

(x) = x

; f

(x) = 2x – x

Решение:

1) Схематично изобразим данную фигуру (рис.

12)

(x) = – x

+ 2x

= , у

= 1

2) Найдем абсциссы точек пересечения этих линий

= 2x – x

– 2х = 0

х = 0, х = 1

3) Найдем площадь фигуры

(x) = x

–

= F(1) – F(0) =

(x) = ; S

= .

4) S

= S

– S

= .

Ответ: S

= .

Пример 9

Вычислить S фигуры, ограниченной линиями:

у=х

+1, у=0, х=0, х=2.

Решение:

F(x) =

S = F(2) – F(0) = 16/4 + 2 – 0/4 + 0 = 6

Ответ: 6.

Пример 10

Вычислить площадь фигуры, ограниченной линиями , , и осью

Это пример для самостоятельного решения. Полное решение и ответ в конце

урока.

Что делать, если криволинейная трапеция расположена под осью ?

Решение:

Выполним чертеж:

На отрезке график функции расположен над осью , поэтому:

Ответ:

Примечание: В задачах на нахождение площадей преподаватели часто

требуют записывать ответ не только точно, но и, в том числе,

приближенно.

Пример 11 : Найти площадь фигуры, ограниченной линиями ,

.Решение:

Выполним чертеж:

На отрезке , по соответствующей формуле:

Ответ:

Пример 12:

Найти площадь фигуры, ограниченной линиями , .

Решение:

Выполним чертеж.

На отрезке , по соответствующей формуле:

Ответ:

Используемые ресурсы:

1. https://infourok.ru/samostoyatelnaya-rabota-po-teme-neopredelenniy-

integral-klass-761699.html

2. http://festival.1september.ru/articles/566339/

3. http://school-collection.edu.ru/catalog/rubr/8a790bee-ba9d-4b2b-9c3a—

6e370cc2df5b/113019/?

4. ЕГЭ: 4000 задач с ответами по математике. Все задания «Закрытый сегмент».

Базовый и профильный уровни /И.В.Ященко, И.Р.Высоцкий, А.В.Забелин и др.;

под редакцией И.В.Ященко. – М.: Издательство «Экзамен», 2016. – 640 с. (Серия

«Банк заданий ЕГЭ»)

5. Математика. ЕГЭ – 2013: экспресс – курс для подготовки к экзамену/ Дмитрий

Гущин. – М, : Издательский дом «Учительская газета», 2013. – 256 с.

(Библиотечка «Учительской газеты». Готовимся к ЕГЭ с лучшими учителями

России

Источник

Определенный интеграл. Площадь криволинейной трапеции. Формула Ньютона-Лейбница. Задание 7

В этой статье мы будем учиться решать задачи на нахождение площади криволинейной трапеции.

Как всегда, начнем с теории. Как вы помните, неопределенный интеграл от функции — это множество всех первообразных F(x) :

∫

В неопределенном интеграле не заданы границы интегрирования, и в результате нахождения неопределенного интеграла от функции f(x) мы получаем множество первообразных, отличающихся друг от друга на постоянную величину С.

Если заданы границы интегрирования, то мы получаем определенный интеграл:

Здесь число — нижний предел интегрирования, число — верхний предел интегрирования. Определенный интеграл — это ЧИСЛО, значение которого вычисляется по формуле Ньютона — Лейбница:

F(a) — это значение первообразной функции f(x) в точке , и, соответственно, F(b) — это значение первообразной функции f(x) в точке .

Для нас с точки зрения решения задач важное значение имеет геометрический смысл определенного интеграла.

Рассмотрим фигуру, изображенную на рисунке:

Зеленая фигура, ограниченая сверху графиком функции y=f(x) , слева прямой x=a , справа прямой x=b , и снизу осью ОХ называется криволинейной трапецией.

Геометрический смысл определенного интеграла:

Определенный интеграл — это число, равное площади криволинейной трапеции — фигуры, ограниченой сверху графиком положительной на отрезке [a;b] функции y=f(x) , слева прямой x=a , справа прямой x=b , и снизу осью ОХ.

Решим задачу из Открытого банка заданий для подготовки к ЕГЭ по математике.

Прототип Задания 7 (№ 323080)

На рисунке изображён график некоторой функции y=f(x) . Функция — одна из первообразных функции f(x) . Найдите площадь закрашенной фигуры.

Закрашенная фигура представляет собой криволинейную трапецию, ограниченную сверху графиком функции y=f(x) , слева прямой x=-10 , справа прямой x=-8 , и снизу осью ОХ.

Площадь этой криволинейной трапеции вычисляется по формуле:

, где F(x) — первообразная функции f(x) .

По условию задачи , поэтому, чтобы найти площадь фигуры, нам нужно найти значение первообразной в точке -8, в точке -10, и затем из первого вычесть второе.

Замечу, что в этих задачах очень часто возникают ошибки именно в вычислениях, поэтому советую аккуратно и подробно их записывать, и ничего не считать «в уме».