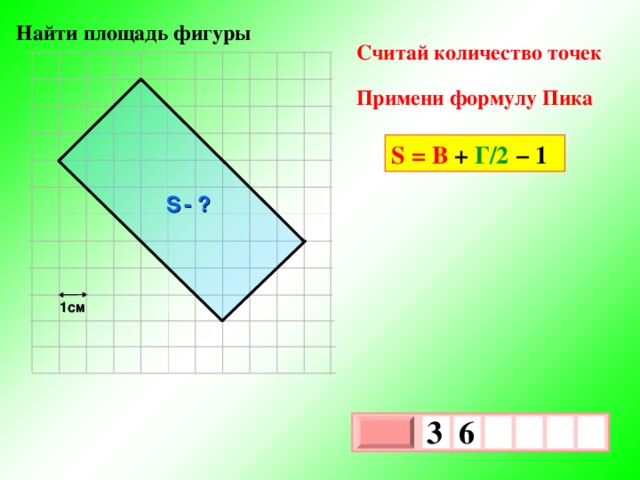
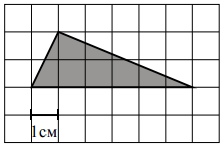
Задания Д4 № 27544
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Аналоги к заданию № 27544: 5093 5095 5165 509986 526205 5097 5099 5101 5103 5105 … Все
Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.
Кодификатор ФИПИ/Решу ЕГЭ: 5.1.1 Треугольник, 5.5.5 Площадь треугольника, параллелограмма, трапеции, круга, сектора
В задании B5 требуется всегда одно и то же: найти площадь фигуры, которая задана точками на координатной плоскости или на клетчатой бумаге. В зависимости от фигуры, все задачи B5 делятся на два типа:
- Площади многоугольников;
- Площади окружностей.
Независимо от типа, надо помнить важнейшее правило, вытекающее из свойств площади: если фигуру разрезать на несколько частей, то сумма площадей этих частей равна площади всей фигуры.
- Глава 1.
- Площадь на координатной сетке
- § 1.
- Площади многоугольников на координатной сетке
- § 2.
- Задача B5: вычисление площади методом обводки
- § 3.
- Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
- § 4.
- Тест к уроку «Площади многоугольников на координатной сетке» (средний)
- § 5.
- Тест к уроку «Площади многоугольников без координатной сетки» (легкий)
- § 6.
- Тест к уроку «Площади многоугольников без координатной сетки» (средний)
- § 7.
- Метод узлов в задаче B5
- § 8.
- Задача B5: метод узлов
- § 9.
- Опасные ошибки в задачах на площади
- Глава 2.
- Площадь без координатной сетки
- § 1.
- Задача B5: площадь фигуры без клеток
- § 2.
- Задача B5: площадь фигур с вершиной в начале координат
- Глава 3.
- Площади кругов и секторов
- § 1.
- Площадь круга
- § 2.
- Задача B5: площадь сектора
- § 3.
- Задача B5: площадь закрашенного сектора
- § 4.
- Задача B5: площадь кольца
- § 5.
- Нестандартная задача B5 на площадь круга
- § 6.
- Семинар: ЕГЭ по математике, задачи B3 на площади
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Использование различных формул площадей многоугольников (страница 2)
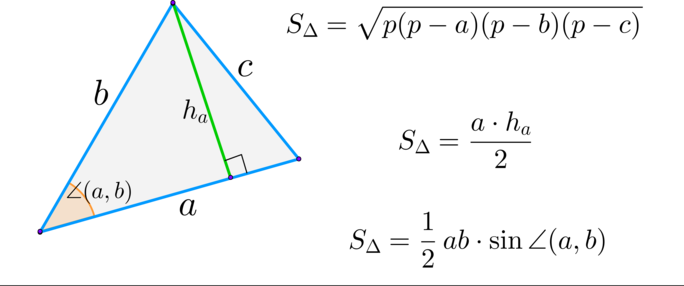
(blacktriangleright) Треугольник:
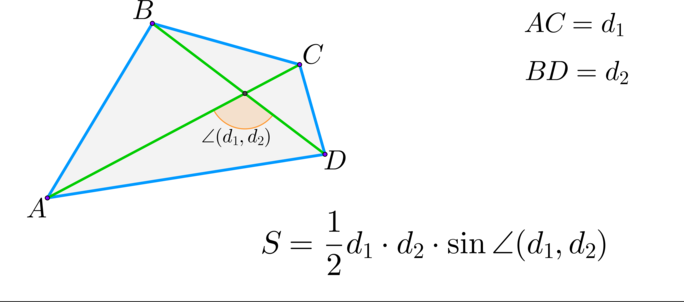
(blacktriangleright) Произвольный выпуклый четырехугольник:
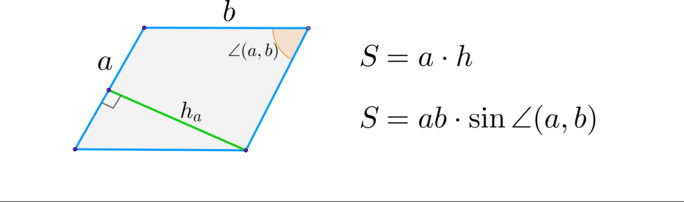
(blacktriangleright) Параллелограмм:
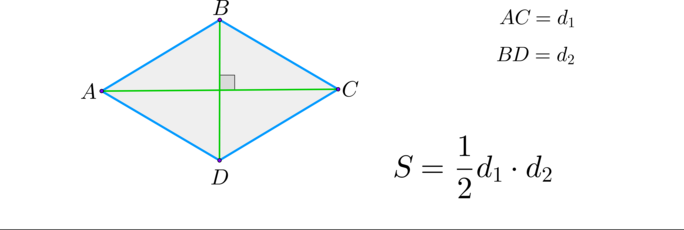
(blacktriangleright) Ромб:
(blacktriangleright) Прямоугольник:
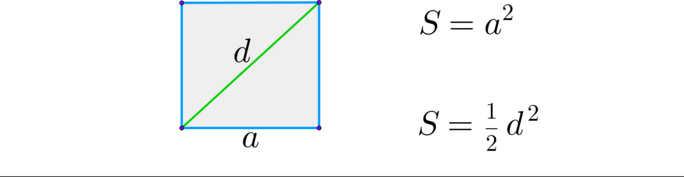
(blacktriangleright) Квадрат:
(blacktriangleright) Трапеция:
Задание
8
#3325
Уровень задания: Равен ЕГЭ
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен (30^circ). Найдите боковую сторону этого треугольника, если его площадь равна (25).
Пусть (a) – боковая сторона треугольника.
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [dfrac12cdot a^2cdot sin30^circ=S=25quadRightarrowquad
a^2=100quadRightarrowquad a=10]
Ответ: 10
Задание
9
#3324
Уровень задания: Равен ЕГЭ
Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
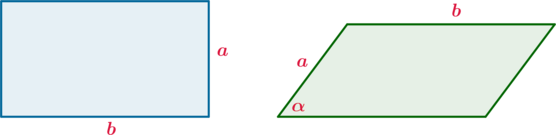
Площадь прямоугольника равна (S_1=ab), площадь параллелограмма равна (S_2=abcdot sinalpha). Из условия следует, что (2S_2=S_1). Следовательно: [2abcdot sinalpha=abquadRightarrowquad sinalpha=dfrac12quadRightarrow
quad alpha=30^circ]
Ответ: 30
Задание
10
#3323
Уровень задания: Равен ЕГЭ
Найдите площадь треугольника, две стороны которого равны (8) и (12), а угол между ними равен (30^circ).
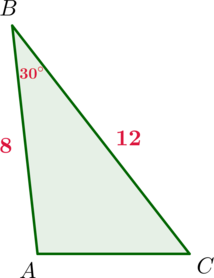
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [S_{ABC}=dfrac12cdot ABcdot BCcdot sinangle B=dfrac12cdot
8cdot 12 cdot dfrac12=24]
Ответ: 24
Задание
11
#3322
Уровень задания: Равен ЕГЭ
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен (150^circ). Боковая сторона треугольника равна (20). Найдите площадь этого треугольника.
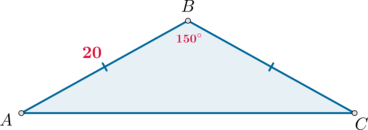
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [S_{ABC}=dfrac12cdot ABcdot BCcdot sinangle B=dfrac12cdot 20^2
cdot dfrac12=100]
Ответ: 100
Задание
12
#3321
Уровень задания: Равен ЕГЭ
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен (30^circ). Боковая сторона треугольника равна (10). Найдите площадь этого треугольника.
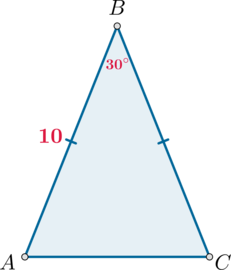
Площадь треугольника равна полупроизведению сторон на синус угла между ними, следовательно, [S_{ABC}=dfrac12cdot ABcdot BCcdot sinangle B=dfrac12cdot 10^2
cdot dfrac12=25]
Ответ: 25
Задание
13
#2281
Уровень задания: Равен ЕГЭ
Катеты прямоугольного треугольника относятся как (5:4), а площадь равна (4,1). Найдите гипотенузу этого треугольника.
Т.к. катеты относятся как (5:4), то их можно обозначить за (4x) и (5x). Тогда необходимо найти гипотенузу, по теореме Пифагора равную (sqrt{25x^2+16x^2}=sqrt{41x^2}).
Т.к. площадь прямоугольного треугольника равна полупроизведению катетов, то (S=0,5cdot 5xcdot 4x=10x^2=4,1). Следовательно, (x^2=0,41).
Значит, гипотенуза равна [sqrt{41cdot 0,41}=sqrt{41cdot 41cdot
0,01}=41cdot 0,1=4,1.]
Ответ: 4,1
Задание
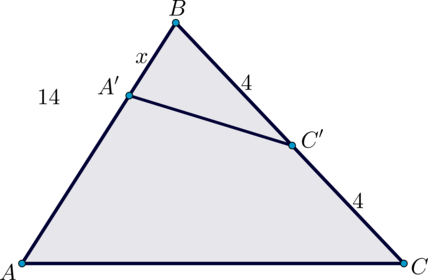
14
#2282
Уровень задания: Сложнее ЕГЭ
Дан треугольник (ABC). На сторонах (AB) и (BC) отмечены точки (A’) и (C’) соответственно. Известно, что (BC’=0,5BC=4), (AB=14), (S_{ABC}=7S_{A’BC’}). Найдите (A’B).
Площадь треугольника (ABC) равна (S_{ABC}=0,5cdot 14 cdot 8cdot
sinangle B).
Площадь треугольника (A’BC’) равна (S_{A’BC’}=0,5cdot A’Bcdot
4cdot sinangle B).
Таким образом, имеем равенство:
[0,5cdot 14 cdot 8cdot
sinangle B=7cdot 0,5cdot A’Bcdot 4cdot sinangle B quad
Leftrightarrow quad A’B=4.]
Ответ: 4

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Задачи на вычисление площадей плоских фигур
Для решения задач на вычисление площадей необходимо знать:
1. Формулы площадей фигур (квадрат, прямоугольник, треугольник, трапеция, параллелограмм, четырёхугольник, круг, сектор круга);
2. Теорему Пифагора;
3. Теорему косинусов;
4. Теорему о сумме углов треугольника;
5. Понятие синуса, косинуса, тангенса и котангенса угла в прямоугольном треугольнике;
6. Процесс решения квадратного уравнения (формулы дискриминанта и корней);
7. Формулы для решения треугольника (отношения высот, медиан, формулы связи радиусов вписанной и описанной окружности с его площадью).
Часть 1. Устные упражнения
- Найдите площадь квадрата, если сторона квадрата равна 4 см.
- Найдите площадь квадрата, если сторона квадрата равна 9 см.
- Найдите площадь квадрата, если периметр равен 24 см.
- Найдите площадь квадрата, если периметр равен 16 см.
- Найдите сторону квадрата, если его площадь равна 1,44 см2.
- Найдите сторону квадрата, если его площадь равна 2,89 см2.
- Найдите площадь прямоугольника, если смежные стороны прямоугольника равны 2,5 см и 3,2 см.
- Найдите площадь прямоугольника, если смежные стороны прямоугольника равны 2,5 см и 1,6 см.
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со смежными сторонами 8 м и 18 м.
- Найдите сторону квадрата, площадь которого равна площади прямоугольника со смежными сторонами 6 м и 24 м.
- Периметр прямоугольника равен 16 см, а длина в 3 раза больше ширины. Найдите его площадь.
- Периметр прямоугольника равен 24 см, а длина в 2 раза больше ширины. Найдите его площадь.
- Найдите периметр прямоугольника, если его площадь равна 72 см2, а длины его сторон относятся как 1:2.
- Найдите периметр прямоугольника, если его площадь равна 50 см2, а длины его сторон относятся как 1:2.
- Сторона параллелограмма равна 16см, а высота, проведенная к ней равна 5 см. Чему равна площадь параллелограмма?
- Сторона параллелограмма равна 12см, а высота, проведенная к ней равна 5 см. Чему равна площадь параллелограмма?
- Найдите площадь треугольника, если сторона равна 16 см, а высота, проведенная к ней равна 5см.
- Найдите площадь треугольника, если сторона равна 20 см, а высота, проведенная к ней равна 6см.
- Найдите площадь прямоугольного треугольника, если катеты равны 4 см и 9 см.
- Найдите площадь прямоугольного треугольника, если катеты равны 5 см и 12 см.
- Найдите площадь ромба, если длины диагоналей равны 8 м и 10 м.
- Найдите площадь ромба, если длины диагоналей равны 12 м и 10 м.
- Найдите площадь трапеции, если основания равны 8см и 12 см, а высота равна 4 см.
- Найдите площадь трапеции, если основания равны 8 см и 4 см, а высота равна 9 см.
- Найдите площадь квадрата, если диагональ равна 2
см.
- Найдите площадь квадрата, если диагональ равна 2
см.
- Найти гипотенузу прямоугольного треугольника, если катеты равны 6 см и 8 см.
- Найти гипотенузу прямоугольного треугольника, если катеты равны 12 см и 5 см.
- Сторона ромба равна 5 см, а одна из его диагоналей – 6 см. Чему равна площадь ромба.
- Площадь прямоугольного треугольника с гипотенузой 26 см, один из катетов которого равен 24 см, равна:
Часть 2. Задачи для фронтальной работы с классом.
- Периметр прямоугольника равен 18 см, а одна из его сторон на 1 см больше другой. Чему равна площадь прямоугольника? (Ответ: 20 см2).
- Периметр прямоугольника равен 24 см, а одна из его сторон в 2 раза меньше другой. Чему равна площадь прямоугольника? (Ответ: 32 см2).
- В прямоугольнике ABCD сторона BС равна 18 см. Расстояние от точки пересечения диагоналей до этой стороны равно 7 см. Найдите площадь треугольника BCD. (Ответ: 126 см2).
- В прямоугольнике ABCD сторона AB равна 12 см. Расстояние от точки пересечения диагоналей до этой стороны равно 8 см. Найдите площадь треугольника ABC. (Ответ: 96 см2).
- Периметр прямоугольника равен 20 см, а одна из его сторон равна 8 см. Прямоугольник имеет такую же площадь, что и квадрат. Чему равен периметр квадрата? (Ответ: 16 см).
- Периметр квадрата равен 24 см. Прямоугольник имеет такую же площадь, что и квадрат, а одна из его сторон равна 9 см. Чему равен периметр прямоугольника? (Ответ: 26 см).
- Стороны параллелограмма равны 10 см и 6 см, а угол между ними равен 150 °. Чему равна площадь этого параллелограмма? (Ответ: 30 см2).
- Стороны параллелограмма равны 12 см и 8 см, а угол между ними равен 30 °. Чему равна площадь этого параллелограмма? (Ответ: 48 см2).
- Чему равна площадь ромба, диагонали которого равны 8 см и 6 см? (Ответ: 24 см2).
- Чему равна площадь ромба, диагонали которого равны 10 см и 12 см? (Ответ: 60 см2).
- Две стороны треугольника равны 12 см и 9 см, а угол между ними 30 °. Чему равна площадь треугольника? (Ответ: 27 см2).
- Найдите площадь треугольника, две стороны треугольника равны 8 см и 6 см, а угол между ними 30 °. (Ответ: 24 см2).
- В прямоугольном треугольнике один из катетов равен 6 см, а его гипотенуза – 10 см. Чему равна площадь треугольника? (Ответ: 24 см2).
- В прямоугольном треугольнике один из катетов равен 5 см, а его гипотенуза – 13 см. Чему равна площадь треугольника? (Ответ: 30 см2).
- Основания трапеции равны 5 см и 9 см, её высота – 6 см. Чему равна площадь трапеции? (Ответ: 42 см2).
- Основания трапеции равны 4 см и 8 см, её высота – 9 см. Чему равна площадь трапеции? (Ответ: 54 см2).
- В равнобедренной трапеции основания равны 6 см и 10 см, а угол при основании равен 45 °. Чему равна площадь трапеции? (Ответ: 16 см2).
- В равнобедренной трапеции основания равны 8 см и 16 см, а угол при основании равен 45 °. Чему равна площадь трапеции? (Ответ: 48 см2).
- В прямоугольной трапеции основания равны 5 см и 9 см, а меньшая боковая сторона — 4 см. Чему равна площадь трапеции? (Ответ: 28 см2).
- В прямоугольной трапеции основания равны 6 см и 10 см, а меньшая боковая сторона — 4 см. Чему равна площадь трапеции? (Ответ: 32 см2).
- Диагонали трапеции взаимно перпендикулярны и равны 12 см и 18 см. Чему равна площадь трапеции? (Ответ: 108 см2).
- Диагонали трапеции взаимно перпендикулярны и равны 14 см и 16 см. Чему равна площадь трапеции? (Ответ: 112 см2).
- В равнобедренной трапеции высота, проведенная из вершины тупого угла, делит большее основание на два отрезка, больший из которых равен 18 см. Найдите площадь трапеции, если её высота равна 12 см. (Ответ: 216 см2).
Часть 3. Самостоятельные и контрольные работы.
Самостоятельная работа по теме
«Площади многоугольников»
Вариант I
1. В треугольнике ABC угол A равен 45°, ВС = 13 см, а высота BDотсекает на стороне AС отрезок DC, равный 12 см. Найдите площадь треугольника ABC и высоту, проведенную к сторонеВС.
2. Одна из диагоналей ромба на 4 см больше другой, а площадь ромба равна 96 см2. Найдите стороны ромба.
Вариант II
1. В треугольнике ABC угол В = 45°, высота AN делит сторону ВСна отрезки BN = 8 см и NC = 6 см. Найдите площадь треугольника ABC и сторону АС.
2. Найдите площадь ромба, если его сторона равна 20 см, а диагонали относятся как 3 : 4.
Вариант III (для более подготовленных учащихся)
1. В треугольнике ABC угол A равен 30°, а угол В равен 75°, высота ВО равна 6 см. Найдите площадь треугольника ABC.
2. Высота ВК ромба ABCD делит сторону AD на отрезки AK = 6 см и KD = 4 см. Найдите площадь ромба и его диагонали.
Самостоятельная работа по теме
«Площадь треугольника»
Вариант I
На рисунке АО = ОВ, OC = 2OD, SAOC = 12 см2. Найдите SBOD.
Вариант II
На рисунке OB = ОC, OD = 3OA, SAOC = 16 см2. Найдите SBOD.
Вариант III (для более подготовленных учащихся)
На рисунке OA = AB, АС || ВD. Докажите, что SOBC = SOAD.
Основания равнобедренной трапеции 12 см и 16 см, а ее диагонали взаимно перпендикулярны. Найдите площадь трапеции.
Самостоятельная работа
Вариант 1
- Сторона треугольника равна 5см, а высота, проведенная к ней, в 2 раза больше стороны. Найдите площадь треугольника.
- Стороны параллелограмма равны 6см и 8см, а угол между ними равен 30º. Найдите площадь параллелограмма.
- В прямоугольной трапеции основания равны 7см и 11см, большая боковая сторона составляет с основанием угол45º. Найдите площадь трапеции.
- В треугольнике ABC стороны AB и BC соответственно равны 14см и 18см. Сторона AB продолжена за точку А на отрезок AM, равный AB. Сторона BC продолжена за точку С на отрезок KC, равный половине BC. Найдите площадь треугольника MBK, если площадь треугольника ABC равна 126см2.
Вариант 2
- Сторона треугольника равна 18см, а высота, проведенная к ней, в 3 раза меньше стороны. Найдите площадь треугольника.
- Стороны параллелограмма равны 4см и 7см, а угол между ними 150º. Найдите площадь параллелограмма.
- В равнобедренной трапеции ABCM большее основание AMравно 20см, высота BH отсекает от AM отрезок AH, равный 6см. Угол BAM равен 45º. Найдите площадь трапеции.
- В ромбе ABCD на стороне BC отмечена точка K такая, чтоKC:BK=3:1. Найдите площадь треугольника ABK, если площадь ромба равна 48см2.
Самостоятельная работа по теме «Площадь»
Вариант 1
- В параллелограмме ABCD угол B тупой. На продолжении стороны AD за вершину D отмечена точка E так, что ∠ECD=60 °,∠CED=90 °, AD=10 см. Найдите площадь параллелограмма. (Ответ: 20 см2).
- Найдите углы параллелограмма, если его площадь равна 20 см2, а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла. (Ответ: 45 °, 135 °).
- В прямоугольнике ABCD BD=12 см. Вершина В удалена от прямой АС на 4 см. Найдите площадь треугольника АВС. (Ответ: 24 см2).
- Периметр равнобедренной трапеции равен 32 см, боковая сторона 5 см, площадь 44 см2. Найдите высоту трапеции. (Ответ: 4 см).
Вариант 2
- В параллелограмме MPKT на стороне МТ отмечена точка E,∠РEМ=90 °, ∠EРТ=45 °, МЕ=4 см, ЕТ=7 см. Найдите площадь параллелограмма. (Ответ: 77 см2).
- Найдите углы параллелограмма, если его площадь равна 20 см2, а высота, проведенная из вершины тупого угла, делит одну из сторон на отрезки 2 см и 8 см, считая от вершины острого угла. (Ответ: 45 °, 135 °).
- Найдите площадь равнобедренного прямоугольного треугольника с гипотенузой 10 см. (Ответ: 25 см2).
- В прямоугольной трапеции площадь равна 30 см2, периметр 28 см, а меньшая боковая сторона 3 см. Найдите большую боковую сторону. (Ответ: 5 см).
Контрольная работа по теме
«Площади многоугольников»
Вариант I
1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.
2. Площадь прямоугольной трапеции равна 120 см2, а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
3. На стороне АС данного треугольника ABC постройте точку Dтак, чтобы площадь треугольника ABD составила одну треть площади треугольника ABC.
Вариант II
1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см2.
2. Найдите площадь трапеции ABCD с основаниями AD и ВС, если AB = 12 см, ВС = 14 см, AD = 30 см, угол B равен 150°.
3. На продолжении стороны KN данного треугольника KMNпостройте точку P так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KMN.
Вариант III (для более подготовленных учащихся)
1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 30°. Найдите площадь параллелограмма.
2. Середина М боковой стороны CD трапеции ABCD соединена отрезками с вершинами A и В. Докажите, что площадь треугольника АВМ в два раза меньше площади данной трапеции.
3. Точки A1, B1, C1 лежат соответственно на сторонах ВС, АС, АВтреугольника ABC, причем АВ1 = 1/3АС, СА1 = 1/3СВ, ВС1 =1/3 BA. Найдите площадь треугольника A1B1C1, если площадь треугольника ABC равна 27 см2.
Контрольная работа по теме
«Площади многоугольников»
Вариант I
1. Смежные стороны параллелограмма равны 32 см и 26 см, а один из его углов равен 150°. Найдите площадь параллелограмма.
2. Площадь прямоугольной трапеции равна 120 см2, а ее высота равна 8 см. Найдите все стороны трапеции, если одно из оснований больше другого на 6 см.
3. На стороне АС данного треугольника ABC постройте точку Dтак, чтобы площадь треугольника ABD составила одну треть площади треугольника ABC.
Вариант II
1. Одна из диагоналей параллелограмма является его высотой и равна 9 см. Найдите стороны этого параллелограмма, если его площадь равна 108 см2.
2. Найдите площадь трапеции ABCD с основаниями AD и ВС, если AB = 12 см, ВС = 14 см, AD = 30 см, угол B равен 150°.
3. На продолжении стороны KN данного треугольника KMNпостройте точку P так, чтобы площадь треугольника NMP была в два раза меньше площади треугольника KMN.
Вариант III (для более подготовленных учащихся)
1. Стороны параллелограмма равны 12 см и 8 см, а угол между высотами, проведенными из вершины тупого угла, равен 30°. Найдите площадь параллелограмма.
2. Середина М боковой стороны CD трапеции ABCD соединена отрезками с вершинами A и В. Докажите, что площадь треугольника АВМ в два раза меньше площади данной трапеции.
3. Точки A1, B1, C1 лежат соответственно на сторонах ВС, АС, АВтреугольника ABC, причем АВ1 = 1/3АС, СА1 = 1/3СВ, ВС1 =1/3 BA. Найдите площадь треугольника A1B1C1, если площадь треугольника ABC равна 27 см2.
Подборка задач из Открытого банка заданий по математике
(с сайта http://mathgia.ru)
- В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 10, а угол, лежащий напротив него, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 10, а острый угол, прилежащий к нему, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 20, а угол, лежащий напротив него, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 30, а острый угол, прилежащий к нему, равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 62, а один из острых углов равен 30°. Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 54, а один из острых углов равен 60° . Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 24, а один из острых углов равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 52, а один из острых углов равен
. Найдите площадь треугольника.
- Сторона равностороннего треугольника равна 48. Найдите его площадь.
- Сторона равностороннего треугольника равна 16. Найдите его площадь.
- Периметр равностороннего треугольника равен 264. Найдите его площадь.
- Высота равностороннего треугольника равна 7. Найдите его площадь.
- В равнобедренном треугольнике боковая сторона равна 94, а угол, лежащий напротив основания, равен
. Найдите площадь треугольника.
- В равнобедренном треугольнике боковая сторона равна 14, а угол, лежащий напротив основания, равен
. Найдите площадь треугольника.
- Периметр равнобедренного треугольника равен 48, а боковая сторона — 15. Найдите площадь треугольника.
- Периметр равнобедренного треугольника равен 324, а боковая сторона — 90. Найдите площадь треугольника.
- Периметр равнобедренного треугольника равен 392, а основание — 192. Найдите площадь треугольника.
- В треугольнике одна из сторон равна 27, а опущенная на нее высота — 11. Найдите площадь треугольника.
- В треугольнике одна из сторон равна 2, а опущенная на нее высота — 17. Найдите площадь треугольника.
- В треугольнике одна из сторон равна 2, другая равна
, а угол между ними равен
. Найдите площадь треугольника.
- В треугольнике одна из сторон равна 28, другая равна
, а угол между ними равен
. Найдите площадь треугольника.
- В ромбе сторона равна 44, одна из диагоналей — 44, а угол, из которого выходит эта диагональ, равен
. Найдите площадь ромба.
- Радиус круга равен 36, а длина ограничивающей его окружности равна
. Найдите площадь круга.
- В ромбе сторона равна 38, одна из диагоналей —
, а угол, лежащий напротив этой диагонали, равен
. Найдите площадь ромба.
- В ромбе сторона равна 22, одна из диагоналей —
, а угол, из которого выходит эта диагональ, равен
. Найдите площадь ромба.
- В равнобедренном треугольнике боковая сторона равна 47, основание —
, а угол, лежащий напротив основания, равен
. Найдите площадь треугольника.
- В прямоугольнике диагональ равна 96, угол между ней и одной из сторон равен 30°, длина этой стороны
. Найдите площадь прямоугольника.
- В прямоугольнике диагональ равна 92, а угол между ней и одной из сторон равен 60°, длина этой стороны равна 46. Найдите площадь прямоугольника.
- В прямоугольном треугольнике один из катетов равен
, острый угол, прилежащий к нему, равен
, а гипотенуза равна 28. Найдите площадь треугольника.
- В прямоугольном треугольнике один из катетов равен 4, угол, лежащий напротив него, равен
, а гипотенуза равна 8. Найдите площадь треугольника.
- Найдите площадь кругового сектора, если радиус круга равен 4, а угол сектора равен
.
- Найдите площадь кругового сектора, если длина ограничивающей его дуги равна
, а угол сектора равен
.
- В прямоугольном треугольнике один из катетов равен 43, острый угол, прилежащий к нему, равен
, а гипотенуза равна 86. Найдите площадь треугольника.
- Основания трапеции равны 3 и 24, одна из боковых сторон равна 7, а тангенс угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 2 и 16, одна из боковых сторон равна 6, а тангенс угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Радиус круга равен 41. Найдите его площадь.
- Основания трапеции равны 10 и 100, одна из боковых сторон равна 5, а синус угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 7 и 42, одна из боковых сторон равна 15, а косинус угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 9 и 27, одна из боковых сторон равна 26, а косинус угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 4 и 12, одна из боковых сторон равна
, а угол между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 9 и 24, одна из боковых сторон равна
, а угол между ней и одним из оснований равен
. Найдите площадь трапеции.
- Основания трапеции равны 5 и 45, одна из боковых сторон равна 13, а синус угла между ней и одним из оснований равен
. Найдите площадь трапеции.
- Одна из сторон параллелограмма равна 15, другая равна 6, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
- Основания трапеции равны 4 и 25, одна из боковых сторон равна
, а угол между ней и одним из оснований равен
. Найдите площадь трапеции.
- Одна из сторон параллелограмма равна 50, другая равна 1, а косинус одного из углов равен
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 8, другая равна 18, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 20, другая равна 29, а тангенс одного из углов равен
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 21, другая равна 3, а один из углов —
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 18, другая равна 25, а синус одного из углов равен
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 13, другая равна 24, а один из углов —
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 17, другая равна 10, а один из углов —
. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 30, другая равна 9, а один из углов —
. Найдите площадь параллелограмма.
- Периметр ромба равен 128, а тангенс одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 20, а тангенс одного из углов равен
. Найдите площадь ромба.
- Одна из сторон параллелограмма равна 20, а опущенная на нее высота равна 23. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 16, а опущенная на нее высота равна 25. Найдите площадь параллелограмма.
- Одна из сторон параллелограмма равна 19, а опущенная на нее высота равна 27. Найдите площадь параллелограмма.
- Периметр ромба равен 80, а косинус одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 84, а косинус одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 144, а косинус одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 72, а тангенс одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 28, а один из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 128, а один из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 108, а синус одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 36, а синус одного из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 32, а синус одного из углов равен
. Найдите площадь ромба.
- Сторона ромба равна 95, а диагональ равна 114. Найдите площадь ромба.
- Сторона ромба равна 90, а диагональ равна 144. Найдите площадь ромба.
- Периметр ромба равен 148, а один из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 112, а один из углов равен
. Найдите площадь ромба.
- Периметр ромба равен 184, а один из углов равен
. Найдите площадь ромба.
- В прямоугольнике одна сторона равна 45, а диагональ равна 53. Найдите площадь прямоугольника.
- В прямоугольнике одна сторона равна 15, а диагональ равна 17. Найдите площадь прямоугольника.
- В прямоугольнике диагональ равна 42, а угол между ней и одной из сторон равен
. Найдите площадь прямоугольника.
- Сторона ромба равна 29, а диагональ равна 42. Найдите площадь ромба.
- В прямоугольном треугольнике гипотенуза равна 52, а один из острых углов равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 24, а один из острых углов равен
. Найдите площадь треугольника.
- В прямоугольном треугольнике гипотенуза равна 52, а один из острых углов равен
. Найдите площадь треугольника.
- Сторона равностороннего треугольника равна 48. Найдите его площадь.
- Сторона равностороннего треугольника равна 16. Найдите его площадь.
- Периметр равнобедренного треугольника равен 48, а боковая сторона — 15. Найдите площадь треугольника.
- Периметр равнобедренного треугольника равен 196, а боковая сторона — 53. Найдите площадь треугольника.
- В прямоугольнике одна сторона равна 13, другая сторона равна 9. Найдите площадь прямоугольника.
- В прямоугольнике одна сторона равна 13, периметр равен 62. Найдите площадь прямоугольника.
- В прямоугольнике одна сторона равна 14, периметр равен 54. Найдите площадь прямоугольника.
- В прямоугольнике одна сторона равна 84, а диагональ равна 91. Найдите площадь прямоугольника.
- В прямоугольнике одна сторона равна 52, а диагональ равна 65. Найдите площадь прямоугольника.
Подборка задач с сайтаhttp://webmath.exponenta.ru/mege/
1 Найдите площадь квадрата, если его диагональ равна 1.
2 Найдите диагональ квадрата, если его площадь равна 2.
3 Найдите сторону квадрата, площадь которого равна площади прямоугольника со сторонами 4 и 9.
4 Найдите площадь прямоугольника, если его периметр равен 18, и одна сторона на 3 больше другой.
5 Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
6 Найдите площадь прямоугольника, если его периметр равен 18, а отношение соседних сторон равно 1:2.
7 Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
8 Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
9 Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
10 Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.
11 Сторона прямоугольника относится к его диагонали, как 4:5, а другая сторона равна 6. Найдите площадь прямоугольника.
12 Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150°.
13 Найдите площадь ромба, если его высота равна 2, а острый угол 30°.
14 Найдите площадь ромба, если его диагонали равны 4 и 12.
15 Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.
16 Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.
17 Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.
18 Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.
19 Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.
20 Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30°.
21 Основания трапеции равны 1 и 3, высота — 1. Найдите площадь трапеции.
22 Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
23 Основания трапеции равны 8 и 34, площадь равна 168. Найдите ее высоту.
24 Основание трапеции равно 13, высота равна 5, а площадь равна 50. Найдите второе основание трапеции.
25 Высота трапеции равна 10, площадь равна 150. Найдите среднюю линию трапеции.
26 Средняя линия трапеции равна 12, площадь равна 96. Найдите высоту трапеции.
27 Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.
28 Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.
29 Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45°.
30 Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.
31 Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.
32 Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
33 Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150°. Найдите площадь трапеции.
34 Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.
35 Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8.
36 Площадь прямоугольного треугольника равна 16. Один из его катетов равен 4. Найдите другой катет.
37 Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.
38 Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.
39 Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.
40 Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.
41 Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
42 Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30°. Найдите боковую сторону треугольника, если его площадь равна 25.
43 Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150°. Найдите боковую сторону треугольника, если его площадь равна 100.
44 Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
45 Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
46 Найдите площадь круга, длина окружности которого равна π1/2 .
47 Площадь круга равна π−1. Найдите длину его окружности.
48 Найдите площадь сектора круга радиуса π−1/2, центральный угол которого равен 90°.
49 Найдите площадь сектора круга радиуса 1, длина дуги которого равна 2.
50 Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны 4·π−1/2 и 2·π−1/2 .
51 Площадь сектора круга радиуса 3 равна 6. Найдите длину его дуги.
52 Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.
53 Площадь треугольника равна 24, а радиус вписанной окружности равен 2. Найдите периметр этого треугольника.
54 Площадь треугольника равна 54, а его периметр 36. Найдите радиус вписанной окружности.
Решение задач по готовым чертежам (из сборника Е.М. Рабиновича «Задачи и упражнения на готовых чертежах», Харьков, 1998 г.)
Площадь треугольника
Площадь четырехугольника
Площадь круга и его частей
РАЗНОЕ
70P Площадь треугольника ABC равна 96. DE — средняя линия. Найдите площадь треугольника CDE.
71P Найдите площадь квадрата, если его диагональ равна 4.
72P Найдите площадь квадрата, если его диагональ равна 6.
73P Даны два квадрата, диагонали которых равны 24 и 25. Найдите диагональ квадрата, площадь которого равна разности площадей данных квадратов.
74P Найдите площадь параллелограмма, если две его стороны равны 6 и 11, а угол между ними равен 30°.
75P Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.
76PСредняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
77P Периметры двух подобных многоугольников относятся как 4:7. Площадь меньшего многоугольника равна 16. Найдите площадь большего многоугольника.
78P Найдите площадь сектора круга радиуса 14, длина дуги которого равна 2.
79P Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны .
Вычисление площадей многоугольников на клетчатой бумаге с применением различных способов
(пригодится на ОГЭ и ЕГЭ)
Рекомендации
Для решения таких заданий, надо знать формулы
вычисления площадей треугольника, прямоугольника,
трапеции, параллелограмма, квадрата!!!!!
Встречаются задачи, где используются свойства
площадей. Фигуру надо разбить на части, площади
которых можно найти по знакомым формулам. Или
наоборот, фигуру надо достроить. Получится большая
фигура, площадь которой мы сможем найти.
На клетчатой бумаге с клетками размером 1 см на 1 см
изображены различные фигуры. Надо найти
площадь. Ответ записать в квадратных сантиметрах
(наименования в ответ не писать)
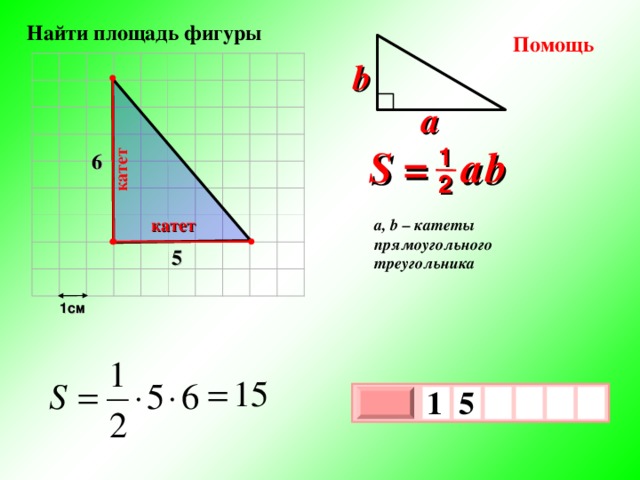
катет
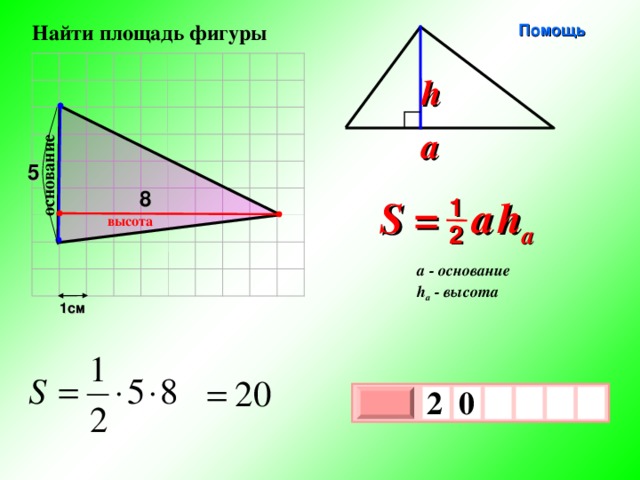
Найти площадь фигуры
Помощь
b
a
S = a b
1
6
2
катет
a, b – катеты прямоугольного треугольника
5
1см
1
5
х
3
х
1
0
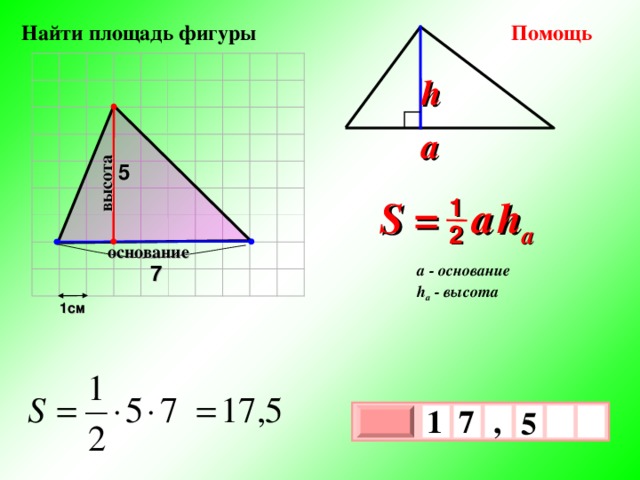
высота
Помощь
Найти площадь фигуры
h
a
5
S = a h a
1
2
основание
7
a — основание
h a — высота
1см
1
,
7
5
х
3
х
1
0
основание
Найти площадь фигуры
Помощь
h
a
5
8
S = a h a
1
высота
2
a — основание
h a — высота
1см
2
0
х
3
х
1
0
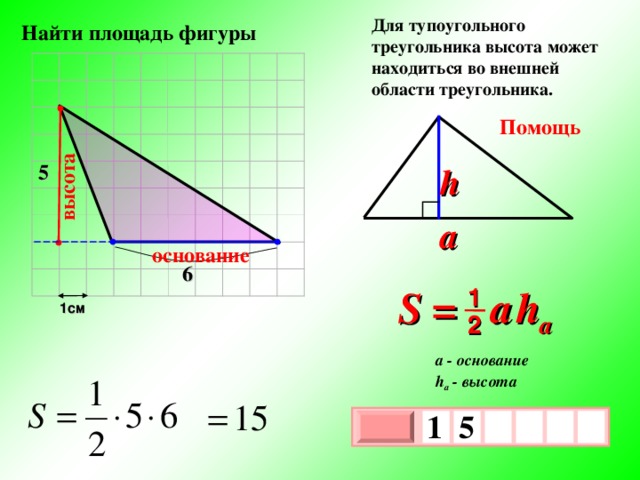
высота
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
Найти площадь фигуры
Помощь
5
h
a
основание
6
S = a h a
1
1см
2
a — основание
h a — высота
1
5
х
3
х
1
0
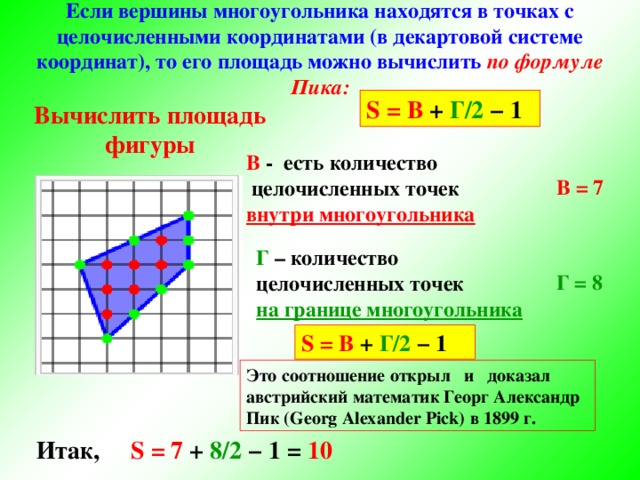
Формула Пика
6
Если вершины многоугольника находятся в точках с целочисленными координатами (в декартовой системе координат), то его площадь можно вычислить по формуле Пика:
S = В + Г/2 − 1
Вычислить площадь фигуры
В — есть количество
целочисленных точек
внутри многоугольника
В = 7
Г – количество
целочисленных точек
на границе многоугольника
Г = 8
S = В + Г/2 − 1
Это соотношение открыл и доказал австрийский математик Георг Александр Пик (Georg Alexander Pick) в 1899 г.
Итак, S = 7 + 8/2 − 1 = 10
6
Вычислить площадь параллелограмма
2
1
4
Первый способ:
1. S = 7·4 = 28
2. S 1 = S 3 , S 2 = S 4
3. 2S 2 = 5·1 = 5
4. 2S 1 = 3·2 = 6
5. S = 28 – 11 = 17
3
1
3
4
2
5
7
Ответ: 17
6
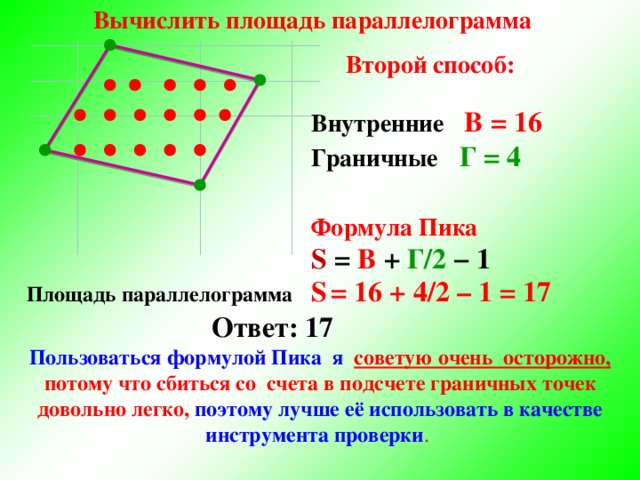
Вычислить площадь параллелограмма
Второй способ:
Внутренние В = 16
Граничные Г = 4
Формула Пика
S = В + Г/2 − 1
Площадь параллелограмма S = 16 + 4/2 – 1 = 17
Ответ: 17
Пользоваться формулой Пика я советую очень осторожно, потому что сбиться со счета в подсчете граничных точек довольно легко, поэтому лучше её использовать в качестве инструмента проверки .
6
основание
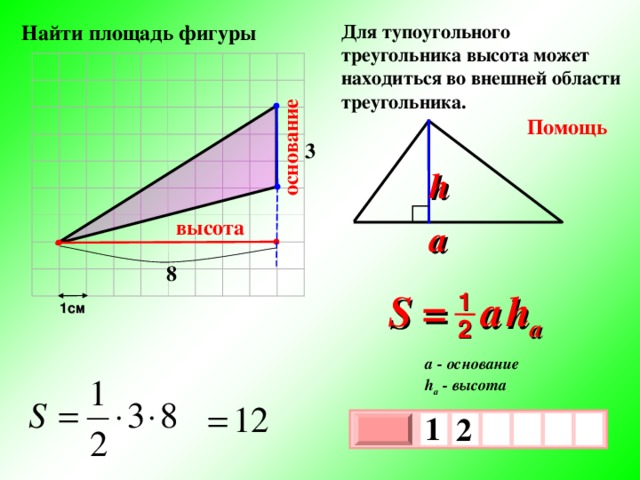
Для тупоугольного треугольника высота может находиться во внешней области треугольника.
Найти площадь фигуры
Помощь
3
h
высота
a
8
S = a h a
1
1см
2
a — основание
h a — высота
1
2
х
3
х
1
0
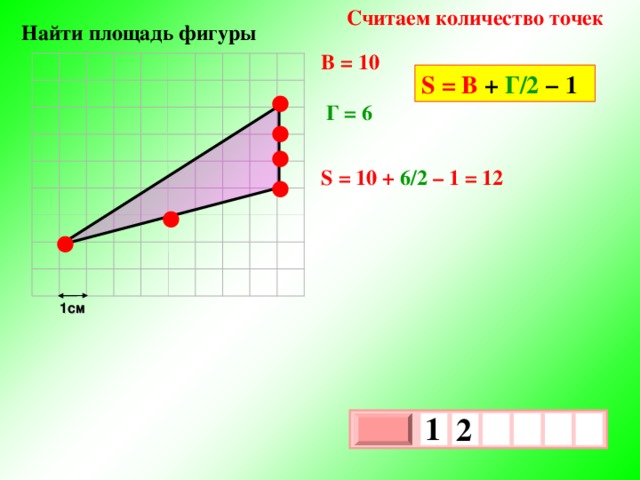
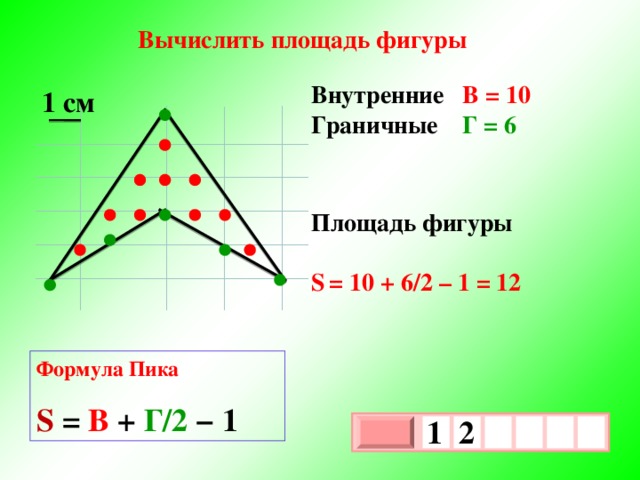
Считаем количество точек
Найти площадь фигуры
В = 10
S = В + Г/2 − 1
●
Г = 6
●
●
S = 10 + 6/2 – 1 = 12
●
●
●
1см
1
2
х
3
х
1
0
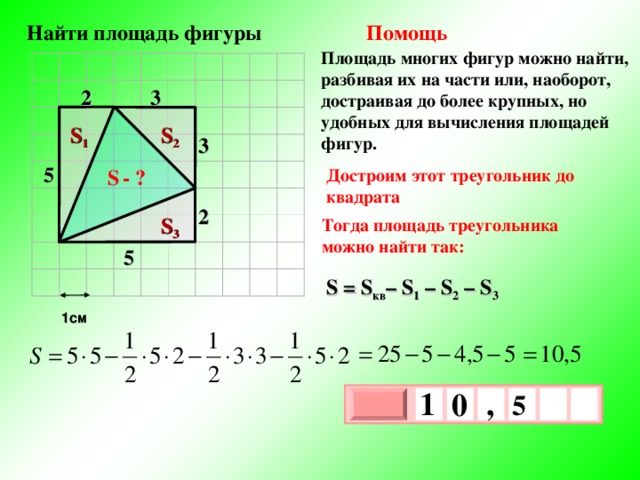
Найти площадь фигуры
Помощь
Площадь многих фигур можно найти, разбивая их на части или, наоборот, достраивая до более крупных, но удобных для вычисления площадей фигур.
2
3
S 1
S 2
3
5
Достроим этот треугольник до квадрата
S — ?
2
S 3
Тогда площадь треугольника можно найти так:
5
S = S кв – S 1 – S 2 – S 3
1см
1
,
0
5
х
3
х
1
0
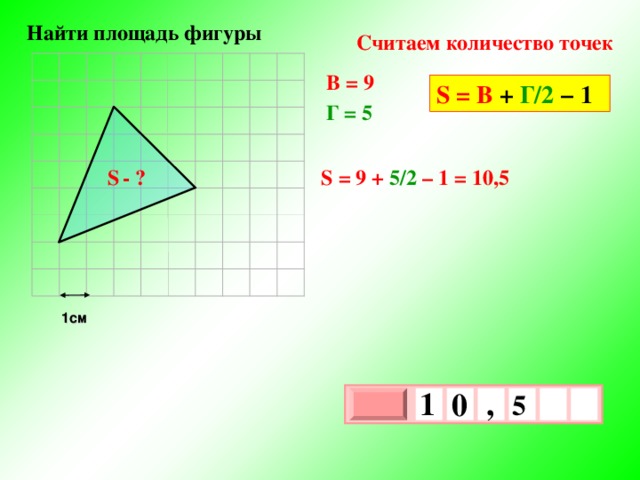
Найти площадь фигуры
Считаем количество точек
В = 9
S = В + Г/2 − 1
Г = 5
S = 9 + 5/2 – 1 = 10,5
S — ?
1см
1
,
0
5
х
3
х
1
0
основание
высота
Найти площадь фигуры
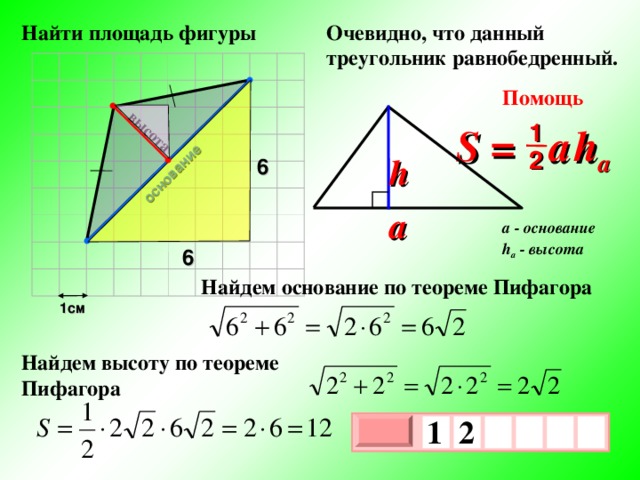
Очевидно, что данный треугольник равнобедренный.
Помощь
1
S = a h a
2
h
6
a
a — основание
h a — высота
6
Найдем основание по теореме Пифагора
1см
Найдем высоту по теореме Пифагора
1
2
х
3
х
1
0
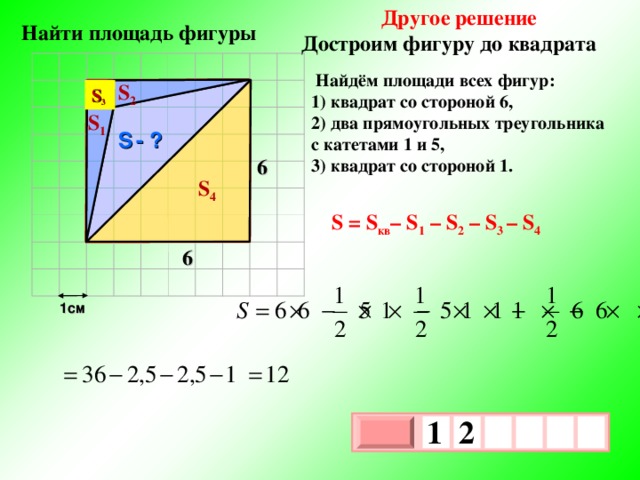
Другое решение
Достроим фигуру до квадрата
Найти площадь фигуры
Найдём площади всех фигур:
1) квадрат со стороной 6,
2) два прямоугольных треугольника с катетами 1 и 5,
3) квадрат со стороной 1.
S 2
S 3
S 1
S — ?
6
S 4
S = S кв – S 1 – S 2 – S 3 – S 4
6
1см
1
2
х
3
х
1
0
Найти площадь фигуры
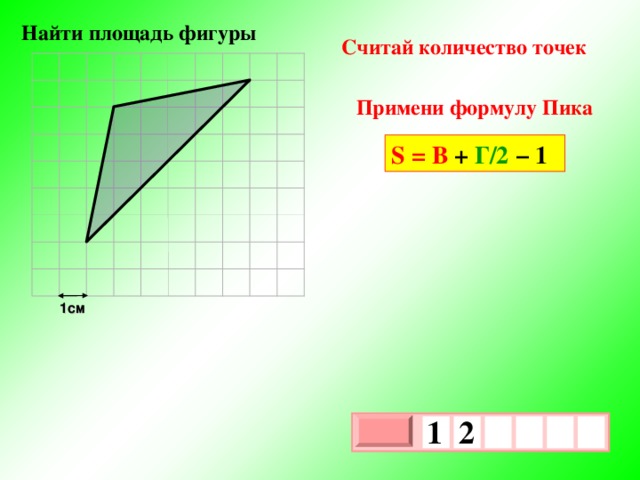
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
1
2
х
3
х
1
0
высота
Найти площадь фигуры
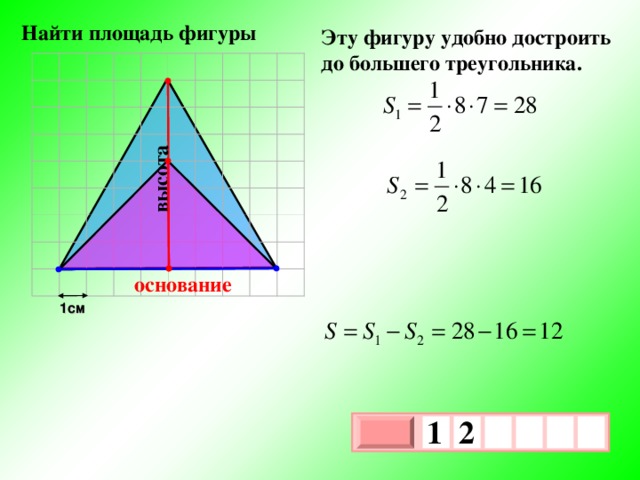
Эту фигуру удобно достроить до большего треугольника.
основание
1см
1
2
х
3
х
1
0
Вычислить площадь фигуры
Внутренние В = 10
Граничные Г = 6
Площадь фигуры
S = 10 + 6/2 – 1 = 12
1 см
Формула Пика
S = В + Г/2 − 1
1
2
х
3
х
1
0
19
высота
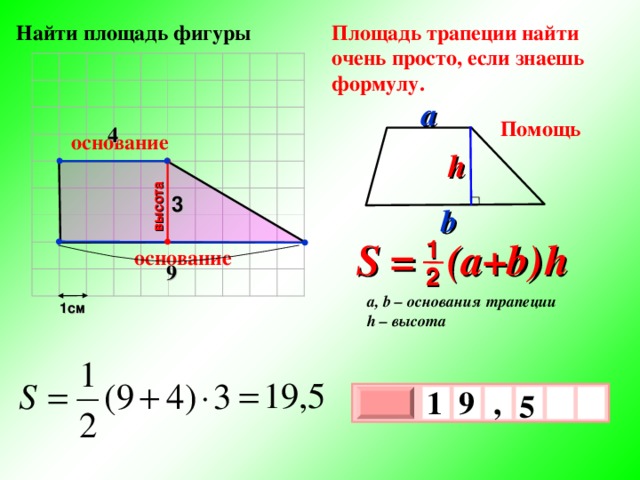
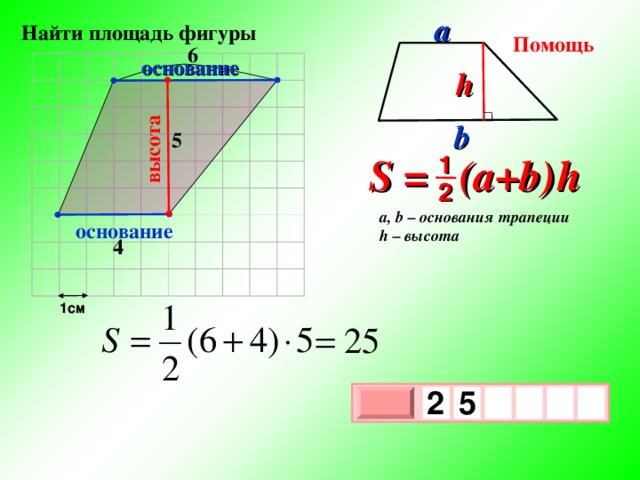
Найти площадь фигуры
Площадь трапеции найти очень просто, если знаешь формулу.
a
Помощь
4
основание
h
3
b
S = (a+b ) h
1
основание
9
2
a, b – основания трапеции
h – высота
1см
1
,
9
5
х
3
х
1
0
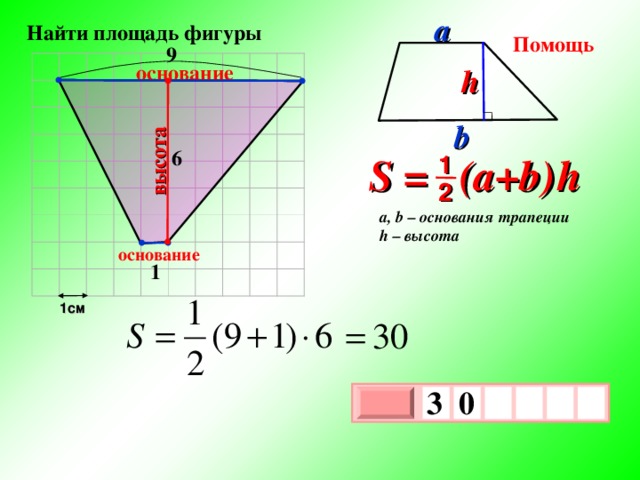
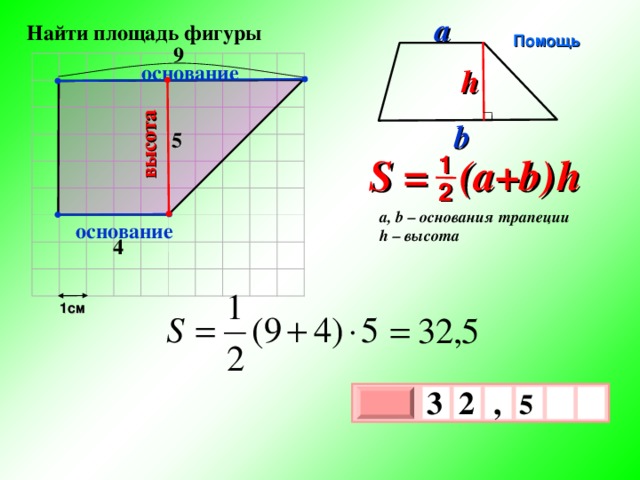
высота
a
Найти площадь фигуры
Помощь
9
основание
h
b
6
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
1
1см
3
0
х
3
х
1
0
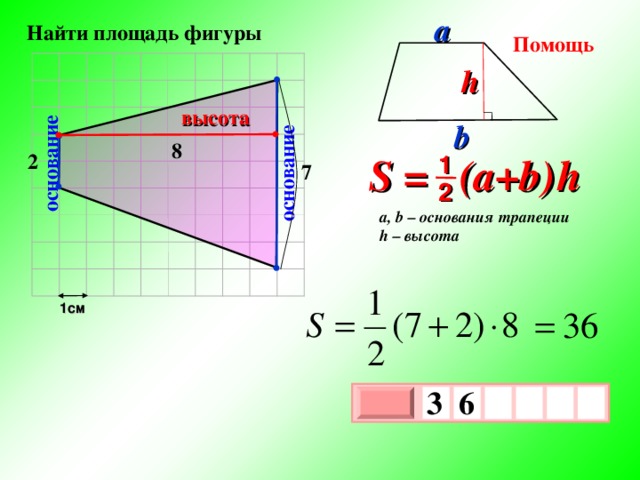
основание
основание
a
Найти площадь фигуры
Помощь
h
высота
b
8
S = (a+b ) h
2
1
7
2
a, b – основания трапеции
h – высота
1см
3
6
х
3
х
1
0
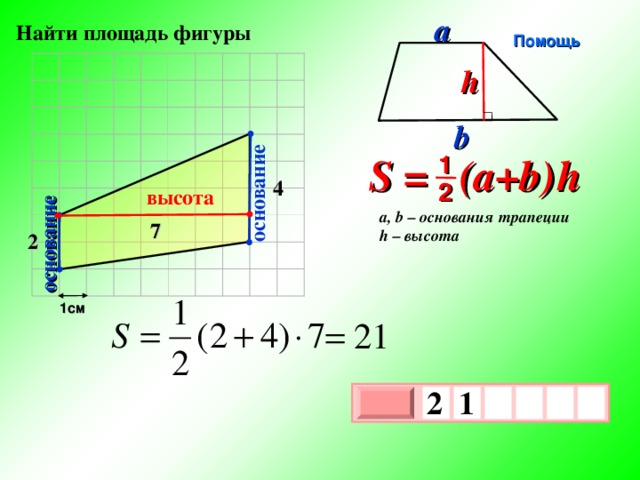
высота
a
Найти площадь фигуры
Помощь
6
основание
h
b
5
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
4
1см
2
5
х
3
х
1
0
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
2
5
х
3
х
1
0
высота
a
Найти площадь фигуры
Помощь
9
основание
h
b
5
S = (a+b ) h
1
2
a, b – основания трапеции
h – высота
основание
4
1см
3
,
2
5
х
3
х
1
0
основание
основание
a
Найти площадь фигуры
Помощь
h
b
S = (a+b ) h
1
4
2
высота
a, b – основания трапеции
h – высота
7
2
1см
2
1
х
3
х
1
0
26
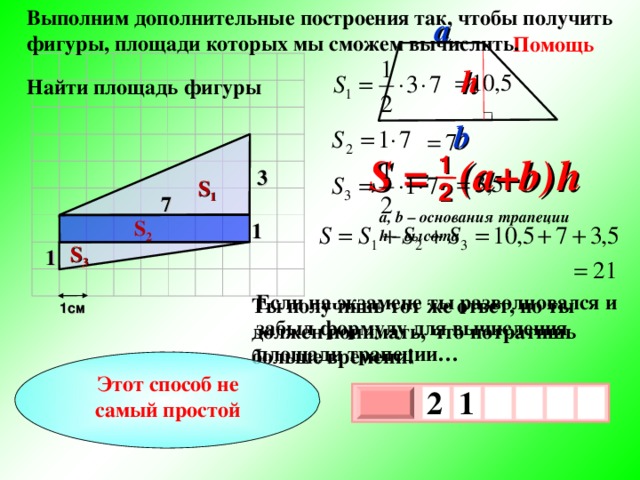
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
a
Помощь
h
Найти площадь фигуры
b
S = (a+b ) h
1
3
S 1
2
7
a, b – основания трапеции
h – высота
S 2
1
S 3
1
Если на экзамене ты разволновался и забыл формулу для вычисления площади трапеции…
Ты получишь тот же ответ, но ты должен понимать, что потратишь больше времени!
1см
Этот способ не самый простой
2
1
х
3
х
1
0
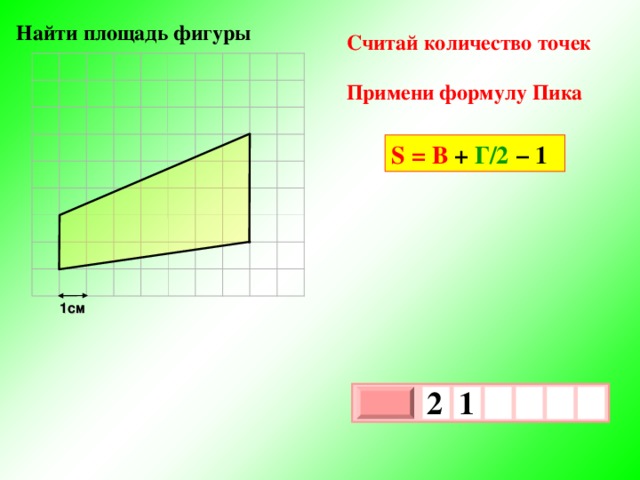
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
2
1
х
3
х
1
0
28
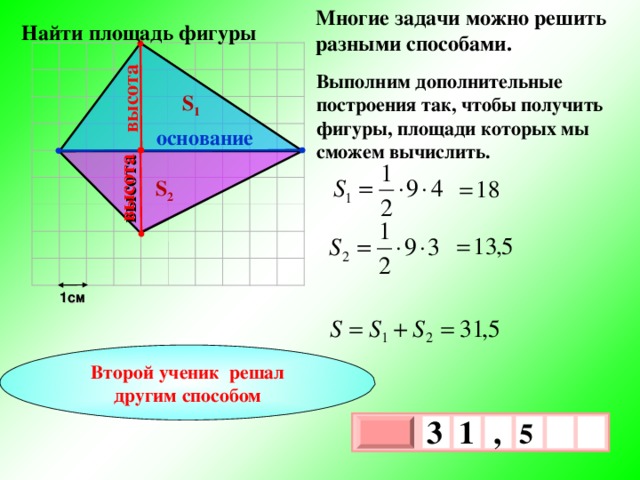
Многие задачи можно решить разными способами.
высота
высота
Найти площадь фигуры
Выполним дополнительные построения так, чтобы получить фигуры, площади которых мы сможем вычислить.
S 1
основание
S 2
1см
Второй ученик решал другим способом
3
,
1
5
х
3
х
1
0
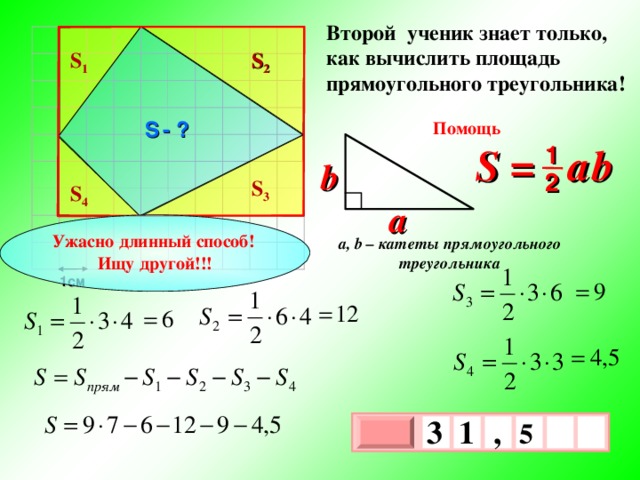
Второй ученик знает только, как вычислить площадь прямоугольного треугольника!
S 2
S 1
S — ?
Помощь
S = a b
1
b
2
S 3
S 4
a
Ужасно длинный способ!
Ищу другой!!!
a, b – катеты прямоугольного треугольника
1см
3
,
1
5
х
3
х
1
0
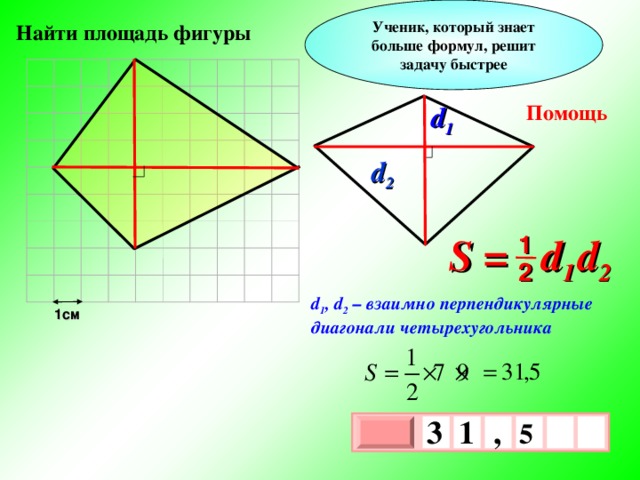
Ученик, который знает больше формул, решит задачу быстрее
Найти площадь фигуры
d 1
Помощь
d 2
S = d 1 d 2
1
2
d 1 , d 2 – взаимно перпендикулярные диагонали четырехугольника
1см
3
,
1
5
х
3
х
1
0
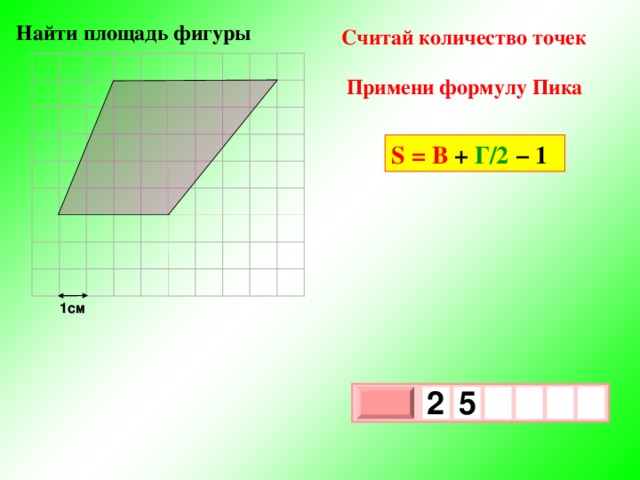
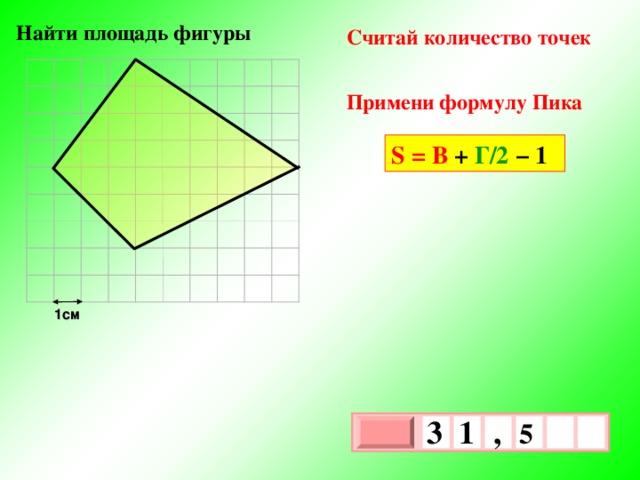
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
3
,
1
5
х
3
х
1
0
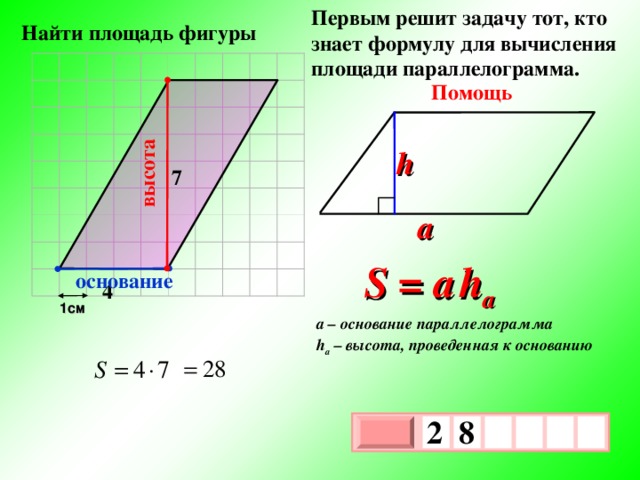
Первым решит задачу тот, кто знает формулу для вычисления площади параллелограмма.
высота
Найти площадь фигуры
Помощь
h
7
a
S = a h a
основание
4
1см
a – основание параллелограмма
h a – высота, проведенная к основанию
2
8
х
3
х
1
0
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
1см
2
8
х
3
х
1
0
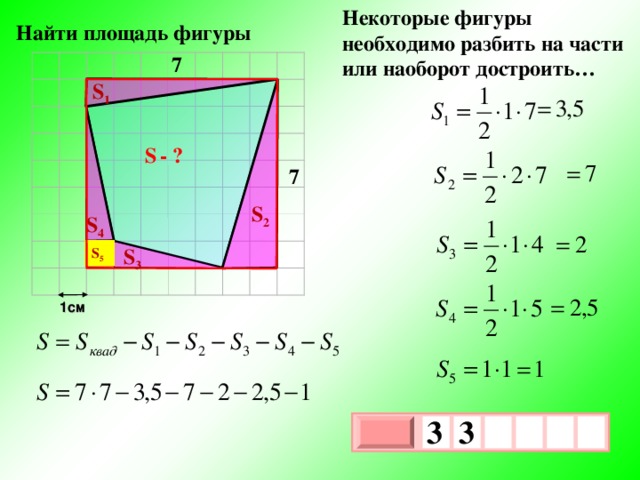
Некоторые фигуры необходимо разбить на части или наоборот достроить…
Найти площадь фигуры
7
S 1
S — ?
7
S 2
S 4
S 3
S 5
1см
3
3
х
3
х
1
0
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
S — ?
1см
3
3
х
3
х
1
0
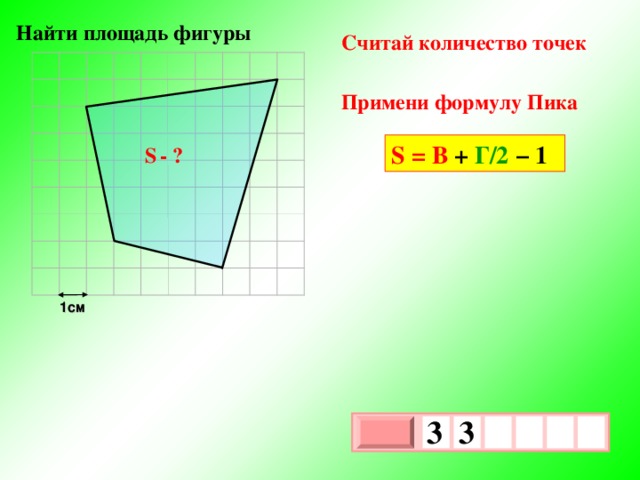
Найти площадь фигуры
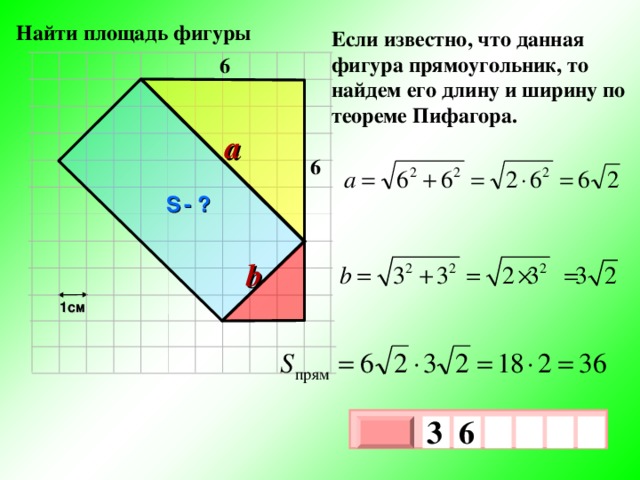
Если известно, что данная фигура прямоугольник, то найдем его длину и ширину по теореме Пифагора.
6
a
6
S — ?
b
1см
3
6
х
3
х
1
0
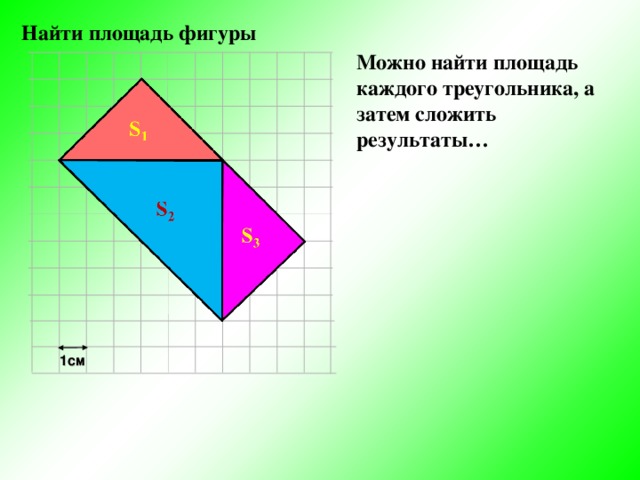
Найти площадь фигуры
Можно найти площадь каждого треугольника, а затем сложить результаты…
1см
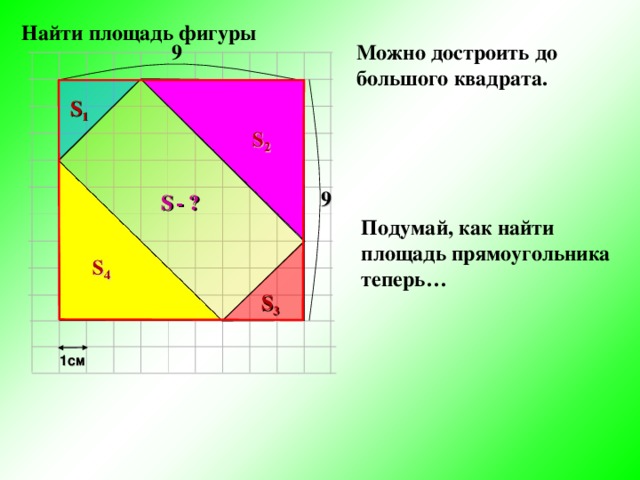
Найти площадь фигуры
9
Можно достроить до большого квадрата.
S 1
9
S — ?
Подумай, как найти площадь прямоугольника теперь…
S 3
1см
Найти площадь фигуры
Считай количество точек
Примени формулу Пика
S = В + Г/2 − 1
S — ?
1см
3
6
х
3
х
1
0
Чтобы уверенно решать задачи по геометрии — даже такие простые — необходимо выучить основные понятия и формулы.
Это формулы площадей фигур — треугольника (5 формул), параллелограмма, ромба, прямоугольника, произвольного четырехугольника, а также круга. Формулы для длины окружности, длины дуги и площади сектора. Для средней линии треугольника и средней линии трапеции.
Надо знать, что такое центральный и вписанный угол. Знать основные тригонометрические соотношения. В общем, учите основы планиметрии.
Больше полезных формул — в нашем ЕГЭ-Справочнике.
Смотри также материал: Как быстро выучить формулы
В этой статье — основные типы заданий №1 Базового ЕГЭ по математике. Задачи взяты из Банка заданий ФИПИ.
Вычисление длин отрезков, величин углов и площадей фигур по формулам
1. На клетчатой бумаге с размером клетки изображена трапеция. Найдите длину средней линии этой трапеции.
Средняя линия трапеции равна полусумме её оснований:
Ответ: 3.
2. Найдите величину угла ABC. Ответ дайте в градусах.
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Соединим точки А и С с центром окружности и проведем диаметры через точки А и С. Видим, что величина центрального угла АОС равна
Тогда
Ответ: 45.
3. Найдите синус угла AOB. В ответе укажите значение синуса, умноженное на
Решение:
Проведем из точки В перпендикуляр к прямой ОА. Из прямоугольного треугольника ОВС по теореме Пифагора:
Осталось умножить найденное значение синуса на
Ответ: 1.
4. Найдите площадь ромба, изображенного на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Самый простой способ — воспользоваться формулой площади ромба, выраженной через его диагонали:
, где
и
— диагонали.
Получим:
Ответ: 12.
5. Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки Ответ дайте в квадратных сантиметрах.
Площадь трапеции равна произведению полусуммы оснований на высоту:
Основания нашей трапеции равны 4 и 8, а высота равна боковой стороне (поскольку трапеция прямоугольная), то есть 3 см. Площадь трапеции
Ответ: 18.
Нахождение площадей многоугольников сложной формы
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ и на авторских задачах.
6. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны
и
. Тогда площадь четырёхугольника равна сумме площадей двух треугольников:
.
Ответ: .
7. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем:
.
Ответ: .
Многие репетиторы рекомендуют в таких задачах пользоваться формулой Пика. В ней нет необходимости, однако эта формула довольно интересна.
Согласно формуле Пика, площадь многоугольника равна В+Г/2-1
где В — количество узлов внутри многоугольника, а Г — количество узлов на границе многоугольника.
Узлами здесь названы точки, в которых пересекаются линии нашей клетчатой бумаги.
Посмотрим, как решается задача 7 с помощью формулы Пика:
Синим на рисунке отмечены узлы внутри треугольника. Зеленым — узлы на границе.
Аккуратно посчитав те и другие, получим, что В = 9, Г = 5, и площадь фигуры равна S = 9 + 5/2 — 1 = 10,5.
Выбирайте — какой способ вам больше нравится.
8. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки
Такой четырехугольник получится, если от квадрата размером отрезать 2 прямоугольника и 4 треугольника. Найдите их на рисунке.
Площадь каждого из больших треугольников равна
Площадь каждого из маленьких треугольников равна
Тогда площадь четырехугольника
9. Авторская задача. Найдите площадь закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
Решение:
На рисунке изображен ромб с вырезанным из него квадратом.
Площадь ромба равна половине произведения его диагоналей.
Площадь вырезанного квадрата равна 4.
Площадь фигуры равна 36 — 4 = 32.
Ответ: 32.
Площадь круга, длина окружности, площадь части круга
Длина дуги во столько раз меньше длины окружности, во сколько раз ее градусная мера меньше, чем полный круг, то есть 360 градусов.
Площадь сектора во столько раз меньше площади всего круга, во сколько раз его градусная мера меньше, чем полный круг, то есть 360 градусов.
10. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна
.
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как
. Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна
(так как
), а длина дуги данного сектора равна
, следовательно, длина дуги в
раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в
раз меньше, чем полный круг (то есть
градусов). Значит, и площадь сектора будет в
раз меньше, чем площадь всего круга.
Ответ: .
11. На клетчатой бумаге нарисован круг площадью 2,8. Найдите площадь закрашенного сектора.
На рисунке изображен сектор, то есть часть круга. Но какая же это часть? Это четверть круга и еще круга, то есть
круга.
Значит, нам надо умножить площадь круга на . Получим:
Ответ: 1,05.
12. На клетчатой бумаге изображены два круга. Площадь внутреннего круга равна 9. Найдите площадь закрашенной фигуры.
Площадь фигуры равна разности площадей двух кругов, один из которых расположен внутри другого. По условию, площадь внутреннего круга равна 9. Радиус внешнего круга относится к радиусу внутреннего как 4 к 3. Площадь круга равна , то есть пропорциональна квадрату радиуса. Значит, площадь внешнего круга в
раза больше площади внутреннего и равна 16. Тогда площадь фигуры равна 16 — 9 = 7.
Ответ: 7.
Задачи на координатной плоскости
13. Найдите площадь четырехугольника, вершины которого имеют координаты (4;2), (8;4), (6;8), (2;6).
Заметим, что этот четырехугольник — квадрат. Сторона квадрата a является гипотенузой прямоугольного треугольника с катетами, равными 2 и 4. Тогда
Ответ: 20
14. Найдите площадь четырехугольника, вершины которого имеют координаты
На рисунке изображен параллелограмм (четырехугольник, имеющий две пары параллельных сторон). Площадь параллелограмма равна произведению основания на высоту. Основание равно 2, высота 8, площадь равна 16.
Ответ: 16.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Геометрия. Применение формул. Задача 1 Базового ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки (1смtimes 1см). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1 см× 1 см) (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1смtimes 1см). Ответ дайте в квадратных сантиметрах.
На клетчатой бумаге с размером клетки 1 см ×1 см изображён треугольник. Найдите его площадь. Ответ дайте в (см^2).
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки (1смtimes 1см). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см ×1 см. Ответ дайте в квадратных сантиметрах.

На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Найдите площадь параллелограмма ABCD, считая стороны квадратных клеток равными 1.
На клетчатой бумаге с размером клетки 1×1 изображена трапеция. Найдите её площадь.
Найдите площадь трапеции, изображенной на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.