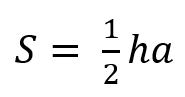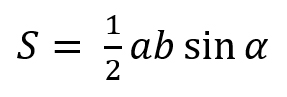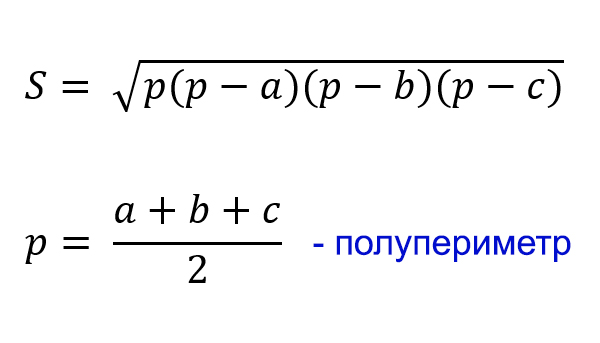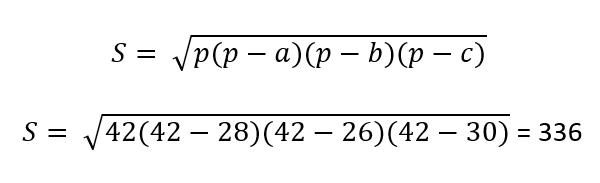Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
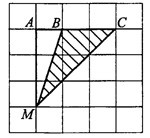
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1см×1см. Ответ дайте в квадратных сантиметрах.
Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см х 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Яндекс: Тренировочная работа ЕГЭ по математике. Вариант 1.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Пробный ЕГЭ по математике, Санкт-Петербург, 19.03.2019. Вариант 2
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402
Найдите площадь треугольника, изображённого на клетчатой бумаге с размером клетки 1 см × 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см 1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1 см
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
Источник: Демонстрационная версия ЕГЭ—2018 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень., Демонстрационная версия ЕГЭ—2017 по математике. Профильный уровень.
Всего: 240 1–20 | 21–40 | 41–60 | 61–80 …
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Задачи на нахождение площади и периметра треугольника
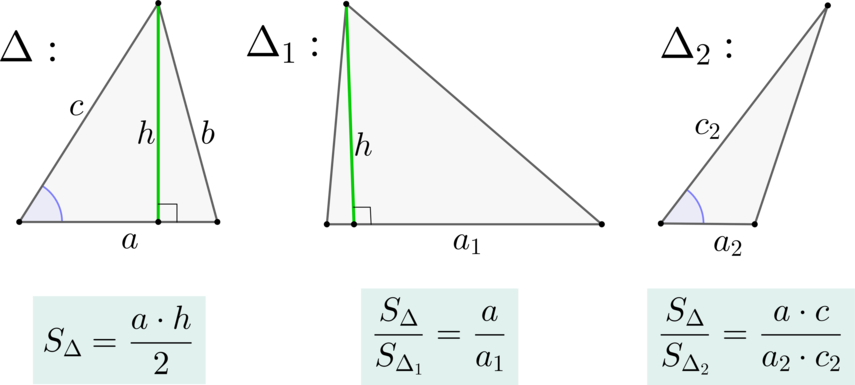
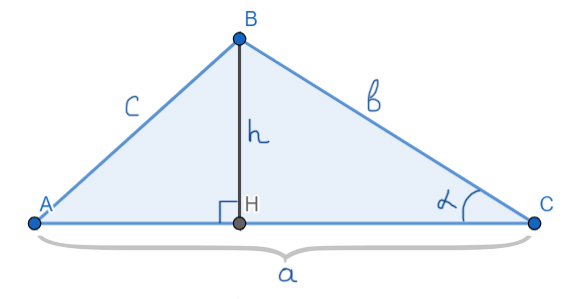
(blacktriangleright) Площадь треугольника равна полупроизведению основания (a) и высоты (h), проведенной к этому основанию.
(blacktriangleright) Формула Герона для площади треугольника:
(large{S_{triangle}=sqrt{p(p-a)(p-b)(p-c)}}), где (p) – полупериметр.
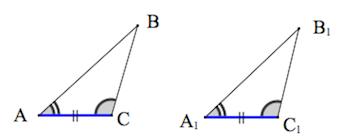
(blacktriangleright) Если треугольники имеют равные высоты ((triangle) и (triangle_{1})), то их площади относятся как основания, к которым эти высоты проведены.
Как следствие: медиана треугольника делит его на два равновеликих (равных по площади) треугольника.
(blacktriangleright) Если треугольники имеют по равному углу ((triangle) и (triangle_{2})), то их площади относятся как произведения сторон, образующих этот угол.
Задание
1
#263
Уровень задания: Равен ЕГЭ
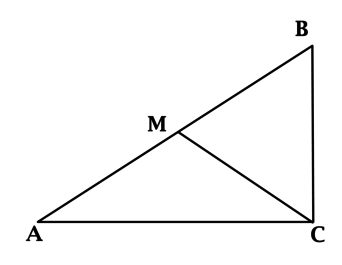
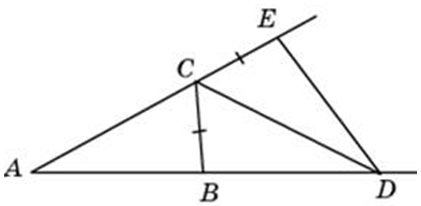
В треугольнике (ABC): (angle C = 90^{circ}), (CM) – медиана, (AC = 4), (CM = 2,5). Найдите периметр треугольника (ABC).
В прямоугольном треугольнике медиана, проведённая к гипотенузе, равна половине гипотенузы, тогда (AB = 2,5 cdot 2 = 5). По теореме Пифагора: (AB^2 = AC^2 + CB^2), откуда находим (CB = 3). Периметр треугольника (ABC) равен (3 + 4 + 5 = 12).
Ответ: 12
Задание
2
#264
Уровень задания: Равен ЕГЭ
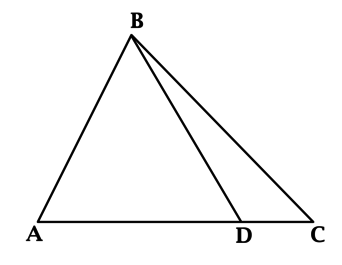
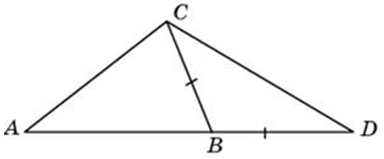
Точка (D) лежит на стороне (AC) треугольника (ABC). Периметр треугольника (ABD) равен (10), периметр треугольника (BDC) равен (7), (BD = 3). Найдите периметр треугольника (ABC).
Периметр треугольника (ABC) равен (AB + AC + BC).
Периметр треугольника (BDC) равен (BD + DC + BC = 7), а (BD = 3), тогда (DC + BC = 4),
периметр треугольника (ABD) равен (AB + BD + AD = 10), тогда (AB + AD = 7).
(AB + AC + BC = AB + AD + DC + BC = 4 + 7 = 11).
Ответ: 11
Задание
3
#265
Уровень задания: Равен ЕГЭ
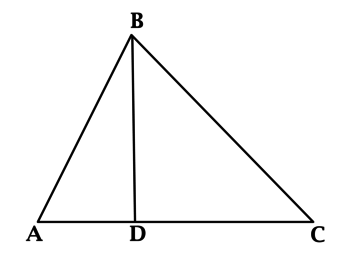
В треугольнике (ABC): (BD) – высота, (AD = 1), (DC = 3), (angle DBC = 45^{circ}). Найдите площадь треугольника (ABC).
(angle BCD = 90^{circ} — angle DBC = 45^{circ} = angle DBC), тогда (BD = DC = 3). Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию, тогда площадь треугольника (ABC) равна (0,5 cdot (3 + 1) cdot 3 = 6).
Ответ: 6
Задание
4
#266
Уровень задания: Равен ЕГЭ
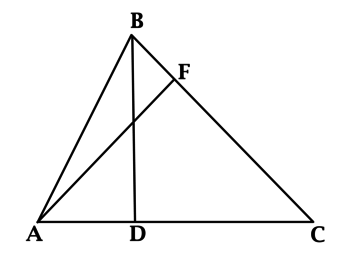
В треугольнике (ABC): (AF) и (BD) – высоты, (AF = 4), (BD = 3), (AC = 6). Найдите (BC).
Площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию. Так как площадь треугольника не зависит от выбора основания, то (0,5 cdot AC cdot BD = 0,5 cdot BC cdot AF), откуда (9 = 0,5 cdot BC cdot 4), значит, (BC = 4,5).
Ответ: 4,5
Задание
5
#2644
Уровень задания: Равен ЕГЭ
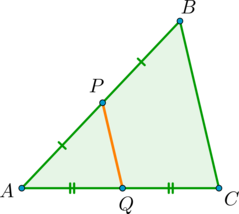
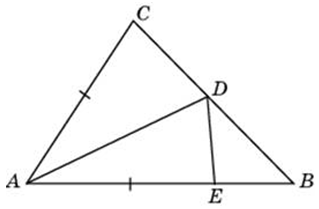
Точки (P) и (Q) – середины сторон (AB) и (AC) треугольника (ABC) соответственно. Найдите периметр треугольника (ABC), если периметр треугольника (APQ) равен (21).
(Задача от подписчиков.)
Т.к. (PQ) – средняя линия (triangle ABC), то (2PQ=BC). Периметр (triangle ABC): [P_{ABC}=AB+AC+BC=2AP+2AQ+2PQ=2(AP+AQ+PQ)=2cdot P_{APQ}=2cdot 21=42.]
Ответ: 42
Задание
6
#1768
Уровень задания: Равен ЕГЭ
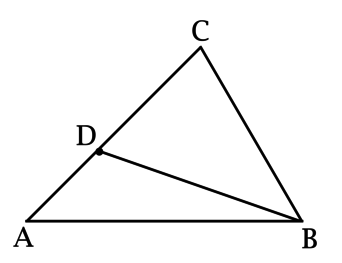
В треугольнике (ABC): (BD) – медиана. Площадь треугольника (ABD) равна (1). Найдите площадь треугольника (ABC).
Так как медиана делит треугольник на два равновеликих (то есть, с равными площадями), то площадь треугольника (BDC) равна площади треугольника (ABD) и равна (1). Тогда площадь треугольника (ABC), равная сумме площадей треугольников (ABD) и (BDC), равна 2.
Покажем подробнее тот факт, что медиана делит треугольник на два равновеликих треугольника:
площадь треугольника равна половине произведения основания на высоту, проведённую к этому основанию, тогда площадь треугольника (ABD) равна (0,5 cdot AD cdot h), где (h) – высота, проведённая из (B) к стороне (AC). Площадь треугольника (BDC) равна (0,5 cdot
CD cdot h), но (CD = AD), тогда (0,5 cdot AD cdot h = 0,5 cdot
CD cdot h) и, значит, площади треугольников (ABD) и (BDC) равны.
Ответ: 2
Задание
7
#1769
Уровень задания: Равен ЕГЭ
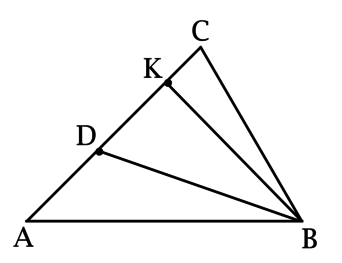
В треугольнике (ABC): точка (D) лежит на (AC), причём (dfrac{AD}{DC} = dfrac{2}{3}). Площадь треугольника (ABD) равна (7,5). Найдите площадь треугольника (BCD).
Построим высоту (BK)
Площадь треугольника (ABD) может быть найдена по формуле: (S_{ABD} = 0,5cdot ADcdot BK).
Аналогично (S_{BCD} = 0,5cdot CDcdot BK), откуда можно сделать вывод:
(dfrac{S_{BCD}}{S_{ABD}} = dfrac{0,5cdot CDcdot BK}{0,5cdot ADcdot BK} = dfrac{CD}{AD} = dfrac{3}{2}), тогда (S_{BCD} = dfrac{3}{2}cdot S_{ABD} = dfrac{3}{2}cdot 7,5 = 11,25).
Ответ: 11,25
Задачи на нахождение площади и периметра равностороннего и равнобедренного треугольника каждый год включаются в программу ЕГЭ по математике. Понимать принцип их решения должны старшеклассники, которые планируют сдавать базовый и профильный уровень аттестационного испытания. Научившись правильно решать задачи на нахождение периметра треугольника в ЕГЭ, школьники смогут оперативно выполнять задания в несколько действий и рассчитывать на получение достаточно высоких баллов по результатам сдачи единого госэкзамена.
Подготовка к аттестационному испытанию вместе со «Школково» — залог вашего успеха
Зачастую во время занятий накануне сдачи единого государственного экзамена перед учащимися встает проблема поиска подходящего источника. Школьного учебника иногда просто не оказывается под рукой в нужный момент. А подобрать все необходимые формулы, к примеру, для вычисления площади прямоугольного треугольника оказывается вовсе не так легко даже в Интернете.
Чтобы успешно пройти выпускное аттестационное испытание, рекомендуем вам заниматься вместе с образовательным порталом «Школково». Наш ресурс предлагает учащимся и преподавателям выстроить процесс подготовки к единому госэкзамену по-новому. Занимаясь вместе с нами, старшеклассники смогут определить те разделы, которые вызывают у них наибольшие трудности, и улучшить собственные знания.
На сайте «Школково» собран весь базовый материал по теме «Вычисление длин и площадей треугольника», который позволит качественно подготовиться к единому государственному экзамену. Данная информация систематизирована и изложена нашими специалистами с учетом их богатого опыта максимально просто и понятно.
Чтобы задачи ЕГЭ на вычисление площади правильного треугольника по трем сторонам не вызывали особых затруднений, мы предлагаем также попрактиковаться в выполнении соответствующих упражнений. Множество подобных заданий представлено в разделе «Каталог». В каждом из них старшеклассники смогут увидеть подробный алгоритм решения и правильный ответ. Базу упражнений в соответствующем разделе мы регулярно обновляем и дополняем.
Выполнять задания на нахождение высоты треугольника или его площади учащиеся из МО и других регионов нашей страны могут в онлайн-режиме. В случае необходимости выполненное упражнение можно сохранить в разделе «Избранное». В дальнейшем задачу, к примеру, на вычисление периметра треугольника можно будет оперативно найти, чтобы обсудить принцип ее решения со школьным преподавателем или репетитором.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Привет! Это первая статья посвящённая ЕГЭ по математике профильного уровня.
В ней речь пойдёт о задачах на площадь треугольника.
Вспомним основные формулы для площади треугольника.
Формулы для площади треугольника
Основная формула:
Площадь треугольника равна половине произведения основания на высоту.
Запасная формула:
Площадь треугольника равна половине произведения двух его сторон на синус угла между ними.
Формула Герона:
Решение задач
Приступим к тренировочным задачам задания №1 из ЕГЭ по математике профильного уровня на площадь треугольника.
Задача (Прямоугольный треугольник)
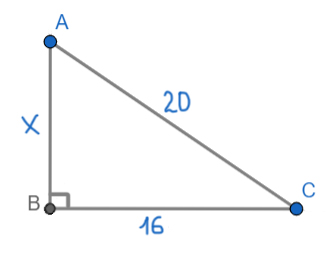
Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 16 и 20.
Решение:
Здесь можно воспользоваться основной формулой для нахождения площади прямоугольного треугольника. Но важно знать, что любой катет — это и есть высота прямоугольного треугольника.
Таким образом, высота будет, к примеру, сторона AB. Тогда основанием будет сторона ВС.
Найдём сторону АВ по теореме Пифагора.
x2 + 162 = 202
x2 = 400 — 256 = 144
x = 12
Тогда площадь будет равна:
S = 0,5 * 12 * 16 = 6 * 16 = 96
Ответ: 96
Задача (Прямоугольный треугольник, закрепление)
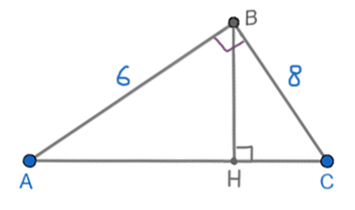
Катеты прямоугольного треугольника равны 6 и 8. Найдите высоту, проведённую к гипотенузе.
Решение:
Найдём гипотенузу по теореме Пифагора.
AC2 = AB2 + BC2
AC2 = 62 + 82 = 100
AC = 10
Мы в прошлой задаче выяснили, что площадь прямоугольного треугольника можно найти, как половину произведения его катетов. А с другой стороны, исходя из основной формулы, площадь равна половине произведения высоты ВН и основания (гипотенузы AC).
S = 0,5*AB*BC = 0,5*BH*AC
BH = AB*BC / AC = 6*8 / 10 = 4,8
Ответ: 4,8
Задача (Три треугольника, одна высота)
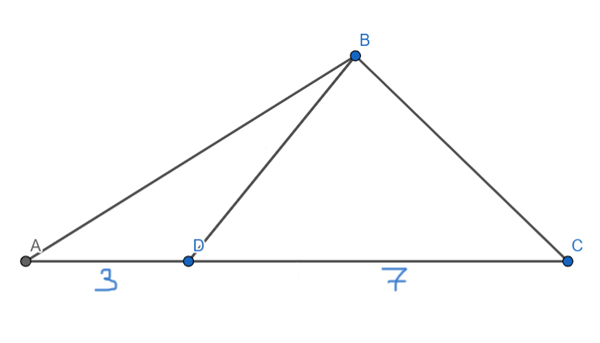
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 100. Найдите площадь треугольника BCD.
Решение:
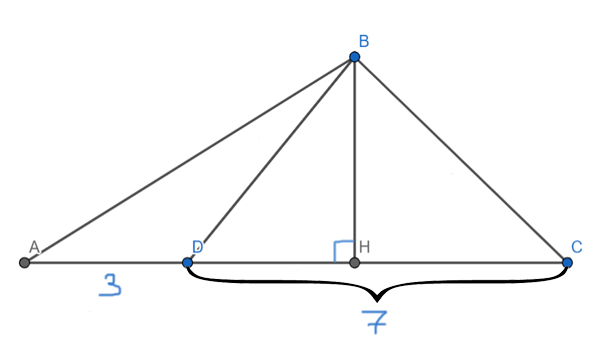
Проведём в треугольнике ABC высоту BH. Оказывается, что ВН является высотой и для треугольника ABD, и для треугольника DBC, и для треугольника ABC.
Применим основную формулу для треугольника ABC и найдём высоту BH.
SABC = 0,5 * AC *BH
SABC = 0,5 * 10 * BH = 100
BH = 100 / (0,5*10) = 20
Теперь применим основную формулу, чтобы найти площадь треугольника BCD.
SDBC = 0,5 * DC * BH
SDBC = 0,5 * 7 * 20 = 70
Ответ: 70
Задача (Запасная формула)
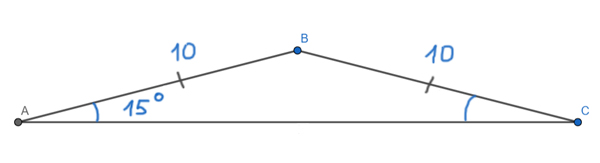
В равнобедренном треугольнике ABC (AB = BC) угол при основании равен 15°. Боковая сторона равна 10. Найдите площадь треугольника ABC.
Решение:
Здесь удобно использовать запасную формулу. Мы знаем две боковые стороны треугольника. Остаётся найти синус угла между ними.
Мы знаем, что углы при основании равны в равнобедренном треугольнике. Поэтому
∠ABC + ∠ВАС + ∠BCA = 180°
∠ABC = 180° — ∠ВАС — ∠BCA
∠ABC = 180° — 15° — 15° = 150°
Синус угла 150° известен. Он равен sin(150°) = sin(30°) = 0,5. Тогда
S = 0,5 * AB*BC * sin(∠ABC)
S = 0,5 * 10*10 * 0,5 = 25
Ответ: 25
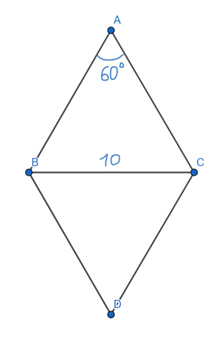
Задача (Треугольники в ромбе)
Найдите площадь ромба, если один из его углов равен 60°, а меньшая диагональ равна 10. В ответе запишите число, делённое на √3.
Решение:
Меньшая диагональ будет находится напротив угла 60°, т.к. второй угол у ромба будет 120°, и напротив этого угла будет находится большая диагональ.
Рассмотрим треугольник ВАС. Мы знаем, что у ромба все стороны равны, поэтому треугольник ВАС равносторонний. Ведь, ВА = АС ⇒ ∠ABC = ∠ACB. Тогда
∠ABC + ∠ACB + ∠BAC = 180°
x = ∠ABC = ∠ACB
x + x + 60° = 180°
2x = 120°
x = 60°
Значит, треугольник ВАС равносторонний. Следовательно, BA = AC = CB = 10.
Чтобы найти площадь ромба, можно разбить его на два одинаковых треугольника: BAC и BDC. Эти два треугольника равны по трём сторонам (BA = AC = CD = DB, BC — общая).
Площадь треугольника BAC легко найти по запасной формуле, ведь две стороны мы знаем, и синус угла между ними тоже известен.
SBAC = 0,5 * BA * AC * sin(60°)
SBAC = 0,5 * 10 * 10 * (√3/2)
SBAC = 25 * √3
Площадь ромба будет равна
SBACD = 2 * SBAC = 2 * 25 * √3 = 50 * √3
В ответе нужно указать число, делённое на √3.
Ответ: 50
Задача (Решаем задачу двумя способами)
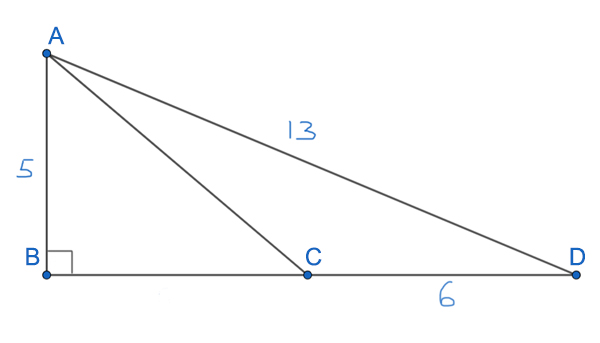
На рисунке AB ⊥ BD, AB = 5, AD = 13 и CD = 6. Найдите площадь треугольника CAD.
Решение:
Первый способ (основная формула)
Нам известна высота треугольника CAD, AB=5. Нам известно основание, на которое она опущена, это CD=6. Применим основную формулу для площади треугольника.
SCAD = ½ * AB * CD
SCAD = ½ * 5 * 6 = 15
Второй способ (запасная формула)
В прямоугольном треугольнике ABD найдём синус ∠BDA.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
sin(∠BDA) = AB/AD = 5/13
Теперь воспользуемся запасной формулой для треугольника CAD.
SCAD = ½ * CD * DA * sin(∠BDA)
SCAD = ½ * 6 * 13 * (5/13) = 15
Ответ: 15
Задача (Формула Герона)
Найдите площадь треугольника, стороны которого равны 28, 26, 30.
Решение:
Решим по формуле Герона.
Найдём полупериметр.
p=(28+26+30)/2 = 42
Тогда
Ответ: 336
На этом всё! Сегодня мы повторили основные формулы для нахождения площади треугольника и порешали задачи на эту темы. Всем удачи!
Все формулы по геометрии. Площади фигур
Чтобы решить задачи по геометрии, надо знать формулы — такие, как площадь треугольника или площадь параллелограмма — а также простые приёмы, о которых мы расскажем.
Для начала выучим формулы площадей фигур. Мы специально собрали их в удобную таблицу. Распечатайте, выучите и применяйте!
Конечно, не все формулы по геометрии есть в нашей таблице. Например, для решения задач по геометрии и стереометрии во второй части профильного ЕГЭ по математике применяются и другие формулы площади треугольника. О них мы обязательно расскажем.
Ты нашел то, что искал? Поделись с друзьями!
А что делать, если надо найти не площадь трапеции или треугольника, а площадь какой-либо сложной фигуры? Есть универсальные способы! Покажем их на примерах из банка заданий ФИПИ.
1. Как найти площадь нестандартной фигуры? Например, произвольного четырёхугольника? Простой приём — разобьём эту фигуру на такие, о которых мы всё знаем, и найдем её площадь — как сумму площадей этих фигур.
Разделим этот четырёхугольник горизонтальной линией на два треугольника с общим основанием, равным . Высоты этих треугольников равны и . Тогда площадь четырёхугольника равна сумме площадей двух треугольников: .
2. В некоторых случаях площадь фигуры можно представить как разность каких-либо площадей.
Не так-то просто посчитать, чему равны основание и высота в этом треугольнике! Зато мы можем сказать, что его площадь равна разности площадей квадрата со стороной и трёх прямоугольных треугольников. Видите их на рисунке? Получаем: .
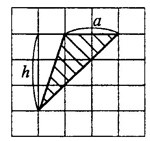
3. Иногда в задании надо найти площадь не всей фигуры, а её части. Обычно речь здесь идет о площади сектора — части круга.Найдите площадь сектора круга радиуса , длина дуги которого равна .
На этом рисунке мы видим часть круга. Площадь всего круга равна , так как . Остается узнать, какая часть круга изображена. Поскольку длина всей окружности равна (так как ), а длина дуги данного сектора равна , следовательно, длина дуги в раз меньше, чем длина всей окружности. Угол, на который опирается эта дуга, также в раз меньше, чем полный круг (то есть градусов). Значит, и площадь сектора будет в раз меньше, чем площадь всего круга.
Читайте также о задачах на тему «Координаты и векторы». Для их решения вспомните, что такое абсцисса точки (это ее координата по ) и что такое ордината (координата по ). Пригодятся также такие понятия, как координаты вектора и длина вектора (она находится по теореме Пифагора), синус и косинус угла, угловой коэффициент прямой, уравнение прямой, а также сумма, разность и скалярное произведение векторов, угол между векторами.
Как найти площадь треугольника
О чем эта статья:
8 класс, 9 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные понятия
Треугольник — это геометрическая фигура, которая получилась из трех отрезков. Их соединили тремя точками, не лежащими на одной прямой. Отрезки принято называть сторонами, а точки — вершинами.
Площадь — это численная характеристика, которая дает нам информацию о размере части плоскости, ограниченной замкнутой геометрической фигурой.
Если значения заданы в разных единицах измерения длины, мы не сможем узнать, какая площадь треугольника получится. Поэтому для правильного решения необходимо перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
- квадратный миллиметр (мм 2 );
- квадратный сантиметр (см 2 );
- квадратный дециметр (дм 2 );
- квадратный метр (м 2 );
- квадратный километр (км 2 );
- гектар (га).
Формула площади треугольника
Для решения задач применяются различные формулы, в зависимости от известных исходных данных. Далее мы рассмотрим способы решения для всех типов треугольников, в том числе частные случаи для равносторонних, равнобедренных и прямоугольных фигур.
Быстро вычислить площадь треугольника поможет наш онлайн-калькулятор. Просто введите известные вам значения и получите ответ в метрах, сантиметрах или миллиметрах.
Научиться быстро щелкать задачки на нахождение площади треугольника помогут курсы по математике от Skysmart!
Общая формула
1. Площадь треугольника через основание и высоту
, где — основание, — высота.
2. Площадь треугольника через две стороны и угол между ними
, где , — стороны, — угол между ними.
3. Площадь треугольника через описанную окружность и стороны
, где , , — стороны, — радиус описанной окружности.
4. Площадь треугольника через вписанную окружность и стороны
, где , , — стороны, — радиус вписанной окружности.
Если учитывать, что — это способ поиска полупериметра, то формулу можно записать следующим образом:
5. Площадь треугольника по стороне и двум прилежащим углам
, где — сторона, и — прилежащие углы.
6. Формула Герона для вычисления площади треугольника
Сначала необходимо подсчитать разность полупериметра и каждой его стороны. Потом найти произведение полученных чисел, умножить результат на полупериметр и найти корень из полученного числа.
, где , , — стороны, — полупериметр, который можно найти по формуле:
Для прямоугольного треугольника
Площадь треугольника с углом 90° по двум сторонам
Площадь треугольника по гипотенузе и острому углу
, где — гипотенуза, — любой из прилегающих острых углов.
Гипотенузой принято называть сторону, которая лежит напротив прямого угла.
Площадь прямоугольного треугольника по катету и прилежащему углу
, где — катет, — прилежащий угол.
Катетом принято называть одну из двух сторон, образующих прямой угол.
Площадь треугольника через гипотенузу и радиус вписанной окружности
, где — гипотенуза, — радиус вписанной окружности.
Площадь треугольника по отрезкам, на которые делит вписанная окружность его гипотенузу
, где , — части гипотенузы.
Площадь прямоугольного треугольника по формуле Герона
, где , — катеты, — полупериметр, который можно найти по формуле:
Для равнобедренного треугольника
Вычисление площади через основание и высоту
, где — основание, — высота, проведенная к основанию.
Поиск площади через боковые стороны и угол между ними
, где — боковая сторона, — угол между боковыми сторонами.
Площадь равностороннего треугольника через радиус описанной окружности
, где — радиус описанной окружности.
Площадь равностороннего треугольника через радиус вписанной окружности
, где — радиус вписанной окружности.
Площадь равностороннего треугольника через сторону
Площадь равностороннего треугольника через высоту
Таблица формул нахождения площади треугольника
У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу, использовать как закладку в тетрадке или учебнике и обращаться к ней по необходимости.
Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
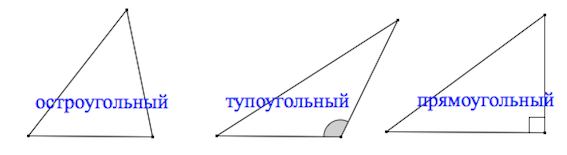
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
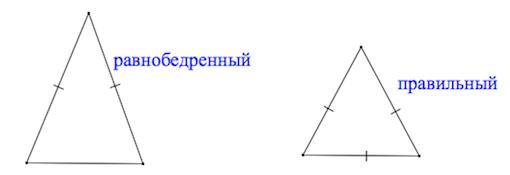
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми , третья сторона называется основанием .
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
3. Сумма углов треугольника равна 180 º .
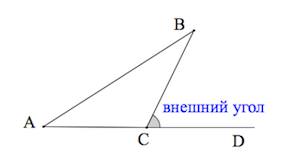
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
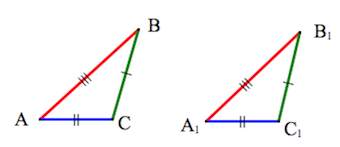
Признаки равенства треугольников
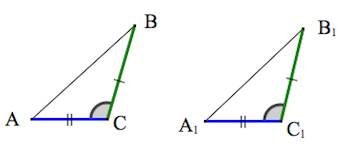
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
2 . Треугольники равны, если у них соответственно равны два угла и прилегающая к ним сторона.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
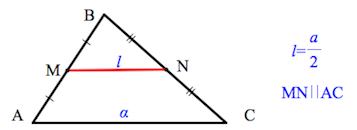
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
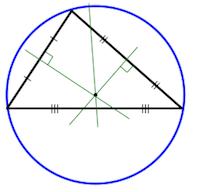
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
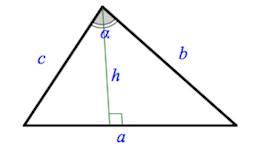
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно
источники:
http://skysmart.ru/articles/mathematic/ploshad-treugolnika
http://egemaximum.ru/treugolnik/
ЕГЭ Профиль №3. Треугольник общего вида
Скачать файл в формате pdf.
ЕГЭ Профиль №3. Треугольник общего вида
| Задача 1. Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30°.
Ответ
ОТВЕТ: 24. |
| Задача 2. Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.
Ответ
ОТВЕТ: 1. |
| Задача 3. У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?
Ответ
ОТВЕТ: 6. |
| Задача 4. В треугольнике ABC угол A равен 40°, внешний угол при вершине B равен 102°. Найдите угол C. Ответ дайте в градусах.
Ответ
ОТВЕТ: 62. |
| Задача 5. Углы треугольника относятся как . Найдите меньший из них.
Ответ
ОТВЕТ: 40. |
| Задача 6. В треугольнике ABC угол A равен 30°, угол В — тупой, CH — высота, угол BCH равен 22°. Найдите угол ACB. Ответ дайте в градусах.
Ответ
ОТВЕТ: 38. |
| Задача 7. В треугольнике ABC AD — биссектриса, угол C равен 50°, угол CAD равен 28°. Найдите угол B. Ответ дайте в градусах.
Ответ
ОТВЕТ: 74. |
| Задача 8. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.
Ответ
ОТВЕТ: 52. |
| Задача 9. В треугольнике ABC угол A равен 72°, а углы B и C — острые. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.
Ответ
ОТВЕТ: 108. |
| Задача 10. Два угла треугольника равны 58° и 72°. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Ответ
ОТВЕТ: 130. |
| Задача 11. В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах. |
| Задача 12. В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения CH и AD, угол BAD равен 26°. Найдите угол AOC. Ответ дайте в градусах. |
| Задача 13. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах. |
| Задача 14. В треугольнике ABC угол A равен 44°, угол C равен 62°. На продолжении стороны AB отложен отрезок BD = BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.
|
| Задача 15. В треугольнике ABC угол B равен 45°, угол C равен 85°, AD — биссектриса, E — такая точка на AB, что AE = AC. Найдите угол BDE. Ответ дайте в градусах.
|
| Задача 16. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах.
|
| Задача 17. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| Задача 18. В треугольнике ABC угол A равен 60°, угол B равен 82°. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах. |
| Задача 19. Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABED. |

Площадь произвольного треугольника равна половине произведения длины его стороны () на высоту (
), проведённую к этой стороне:
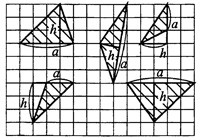
На рисунке 1 приведены чертежи некоторых треугольников, у которых обозначены одна из сторон и высота, проведённая к этой стороне
.
Как правило, удобно брать ту сторону, которая проходит по линиям клетчатой бумаги (или же проходит параллельно осям координат).
Рис. 1.
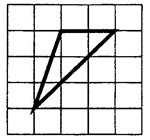
Задача 1. На клетчатой бумаге с клетками размером 1 см х 1 см изображён треугольник (см. рис. 2). Найдите его площадь в квадратных сантиметрах.
Решение.
1-й способ.
Рис. 2.
Площадь произвольного треугольника равна половине произведения длины его стороны () на высоту (
), проведённую к этой стороне. Проведём высоту
. Треугольник тупоугольный, поэтому высота проводится вне треугольника.
Рис. 3.
На рисунке 3 сторона = 2 см, высота
= 3 см.
см².
Ответ: 3.
Заметим, что так как клетки имеют размер 1 см х 1 см, то площадь в квадратных сантиметрах получится, если мы будем по рисунку считать размер отрезков в клетках. Поэтому единицы длины в этих задачах можно и не писать.
2-й способ.
Достроим треугольник до прямоугольного треугольника
(см. рис. 4).
Рис. 4.
Тогда искомую площадь треугольника можно найти как разность площадей двух прямоугольных треугольников
и
.
Катеты первого из них равны 3 см и 3 см, катеты второго — Зсм и 1 см.
Площадь прямоугольного треугольника равна половине произведения его катетов, следовательно,
Ответ: 3.
Главная > ЕГЭ по математике > Площадь треугольника — задание 3
Площадь треугольника — задание 3 — видеоурок
На этом видео уроке для подготовке к экзамену в 11 классе по математике — ЕГЭ. Объясняется как находить площадь треугольника и площадь прямоугольного треугольника. Решаются задачи из КИМ на нахождение площади треугольников а также площади различных фигур разбив их на треугольники.