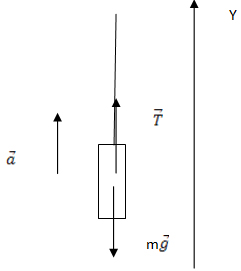
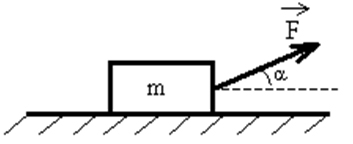
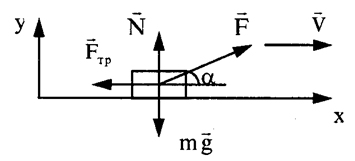
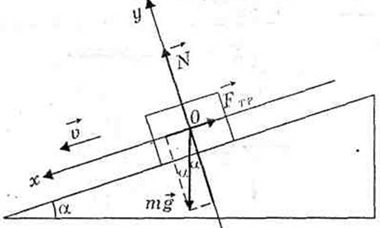
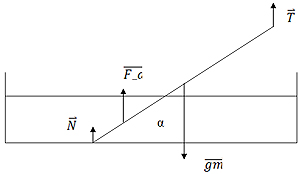
Брусок массой 100 г перемещают с постоянной скоростью вертикально вниз вдоль шероховатой вертикальной стены, действуя на него силой
Эта сила равна по модулю 5 Н и направлена под углом α = 30° к горизонтали так, как показано на рисунке. Чему равен модуль силы трения, действующей на брусок?
Спрятать решение
Решение.
По условию ускорению бруска равно нулю. При движении бруска вниз возникает сила трения, направленная вертикально вверх. Тогда второй закон Ньютона для бруска в проекции на вертикальную ось приобретает вид:
Отсюда модуль силы трения равен
Ответ: 3,5.
Каталог заданий
Версия для печати и копирования в MS Word
1
Тип 2 № 11261
Брусок массой 100 г перемещают с постоянной скоростью вертикально вниз вдоль шероховатой вертикальной стены, действуя на него силой
Эта сила равна по модулю 5 Н и направлена под углом α = 30° к горизонтали так, как показано на рисунке. Чему равен модуль силы трения, действующей на брусок?
Аналоги к заданию № 11261: 11295 Все
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО
Решение
·
·
Сообщить об ошибке · Помощь
Задача 1
К одному концу лёгкой пружины жёсткостью k = 100 Н/м прикреплён массивный груз, лежащий на горизонтальной плоскости, другой конец пружины закреплён неподвижно (см. рисунок). Коэффициент трения груза по плоскости Груз смещают по горизонтали, растягивая пружину, затем отпускают с начальной скоростью, равной нулю. Груз движется в одном направлении и затем останавливается в положении, в котором пружина уже сжата. Максимальное растяжение пружины, при котором груз движется таким образом, равно d = 15 см. Найдите массу m груза.
Решение
1. Начальная энергия системы равна потенциальной энергии растянутой пружины: После того, как пружину отпустили, она остановится в положении, при котором она сжата на величину
Тогда конечная энергия системы равна потенциальной энергии сжатой пружины:
Изменение полной энергии системы равно работе силы трения
где — модуль силы реакции опоры.
2. В момент, когда груз остановился, по второму закону Ньютона равнодействующая всех сил стала равна нулю. Пружина сжата, поэтому сила упругости пружины направлена вправо. Её уравновешивает сила трения покоя, которая направлена против возможного движения, причём эта сила максимальна, т. к. по условию начальное положение пружины соответствует максимальному растяжению пружины, при котором груз движется таким образом.
Запишем закон Ньютона для горизонтальной и вертикальной осей:
3. Подставим полученное выражение для в равенство из пункта 1:
После подстановки получим
Ответ:
Задача 2
Из пружинного пистолета выстрелили вертикально вниз в мишень, находящуюся на расстоянии 2 м от него. Совершив работу 0,12 Дж, пуля застряла в мишени. Какова масса пули, если пружина была сжата перед выстрелом на 2 см, а ее жесткость 100 Н/м?
Решение
Согласно закону сохранения механической энергии, имеем два равенства:
где и
— скорости летящей пули соответственно на высоте и непосредственно перед мишенью. Вся энергия подлетевшей к мишени пули потрачена на механическую работу, так что
Решая полученную систему уравнений, находим массу пули:
Задача 3
Небольшая шайба после толчка приобретает скорость v = 2 м/с и скользит по внутренней поверхности гладкого закрепленного кольца радиусом R = 0,14 м. На какой высоте h шайба отрывается от кольца и начинает свободно падать?
Решение
Согласно закону сохранения энергии:
, (1)
где — скорость шайбы в момент отрыва от кольца на высоте
.
В точке отрыва сила нормальной реакции опоры равна 0; . Центростремительное ускорение шайбы
найдём из второго закона Ньютона (см. рис.):
. (2)
. (3)
Объединяя (1), (2) и (3), получим:
м.
Ответ: 0,18.
Задача 4
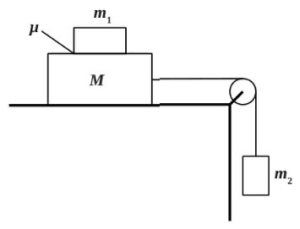
Грузы массами M = 1 кг и m связаны легкой нерастяжимой нитью, переброшенной через блок, по которому нить может скользить без трения (см. рис.). Груз массой М находится на шероховатой наклонной плоскости (угол наклона плоскости к горизонту а = 30°, коэффициент трения = 0,3). Чему равно минимальное значение массы m, при котором система грузов еще не выходит из первоначального состояния покоя?
Решение
Если масса m достаточно мала, но грузы ещё покоятся, то сила трения покоя, действующая на груз массой М, направлена вверх вдоль наклонной плоскости. Запишем второй закон Ньютона для каждого из покоящихся тел в проекциях на оси введенной системы координат. На первое тело действуют сила тяжести, сила нормальной реакции опоры, сила натяжения нити и сила трения:
(ось направлена вниз вдоль наклонной плоскости);
(ось направлена вверх перпендикулярно наклонной плоскости).
На второе тело действуют сила тяжести и сила натяжения нити:
(ось направлена вертикально вниз).
Учитывая, что (нить легкая, между блоком и нитью трения нет), то
(сила трения покоя). Получим:
кг.
Ответ: 0,24.
Задача 5
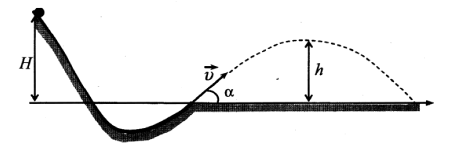
Тело, брошено с поверхности земли со скоростью v под углом a к горизонту. Сопротивление воздуха пренебрежимо мало.
Установите соответствие между физическими величинами, характеризующими движение тела, и формулами, по которым их можно определить.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры.

Решение
Рассмотрим динамику движения тела, брошенного под углом к горизонту с начальной скоростью
. В задаче нас интересует вертикальное движение тела.
Из рисунка видно, что проекция начальной скорости на ось Oy равна
.
Проекция ускорения равна
,
где м/с2 – ускорение свободного падения. Таким образом, скорость тела вдоль оси Oy будет меняться по закону
.
Можно заметить, что в точке максимального подъема скорость , получаем уравнение
То есть для буквы «А» соответствует формула под номером 4.
Для определения максимальной высоты , запишем формулу движения тела, подброшенного вертикально вверх:
и, учитывая, что ,
, а время для достижения максимальной высоты составляет
, получаем выражение:
.
То есть для буквы «Б» соответствует формула под номером 1.
Ответ: А4, Б1.
Задача 6
Воздушный шар объемом V = 2500 м3 с массой оболочки = 400 кг имеет внизу отверстие, через которое воздух в шаре нагревается горелкой. До какой минимальной температуры t1 нужно нагреть воздух в шаре, чтобы шар взлетел вместе с грузом (корзиной и воздухоплавателем) массой
= 200 кг? Температура окружающего воздуха t = 7 °С, его плотность
= 1,2 кг/м3. Оболочку шара считать нерастяжимой.
Решение
Шар взлетает, когда сила тяжести, действующая на него, равна силе Архимеда
, (1)
где m — масса воздуха в шаре. Из уравнения Менделеева-Клапейрона
,
, (2)
где ,
,
— молярная масса воздуха. Объединяя (1) и (2), получим:
К
соответственно °С.
Ответ: 350.
Задача 7
Брусок массой m1 = 500 г соскальзывает по наклонной плоскости с некоторой высоты h и, двигаясь по горизонтальной поверхности, сталкивается с неподвижным бруском массой m2 = 300 г. Считая столкновение абсолютно неупругим, определите высоту h, если общая кинетическая энергия брусков после столкновения равна 2,5 Дж. Трением при движении пренебречь. Считать, что наклонная плоскость плавно переходит в горизонтальную.
Решение
Кинетическая энергия брусков после столкновения где v — скорость системы после удара, определяемая из закона сохранения импульса на горизонтальном участке: m1v1 = (m1 + m2)v.
Исключая из системы уравнений скорость v, получим:
Кинетическая энергия первого бруска перед столкновением определяется из закона сохранения механической энергии при скольжении по наклонной плоскости: что даёт выражение
Подставляя значения масс и энергии из условия, получим численное значение h = 0,8 м
Ответ: h = 0,8 м.
Задача 8
Небольшой груз, прикрепленный к нити длиной l = 15 см, вращается вокруг вертикальной оси так, что нить отклоняется от вертикали на угол a = 60°. С какой скоростью движется груз?
Решение
На груз действуют сила натяжения нити и сила тяжести
, как указано на рисунке.
В инерциальной системе отсчёта, связанной с Землёй, ускорение тела определяется вторым законом Ньютона:
Здесь — центростремительное ускорение. Решая полученную систему, получим:
м/с.
Ответ: 1,5.
Задача 9
Камень массой m = 4 кг падает под углом a = 30° к вертикали со скоростью 10 м/с в тележку с песком общей массой M = 16 кг, покоящуюся на горизонтальных рельсах. Определите скорость тележки с камнем после падения в нее камня.
Решение
Общая инерция камня, падающего в тележку, равна . Величина инерции, в горизонтальном направлении от падения камня составит
. Тогда из закона сохранения инерции, учитывая, что тележка вначале была неподвижной, а после падения в нее камня увеличила свою массу на массу камня, получаем
,
откуда
и

Ответ: 1.
Задача 10
Два груза одинаковой массы М, связанные нерастяжимой и невесомой нитью, движутся прямолинейно по гладкой горизонтальной поверхности под действием горизонтальной силы F, приложенной к одному из грузов (см. рис.). Минимальная сила F, при которой нить обрывается, равна 12 Н. При какой силе натяжения обрывается нить?
Решение
Сила, под действием которой движутся грузы массой M – это равнодействующая, то есть учитывающая силу трения. Следовательно, из второго закона Ньютона можно записать , где
— ускорение, с которым движутся грузы. Сила натяжения нити T создается последним грузом, который перемещается с тем же ускорением
, но имеет массу M, т.е.
. Выражая ускорение как
, получаем силу натяжения, равную
Н.
Ответ: 6.
Задача 11
Груз, лежащий на столе, связан легкой нерастяжимой нитью, переброшенной через идеальный блок, с грузом массой 0,25 кг. На первый груз действует горизонтальная постоянная сила F, равная 9 Н (см. рис.). Второй груз движется с ускорением 2 м/с2, направленным вверх. Трением между грузом и поверхностью стола пренебречь. Какова масса первого груза?
Решение
На второй груз действует сила тяжести и противоположная сила тяги первого груза
Н (трение здесь не учитывается). Таким образом, для системы из двух грузов массами
и
можем записать
,
где — масса первого груза. Отсюда получаем:
Подставляем числовые значения, находим
кг.
Ответ: 3.
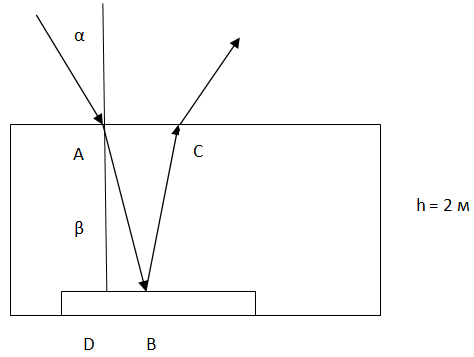
Задача 12
Маленький шарик падает сверху на наклонную плоскость и упруго отражается от неё. Угол наклона плоскости к горизонту равен На какое расстояние по горизонтали перемещается шарик между первым и вторым ударами о плоскость? Скорость шарика непосредственно перед первым ударом направлена вертикально вниз и равна 1 м/с.
Решение
Выберем следующую систему координат: ось направим вдоль плоскости, а ось
— перпендикулярно ей. Тогда кинематические уравнения движения шарика имеют вид:
В момент второго соударения шарика с плоскостью
Решая систему уравнений, получаем:
и
Из рисунка видно, что
Ответ:
Задача 13
На гладкой горизонтальной поверхности стола покоится горка с двумя вершинами, высоты которых h и 5/2*h (см. рисунок). На правой вершине горки находится шайба. От незначительного толчка шайба и горка приходят в движение, причём шайба движется влево, не отрываясь от гладкой поверхности горки, а поступательно движущаяся горка не отрывается от стола. Скорость шайбы на левой вершине горки оказалась равной v. Найдите отношение масс шайбы и горки.
Решение
На систему тел «шайба + горка» действуют внешние силы (тяжести и реакции стола), направленные по вертикали, поэтому проекция импульса системы на горизонтальную ось Ох системы отсчёта, связанной со столом, сохраняется.
В начальный момент , а в момент
. Из закона сохранения импульса
получим:
, где m — масса шайбы, М — масса горки.
Работа сил тяжести определяется изменением потенциальной энергии, а суммарная работа сил реакции равна нулю, так как поверхности гладкие. Следовательно, полная механическая энергия системы тел, равная сумме кинетической и потенциальной, сохраняется. Так как потенциальная энергия горки не изменилась, получаем уравнение
.
Решение системы дает отношение масс
.
Ответ: .
Задача 14
Снаряд, движущийся со скоростью v0 разрывается на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая движется в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆E. Скорость осколка, движущегося вперёд по направлению движения снаряда, равна v1. Найдите массу m осколка.
Решение
Введём обозначение: v2 — модуль скорости летящего назад осколка снаряда. Система уравнений для решения задачи:
Выразим v2 из первого уравнения: — и подставим во второе уравнение. Получим:
. Отсюда следует:

Ответ: 
Задача 15
Снаряд массой 2m разрывается в полёте на две равные части, одна из которых продолжает движение по направлению движения снаряда, а другая — в противоположную сторону. В момент разрыва суммарная кинетическая энергия осколков увеличивается за счёт энергии взрыва на величину ∆Е. Модуль скорости осколка, движущегося по направлению движения снаряда, равен v1, а модуль скорости второго осколка равен v2. Найдите ∆Е.
Решение
Введём обозначение: v0 — модуль скорости снаряда до разрыва. Система уравнений для решения задачи:
Выразим v0 из первого уравнения: и подставим во второе уравнение. Получим:
.
Отсюда следует:
.
Ответ: .
Задача 16
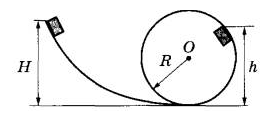
При выполнении трюка «Летающий велосипедист» гонщик движется по гладкому трамплину под действием силы тяжести, начиная движение из состояния покоя с некоторой высоты (см. рисунок). На краю трамплина скорость гонщика направлена под углом α = 60° к горизонту. Пролетев по воздуху, он приземляется на горизонтальный стол, поднявшись в полёте на высоту h над краем трамплина. С какой высоты H начинал движение гонщик?
Решение
Применим закон сохранения энергии и найдём скорость велосипедиста при отрыве от трамплина.
Рассмотрим проекции скорости на горизонтальную и вертикальную оси:
В тот момент, когда велосипедист достигнет наивысшей точки полёта вертикальная проекция его скорости станет равной нулю, при этом в горизонтальном направлении он пролетит половину пути. Найдём время, за которое велосипедист достигнет наивысшей точки.
Координата зависит от времени по закону
Значит, максимальная высота полёта велоспедиста
Откуда
Ответ:
Задача 17
После толчка льдинка закатилась в яму с гладкими стенками, в которой она может двигаться практически без трения. На рисунке приведен график зависимости энергии взаимодействия льдинки с Землей от её координаты в яме.
В некоторый момент времени льдинка находилась в точке А с координатой и двигалась влево, имея кинетическую энергию, равную 2 Дж. Сможет ли льдинка выскользнуть из ямы? Ответ поясните, указав, какие физические закономерности вы использовали для объяснения.
Решение
1) Льдинка сможет выскользнуть из ямы через ее правый край.
2) Трения при движении льдинки нет, поэтому ее механическая энергия сохраняется. Запас кинетической энергии льдинки в точке A позволяет ей подняться до уровня, где ее потенциальная энергия составит 4 Дж.
3) Левый край ямы поднят до большей высоты. Следовательно, этого края льдинка не достигнет и заскользит вправо. Правый же край ямы ниже: на верху этого края потенциальная энергия льдинки меньше 4 Дж. Поэтому льдинка выскользнет из ямы через правый край.
Задача 18
Гладкий клин массой M с углом при основании стоит на горизонтальной плоскости, часть которой под ним и левее — гладкая, а часть — справа от него — шероховатая (см. рис.). На вершине клина, на высоте H над плоскостью находится маленький брусок массой m, коэффициент трения которого о шероховатую часть плоскости равен
Брусок отпускают без начальной скорости, он скатывается по клину и далее скользит по шероховатой плоскости и останавливается на некотором расстоянии L по горизонтали от своего начального положения. Найдите это расстояние L, если в точке перехода с клина на плоскость есть гладкое закругление, так что скорость бруска при переходе с клина на плоскость не уменьшается.
Решение
При соскальзывании бруска с клина выполняются законы сохранения горизонтальной проекции импульса и механической энергии данной системы тел:
где v и V — скорости бруска и клина, соответственно, после соскальзывания бруска с клина. Из этих уравнений следует, что скорость бруска перед его попаданием на шероховатый участок плоскости равна:
До попадания на этот участок брусок сдвинется из начального положения по горизонтали без трения на расстояние равное, очевидно, длине основания клина, а затем пройдёт по шероховатой плоскости расстояние
на котором его кинетическая энергия будет израсходована на работу против силы сухого трения скольжения. По закону Амонтона — Кулона эта сила равна
так как сила N давления бруска на неподвижную горизонтальную плоскость равна mg. Таким образом,
и
Искомое расстояние L в результате равно сумме l1 и l2:
Ответ:
Задача 19
В системе, изображённой на рисунке, трения нет, блоки невесомы, нить невесома и нерастяжима, m1 = 2 кг, m2 = 4 кг, m3 = 1 кг. Найдите модуль и направление ускорения груза массой m3.
Решение
1. Введём на рисунке неподвижную систему координат, у которой ось x горизонтальна и направлена вправо, а ось y направлена вертикально вниз. Обозначим также силы, определяющие ускорения тел вдоль направлений их движения: силу T натяжения нити, которая, как следует из условия задачи, постоянна по модулю вдоль всей нити, и силу тяжести
2. Записывая второй закон Ньютона в проекциях на оси x и y для трёх грузов, имеем:
3. Поскольку нить нерастяжима, из постоянства её длины получаем следующее соотношение для координат грузов:
Отсюда следует связь между ускорениями грузов:
4. Решая полученную систему уравнений, находим модуль искомого ускорения:
вектор направлен вниз.
Ответ: вектор
направлен вниз.
Задача 20
К двум вертикально расположенным пружинам одинаковой длины подвесили однородный стержень длиной L = 30 см. Если к этому стержню подвесить груз массой m = 3 кг на расстоянии d = 5 см от правой пружины, то стержень будет расположен горизонтально, и растяжения обеих пружин будут одинаковы (см. рисунок). Жёсткость левой пружины в 2 раза меньше, чем правой. Чему равна масса стержня М? Сделайте рисунок с указанием используемых в решении сил.
Решение
1. Укажем на рисунке силы действующие на стержень. Приравняем моменты сил, действующих на стержень, относительно центра стержня, т.е. точки А:
Учтем, что стержень расположен горизонтально, т.е. удлинения пружин равны, а также, что жесткость правой пружины в два раза больше левой:
2. Приравняем моменты сил, действующих на стержень, относительно точки Б, которая находится в месте крепления правой пружины:
3. Найдем массу стержня:
Ответ:
Задача 21
Найдите модуль ускорения a груза массой m в системе, изображённой на рисунке. Трения нет, блоки невесомы, нити лёгкие и нерастяжимые, их участки, не лежащие на блоках, вертикальны, масса второго груза M, ускорение свободного падения равно g.
Решение
Введём координатную ось Х, направленную вниз, и отметим на ней координаты грузов М и m: xM и xm (см. рис.). Пронумеруем блоки цифрами 1, 2, 3 и укажем на рисунке силы натяжения нитей и силы тяжести, действующие на грузы. Согласно условию, в силу невесомости нитей и блоков, а также отсутствия сил трения, первая нить, охватывающая блоки 1 и 2, натянута с силой T, а вторая — с силой 2T, так что на груз m действует направленная вверх сила 4T. Если сместить груз М вдоль оси Х вниз на расстояние ΔxM, то в силу нерастяжимости нитей блок 2 сместится, как следует из рисунка, на −ΔxM/2, а блок 3 и груз m — на Δxm = −ΔxM/4. Таким образом, ΔxM + 4Δxm = 0.
Отсюда получаем уравнение кинематической связи: A + 4a = 0, где A и a — проекции ускорений грузов М и m на ось Х. Уравнения движения грузов (второй закон Ньютона) в проекциях на ось Х имеют вид: МA = Мg – T, ma = mg – 4T. Решая полученную систему из трех уравнений, находим, что модуль ускорения груза М равен:
Ответ:
Задача 22
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рисунок). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Решение
1. Изобразим на рисунке силы, действующие на стержень, и систему координат Оху.
Здесь — сила натяжения нити,
— сила тяжести,
и
— вертикальная и горизонтальная составляющие силы, действующей на стержень со стороны шарнира.
2. В положении равновесия равны нулю сумма моментов сил, действующих на стержень, относительно оси, проходящей через точку А перпендикулярно плоскости рисунка, сумма горизонтальных и сумма вертикальных составляющих сил, действующих на стержень:
где
— длина стержня; (1)
(2)
(3)
3. Модуль силы реакции шарнира
Из (1) получим Окончательно
Ответ:
Задача 23
Из двух ровных досок сделан желоб, представляющий собой двугранный угол с раствором Желоб закреплен так, что его ребро горизонтально, а доски симметричны относительно вертикали. В желобе на боковой поверхности лежит цилиндр массой
Коэффициент трения между досками и цилиндром равен
К торцу цилиндра приложена горизонтально направленная сила
Найдите модуль ускорения цилиндра.
Решение
Изобразим вид на желоб со стороны торца цилиндра. На цилиндр в плоскости чертежа действуют направленная вниз сила тяжести
и две равные по модулю силы реакции
досок, направленные перпендикулярно стенкам желоба. Так как цилиндр не движется в вертикальном направлении, то, в соответствии со вторым законом Ньютона, сумма проекций этих трех сил на вертикаль равна нулю:
где
Отсюда В горизонтальном направлении (вдоль желоба) на цилиндр действуют сила
а также, в противоположном направлении, две силы сухого трения
Предположим, что цилиндр будет двигаться по желобу. Тогда по закону Амонтона — Кулона для силы сухого трения скольжения можно записать:
Записывая второй закон Ньютона в проекции на горизонтальную ось, направленную вдоль ребра желоба, получим:
где — модуль искомого ускорения цилиндра. Заметим, что
Это означает, что приложенная к торцу цилиндра сила превышает силу трения покоя, то есть цилиндр и в самом деле будет скользить вдоль желоба.
Следовательно, Подставляя числовые данные и проверяя размерность, окончательно получим:
Ответ:
Задача 24
Равносторонний треугольник, состоящий из трёх жёстких лёгких стержней, может вращаться без трения вокруг горизонтальной оси, совпадающей с одной из его сторон. В точке пересечения двух других его сторон к треугольнику прикреплён массивный грузик (см. рисунок). Как и во сколько раз изменится период малых колебаний грузика около его положения равновесия, если ось вращения наклонить под углом к горизонту?
Решение
Обозначим расстояние от оси вращения треугольника до грузика через Тогда период колебаний при горизонтальном положении оси равен, очевидно,
После наклона оси на угол возвращающая сила при отклонении треугольника от положения равновесия уменьшится: составляющая силы тяжести вдоль оси, равная
(здесь
— масса грузика), будет компенсироваться силами реакции со стороны подшипников, в которых закреплена эта ось, а в направлении, перпендикулярном оси, будет действовать эффективная «сила тяжести», равна
Поэтому период малых колебаний грузика при наклоненной оси будет равен
Таким образом, период колебаний увеличится в раз.
Ответ: период колебаний увеличится в раз.
Задача 25
На гладкой горизонтальной плоскости лежат два груза массами и
соединённые невесомой нерастяжимой нитью, перекинутой через два неподвижных (А и В) и один подвижный (О) невесомые блоки, как показано на рисунке. Оси блоков горизонтальны, трения в осях блоков нет. К оси О подвижного блока приложена направленная вертикально вниз сила F = 4 Н. Найдите ускорение этой оси. Сделайте схематический рисунок с указанием сил, действующих на грузы и блок.
Решение
Нарисуем силы Т натяжения нити, одинаковые, в силу условия задачи, вдоль всей нити и действующие на грузы и блок О (см. рисунок). Введём систему координат XY, как показано на рисунке, и запишем уравнения движения грузов в проекции на ось X:
В силу невесомости блока О имеем или
В силу нерастяжимости нити (длиной L) и неподвижности блоков А и В (их координаты и
постоянны) имеется следующая кинематическая связь между координатами
и
грузов и координатой
блока О (здесь
— радиус блоков А и В, R — радиус блока О):
или
и значит
Решаем записанную систему уравнений и получаем ответ:
Ответ:
Задача 26
Два вращающихся вала соединены замкнутым ремнём, который не проскальзывает относительно валов. Радиус первого вала равен R, радиус второго вала равен 2R. Чему равно отношение угловой скорости точки A к угловой скорости вращения первого вала
Решение
Скорость движения точек первого вала, находящихся на расстоянии от его центра, даётся формулой
Угловая скорость вращения точки А равна угловой скорости вращения второго вала. Валы связаны ремнём, поэтому скорости ободов
у валов одинаковы, а их угловые скорости
В итоге получаем
Ответ: 0,5.
Задача 28
Два велосипедиста совершают кольцевую гонку с одинаковой угловой скоростью. Положения и траектории движения велосипедистов показаны на рисунке. Чему равно отношение центростремительных ускорений велосипедистов ?
Решение
При движении по окружности угловая и линейная
скорости тела связаны с радиусом окружности
соотношением:
Центростремительное ускорение равно
Поскольку велосипедисты едут с одинаковым угловыми скоростями, для отношения центростремительных ускорения велосипедистов имеем:
Ответ: 2.
Задача 29
Прибор наблюдения обнаружил летящий снаряд и зафиксировал его горизонтальную координату и высоту
м над Землёй (см. рисунок). Через 3 с снаряд упал на Землю и взорвался на расстоянии
м от места его обнаружения. Известно, что снаряды данного типа вылетают из ствола пушки со скоростью 800 м/с. Какова была максимальная высота Н траектории снаряда, если считать, что сопротивление воздуха пренебрежимо мало? Пушка и место взрыва находятся на одной горизонтали.
Первое решение
Найдём горизонтальную скорость снаряда:
Найдём вертикальную проекцию скорости снаряда в момент обнаружения:
Определим, за какое время снаряд долетел из верхней точки траектории в точку, в которой был зафиксирован:
Таким образом, время опускания снаряда составляет
Таким образом, максимальная высота снаряда:
Второе решение
Найдём горизонтальную скорость снаряда: эта скорость остается постоянной на протяжении всего полета. Определим величину вертикальной проекции скорости в начальный момент:
Используя формулу для максимальной высоты брошенного под углом к горизонту тела, получаем:
Ответ: около 16 км.
Задача 30
К концу вертикального стержня привязана лёгкая нерастяжимая нить с маленьким грузиком на конце. Грузик раскрутили на нити так, что она отклонилась от вертикали на угол α = 30º (см. рисунок). Как и во сколько раз надо изменить угловую скорость ω вращения грузика вокруг стержня для того, чтобы этот угол стал равным β = 60º?
Решение
1. Обозначим силу натяжения нити T, массу грузика m, длину нити l, радиус окружности, по которой вращается грузик, R, и изобразим систему на рисунке (см. рисунок).
2. Запишем уравнение движения грузика по окружности вокруг стержня в проекциях на вертикальную ось и на радиус окружности с учётом выражения для центростремительного ускорения грузика:
,
.
3. Из написанных соотношений следует, что , а
.
4. Для того, чтобы угол отклонения нити стал равным β, угловая скорость вращения грузика должна увеличиться в
раза.
Ответ: 1,3 раза.
Задача 31
В аттракционе человек массой 80 кг движется на тележке по рельсам и совершает «мертвую петлю» в вертикальной плоскости. Каков радиус круговой траектории, если при скорости 10 м/с, направленной вертикально вверх, сила нормального давления человека на сидение тележки равна 1 600 Н? Ускорение свободного падения равно
Задача 32
На рисунке приведен график зависимости проекции скорости тела от времени. Чему равна проекция ускорения тела в момент времени 45 с? Ответ выразите в м/с2.
Решение
Из графика видно, что скорость в интервале времени от 40 с до 50 с меняется линейно, значит, ускорение постоянно. На всём этом интервале времени ускорение такое же, как и в момент времени 45 с. Найдём это ускорение:
Ответ: 2.
Задача 32
Два небольших тела с массами 2 кг и 3 кг висят на разных концах невесомой нерастяжимой нити, перекинутой через гладкий неподвижный блок. Первое тело находится на высоте 40 см ниже второго. Тела пришли в движение без начальной скорости. Через какое время они окажутся на одной высоте? Сделайте схематический рисунок с указанием сил, действующих на тела. Обоснуйте применимость используемых законов к решению задачи.
Решение
Задача 33
Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,3. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.
Решение
Задача 34
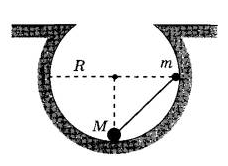
Небольшие шарики, массы которых m и M, соединены лёгким стержнем и помещены в гладкую сферическую выемку радиусом R = 20 см. В начальный момент шарики удерживаются в положении, изображённом на рисунке. Когда их отпустили без толчка, шарики стали скользить по поверхности выемки. Минимальная высота, на которой оказался шарик m в процессе движения, равна 4 см от нижней точки выемки. Определите отношение масс M и m.
Решение
Задача 35
Небольшой брусок массой m начинает соскальзывать с высоты H по гладкой горке, переходящей в мёртвую петлю (см. рисунок). Определите высоту отрыва бруска, если высота горки H. Радиус окружности R. Сделайте рисунок с указанием сил, поясняющий решение.
Решение
Направим ось Ох вдоль ускорения и пусть сила тяжести образует с этой осью угол α Запишем второй закон Ньютона для бруска на высоте h:
Выразим отсюда скорость бруска, учитывая, что и по третьему закону Ньютона
:
На высоте h брусок обладает как кинетической, так и потенциальной энергией. Из закона сохранения энергии найдём искомую высоту H:
откуда
Задача 36
В маленький шар массой M=100г, висящий на нити длиной l=50 см, попадает и застревает в нем пулька массой m=20г, летящая под углом 30 град к горизонту (см рисунок). Какую скорость v имела пуля перед попаданием в шар, если после соударения шар с застрявшей в нем пулей отклонился по вертикали на угол 60 град? Сопротивлением воздуха пренебречь. Какие законы вы использовали для описания взаимодействия пульки с шаром и подьема тел? Обоснуйте их применимость к данному случаю.
Решение
Задача 37
При выполнение трюка летающий велосипедист гонщик движется по трамплину под действием силы тяжести, начиная движение из состояния покоя с высоты H. На краю трамплина скорость гонщика направлена под таим углом к горизонту, что дальность его полета максимальна. Пролетев по воздуху, гонщик приземляется на горизонтальный стол, находящейся на той же высоте, что и край трамплина. Какова высота полета h на этом трамплине? Сопротивлением воздуха и трением пренебречь.
Решение

В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т.е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.
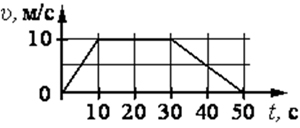
Задание 1. На рисунке представлен график зависимости модуля скорости от времени t. Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.
Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость v = 10 м/с, т.е.
| S = | (30 + 20) с | 10 м/с = 250 м. |
| 2 |
Ответ. 250 м.
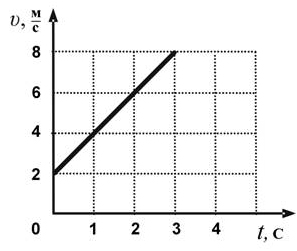
Задание 2. Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени t. Определите модуль силы натяжения троса в течение подъема.
Рис. 1
Рис. 2
Решение. По графику зависимости проекции скорости v груза на ось, направленную вертикально вверх, от времени t, можно определить проекцию ускорения груза
| a = | ∆v | = | (8 – 2) м/с | = 2 м/с2. |
| ∆t | 3 с |
На груз действуют: сила тяжести 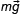
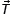
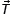
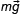
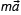
Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем
T – mg = ma (2);
из формулы (2) модуль силы натяжения
Т = m(g + a) = 100 кг (10 + 2) м/с2 = 1200 Н.
Ответ. 1200 Н.
Задание 3. Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью 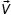
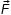
Рис. 1
Рис. 2
Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.
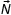
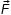
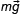
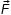
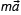
Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения 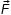
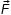
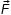
N = 16 Н · 1,5 м/с = 24 Вт.
Ответ. 24 Вт.
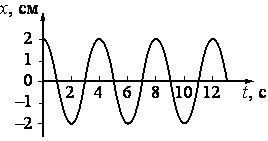
Задание 4. Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения x груза от времени t. Определите, чему равна масса груза. Ответ округлите до целого числа.
Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза х от времени t, определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π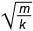
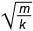 = = |
T | ; | m | = | T2 | ; m = k | T2 | ; m = 200 H/м | (4 с)2 | = 81,14 кг ≈ 81 кг. |
| 2π | k | 4π2 | 4π2 | 39,438 |
Ответ: 81 кг.
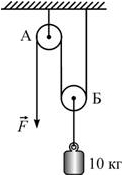
Задание 5. На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите два верных утверждения и укажите в ответе их номера.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н.
- Изображенная на рисунке система блоков не дает выигрыша в силе.
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 3h.
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 2h.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:
- Для того чтобы медленно поднять груз на высоту h, нужно вытянуть участок веревки длиной 2h.
- Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
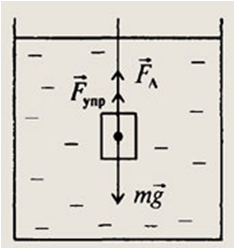
Ответ. 45.
Задание 6. В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?
Для каждой величины определите соответствующий характер изменения:
- Увеличивается;
- Уменьшается;
- Не изменяется.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Модуль силы натяжения нити |
Модуль действующей на груз силы тяжести |
Рис. 1
Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити Fупр, направленная вдоль нити вверх; сила тяжести 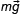
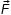
Плотность железа 7800 кг/м3, а алюминиевого груза 2700 кг/м3. Следовательно, Vж < Va. Тело в равновесии, равнодействующая всех сил, действующих на тело равна нулю. Направим координатную ось OY вверх. Основное уравнение динамики с учетом проекции сил запишем в виде Fупр + Fa – mg = 0; (1) Выразим силу натяжения Fупр = mg – Fa (2); архимедова сила зависит от плотности жидкости и объема погруженной части тела Fa = ρgV п.ч.т. (3); Плотность жидкости не меняется, а объем тела из железа меньше Vж < Va, поэтому архимедова сила, действующая на железный груз будет меньше. Делаем вывод о модуле силы натяжения нити, работая с уравнение (2), он возрастет.
Ответ. 13.
Задание 7. Брусок массой m соскальзывает с закрепленной шероховатой наклонной плоскости с углом α при основании. Модуль ускорения бруска равен a, модуль скорости бруска возрастает. Сопротивлением воздуха можно пренебречь.
Установите соответствие между физическими величинами и формулами, при помощи которых их можно вычислить. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
|
ФИЗИЧЕСКАЯ ВЕЛИЧИНА |
ФОРМУЛА |
|
А) Модуль силы реакции, действующей на брусок со стороны наклонной плоскости |
1) mg |
|
Б) Коэффициент трения бруска о наклонную плоскость |
3) mg cosα |
Решение. Данная задача требует применение законов Ньютона. Рекомендуем сделать схематический чертеж; указать все кинематические характеристики движения. Если возможно, изобразить вектор ускорения и векторы всех сил, приложенных к движущемуся телу; помнить, что силы, действующие на тело, – результат взаимодействия с другими телами. Затем записать основное уравнение динамики. Выбрать систему отсчета и записать полученное уравнение для проекции векторов сил и ускорений;
Следуя предложенному алгоритму, сделаем схематический чертеж (рис. 1). На рисунке изображены силы, приложенные к центру тяжести бруска, и координатные оси системы отсчета, связанной с поверхностью наклонной плоскости. Так как все силы постоянны, то движение бруска будет равнопеременным с увеличивающейся скоростью, т.е. вектор ускорения направлен в сторону движения. Выберем направление осей как указано на рисунке. Запишем проекции сил, на выбранные оси.
Рис. 1
Запишем основное уравнение динамики:
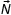
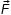
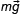
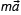
Запишем данное уравнение (1) для проекции сил и ускорения.
На ось OY: проекция силы реакции опоры положительная, так как вектор совпадает с направлением оси OY Ny = N; проекция силы трения равна нулю так как вектор перпендикулярен оси; проекция силы тяжести будет отрицательная и равная mgy = –mgcosα; проекция вектора ускорения ay = 0, так как вектор ускорения перпендикулярен оси. Имеем N – mgcosα = 0 (2) из уравнения выразим силу реакции действующей на брусок, со стороны наклонной плоскости. N = mgcosα (3). Запишем проекции на ось OX.
На ось OX: проекция силы N равна нулю, так как вектор перпендикулярен оси ОХ; Проекция силы трения отрицательная (вектор направлен в противоположную сторону относительно выбранной оси); проекция силы тяжести положительная и равна mgx = mgsinα (4) из прямоугольного треугольника. Проекция ускорения положительная ax = a; Тогда уравнение (1) запишем с учетом проекции mgsinα – Fтр = ma (5); Fтр = m(gsinα – a) (6); Помним, что сила трения пропорциональна силе нормального давления N.
По определению Fтр = μN (7), выразим коэффициент трения бруска о наклонную плоскость.
| μ = | Fтр | = | m(gsinα – a) | = tgα – | a | (8). |
| N | mgcosα | gcosα |
Выбираем соответствующие позиции для каждой буквы.
Ответ. A – 3; Б – 2.
Задание 8. Газообразный кислород находится в сосуде объемом 33,2 литра. Давление газа 150 кПа, его температура 127° С. Определите массу газа в этом сосуде. Ответ выразите в граммах и округлите до целого числа.
Решение. Важно обратить внимание на перевод единиц в систему СИ. Температуру переводим в Кельвины T = t°С + 273, объем V = 33,2 л = 33,2 · 10–3 м3; Давление переводим P = 150 кПа = 150 000 Па. Используя уравнение состояния идеального газа
| PV = | m | RT, (уравнение Менделеева –Клапейрона) |
| μ |
выразим массу газа.
и подставим числовые значения в полученное уравнение.
| m = | 1,5 · 105 ·33,2 · 10–3 · 32 · 10–3 | = 0,0479 кг = 47,9 г ≈ 48 г |
| 8,31 · 400 |
Обязательно обращаем внимание, в каких единица просят записать ответ. Это очень важно.
Ответ. 48 г.
Задание 9. Идеальный одноатомный газ в количестве 0,025 моль адиабатически расширился. При этом его температура понизилась с +103°С до +23°С. Какую работу совершил газ? Ответ выразите в Джоулях и округлите до целого числа.
Решение. Во-первых, газ одноатомный число степеней свободы i = 3, во-вторых, газ расширяется адиабатически – это значит без теплообмена Q = 0. Газ совершает работу за счет уменьшения внутренней энергии. С учетом этого, первый закон термодинамики запишем в виде 0 = ∆U + Aг; (1) выразим работу газа Aг = –∆U (2); Изменение внутренней энергии для одноатомного газа запишем как
Проведем вычисления подставив (3) в (2). Не забываем перевести температуру из градусов Цельсия в Кельвины.
| Aг = – | 3 | 0,025 · 8,31 · (–80) = 24,93 (Дж) ≈ 25Дж |
| 2 |
Ответ. 25 Дж.
Задание 10. Относительная влажность порции воздуха при некоторой температуре равна 10 %. Во сколько раз следует изменить давление этой порции воздуха для того, чтобы при неизменной температуре его относительная влажность увеличилась на 25 %?
Решение. Вопросы, связанные с насыщенным паром и влажностью воздуха, чаще всего вызывают затруднения у школьников. Воспользуемся формулой для расчета относительной влажности воздуха
| φ = | Pв.п. | · 100 % (1); |
| Pн.п. |
По условию задачи температура не изменяется, значит, давление насыщенного пара остается тем же. Запишем формулу (1) для двух состояний воздуха.
| φ1 = | P1в.п. | · 100 % (2); |
| Pн.п. |
и
| φ2 = | P2в.п. | · 100 % (3); |
| Pн.п. |
φ1 = 10 % ; φ2 = 35 %
Выразим давления воздуха из формул (2), (3) и найдем отношение давлений.
| P2 | = | φ2 | = | 35 | = 3,5 |
| P1 | φ1 | 10 |
Ответ. Давление следует увеличить в 3,5 раза.
Задание 11. Горячее вещество в жидком состоянии медленно охлаждалось в плавильной печи с постоянной мощностью. В таблице приведены результаты измерений температуры вещества с течением времени.
|
Время, мин |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
|
Температура, °С |
250 |
242 |
234 |
232 |
232 |
232 |
230 |
216 |
Выберите из предложенного перечня два утверждения, которые соответствуют результатам проведенных измерений и укажите их номера.
- Температура плавления вещества в данных условиях равна 232°С.
- Через 20 мин. после начала измерений вещество находилось только в твердом состоянии.
- Теплоемкость вещества в жидком и твердом состоянии одинакова.
- Через 30 мин. после начала измерений вещество находилось только в твердом состоянии.
- Процесс кристаллизации вещества занял более 25 минут.
Решение. Так как вещество охлаждалось, то его внутренняя энергия уменьшалась. Результаты измерения температуры, позволяют определить температуру, при которой вещество начинает кристаллизоваться. Пока вещество переходит из жидкого состояния в твердое, температура не меняется. Зная, что температура плавления и температура кристаллизации одинаковы, выбираем утверждение:
1. Tемпература плавления вещества в данных условиях равна 232°С.
Второе верное утверждение это:
4. Через 30 мин. после начала измерений вещество находилось только в твердом состоянии. Так как температура в этот момент времени, уже ниже температуры кристаллизации.
Ответ. 14.
Задание 12. В изолированной системе тело А имеет температуру +40°С, а тело Б температуру +65°С. Эти тела привели в тепловой контакт друг с другом. Через некоторое время наступило тепловое равновесие. Как в результате изменилась температура тела Б и суммарная внутренняя энергия тела А и Б?
Для каждой величины определите соответствующий характер изменения:
- Увеличилась;
- Уменьшилась;
- Не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Температура тела Б |
Суммарная внутренняя энергия тел А и Б |
Решение. Если в изолированной системе тел не происходит никаких превращений энергии кроме теплообмена, то количество теплоты, отданное телами, внутренняя энергия которых уменьшается, равно количеству теплоты, полученному телами, внутренняя энергия которых увеличивается. (По закону сохранения энергии.) При этом суммарная внутренняя энергия системы не меняется. Задачи такого типа решаются на основании уравнения теплового баланса.
| ∆U = ∑ | n | ∆Ui = 0 (1); |
i = 1 |
где ∆U – изменение внутренней энергии.
В нашем случае в результате теплообмена внутренняя энергия тела Б уменьшается, а значит уменьшается температура этого тела. Внутренняя энергия тела А увеличивается, так как тело получило количество теплоты от тела Б, то температура его увеличится. Суммарная внутренняя энергия тел А и Б не изменяется.
Ответ. 23.
Задание 13. Протон p, влетевший в зазор между полюсами электромагнита, имеет скорость 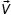
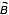
Решение. На заряженную частицу магнитное поле действует с силой Лоренца. Для того чтобы определить направление этой силы, важно помнить мнемоническое правило левой руки, не забывать учитывать заряд частицы. Четыре пальца левой руки направляем по вектору скорости, для положительно заряженной частицы, вектор 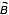
Ответ. от наблюдателя.
Задание 14. Модуль напряженности электрического поля в плоском воздушном конденсаторе емкостью 50 мкФ равен 200 В/м. Расстояние между пластинами конденсатора 2 мм. Чему равен заряд конденсатора? Ответ запишите в мкКл.
Решение. Переведем все единицы измерения в систему СИ. Емкость С = 50 мкФ = 50 · 10–6 Ф, расстояние между пластинами d = 2 · 10–3 м. В задаче говорится о плоском воздушном конденсаторе – устройстве для накопления электрического заряда и энергии электрического поля. Из формулы электрической емкости
выразим электрический заряд q = C · U (2). Используя связь напряженности электрического поля E и напряжения U, запишем формулу
где d – расстояние между пластинами.
Выразим напряжение U = E · d (4); Подставим (4) в (2) и рассчитаем заряд конденсатора.
q = C · Ed = 50 · 10–6 · 200 · 0,002 = 20 мкКл
Обращаем внимание, в каких единицах нужно записать ответ. Получили в кулонах, а представляем в мкКл.
Ответ. 20 мкКл.
Задание 15.
Рис. 1
Ученик провел опыт по преломлению света, представленный на фотографии. Как изменяется при увеличении угла падения угол преломления света, распространяющегося в стекле, и показатель преломления стекла?
- Увеличивается
- Уменьшается
- Не изменяется
- Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
|
Угол преломления |
Показатель преломления стекла |
Решение. В задачах такого плана вспоминаем, что такое преломление. Это изменение направления распространения волны при прохождении из одной среды в другую. Вызвано оно тем, что скорости распространения волн в этих средах различны. Разобравшись из какой среды в какую свет распространяется, запишем закона преломления в виде
где n2 – абсолютный показатель преломления стекла, среда куда идет свет; n1 – абсолютный показатель преломления первой среды, откуда свет идет. Для воздуха n1 = 1. α – угол падения луча на поверхность стеклянного полуцилиндра, β – угол преломления луча в стекле. Причем, угол преломления будет меньше угла падения, так как стекло оптически более плотная среда – среда с большим показателем преломления. Скорость распространения света в стекле меньше. Обращаем внимание, что углы измеряем от перпендикуляра, восстановленного в точке падения луча. Если увеличивать угол падения, то и угол преломления будет расти. Показатель преломления стекла от этого меняться не будет.
Ответ.
Задание 16. Медная перемычка в момент времени t0 = 0 начинает двигаться со скоростью 2 м/с по параллельным горизонтальным проводящим рельсам, к концам которых подсоединен резистор сопротивлением 10 Ом. Вся система находится в вертикальном однородном магнитном поле. Сопротивление перемычки и рельсов пренебрежимо мало, перемычка все время расположена перпендикулярно рельсам. Поток Ф вектора магнитной индукции через контур, образованный перемычкой, рельсами и резистором, изменяется с течением времени t так, как показано на графике.
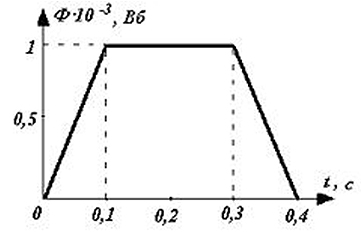
Используя график, выберите два верных утверждения и укажите в ответе их номера.
- К моменту времени t = 0,1 с изменение магнитного потока через контур равно 1 мВб.
- Индукционный ток в перемычке в интервале от t = 0,1 с t = 0,3 с максимален.
- Модуль ЭДС индукции, возникающей в контуре, равен 10 мВ.
- Сила индукционного тока, текущего в перемычке, равна 64 мА.
- Для поддержания движения перемычки к ней прикладывают силу, проекция которой на направление рельсов равна 0,2 Н.
Решение. По графику зависимости потока вектора магнитной индукции через контур от времени определим участки, где поток Ф меняется, и где изменение потока равно нулю. Это позволит нам определить интервалы времени, в которые в контуре будет возникать индукционный ток. Верное утверждение:
1) К моменту времени t = 0,1 с изменение магнитного потока через контур равно 1 мВб ∆Ф = (1 – 0) · 10–3 Вб; Модуль ЭДС индукции, возникающей в контуре определим используя закон ЭМИ
| Ɛ = | – | ∆Ф | = | – | 1 ·10–3 | = 0,01 В = 10 мВ |
| ∆t | 0,1 |
Ответ. 13.
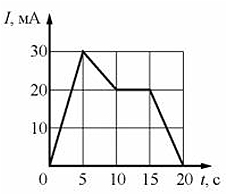
Задание 17.
По графику зависимости силы тока от времени в электрической цепи, индуктивность которой равна 1 мГн, определите модуль ЭДС самоиндукции в интервале времени от 5 до 10 с. Ответ запишите в мкВ.
Решение. Переведем все величины в систему СИ, т.е. индуктивность 1 мГн переведем в Гн, получим 10–3 Гн. Силу тока, показанной на рисунке в мА также будем переводить в А путем умножения на величину 10–3.
Формула ЭДС самоиндукции имеет вид
где L – индуктивность цепи; ∆I – изменение тока; ∆t – интервал времени (при котором происходит изменение тока).
Модуль ЭДС самоиндукции будет иметь вид
при этом интервал времени дан по условию задачи
∆t = 10 c – 5 c = 5 c
секунд и по графику определяем интервал изменения тока за это время:
∆I = 30 · 10–3 – 20 · 10–3 = 10 · 10–3 = 10–2 A.
Подставляем числовые значения в формулу (2), получаем
|Ɛ| = 2 ·10–6 В, или 2 мкВ.
Ответ. 2.
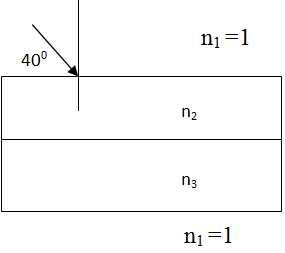
Задание 18. Две прозрачные плоскопараллельные пластинки плотно прижаты друг к другу. Из воздуха на поверхность первой пластинки падает луч света (см. рисунок). Известно, что показатель преломления верхней пластинки равен n2 = 1,77. Установите соответствие между физическими величинами и их значениями. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
|
ФИЗИЧЕСКАЯ ВЕЛИЧИНА |
ЕЕ ЗНАЧЕНИЕ |
|
А) Синус угла падения луча на границу 2-3 между пластинами |
1) ≈ 0,698 |
|
2) ≈ 0,433 |
|
|
Б) Угол преломления луча при переходе границы 3-1 ( в радианах) |
3) ≈ 0,363 |
|
4) ≈ 0,873 |
Решение. Для решения задач о преломлении света на границе раздела двух сред, в частности задач на прохождение света через плоскопараллельные пластинки можно рекомендовать следующий порядок решения: сделать чертеж с указанием хода лучей, идущих из одной среды в другую; в точке падения луча на границе раздела двух сред провести нормаль к поверхности, отметить углы падения и преломления. Особо обратить внимание на оптическую плотность рассматриваемых сред и помнить, что при переходе луча света из оптически менее плотной среды в оптически более плотную среду угол преломления будет меньше угла падения. На рисунке дан угол между падающим лучом и поверхностью, а нам нужен угол падения. Помним, что углы определяются от перпендикуляра, восстановленного в точке падения. Определяем, что угол падения луча на поверхность 90° – 40° = 50°, показатель преломления n2 = 1,77; n1 = 1 (воздух).
Запишем закон преломления
для границы 1-2:
| sinβ = | sin50 | = 0,4327 ≈ 0,433 |
| 1,77 |
Построим примерный ход луча через пластинки. Используем формулу (1) для границы 2–3 и 3–1. В ответе получаем
А) Синус угла падения луча на границу 2–3 между пластинками – это 2) ≈ 0,433;
Б) Угол преломления луча при переходе границы 3–1 (в радианах) – это 4) ≈ 0,873.
Ответ. 24.
Задание 19. Определите, сколько α – частиц и сколько протонов получается в результате реакции термоядерного синтеза



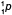
|
Количество α-частиц |
Количество протонов |
Решение. При всех ядерных реакциях соблюдаются законы сохранения электрического заряда и числа нуклонов. Обозначим через x – количество альфа частиц, y– количество протонов. Составим уравнения



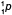
решая систему имеем, что x = 1; y = 2
Ответ. 1 – α-частица; 2 – протона.
Задание 20. Модуль импульса первого фотона равен 1,32 · 10–28 кг·м/с, что на 9,48 · 10–28 кг·м/с меньше, чем модуль импульса второго фотона. Найдите отношение энергии E2/E1 второго и первого фотонов. Ответ округлите до десятых долей.
Решение. Импульс второго фотона больше импульса первого фотона по условию значит можно представить p2 = p1 + Δp (1). Энергию фотона можно выразить через импульс фотона, используя следующие уравнения. Это E = mc2 (1) и p = mc (2), тогда
E = pc (3),
где E – энергия фотона, p – импульс фотона, m – масса фотона, c = 3 · 108 м/с – скорость света. С учетом формулы (3) имеем:
Ответ округляем до десятых и получаем 8,2.
Ответ. 8,2.
Задание 21. Ядро атома претерпело радиоактивный позитронный β – распад. Как в результате этого изменялись электрический заряд ядра и количество нейтронов в нем?
Для каждой величины определите соответствующий характер изменения:
- Увеличилась;
- Уменьшилась;
- Не изменилась.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Электрический заряд ядра |
Количество нейтронов в ядре |
Решение. Позитронный β – распад в атомном ядре происходит при превращений протона в нейтрон с испусканием позитрона. В результате этого число нейтронов в ядре увеличивается на единицу, электрический заряд уменьшается на единицу, а массовое число ядра остается неизменным. Таким образом, реакция превращения элемента следующая:
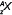
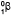
Ответ. 21.
Задание 22. В лаборатории было проведено пять экспериментов по наблюдению дифракции с помощью различных дифракционных решеток. Каждая из решеток освещалась параллельными пучками монохроматического света с определенной длиной волны. Свет во всех случаях падал перпендикулярно решетке. В двух из этих экспериментов наблюдалось одинаковое количество главных дифракционных максимумов. Укажите сначала номер эксперимента, в котором использовалась дифракционная решетка с меньшим периодом, а затем – номер эксперимента, в котором использовалась дифракционная решетка с большим периодом.
|
Номер эксперимента |
Период дифракционной решетки |
Длина волны падающего света |
|
1 |
2d |
λ/2 |
|
2 |
d |
λ |
|
3 |
2d |
λ |
|
4 |
d/2 |
λ/2 |
|
5 |
d/2 |
2λ |
Решение. Дифракцией света называется явление светового пучка в область геометрической тени. Дифракцию можно наблюдать в том случае, когда на пути световой волны встречаются непрозрачные участки или отверстия в больших по размерам и непрозрачных для света преградах, причем размеры этих участков или отверстий соизмеримы с длиной волны. Одним из важнейших дифракционных устройств является дифракционная решетка. Угловые направления на максимумы дифракционной картины определяются уравнением
dsinφ = k λ (1),
где d – период дифракционной решетки, φ – угол между нормалью к решетке и направлением на один из максимумов дифракционной картины, λ – длина световой волны, k – целое число, называемое порядком дифракционного максимума. Выразим из уравнения (1)
Подбирая пары согласно условию эксперимента, выбираем сначала 4 где использовалась дифракционная решетка с меньшим периодом, а затем – номер эксперимента, в котором использовалась дифракционная решетка с большим периодом – это 2.
Ответ. 42.
Задание 23. По проволочному резистору течет ток. Резистор заменили на другой, с проволокой из того же металла и той же длины, но имеющей вдвое меньшую площадь поперечного сечения, и пропустили через него вдвое меньший ток. Как изменятся при этом напряжение на резисторе и его сопротивление?
Для каждой величины определите соответствующий характер изменения:
- Увеличится;
- Уменьшится;
- Не изменится.
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Напряжение на резисторе |
Сопротивление резистора |
Решение. Важно помнить от каких величин зависит сопротивление проводника. Формула для расчета сопротивления имеет вид
где ρ – удельное сопротивление проводника; l – длина проводника; S – площадь поперечного сечения. Для полного ответа на вопрос задачи необходимо записан формулу
закона Ома для участка цепи, из формулы (2), выразим напряжение
U = IR (3).
По условию задачи второй резистор изготовлен из проволоки того же материала, той же длины, но разной площади поперечного сечения. Площадь в два раза меньшая. Подставляя в (1) получим, что сопротивление увеличивается в 2 раза, а сила тока уменьшается в 2 раза, следовательно, напряжение не изменяется.
Ответ. 13.
Задание 24. Период колебаний математического маятника на поверхности Земли в 1, 2 раза больше периода его колебаний на некоторой планете. Чему равен модуль ускорения свободного падения на этой планете? Влияние атмосферы в обоих случаях пренебрежимо мало.
Решение. Математический маятник – это система, состоящая из нити, размеры которой много больше размеров шарика и самого шарика. Трудность может возникнуть если забыта формула Томсона для периода колебаний математического маятника.
T = 2π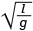
l – длина математического маятника; g – ускорение свободного падения.
По условию
Используя формулу Томсона для периода колебаний математического маятника T = 2π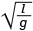
| Tз | =  (4). (4). |
| Tп |
Выразим из (3) gп = 14,4 м/с2. Надо отметить, что ускорение свободного падения зависит от массы планеты и радиуса
Ответ. 14,4 м/с2.
Задание 25. Прямолинейный проводник длиной 1 м, по которому течет ток 3 А, расположен в однородном магнитном поле с индукцией В = 0,4 Тл под углом 30° к вектору 
Решение. Если в магнитное поле, поместить проводник с током, то поле на проводник с током будет действовать с силой Ампера. Запишем формулу модуля силы Ампера
FА = ILBsinα;
FА = 0,6 Н
Ответ. FА = 0,6 Н.
Задание 26. Энергия магнитного поля, запасенная в катушке при пропускании через нее постоянного тока, равна 120 Дж. Во сколько раз нужно увеличить силу тока, протекающего через обмотку катушки, для того, чтобы запасенная в ней энергия магнитного поля увеличилась на 5760 Дж.
Решение. Энергия магнитного поля катушки рассчитывается по формуле
По условию W1 = 120 Дж, тогда W2 = 120 + 5760 = 5880 Дж.
| I12 = | 2W1 | ; I22 = | 2W2 | ; |
| L | L |
Тогда отношение токов
Ответ. Силу тока нужно увеличить в 7 раз. В бланк ответов Вы вносите только цифру 7.
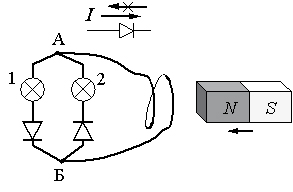
Задание 27. Электрическая цепь состоит из двух лампочек, двух диодов и витка провода, соединенных, как показано на рисунке. (Диод пропускает ток только в одном направлении, как показано на верхней части рисунка). Какая из лампочек загорится, если к витку приближать северный полюс магнита? Ответ объясните, указав, какие явления и закономерности вы использовали при объяснении.
Решение. Линии магнитной индукции выходят из северного полюса магнита и расходятся. При приближении магнита магнитный поток через виток провода увеличивается. В соответствии с правило Ленца магнитное поле, создаваемое индукционным током витка, должно быть направлено вправо. По правилу буравчика ток должен идти по часовой стрелке (если смотреть слева). В этом направлении пропускает диод, стоящий в цепи второй лампы. Значит, загорится вторая лампа.
Ответ. Загорится вторая лампа.
Задание 28. Алюминиевая спица длиной L = 25 см и площадью поперечного сечения S = 0,1 см2 подвешена на нити за верхний конец. Нижний конец опирается на горизонтальное дно сосуда, в который налита вода. Длина погруженной в воду части спицы l = 10 см. Найти силу F, с которой спица давит на дно сосуда, если известно, что нить расположена вертикально. Плотность алюминия ρа = 2,7 г/см3, плотность воды ρв = 1,0 г/см3. Ускорение свободного падения g = 10 м/с2
Решение. Выполним поясняющий рисунок.
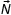
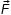
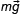
По определению масса спицы m и модуль архимедовой силы выражаются следующим образом : m = SLρa (1);
Fa = Slρвg (2)
Рассмотрим моменты сил относительно точки подвеса спицы.
М(Т) = 0 – момент силы натяжения; (3)
М(N) = NLcosα – момент силы реакции опоры; (4)
| М(Fa) = Slρв g (L – | 1 | ) cosα – момент архимедовой силы ; (5) |
| 2 |
| М(mg) = SLρa g | L | cosα – момент силы тяжести; (6) |
| 2 |
С учетом знаков моментов запишем уравнение
| NLcosα + Slρв g (L – | l | ) cosα = SLρa g | L | cosα (7) |
| 2 | 2 |
учитывая, что по третьему закону Ньютона сила реакции дна сосуда равна силе Fд с которой спица давит на дно сосуда запишем N = Fд и из уравнения (7) выразим эту силу:
| Fд = [ | 1 | Lρa – (1 – | l | )lρв]Sg (8). |
| 2 | 2L |
Подставим числовые данные и получим, что
Fд = 0,025 Н.
Ответ. Fд = 0,025 Н.
Задание 29. Баллон, содержащий m1 = 1 кг азота, при испытании на прочность взорвался при температуре t1 = 327°С. Какую массу водорода m2 можно было бы хранить в таком баллоне при температуре t2 = 27°С, имея пятикратный запас прочности? Молярная масса азота M1 = 28 г/моль, водорода M2 = 2 г/моль.
Решение. Запишем уравнение состояния идеального газа Менделеева – Клапейрона для азота
Из уравнения состояния азота следует, что давление, при котором взорвался баллон,
| p1 = | m1 | · | RT1 | , (2) |
| M1 | V |
где V – объем баллона, T1 = t1 + 273°C. По условию водород можно хранить при давлении p2 = p1/5; (3) Учитывая, что
| p2 = | m2 | · | RT2 | (4) |
| M2 | V |
можем выразить массу водорода работая сразу с уравнениями (2), (3), (4). Конечная формула имеет вид:
| m2 = | m1 | M2 | T1 | (5). | ||
| 5 | M1 | T2 |
После подстановки числовых данных m2 = 28 г.
Ответ. m2 = 28 г.
Задание 30. В идеальном колебательном контуре амплитуда колебаний силы тока в катушке индуктивности Im = 5 мА, а амплитуда напряжения на конденсаторе Um = 2,0 В. В момент времени t напряжение на конденсаторе равно 1,2 В. Найдите силу тока в катушке в этот момент.
Решение. В идеальном колебательном контуре сохраняется энергия колебаний. Для момента времени t закон сохранения энергий имеет вид
| C | U2 | + L | I2 | = L | Im2 | (1) |
| 2 | 2 | 2 |
Для амплитудных (максимальных) значений запишем
| C | Um2 | = L | Im2 | (2) |
| 2 | 2 |
Из равенства (1) следует :
а из уравнения (2) выразим
Подставим (4) в (3). В результате получим:
I = Im 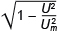
Таким образом, сила тока в катушке в момент времени t равна
I = 4,0 мА.
Ответ. I = 4,0 мА.
Задание 31. На дне водоема глубиной 2 м лежит зеркало. Луч света, пройдя через воду, отражается от зеркала и выходит из воды. Показатель преломления воды равен 1,33. Найдите расстояние между точкой входа луча в воду и точкой выхода луча из воды, если угол падения луча равен 30°
Решение. Сделаем поясняющий рисунок
α – угол падения луча;
β – угол преломления луча в воде;
АС – расстояние между точкой входа луча в воду и точкой выхода луча из воды.
По закону преломления света
где n2 – показатель преломления воды; n1 – показатель преломления воздуха. n1 = 1. Тогда формулу (1) можно записать
Выразим
Рассмотрим прямоугольный ΔАDВ. В нем АD = h, тогда DВ = АD
| tgβ = htgβ = h | sinα | = h | sinβ | = h | sinα | (4) |
| cosβ |  |
 |
Получаем следующее выражение:
| АС = 2 DВ = 2h | sinα | (5) |
 |
Подставим числовые значения в полученную формулу (5)
АС = 1,63 м
Ответ. 1,63 м.
Задание 17589
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18256
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18335
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 17541
Установление соответствия
Решение
→
Задание 18222
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18625
Введите ответ в поле ввода
Решение
→
Задание 17501
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 18523
Введите ответ в поле ввода
Решение
→
Задание 22669
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→
Задание 22708
Введите ответ в поле ввода
Решение
→
Задание 18382
Установление соответствия
Решение
→
Задание 19100
Введите ответ в поле ввода
Решение
→
Задание 22793
Внимательно прочитайте текст задания и выберите верный ответ из списка
Решение
→