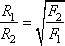Условимся считать изображение на пленке фотоаппарата резким, если вместо идеального изображения в виде точки на пленке получается изображение пятна диаметром не более некоторого предельного значения. Поэтому, если объектив находится на фокусном расстоянии от пленки, то резкими считаются не только бесконечно удаленные предметы, но и все предметы, находящиеся дальше некоторого расстояния d. Оцените предельный размер пятна, если при фокусном расстоянии объектива 50 мм и диаметре входного отверстия 5 мм резкими оказались все предметы, находившиеся на расстояниях более 5 м от объектива. Сделайте рисунок, поясняющий образование пятна.
Спрятать решение
Решение.
Лучи, идущие от предмета на расстоянии d, собираются на расстоянии f, которое больше фокусного расстояния, и поэтому образуют на пленке пятно диаметром Из подобия треугольников получаем соотношение:
(1).
Из формулы тонкой линзы находим:
(2). Из (1) и (2) получаем окончательно:
Ответ:
Спрятать критерии
Критерии проверки:
|
Критерии оценки выполнения задания |
Баллы |
|
Приведено полное правильное решение, включающее следующие элементы: 1) верно записаны формулы, выражающие физические законы, применение которых необходимо для решения задачи выбранным способом (в данном решении — формула тонкой линзы); 2) проведены необходимые математические преобразования и расчеты, приводящие к правильному числовому ответу, и представлен ответ (включая единицы измерения). При этом допускается решение «по частям» (с промежуточными вычислениями). |
3 |
|
Представленное решение содержит п.1 полного решения, но и имеет один из следующих недостатков: — в необходимых математических преобразованиях или вычислениях допущена ошибка; ИЛИ — необходимые математические преобразования и вычисления логически верны, не содержат ошибок, но не закончены; ИЛИ — не представлены преобразования, приводящие к ответу, но записан правильный числовой ответ или ответ в общем виде; ИЛИ — решение содержит ошибку в необходимых математических преобразованиях и не доведено до числового ответа. |
2 |
|
Представлены записи, соответствующие одному из следующих случаев: — представлены только положения и формулы, выражающие физические законы, применение которых необходимо для решения задачи, без каких-либо преобразований с их использованием, направленных на решение задачи, и ответа; ИЛИ — в решении отсутствует ОДНА из исходных формул, необходимая для решения задачи (или утверждение, лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. ИЛИ — в ОДНОЙ из исходных формул, необходимых для решения задачи (или утверждении, лежащем в основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися формулами, направленные на решение задачи. |
1 |
|
Все случаи решения, которые не соответствуют вышеуказанным критериям выставления оценок в 1, 2, 3 балла. |
0 |
Решу егэ физика 3104
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 7 № 3104
Подвешенный на пружине груз совершает вынужденные гармонические колебания под действием внешней силы, изменяющейся с частотой Установите соответствие между физическими величинами, характеризующего этот процесс, и частотами их изменения.
К каждому элементу первого столбца подберите соответствующий элемент из второго и внесите в строку ответов выбранные цифры под соответствующими буквами.
А) Кинетическая энергия груза
Б) Ускорение груза
Под действием силы, меняющейся с частотой груз на пружине совершает вынужденные гармонические колебания с такой же частотой. Следовательно, закон изменения со временем высоты груза относительно положения устойчивого равновесия имеет вид Таким образом, закон изменения ускорения со временем: Отсюда получаем, что частота изменения ускорения груза также равна (Б — 2).
Скорость изменяется по закону: Отсюда получаем, что кинетическая энергия груза изменяется по закону
Следовательно, частота изменения кинетической энергии равна (А — 3). Наконец, закон изменения потенциальной энергии груза:
Таким образом, период ее изменения равен (В — 2).
Разве частота изменения и потенциальной, и кинетической энергий не 2V?
В случае вертикальных колебаний груза на пружине надо быть очень аккуратным в терминологии. Попробую пояснить, в чем тут дело (при этом, к сожалению, не могу гарантировать, что все создатели задач для ЕГЭ дают себе отчет в данном вопросе, расскажу так, как есть на самом деле).
С кинетической энергия груза все просто, она действительно изменяется с удвоенной частотой, а вот с потенциальной энергией надо быть осторожнее. Потенциальная энергия всегда связана с работой некоторой потенциальной силы. При вертикальных колебаниях в пружинном маятнике есть две такие силы: меняется как потенциальная энергия груза в поле тяжести (), так и потенциальная энергия деформации пружины (). Как отмечено в решении, потенциальная энергия груза изменяется по гармоническому закону с такой же частотой, с которой происходят колебания, так как она определяется только высотой тела над поверхностью Земли. А вот энергия пружины вообще изменяется не по гармоническому закону.
Почему так? Ответ очень прост. У вертикального пружинного маятника положение равновесия соответствует растянутой пружине: когда мы подвешиваем груз, он сразу растягивает пружину на некоторую величину, которую можно найти из второго закона Ньютона для тела: . При этом, если мы будем искать энергию пружины, то обязаны учитывать это начальное растяжение. В результате, при колебаниях потенциальная энергия пружины изменяется по закону:
Легко видеть, что в законе изменения энергии пружины со временем есть и, и, то есть частота колебаний получается тоже.
—>
Задание 7 № 3104
Попробую пояснить, в чем тут дело при этом, к сожалению, не могу гарантировать, что все создатели задач для ЕГЭ дают себе отчет в данном вопросе, расскажу так, как есть на самом деле.
Phys-ege. sdamgia. ru
26.07.2019 2:00:34
2019-07-26 02:00:34
Источники:
Http://phys-ege. sdamgia. ru/problem? id=3104
Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения » /> » /> .keyword { color: red; } Решу егэ физика 3104
Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения
Гущин решу егэ физика. Подготовка к ЕГЭ по физике: примеры, решения, объяснения
2) СТРУКТУРА КИМов — 2018 и 2019 по сравнению с 2017г. несколько ИЗМЕНИЛАСЬ: Вариант экзаменационной работы будет состоять из двух частей и включит в себя 32 задания. Часть 1 будет содержать 24 задания с кратким ответом, в том числе задания с самостоятельной записью ответа в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр. Часть 2 будет содержать 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (25–27) и 5 заданий (28–32), для которых необходимо привести развернутый ответ. В работу будут включены задания трех уровней сложности. Задания базового уровня включены в часть 1 работы (18 заданий, из которых 13 заданий с записью ответа в виде числа, двух чисел или слова и 5 заданий на соответствие и множественный выбор). Задания повышенного уровня распределены между частями 1 и 2 экзаменационной работы: 5 заданий с кратким ответом в части 1, 3 задания с кратким ответом и 1 задание с развернутым ответом в части 2. Последние четыре задачи части 2 являются заданиями высокого уровня сложности. Часть 1 экзаменационной работы будет включать два блока заданий: первый проверяет освоение понятийного аппарата школьного курса физики, а второй – овладение методологическими умениями. Первый блок включает 21 задание, которые группируются, исходя из тематической принадлежности: 7 заданий по механике, 5 заданий по МКТ и термодинамике, 6 заданий по электродинамике и 3 по квантовой физике.
Новым заданием базового уровня сложности является последнее задание первой части (24 позиция), приуроченное к возвращению курса астрономии в школьную программу. Задание имеет характеристику типа «выбор 2 суждений из 5». Задание 24, как и другие аналогичные задания в экзаменационной работе, оценивается максимально в 2 балла, если верно указаны оба элемента ответа, и в 1 балл, если в одном из элементов допущена ошибка. Порядок записи цифр в ответе значения не имеет. Как правило, задания будут иметь контекстный характер, т. е. часть данных, необходимых для выполнения задания будут приводиться в виде таблицы, схемы или графика.
В соответствии с этим заданием в кодификаторе добавился подраздел «Элементы астрофизики» раздела «Квантовая физика и элементы астрофизики», включающий следующие пункты:
· Солнечная система: планеты земной группы и планеты-гиганты, малые тела Солнечной системы.
· Звёзды: разнообразие звездных характеристик и их закономерности. Источники энергии звезд.
· Современные представления о происхождении и эволюции Солнца и звёзд. Наша галактика. Другие галактики. Пространственные масштабы наблюдаемой Вселенной.
· Современные взгляды на строение и эволюцию Вселенной.
Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М. Ю. Демидовой https://www. youtube. com/watch? v=JXeB6OzLokU либо в документе, приведенном ниже.
Подготовка к ОГЭ и ЕГЭ
Среднее общее образование
Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)
Линия УМК А. В. Грачева. Физика (7-9)
Линия УМК А. В. Перышкина. Физика (7-9)
Подготовка к ЕГЭ по физике: примеры, решения, объяснения
Лебедева Алевтина Сергеевна, учитель физики, стаж работы 27 лет. Почетная грамота Министерства образования Московской области (2013 год), Благодарность Главы Воскресенского муниципального района (2015 год), Грамота Президента Ассоциации учителей математики и физики Московской области (2015 год).
В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т. е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.
На рисунке представлен график зависимости модуля скорости от времени T . Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость V = 10 м/с, т. е.
| S = | (30 + 20) С | 10 м/с = 250 м. |
| 2 |
Ответ. 250 м.
Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени T . Определите модуль силы натяжения троса в течение подъема.


Решение. По графику зависимости проекции скорости V груза на ось, направленную вертикально вверх, от времени T , можно определить проекцию ускорения груза
| A = | ∆V | = | (8 – 2) м/с | = 2 м/с 2 . |
| ∆T | 3 с |
На груз действуют: сила тяжести, направленная вертикально вниз и сила натяжения троса, направленная вдоль троса вертикально вверх смотри рис. 2. Запишем основное уравнение динамики. Воспользуемся вторым законом Ньютона. Геометрическая сумма сил действующих на тело равна произведению массы тела на сообщаемое ему ускорение.
Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем
T – Mg = Ma (2);
Из формулы (2) модуль силы натяжения
Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.
Ответ . 1200 Н.
Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью модуль которой равен 1, 5 м/с, прикладывая к нему силу так, как показано на рисунке (1). При этом модуль действующей на тело силы трения скольжения равен 16 Н. Чему равна мощность, развиваемая силой F ?


Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.
Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения тр. и сила, с которой тело тащат. Проекция силы трения отрицательная, так как вектор силы не совпадает с направлением оси Х . Проекция силы F положительная. Напоминаем, для нахождения проекции опускаем перпендикуляр из начала и конца вектора на выбранную ось. С учетом этого имеем: F cosα – F тр = 0; (1) выразим проекцию силы F , это F cosα = F тр = 16 Н; (2) тогда мощность, развиваемая силой, будет равна N = F cosα V (3) Сделаем замену, учитывая уравнение (2), и подставим соответствующие данные в уравнение (3):
N = 16 Н · 1,5 м/с = 24 Вт.
Ответ. 24 Вт.
Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения X груза от времени T . Определите, чему равна масса груза. Ответ округлите до целого числа.

Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза Х от времени T , определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π выразим массу M груза.
| = | T | ; | M | = | T 2 | ; M = K | T 2 | ; M = 200 H/м | (4 с) 2 | = 81,14 кг ≈ 81 кг. |
| 2π | K | 4π 2 | 4π 2 | 39,438 |
Ответ: 81 кг.
На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите Два верных утверждения и укажите в ответе их номера.

Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н. Изображенная на рисунке система блоков не дает выигрыша в силе. H , нужно вытянуть участок веревки длиной 3H . Для того чтобы медленно поднять груз на высоту HH .
Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:
Для того чтобы медленно поднять груз на высоту H , нужно вытянуть участок веревки длиной 2H . Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?
Увеличивается; Уменьшается; Не изменяется.

Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити F упр, направленная вдоль нити вверх; сила тяжести, направленная вертикально вниз; архимедова сила A , действующая со стороны жидкости на погруженное тело и направленная вверх. По условию задачи масса грузов одинакова, следовательно, модуль действующей на груз силы тяжести не меняется. Так как плотность грузов разная, то объем тоже будет разный
Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж
Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М.
Testet. ru
29.07.2018 9:26:26
2018-07-29 09:26:26
Источники:
Http://testet. ru/biogafii/gushchin-reshu-ege-fizika-podgotovka-k-ege-po-fizike-primery. html
Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике » /> » /> .keyword { color: red; } Решу егэ физика 3104
Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике
Решу егэ по физике онлайн. Материалы для подготовки к егэ по физике
ЕГЭ по физике – экзамен, который не входит в перечень испытаний обязательных для сдачи всеми выпускниками. Физику выбирают потенциальные студенты инженерных специальностей. Причем, каждый ВУЗ устанавливает свою планку – в престижных учебных заведениях она может быть очень высокой. Это должен понимать выпускник, начиная подготовку к экзамену. Цель экзамена – проверка уровня знаний и умений, полученных в ходе школьного обучения, на соответствие нормам и стандартам, указанным в программе.
- На экзамен отводится практически 4 часа – 235 минут, это время необходимо правильно распределить между заданиями, чтобы успешно справиться со всеми, не теряя ни одной минуты. Разрешается брать с собой калькулятор, поскольку для выполнения заданий требуется множество сложных расчетов. Также можно взять линейку. Работа состоит из трех частей, каждая имеет свои особенности, состоит из заданий разного уровня сложности.
Физика относится к сложным предметам, приблизительно каждый 15-1 сдает этот экзамен ежегодно, чтобы поступить в технический ВУЗ. Предполагается, что выпускник с такими целями не будет учить предмет «с нуля», чтобы подготовиться к ЕГЭ.
Чтобы удачно пройти испытание, необходимо:
- Начинать повторение материала заранее, подходить к вопросу комплексно; Активно применять теорию на практике – решать много заданий разного уровня сложности; Заниматься самообразованием; Проходить онлайн тестирование по вопросам за прошлые годы.
Подготовка к ОГЭ и ЕГЭ
Среднее общее образование
Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)
Линия УМК А. В. Грачева. Физика (7-9)
Линия УМК А. В. Перышкина. Физика (7-9)
Подготовка к ЕГЭ по физике: примеры, решения, объяснения
Лебедева Алевтина Сергеевна, учитель физики, стаж работы 27 лет. Почетная грамота Министерства образования Московской области (2013 год), Благодарность Главы Воскресенского муниципального района (2015 год), Грамота Президента Ассоциации учителей математики и физики Московской области (2015 год).
В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т. е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.
На рисунке представлен график зависимости модуля скорости от времени T . Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость V = 10 м/с, т. е.
| S = | (30 + 20) С | 10 м/с = 250 м. |
| 2 |
Ответ. 250 м.
Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени T . Определите модуль силы натяжения троса в течение подъема.


Решение. По графику зависимости проекции скорости V груза на ось, направленную вертикально вверх, от времени T , можно определить проекцию ускорения груза
| A = | ∆V | = | (8 – 2) м/с | = 2 м/с 2 . |
| ∆T | 3 с |
На груз действуют: сила тяжести, направленная вертикально вниз и сила натяжения троса, направленная вдоль троса вертикально вверх смотри рис. 2. Запишем основное уравнение динамики. Воспользуемся вторым законом Ньютона. Геометрическая сумма сил действующих на тело равна произведению массы тела на сообщаемое ему ускорение.
Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем
T – Mg = Ma (2);
Из формулы (2) модуль силы натяжения
Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.
Ответ . 1200 Н.
Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью модуль которой равен 1, 5 м/с, прикладывая к нему силу так, как показано на рисунке (1). При этом модуль действующей на тело силы трения скольжения равен 16 Н. Чему равна мощность, развиваемая силой F ?


Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.
Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения тр. и сила, с которой тело тащат. Проекция силы трения отрицательная, так как вектор силы не совпадает с направлением оси Х . Проекция силы F положительная. Напоминаем, для нахождения проекции опускаем перпендикуляр из начала и конца вектора на выбранную ось. С учетом этого имеем: F cosα – F тр = 0; (1) выразим проекцию силы F , это F cosα = F тр = 16 Н; (2) тогда мощность, развиваемая силой, будет равна N = F cosα V (3) Сделаем замену, учитывая уравнение (2), и подставим соответствующие данные в уравнение (3):
N = 16 Н · 1,5 м/с = 24 Вт.
Ответ. 24 Вт.
Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения X груза от времени T . Определите, чему равна масса груза. Ответ округлите до целого числа.

Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза Х от времени T , определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π выразим массу M груза.
| = | T | ; | M | = | T 2 | ; M = K | T 2 | ; M = 200 H/м | (4 с) 2 | = 81,14 кг ≈ 81 кг. |
| 2π | K | 4π 2 | 4π 2 | 39,438 |
Ответ: 81 кг.
На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите Два верных утверждения и укажите в ответе их номера.

Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н. Изображенная на рисунке система блоков не дает выигрыша в силе. H , нужно вытянуть участок веревки длиной 3H . Для того чтобы медленно поднять груз на высоту HH .
Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:
Для того чтобы медленно поднять груз на высоту H , нужно вытянуть участок веревки длиной 2H . Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?
Увеличивается; Уменьшается; Не изменяется.

Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити F упр, направленная вдоль нити вверх; сила тяжести, направленная вертикально вниз; архимедова сила A , действующая со стороны жидкости на погруженное тело и направленная вверх. По условию задачи масса грузов одинакова, следовательно, модуль действующей на груз силы тяжести не меняется. Так как плотность грузов разная, то объем тоже будет разный
Плотность железа 7800 кг/м 3 , а алюминиевого груза 2700 кг/м 3 . Следовательно, V ж ЕДИНЫЙ ГОСУДАРСТВЕННЫЙ ЭКЗАМЕН ПО ФИЗИКЕ ДЛИТСЯ 235 мин
2) СТРУКТУРА КИМов — 2018 и 2019 по сравнению с 2017г. несколько ИЗМЕНИЛАСЬ: Вариант экзаменационной работы будет состоять из двух частей и включит в себя 32 задания. Часть 1 будет содержать 24 задания с кратким ответом, в том числе задания с самостоятельной записью ответа в виде числа, двух чисел или слова, а также задания на установление соответствия и множественный выбор, в которых ответы необходимо записать в виде последовательности цифр. Часть 2 будет содержать 8 заданий, объединенных общим видом деятельности – решение задач. Из них 3 задания с кратким ответом (25–27) и 5 заданий (28–32), для которых необходимо привести развернутый ответ. В работу будут включены задания трех уровней сложности. Задания базового уровня включены в часть 1 работы (18 заданий, из которых 13 заданий с записью ответа в виде числа, двух чисел или слова и 5 заданий на соответствие и множественный выбор). Задания повышенного уровня распределены между частями 1 и 2 экзаменационной работы: 5 заданий с кратким ответом в части 1, 3 задания с кратким ответом и 1 задание с развернутым ответом в части 2. Последние четыре задачи части 2 являются заданиями высокого уровня сложности. Часть 1 экзаменационной работы будет включать два блока заданий: первый проверяет освоение понятийного аппарата школьного курса физики, а второй – овладение методологическими умениями. Первый блок включает 21 задание, которые группируются, исходя из тематической принадлежности: 7 заданий по механике, 5 заданий по МКТ и термодинамике, 6 заданий по электродинамике и 3 по квантовой физике.
Новым заданием базового уровня сложности является последнее задание первой части (24 позиция), приуроченное к возвращению курса астрономии в школьную программу. Задание имеет характеристику типа «выбор 2 суждений из 5». Задание 24, как и другие аналогичные задания в экзаменационной работе, оценивается максимально в 2 балла, если верно указаны оба элемента ответа, и в 1 балл, если в одном из элементов допущена ошибка. Порядок записи цифр в ответе значения не имеет. Как правило, задания будут иметь контекстный характер, т. е. часть данных, необходимых для выполнения задания будут приводиться в виде таблицы, схемы или графика.
В соответствии с этим заданием в кодификаторе добавился подраздел «Элементы астрофизики» раздела «Квантовая физика и элементы астрофизики», включающий следующие пункты:
· Солнечная система: планеты земной группы и планеты-гиганты, малые тела Солнечной системы.
· Звёзды: разнообразие звездных характеристик и их закономерности. Источники энергии звезд.
· Современные представления о происхождении и эволюции Солнца и звёзд. Наша галактика. Другие галактики. Пространственные масштабы наблюдаемой Вселенной.
· Современные взгляды на строение и эволюцию Вселенной.
Подробнее о структуре КИМ-2018 Вы можете узнать, посмотрев вебинар с участием М. Ю. Демидовой https://www. youtube. com/watch? v=JXeB6OzLokU либо в документе, приведенном ниже.
Подготовка к ОГЭ и ЕГЭ
Среднее общее образование
Линия УМК А. В. Грачева. Физика (10-11) (баз., углубл.)
Линия УМК А. В. Грачева. Физика (7-9)
Линия УМК А. В. Перышкина. Физика (7-9)
Подготовка к ЕГЭ по физике: примеры, решения, объяснения
Лебедева Алевтина Сергеевна, учитель физики, стаж работы 27 лет. Почетная грамота Министерства образования Московской области (2013 год), Благодарность Главы Воскресенского муниципального района (2015 год), Грамота Президента Ассоциации учителей математики и физики Московской области (2015 год).
В работе представлены задания разных уровней сложности: базового, повышенного и высокого. Задания базового уровня, это простые задания, проверяющие усвоение наиболее важных физических понятий, моделей, явлений и законов. Задания повышенного уровня направлены на проверку умения использовать понятия и законы физики для анализа различных процессов и явлений, а также умения решать задачи на применение одного-двух законов (формул) по какой-либо из тем школьного курса физики. В работе 4 задания части 2 являются заданиями высокого уровня сложности и проверяют умение использовать законы и теории физики в измененной или новой ситуации. Выполнение таких заданий требует применения знаний сразу из двух трех разделов физики, т. е. высокого уровня подготовки. Данный вариант полностью соответствует демонстрационному варианту ЕГЭ 2017 года, задания взяты из открытого банка заданий ЕГЭ.
На рисунке представлен график зависимости модуля скорости от времени T . Определите по графику путь, пройденный автомобилем в интервале времени от 0 до 30 с.

Решение. Путь, пройденный автомобилем в интервале времени от 0 до 30 с проще всего определить как площадь трапеции, основаниями которой являются интервалы времени (30 – 0) = 30 c и (30 – 10) = 20 с, а высотой является скорость V = 10 м/с, т. е.
| S = | (30 + 20) С | 10 м/с = 250 м. |
| 2 |
Ответ. 250 м.
Груз массой 100 кг поднимают вертикально вверх с помощью троса. На рисунке приведена зависимость проекции скорости V груза на ось, направленную вверх, от времени T . Определите модуль силы натяжения троса в течение подъема.


Решение. По графику зависимости проекции скорости V груза на ось, направленную вертикально вверх, от времени T , можно определить проекцию ускорения груза
| A = | ∆V | = | (8 – 2) м/с | = 2 м/с 2 . |
| ∆T | 3 с |
На груз действуют: сила тяжести, направленная вертикально вниз и сила натяжения троса, направленная вдоль троса вертикально вверх смотри рис. 2. Запишем основное уравнение динамики. Воспользуемся вторым законом Ньютона. Геометрическая сумма сил действующих на тело равна произведению массы тела на сообщаемое ему ускорение.
Запишем уравнение для проекции векторов в системе отсчета, связанной с землей, ось OY направим вверх. Проекция силы натяжения положительная, так как направление силы совпадает с направлением оси OY, проекция силы тяжести отрицательная, так как вектор силы противоположно направлен оси OY, проекция вектора ускорения тоже положительная, так тело движется с ускорением вверх. Имеем
T – Mg = Ma (2);
Из формулы (2) модуль силы натяжения
Т = M (G + A ) = 100 кг (10 + 2) м/с 2 = 1200 Н.
Ответ . 1200 Н.
Тело тащат по шероховатой горизонтальной поверхности с постоянной скоростью модуль которой равен 1, 5 м/с, прикладывая к нему силу так, как показано на рисунке (1). При этом модуль действующей на тело силы трения скольжения равен 16 Н. Чему равна мощность, развиваемая силой F ?


Решение. Представим себе физический процесс, заданный в условии задачи и сделаем схематический чертеж с указанием всех сил, действующих на тело (рис.2). Запишем основное уравнение динамики.
Выбрав систему отсчета, связанную с неподвижной поверхностью, запишем уравнения для проекции векторов на выбранные координатные оси. По условию задачи тело движется равномерно, так как его скорость постоянна и равна 1,5 м/с. Это значит, ускорение тела равно нулю. По горизонтали на тело действуют две силы: сила трения скольжения тр. и сила, с которой тело тащат. Проекция силы трения отрицательная, так как вектор силы не совпадает с направлением оси Х . Проекция силы F положительная. Напоминаем, для нахождения проекции опускаем перпендикуляр из начала и конца вектора на выбранную ось. С учетом этого имеем: F cosα – F тр = 0; (1) выразим проекцию силы F , это F cosα = F тр = 16 Н; (2) тогда мощность, развиваемая силой, будет равна N = F cosα V (3) Сделаем замену, учитывая уравнение (2), и подставим соответствующие данные в уравнение (3):
N = 16 Н · 1,5 м/с = 24 Вт.
Ответ. 24 Вт.
Груз, закрепленный на легкой пружине жесткостью 200 Н/м, совершает вертикальные колебания. На рисунке представлен график зависимости смещения X груза от времени T . Определите, чему равна масса груза. Ответ округлите до целого числа.

Решение. Груз на пружине совершает вертикальные колебания. По графику зависимости смещения груза Х от времени T , определим период колебаний груза. Период колебаний равен Т = 4 с; из формулы Т = 2π выразим массу M груза.
| = | T | ; | M | = | T 2 | ; M = K | T 2 | ; M = 200 H/м | (4 с) 2 | = 81,14 кг ≈ 81 кг. |
| 2π | K | 4π 2 | 4π 2 | 39,438 |
Ответ: 81 кг.
На рисунке показана система из двух легких блоков и невесомого троса, с помощью которого можно удерживать в равновесии или поднимать груз массой 10 кг. Трение пренебрежимо мало. На основании анализа приведенного рисунка выберите Два верных утверждения и укажите в ответе их номера.

Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 100 Н. Изображенная на рисунке система блоков не дает выигрыша в силе. H , нужно вытянуть участок веревки длиной 3H . Для того чтобы медленно поднять груз на высоту HH .
Решение. В данной задаче необходимо вспомнить простые механизмы, а именно блоки: подвижный и неподвижный блок. Подвижный блок дает выигрыш в силе в два раза, при этом участок веревки нужно вытянуть в два раза длиннее, а неподвижный блок используют для перенаправления силы. В работе простые механизмы выигрыша не дают. После анализа задачи сразу выбираем нужные утверждения:
Для того чтобы медленно поднять груз на высоту H , нужно вытянуть участок веревки длиной 2H . Для того чтобы удерживать груз в равновесии, нужно действовать на конец веревки с силой 50 Н.
В сосуд с водой полностью погружен алюминиевый груз, закрепленный на невесомой и нерастяжимой нити. Груз не касается стенок и дна сосуда. Затем в такой же сосуд с водой погружают железный груз, масса которого равна массе алюминиевого груза. Как в результате этого изменятся модуль силы натяжения нити и модуль действующей на груз силы тяжести?
Увеличивается; Уменьшается; Не изменяется.

Решение. Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования: это масса тела и жидкость, в которую погружают тело на нити. После этого лучше выполнить схематический рисунок и указать действующие на груз силы: сила натяжения нити F упр, направленная вдоль нити вверх; сила тяжести, направленная вертикально вниз; архимедова сила A , действующая со стороны жидкости на погруженное тело и направленная вверх. По условию задачи масса грузов одинакова, следовательно, модуль действующей на груз силы тяжести не меняется. Так как плотность грузов разная, то объем тоже будет разный
Заготовьте этот чудесный, овощной салат, и у вас зимой всегда будет наготове вкусный перекус. У приятный, кисло-сладкий привкус и летний аромат. Овощи тушатся в томатном соусе, поэтому в салате образуется вкусная подливка, которая идеально смягчит гарнир
Описание сделанный своими руками уже долгое количество времени считается не просто вкусным и полезным, а еще и целебным! Не зря в Китае грушевые деревья считаются символом долголетия. Срок их существования намного больше, чем у остальных деревьев. А грек
Здравствуйте, мои дорогие Умные Хозяйки и Хозяева! Признавайтесь, кому уже надоело есть просто так пасхальные яйца😀😀😀?! Для вас рецепт простой и вкусной закуски, которую можно приготовить буквально за пять минут👏! Получается ярко, интересно, красиво! Не с
Дидактические игры по экологическому воспитанию для старших дошкольников. Дидактические игры экологического содержания помогают увидеть целостность отдельного организма и экосистемы, осознать уникальность каждого объекта природы, понять, что неразумное вм
Анализируем условие задачи и выделяем те параметры, которые не меняются в ходе исследования это масса тела и жидкость, в которую погружают тело на нити.
Rybokean. ru
04.01.2018 9:49:40
2018-01-04 09:49:40
Источники:
Http://rybokean. ru/reshu-ege-po-fizike-onlain-materialy-dlya-podgotovki-k-ege-po. html
Канал видеоролика: Физика для ЕГЭ
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Физике (листай):
С этим видео ученики смотрят следующие ролики:

8 задание 1 варианта ЕГЭ 2020 по физике М.Ю. Демидовой (30 вариантов)
Физика для ЕГЭ

9 задание 1 варианта ЕГЭ 2020 по физике М.Ю. Демидовой (30 вариантов)
Физика для ЕГЭ

6 задание 1 варианта ЕГЭ 2020 по физике М.Ю. Демидовой (30 вариантов)
Физика для ЕГЭ

7 задание 1 варианта ЕГЭ 2020 по физике М.Ю. Демидовой (30 вариантов)
Физика для ЕГЭ
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
19.11.2019
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
ЕГЭ 2017. Физика. Демидова М. Ю. 30 вариантов. Вариант 4. Решение
Задание 1. Координата тела x меняется с течением времени согласно закону x = 2 — 4t + t^2, где все величины выражены в СИ. Определите проекцию ускорения ax этого тела.
Решение.
Ускорение – это скорость изменения скорости, то есть производная от скорости. Скорость – это производная пути по времени. Используя функцию изменения координаты x найдем сначала проекцию скорости
,
а затем, проекцию ускорения:
м/с2.
Ответ: 2.
Задание 2. Две планеты с одинаковыми массами обращаются по круговым орбитам вокруг звезды. Для первой из них сила притяжения к звезде в 9 раз меньше, чем для второй. Каково отношение R1/R2 радиусов орбит первой и второй планет?
Решение.
Планеты притягиваются друг к другу по закону всемирного притяжения . Для первой планеты массы m и радиусом R1 имеем:
,
а для второй с массой m и радиусом R2:
.
Тогда отношение радиусов этих планет есть величина
В задаче сказано, что , следовательно,
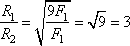
Ответ: 3.
Задание 3. Тело массой 3,6 кг движется по прямой в одном направлении. Под действием постоянной силы за 10 с импульс тела изменился на 60 кг • м/с. Определите модуль силы, действующей на тело.
Решение.
За 10 секунд импульс изменился на 60, это значит, что условно в начальный момент времени импульс был равен 0, а через 10 с стал равен 60, то есть , откуда
.
Так как сила была постоянна, то и ускорение тела было постоянно. Тело за 10 с набрало скорость v=60/m, значит, ускорение равно
.
Модуль силы, действующей на тело, равен
Н.
Ответ: 6.
Задание 4. Шарик массой 0,2 кг, подвешенный на лёгкой пружине, совершает свободные гармонические колебания вдоль вертикальной прямой. Какой должна быть масса шарика, чтобы частота его свободных вертикальных гармонических колебаний на этой же пружине была в 2 раза меньше?
Решение.
Частота колебаний пружинного маятника с грузом массой m=0,2 кг и жесткостью пружины k определяется формулой
.
Для частоты в 2 раза меньше, то есть для v/2 эта формула запишется в виде
.
Из последнего выражения видно, что массу груза нужно увеличить в 4 раза, то есть нужно взять кг.
Ответ: 0,8.
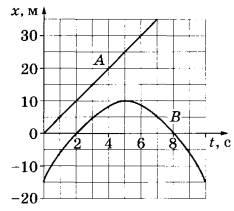
Задание 5. На рисунке приведены графики зависимости координаты от времени для двух тел: A и B, движущихся по прямой, вдоль которой и направлена ось Ох. Выберите два верных утверждения о характере движения тел.
1) Тело А движется равноускоренно, а тело В — с переменным ускорением.
2) Скорость тела В в момент времени t = 5 с равна 0 м/с.
3) Скорость тела А в момент времени t = 5 с равна 25 м/с.
4) Проекция ускорения тела В на ось Ох отрицательна.
5) Проекция скорости тела В на ось Ох на интервале времени от t1 = 0 до t2 = 2 с отрицательна.
Решение.
1) Для тела А имеем линейную зависимость перемещения от времени. Это значит, что тело движется с одной и той же скоростью, то есть равномерно. Для тела В имеем кривую, которая получается при уменьшающемся ускорении.
2) В момент времени t=5 с тело B меняет направление своего движения, а значит, имеем нулевую скорость.
3) При t=5 с тело A имеем координату x=25, следовательно, скорость тела в этот момент равна м/с.
4) Из графика видно, что координата x тела B сначала меняется быстрее, затем все медленнее и медленнее, пока при t=5 не перестанет меняться вовсе. Затем, эта координата начинает уменьшаться со все возрастающей скоростью. Это говорит о том, что тело B движется с постоянным замедлением скорости, то есть с отрицательным ускорением.
5) В интервале времени от 0 до 2 с тело движется в одном направлении с увеличивающейся скоростью, следовательно, проекция скорости на ось Ox – положительная.
Ответ: 24.
Задание 6. На шероховатой наклонной плоскости покоится деревянный брусок. Угол наклона плоскости уменьшили. Как изменились при этом сила трения покоя, действующая на брусок, и коэффициент трения бруска о плоскость? Для каждой величины определите соответствующий характер изменения:
1) увеличилась
2) уменьшилась
3) не изменилась
Решение.
Так как брусок покоится на месте, то сила трения покоя уравновешивает силу соскальзывания бруска (тангенциальную силу). При уменьшении угла наклона тангенциальная сила уменьшается, следовательно, в соответствии с третьим законом Ньютона, сила трения покоя также уменьшается.
Коэффициент трения бруска о поверхность зависит только от материала соприкасающихся плоскостей и их площади, то есть он не изменится.
Ответ: 23.
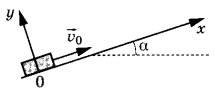
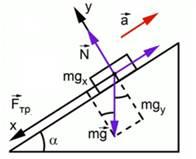
Задание 7. После удара шайба массой m начала скользить с начальной скоростью v0 вверх по плоскости, установленной под углом а к горизонту (см. рисунок). Переместившись вдоль оси Ох на расстояние s, шайба соскользнула в исходное положение. Коэффициент трения шайбы о плоскость равен µ. Формулы А и Б позволяют рассчитать значения физических величин, характеризующих движение шайбы.
Установите соответствие между формулами и физическими величинами, значение которых можно рассчитать по этим формулам.
|
ФОРМУЛЫ |
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) модуль ускорения шайбы при её движении вверх 2) модуль работы силы трения при движении шайбы вверх 3) модуль работы силы трения при движении шайбы от старта до финиша 4) модуль ускорения шайбы при её движении вниз |
Решение.
На рисунке ниже показаны силы, действующие на тело, при его движении по наклонной плоскости.
Равнодействующая сила, действующая на тело, движущееся вверх по наклонной плоскости, складывается из трех сил: силы тяжести, силы реакции опоры и силы трения. Проекция этих трех сил на ось Ox дает:
,
Сила трения равна проекции силы тяжести на ось Oy, умноженная на коэффициент трения µ:
,
и для равнодействующей силы можно записать
А) Здесь имеем формулу — это работа силы трения. Ответ под номером 2.
Б) Модуль ускорения шайбы при ее движении вверх – ответ под номером 1.
Ответ: 21.
Задание 8. Температура неона уменьшилась с 27 °С до -23 °С. Во сколько раз уменьшилась средняя кинетическая энергия его молекул?
Решение.
Кинетическую энергию молекул можно найти по формуле . Для первой температуры T=27+273=300 K, имеем:
,
для второй T=-23+273=250 K:
,
и их отношение дает
.
Ответ: 1,2.
Задание 9. Парциальное давление водяных паров, содержащихся в воздухе при температуре 100 °С, равно 70 кПа. Определите относительную влажность воздуха.
Решение.
Относительная влажность воздуха определяется выражением
,
где — парциальное давление газа;
— равновесное давление насыщенного пара.
Давление насыщенного пара выбираем из таблицы, имеем . Следовательно, относительная влажность равна
.
Ответ: 70.
Задание 10. Тепловая машина с КПД 30 % за цикл работы получает от нагревателя количество теплоты, равное 5 кДж. Какое количество теплоты машина отдаёт за цикл холодильнику?
Решение.
КПД тепловой машины можно определить формулой
,
где — количество теплоты, полученное от нагревателя;
— количество теплоты, отданное холодильнику. В задаче дано
Дж и КПД 30%, имеем:
,
подставляем числовые значения, имеем:
Дж
что составляет 3,5 кДж.
Ответ: 3,5.
Задание 11. Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления р газа от объёма V. Количество вещества газа при этом не меняется. Из приведённого ниже списка выберите два правильных утверждения, характеризующие процессы на графике, и укажите их номера.
1) Абсолютная температура газа минимальна в состоянии 2.
2) В процессе 1-2 абсолютная температура газа изобарно увеличилась в 2 раза.
3) В процессе 2-3 абсолютная температура газа изохорно уменьшилась в 2 раза.
4) Концентрация газа минимальна в состоянии 1.
5) В ходе процесса 1-2-3 среднеквадратическая скорость теплового движения молекул газа уменьшается в 4 раза.
Решение.
1) Из уравнения состояния идеального газа для участка 1-2 следует, что
, значит
и уменьшение объема влечет уменьшение температуры. На участке 2-3 имеем
и
, следовательно, с уменьшением давления происходит уменьшение температуры. Таким образом, минимум температуры будет наблюдаться в точке 3.
2) В п. 1 уже было показано, что температура изобарно уменьшилась.
3) На участке 2-3 имеем изохорный процесс, при котором температура уменьшается пропорционально давлению. Для данного процесса будет справедливо отношение:
,
откуда, температура в точке 3
,
то есть уменьшается в 2 раза.
4) Концентрация газа минимальна в точке максимума объема. Точка 1 является точкой, где объем максимален, следовательно, и концентрация газа в ней минимальна.
5) Среднеквадратическая скорость молекул меняется пропорционально температуре по закону . В ходе процесса 1-2-3 температура сначала уменьшилась (на участке 1-2) в
2 раза, а затем, на участке 2-3 – еще в 2 раза (см. п. 3). Таким образом, температура уменьшилась в 4 раза, и среднеквадратическая скорость уменьшилась в 16 раз.
Ответ: 34.
Задание 12. В цилиндре под поршнем находятся жидкость и её насыщенный пар (см. рисунок). Как будут изменяться масса пара и давление в жидкости у её поверхности при медленном перемещении поршня вниз при постоянной температуре, пока поршень не коснётся поверхности жидкости?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Решение.
При медленном перемещении поршня часть молекул пара будет постоянно переходить в жидкость, и масса пара будет уменьшаться. При этом давление пара на жидкость (и жидкости на пар) будет постоянно. Таким образом, масса пара будет уменьшаться, а давление в жидкости у ее поверхности оставаться постоянным.
Ответ: 23.
Задание 13. На рисунке показаны сечения двух параллельных длинных прямых проводников и направления токов в них. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке А, находящейся на прямой, соединяющей проводники? Ответ запишите словом (словами).
Решение.
Вектор магнитной индукции направлен по касательной к магнитным линиям, циркулирующие вокруг проводника с током. Направление магнитных линий можно найти по правилу буравчика. Для первого проводника с током I1 направляем буравчик резьбой вглубь рисунка (от наблюдателя) и крутим ручку так, чтобы направление движения буравчика совпадало с направление движения тока в проводнике. Для первого проводника получаем, что магнитные линии будут циркулировать по часовой стрелке, следовательно, в точке А вектор магнитной индукции будет направлен вертикально вниз.
Аналогично для второго проводника с током I2. По правилу буравчика получаем движение магнитных линий против часовой стрелки и вектор магнитной индукции в точке А будет направлен вертикально вверх.
Результирующий вектор магнитной индукции – это суперпозиция (в данном случае просто сложение) двух векторов. Так как токи в проводниках равны, то вектор магнитной индукции, направленный вверх будет больше вектора магнитной индукции, направленный вниз (так как второй проводник ближе к точке А) и результирующий вектор будет направлен вверх.
Ответ: вверх.
Задание 14. Пять одинаковых резисторов соединены в электрическую цепь, через которую течёт ток I = 6 А (см. рисунок). Идеальный вольтметр показывает напряжение U = 15 В. Чему равно сопротивление одного резистора?
Решение.
Через сопротивление, к которому подключен вольтметр, течет ток I=6:2=3 А, так как в точке ветвления ток разделяется на два равных потока (так как сопротивление каждой линии одинаково). Тогда по закону Ома, имеем:
Ом.
Ответ: 5.
Задание 15. Луч света падает на плоское зеркало. Угол падения равен 30°. Чему равен угол между отражённым лучом и плоскостью зеркала?
Решение.
Согласно законам оптики угол падения равен углу отражения, то есть 30 градусов. Тогда угол между этими двумя лучами будет составлять (см. рисунок)
30+30=60 градусов.
Ответ: 60.
Задание 16. На рисунке приведён график зависимости силы тока от времени в колебательном контуре, образованном конденсатором и катушкой, индуктивность которой равна 0,3 Гн. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
1) Период электромагнитных колебаний равен 5 мс.
2) Максимальное значение энергии электрического поля конденсатора равно 0,9 мкДж.
3) В момент времени 3 мс заряд конденсатора равен нулю.
4) В момент времени 4 мс энергия магнитного поля катушки достигает своего минимума.
5) За первые 6 мс энергия магнитного поля катушки достигла своего максимума 2 раза.
Решение.
1) в колебательном контуре колебание начинается с разрядки конденсатора, что приводит к появлению тока в цепи, затем, возникающая ЭДС в катушке, вновь начинает заряжать конденсатор, но с противоположной полярностью. После этого процесс повторяется, то начинает течь в обратную сторону и повторная зарядка конденсатора (график тока в отрицательной области) с прежней полярностью завершает колебательный процесс. Таким образом, период колебаний составляет 4 мс.
2) Согласно закону сохранения энергии можно записать, что
Из графика видно, что мА, следовательно,
то есть 5,4 мкДж.
3) В точке, где ток максимален, конденсатор полностью разряжен (вне зависимости от знака тока).
4) Верно, при t=4 мс, заканчивается период одного колебания и вся энергия сосредотачивается в конденсаторе.
5) В диапазоне 6 с видим три пика тока, следовательно, катушка трижды достигала своего максимума по энергии.
Ответ: 34.
Задание 17. Плоский конденсатор с воздушным зазором между обкладками подключён к источнику постоянного напряжения. Как изменятся напряжённость поля в зазоре между обкладками конденсатора и величина заряда на его обкладках, если увеличить зазор между ними?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Решение.
Напряженность поля между обкладками плоского конденсатора определяется выражением
,
где U – величина приложенного напряжения; d – расстояние между обкладками конденсатора. Из этой формулы видно, что при увеличении зазора d напряженность поля E между обкладками будет уменьшаться.
Величина заряда на обкладках q пропорциональна емкости конденсатора C:
,
а емкость C, в свою очередь, зависит от расстояния d между обкладками по формуле
,
где — абсолютная диэлектрическая проницаемость; S – площадь обкладок конденсатора. Объединяя последние две формулы, имеем:
,
то есть с увеличением d заряд q будет уменьшаться.
Ответ: 22.
Задание 18. Установите соответствие между формулами для расчёта физических величин в цепях постоянного тока и названиями этих величин. В формулах использованы обозначения: R — сопротивление резистора; I — сила тока; U — напряжение на резисторе.
|
ФОРМУЛЫ |
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ 1) напряжение на резисторе 2) сила тока 3) мощность электрического тока 4) работа электрического тока |
Решение.
А) Выражение — мощность тока. Вариант ответа под номером 3.
Б) Величина — сила тока, что следует из закона Ома. Ответ под номером 2.
Ответ: 32.
Задание 19. На рисунке представлен фрагмент Периодической системы элементов Д. И. Менделеева. Под названием каждого элемента приведены массовые числа его основных стабильных изотопов. При этом нижний индекс около массового числа указывает (в процентах) распространённость изотопа в природе.
Укажите число протонов и число нейтронов в ядре наиболее распространённого стабильного изотопа цинка.
Решение.
Цинк, обозначение Zn имеет порядковый номер 30. Это означает, что в атоме цинка находится 30 протонов. Из таблицы видно, что наиболее распространенный изотоп цинка имеет массовое число 64, то есть сумма протонов и нейтронов в ядре этого изотопа равна 64. Отсюда получаем число нейтронов: 64-30=34.
Ответ: 3034.
Задание 20. Период полураспада изотопа висмута равен пяти дням. Какая масса этого изотопа осталась через 10 дней в образце, содержавшем первоначально 80 мг
?
Решение.
Закон радиоактивного распада изотопа имеет вид:
,
где мг – начальный объем изотопа; t=10 дней – период распада; T=5 дней – период полураспада. Таким образом, получаем, что через 10 дней останется
мг.
Ответ: 20.
Задание 21. Ядро испытывает альфа-распад. Как при этом изменяются заряд ядра и число нейтронов в ядре?
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Решение.
При альфа-распаде порядковый номер уменьшается на 2 единицы, то есть ядро теряет 2 протона, а массовое число на 4 единицы, то есть происходит потеря еще и двух нейтронов (массовое число – это сумма протонов и нейтронов). При потере 2 протонов положительный заряд ядра уменьшается. Число нейтронов в ядре также уменьшается как было сказано ранее.
Ответ: 22.
Задание 22. С помощью барометра проводились измерения атмосферного давления. Верхняя шкала барометра проградуирована в кПа, а нижняя шкала — в мм рт. ст. Погрешность измерений давления равна цене деления шкалы барометра. Чему равно атмосферное давление по результатам этих измерений?
Запишите в ответ показания барометра с учётом погрешности измерений.
Решение.
Ответ нужно дать в мм. рт. ст. Поэтому смотрим на нижнюю шкалу барометра, по которой видим уровень атмосферного давления в 746 мм. рт. ст. Цена одного деления шкалы равна 1 мм. рт. ст., следовательно, имеем наблюдение
мм. рт. ст.
Ответ: .
Задание 23. Необходимо экспериментально изучить зависимость частоты свободных электромагнитных колебаний в колебательном контуре от величины индуктивности катушки. Какие две установки следует использовать для проведения такого исследования?
В ответ запишите номера выбранных установок.
Решение.
Период колебаний в колебательном контуре определяется выражением
и так как нужно исследовать данную величину при различных индуктивностях L, то следует взять две установки с одинаковой емкостью, но разными индуктивностями. Этому условию удовлетворяют установки под номерами 3 и 5.
Ответ: 35.
Задание 24. Тело массой 2 кг брошено с некоторой высоты вертикально вверх с начальной скоростью v0 и упало на землю со скоростью 2v0. Потенциальная энергия тела относительно поверхности земли в момент броска была равна 75 Дж. С какой начальной скоростью бросили тело? Сопротивлением воздуха пренебречь.
Решение.
Потенциальная энергия определяется выражением , откуда высота броска h, равна
метра.
Тело упало на землю со скоростью м/с, значит, его кинетическая энергия составляла
Дж. Из закона сохранения энергии можно сказать, что потенциальная энергия тела в самой верхней своей точке полностью перешла в кинетическую при подлете к земле, то есть
,
откуда максимальная высота полета тела
метров.
Отсюда делаем вывод, что тело было брошено с начальной скоростью и поднялось на высоту
метра. При движении вертикально вверх начальная скорость уменьшается на величину ускорения свободного падения g и в максимальной точке становится равна 0, то есть
,
откуда
.
Подставим данное значение в формулу вычисления высоты
,
получим:
Выражаем скорость, имеем:
Ответ: 5.
Задание 25. На рисунке изображён график изменения состояния одноатомного идеального газа в количестве 20 моль. Какая температура соответствует состоянию 2, если в состоянии 1 она равна 300 К?
Решение.
Запишем уравнение Менделеева-Клайперона для идеального газа:
.
где p, V — давление и объем газа; v=20 моль – количество газа; R=8,31 – универсальная газовая постоянная. Так как график исходит из точки 0, то имеем линейную зависимость между давлением и объемом вида , где
— некоторый коэффициент. Тогда в точке 1 уравнение примет вид:
В точке 2 имеем:
,
откуда
К.
Ответ: 1200.
Задание 26. Прямолинейный проводник длиной l = 0,1 м, по которому течёт ток I, расположен в однородном магнитном поле под углом 90° к вектору В. Модуль индукции магнитного поля В = 0,5 Тл. Сила, действующая на проводник со стороны магнитного поля, F = 0,2 Н. Чему равна сила тока I?
Решение.
На проводник с током будет действовать сила Ампера, вычисляемая как
и при , имеем
.
Из этого выражения находим силу тока в проводнике:
А.
Ответ: 4.
Задание 27. В вертикальном цилиндре с гладкими стенками под массивным металлическим поршнем находится идеальный газ. В первоначальном состоянии 1 поршень опирается на жёсткие выступы на внутренней стороне стенок цилиндра (рис. 1), а газ занимает объём V₀ и находится под давлением р₀, равным внешнему атмосферному. Его температура в этом состоянии равна Т₀. Газ медленно нагревают, и он переходит из состояния 1 в состояние 2, в котором давление газа равно 2р₀, а его объём равен 2V₀ (рис. 2). Количество вещества газа при этом не меняется. Постройте график зависимости давления газа от его температуры при переходе из состояния 1 в состояние 2. Ответ поясните, указав, какие явления и закономерности Вы использовали для объяснения.
Решение.
Определим температуру Т₂ конечного состояния газа. Запишем уравнение Клапейрона — Менделеева для газа в состояниях 1 и 2:
откуда .
Покажем силы, приложенные к поршню, когда он уже не опирается на выступы на стенках цилиндра. Сила тяжести mg и сила давления на поршень со стороны атмосферы постоянны. Поскольку поршень перемещается медленно, сумму приложенных к нему сил считаем равной нулю. Отсюда следует, что сила давления на поршень со стороны газа
тоже постоянна. Значит, её модуль равен
(S — площадь горизонтального сечения поршня) при любом положении поршня выше первоначального.
Таким образом, при
процесс нагревания газа изобарный (
). Определим температуру начала этого процесса
:
откуда .
На отрезке температур процесс нагревания газа изохорный (
). давление газа увеличивается от
до
прямо пропорционально его температуре:
.
Ответ: а) при давление газа
;
б) при процесс нагревания газа изобарный:
. График, изображающий зависимости из п. а) и б), представляет собой ломаную линию.
Задание 28. Однородный тонкий стержень массой m = 1 кг одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную горизонтальную доску, образуя с ней угол а = 30°. Под действием горизонтальной силы F доска движется поступательно влево с постоянной скоростью (см. рисунок). Стержень при этом неподвижен. Найдите коэффициент трения стержня по доске µ, если F = 1 Н. Трением доски по опоре и трением в шарнире пренебречь.
Решение.
В инерциальной системе отсчёта Оху, связанной с Землёй, доска движется поступательно с постоянной скоростью. Поэтому сумма проекций на ось Ох всех сил, приложенных к доске, равна нулю (рис. а): .
На рис. б показаны все силы, приложенные к стержню. Силы реакции шарнира и доски представлены горизонтальными и вертикальными составляющими: и
соответственно. По третьему закону Ньютона
, поэтому
. (1)
По условию задачи стержень покоится, поэтому сумма моментов сил относительно оси шарнира А равна нулю. Обозначив длину стержня через L, запишем это условие:
.
Доска движется относительно стержня, поэтому сила трения является силой трения скольжения: . (3)
Из (1) и (3) следует, что . Поэтому уравнение (2) приводится к виду
,
откуда
Ответ: 0,23.
Задание 29. В школьном физическом кружке изучали уравнение теплового баланса. В одном из опытов использовали два калориметра. В первом калориметре находилась вода при 50 °С, во втором — 200 г льда и 200 г воды при 0 °С. Какая масса воды находилась первоначально в первом калориметре, если после добавления в него всего содержимого второго в первом калориметре установилась температура 2 °С? Теплоёмкостью калориметров пренебречь.
Решение.
Количество теплоты, полученное льдом при его таянии при 0 °С:
(1)
Количество теплоты, полученное водой при её нагревании от 0 °С до температуры t0 = 2 °С:
. (2)
Количество теплоты, отданное водой при её охлаждении от температуры t до температуры t0:
. (3)
Уравнение теплового баланса:
(4)
Объединяя (1)-(4), получаем:
Ответ: 344 г.
Задание 30. Источник тока, два резистора и ключ включены в цепь, как показано на рисунке. На резисторе R₂ при разомкнутом ключе выделяется мощность Р₂ = 1 Вт, а при замкнутом — мощность Р₂’ = 16 Вт. Какая мощность выделяется на резисторе R₁ при разомкнутом ключе? Внутренним сопротивлением источника пренебречь.
Решение.
Ток в цепи до замыкания ключа K
,
где E — ЭДС источника. Мощность, выделяемая соответственно на резисторах R₁ и R₂,
Так как после замыкания ключа ток через резистор R₁ не течёт, искомая мощность, выделяемая на резисторе R₂ после замыкания ключа K,
.
Объединяя уравнения, получаем:
,
откуда
Вт.
Ответ: 3 Вт.
Задание 31. Фотокатод с работой выхода Дж освещается монохроматическим светом с частотой
Гц. Вылетевшие из катода электроны попадают в однородное магнитное поле с индукцией
Тл перпендикулярно линиям индукции этого поля и движутся по окружностям. Каков максимальный радиус такой окружности?
Решение.
Для определения максимальной скорости движения электрона воспользуемся уравнением Эйнштейна для фотоэффекта:
,
откуда
.
Электрон в магнитном поле движется по окружности радиусом R со скоростью v и центростремительным ускорением . Ускорение вызывается силой Лоренца (F = evB) в соответствии со вторым
законом Ньютона:
Подставляя в выражение для радиуса траектории максимальную скорость электрона, получим:
Ответ: 8 мм.
- 10.03.2023
Четвертая тренировочная работа от Статграда по физике в формате ЕГЭ 2023 года. Работа проводилась 7 марта 2023 года. Разбираем все задания из варианта в формате видеоурока.
Ответы на каждое задание будут по ходу видео, вместе с разбором.
- Другие варианты ЕГЭ по физике
Есть вопросы? Задавайте в комментариях ниже.
Вариант с видеоразбором
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить