Добрый день!
Не очень понимаю, что Вы называете объединенным газовым законом. Если , то ответ на Ваш вопрос очень прост. Этот закон попросту нельзя здесь использовать, как и любой другой газовый закон (Бойля-Мариотта, Гей-Люссака, Шарля), поскольку они верны только для постоянного количества вещества,а у нас количество вещества изменяется.
Закон , на самом деле, ведь просто следствие уравнения Клапейрона-Менделеева в случае, если
. Действительно,
. Таким образом, данный закон неформально можно называть законом «изоколичества вещества». А закон Шарля — это «изобрано/изоколичественный» закон.
2017-04-24
В сосуде объемом $V = 3 cdot 10^{-2} м^{3}$ находится $m_{1} = 4 cdot 10^{-3} г$ гелия, $m_{2} = 70 cdot 10^{-3} г$ азота и $N = 5 cdot 10^{21}$ молекул водорода. Каково давление смеси, если ее температура $T = 300 К$?
Решение:
Найдем парциальное давление гелия $p_{1}$. Считая, что гелий распределен по всему объему сосуда, укажем параметры его состояния: $p_{1}, V, T$. Свяжем эти параметры состояния уравнением Менделеева-Клапейрона: $p_{1}V = frac{m_{1}}{ mu_{1}} RT$, где $mu_{1} = 4 cdot 10^{-3} кг/моль$ — молярная масса гелия. Отсюда $p_{1} = frac{m_{1}}{ mu_{1}} frac{RT}{V}$. Аналогично нашем парциальное давление азота $p_{2}: p_{2} = frac{m_{2}}{ mu_{2}} frac{RT}{V}$, где $mu_{2} = 28 cdot 10^{-3} кг/моль$ — молярная масса азота. Для нахождения парциального давления водорода $p_{3}$ воспользуемся уравнением состояния:
$p_{3}V = N k_{Б} T Rightarrow p_{3} = frac{Nk_{Б}T}{V}$. По закону Дальтона давление смеси: $p = p_{1} + p_{2} + p_{3} = frac{m}{ mu_{1}} frac{RT}{V} + frac{m_{2}}{ mu_{2}} frac{RT}{V} + frac{Nk_{Б}T}{V} = frac{T}{V} left ( frac{m_{1}}{ mu_{1}} R + frac{m_{2}}{ mu_{2}} R + N k_{Б} right ) = frac{T}{V} left ( frac{m_{1}}{ mu_{1}} R + frac{m_{2}}{ mu_{2}} R + N frac{R}{N_{A}} right ) = frac{RT}{V} left ( frac{m_{1}}{ mu_{1}} + frac{m_{2}}{ mu_{2}} + frac{N}{N_{A}} right ) = 9,8 cdot 10^{3} Па$.
Как выглядит задача?
Обратите внимание!
Задача содержит в себе два полноценных вопроса: по расчётной и по теоретической (обоснование) частям задачи.
На горизонтальной поверхности неподвижно закреплена абсолютно
гладкая полусфера радиусом R = 2,5 м. С её верхней точки из состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно. Найдите скорость тела в момент отрыва от сферы. Сопротивлением воздуха пренебречь. Обоснуйте применимость используемых законов к решению задачи.
Как оценивается задача?
Задание оценивается по двум критериям:
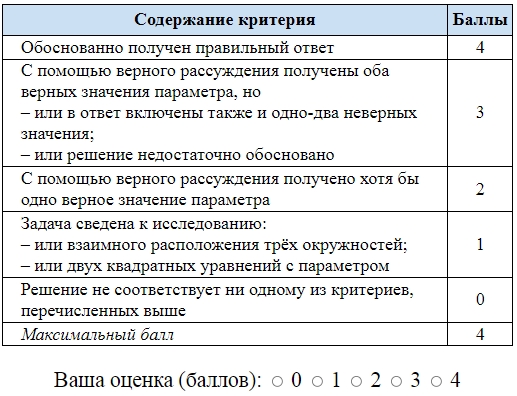
- Критерий 1 оценивает обоснование возможности использования законов и закономерностей (1 балл).
- Критерий 2 – стандартные требования к оформлению расчётной задачи второй части (3 балла).
Итого: максимально можно получить 4 первичных балла.
Как написать обоснование?
- Заново прочитать условие задачи.
- Найти в нем слова-ключи и подчеркнуть их.
- На основе слов-ключей и физических законов сформулировать обоснование.
P.S. Слова-ключи – это подсказки от авторов, наводящие на решение задачи.
Выделим слова-ключи в задаче из примера:
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом R = 2,5 м. С её верхней точки из состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно. Найдите скорость тела в момент отрыва от сферы. Сопротивлением воздуха пренебречь. Обоснуйте применимость используемых законов к решению задачи.
Найденные слова-ключи: абсолютно гладкая поверхность, из состояния покоя, маленькое тело, отрыв, свободное падение, сопротивления воздуха нет.
Теперь на основе найденных слов-ключей сформулируем обоснование:
- Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
- Так как по условию задачи дано маленькое тело, то его можно рассматривать как материальную точку.
- Тело начинает движение из состояния покоя, значит его начальная скорость равна 0.
- Сопротивлением воздуха можно пренебречь, а сфера имеет абсолютно гладкую поверхность, следовательно трения при движении тела по сфере нет, поэтому его механическая энергия при движении по поверхности сферы сохраняется. (Силы сопротивления и трения не вводим, записываем ЗСЭ).
- Поскольку тело описывается моделью материальной точки, условие его отрыва от поверхности сферы 2-м законом Ньютона. В момент отрыва сила реакции опоры N = 0. (отрыв => сила реакции опоры в момент отрыва N=0).
Мы видим, что каждому слову-ключу соответствует определенный пункт в обосновании к решению данной задачи. Таким образом, обоснование формируется путем анализа слов-ключей, найденных в тексте условия, и законов, применяемых для решения данной задачи.
Лайфхак: Зачастую проще сначала решить задачу на черновике. Глядя на использованные при решении законы и формулы, распознать слова-ключи в условии становится намного легче. Поэтому рекомендуется сначала решить задачу на черновике и только потом начинать писать обоснование.
Важно:
- Чтобы ваше решение всей задачи выглядело красиво и логично, на «беловик» (листы КИМ) переписывается сначала обоснование, а потом уже текст решения, как это и было сделано в авторском примере, приведённом выше.
- Приведённые слова-ключи не всегда встречаются в тексте условий задач в том виде, в котором они приведены в данном пособии. Приведённые слова отражают лишь общий смысл фраз, которые нужно искать.
- Например, существуют следующие аналоги слова-ключа «гладкая поверхность»: абсолютно гладкое тело, коэффициент трения отсутствует / пренебрежимо мал, трения нет, потери на трение пренебрежимо малы.
Обоснование
- Рассмотрим задачу в системе отсчёта, связанной с 3емлёй. Будем считать эту систему отсчёта инерциальной (ИСО).
- Так как по условию задачи дано маленькое тело, то его можно рассматривать как материальную точку.
- Тело начинает движение из состояния покоя, значит его начальная скорость равна 0.
- Сопротивлением воздуха можно пренебречь, а сфера имеет абсолютно гладкую поверхность, следовательно трения при движении тела по сфере нет, поэтому его механическая энергия при движении по поверхности сферы сохраняется. (Силы сопротивления и трения не вводим, записываем ЗСЭ).
- Поскольку мы имеем дело с моделью материальной точки, условие его отрыва от поверхности сферы описывается вторым законом Ньютона. В момент отрыва сила реакции опоры N = 0. (Отрыв -> сила реакции опоры в момент отрыва N = 0).
Решение
- Запишем закон сохранения энергии для двух состояний тела (на вершине сферы и в момент отрыва):
где m – масса тела, v – скорость тела в момент отрыва.
- Запишем в точке отрыва второй закон Ньютона в проекциях на ось x:
- Используя (1), (2) и условие
Ответ: ≃ 4 м/с.
Перечень слов-ключей
Важно: существует огромное число вариаций задач и совокупностей условий, поэтому в данной таблице приведены только самые основные следствия, на которые указывают слова-ключи.
СКАЧАТЬ ШПАРГАЛКУ ПО МАТЕМАТИКЕ ДЛЯ ЕГЭ
30 задание в ЕГЭ по физике 2022
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
На чтение 1 мин Просмотров 39 Опубликовано 5 марта, 2023
Тригонометрические уравнения решу ЕГЭ 2022 профиль с ответами Решение и ответы на задачи на официальном сайте источника онлайн.
Задание №1 ЕГЭ 2022 профильный уровень тригонометрические уравнения 6 задач решу ЕГЭ с ответами и решением для подготовки, решаем примеры
Варианты ответов и решение задачи ТУТ: https://100ballnik.com/%d1%82%d1%80%d0%b8%d0%b3%d0%be%d0%bd%d0%be%d0%bc%d0%b5%d1%82%d1%80%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%b8%d0%b5-%d1%83%d1%80%d0%b0%d0%b2%d0%bd%d0%b5%d0%bd%d0%b8%d1%8f-%d1%80%d0%b5%d1%88%d1%83-%d0%b5/
Ответы и решение задачи онлайн
Оставляйте комментарии на сайте, обсуждайте их решения и ответы, предлагайте альтернативные варианты ответов.
На чтение 12 мин. Просмотров 7 Опубликовано 11.03.2023
Содержание
- Поделиться
- Решать варианты егэ 2022 базового уровня:
- Решать варианты егэ 2022 по математике (профильный уровень)
- Решу егэ
Поделиться
Варианты, ответы и решения пробного ЕГЭ 2022 по математике базовый и профильный уровень для 11 класса, официальная дата проведения пробного ЕГЭ 2022 19 марта.
Решать варианты егэ 2022 базового уровня:
Задания с ответами:
1)На рок-фестивале выступают группы — по одной от каждой из заявленных стран. Порядок выступления определяется жребием. Какова вероятность того, что группа из Дании будет выступать после группы из Швеции и после группы из Норвегии? Результат округлите до сотых.
Правильный ответ: 0,33
2)Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150°. Найдите радиус окружности, описанной около этого треугольника.
Правильный ответ: 1
3)В правильной треугольной пирамиде SABC медианы основания ABC пересекаются в точке O. Площадь треугольника ABC равна 4; объем пирамиды равен 6. Найдите длину отрезка OS.
Правильный ответ: 4,5
4)Один мастер может выполнить заказ за 12 часов, а другой — за 6 часов. За сколько часов выполнят заказ оба мастера, работая вместе?
Правильный ответ: 4
5)Игральную кость бросали до тех пор, пока сумма всех выпавших очков не превысила число 3. Какова вероятность того, что для этого потребовалось два броска? Ответ округлите до сотых.
Правильный ответ: 0,42
6)За прохождение каждого уровня платной сетевой игры можно получить от одной до трех звезд. При этом со счета участника игры списывается 75 рублей при получении одной звезды, 60 рублей — при получении двух звезд и 45 рублей при получении трех звезд.
Миша прошел несколько уровней игры подряд. а) Могла ли сумма на его счете уменьшиться при этом на 330 рублей? б) Сколько уровней игры прошел Миша, если сумма на его счете уменьшилась на 435 рублей, а число полученных им звезд равно 13? в) За пройденный уровень начисляется 5000 очков при получении трех звезд, 3000 — при получении двух звезд и 2000 — при получении одной звезды.
Правильный ответ: а-да, б-7, в-780 рублей
2)В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.
Правильный ответ: 0,14
5)В правильной треугольной пирамиде SABC точка M – середина ребра AB, S – вершина. Известно, что BC = 3, а площадь боковой поверхности пирамиды равна 45. Найдите длину отрезка SM.
Правильный ответ: 10
6)На рисунке изображён график функции y = f(x), определённой на интервале (−4; 4). Найдите корень уравнения f '(x) = 0.
Правильный ответ: 2
8)Имеются два сосуда. Первый содержит 30 кг, а второй – 20 кг раствора кислоты различной концентрации. Если эти растворы смешать, то получится раствор, содержащий 68% кислоты. Если же смешать равные массы этих растворов, то получится раствор, содержащий 70% кислоты. Сколько килограммов кислоты содержится в первом сосуде?
Правильный ответ: 18
10)Стрелок в тире стреляет по мишени до тех пор, пока не поразит её. Известно, что он попадает в цель с вероятностью 0,2 при каждом отдельном выстреле. Какое наименьшее количество патронов нужно дать стрелку, чтобы он поразил цель с вероятностью не менее 0,6?
Правильный ответ: 5
15)В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Правильный ответ: 4 года
16)В полуокружности с диаметром MN расположены две окружности с центрами O1 и O2, касающиеся друг друга, полуокружности и прямой MN (при этом точки касания c полуокружностью — это соответственно A и B). а) Докажите, что прямые O1A, O2B и MN пересекаются в одной точке. б) Радиусы окружностей равны 2 и 5. Найдите радиус полуокружности.
18)На доске написано более 27, но менее 45 целых чисел. Среднее арифметическое этих чисел равно −5, среднее арифметическое всех положительных из них равно 9, а среднее арифметическое всех отрицательных из них равно − 18. а) Сколько чисел написано на доске? б)
2)В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел выпадет ровно два раза.
Правильный ответ: 0,375
3)Через концы А и В дуги окружности с центром О проведены касательные АС и ВС. Угол СAB равен 32°. Найдите угол AОB. Ответ дайте в градусах.
Правильный ответ: 64
5)Объем параллелепипеда ABCDA B C D 1 1 1 1 равен 9. Найдите объем треугольной пирамиды ABCA1 .
Правильный ответ: 1,5
8)Расстояние между пристанями A и B равно 120 км. Из A в B по течению реки отправился плот, а через час вслед за ним отправилась яхта, которая, прибыв в пункт B, тотчас повернула обратно и возвратилась в A. К этому времени плот прошел 24 км. Найдите скорость яхты в неподвижной воде, если скорость течения реки равна 2 км/ч. Ответ дайте в км/ч.
Правильный ответ: 22
10)Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99.
Правильный ответ: 0,0296
15)Планируется открыть вклад на 4 года, положив на счет целое число миллионов рублей. В конце каждого года сумма, лежащая на вкладе, увеличивается на 10%, а в начале третьего и четвертого года вклад пополняется на 3 миллиона рублей. Найдите наименьший первоначальный вклад, при котором начисленные проценты за весь срок будут более 5 миллионов рублей.
Правильный ответ: 9 млн. руб
16)Дан треугольник ABC со сторонами AB = 4, BC = 5 и AC = 6. а) Докажите, что прямая, проходящая через точку пересечения медиан и центр вписанной окружности, параллельна стороне BC. б) Найдите длину биссектрисы треугольника ABC, проведенной из вершины A.
Правильный ответ: 3 корень из 2
18)В каждой из девяти ячеек строки слева направо в некотором (возможно, ином) порядке расставлены по одному 9 чисел: 1, 2, 3, 4, 5, 6, 7, 8 и 9. а) Могло ли оказаться так, что среди любых четырёх подряд (идущих слева направо) из этих чисел есть ровно одно, делящееся на 3, и ровно одно, делящееся на 4? б)
Могло ли оказаться так, что среди любых четырёх подряд (идущих слева направо) из этих чисел есть ровно одно, делящееся на 3, а среди любых двух подряд (идущих слева направо) из этих чисел есть ровно одно простое число? в) Какое наибольшее значение может принимать произведение суммы всех чисел, стоящих на нечётных местах, и суммы всех чисел, стоящих на чётных местах этой строки?
2)Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Какое наибольшее количество шоколадок можно получить, потратив не более 200 рублей в воскресенье?
Правильный ответ: 7
4)На диаграмме показана среднемесячная температура воздуха в Симферополе за каждый месяц 1988 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было осенью месяцев, когда среднемесячная температура превышала 12 градусов Цельсия.
Правильный ответ: 1
5)На рисунке изображён план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Щало, изображённого на плане. Ответ округлите до целого числа.
Правильный ответ: 4
6)Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
Правильный ответ: 6
10)Дачный участок имеет форму квадрата, стороны которого равны 30 м. Размеры дома, расположенного на участке и имеющего форму прямоугольника, — 8 м × 5 м. Найдите площадь оставшейся части участка. Ответ дайте в квадратных метрах.
Правильный ответ: 860
11)Игральную кость с 6 гранями бросают дважды. Найдите вероятность того, что хотя бы раз выпало число, большее 3.
Правильный ответ: 0,75
12)В городском парке имеется пять аттракционов: карусель, колесо обозрения, автодром, «Ромашка» и «Весёлый тир». В кассах продаётся шесть видов билетов, каждый из которых позволяет посетить один или два аттракциона. Сведения о стоимости билетов представлены в таблице.
Андрей хочет посетить все пять аттракционов, но имеет в наличии только 900 рублей. Какие виды билетов он должен купить? В ответе укажите номера (в порядке возрастания номеров), соответствующие видам билетов, без пробелов, запятых и других дополнительных символов.
Правильный ответ: 234
13)Плоскость, проходящая через точки A, B и C (см. рис.), разбивает тетраэдр на два многогранника. Сколько рёбер у получившегося многогранника с большим числом вершин?
Правильный ответ: 9
14)На рисунке изображён график функции y = f(x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в соответствие каждому интервалу характеристику функции или её производной.
Правильный ответ: 2143
15)В окружности с центром O AC и BD – диаметры. Центральный угол AOD равен . Найдите вписанный угол ACB. Ответ дайте в градусах.
Правильный ответ: 35
16)Даны два конуса. Радиус основания и образующая первого конуса равны, соответственно, 2 и 4, а второго — 6 и 8. Во сколько раз площадь боковой поверхности второго конуса больше площади боковой поверхности первого?
Правильный ответ: 6
18)Пять жильцов многоквартирного дома — Андрей, Борис, Виктор, Денис и Егор — имеют различный возраст. При этом известно, что возраст Андрея больше, чем сумма возрастов Бориса и Виктора, Виктор старше Дениса, но младше Егора. Выберите утверждения, которые следуют из приведённых данных. 1) Андрей самый старший из жильцов 2) Егор старше Бориса 3) Андрей старше Дениса 4) Борис старше Егора.
Правильный ответ: 3
19)Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число.
Правильный ответ: 1124
20)На изготовление 475 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?
Правильный ответ: 25
21)Три луча, выходящие из одной точки, разбивают плоскость на 3 разных угла, измеряемых целым числом градусов. Наибольший угол в 2 раза больше наименьшего. Сколько значений может принимать величина среднего угла?
Правильный ответ: 17
Готовитесь к ЕГЭ 2022? Прорешайте типовые варианты статграда:
Решать варианты егэ 2022 по математике (профильный уровень)
Информация о генераторе вариантов:

Источники заданий:
1) Прототипы из fipi.ru;
2) Прототипы из os.fipi.ru;
3) Прототипы с реальных ЕГЭ всех лет;
4) Прототипы с mathege.ru.
На каждую позицию рандомно выпадает случайное задание из базы заданий.
Описание каждой из позиций №1–18:



• Задание 4. Вычисления и преобразования – на данный момент 10 прототипов.
• Задание 5. Стереометрия – на данный момент 10 прототипов.





Условия прототипов заданий первой части взяты у Евгения Пифагора из его видеокурса: «1–11 задания ЕГЭ профиль (первая часть с нуля)».
• Задание 12. Уравнения – на данный момент 10 прототипов.
• Задание 13. Стереометрическая задача – на данный момент 4 прототипа.
• Задание 14. Неравенства – на данный момент 10 прототипов.
• Задание 15. Финансовая математика – на данный момент 9 прототипов.
• Задание 16. Планиметрическая задача – на данный момент 4 прототипа.
• Задание 17. Задача с параметром – на данный момент 7 прототипов.
• Задание 18. Числа и их свойства – на данный момент 9 прототипов.


Примеры заданий, развёрнутая часть.

Время выполнения варианта.



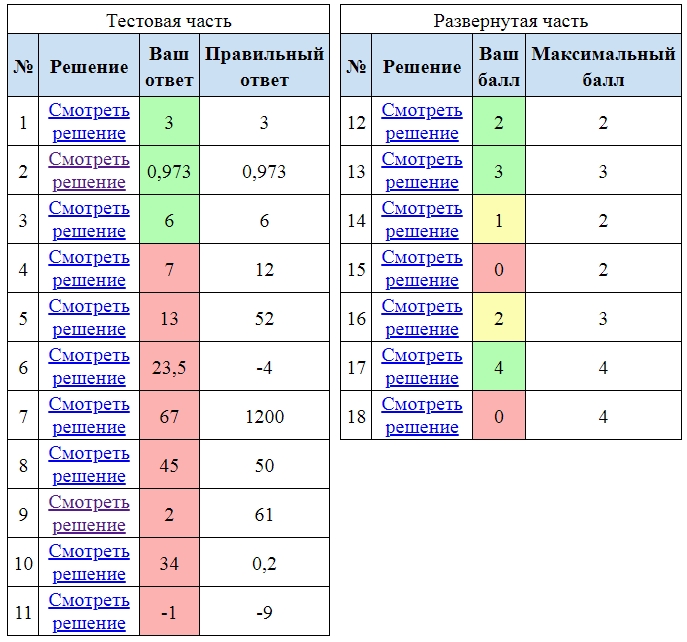
Итог работы, ссылки на подробные решения всех задач.
Теги: тренировочные варианты, 11 класс, 2021, с ответами, новый вариант, профиль, пробный егэ.
Решу егэ
В школах № 1 и № 2 учащиеся писали тест. Из каждой школы тест писали по крайней мере два учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл был целым числом. После этого, один из учащихся, писавших тест, перешел из школы № 1 в школу № 2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе № 1 уменьшиться в 10 раз?
б) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе № 2 равняться 7?
в) Средний балл в школе № 1 уменьшился на 10%, средний балл в школе № 2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе № 2.