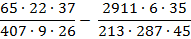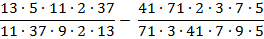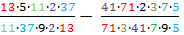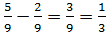Дроби появились в глубокой древности, когда древний человек решил разделить добычу с себе подобным. При разделе добычи, при измерениях величин, да и в других похожих случаях люди столкнулись с необходимостью делить что-то на равные части, т. е. наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удавалось выразить натуральным числом, приходилось учитывать и части употребляемой меры. Так возникли дроби. Так русское слово дробь, как и его аналоги в других языках, происходят от латинского слова fractura, которое, в свою очередь, является переводом арабского с тем же значением: ломать, раздроблять. Первой дробью, с которой познакомились люди, была половина. Следующей дробью была треть. В древности у разных народов использовались разные дроби и разные записи дробей.
Оцени ответ
Руководитель:
Яруллина Гульсиня Ситдиковна
Учреждение:
Школа МБОУ «Гимназия №1» г. Абдулино
В данном исследовательском проекте по математике на тему «Обыкновенные дроби в жизни людей» автор изучает историю возникновения дробей, даёт определение «обыкновенная дробь», а также наглядно показывает обыкновенные дроби.
Подробнее о проекте:
В авторском исследовательском проекте по математике «Обыкновенные дроби в жизни людей» ученик 5 класса стремится показать, что дроби нужны не только в математике, но и в повседневной жизни. Учащийся дает развернутое определение понятия «дроби в математике», а также приводит подробную характеристику обыкновенных дробей.
Автор творческого проекта по математике на тему «Обыкновенные дроби в жизни людей» изучил использование обыкновенных дробей в профессиональной деятельности человека, а также порассуждал и аргументированно доказал важность знания и применения дробей для профессии «Разметчик». Также в работе можно найти определение других математических дробей.
Оглавление
Введение
1. Теоретическая часть.
1.1 Понятие дроби.
1.2 История возникновения дробей.
1.3 Использование обыкновенных дробей в профессиональной деятельности человек.
1.3.1 Дроби для профессии «Разметчик».
2. Практическая часть.
2.1. Мои наблюдения.
Заключение
Список использованной литературы
Введение
Уважаемые друзья! Ответственно вам сообщаю, есть люди, которые считают, будто дробям нет места в нашей жизни. За примерами далеко ходить не надо. Когда я учился в начальных классах, думал: «Зачем математики придумали дроби?» Наверное, только для того, чтобы портить жизнь школьникам. Другого объяснения не знал, пока не начали изучать в 5 классе тему «Дроби»
С первого знакомства с дробями было понятно, что они очень необычные числа, начиная с их непривычной записи и заканчивая сложными правилами действий с ними.
В обычной жизни, и взрослым, и детям каждый день приходится сталкиваться с проблемой деления целого на части, и даже в определенный момент кажется, что нас больше окружают не целые, а дробные числа, что является актуальностью данной темы.
Мне стало интересно узнать: как и когда появились дроби? В какой сфере жизни больше всего практически их применяют? Хотелось в ходе исследования этого вопроса убедиться и убедить других в необходимости дробей в повседневной жизни.
Объект исследования: обыкновенные дроби
Предмет исследования: использование дробей в нашей повседневной жизни.
Цель: показать, что дроби нужны не только в математике, но и в повседневной жизни.
Задачи:
- Узнать, что такое дробь, какие виды дроби существуют
- Изучить историю возникновения дробей.
- Рассмотреть применение дробей в повседневной жизни.
- Оценить достижения науки в данной области.
Понятие дроби
Дробь в математике — число, состоящее из одной или нескольких частей (долей) единицы. Дробь выражается отношением двух целых чисел m/n, где n — показывает на сколько долей разделена единица, а m – показывает сколько таких долей содержится в дроби.
В математике применяются следующие виды дробей:
- обыкновенная дробь;
- правильная дробь;
- неправильная дробь;
- смешанная дробь;
- десятичная дробь.
Дроби разные нужны, дроби всякие важны
Обыкновенная дробь имеет вид n/m или m/n где m и n — натуральные числа. Делимое (m) — называют числителем дроби, делитель (n) — называют знаменателем данной дроби. Горизонтальная или косая линия в дроби обозначает деление. Черта наклонная называется — «солидус», а горизонтальная – «винкулум».
Если числитель дроби меньше знаменателя, то дробь называется правильной (например 3/7), если больше или равен — неправильной (например 7/3).
Числа, в состав которых входит целое число и правильная дробь, называются смешанными. Целое число называют целой частью смешанного числа, а правильная дробь называется дробной частью смешанного числа. Например, для смешанной дроби число 3 — целая часть, 2/5 — дробная.
Десятичная дробь, это дробь, которая записывается без знаменателя.
Выглядят они так: 5,6; 3,17; 0,17 и т.д. На самом деле это особая запись обыкновенных дробей, у которых знаменатель равен 10, 100, 1000 и т. д.
История возникновения дробей
Память человечества не сохранила для нас имя изобретателя колеса. Также невозможно назвать точно даже тот отрезок времени, когда появились дроби.
Можно предположить, что потребность делить целое на части возникала ещё в первобытном обществе. Могло быть и так…
Были у древнего человека жена и двое детей. Вот пошла однажды древняя женщина собирать плоды и нашла всего лишь 1 яблоко. Детей у неё двое, а яблоко одно. Наверное, она догадалась: взяла каменный нож да и разделила это яблоко на 2 половины.
А в это время самый — самый древний человек пошёл на охоту и убил самого — самого древнего кабана. Пришёл домой и разделил свою добычу на четыре равные части: себе, жене, сыну и дочке. Конечно, эти древние люди и не догадывались, что, разделив целое число на части, они занимались таким трудным разделом математики, который впоследствии назовут «дроби». Итак, дроби появились в тот период времени, когда в трудовой деятельности людей появилась потребность более точно измерять какие-то величины, хотя делением на части люди пользовались, наверное, с древнейших времён.
Дроби в Древнем Египте
На протяжении многих веков египтяне именовали дроби «ломаным числом», а первая дробь, с которой они познакомились, была 1/2 . За ней последовали 1/4, 1/8 , 1/16, … затем 1/3, 1/6, … т.е. самые простые дроби, называемые единичными или основными дробями.
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
Одним из первых известных упоминаний о дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей.
Египтяне ставили иероглиф (ер, «один из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби.
Остальные дроби они записывали в виде суммы долей. Дробь 7/8 они записывали в виде ½ ¼ 1/8, но знак «+» не указывали. А сумму 4+1/3 записывали в виде 41/3. Такая запись смешанных чисел (без знака «+») сохранилась до сих пор.
Вавилонские дроби
Жители древнего Вавилона примерно за 3000 лет до нашей эры создали систему мер аналогичную нашей метрической, только в основе её лежало не число 10, а число 60, в которой меньшая единица измерения составляла 1/60 часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.
Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы. Число 60 прекрасно делится на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. Шестидесятые доли были привычны в жизни вавилонян.
Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.
Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическимидробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Дроби в Древней Греции
Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали, как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали, как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит оно от слова «дробить, разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
| 1/2 — половина, полтина | 1/3 – треть |
| 1/4 – четь | 1/6 – полтреть |
| 1/8 — полчеть | 1/12 –полполтреть |
| 1/16 — полполчеть | 1/24 – полполполтреть (малая треть) |
| 1/32 – полполполчеть (малая четь) | 1/5 – пятина |
| 1/7 — седьмина | 1/10 — десятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Дроби в других государствах древности
В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Использование обыкновенных дробей в профессиональной деятельности человека
Живя в окружении дробей, мы не всегда их явно замечаем. И все же, мы сталкиваемся с ним очень часто: дома, на улице, в магазине, на работе и так далее. Покажу лишь малую часть того, где мы можно увидеть присутствие дробей.
В медицине. Чтобы приготовить необходимое лекарство нужно знать его состав, записанный с помощью дробей, или, когда врач назначает больному ½ таблетки.
Дроби в кулинарии. Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Дроби в музыке. Учащиеся музыкальной школы знакомятся с дробями раньше, чем в общеобразовательной школе. С первых дней занятий дети знакомятся с такими понятиями как размер и длительности нот. Древнегреческий философ Пифагор (570 г. до н. э.), один из самых первых установил связь музыки и математики. Он создал учение о звуке. Пифагор связал длительность звучания нот с дробями.
Счёт длительностей в музыке ведётся от целой ноты, которая считается до четырёх. В целой ноте 2 половинные, 4 четверти, 8 восьмых, 16 шестнадцатых. Так музыка живёт в согласии с математикой.
Дроби в географии: Материк Евразия занимает 1/3 часть суши;
Масштаб карты равен 1/50000
Участки земной поверхности изображаются на карте в уменьшенном виде, для этого используется понятие масштаба: отношение длины отрезка на карте к длине соответствующего отрезка на местности.
Например, масштаб карты 1/10000 означает, что 1см на карте соответствует 10000 см на местности.
Дроби в спорте. Когда смотрим ½ финала матча по футболу.
Дроби в пропорции человека тоже связаны с дробями. Голова маленького ребенка составляет 1/5 часть роста человека. Голова подростка – 1/6. А голова взрослого человека – 1/8 часть роста. Основываясь на этих данных, была создана кукла «Барби».
Дроби в юридической деятельности. Взрослые в жизни встречаются с такими ситуациями: в наследство каждый по завещанию получили, например А- 1/8 имущества наследодателя; Б. – 6/17; В. — завещано всё остальное . Какие доли достались каждому из наследников?
Дроби для портных. Портной при раскрое одежды использует дроби. (рукав длины три четверти — ¾ или брюки длины 7/8)
В настоящее время невозможно представить ни одну отрасль промышленности или сельского хозяйства, или строительства, где бы в расчётах не встречалось дробных чисел.
Дроби для профессии «Разметчик»
На машиностроительных заводах есть очень увлекательная профессия, называется она — разметчик. Разметчик намечает на заготовке линии, по которым эту заготовку следует обрабатывать, чтобы придать ей необходимую форму.
Разметчику приходится решать интересные и подчас нелегкие геометрические задачи, производить арифметические расчеты и т. д.
«Понадобилось как-то распределить 7 одинаковых прямоугольных пластинок равными долями между 12 деталями. Принесли эти 7 пластинок разметчику и попросили его, если можно, разметить пластинки так, чтобы не пришлось дробить ни одной из них на очень мелкие части. Значит, простейшее решение — резать каждую пластинку на 12 равных частей — не годилось, так как при этом получалось много мелких долей. Как же быть?
Возможно ли деление данных пластинок на более крупные доли? Разметчик подумал, произвел какие-то арифметические расчеты с дробями и нашел все-таки самый экономный способ деления данных пластинок.
Впоследствии он легко дробил 5 пластинок для распределения их равными долями между шестью деталями, 13 пластинок для 12 деталей, 13 пластинок для 36 деталей, 26 для 21 и т.п.
Оказывается, разметчик представил дробь 712 в виде суммы единичных дробей 13 + 14. Значит, если из 7 данных пластинок 4 разрезать на три равные части каждую, то получим 12 третей, то есть по одной трети для каждой детали. Остальные 3 пластинки разрежем 4 равные части каждую, получим 12 четвертей, то есть по одной четверти для каждой детали. Аналогично, используя представления дробей в виде суммы единичных дробей 56 = 12+13; 1312 =13+34; 1336 =14+19.
Практическая часть. Мои наблюдения
Дроби в часах. «Встреча». Видеоролик. (Приложение 1)
Мы часто отвечаем на вопрос «который час?» дробями. «Без четверти пять» без пятнадцати минут пять; «Сейчас три часа без четверти» -2 час 45 минут; «Половина второго» -1 час 30 минут.
Ситуация 1. В парке стоит молодой человек с букетом цветов:
- Извините. Не подскажете который час? — спрашивает у прохожего.
- «Без четверти пять», — отвечает прохожий.
- Что опаздывает?
- Да, на целых ¾ часа.
- Сочувствую.
- Спасибо.
Дроби в кулинарии. «Пряники». Видеоролик. (Приложение 2)
Поварам нужны дроби для соблюдения пропорции при приготовлении блюда. В рецептах очень часто используются такие фразы, например, как одна вторая стакана, четверть столовой ложки.
Ситуация 2. Ученик в одежде повара. Готовит тесто для пряников.
— Для пряников понадобится 1 яйцо, один с четвертью стакана муки, две с половиною столовой ложки меда, треть чайной ложки соли, половина чайной ложки имбиря. Всё тщательно перемешиваем и печем пряники.
Дроби в кулинарии. «Пирожное». Видеоролик (Приложение 3)
Приготовленные блюда нужно умело делить на порции.
Ситуация 3. На столе стоит тарелка. В ней 5 пирожное.
— На день рождения пришли 6 друзей. Передо мной встал вопрос: «Как поровну разделить 5 пирожное между 6 человек»?
Решение было такое: нужно 5 пирожное разделить пополам каждый. Затем ещё 2 пирожное разделить на 3 части. Получается 6 абсолютно равных частей.
Дроби в математике.
Учитель математики после изучения сокращения дробей задал домашнее задание. Найти значение выражения рациональным способом.
65 : (407 : 9) 22 (37 : 26) — (2911 : 213) 6 (35: 287) : 45
На первый взгляд, обыкновенные натуральные числа. Сначала надо решить действия в скобках, потом делить и умножать. Но, здесь должна быть какая-то хитрость?! Надо найти рациональный способ. Я решил данное выражение так:
1) Записал выражение в виде дроби.
2) Преобразовал каждое натуральное число в виде произведения двух множителей.
3) В полученных дробях получились числа, которых можно сократить.
4) Получил ответ
Заключение
При выполнении своего проекта, я узнал много нового и интересного о дробях. Думаю, что эти знания пригодятся в учебе. Прочитал много книг и разделов из энциклопедий. Познакомился с первыми дробями, которыми оперировали люди, узнал новые для меня имена ученых, внесших свой вклад в развитие учения о дробях. А особенно то, что дроби используются почти во всех сферах деятельности человека, а это значит, что людям всех профессий нужно обязательно изучать дроби! Уметь решать задачи на дроби, знать правила сложения и вычитания, умножения и деления дробей.
Без знания математики, особенно знания дробей вся современная жизнь была бы невозможна. Например, у нас не было бы хороших домов, потому что строители должны уметь измерять, считать, сооружать. Наша одежда была бы очень грубой, так как ее нужно хорошо скроить, то есть точно все измерить, Не было бы ни какой большой промышленности, ни какой коммерции.
И конечно, не было бы радио, телевидения, кино, телефона и тысяч других вещей, составляющих часть нашей цивилизации. Использование дробей, измерения «на сколько?», «как долго?» являются жизненно необходимой частью мира, в котором мы живем.
В заключении можно сказать, что дроби бывают разные, дроби бывают важные. Знание понятия математическая дробь очень важно!
Считаю, что материалы моей работы будут интересными для других учащихся. Они могут быть использованы как на уроке, так и для проведения учителями внеклассных мероприятий по математике.
Список использованной литературы
- Анищенко Е. А. Число как основное понятие математики. Мариуполь, 2002.
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика. 5 класс: учеб.для общеобразовательных учреждений/- 26-е изд., стер. – М.: Мнемозина, 2009. — 280 с.
- Гейзер Г.И. История математики в школе. Пособие для учителей. – М.: Просвещение, 1981. – 239 с.
- Математика. 5 класс: учеб.для общеобразоват. учреждений. [СМ. Никольский, М.К.Потапов, Н.Н.Решетников, А.В. Шевкин]. — 11-е изд, дораб. — М.: Просвещение, 2016. — 272 с. — (МГУ — школе).
- Математический энциклопедический словарь. – М., 1988.
Если страница Вам понравилась, поделитесь в социальных сетях:
Я думаю тебе нужна ( обыкновенная дробь)
Жила-была обыкновенная дробь. Обыкновенная, как и любая, состоящая из числителя и знаменателя, разделённых чёрточкой. Она была довольно симпатичной, но вот только ей так хотелось быть похожей на десятичную! Особенно ей нравились бесконечные десятичные дроби: ведь это так замечательно и заманчиво – уноситься вдаль, в даль, которой нет конца! Сколько там интересного можно повидать. Но обыкновенная дробь продолжала оставаться обыкновенной. А ещё ей было обидно, что её называют обыкновенной. Разве она обыкновенная? Она необыкновенная! Так удивительно – ни у каких чисел больше нет числителя и знаменателя, а у неё есть. Но всё же ей так хотелось иногда стать бесконечной десятичной дробью. И вот однажды… Однажды кто-то придумал числитель разделить на знаменатель. И, оказывается, так просто обыкновенная дробь может стать десятичной! А наша дробь как раз оказалась бесконечной! И понеслась она далеко-далеко, в далёкие края!
Обновлено: 11.03.2023
Итоги конкурса 2012 года
Члены жюри отметили лучшие сказки учащихся, при этом учли голосование на сайте.
1 место Почтовый Артур, 5 “Б” класс (сказка № 3 и сказка № 18).
2 место разделили Мишкина Анна, 5 “Б” (сказка №8), Шелегова Дарья, 5 “А” (сказка №15) и Фролова Анастасия, 5 “Б” (сказка №4).
3 место разделили Мешкова Карина, 5 “В” (сказка №19), Слабодич Виктория, 5 “А” (сказка №17), Миклуш Елизавета, 5 “Б” (сказка №14), и Стельмахов Александр, 5 “Б” (сказка №2).
Награждение участников будет проходить традиционно на школьной рабочей линейке в конце третьей четверти.
Сказки, взятые из Интернета, при подведении итогов не учитывались!
Сказка про десятичную дробь
Однажды пошли слухи, что у десятичной дроби
украли запятую, а она сама сидит в пещере и
плачет. Но когда случается где-нибудь беда, там
сразу появляется Скуби-ду-би-ду, и всегда всех
выручает.
И вот однажды он пошел в эту пещеру, где сидела
десятичная дробь. Десятичная дробь ему всё
рассказала. Оказывается запятую украл её лучший
друг – Шегги и теперь ей стыдно выходить из
пещеры потому, что она стала обыкновенным числом.
И тогда Скуби пошёл искать её друга Шегги. И вот,
наконец, нашел его и увидел, где спрятана запятая.
Она висела у него на шее. Тогда Скуби стал думать,
как её спасти. И когда Шегги лёг спать, он
пробрался и снял с шеи запятую, отнёс в пещеру и
отдал десятичной дроби. И всё встало на свои
места. Но Шегги проснувшись, не обнаружил на шее
запятой, побежал скорее в пещеру, но там поджидал
его сюрприз… Десятичная дробь позвала своих
друзей и они наказали Шегги за воровство. Но как
они его наказали для нас останется загадкой.
Андреева Анжелика, ученица 5Б класса
Сказка про параллельные прямые
Жили-были параллельные прямые a и b. Однажды они
пошли в лес за ёлкой. Долго выбирали и наконец
нашли. Хотели срубить, но оказалось, что не могут.
Потому что они не пересекаются, а всегда идут
прямо параллельно друг другу.
Федякова Елена, ученица 7Б класса
Жили-были в математическом поселке АРАБЕЛЛА
два числа-друга. Одного звали АЛЬ-ДЖЕБР, а другого
АЛЬ-МУКАБАЛА. АЛЬ-ДЖЕБР – это число было очень
порядочное и воспитанное, никогда не грубило
другим числам, всегда слушалось своих родителей
и ни разу в своей жизни не обмануло взрослого
человека. А другое число, АЛЬ-МУКАБАЛА, было
хулиганом и грубияном. Оно постоянно ввязывалось
в драки, донимало всех подряд, начиная от
маленьких и заканчивая большими, никогда не
прислушивалось к советам других. За их поступки
их начали называть так: АЛЬ-ДЖЕБР –
положительным числом, а АЛЬ-МУКАБАЛА –
отрицательным числом. И до наших дней дошёл этот
миф. Учёные-математики придумали положительные и
отрицательные числа в математической науке.
Емельянова Анастасия, 5А класс
Сказка о координатной прямой
Сказка о координатной прямой
Творческие работы учащихся
- Для учеников 1-11 классов и дошкольников
- Бесплатные сертификаты учителям и участникам
Учитель: Порубова О. В.
Жили-были на свете две подружки дроби. Одну звали , а другую , Жили себе счастливо, не тужили.
Жили с тех пор дроби счастливо, в мире и согласии!
МКОУ СОШ №6 г. Омутнинска
Порубова Ольга Васильевна
Сказка ложь, да в ней намёк, добрым молодцам урок.
Учитель: Порубова Ольга Васильевна.
В городе Дробики жили дроби. Они жили очень дружно и весело. У одной дроби вырос огромный арбуз. Она обрадовалось хорошему урожаю, и захотела угостить весь город.
Она привезла на тележке на главную площадь города, где уже собрались остальные жители города. Когда они начали делить, то всем хотелось большой кусочек вкусного и ароматного арбуза, и они начали ссориться. Так они сорились, а дробь стояла в стороне и плакала, ей было обидно, что они не могли придти к одному мнению. Немножко успокоившись, дробь побрела домой тяжело вздыхая.
Тогда дробь пошла домой, для того, чтобы взять с собой еду и теплую накидку. По дороге она встречала много знакомых. Так она шла, шла и дошла до речки, речка была глубокая, и течение в реке было быстрое. Дробь села на камень и призадумалась, как же ей перебраться на противоположный берег. Вдруг невдалеке она увидела старичка, дробь обрадовалась и побежала к нему.
— Много уважаемый старичок, не будете ли Вы столь любезны, перевести меня на тот берег, мне очень нужно попасть в снежную страну, — сказала дробь старичку.
— Конечно, я тебе помогу, — ответил старичок.
Перебравшись на другую сторону, дробь поблагодарила старичка и пошла дальше. Так она дошла до горы и увидела, что гора очень высокая и взбираться по ней придется очень долго, и на вершине горы лежит снег и стоит густой туман. Но дробь не испугалась, она смело и отважно стала карабкаться на гору. Добравшись до самой вершины горы, она увидела волшебное дерево. Дерево было необычайно красиво, у него были золотые листья, а на ветвях дерева сидели птицы, которых дробь раньше никогда прежде не видела.
Прилетев в город, волшебники дроби взяли всех за руки и произнесли волшебное заклинание, в один момент все помирились, и больше не ссорились. У всех было хорошее настроение и все с аппетитом ели вкусный арбуз.
жило-было целое число. и никто не хотел с ним дружить. и решило тогда число разделиться на части, чтобы эти части дружили между собой. и разделилось оно на несколько частей, которые назвали дробями=))
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала один
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала один
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала один
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала одиннн
Жила-была девочка Наташа. она любила математику да тех пор, пока не началась тема » дроби «.
Тихим зимним вечерком наташа думала над очередной задачей как вдруг откуда ни возьмись .
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала одиннн
Жили-были две дроби соседки с разными знаменателями. Одна была с добрым, мягким знаменателем, а другая – с вредным. Никак они не могли поладить между собой, не получалось между ними дружбы.
Вскоре надоело вредной дроби жить одной, без друзей, и решила она измениться. Долго старалась… и вскоре, другим стал ее числитель, а знаменатель стал — добрым и мягким.
И стали с тех пор дружить дроби, и появились у них добрые общие друзья!
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала один
Сказка про дробь.
Жили – были числитель и знаменатель. Числителя звали два, а знаменателя тринадцать. Жили они хорошо. Ученики писали их в тетрадках, они видели себя в книжках, но хотели они еще брата или сестру. Тогда пошли они к тетушке математике и попросили ее поменять два и тринадцать местами. Тетушка долго не соглашалась. Но два и тринадцать рассказали, что у них нет ни брата, ни сестры. Математика пожалела и согласилась. Она поменяла два и тринадцать местами и получилась неправильная дробь тринадцать вторых, из этой дроби появился брат шесть целых, но хоть он появился позже, все равно был старше всех. А тринадцать поменяла свое имя и стала один
Обыкновенная дробь — это целое число (числитель) , деленное на другое целое число (знаменатель) .
Дроби бывают правильные, когда числитель меньше знаменателя, и неправильные, когда больше.
3/5 или 4/7 — это правильные дроби. 4/3 или 29/17 — это неправильные дроби.
Еще дроби бывают десятичные, это когда в знаменателе стоит 10 в какой-то степени.
Обычно они записываются через запятую. Например, 4/10 = 0,4; 8/100 = 0,08 и так далее.
Десятичные дроби бывают конечными, как только что приведенные, и бесконечными.
Например, дробь 3/5 = 0,6 — конечная, а дробь 4/7 = 0,571428571428. -бесконечная.
Бесконечные периодические дроби обычно записывают с периодом в скобках. 4/7 = 0,(571428).
Это значит, что период повторяется бесконечное количество раз.
Любую обыкновенную дробь можно представить в виде конечной или бесконечной периодической.
И, наконец, есть непериодические дроби, например Пи = 3,14159265358.
У них периода нет, и такую дробь нельзя представить в виде обыкновенной.
________________________________________
Жила-была обыкновенная дробь. Обыкновенная, как и любая, состоящая из числителя и знаменателя, разделённых чёрточкой. Она была довольно симпатичной, но вот только ей так хотелось быть похожей на десятичную! Особенно ей нравились бесконечные десятичные дроби: ведь это так замечательно и заманчиво – уноситься вдаль, в даль, которой нет конца! Сколько там интересного можно повидать. Но обыкновенная дробь продолжала оставаться обыкновенной. А ещё ей было обидно, что её называют обыкновенной. Разве она обыкновенная? Она необыкновенная! Так удивительно – ни у каких чисел больше нет числителя и знаменателя, а у неё есть. Но всё же ей так хотелось иногда стать бесконечной десятичной дробью. И вот однажды… Однажды кто-то придумал числитель разделить на знаменатель. И, оказывается, так просто обыкновенная дробь может стать десятичной! А наша дробь как раз оказалась бесконечной! И понеслась она далеко-далеко.
N ты неправильно написал ГДЕ НАПИСАННО 3/5 или 4/7 ЗНАМЕНАТЕЛИ ДОЛЖНЫ БЫТЬ ТОЖЕ САМЫМ НАПРИМЕР 3 5 И 4 5 Я В 5 КЛАССЕ
Жила-была обыкновенная дробь. Обыкновенная, как и любая, состоящая из числителя и знаменателя, разделённых чёрточкой. Она была довольно симпатичной, но вот только ей так хотелось быть похожей на десятичную! Особенно ей нравились бесконечные десятичные дроби: ведь это так замечательно и заманчиво – уноситься вдаль, в даль, которой нет конца! Сколько там интересного можно повидать. Но обыкновенная дробь продолжала оставаться обыкновенной. А ещё ей было обидно, что её называют обыкновенной. Разве она обыкновенная? Она необыкновенная! Так удивительно – ни у каких чисел больше нет числителя и знаменателя, а у неё есть. Но всё же ей так хотелось иногда стать бесконечной десятичной дробью. И вот однажды… Однажды кто-то придумал числитель разделить на знаменатель. И, оказывается, так просто обыкновенная дробь может стать десятичной! А наша дробь как раз оказалась бесконечной! И понеслась она далеко-далеко, в далёкие края!
Читайте также:
- Лебеди сочинение 2 класс
- Я себя презираю а вас ненавижу сочинение
- Русский язык настоящий сильный где нужно строгий сочинение рассуждение
- Моя малая родина сочинение на английском
- Мир счастье братство людей вот что нужно нам на этом свете сочинение
Муниципальное бюджетное общеобразовательное учреждение
города Новосибирска
«Средняя общеобразовательная школа № 156
с углубленным изучением предметов художественно-эстетического цикла» МБОУ СОШ № 156
г. Новосибирск, ул. Гоголя, 35-а, тел. 224-75-29, E-mail: sсh_156_nsk@nios.ru
Проектная работа
Зачем людям
нужны дроби
Выполнила:
Сташкова Дарья Алексеевна
5 Б класс
МБОУ СОШ № 156
Руководитель:
Бурдыгина Ирина Николаевна
учитель математики ВКК,
классный руководитель
НОВОСИБИРСК 2013
СОДЕРЖАНИЕ
- Введение……………………………………………………………………..стр. 3
- Что такое дробь………………………………………………………………стр.4
- История возникновения дробей…………………………………………… стр. 5
- Дроби в Древнем Риме……………………………………….…..стр. 5
- Дроби в Древнем Египте…………………………………………стр. 5
- Вавилонские дроби……………………………………………….стр. 6
- Дроби в Древней Греции………………………………….………стр. 7
- Дроби в Древнем Китае…………………………………………..стр. 7
- Дроби на Руси…………………………………………………….стр. 8
- Дроби в других государствах древности………………………..стр. 8
- Десятичные дроби………………………………………………..стр. 9
- Дроби в музыке ………………………………………………….стр. 10
- Заключение ………………………………………………………………….стр. 11
- Список литературы………………………………………………………….стр. 12
- Приложение № 1……………………………………………………………стр. 13
- Приложение № 2……………………………………………………………стр. 19
ВВЕДЕНИЕ
Человек подобен дроби: в знаменателе — то, что он о себе
думает, в числителе — то, что он есть на самом деле.
Чем больше знаменатель, тем меньше дробь.
(Л.Н. Толстой)
Необходимость в дробных числах возникла у человека на весьма ранней стадии развития. Уже дележ добычи, состоявший из нескольких убитых животных, между участниками охоты, когда число животных оказывалось не кратным числу охотников, могло привести первобытного человека к понятию о дробном числе.
Наряду с необходимостью считать предметы у людей с древних времён появилась потребность измерять длину, площадь, объём, время и другие величины. Результат измерений не всегда удаётся выразить натуральным числом, приходится учитывать и части употребляемой меры. Исторически дроби возникли в процессе измерения.
Потребность в более точных измерениях привела к тому, что начальные единицы меры начали дробить на 2, 3 и более частей. Более мелкой единице меры, которую получали как следствие раздробления, давали индивидуальное название, и величины измеряли уже этой более мелкой единицей.
Цель работы: доказать, что дроби необходимы людям;
Задачи:
- познакомиться с различными видами дробей;
- собрать материал об истории возникновения и развития дробей;
- обобщить собранные материалы;
- провести анкетирование;
- заинтересовать слушателей информацией о дробях;
- ответить на вопрос, сформулированный в названии работы.
Результаты анкетирования в 5Б классе показали, что ребята понимают необходимость использования дробей в повседневной жизни, диаграммы представлены в приложении №2. А значит, выбранная мною тема имеет не только многовековую историю, но и будет актуальна всегда. А в качестве практической части я собрала около полусотни старинных задач из различных источников на дроби, составив небольшой сборник.
ЧТО ТАКОЕ ДРОБЬ
Дробь в математике – число, состоящее из одной или нескольких частей (долей) единицы. По способу записи дроби бывают обыкновенными и десятичными. Обыкновенная (простая) дробь имеет вид , где
или
. Горизонтальная или косая черта обозначает знак деления, в результате чего получается частное. Делимое называется числителем дроби, а делитель — знаменателем. Черта наклонная называется «солидус», а горизонтальная – «винкулум».
Правильной называется дробь, у которой модуль числителя меньше модуля знаменателя. Дробь, не являющаяся правильной, называется неправильной, она по модулю больше или равна 1. Например, — правильные дроби, а
— неправильные дроби. Всякое целое число можно представить в виде неправильной обыкновенной дроби со знаменателем 1.
Дробь, записанная в виде целого числа и правильной дроби, называется смешанной дробью и понимается как сумма этого числа и дроби. Любое рациональное число можно записать в виде смешанной дроби. Например — смешанные дроби. Чтобы из неправильной дроби выделить целую часть надо:
- разделить с остатком числитель на знаменатель;
- полученное неполное частное записать в целую часть;
- остаток записать в числитель дроби;
- делитель записать в знаменатель дроби.
На рисунке показано выделение целой части из неправильной дроби .
Десятичная дробь — это дробь, знаменатель которой есть целая степень числа 10. (Например: ). Такие дроби договорились записывать без знаменателя, то есть 0,6; 0,11; 0,037. Часть записи, которая стоит до запятой, является целой частью числа (дроби), а стоящая после запятой — дробной частью. Всякую обыкновенную дробь можно преобразовать в десятичную, которая может быть конечной или бесконечной. Например
или
ИСТОРИЯ ВОЗНИКНОВЕНИЯ ДРОБЕЙ
Дроби в Древнем Риме
У римлян основной единицей измерения массы, а также и денежной единицей служил «асс». Асс делился на 12 равных частей — унций. Из них складывали все дроби со знаменателем 12, то есть 1/12, 2/12, 3/12… Со временем унции стали применяться для измерения любых величин.
Так возникли римские двенадцатеричные дроби, то есть дроби, у которых знаменателем всегда было число 12. Вместо 1/12 римляне говорили «одна унция», 5/12 – «пять унций» и т.д. Три унции назывались четвертью, четыре унции – третью, шесть унций – половиной.
Сейчас иногда говорят: «скрупулёзно изучен этот вопрос». Это значит, что вопрос изучен до конца, что ни одной самой малой неясности не осталось. А происходит странное слово «скрупулёзно» от римского названия 1/288 асса – «скрупулус». В ходу были и такие названия: «семис» — половина асса, «секстанс»- шестая его доля, «семиунция» — половина унции, т.е. 1/24 асса и т.д. Всего применялось 18 различных названий дробей. Чтобы работать с дробями, надо было помнить для этих дробей таблицу сложения и таблицу умножения. Поэтому римские купцы твёрдо знали, что при сложении триенса (1/3 асса) и секстанса получается семис, а при умножении беса (2/3 асса) на сескунцию (2/3 унции, т.е.1/8 асса) получается унция. Для облегчения работы составлялись специальные таблицы, некоторые из которых дошли до нас.
Дроби в Древнем Египте
На протяжении многих веков египтяне именовали дроби «ломаным числом», а первая дробь, с которой они познакомились, была 1/2 . За ней последовали 1/4, 1/8 , 1/16, … затем 1/3, 1/6, … т.е. самые простые дроби, называемые единичными или основными дробями.
У них числитель всегда единица. Лишь значительно позже у греков, затем у индийцев и других народов стали входить в употребление и дроби общего вида, называемые обыкновенными, у которых числитель и знаменатель могут быть любыми натуральными числами. В Древнем Египте архитектура достигла высокого развития. Чтобы строить грандиозные пирамиды и храмы, чтобы вычислять длины, площади и объемы фигур, необходимо было знать арифметику.
Из расшифрованных сведений на папирусах ученые узнали, что египтяне 4000 лет назад имели десятичную систему счисления, умели решать многие задачи, связанные с потребностями строительства, торговли и военного дела.
Одним из первых известных упоминаний о дробях является математический папирус Ринда. Три более древних текста, в которых упоминаются дроби — это Египетский математический кожаный свиток, Московский математический папирус и Деревянная табличка Ахмима. Папирус Ринда включает таблицу египетских дробей для рациональных чисел вида 1/n, а также 84 математических задачи, их решения и ответы, записанные в виде египетских дробей. Египтяне ставили иероглиф (ер, «один из» или ре, рот) над числом для обозначения единичной дроби в обычной записи, а в священных текстах использовали линию. У них также были специальные символы для дробей 1/2, 2/3 и 3/4, которыми можно было записывать также другие дроби.
Остальные дроби они записывали в виде суммы долей. Дробь 7/8 они записывали в виде , но знак «+» не указывали. А сумму
записывали в виде
. Такая запись смешанных чисел (без знака «+») сохранилась до сих пор.
Вавилонские дроби
Жители древнего Вавилона примерно за 3000 лет до нашей эры создали систему мер аналогичную нашей метрической, только в основе её лежало не число 10, а число 60, в которой меньшая единица измерения составляла 1/60 часть высшей единицы. Полностью эта система выдерживалась у вавилонян для измерения времени и углов, и мы унаследовали от них деление часа и градуса на 60 минут, а минуты на 60 секунд.
Исследователи по-разному объясняют появление у вавилонян шестидесятеричной системы. Число 60 прекрасно делится на 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 и 60, что значительно облегчает всякие расчеты. Шестидесятые доли были привычны в жизни вавилонян. Вот почему они пользовались шестидесятеричными дробями, имеющими знаменателем всегда число 60 или его степени: 602, 603 и т.д. В этом отношении шестидесятеричные дроби можно сравнить с нашими десятичными дробями.
Вавилонская математика оказала влияние на греческую математику. Следы вавилонской шестидесятеричной системы счисления удержались в современной науке при измерении времени и углов. До наших дней сохранилось деление часа на 60 мин., минуты на 60 с, окружности на 360˚, градуса на 60 мин., минуты на 60с.
Вавилоняне внесли ценный вклад в развитие астрономии. Шестидесятеричными дробями пользовались в астрономии ученые всех народов до XVII века, называя их астрономическими дробями. В отличие от них, дроби общего вида, которыми пользуемся мы, были названы обыкновенными.
Дроби в Древней Греции
Греки работали с обыкновенными дробями не часто, поэтому использовали различные обозначения. Герон и Диофант, самые известные арифметики среди древнегреческих математиков, записывали дроби в алфавитной форме, причем числитель располагали под знаменателем. Но в принципе предпочтение отдавалось либо дробям с единичным числителем, либо шестидесятеричным дробям.
Недостатки греческой системы счисления относят к их любви к строгости, которое заметно увеличило трудности, связанные с анализом отношения несоизмеримых величин. Слово «число» греки понимали как набор единиц, поэтому то, что мы теперь рассматриваем как единое число – дробь, – греки понимали как отношение двух целых чисел. Именно этим объясняется, почему обыкновенные дроби редко встречались в греческой арифметике.
Дроби в Древнем Китае
В Древнем Китае уже пользовались десятичной системой мер, обозначали дробь словами, используя меры длины чи: цуни, доли, порядковые, шерстинки, тончайшие, паутинки. Дробь вида 2,135436 выглядела так: 2 чи, 1 цунь, 3 доли, 5 порядковых, 4 шерстинки, 3 тончайших, 6 паутинок. Так записывались дроби на протяжении двух веков, а в V веке китайский ученый Цзу-Чун-Чжи принял за единицу не чи, а чжан = 10 чи, тогда эта дробь выглядела так: 2 чжана, 1 чи, 3 цуня, 5 долей, 4 порядковых, 3 шерстинки, 6 тончайших, 0 паутинок.
Дроби на Руси
В русском языке слово «дробь» появилось лишь в VIII веке. Происходит оно от слова «дробить, разбивать, ломать на части». В русских рукописных арифметиках XVII в. дроби называли долями, позднее «ломаными числами». В старых руководствах существуют следующие названия дробей на Руси:
|
1/2 — половина, полтина |
1/3 – треть |
|
1/4 – четь |
1/6 – полтреть |
|
1/8 — полчеть |
1/12 –полполтреть |
|
1/16 — полполчеть |
1/24 – полполполтреть (малая треть) |
|
1/32 – полполполчеть (малая четь) |
1/5 – пятина |
|
1/7 — седьмина |
1/10 — десятина |
Славянская нумерация употреблялась в России до XVI века, затем в страну начала постепенно проникать десятичная система счисления. Она окончательно вытеснила славянскую нумерацию при Петре I.
Дроби в других государствах древности
В китайской «Математике в девяти разделах» уже имеют место сокращения дробей и все действия с дробями. У индийского математика Брахмагупты найдена достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной черты, а просто размещаются один над другим.
Арабы первыми начали отделять чертой числитель от знаменателя.
Леонардо Пизанский уже записывает дроби, помещая в случае смешанного числа, целое число справа, но читает так, как принято у нас. В XV – XVI столетиях учение о дробях приобретает уже знакомый нам теперь вид и оформляется приблизительно в те самые разделы, которые встречаются в наших учебниках.
Следует отметить, что раздел арифметики о дробях долгое время был одним из наиболее трудных. Недаром у немцев сохранилась поговорка: «Попасть в дроби», что означало – зайти в безвыходное положение. Считалось, что тот, кто не знает дробей, не знает и арифметики.
Десятичные дроби
Появились десятичные дроби в трудах арабских математиков в Средние века и независимо от них в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби того же типа, только шестидесятеричные.
Позднее учёный Гартман Бейер (1563-1625) выпустил сочинение «Десятичная логистика», где писал: «…я обратил внимание на то, что техники и ремесленники, когда измеряют какую-нибудь длину, то очень редко и лишь в исключительных случаях выражают её в целых числах одного наименования; обыкновенно им приходится или брать мелкие меры, или обращаться к дробям. Точно так же астрономы измеряют величины не только в градусах, но и в долях градуса, т.е. минутах, секундах и т.п. Их деление на 60 частей не так удобно, как деление на 10, на 100 частей и т.д., потому что в последнем случае гораздо легче складывать, вычитать и вообще производить арифметические действия; мне кажется, что десятичные доли, если бы ввести вместо шестидесятеричных, пригодились бы не только для астрономии, но и для всякого рода вычислений».
Сегодня мы пользуемся десятичными дробями естественно и свободно. Однако то, что кажется естественным нам, служило настоящим камнем преткновения для учёных Средневековья. В Западной Европе XVIв. вместе с широко распространённой десятичной системой в расчётах применялись шестидесятеричные дроби, восходящие ещё к древней традиции вавилонян. Понадобился светлый ум нидерландского математика Симона Стевина, чтобы привести запись и целых, и дробных чисел в единую систему. По-видимому, толчком создания десятичных дробей послужили составленные им таблицы сложных процентов. В 1585 г. он опубликовал книгу «Десятина», в которой объяснил десятичные дроби.
С начала XVII века начинается интенсивное проникновение десятичных дробей в науку и практику. В Англии в качестве знака, отделяющего целую часть от дробной, была введена точка. Запятая, как и точка, в качестве разделительного знака была предложена в 1617 году математиком Непером.
Развитие промышленности и торговли, науки и техники требовали все более громоздких вычислений, которые с помощью десятичных дробей легче было выполнять. Широкое применение десятичные дроби получили в XIX веке после введения тесно связанной с ними метрической системы мер и весов. Например, в нашей стране в сельском хозяйстве и промышленности десятичные дроби и их частный вид – проценты – применяются намного чаще, чем обыкновенные дроби.
Дроби в музыке
В греческих сочинениях по математике дробей не встречалось. Греческие ученые считали, что математика должна заниматься только целыми числами. Возиться с дробями они предоставляли купцам, ремесленникам, а также астрономам, землемерам, механикам и другому «черному люду». Но старая пословица гласит: «Гони природу в дверь — она влетит в окно». Поэтому и в строго научные сочинения греков дроби проникали «с заднего хода». Кроме арифметики и геометрии, в греческую науку входила музыка.
Музыкой греки называли учение о гармонии. Это учение опиралось на ту часть нашей арифметики, в которой говорится об отношениях и пропорциях. Греки знали: чем длиннее натянутая струна, тем ниже получается звук, который она издает, а короткая струна издает высокий звук. Но у всякого музыкального инструмента не одна, а несколько струн. Для того чтобы все струны при игре звучали «согласно», приятно для слуха, длины звучащих частей их должны быть в определенном отношении. Поэтому учение об отношениях и дробях использовалось в греческой теории музыки.
Пифагорейцы, много занимавшихся музыкой и обожествлявшие число, считали, что Земля имеет форму шара и находится в центре Вселенной: ведь нет никаких оснований, чтобы она была смещена или вытянута в какую-то одну сторону. Солнце же, Луна и 5 планет (Меркурий, Венера, Марс, Юпитер и Сатурн) движутся вокруг Земли. Расстояния от них до нашей планеты таковы, что они как бы составляют семиструнную арфу, и при их движении возникает прекрасная музыка – музыка сфер. Обычно люди не слышат её из-за суеты жизни, и лишь после смерти некоторые из них смогут насладиться ею. А Пифагор слышал её при жизни.
Его ученики – пифагорейцы, много занимавшиеся музыкой и обожествлявшие число, исследовали, насколько повышается тон струны, если её прижать посередине, или на четверть расстояния одного из концов, или на треть. Обнаружилось, что одновременное звучание двух струн приятно для слуха, если длины их относятся как 1:2, или 2:3, или 3:4, что соответствует музыкальным интервалам в октаву, квинту и кварту. Гармония оказалась тесно связанной с дробями, что подтверждало основную мысль пифагорейцев: «число правит миром»…
Так дроби сыграли определяющую роль в музыке. И сейчас в общепринятой нотой записи длинная нота – целая – делится на половинки (вдвое короче), четверти, восьмые, шестнадцатые и тридцать вторые.
ЗАКЛЮЧЕНИЕ
Без знания дробей никто не может
признаться знающим арифметику.
Цицерон
В процессе познания действительности математика играет все возрастающую роль. Сегодня нет такой области знаний, где в той или иной степени не использовались бы математические понятия и методы. Проблемы, решение которых раньше считалось невозможным, успешно решаются благодаря применению математики, тем самым расширяются возможности научного познания.
Математика всегда была неотъемлемой и существеннейшей составной частью человеческой культуры, она является ключом к познанию окружающего мира, базой научно-технического прогресса и важной компонентой развития личности. Сегодня можно с уверенностью сказать, что дроби – неотъемлемая часть нашей жизни.
Переход в расчетах на десятичные дроби очень скоро помог
практике. Особенно хочется подчеркнуть, как важны точные расчеты. В истории стран можно прочитать много примеров того, как неточные инженерные расчеты приводили к разрушению мостов, зданий, церквей и других сооружений. Изобретение десятичных дробей существенно продвинуло науку в создании счетных машин. Кроме торговли, производства, картографии пользу испытала и наука. Ученые-физики теперь могли указывать размеры мельчайших частиц-атомов, из которых состоят все тела. Медики могли выразить размеры болезнетворных бактерий, по размерам определить, какие бактерии заразили организм и с какой болезнью надо бороться. А закончить мне хотелось бы стихотворением В. Лифшица «Три десятых», которое показывает, к чему может привести незнание дробей.
|
Это кто Из портфеля Швыряет в досаде Ненавистный задачник, Пенал и тетради И сует свой дневник, Не краснея при этом, Под дубовый буфет, Чтоб лежал под буфетом?.. *** Познакомьтесь, пожалуйста: Костя Жигалин. Жертва вечных придирок, – Он снова провален И шипит, на растрепанный Глядя задачник: – Просто мне не везет! Просто я неудачник!.. *** В чем причина Обиды его и досады? Что ответ не сошелся Лишь на три десятых! И к нему, безусловно, Придирается строгая Марья Петровна. *** Три десятых… Скажи про такую ошибку И пожалуй, на лицах Увидишь улыбку. Три десятых… И все же об этой ошибке Я прошу вас послушать меня Без улыбки… |
Если б, строя ваш дом, Тот, в котором живете, Архитектор немножко Ошибся в расчете,– Что б случилось, Ты знаешь ли, Костя Жигалин? Этот дом Превратился бы В груду развалин! *** Ты вступаешь на мост. Он надежен и прочен. А не будь инженер В чертежах своих точен, Ты бы, Костя, Свалившись В холодную реку, Не сказал бы спасибо Тому человеку! *** Вот турбина. В ней вал Токарями Расточен. Если б токарь В работе Не очень был точен, Совершилось бы, Костя, Большое несчастье: Разнесло бы турбину На мелкие части! *** |
Три десятых – И стены возводятся Косо. Три десятых – И рухнут вагоны С откоса. Ошибись Только на три десятых Аптека, – Станет ядом лекарство, Убьет человека! *** Мы громили и гнали Фашистскую банду. Твой отец подавал Батарее команду. Ошибись он при этом Хоть на три десятых, – Не настигли б снаряды Фашистов проклятых. *** Ты подумай об этом, Мой друг, хладнокровно, И скажи – Не права ль была Марья Петровна? Если честно подумаешь, Костя, об этом, То недолго лежать Дневнику под буфетом! *** |
СПИСОК ЛИТЕРАТУРЫ:
- Виленкин Н.Я. «За страницами учебника математики. Арифметика» (М. Просвещение, 2008)
- Выгодский М. Я. «Арифметика и алгебра в Древнем мире» (М. Наука,1967)
- Глейзер Г. И. «История математики в школе» (М. Просвещение,1964)
- Депман И. Я. «История арифметики» (М. Просвящение, 1959)
- Шевкин А. В. «Текстовые задачи по математике 5-6»(М. Илекса, 2011)
ПРИЛОЖЕНИЕ № 1
«Но несть тот арифметчик,
Иже в целых ответчик,
А в долях ничтоже
Отвещате возможе.
Тем же о ты радеяй,
Буди в частях умеяй».
«Арифметика» русского математика
XVIII века Л.Ф. Магницкого
Небольшой сборник старинных задач по математике
по теме «Дроби»
- (Франция, XVII -XVIII вв.). Трое хотят купить дом за 24 000 ливров. Они условились, что первый даст половину, второй — одну треть, а третий — оставшуюся часть. Сколько даст каждый?
- Бутыль, наполненная вином, весит 950 г. Когда из нее вылили половину вина, она стала весить 550 г. Сколько весит вино? Сколько весит пустая бутыль?
- Из «Арифметики» Л.Ф. Магницкого. Некто оставил в наследство жене, дочери и трем сыновьям 48 000 рублей и завещал жене — всей суммы, а каждому из сыновей вдвое больше, чем дочери. Сколько досталось каждому из наследников?
- Отец дает денег своим детям. Старшему — половину всего и 1 рубль, среднему — половину остатка и еще 1 рубль, младшему — половину остатка и еще 3 рубля. И таким образом всю сумму раздал. Сколько было денег?
- Крестьянин, покупая товары, сначала уплатил первому купцу половину своих денег и еще 1 рубль; потом уплатил второму купцу половину оставшихся денег да еще 2 рубля и, наконец, уплатил третьему купцу половину оставшихся денег да еще 1 рубль. После этого денег у крестьянина совсем не осталось. Сколько денег было у крестьянина первоначально?
- Крестьянка продавала на рынке яйца. Первая покупательница купила у нее половину яиц и еще пол-яйца, вторая — половину остатка и еще пол-яйца, а третья — последние 10 яиц. Сколько яиц принесла крестьянка на рынок?
- К табунщику пришли три казака покупать лошадей. «Хорошо, я вам продам лошадей, — сказал табунщик, — первому продам я полтабуна и еще половину лошади, второму — половину оставшихся лошадей и еще пол-лошади, третий также получит половину оставшихся лошадей с полулошадью. Себе же оставлю только 5 лошадей». Удивились казаки, как это табунщик будет делить лошадей на части. Но после некоторых размышлений они успокоились, и сделка состоялась. Сколько же лошадей продал табунщик каждому из казаков?
- Купивши комод за 36 р., я потом вынужден был продать его за 7/12 цены. Сколько рублей я потерял при этой продаже?
- Сыну 8 лет, его возраст составляет 2/9 возраста отца. А возраст отца составляет 3/5 возраста дедушки. Сколько лет дедушке?
- Из папируса Ахмеса (Египет, ок. 2000 г. до н. э.) Приходит пастух с 70 быками. Его спрашивают: — Сколько приводишь ты из своего многочисленного стада? Пастух отвечает: — Я привожу две трети от трети скота. Сочти! Сколько быков в стаде?
- На ветке сидели воробьи. Когда третья часть воробьев улетела, то их осталось 6. Сколько воробьев было на ветке первоначально?
- Из «Арифметики» Л.Н. Толстого. Муж и жена брали деньги из одного сундука, и ничего не осталось. Муж взял 7/10 всех денег, а жена 690 р. Сколько было всех денег?
- Решите двумя способами задачи из египетских папирусов:
А) Количество и его четвертая часть дают вместе 15. Найти количество.
Б) Число и его половина составляют 9. Найти число.
- Из бочки вылили сначала 1/2 находившейся в ней воды, потом 1/3, 1/15 и 1/10. Какую часть воды вылили?
- Некто отпил полчашки черного кофе и долил ее молоком. Потом он отпил 1/3 чашки и долил ее молоком. Потом отпил 1/6 чашки и долил ее молоком. Наконец, он допил содержимое чашки до конца. Чего выпито больше: кофе или молока?
- Два пешехода вышли в одно время навстречу друг другу из двух деревень. Первый может пройти расстояние между двумя деревнями за 8 ч, а второй — за 6 ч. На какую часть расстояния они приближаются за 1 ч?
- Для постройки купальни наняты три плотника; первый сделал в день 2/33 всей работы, второй 1/11, третий 7/55 . Какую часть всей работы сделали все они в день?
- Для переписки сочинения наняты 4 писца. Первый мог бы один переписать сочинение в 24 дня, второй — в 36 дней, третий — в 20 и четвертый — в 18 дней. Какую часть сочинения перепишут они в один день, если будут работать вместе?
- Прохожий, догнавший другого, спросил: «Как далеко до деревни, которая у нас впереди?» Ответил другой прохожий: «Расстояние от той деревни, от которой ты идешь, равно третьей части всего расстояния между деревнями, а если еще пройдешь 2 версты, тогда будешь ровно посередине между деревнями». Сколько верст осталось еще идти первому прохожему?
- Задача Адама Ризе (XVI в.) Трое выиграли некоторую сумму денег. На долю первого пришлась 1/4 этой суммы, на долю второго — 1/7, а на долю третьего 17 флоринов. Как велик весь выигрыш?
- Некто за — аршина сукна заплатил 3 алтына. Сколько надо заплатить за 100 аршин такого же сукна?
- Некто купил 96 гусей. Половину гусей он купил, заплатив по 2 алтына и 7 полушек за каждого гуся. За каждого из остальных гусей он заплатил по 2 алтына без полушки. Сколько стоит покупка?
- Некто израсходовал половину своих денег и 1/3 остатка. После этого у него осталось 60 рублей. Сколько денег было у него первоначально?
- Задача Бхаскары (Индия, XII в.) Из множества чистых цветков лотоса были принесены в жертву: Шиве — третья доля этого множества, Вишну — пятая и Солнцу — шестая; четвертую долю получил Бхавани, а остальные шесть цветков получил уважаемый учитель. Сколько было цветков?
- Капитан на вопрос «Сколько людей имеет он в своей команде?» ответил, что 2/5 его команды в карауле, 2/7 —в работе, 1/4 — в лазарете, да еще 27 человек налицо. Спрашивается число людей его команды.
- Из «Азбуки» Л.К Толстого. Мужик вышел пешком из Тулы в Москву в 5 ч утра. В 12 ч выехал барин из Тулы в Москву. Мужик идет 5 верст в каждый час, а барин едет 11 верст в каждый час. На какой версте барин догонит мужика?
- Из «Всеобщей арифметики» И. Ньютона. Два почтальона А и В находятся друг от друга на расстоянии 59 миль. Утром они отправляются друг другу навстречу. А проходит в два часа 7 миль, В — в три часа 8 миль, но В выходит часом позднее, чем А. Сколько миль пройдет А до встречи с В?
- Задача Герона Александрийского (I е.) Бассейн емкостью 12 кубических единиц получает воду через две трубы, из которых одна дает в каждый час кубическую единицу, а другая в каждый час — четыре кубические единицы. В какое время наполнится бассейн при совместном действии обеих труб?
- Задача С.А. Рачинского. Нужно проверить 360 тетрадей диктанта. Один учитель может проверить их за 15 ч, другой — за 10 ч, третий — за 6 ч. За сколько часов они проверят тетради втроем?
- Путешественник идет из одного города в другой 10 дней, а другой путешественник тот же путь проходит за 15 дней. Через сколько дней встретятся путешественники, если выйдут одновременно навстречу друг другу из этих городов?
- Из «Арифметики» Л.Ф. Магницкого. Один человек выпьет кадь пития в 14 дней, а с женою выпьет ту же кадь в 10 дней. Спрашивается, за сколько дней жена его отдельно выпьет ту же кадь.
- Старинная задача (Китай, II в.). Дикая утка от южного моря до северного моря летит 7 дней. Дикий гусь от северного моря до южного моря летит 9 дней. Теперь дикая утка и дикий гусь вылетают одновременно. Через сколько дней они встретятся?
- Старинная задача (Армения, VII в.). В городе Афинах был водоем, в который проведены три трубы. Одна из труб может наполнить водоем за 1 ч, другая, более тонкая, — за 2 ч, третья, еще более тонкая, — за 3 ч. Итак, узнай, в какую часть часа все три трубы вместе наполняют водоем.
- Лошадь съедает воз сена за месяц, коза — за два месяца, овца — за три месяца. За какое время лошадь, коза и овца вместе съедят такой же воз сена?
- Четыре плотника хотят построить дом. Первый плотник может построить дом за 1 год, второй — за 2 года, третий — за 3 года, четвертый — за 4 года. Спрашивается, за сколько лет они построят дом при совместной работе.
- Из «Всеобщей арифметики» И. Ньютона. Трое рабочих могут выполнить некоторую работу, при этом А может выполнить ее 1 раз за 3 недели, В — 3 раза за 8 недель, С — 5 раз за 12 недель. Спрашивается, в какое время они смогут выполнить эту работу все вместе. (Считать в неделе 6 рабочих дней по 12 ч.)
- Мастер сплавил 3 куска серебра в 1/6 фунта, в 1/4 фунта и в 1/8 фунта, сделал из него ложки и продал их. Сколько получил он денег, если фунт серебра ценил в 24 рубля да за работу взял 8 р.?
- За 11 копеек куплены одна пятириковая (в 1/5 фунта) и одна шестириковая (в 1/6 фунта) стеариновые свечи. Сколько стоит фунт стеариновых свечей?
- Древнеримская задача (II в.) Некто, умирая, завещал: если у моей жены родится сын, то пусть ему будет дано 2/3 имения, а жене — остальная часть. Если же родится дочь, то ей 1/3, а жене 2/3. Родилась двойня — сын и дочь. Как разделить имение?
- Из Акмимского папируса (VI в.). Некто взял из сокровищницы 1/13. Из того, что осталось, другой взял1/17 . Оставил же в сокровищнице 150. Мы хотим узнать, сколько было в сокровищнице первоначально.
- Старинная задача (Индия, XI в.)
Есть кадамба цветок,
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Вся в цвету сименгда,
И на ней третья часть поместилась.
Разность их ты найди,
Ее трижды сложи
И тех пчел на Кутай посади.
Лишь одна не нашла
Себе места нигде,
Все летала то взад, то вперед и везде
Ароматом цветов наслаждалась.
Назови теперь мне,
Подсчитавши в уме,
Сколько пчелок всего здесь собралось.
- Старинная задача (Армения, VII в.). Один купец прошел через три города, и взыскали с него в первом городе пошлины половину и треть имущества, во втором городе половину и треть (с того, что осталось), и в третьем городе снова взыскали половину и треть (с того, что у него было); и когда он прибыл домой, у него осталось 11 дахеканов (денежных единиц). Итак, узнай, сколько всего дахеканов было вначале у купца.
- Из «Арифметики» Л. Ф. Магницкого. Некто пришел в ряд, купил игрушек для малых ребят: за первую игрушку заплатил 1/5 часть всех своих денег, за другую — 3/7 остатка от первой покупки, за третью игрушку заплатил 3/5 остатка от второй покупки, а по приезде в дом нашел остальных в кошельке денег 1 рубль 92 копейки. Спрашивается, сколько в кошельке денег было и сколько за каждую игрушку денег заплачено.
- Надгробная надпись на могиле Диофанта имеет следующее содержание: «Диофант провел шестую часть своей жизни в детстве, двенадцатую — в юности, после седьмой части, проведенной в бездетном супружестве, и еще пяти лет, у него родился сын, умерший по достижении половины числа лет жизни отца, после чего Диофант прожил только 4 года». Сколько лет жил Диофант?
- Смешаны два сорта кофе: 101/2 пуда первого сорта по 6 гривен за фунт и 21 пуд второго сорта по 12 рублей за пуд. Что стоит фунт смеси?
- Задача Метродора. Корона весит 60 мин (греческая мера) и состоит из сплава золота, меди, олова и железа. Золото и медь составляют 2/3, золото и олово 3/4, золото и железо — 3/5 общего веса. Определить вес каждого металла в отдельности.
- Задача из «Арифметики» известного среднеазиатского математика IX века Мухаммеда ибн-Мусы альХорезми (в упрощенном варианте) Найти число, зная, что если отнять от него одну треть и одну четверть, то получится 10.
ПРИЛОЖЕНИЕ № 2
Анкета,
которую я предложила в 5Б классе
- Знаешь ли ты, что такое дробь?
- Используются ли дроби в повседневной жизни?
- Какие виды дробей ты знаешь?