Симметрия вокруг нас
- Авторы
- Руководители
- Файлы работы
- Наградные документы
Кульпина Г.А. 1
1МБОУ «СОШ№7»
Богданова Т.И. 1
1МБОУ»СОШ№7″
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
|
Стоя пред черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Л.Н. Толстой |
С давних времен математика считается одной из главных наук. Математика одна из древнейших и необходимых для прогресса разных дисциплин наука.
Числа, формулы, геометрические фигуры в математике, внешне холодные и сухие, но полные внутренней красоты.
–»Можно ли с помощью симметрии создать порядок, красоту и совершенство?», «Во всём ли в жизни должна быть симметрия?»– эти вопросы я поставила перед собой уже давно, и попробую ответить на них в этой работе.
Предметом данного исследования является симметрия как одна из математических основ законов красоты, взаимосвязи науки математики с окружающими нас живыми и неживыми объектами.
Актуальность проблемы заключена в том, чтобы показать, что красота является внешним признаком симметрии и, прежде всего, имеет математическую основу.
Цель работы — на примерах найти и показать симметрию как основу красоты в природе, технике, архитектуре и искусстве.
На основе данной цели были сформулированы следующие задачи исследования:
— определить сущность симметрии;
— рассмотреть, как проявляется симметрия в окружающем нас мире.
Методы исследования:
— обработка, анализ научных источников;
— анализ научной литературы, учебников и пособий по исследуемой проблеме.
Многие люди даже не задумываются, проходя мимо обычных, на первый взгляд, вещей о том, какой удивительной формой эти объекты обладают и с какой точностью они созданы природой или человеком. Симметрия окружает нас, находя своё проявление, как в живой, так и в неживой природе.
В данной работе была сделана попытка систематизации литературных источников по данной проблематике в общее понятие симметрии и в теоретической главе рассмотрены гипотезы появления симметрии в природе, красота симметрии в архитектуре, необходимость симметрии в технике. В практической части данной работы были проведены небольшие опыты, доказывающие необходимость симметрии в технике и показывающие красоту симметрии в искусстве и народном творчестве народов Кузбасса.
На протяжении веков симметрия остается предметом, который очаровывает философов, астрономов, математиков, художников, архитекторов и физиков. Древние греки были совершенно одержимы ею – и даже сегодня мы, как правило, сталкиваемся с симметрией во всем от расположения мебели до стрижки волос.
Просто имейте в виду: как только вы осознаете это, вы, вероятно, испытаете непреодолимое желание искать симметрию во всем, что видите.
Глава 1. Теоретические аспекты симметрии
Возникновение симметрии
Симметрия является фундаментальным свойством природы, представление о котором, как отмечал академик В.И. Вернадский, «слагалось в течение десятков, сотен, тысяч поколений». «Изучение археологических памятников показывает, что человечество на заре своей культуры уже имело представление о симметрии и осуществляло ее в рисунке и в предметах быта. Надо полагать, что применение симметрии в первобытном производстве определялось не только эстетическими мотивами, но в известной мере и уверенностью человека в большей пригодности для практики правильных форм». Это слова другого нашего замечательного соотечественника, посвятившего изучению симметрии всю свою долгую жизнь, академика А.В. Шубникова.
Термин «симметрия» придумал скульптор Пифагор Регийский. Древние греки полагали, что Вселенная симметрична просто потому, что она прекрасна. Первую научную школу в истории человечества создал Пифагор Самосский. «Симметрия – это некая «средняя мера», — считал Аристотель, а Римский врач Гален (2 в. н. э.) под симметрией понимал покой души и уравновешенность.
Толковый словарь русского языка С.И. Ожегова и Н.Ю. Шведовой под симметрией понимают — соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости. В Толковом словаре иностранных слов Л.П. Крысина «Симметрия (нем. Symmetrie, франц. symetrie, греч. symmetria) – соразмерность, пропорциональность в расположении частей чего-нибудь по обе стороны от середины, центра». Большая энциклопедия Кирилла и Мефодия трактует симметрию — соразмерность, в широком смысле – инвариантность (неизменность) структуры, свойств, формы материального объекта относительно его преобразований (т.е. изменений ряда физических свойств).
С симметрией мы встречаемся везде – в природе, технике, искусстве, науке. Понятие симметрии проходит через всю многовековую историю человеческого творчества. Оно встречается уже у истоков человеческого знания; его широко используют все без исключения направления современной науки. Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
В научном мире существует несколько гипотез, с помощью которых пытаются объяснить, как возникла симметрия в пространстве нашего мира. Согласно одной из них, все, что растет вверх или вниз, подчинено закону радиально-лучевой симметрии. А то, что формируется параллельно земной поверхности или под наклоном к ней, принимает зеркально-симметричную форму. Эти свойства пытаются объяснить земным притяжением от центра планеты и различной степенью освещенности объектов солнечным светом в зависимости от их расположения.
Симметрия пронизывает наш мир гораздо глубже, нежели это можно увидеть глазами. Осмысливание этого факта происходило в течение многих веков. В результате само понятие симметрии претерпело существенную эволюцию. От тех времен до наших дней понятие «симметрия» прошло длинный путь развития. Из чисто геометрического понятия оно превратилось в фундаментальное понятие, лежащее в основе законов природы. Мы знаем теперь, что симметрия – это не только то, что можно видеть глазами. Симметрия не просто вокруг нас, она сама в основе всего.
Чтобы иметь более точное представление о том, что же такое симметрия, нужно рассмотреть её виды.
Виды симметрии
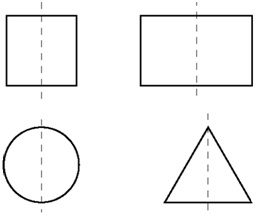
С точки зрения геометрии выделяют три основных вида симметрии: центральная, осевая и зеркальная.
Центральная симметрия (или симметрия относительно точки) – это преобразование плоскости (или пространства), при котором единственная точка (точка О – центр симметрии) остаётся на месте, остальные же точки меняют своё положение: вместо точки А получаем точку А1 такую, что точка О середина отрезка АА1. Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно точки О, нужно через каждую точку фигуры Ф провести луч, проходящий через точку О (центр симметрии), и на этом луче отложить точку, симметричную выбранной относительно точки О. Множество построенных, таким образом, точек даст фигуру Ф1.
Большой интерес вызывают фигуры, имеющие центр симметрии: при симметрии относительно точки О любая точка фигуры Ф преобразуется опять же в некоторую точку фигуры Ф. Таких фигур в геометрии встречается много. Например: отрезок (середина отрезка – центр симметрии), прямая (любая её точка – центр её симметрии), окружность (центр окружности – центр симметрии), прямоугольник (точка пересечения его диагоналей – центр симметрии). Много центрально симметричных объектов в живой и неживой природе. Часто люди сами создают объекты, имеющие центр симметрии.
Осевая симметрия (или симметрия относительно прямой) – это преобразование плоскости (или пространства), при котором только точки прямой р остаются на месте (эта прямая является осью симметрии), остальные же точки меняют своё положение: вместо точки В получаем такую точку В1, что прямая р является серединным перпендикуляром к отрезку ВВ1. Чтобы построить фигуру Ф1, симметричную фигуре Ф, относительно прямой р, нужно для каждой точки фигуры Ф построить точку, симметричную ей относительно прямой р. Множество всех этих построенных точек и дают искомую фигуру Ф1. Много существует геометрических фигур, имеющих ось симметрии.
У прямоугольника их две, у квадрата – четыре, у круга – любая прямая, проходящая через его центр. Если присмотреться к буквам алфавита, то и среди них можно найти, имеющие горизонтальную или вертикальную, а иногда и обе оси симметрии. Объекты, имеющие оси симметрии достаточно часто встречаются в живой и неживой природе. В своей деятельности человек создаёт много объектов, имеющих несколько осей симметрии.
Плоскостная (зеркальная) симметрия (или симметрия относительно плоскости) – это преобразование пространства, при котором только точки одной плоскости сохраняют своё местоположение (α-плоскость симметрии), остальные точки пространства меняют своё положение: вместо точки С получается такая точка С1, что плоскость α проходит через середину отрезка СС1, перпендикулярно к нему.
Чтобы построить фигуру Ф1, симметричную фигуре Ф относительно плоскости α, нужно для каждой точки фигуры Ф выстроить симметричные относительно α точки, они в своём множестве и образуют фигуру Ф1.
Чаще всего в окружающем нас мире вещей и объектов нам встречаются объёмные тела. И некоторые из этих тел имеют плоскости симметрии, иногда даже несколько. И сам человек в своей деятельности создаёт объекты, имеющие плоскости симметрии.
Глава 2. Симметрия вокруг нас
2.1. Симметрия в природе
Симметрией обладают объекты и явления живой природы. Она позволяет живым организмам лучше приспособиться к среде обитания, защитить себя от недоброжелателей и просто выжить.
Для начала давайте рассмотрим, какие виды симметрии встречаются в растительном мире. Например, для листьев характерна зеркальная симметрия. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.
Центральную симметрию можно наблюдать у следующих цветов: лук, цветок одуванчика, цветок кувшинки, цветок мать и мачехи. Цветок ромашки обладает центральной симметрией, только в случае четного количества лепестков. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Нередки случаи и переносной симметрии в растительном мире, например: веточки акации, рябины и многие другие.
Двусторонняя симметрия ярче всего представлена в биологии. Одним из примеров подобной симметрии являются красивые и конструктивно непростые узоры у бабочек на крыльях. Двусторонняя симметрия возникла в связи с потребностью организмов передвигаться в пространстве в соответствии с определёнными целями. В первую очередь, она затронула органы движения: ноги у пауков, ракообразных, амфибий, насекомых, млекопитающих и рептилий, крылья у летучих мышей и птиц, плавники у миног, кальмаров, тюленей, рыб, дельфинов и китов. Органы, которые управляют движением, нервная система человека и животных тоже имеют подобную симметрию. Очевидно, что так проще координировать работу ног, крыльев или плавников для того, чтобы активнее передвигаться в пространстве, не сталкиваясь с различными предметами, поддерживая равновесие тела, осуществлять точное приземление и совершать другие движения. Таким образом, мы рассмотрели некоторые виды симметрии.
Симметрия – базовое свойство большинства живых существ. Быть симметричным очень удобно. Подумайте сами: если у вас со всех сторон есть глаза, уши, носы, рты и конечности, то вы успеете вовремя почувствовать что-то подозрительное, с какой бы стороны оно ни подкрадывалось, и, в зависимости от того, какое оно, это подозрительное, — съесть его или, наоборот, от него удрать. Симметрия в животном мире определяется в соответствие размеров, форм и очертаний, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Ярким примерами симметрии у животных можно считать бабочку, жука плавунца, морскую звезду, лягушку (см. Приложение 1).
2.2. Симметрия в архитектуре
Особенно интересно проявление симметрии в древнерусских постройках, в частности в деревянных церквах, которыми издавна славилась Россия. В XVII—XVIII вв. на Руси были распространены так называемые ярусные храмы, завершавшиеся поставленными друг на друга, уменьшающимися по величине срубами. Старая русская архитектура дает много и других примеров использования симметрии. Достаточно назвать колокольни, звонницы, сторожевые башни, внутренние опорные столбы. Более поздние каменные русские храмы, дворцы, садово-парковые ансамбли тоже несут на себе явный отпечаток симметрии.
От нее в первую очередь зависит впечатление, которое производит архитектурное сооружение.
Как и в любом деле, абсолютизация одной идеи не могла привести ни к чему хорошему. Симметрия в искусстве не составила исключения. «Красота неправильная», асимметрия, стала пробивать себе дорогу в искусстве, ибо сведение красоты только к симметрии ограничивало богатство ее внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в единстве противоположностей. Вот почему именно единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами, как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
Примером удивительного сочетания симметрии и асимметрии является храм Василия Блаженного на Красной площади в Москве. Эта причудливая композиция из десяти храмов, каждый из которых обладает центральной симметрией, в целом не имеет ни зеркальной, ни поворотной симметрии. Симметричные архитектурные детали собора кружатся в своем асимметричном, беспорядочном танце вокруг его центрального шатра: они то поднимаются, то опускаются, то, как бы набегают друг на друга, то отстают, создавая впечатление радости и праздника. Без своей удивительной асимметрии храм Василия Блаженного просто немыслим!
Архитектурные сооружения, созданные человеком, в большей своей части симметричны. Они приятны для глаза, их люди считают красивыми.
Здания симметричной формы характеризуют собой строгость, вызывает чувство организованности и скованности. Яркими примерами в архитектуре являются: Казанский собор в Санкт-Петербурге (выполнен в стиле классицизма); Кафедральный собор Дуомо в Милане (выполнен в стиле готики), обладает зеркальной — осевой симметрией; Собор Святого Петра в Риме; дворец Лувр; ну и, конечно же, Нотр-Дам-Де-Пари и Эйфелева Башня (см. Приложение 2).
2.3. Симметрия в технике
Симметрия в технике. Симметричная форма дирижабля, самолета, подводной лодки, автомобиля и т.д. обеспечивает хорошую обтекаемость воздухом или водой, а значит, и минимальное сопротивление движению. В технике красота, соразмерность механизмов часто бывает связана с их надежностью, устойчивостью в работе.
Что будет, если произойдет нарушение симметрии в технических устройствах, мы проверили опытным путем, результаты которых представлены в главе 4 (см. Приложение 3).
2.4. Симметрия кристаллов
Симметрия проявляется в многообразных структурах и явлениях неорганического мира и живой природы. В мир неживой природы очарование симметрии вносят кристаллы. Каждая снежинка — это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией — поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией (см. Приложение 4).
2.5. Симметрия в живописи
|
«Искусство живописи есть не что иное, как искусство выражать невидимое, через видимое» Фромантес |
Для анализа симметрии изображения лучше взять картину гениального итальянского художника Леонардо да Винчи «Мадонна Литта». Фигуры мадонны и ребенка вписываются в правильный треугольник, который вследствие своей симметричности особенно ясно воспринимается глазом зрителя. Благодаря этому мать и ребенок сразу же оказываются в центре внимания, как бы выдвигаются на передний план. Внутренняя симметрия картины хорошо ощущается (см. Приложение 4).
2.6. Литература и симметрия
Вспомним хотя бы закон возмездия в греческой трагедии, где виновный становится жертвой такого же преступления.
В «Евгении Онегине» А.С. Пушкина мы наблюдаем симметрию положений: «Онегин, отвергнувший когда-то любовь Татьяны, сам через несколько лет вынужден испытывать горечь отвергнутой любви». В трагедии А.С. Пушкина «Борис Годунов» прекрасно выписана симметрия образов. Убийцу царственного наследника, занявшего престол, сменяет на троне такой же умный, такой же наглый и беспощадный убийца юноши-царевича.
Рассмотрим буквы русского языка с точки зрения симметрии:
А; Д; Л; М; П; Е; Ф; Ш. (вертикальная ось симметрии)
В; Е; З; К; С; Э; Ю. (горизонтальная ось симметрии)
Ж; Н; О; Х. (и вертикальные и горизонтальные оси симметрии)
Б; Г; И; Й; Р; У; Ц; Ч; Щ; Я. (ни вертикальные, ни горизонтальные оси)
В русском языке есть «симметричные» слова – палиндромы, которые можно читать одинаково в двух направлениях:
Шалаш, казак, радар, Алла, Анна, кок, поп, топот
Могут быть палиндромическими и предложения. Написаны тысячи таких предложений.
А роза упала на лапу Азора. (А. Фет)
Я иду с мечем судия. (Т. Державин)
Симметрией обладают так называемые фигурные стихи, текст которых имеет очертание какого-либо предмета-звезды, креста, треугольника, пирамиды…
«О, где же те мечты? Где радости, печали,
Светившие нам столько долгих лет?
От их огней в туманной дали
Чуть виден слабый свет
И те пропали,
Их нет».
(А. Апухтин).
Сведение красоты только к симметрии ограничивало богатство ее внутреннего содержания, лишало красоту жизни. Истинную красоту можно постичь только в единстве противоположностей. Вот почему единство симметрии и асимметрии определяет сегодня внутреннее содержание прекрасного в искусстве. Симметрия воспринимается нами как покой, скованность, закономерность, тогда как асимметрия означает движение, свободу, случайность.
В «Фаусте» Гете противопоставляет в образах Прекрасной Елены и одноглазой, однозубой старухи Форкиды красоту симметрии и уродство асимметрии. В «Сказке о царе Салтане» Пушкин рисует величавую Царевну-Лебедь со звездой во лбу (красота – симметрия) и окривевших злодеек – ткачиху с поварихой (уродство – асимметрия).
Глава 3. Симметрия родного края
3.1. Симметрия в архитектуре Кемеровской области
В 1928-30 годах строились корпуса окружной больницы (сейчас третья городская больница), здание Госбанка и центрального универмага на улице Кирова, городская гостиница и химический техникум на Притомском участке. Все эти здания были построены в конструктивистском стиле со свойственной ему лаконичностью, функциональностью и отсутствием украшений. Уникальным в своем роде образцом «каменного» конструктивизма является здание Дворца труда 1927 года проекты кемеровских архитекторов конца 30-х годов еще стилистически очень близки к конструктивизму, это, скорее, постконструктивизм, чем неоклассицизм. В предвоенные годы ещё жива традиция проведения открытых архитектурных конкурсов на проекты наиболее значительных зданий. В результате одного из таких конкурсов в 1937 году по проекту архитекторов Д. Зезина и С. Скобликова строится кинотеатр «Москва», наиболее яркий образец архитектуры переходного периода, в котором уже ясно видно возвращение таких классических принципов, как симметрия, закрытость композиции, сдержанное применение декоративных элементов (см. Приложения 5,6).
3.2. Симметрия национального узора
По материалам музейных коллекций и по имеющимся в научной литературе сведениям у народов Притомья можно выделить следующие типы народного декоративного искусства: вышивку, аппликацию, тканый орнамент, художественную обработку кости, рога и дерева, изготовление женских украшений. Преобладают характерные для северосибирского типа мотивы орнамента, выполненные тамбурным швом: зигзаг, зигзаг с петлей в изломе, прямые параллельные линии, узкие полосы, концентрические круги. В основном все рисунки симметричные. В вышивке кисета ярко проиллюстрировано характерное для шорского орнамента несоблюдение симметрии: на лицевой стороне беспорядочно расположены мифические фигурки наряду с пятилучевыми розетками. В орнаментации пряслиц и колец для нарт четко прослеживается одна из характерных черт шорского декора – нарушение симметрии. Она присутствует и в орнаменте подставки для ружья из рога марала, и в декоре рукояток ножей, плеток (см. Приложение 7).
Глава 4. Опыты применения симметрии
В основу моего исследования было взято одно из направлений японского искусства оригами — аэрогами (от яп. «гами» — бумага и лат. «аэро» — воздух). Для опыта мы так же использовали самолетики их бумаги, одинакового размера, массы, рода материала, но разные по симметрии; парашюты из бумаги соответственно одинакового размера, массы, из одного материала, но разные по симметрии; нитки, пластилин, ленту для измерения длины, секундомер.
Результаты эксперимента:
|
Вид самолета, парашюта |
Количество экспериментов |
Дальность полета /скорость |
Курс |
Характер полета |
|
С симметричными крыльями |
10 |
4,3 м |
прямой |
Плавный, бреющий |
|
С правым узким крылом |
10 |
2,1 м |
отклонен вправо |
Резкий поворот вправо и уход на посадку |
|
С левым узким крылом |
10 |
2,1 м |
отклонен влево |
Резкий поворот влево и уход на посадку |
|
С правым коротким крылом |
10 |
1.2 м |
отклонен влево |
Взлет и пике |
|
С левым коротким крылом |
10 |
1.1 м |
отклонен вправо |
Взлет и пике |
|
Симметричный квадрат парашюта |
10 |
3 сек |
прямой |
Плавный |
|
Несимметричный парашют |
10 |
0,9 сек |
вниз |
Кувырком, с переворотом |
|
Круглый парашют |
10 |
2 сек |
прямо |
Плавно |
|
Гафрированный круглый парашют |
10 |
1,3 сек |
вниз |
Раскачиваясь |
|
Гафрированный несимметричный парашют |
10 |
1,1 сек |
вниз |
Кувырком с переворотом |
Симметричный самолет и парашют демонстрируют лучшие показатели полета.
Еще одним экспериментом, демонстрирующим центральную симметрию является вырезание снежинок. Мы предлагаем в качестве эксперимента вырезать собственное имя на снежинке и посмотреть, как оно будет выглядеть в центральной симметрии (см. Приложение 9).
Так же мною были проведены эксперименты с зеркальной симметрией (см. Приложение 8).
Заключение
Сфера влияния симметрии поистине безгранична. Природа – наука — искусство. Всюду мы видим противоборство, а часто и единство двух великих начал — симметрии и асимметрии, которые во многом и определяют гармонию природы, мудрость науки и красоту искусства.
Симметрия, проявляясь в самых различных объектах материального мира, несомненно, отражает наиболее общие, наиболее фундаментальные его свойства. Поэтому исследование симметрии разнообразных природных объектов и сопоставление его результатов является удобным и надежным инструментом познания основных закономерностей существования материи.
Список использованной литературы
Жёлудев И.С. Симметрия и её приложения. – М.: Энергоатомиздат, 1983.
Карпенков С.Х. Концепция современного естествознания: Учебник для вузов. – М.: ЮНИТИ, 2000.
«Концепции современного естествознания». Лекции для студентов заочного отделения УГАТУ. Уфа, 2005.
Сонин А.С. Постижение совершенства: симметрия, асимметрия, диссимметрия, антисимметрия. – М.: ЗНАНИЕ, 1997.
Трофимов В. Введение в геометрическом многообразии с симметриями М.: МГУ, 1999.
Урманцев Ю.А. Симметрия природы и природа симметрии. – М.: МЫСЛЬ, 1974.
Харитонов А.С. Феномен симметрии. — ЮНИТИ, 1999.
Хорошавина С.Г. Курс лекций «Концепция современного естествознания». Ростов н/Д: Феникс, 2000.
Шубников А.В. Избранные труды по кристаллографии. – М.: НАУКА, 1995.
www.numanities.edu.ru
www.nrc.edu.ru
www.toe-krsh.narod.ru
Приложение 1
Рисунок 1 — Примеры симметрии в природе
Приложение 2
Рисунок 2 – Примеры симметрии и асимметрии в архитектуре
Приложение 3
Рисунок 3 – Примеры симметрии в технике
Приложение 4
Рисунок 4 – Пример симметрии кристалла (снежинки)
Рисунок 5 – Пример симметрии в живописи
Приложение 5
Рисунок 6 – Пример симметрии в архитектуре г. Кемерово
Приложение 6
Рисунок 7 — Музей-заповедник «Кузнецкая крепость»
Рисунок 8 – Скульптурная композиция в г. Новокузнецке
Приложение 7
Рисунок 9 — Национальный орнамент коренных жителей Кузбасса
Приложение 8
Рисунок 10 — Зеркальная симметрия (проверено на себе)
Приложение 9
Рисунок 11 – Центральная симметрия сделанная своими руками (на примере снежинки с именем)
Просмотров работы: 8829
Симметрия вокруг нас
Клубков Владислав
8 Б класс, МОУ «СОШ № 93»
Г. Саратов
Что же такое симметрия? Какой глубокий смысл заложен в этом понятии?
Почему симметрия буквально пронизывает весь окружающий нас мир?
Ответы на эти вопросы каждый из нас может получить, прочитав данный реферат.
Материал моего реферата распадается на две части. В первой части работы рассматривается симметрия положений, форм, структур. Это та симметрия, которую можно непосредственно видеть. Она может быть названа геометрической симметрией. Во второй части моего реферата рассматривается симметрия физических явлений и законов природы. Эта симметрия лежит в самой основе естественнонаучной картины мира; её можно назвать физической симметрией.
А вы смогли бы привести немало примеров, демонстрирующих правильность формы (симметричность) объектов или предметов, созданных человеком? Отвечая на этот вопрос, хочется отметить прежде всего, архитектурные ссоружения. Например, здание Большого театра в Москве. Практически все транспортные средства, начиная с телеги и кончая реактивным лайнером.
Предметы домашнего обихода (мебель, посуда). Некоторые музыкальные инструменты: обычная гитара, скрипка, барабан…
Кто не любовался симметричными формами снежинок, кристаллов, листьев, цветов? Симметричны животные, рыбы, птицы, насекомые. Симметрично человеческое тело. Действительно, симметричные объекты окружают нас буквально со всех сторон. Не только объекты. Симметрия присутствует также в регулярности смены дня и ночи, времен года. Она проявляется в ритмическом построении стихотворения. Фактически мы имеем дело с симметрией везде, где наблюдается какая-либо упорядоченность. Симметрия, понимаемая в самом широком смысле, противостоит хаосу, беспорядку.
Термин « симметрия » по-гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей». Математически строгое представление о симметрии сформировалось сравнительно недавно – в ХIХ веке. В наиболее простой трактовке (по Г. Вейлю) современное определение симметрии выглядит примерно так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали.
Можно сказать, что существуют три последовательные ступени в нашем знании о мире. На низшей ступени находятся явления; на следующей ступени – законы природы; наконец, на третьей ступени – принципы симметрии. Законы природы управляют явлениями, а принципы симметрии управляют законами природы. Если законы природы позволяют предсказывать явления, то принципы симметрии позволяют предсказывать законы природы. Главенствующую роль принципов симметрии предопределяет в конечном счете фактическое присутствие симметрии во всем, что нас окружает.
Принципы симметрии играют исключительно важную роль в великом таинстве, именуемом научным познанием мира. Любая научная классификация основана на выявлении свойств симметрии классифицируемых объектов.
Объекты или явления группируют по общности их свойств, сохраняющейся при определённых преобразованиях.
Яркий пример – периодическая система элементов, предложенная великим русским химиком Д.И.Менделеевым (1834 – 1907). От периода к периоду сохраняется общность свойств элементов, входящих в один и тот же столбец таблицы Менделеева, например, лития, натрия, калия, рубидия, цезия. Характер изменения свойств элементов в пределах периода является общим для разных периодов.
Соображения симметрии лежат в основе всех классификаций.
Кристаллы, например, классифицируют по типу симметрии кристаллической решетки, по свойствам межатомных сил связи, по электрическим и иным свойствам. Классификация атомов основывается на общности и различиях в структуре их спектров излучения.
Когда мы смотрим на нагромождения камней у подножия горы, на неправильную линию холмов на горизонте, на причудливые извивы берегов реки или озера, на фантастические формы облаков, у нас может возникнуть мысль, что симметрия в неорганическом мире – отнюдь не частый гость.
И в то же время встречается точка зрения, что симметрия и строгая точность холодна и враждебна живому. Наверное, не случайно безжизненный замок
Снежной королевы из известной сказки Андерсена часто изображают как в высшей степени симметричное сооружение, сверкающее отполированными зеркальными гранями правильных форм. Так кто же прав – тот, кто видит в неживой природе нагромождение беспорядка, или, напротив, тот, кто видит в ней господство холодной точности и симметрии? Строго говоря, неверны обе крайние точки зрения. Конечно, воздействие на облик земной поверхности таких природных факторов, как ветер, вода, солнечный свет, весьма стихийно и часто носит беспорядочный характер. Однако песчаные дюны в пустыне, галька на морском берегу, кратер потухшего вулкана имеют, как правило, геометрически правильные формы. Конечно, груда камней у подножия беспорядочна; однако каждый камень является огромной колонией криссталов, представляющих собой в высшей степени симметричные «постройки» из атомов и молекул. Именно криссталы вносят в мир неживой природы очарование симметрии.
Кто из нас зимой не любовался снежинками? Каждая снежинка – это маленький крисстал замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают симметрией – поворотной симметрией 6-го порядка и, кроме того, зеркальной симметрией.
Все твердые тела состоят из криссталов. В большинстве случаев отдельные криссталы очень малы (меньше песчинки); однако в некоторых случаях криссталы вырастают до внушительных размеров, и тогда они предстают перед нами во всей своей геометрически правильной красоте.
Криссталы – это многогранники достаточно правильной формы с плоскими гранями и прямыми ребрами.
Существуют криссталы топаза (фторосиликата алюминия), берилла (соединения, в которое входят бериллий, кремний, алюминий), дымчатого кварца. Крисстал берилла относится к одному из криссталических разновидностей этого соединения; перед нами гелиодор. Другие разновидности берилла: сине-зеленый аквамарин, ярко-зеленый изумруд, розоватый воробьевит.
Разная окраска гелиодора обусловлена примесью ионов трехвалентного железа. Весьма распространен в природе кварц (кремнезем), представляющий собой окись кремния. Самая чистая и прозрачная разновидность кварца – горный хрусталь; далее следует дымчатый кварц. Кварц встречается и в виде фиолетового аметиста, красного сердолика, черного оникса, серого халцедона. Кварц – это также точильный камень, кремень, простой песок.
Симметрия внешней формы кристаллов хорошо видна. Существует три формы кристаллов алмаза: октаэдр, ромбический додекаэдр, гексагональный октаэдр. Симметрия внешней формы кристалла является следствием его внутренней симметрии – упорядоченного взаимного расположения в пространстве атомов (молекул). Иначе говоря, симметрия кристалла связана с существованием пространственной решетки из атомов – так называемой кристаллической решетки.
Поразительно, насколько широким по охвату различных вопросов оказался разговор о месте и роли симметрии. Он был бы значительно шире, если бы мы включили в него вопросы, связанные не только с научной деятельностью человека, но также и другие стороны его деятельности, например технику, архитектуру, искусство. Симметрия в технике и архитектуре очевидна. Что же касается живописи, музыки, поэзии, то здесь, как мне кажется, господство симметрии сомнительно… Прежде всего заметим, что человеческое творчество во всех своих проявлениях тяготеет к симметрии.
«Стоя перед чёрной доской и рисуя на ней мелом разные фигуры, я вдруг был поражён мыслью: почему симметрия приятна глазу? Это врожденное чувство, отвечал я сам себе».
Л.Н.Толстой
Многие люди даже не задумываются, проходя мимо обычных, на первый взгляд, вещей о том, какой удивительной формой эти объекты обладают и с какой точностью они созданы природой или человеком. Симметрия окружает нас, находя своё проявление, как в живой, так и в неживой природе.
Термин «симметрия» в переводе с греческого означает соразмерность, пропорциональность, гармония. Как предполагают, ввел в обиход данный термин Пифагор (VI в. до н. э.), обозначив им пространственную закономерность в расположении одинаковых фигур или их частей. Он же определил отклонение от симметрии как асимметрию.
Для симметричной организации композиции характерна уравновешенность её частей по массам, по тону, цвету и даже по форме. В таких случаях одна часть почти зеркально похожа на вторую. В симметричных композициях чаще всего имеется ярко выраженный центр. Как правило, он совпадает с геометрическим центром картинной плоскости.
Симметрия пронизывает наш мир гораздо глубже, нежели это можно увидеть глазами. Осмысливание этого факта происходило в течение многих веков. В результате само понятие симметрии претерпело существенную эволюцию. От тех времен до наших дней понятие «симметрия» прошло длинный путь развития. Из чисто геометрического понятия оно превратилось в фундаментальное понятие, лежащее в основе законов природы. Мы знаем теперь, что симметрия – это не только то, что можно видеть глазами. Симметрия не просто вокруг нас, она сама в основе всего. С самой общей точки зрения, понятие симметрии связано с инвариантностью по отношению к каким-либо преобразованиям. Инвариантность может быть чисто геометрической (сохранение геометрической формы), но может и не иметь отношения к геометрии, например сохранение энергии или биологических свойств. Точно так же преобразования могут иметь геометрический характер (повороты, переносы, перестановки), а могут и не иметь его (замена частиц античастицами, переход от одного поколения к другому).
Чтобы иметь более точное представление о том, что же такое симметрия, нужно рассмотреть её три основных вида: зеркальная симметрия; центральная симметрия; переносная симметрия.
Рассмотрим поподробнее каждый вид. Начнём с зеркальной симметрии. Иногда данный вид ещё называют плоскостная симметрия. Одна половинка симметричного объекта является зеркальным отражением другой половинки. Если поставить зеркальце вдоль прочерченной ровно посередине рисунка прямой, то отражённая в зеркале половинка фигуры дополнит её до целой. Поэтому такая симметрия и называется зеркальной, а прямая, вдоль которой поставлено зеркало, называется осью симметрии. В простейшем случае, если плоскую фигуру имеющую ось симметрии загнуть вдоль оси, то обе её части совпадут.
Следующий вид, который мы рассмотрим – центральная симметрия. Её ещё называют – поворотная симметрия. Данный вид симметрии характеризуется наличием центра симметрии – неподвижной точки (назовём эту точку «О»). Эта точка обладает определённым свойством, заключающемся в том, что при повороте на 180 градусов центрально симметричная фигура переходит сама в себя. Яркими примерами центрально симметричных фигур могут быть снежинки.
Последний вид симметрии – переносная или по-другому трансляционная. Это параллельный перенос вдоль прямой. Данный вид симметрии характерен для архитектуры или искусства. В природе же такая симметрия встречается редко и чаще всего не обладает 100% точностью.
Симметрия в природе – это мир вокруг нас. Наука, изучающая её, называется биосимметрией. Симметрией обладают объекты и явления живой природы. Она позволяет живым организмам лучше приспособиться к среде обитания, защитить себя от недоброжелателей и просто выжить.
Для начала давайте рассмотрим, какие виды симметрии встречаются в растительном мире. Например, для листьев характерна зеркальная симметрия. Многие листья деревьев и лепестки цветов симметричны относительно среднего стебля.
Центральную симметрию можно наблюдать у следующих цветов: лук, цветок одуванчика, цветок кувшинки, цветок мать и мачехи. Цветок ромашки обладает центральной симметрией, только в случае четного количества лепестков. Её сердцевина представляет собой окружность, и поэтому центрально симметрична, так как мы знаем, что окружность имеет центр симметрии. Нередки случаи и переносной симметрии в растительном мире, например: веточки акации, рябины и многие другие.
Симметрия – базовое свойство большинства живых существ. Быть симметричным очень удобно. Подумайте сами: если у вас совсех сторон есть глаза, уши, носы, рты и конечности, то вы успеете вовремя почувствовать что-то подозрительное, с какой бы стороны оно ни подкрадывалось, и, в зависимости от того, какое оно, это подозрительное, — съесть его или, наоборот, от него удрать. Симметрия в животном мире определяется в соответствие размеров, форм и очертаний, а также относительное расположение частей тела, находящихся на противоположных сторонах разделяющей линии. Ярким примерами симметрии у животных можно считать бабочку, жука плавунца, морскую звезду, лягушку.
Можно сказать, что каждое животное (насекомое, рыба, птица) состоит из двух энантиоморфов – правой и левой половин. Энантиоморфами являются также парные детали, одна из которых попадает в правую, а другая в левую половину тела животного. Так, энантиоморфами являются правое и левое ухо, правый и левый глаз Примером могут являться оленьи рога. Симметрия в животном мире диктуется условиями жизни. Это хорошо видно на примере рыбы камбалы. У камбалы, как и у других рыб, имеется вертикальная плоскость симметрии. Взрослая камбала лежит на дне. Ее глаза, рот, плавники переползают на одну сторону, и ее плоскость симметрии поворачивается на 90º. Камбала приобретает симметрию тела вращения, т.е. поворотную центральную симметрию.Примером симметрии можно считать и паутину. Пауки создают совершенные круговые сети. Сеть паутины состоит из равно отдаленных радиальных уровней, которые распространяются из центра по спирали, переплетаясь друг с другом с максимальной прочностью. Также симметрию в животном мире можно встретить, глядя на лебедя, плывущего по воде. На воде появляется его зеркальное отражение, что придаёт чувство покоя и уравновешенности.
С симметрией мы часто встречаемся в искусстве, архитектуре, технике, быту. Так фасады многих зданий обладают осевой симметрией. В большинстве случаев симметричны относительно оси или центра узоры на коврах, тканях, комнатных обоях. Теперь более подробно о симметрии в архитектуре. Архитектурные сооружения, созданные человеком, в большей своей части симметричны. Они приятны для глаза, их люди считают красивыми. С чем это связано? Здесь можно высказать только предположения.
Во-первых, все мы с вами живем в симметричном мире, который обусловлен условиями жизни на планете Земля, прежде всего существующей здесь гравитацией. И, скорее всего, подсознательно человек понимает, что симметрия это форма устойчивости, а значит существования на нашей планете. Поэтому в рукотворных вещах он интуитивно стремится к симметрии. Золотым веком симметрии в скульптуре и архитектуре была античность. Греко-римская любовь к пропорциям, как высшим ценностям вознесли симметрию на самую высшую точку в скульптуре того времени. Великолепные храмы того времени были переполнены симметрии, но спустя несколько веков, она всё чаще и чаще стала исчезать из архитектуры. Строители храмов, упраздняя симметрию, боролись даже с замыслом архитекторов, заменяя положенные шесть колон – пятью, четыре – тремя. Здания симметричной формы характеризуют собой строгость, вызывает чувство организованности и скованности. Яркими примерами в архитектуре являются: Казанский собор в Санкт-Петербурге (выполнен в стиле классицизма); Кафедральный собор Дуомо в Милане (выполнен в стиле готики), обладает зеркальной-осевой симметрией; Собор Святого Петра в Риме; дворец Лувр; ну и, конечно же, Нотр-Дам-Де-Пари и Эйфелева Башня.
Таким образом, нам удалось познакомиться с понятием симметрии. Объяснение законов симметрии важно для понимания красоты, гармонии, жизни.Принципы симметрии играют важную роль в физике и математике, химии и биологии, технике и архитектуре, живописи и скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своем многообразии картиной явлений, в свою очередь также подчиняются принципам симметрии.
Список используемой литературы
- Егоров-Тимченко Ю.К. Кристаллография и кристаллохимия [Текст] / Ю.К. Егоров-Тимченко.- М.: КДУ, 2009.-592с.
- Атанасян Л.С. Геометрия: Учеб. Для 7-9 кл.ср.шк. [Текст]/Л.С Анатасян, В.Ф Бутузов, С.Б. Кадомцев.-М: Просвещение,1992.-335с.
- Бурла А.М. Симметрия [Электронный ресурс]. — Режим доступа: http://pandia.ru/text/77/404/36312.php (дата обращения – 26.01.16).
- Дутова Е.Г. Симметрия вокруг нас [Электронный ресурс]. — Режим доступа: http://infourok.ru/issledovatelskaya-rabota-na-temu-simmetriya-vokrug-nas-384931.html (дата обращения 26.01.16).
- Симметрия как закономерность [Электронный ресурс]:- Режим доступа: http://www.studfiles.ru/preview/2378656/ (дата обращения – 26.01.2016).
Сочинение: Симметрия — символ красоты, гармонии и совершенства
Районная научно-практическая конференция
школьников « К вершинам знаний»
Секция « Естественно-математические дисциплины»
Тема « Симметрия – символ красоты, гармонии и совершенства»
Выполнила: Нуралинова Евгения Сергеевна
МОУ Рождественская СОШ, 8 класс.
Руководитель: Митина Светлана Петровна,
учитель математики
1 квалификационной категории.
Контактный телефон: 26-539.
2010 год.
Оглавление
§1. Введение
§2. Что такое симметрия? Ее виды в геометрии
§3. Проявление симметрии в живой и неживой природе
§4. Применение законов симметрии человеком
§5. Заключение
§6. Литература
§7. Приложения
§1. Введение
Когда мы проходили по геометрии тему «Симметрия», то на нее было отведено очень мало времени, а мне показалось эта тема интересной, и я решила взять ее для исследования. Мне захотелось побольше узнать по данному вопросу, ведь я уже ни раз слышала данный термин на других предметах и в быту. Приступив к исследованию, я заметила, что симметрия не только математическое понятие, она проявляется как нечто прекрасное в живой и неживой природе, а также в творениях человека. Поэтому я поставила перед собой такие проблемные вопросы:
— Как проявляется гармоничность симметрии в природе;
— Какие виды симметрий, встречаются в природе;
— Как применяет красоту симметрии в своих творениях человек?
Поэтому тему своего исследования я назвала «Симметрия — символ красоты, гармонии и совершенства».
§2. Что такое симметрия? Ее виды в геометрии.
О, симметрия! Гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты в Эйфелевой башне, в малой мошке,
Ты в елочке, что у лесной дорожки.
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза!
А что же такое симметрия? В толковом словаре С.И. Ожегова симметрия истолковывается, как «соразмерность, одинаковость в расположении частей чего-нибудь по противоположным сторонам от точки, прямой или плоскости». Из этого же словаря я узнала, что слово гармония означает «согласованность, стройность в сочетании чего-нибудь». Мы видим, что симметрия и гармония связаны между собой.
В начале я рассмотрю какие виды симметрии встречаются в школьном курсе геометрии, а это:
— центральная (относительно точки)
— осевая ( относительно прямой)
— зеркальная (относительно плоскости).
Центральная симметрия.
Фигура называется симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре. Точка О называется центром симметрии фигуры. Говорят также, что фигура обладает центральной симметрией (см.рис. 1).
Осевая симметрия.
Фигура называется симметричной относительно прямой а, если для каждой точки фигуры симметричная ей точка относительно прямойа, также принадлежит этой фигуре. Прямаяа называется осью симметрии фигуры. Говорят также, что фигура обладает осевой симметрией (см. рис. 2).
Зеркальная симметрия.
Зеркальной симметрией (симметрией относительно плоскости) называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей относительно этой плоскости точку М1(см. Рис 3).
Теперь я хочу, понаблюдав и изучив специальную литературу, посмотреть, где найдет свое отображение симметрия. Почему мы находим одни вещи красивыми, а другие нет? Почему смотреть на симметричные изображения приятнее, нежели на асимметричные?
§3. Проявление симметрии в живой и неживой природе
Красота в природе не создаётся, а лишь фиксируется, выражается. Рассмотрим проявление симметрии с «глобального», а именно с нашей планеты Земля.
То, что Земля — шар, стало известно образованным людям еще в древности. Земля в представлении большинства начитанных людей до эпохи Коперника была центром мироздания. Поэтому прямые, проходящие через центр Земли, они считали центром симметрии Вселенной. Поэтому даже макет Земли – глобус имеет ось симметрии (см. рис. 4).
· Далее я рассмотрела проявление симметрии в живой природе. Почти все живые существа построены по законам симметрии, недаром в переводе с греческого слово «симметрия» означает «соразмерность».
Среди цветов, например, наблюдается поворотная симметрия. Многие цветы можно повернуть так, что каждый лепесток займет положение соседнего, цветок совместится с самим собой. Минимальный угол такого поворота для различных цветов неодинаков. Для ириса он равен 120° (см. рис. 5), для колокольчика – 72° (см. рис. 6), для нарцисса – 60° (см. рис. 7). В расположении листьев на стеблях растений наблюдается винтовая симметрия. Располагаясь винтом по стеблю, листья как бы раскидываются в разные стороны и не заслоняют друг друга от света (см. рис. 8), хотя сами листья тоже имеют ось симметрии (см. рис. 9). Рассматривая общий план строения какого-либо животного, мы замечаем обычно известную правильность в расположении частей тела или органов, которые повторяются вокруг некоторой оси или занимают одно и то же положение по отношению к некоторой плоскости. Эту правильность называют симметрией тела. Явления симметрии столь широко распространены в животном мире, что весьма трудно указать группу, в которой никакой симметрии тела подметить нельзя. Симметрией обладают и маленькие насекомые, и крупные животные (см.рис. 10,11, 12).
· Среди бесконечного разнообразия форм неживой природы в изобилии встречаются такие совершенные образы, чей вид неизменно привлекает наше внимание. Наблюдая за красотой природы, можно заметить, что при отражении предметов в лужах, озерах проявляется зеркальная симметрия.
Видите? Это же голая зеркальность!
Глупая, глупая природа, ни о чем она не заботится так рьяно,
как о равновесии (см. рис. 13).
(Венедикт Ерофеев)
В мир неживой природы очарование симметрии вносят кристаллы (см.рис.14). Каждая снежинка- это маленький кристалл замерзшей воды. Форма снежинок может быть очень разнообразной, но все они обладают поворотной симметрией и, кроме того, зеркальной симметрией (см. рис. 15).
А что такое кристалл? Твердое тело, имеющее естественную форму многогранника. Соль, лед, песок и т.д. состоят из кристаллов. Прежде всего Ромэ-Делиль подчёркивал правильную геометрическую форму кристаллов исходя из закона постоянства углов между их гранями. Он писал: «К разряду кристаллов стали относить все тела минерального царства, для которых находили фигуру геометрического многогранника…» Правильная форма кристаллов возникает по двум причинам. Во-первых, кристаллы состоят из элементарных частичек — молекул, которые сами имеют правильную форму. Во-вторых, «такие молекулы имеют замечательное свойство соединяться между собой в симметричном порядке».
Почему же так красивы и привлекательны кристаллы? Их физические и химические свойства определяются их геометрическим строением. В кристаллографии (науке о кристаллах) существует даже раздел, который называется «Геометрическая кристаллография». В 1867 году генерал от артиллерии, профессор Михайловской академии в Петербурге А.В. Гадолин строго математически вывел все сочетания элементов симметрии, характеризующие кристаллические многогранники. Например, гранат попадает в первую, так называемую кубическую систему, все кристаллы которой имеют те же элементы симметрии, что и куб
(форму куба имеют, например, кристаллы поваренной соли). Всего существует 32 вида симметрий идеальных форм кристалла.
Легко вообразить, какая бы царила на Земле неразбериха, если бы симметрия в природе была нарушена!
§4. Применение законов симметрии человеком
Увидев проявление симметрии в природе, мне захотелось узнать, применяет ли человек эти закономерности в своих творениях.
Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле — как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство». Г. Вейль под симметрией понимал «неизменность какого-либо объекта, при определенного, рода преобразованиях; предмет является симметричным, в том случае, когда его можно подвергнуть какой-нибудь операции, после которой он будет выглядеть так же, как и до преобразования». Определенную главу Г. Вейль посвятил орнаментной симметрии. Упорядоченность и подчиненность определенному набору правил мы обнаруживаем в узорах и орнаментах (см. рис. 16).
Нельзя не увидеть симметрию и в ограненных драгоценных камнях. Многие гранильщики стараются придать бриллиантам форму тетраэдра, куба, октаэдра или икосаэдра. Так как гранат имеет те же элементы что и куб, он высоко ценится знатоками драгоценных камней. Художественные изделия из гранатов были обнаружены в могилах Древнего Египта, относящихся еще к додинастическому периоду (свыше двух тысячелетий до н.э.).
В коллекциях Эрмитажа особым вниманием пользуются золотые украшения древних скифов. Необычайно тонка художественная работа золотых венков, диадем, дерева и украшенных драгоценными красно-фиолетовыми гранатами (см.рис. 17, 18).
Одним из самых наглядных использований законов симметрии в жизни служат строения архитектуры. Это то, что чаще всего мы можем увидеть. В архитектуре оси симметрии используются как средства выражения архитектурного замысла. Примеров использования симметрии в архитектуре множество, одним из них является прекрасный Новосибирский театр оперы и балета (см. рис. 19). И даже у нас, в г. Купино есть здание, имеющее симметрию – здание Администрации Купинского района (см. рис. 20).
Еще одним примером использования человеком симметрии в своей практике — это техника. В технике оси симметрии наиболее четко обозначаются там, где требуется оценить отклонение от нулевого положения, например на руле грузовика или на штурвале корабля. Или одно из важнейших изобретений человечества, имеющих центр симметрии, является колесо (см. рис. 21), также центр симметрии есть у пропеллера и других технических средств.
Симметрию можно заметить даже там, на что никогда не обращал внимание. Например, если вы поместите буквы перед зеркалом, расположив его параллельно строке, то заметите, что те из них, у которых ось симметрии проходит горизонтально, можно прочесть и в зеркале. А вот те, у которых ось расположена вертикально или отсутствует вовсе, становятся «нечитабельными».
Существуют языки, в которых начертание знаков опирается на наличие симметрии. Так, в китайской письменности иероглиф означает именно истинную середину.
Симметрия также есть и в числах, например, √12345678987654321=111111111; √123454321=11111 и т.д.
симметрия центральная осевая зеркальная геометрия
Заключение
Изучив и исследовав тему «Симметрии» я узнала, что помимо осевой, зеркальной и центральной видов симметрии, которые мы изучаем в школьном курсе, существуют и другие виды симметрии, например в природе – поворотная, винтовая, в кристаллографии вообще — 32 вида.
Таким образом, изучая симметрию законов природы, рано или поздно удается глубже проникнуть в сущность живого, объяснить ход эволюции и дать возможность человеку чаще применять данные законы симметрии в жизни.
Рассматривая архитектуру зданий, предметы украшения и быта, технические изобретения, мы видим в них присутствие центральной, поворотной, переносной, осевой и зеркальной видов симметрии, которые дают ощущение спокойной уверенности и эстетической привлекательности.
Симметрия, проявляясь в самых различных объектах природного мира, несомненно, отражает наиболее общие ее свойства. Поэтому изучение симметрии разнообразных природных объектах и сопоставление его (изучения) результатов удобным и надежным инструментом познания гармонии мира.
Литература
1) Тарасов Л.В. Этот удивительно симметричный мир. – М.: Просвещение, 1982.
2) Гончарова С.Г., Кукин Г.П. Конструктор «В мире симметрии» //Математика в школе. – 1996. — № 3. – С. 60.
3) Кошелев А.И. Проявление симметрии в различных формах материи.
4) Вейль Г. Симметрия. М.: Едиториал УРСС, 2003
5) Климова Н.Т. Народный орнамент в композиции художественных изделий. — М.: Изобразительное искусство, 1993.
6) О. Иванова. Этот симметричный мир. — Первое сентября. – 2006 № 6.
Приложения
Симметрия и ее виды в геометрии.
Симметрия в природе
Классы симметрии
По тому, сколько симметрий имеют фигуры, можно проводить их классификацию. Множество симметрий правильного n-угольника состоит из 2n преобразований: n-поворотов и n-осевых симметрий. Класс симметрий обозначается через Dn.
Задавая класс симметрии можно самим конструировать фигуры.
Я построила фигуру с симметрией D8, D12.
Симметрия в природе
В основе строения любой живой формы лежит принцип симметрии. Я убедилась в этом сама.
Листья растений обладают осевой симметрией, а в строении некоторых цветов (например, кактусов) присутствует центральная симметрия.
Зеркальная симметрия характерна для представителей животного мира. Эта симметрия очень ярко выражена у бабочек. Симметрия левого и правого крыла проявляются здесь с почти математической строгостью.
Еще более ярко и систематически симметричность обнаруживается в неживой природе, например в кристаллах. Сахар и поваренная соль, лед и песок состоят из множества кристалликов. Даже обыкновенная глина представляет собой нагромождение мельчайших кристалликов. Кристаллы – это твердые тела, имеющие естественную форму многогранников.
Каждая снежинка – это маленький кристалл замершей воды. Сфотографировать и увеличить фото снежинки у меня не получилось, поэтому я нашла фотографии в интернете.
Симметрия внутри нас
Несмотря на то, что огромное количество предметов, обладающих симметрией находится вокруг нас, в нашем теле есть органы, которым тоже не чуждо понятие симметрия. Почти все подобные органы симметричны относительно той или иной оси (т.е. осевая симметрия). Например: легкие, почки, глаза, руки, ноги .
Симметрия в предметах декоративно-прикладного искусства
Принцип симметрии используется в построении орнамента. Орнамент предназначен для украшения различных предметов и архитектурных сооружений.
Я попробовала сама построить орнамент:
- построила квадрат АВСD;
- провела диагонали;
- отметила точку пересечения диагоналей-точку О;
- выполнила поворот относительно точки О, построила квадраты.
- Из центра квадратов провела дуги, радиусы которых равны сторонам квадрата
Симметрия в музыке
Я занимаюсь в музыкальной школе, поэтому мне было интересно определить, присутствует ли симметрия в музыке.
Когда учат играть на музыкальных инструментах, то всегда начинают с гамм. В них ноты располагаются симметрично на нотном стане:
В построении музыкальных произведений также присутствует симметрия. Секвенция — разновидность трансляции. Многократное повторение небольшого мотива разных ступеней лада, как в восходящем, так и в нисходящем направлении.
Симметрия в технике
Практически все технические объекты обладают симметрией. Симметрия в технике обеспечивает хорошую обтекаемость воздухом или водой, а значит минимальное сопротивление движению.
Колёса, различные механизмы обладают осевой и центральной симметрией.
Симметрия в русском языке
В русском алфавите 33 буквы и некоторые из них обладают осевой и центральной симметрией.
Так же я нашла слова, которые обладают осевой симметрией, например:
шалаш, оно, топот, око, дед, кабак.
В русском языке есть даже фразы, которые обладают симметрией (их называют палиндромами), например:
- город дорог;
- барин и раб;
- бел хлеб;
- Лёша на полке клопа нашёл;
- Вор в лесу сел в ров.
Симметрия в физике
В физике существует понятие «центр тяжести тела».
Центр тяжести — это геометрическая точка, через которую проходит равнодействующая всех сил тяжести, действующих на частицы этого тела при любом положении последнего в пространстве.
Центр тяжести плоской фигуры, обладающей симметрией, совпадает с центром симметрии, если фигура имеет ось симметрии, то центр лежит на оси симметрии. Я в этом убедились, проведя эксперимент.
Я вырезала прямоугольник, провела его диагонали и отметила точку их пересечения. Эта точка лежит на пересечении осей симметрии прямоугольника. Она и является центром тяжести прямоугольника. Если вырезать круг, то центр тяжести будет лежать в точке пересечения диаметров круга. Эта точка является и центром симметрии.
Если определять центр тяжести несимметричной фигуры, то это можно сделать с помощью груза, подвешенного на нитке.
Симметрия в геометрии
Любой из графиков, построенных ниже, можно было получить из графика функции y путём параллельного переноса.
С помощью программы «Математический конструктор» я легко справилась с построением графиков, а когда строила графики самостоятельно на листе в клетку, то не все графики смогла построить. Например, трудно было определить по точкам, как будет располагаться график функции.
Программа построения графиков помогла разобраться. График этой функции-парабола, ветви которой симметричны относительно прямой
х=-2,5. Самым сложным было построить график функции, содержащей модуль. Я решила сразу воспользоваться программой. Построила график функции
График этой функции тоже симметричен относительно прямо х=-2,5 , но значения функции могут быть только неотрицательными
Оба графика симметричны относительно оси Оу.
Заключение
В процессе своей работы я расширила свои знания о симметрии, убедилась, что симметрия присутствует во многих областях жизни, с ней мы сталкиваемся в живой и не живой природе, при изучении различных предметов. Симметрия действительно создаёт порядок, красоту и совершенство в окружающем нас мире.
Симметрия – это фундаментальное свойство природы, с которым связаны различные законы и свойства.
Источники информации
- Атанасян Л.С. Учебник по геометрии для 7 – 9 классов.
- Атанасян Л.С. учебник по геометрии для 10-11 классов.
- Интернет.
Проект выполнили: Алифанова Марина и Маринина Евгения.
Тема исследования: «Симметрия вокруг нас».
Проблема исследования : Какое место в нашей жизни занимает симметрия?
Актуальность : Симметрия окружает человека, находя своё проявление как в живой, так и в неживой природе. Объяснение законов симметрии важно для понимания красоты, гармонии, жизни.
Цель исследования: Показать прямую связь окружающего мира и симметрии,показать пользу и красоту практического применения симметрии в жизни.
Гипотеза исследования: В окружающем мире было бы меньше порядка, красоты и гармонии, если бы не было симметрии.
Задачи исследования:
1) Изучить различные источники информации для определения понятия симметрии и её основных видов.
2) Выявить как используется симметрия в окружающем нас мире и в повседневной жизни.
3) Выяснить значение симметрии для обеспечения порядка,красоты и гармонии в окружающем нас мире.
4) Сделать выводы и дать рекомендации.
Методы исследования:
1) Изучение информации.
2)Анкетирование.
4)Эксперимент.
5) Анализ.
Этапы исследования
I.Изучение источников информации.
Результат:
Симметрия — соответствие, неизменность проявляемые при каких-либо изменениях, преобразованиях.
Симметрия бывает разных видов:зеркальная, осевая, центральная, вращательная, скользящая, радиальная, билатеральная.
Рассмотрим развитие симметрии от древнейших времен до современности.
Историческая хронология событий
Итог: Дали точное определение симметрии и показали ,что представления о симметрии и её следствиях в разных областях деятельности использовались человечеством с древнейших времён.
II.Провести анкетирование среди учащихся о повседневном использование симметрии в жизни.
Анкета
Здравствуйте ,уважаемые учащиеся 7-8ых классов МКОУ «Большечапурниковская СШ».
Мы студентки 1 курса ВГСПУ проводим анкету с целью исследования ваших представлений о симметрии. Все результаты буду проанализированы и представлены в нашем исследовательском проекте «Симметрия вокруг нас». Все результаты будут переданы вашему классному руководителю.
Ваше мнение очень важно для нас !
Инструкция:
Анкета состоит из 7 вопросов, на каждый из которых вам нужно ответить. Ответы представлены в виде качественной шкалы с 3 вариантами ответов : а)да, б)нет, в) затрудняюсь ответить. Вам нужно выбрать один из предложенных вариантов ответов. Так же вам предлагается варианты ответов в виде высказывания вашего мнения, где вам нужно коротко и ясно изъясниться. Желаем удачи!
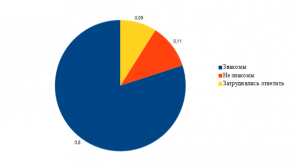
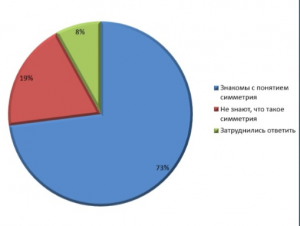
1. Знакомы ли вы с понятием слова симметрия?
а) Да
б) Нет
в) Затрудняюсь ответить
Итог: большинство опрошенных знакомы с понятием симметрия.
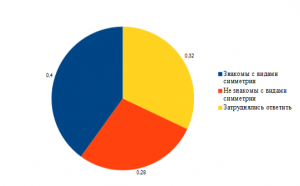
2. Знакомы ли вы с видами симметрии ?
а) Да
б) Нет
в) Затрудняюсь ответить
Итог: большинство опрошенных знакомы с видами симметрии.
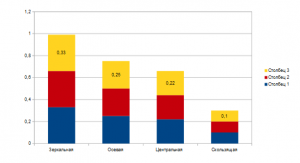
3. Приведите примеры симметрии ,которые вам известны?
__________________________________________
Итог: самым популярным видом симметрии среди опрошенных является зеркальная симметрия.
4. Является ли симметрия обязательной частью нашей жизни?
а) Да
б) Нет
в) Затрудняюсь ответить
Итог: большинство опрошенных считают, что симметрия является обязательной частью нашей жизни.
5.Во всём ли проявляется симметрия?
а) Да
б) Нет
в) Затрудняюсь ответить
Итог: большинство опрошенных ответили, что симметрия проявляется во всем.
6.Всё ли симметричное красиво ?
а) Да
б) Нет
в) Затрудняюсь ответить
Итог: большинство опрошенных ответили,что все симметричное красиво.
7. Как симметрия проявляется в творчестве человека ? (Выскажите своё мнение.)
_________________________________________
Итог:
По результатам опроса мы можем сделать вывод, большинство респондентов встречались с понятием симметрия. По результатам опроса было установлено,что симметрия создаёт красоту и гармонию в нашем мире.
III.Эксперимент:поиск симметрии в окружающем нас мире.
— Следует разбиться на 3 группы : 1 группа ищет примеры симметрии в природе , 2 группа ищет примеры симметрии в технике , 3 группа ищет примеры симметрии в архитектуре .
— Каждой группе предлагается запечатлеть с помощью фотоаппарата примеры симметрии соответственно своей теме .
— Средствами графического редактора показать на фотографиях виды симметрии, относящееся к специальной теме своей группы.
— Представить результаты своей работы в виде фотографий.
Результат 1 группы ,которые рассматривали симметрию в природе.
Результат 2 группы ,которые рассматривали симметрию в технике.
Результат 3 группы ,которые рассматривали симметрию в архитектуре .
Итог:
В результате проведения проекта, мы пришли к выводу, что симметрия применяется везде в нашей повседневной жизни : природе, технике, архитектуре, математике, физике, она противостоит хаосу, беспорядку. Симметрия присутствует в нашей жизни буквально во всем, но мы настолько к ней привыкли, что не замечаем этого.
IV.Подведение итогов. Выводы и рекомендации.
Презентация
Выводы:
Подводя итоги исследования, можно с точностью сказать, что мы достигли реализации поставленной цели и доказали выдвинутую гипотезу. Природа устроена в соответствии с законами симметрии, всё живое и неживое в природе обладает свойством симметрии. Знание о симметрии в повседневной жизни для человека очень важно. Её можно применять в своей деятельности: в строительстве, в создании предметов быта, в украшении одежды, в оформлении интерьера жилища.
В своей работе мы рассматривали симметрию в окружающем нас мире и выявили, что:
- симметрия встречается как в живой, так и в неживой природе.
- симметрия является одним из принципов гармонического построения мира.
- действительно, симметрию мы можем наблюдать везде.
Ссылки на используемые сервисы интернета:
1.Симметрия вокруг нас URL: https://nsportal.ru/ap/library/drugoe/2014/04/13/simmetriya-vokrug-nas (Дата обращения: 01.07.2019).
2. Значение слова симметрия URL: https://dic.academic.ru/ (Дата обращения: 01.07.2019).
3.Википедия URL: https://ru.wikipedia.org (Дата обращения: 02.07.2019).
4. Урок на тему «Симметрия вокруг нас» URL: https://urok.1sept.ru (Дата обращения: 02.07.2019).
5.Создание тизера URL: https://www.powtoon.com/home/? (Дата обращения: 02.07.2019)
6.Создание ленты времени URL: https://www.timetoast.com/ (Дата обращения: 03.07.2019)
7. Разработка онлайн-презентаций URL: https://prezi.com/dashboard/next/(Дата обращения: 04.07.2019)
8. Создание интерактивных книг-комиксов URL:http://www.toondoo.com/ (Дата обращения: 05.07.2019)
Муниципальное
бюджетное общеобразовательное учреждение
«Татарская
средняя общеобразовательная школа»
«Муниципальная
конференция научно-исследовательских работ обучающихся общеобразовательных
организаций Черлакского муниципального района Омской области «Шаги в науку»
Научно-исследовательская
работа
Направление
работы: математика
Тема
«Симметрия вокруг нас»
Автор:
Кабацкий Е. Е.
Руководитель:
Гриценко Т. Р.
Содержание
Введение
……………………………………………………………….……. 2
Глава 1 Теоретическая часть
1.1 Понятие симметрии и
ее виды………………………..……………….. 4
1.2 Симметрия
в живой природе………..…………………………….…….9
1.3 Симметрия
в неживой природе…………………………………………….12
1.4 Симметрия
в творениях рук человека
Глава
2 Практическая часть.
2.1 Действительно ли симметрия приятна глазу?……………………………………13
2.2
Симметрия вокруг меня…………………………………………….……15
Заключение.………………………………………………………………………18
Источники
информации …………………………………………………… 19
Приложение
…………………………………………………………………. 20
Введение
Впервые
с понятием симметрия я столкнулся, когда решал вариант КИМ ВПР по математике за
6 класс. Это было задание под №12. Оно меня очень заинтересовало, но
учительница сказала, что это задания на симметрию и мы будем разбирать их
позже, после изучения темы «Симметрия».
Раньше,
я не обращал внимания на то, что симметрия окружает нас повсюду. Она
встречается не только в математике, но в живой и не живой природе, в творениях
рук человека. На объекты обладающие симметрией приятно
смотреть. Симметрия вызывает чувства организованности и спокойствия.
Тема
«Симметрия вокруг нас» заинтересовала меня. Я решил взять её для своего
исследования. Мне захотелось, как можно больше узнать
о симметрии. Научиться определять виды симметрии,
решать задачи на симметрию, находить симметрию в окружающем мире.
Актуальность.
Выбранная нами тема актуальна, так как симметрия
повсюду вокруг нас – в науке, искусстве, природе, технике,
быту. Создавая симметрию,
природа стремится к красоте, гармонии и совершенству. Симметрия кроется в
формах транспорта, архитектуре, мебели, одежде, орнаментах и бордюрах и т. д.
Понятие симметрии используют все без исключения направления современной науки.
Принципы симметрии играют важную роль в научном познании мира. Все законы
природы подчиняются принципам симметрии.
Проблема: В
школьном курсе математике отведено на изучение темы «Симметрия» всего несколько
уроков. Задачи на симметрию встречаются в различных проверочных работах. Зеркальная
симметрия и поворот в курсе математики за 6 класс по учебнику Г. В. Дорофеев и
другие не изучается, а задачи на ВПР на поворот встречаются.
Цели: изучить
понятие симметрии и виды симметрии, научиться решать задачи на симметрию,
исследовать проявление симметрии в различных объектах окружающих нас.
Задачи:
1)
изучить литературу и интернет ресурсы по теме
2)
рассмотреть основные виды симметрии;
3)
решить задачи из учебника и ВПР на симметрию применяя полученные знания
3)
найти симметричные объекты в окружающем мире
4)
доказать, что нас окружают симметричные предметы.
5)
провести мини исследование «Действительно ли симметрия приятна глазу?»
Предмет исследования:
симметрия.
Объект исследования:
понятие и
виды симметрии, симметрия в окружающем мире
Гипотеза: симметрия не только практична, но и приятна глазу
человека, поэтому симметрия широко используется во всех проявлениях
жизнедеятельности человека, мы сталкиваемся с ней повседневно, она нас окружает
нас.
Методы исследования: поиск и подборка, анализ, систематизация,
исследование, выполнение рисунков, чертежей и фотографий.
Новизна
моей работы заключается в том, что в нашей
школе исследованием темы «Симметрия вокруг нас» ранее никто
не занимался.
Практическая
значимость.
Написанная
нами работа даст возможность учащимся применять полученные знания при решении
предметных задач, при изучении тем на других предметах, а также в
повседневной жизни.
Глава
1. Теоретическая часть
1.1 Понятие
симметрии и её виды.

симметрии и её виды в различных источниках раскрываются примерно одинаково. «Слово
«симметрия» греческого происхождения. Оно, как слово «гармония», означает
«соразмерность», «наличие определенного порядка, закономерности в распоряжении
частей»» [Дорофеев]. Снежинка, бабочка, птица, отражение в воде, — это лишь
некоторые примеры проявления симметрии в природе.
С
давних времен люди использовали симметрию в архитектуре, предметах быта,
орнаментах.
В
математике рассматриваются различные виды симметрии.
В
учебнике по математике за 6 класс Г. В. Дорофеева др. мы знакомимся с осевой,
центральной, а также с зеркальной симметрией. Решая задания ВПР по математике,
мне попалась задача на поворотную симметрию. Поворотную симметрию я изучал из интернет
ресурсов.
Осевая
симметрия
Возьмём лист
бумаги. Проведем на нем какую – ни будь прямую и перегнем лист по этой прямой.
Проткнём сложенный лист иглой (рис. а). Развернув лист, мы увидим две
точки, расположенные по разные стороны от этой прямой (рис. б). Говорят,
что эти точки симметричны относительно прямой
линии сгиба .
Проведем
через полученные точки прямую и обозначим её буквой l.
С помощью инструментов мы можем убедиться, что прямая lперпендикулярна
линии сгиба, а точки находятся от неё на одинаковом расстоянии (рис. в ).
Это важное свойство симметричных точек. С его помощью можно строить точки,
симметричные относительно некоторой прямой, и без перегибания листа бумаги.
Пусть
дана прямая lи
точка M (рис.
а). Построим точку, симметричную точкеMотносительно
прямойl. Для этого проведём
через точку Mпрямую,
перпендикулярную l (рис.
б);
Отметим
на ней точку K,
расположенную на таком же расстоянии от прямой l,
что и точка M
(рис. в).
Точка К
симметрична точке М относительно прямой l
.

рисунок ниже: четырёхугольники ABCD
и A1B1C1D1
симметричны относительно прямой k.
Симметричные вершины обозначены одной и той же буквой, но с добавлением индекса
– цифры, поставленной внизу. Называя четырёхугольник ABCD,
мы обходим его по часовой стрелке, а симметричный ему четырёхугольникA1B1C1D1
– против часовой стрелке. Это означает что осевая
симметрия меняет направление обхода на противоположное.
Если перегнуть рисунок по прямой k
, то четырёхугольники A1B1C1D1
и ABCD
совпадут . Иными словами, эти четырёхугольники равны .
Если
фигуры симметричны, то они равны .
В пространстве аналогов осевой симметрии является симметрия относительно
плоскости – зеркальная симметрия. Отражение в воде – примерзеркальной
симметрии в природе. С этой симметрией мы постоянно встречаемся, глядя на себя
в зеркале.
Зеркальная симметрия, как и осевая, меняет ориентацию предмета. Если мы, стоя
перед зеркалом, закружимся по часовой стрелке, то наше отражение будет кружиться
против часовой стрелки.
Заметим ещё один интересный факт: всё то, что мы делаем правой рукой, наше отражение
делает левой, и наоборот.
Центральная симметрия
характеризуется наличием центра симметрии —
точки О, обладающей определённым свойством. Можно сказать, что точка О
является центром симметрии, если при повороте вокруг точки О на 180°
фигура переходит сама в себя. На рисунке ниже каждая пара отрезков ОА и ОА1,
ОВ и ОВ1, ОС и ОС1 равна и лежит на одой прямой. Фигуры
симметричные относительно некоторой точки, равны.
Поворот
Если
одна фигура получена из другой фигуры поворотом всех её точек относительно
центра O на один и тот же угол в одном и том
же направлении, то такое преобразование фигуры называется поворотом.
Чтобы
поворот имел место, должен быть задан центр O и угол поворота α.

наоборот — отрицательный угол поворота. Треугольник ABC повёрнут
в положительном направлении (приблизительно на α=45 градусов).
Если
угол поворота равен 180 или −180 градусам, то фигура
отображается как центрально симметричная данной, и этот поворот называется
центральной симметрией.

которые взаимно повёрнуты.
В
заданиях 12 ВПР по математике за 6 класс встречаются задачи на отрицательный и
положительный поворот на угол в 900 смотрите приложение задача №5.
Зеркальная симметрия
хорошо знакома каждому человеку из повседневного наблюдения. Как показывает
само название, зеркальная симметрия связывает любой предмет и его отражение в
плоском зеркале. Говорят, что одна фигура (или тело) зеркально симметрично
другой, если вместе они образуют зеркально симметричную фигуру (или тело).
Зеркальная симметрия — это
тип симметрии объекта, когда объект при операции отражения переходит
в себя. Это математическое понятие в оптике описывает соотношение объектов и их
(мнимых) изображений при отражении в плоском зеркале. Проявляется во многих
законах природы (в кристаллографии, химии, физике, биологии и т. д.,
а также в искусстве и искусствоведении). На рисунке ниже точки А и В называются
симметричными относительно плоскости а (плоскость симметрии), если
плоскость а проходит через середину отрезка АВ и перпендикулярна к этому
отрезку. Каждая точка плоскости а считается симметричной сама себе.


1.2 Симметрия в живой
природе
Симметрией
обладают объекты и явления живой природы. Она не только радует глаз и
вдохновляет поэтов всех времен и народов, а позволяет живым организмам
лучше приспособиться к среде обитания и просто выжить. В живой природе огромное
большинство живых организмов обнаруживает различные виды симметрий.
Изображения
на плоскости многих предметов окружающего нас мира имеют ось симметрии или
центр симметрии. Многие листья деревьев и лепестки цветов симметричны
относительно среднего стебля.
Среди
цветов наблюдаются поворотные симметрии разных порядков. Многие цветы обладают
характерным свойством: цветок можно повернуть так, что каждый лепесток займёт
положение соседнего, цветок же совместится с самим собой.
Осевая
симметрия встречается и в животном мире. Так у бабочки симметрия левого правого
крыльев проявляется с математической строгостью. Симметрия форм и окраски
растений и животных придает им красоту.
Всех
животных делят на одноклеточных и многоклеточных.
Наличие форм симметрии прослеживается уже у простейших – одноклеточных
(инфузории, амёбы).
У
подавляющего большинства животных части тела расположены симметрично. Лишь у
немногих (например, у некоторых губок и простейших) тело имеет неправильную,
лишенную симметрии форму (например, амеба протей).
Можно
сказать, что каждое животное состоит из правой и левой половин. Например,
правое и левое ухо, правый и левый глаз, правый и левый рог и т.д. Симметрия
животным также служит для равновесия движения
Отметим,
наконец, зеркальную симметрию человеческого тела (речь идёт о внешнем облике и
строении скелета).
Эта
симметрия всегда являлась и является основным источником нашего эстетического
восхищения хорошо сложенным человеческим телом.
Человеческое
тело, так же как и тело других позвоночных, в основе своей построено
симметрично. Общие принципы строения организма человека заложены миллиарды лет
назад, когда формировался генетический код, и возникла первая клетка. В наших
генах содержится значительная часть генофонда древних рыб, первых хордовых и
некоторых беспозвоночных животных. Одним из признаков, переданных нам, является
двухсторонняя симметрия человеческого тела. Среди врачей существует мнение, что
причинами наших болезней являются не только и не столько вирусы и прочие
вредные факторы среды, сколько генетически обусловленные нарушения конструкции
тела. «Симметричные» животные живут дольше, чем «несимметричные», что также и
показатель лучшей способности к воспроизводству. Асимметрия лица – это
показатель старения.
В
природе почти везде можно найти симметрию. Спил дерева, цветок, плоды многих
растений. Посмотрим в более глобальном масштабе: планеты, звезды, звездные
системы – все относительно симметрично.
Необходимо
отметить, что в природе невозможна идеальная математическая симметрия. Отсюда
можно сделать вывод: в реальной жизни не может быть совершенной симметрии.
1.3. Симметрия в неживой
природе

симметрии и порядка, но это не так.
Сколько вопросов возникает у человека, глядящего на снежинки. Именно
кристаллы вносят в мир неживой природы очарование симметрии.

снежинка – это маленький кристалл замёрзшей воды. Форма снежинок может быть очень
разнообразной, но все они имеют форму шестиугольника и обладают симметрией –
поворотной, зеркальной и осевой.
Единственная горизонтальная симметрия, которую мы встречаем в
природе, — отражение в зеркале воды. Возможно, в необычности такой симметрии и
заключается её завораживающая сила.
Получается,
что всякий раз, когда мы, говорим о гармонии, красоте, мы тем самым касаемся
симметрии.
1.4.
Симметрия в творениях рук человека
Симметрия – царица
архитектурного совершенства. Известный французский
архитектор Ле Корбюзье сказал: «Человеку необходим порядок: без него все его
действия теряют согласованность, логическую взаимосвязь. Чем совершеннее
порядок, тем спокойнее и увереннее чувствует себя человек». Нагляднее всего
видна симметрия в архитектуре. Наиболее ярко симметрия проявляется в античных
сооружениях Древней Греции, предметах роскоши и орнаментов, украшавших их. С
тех пор и до наших дней симметрия в сознании человека стала объективным
признаком красоты.
Соблюдение
симметрии является первым правилом архитектора при проектировании любого
сооружения. Стоит только посмотреть на великолепное произведение проекту архитектора И.
Г. Хворинова Омский академический театр драмы, чтобы убедиться в этом.
Принципы
симметрии являются основополагающими для любого архитектора, но вопрос о
соотношении между симметрией и асимметрией каждый архитектор решает по-разному.
Асимметричное в целом сооружение может являть собой гармоническую композицию
симметричных элементов.
Архитектурные
сооружения, созданные человеком, в большей своей части симметричны. Они приятны
для глаза, их люди считают красивыми.
С
симметрией мы встречаемся везде – в природе, технике, архитектуре, быту,
искусстве, науке, музыке, литературе. Понятие симметрии проходит через всю
многовековую историю человеческого творчества. Принципы симметрии играют важную
роль в физике и математике, химии и биологии, технике и архитектуре, живописи и
скульптуре, поэзии и музыке. Законы природы, управляющие неисчерпаемой в своём
многообразии картиной явлений, в свою очередь, подчиняются принципам симметрии.
Свойство
симметричности, присущее живой природе, человек использовал в своих
достижениях: изобрел самолет, технику, бытовые приборы, электронные устройства,
создал уникальные здания архитектуры.
Симметрия
воспринимается человеком как проявление закономерности, а значит внутреннего
порядка. Внешне этот внутренний порядок воспринимается как красота.
Глава 2. Практическая
часть.
2.1. Действительно ли симметрия приятна глазу
Герман
Вейль сказал: «Симметрия является той идеей, посредством которой человек на
протяжении веков пытался постичь и создать порядок, красоту и совершенство»[1].
Лев
Николаевич Толстой говорил «Стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был
поражен мыслью: почему симметрия приятна глазу? Что такое симметрия? Это
выраженное чувство, отвечал я сам себе. На чём же оно основано?»[3]. Мы тоже
задались этим вопросом. Действительно ли симметрия приятна глазу человека? И
провели мини исследование. Предлагали учащимся 6-11 классов посмотреть на три
рисунка (см. приложение) на которых были изображены по 6 картинок. Каждая из
картинок обладала симметрией или асимметрией. На первом рисунке было 2 бабочки,
обладающих симметрией и 4 асимметрией. На втором рисунке были архитектурные
сооружения, 4 картинки симметричных и 2 не имеющих симметрии. На третьем
рисунке были 3 симметричных композиции и 3 асимметричных. Результат нас
удивил. Из 48 участников исследования практически все выбрали объекты с
симметрией. Наша гипотеза, что симметрия приятна глазу человека, подтвердилась.
Результаты представлены ниже в виде таблицы и диаграммы.
|
Рисунок 1 Живая природа (Бабочки) |
Рисунок 2 Неживая природа (Архитектура) |
Рисунок 3 Композиции |
|
|
Симметрия, |
44 — 92 |
47 — 98 |
45 — 94 |
|
Асимметрия, |
4 — 8 |
1 — 2 |
3 — 6 |
2.1. Симметрия вокруг
меня
В
данной части работы, используя полученные мною знания, я исследовал некоторые
объекты окружающие меня на наличие симметрии.
|
Мои Если |
|
|
|
|
|
Домашние
|
|
|
|
Мой стул (осевая и |
|
Узор
|
Форма |
|
Корпус |
|
|
|
|
Вывод:
Вокруг меня чаще всего встречается осевая и зеркальная симметрии. В природе
невозможна идеальная математическая симметрия. В реальной жизни не может быть
совершенной идеальной симметрии.
ЗАКЛЮЧЕНИЕ
Подводя
итог своей работы, я сделал вывод. Поставленные мною цели и задачи достигнуты. Я
изучил
понятие симметрии и виды симметрии, умею решать задачи на симметрию,
исследовал проявление симметрии в различных объектах окружающих меня. Задачи на
симметрию в приложении. Моё исследование подтвердило гипотезу о том, что
симметрия не только практична, но и приятна глазу человека, поэтому симметрия
широко используется во всех проявлениях жизнедеятельности человека. Она
присутствует в нашей жизни буквально во всём, но мы настолько к ней привыкли, что
не замечаем этого. Данную работу можно использовать на уроках математики и при
подготовке к ВПР и ОГЭ.
Источники информации
1. Вейль
Г. Симметрия. М.: Едиториал УРСС, 2003
2. Дорофеев
Г. В. И др.. Математика 6 класс. М.: Просвещение, 2017
3. https://ilibrary.ru/text/1310/p.19/index.html
4. http://obuchonok.ru/node/2260
5. https://urokimatematiki.ru/prezentaciya-dvizheniya-zerkalnaya-simmetriya-965.html
6. http://www.desktopwallpapers4.me/nature/snowy-peak-reflecting-in-the-lake-38321/
7. https://www.yaklass.ru/p/geometria/9-klass/dvizhenie-10434/parallelnyi-perenos-i-povorot-9251/re-35537b4b-fe94-48de-8388-56489b9264e2
8. https://www.pinterest.ru/pin/137570963589521631/
Приложение.
Задания из КИМ
ВПР и ОГЭ
Задания
из КИМ ВПР по математике
1. Задание
12
На
рис. 1 на клетчатой бумаге изображены фигуры, симметричные относительно
изображённой прямой. Нарисуйте на рис. 2 фигуру, симметричную заштрихованной
фигуре относительно данной прямой.
2. Задание
12 № 87
На
рис. 1 на клетчатой бумаге изображены фигуры, симметричные относительно
изображённой прямой. Нарисуйте на рис. 2 фигуру, симметричную заштрихованной
фигуре относительно данной прямой.
3. Задание
12 № 471
На
левом рисунке фигуру 1 зеркально отразили относительно
пунктирной
линии так, что получилась фигура 2. Нарисуйте,
какая
фигура получится, если то же самое сделать с фигурой 3
на
правом рисунке.
4. Задание
12 № 666
Лёня
закрасил несколько клеточек на квадратном листке и сложил его по диагонали.
Получился отпечаток.
Затем
на таком же листке Лёня закрасил несколько клеточек и тоже сложил листок по
диагонали. Нарисуйте получившийся отпечаток.
5. Задание
12 № 693
Когда
фигуру A повернули на 90° против часовой стрелки
относительно
точки О, получилась фигура В. Нарисуйте
фигуру,
которая получится, если повернуть фигуру С на
90°
против часовой стрелки относительно точки M.
Задание
из КИМ ОГЭ
6.
Задание 15

Сколько всего осей симметрии
имеет фигура,
изображённая
на рисунке?