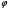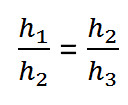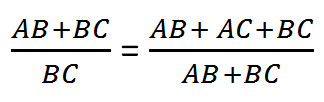Сочинение по математике 6 класс золотое сечение

ДОКЛАД

на тему: “Золотое сечение”

Выполнила ученица 6б класса:                Теремкова
Катя

Учитель:    Тивирикина Ирина Александровна

Золотое сечение – гармоническая пропорция.

В математике пропорцией  называют
равенство двух отношений:

a : b = c : d.

Отрезок прямой AB можно разделить на
две части следующими способами:

·
на
две равные части – AB : AC = AB : BC;

·
на
две неравные части в любом отношении (такие части пропорции не образуют);

·
таким
образом, когда AB : AC = AC : BC.

Последнее и есть золотое деление или деление отрезка в
крайнем и среднем отношении.

Золотое
сечение
– это такое пропорциональное деление отрезка на неравные части, при котором
весь отрезок так относится к большей части, как сама большая часть относится к меньшей;
или другими словами, меньший отрезок так относится к большему, как больший ко
всему:

           a : b = b : c
или
                  c : b = b : a.

Даже не вдаваясь в
расчеты, золотое сечение можно без труда обнаружить в природе. Так, под него
попадают соотношение хвоста и тела ящерицы, расстояния между листьями на ветке,
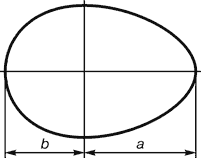
есть золотое сечение и в форме яйца, если условную линию провести через его
наиболее широкую часть.

 В
результате решения одной из задач Леонардо Фибоначчи вышел на последовательность
чисел, известную сейчас как ряд Фибоначчи: 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д.
На отношение этой последовательности к золотой пропорции обратил внимание
Кеплер: «Устроена она так, что два младших члена этой нескончаемой пропорции в
сумме дают третий член, а любые два последних члена, если их сложить, дают
следующий член, причем та же пропорция сохраняется до бесконечности».

Проявления спиральных форм золотого сечения в природе – это  раковина
улитки, расположение семян подсолнечника, узоры паутины, движение урагана,
строение ДНК и даже структура галактик заключают в себе ряд Фибоначчи.

Модельеры и дизайнеры одежды все расчеты делают, исходя из
пропорций золотого сечения. Человек – это универсальная форма для проверки
законов золотого сечения. Конечно, от природы далеко не у всех людей пропорции
идеальны, что создает определенные сложности с подбором одежды. В дневнике
Леонардо да Винчи есть рисунок вписанного в окружность обнаженного человека,
находящегося в двух наложенных друг на друга позициях. Опираясь на исследования
римского архитектора Витрувия, Леонардо подобным образом пытался установить
пропорции человеческого тела. Позднее французский архитектор Ле Корбюзье,
используя «Витрувианского человека» Леонардо, создал собственную шкалу
«гармонических пропорций», повлиявшую на эстетику архитектуры XX века. Адольф
Цейзинг, исследуя пропорциональность человека, проделал колоссальную работу. Он
измерил порядка двух тысяч человеческих тел, а также множество античных статуй
и вывел, что золотое сечение выражает среднестатистический закон. В человеке
ему подчинены практически все части тела, но главный показатель золотого
сечения это деление тела точкой пупа.

В результате измерений
исследователь установил, что пропорции мужского тела 13:8 ближе к золотому
сечению, чем пропорции женского тела – 8:5.

Художник Василий Суриков говорил, «что в композиции есть
непреложный закон, когда в картине нельзя ничего ни убрать, ни добавить, даже
лишнюю точку поставить нельзя, это настоящая математика». Долгое время
художники следователи этому закону интуитивно, но после Леонардо да Винчи
процесс создания живописного полотна уже не обходится без решения
геометрических задач.

 Например, Альбрехт Дюрер
для определения точек золотого сечения использовал изобретенный им
пропорциональный циркуль. Искусствовед Ф. В. Ковалев, подробно исследовав
картину Николая Ге «Александр Сергеевич Пушкин в селе Михайловском», отмечает,
что каждая деталь полотна будь-то камин, этажерка, кресло или сам поэт строго
вписаны в золотые пропорции.                                                Исследователи
золотого сечения без устали изучают и замеряют шедевры архитектуры, утверждая,
что они стали таковыми, потому что созданы по золотым канонам: в их списке
Великие пирамиды Гизы, Собор Парижской Богоматери, Храм Василия Блаженного,
Парфенон. И сегодня в любом искусстве пространственных форм стараются следовать
пропорциям золотого сечения, так как они, по мнению искусствоведов, облегчают
восприятие произведения и формируют у зрителя эстетическое ощущение.

Слово, звук и кинолента Формы временного искусства по-своему
демонстрируют нам принцип золотого деления. Литературоведы, к примеру, обратили
внимание, что наиболее популярное количество строк в стихотворениях позднего
периода творчества Пушкина соответствует ряду Фибоначчи – 5, 8, 13, 21, 34. Действует
правило золотого сечения и в отдельно взятых произведениях русского классика.
Так кульминационным моментом «Пиковой дамы» является драматическая сцена
Германа и графини, заканчивающаяся смертью последней. В повести 853 строки, а
кульминация приходится на 535 строке (853:535=1,6) – это и есть точка золотого
сечения. Советский музыковед Э. К. Розенов отмечает поразительную точность
соотношений золотого сечения в строгих и свободных формах произведений Иоганна
Себастьяна Баха, что соответствует вдумчивому, сосредоточенному, технически
выверенному стилю мастера. Это справедливо и в отношении выдающихся творений
других композиторов, где на точку золотого сечения обычно приходится наиболее
яркое или неожиданное музыкальное решение. Кинорежиссер Сергей Эйзенштейн
сценарий своего фильма «Броненосец Потёмкин» сознательно согласовывал с
правилом золотого сечения, разделив ленту на пять частей. В первых трех
разделах действие разворачивается на корабле, а в последних двух – в Одессе.
Переход на сцены в городе и есть золотая середина фильма.

Закономерности золотого сечения и чисел Фибоначчи проявляются
также в переходах энергии, в процессах, происходящих с элементарными частицами,
составляющих химические соединения, в космических системах, в генной структуре
ДНК. Аналогичные процессы происходят и в организме человека, проявляясь в
биоритмах его жизни, в действии органов, например, головного мозга или зрения.
Алгоритмы и закономерности золотых пропорций широко используются в современной
кибернетике и информатике. Одна из несложных задач, которую дают решать
начинающим программистам, — написать формулу и определить, сумму чисел
Фибоначчи до определенного числа, используя языки программирования.

Золотое сечение в фотографии — основной и мощный инструмент для получения
динамичных, интересных снимков. При пересечении горизонтальной и
вертикальной линии образуется особая точка – «точка силы» или «узел внимания».
Их четыре – именно в этих точках лучше располагать главные объекты кадра,
именно на них останавливается взгляд в независимости от формата кадра или
картины.

Слайд 1

Проект Золотое сечение Выполнили: ученицы 6 “ б ” класса ФКОУ СОШ имени А.Н. Радищева Кусакина А настасия и Кажаева Марина 2018 ФКОУ СОШ имени А.Н. Радищева

Слайд 2

Цель проекта: расширение знаний о золотом сечении и исследование гармонии окружающего мира, вытекающей из принципа золотого сечения. Задачи проекта: найти дополнительную информацию о золотом сечении, показать его практическое применение в разных сферах и провести эксперимент с элементами золотого сечения. Гипотеза: золотое сечение — основополагающий принцип красоты и гармонии.

Слайд 3

Определение Золотого сечения Золотое сечение – гармоническая пропорция. В математике пропорцией (лат. proportio ) называют равенство двух отношений: a : b = c : d. Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей. b: a= c:b ≈ 1,618

Слайд 4

История Золотого сечения Как научное понятие золотое сечение вошло в обиход во времена Пифагора, а именно в VI веке до нашей эры. До Пифагора знания о подобном соотношении на практике использовали в Древнем Египте и Вавилоне. Ярким свидетельством этого являются пирамиды, для построения которых использовали именно такую золотую пропорцию.

Слайд 5

Золотое сечение в математике

Слайд 6

Золотое сечение в архитектуре Архитекторы ещё в древности знали о существовании золотого сечения. Они пытались добиться максимальной прочности и гармонии резиденций царствующих особ, церквей, ратуш и зданий, имеющих особое социальное значение в обществе. Парфенон Собор Василия Блаженного Собор Парижской Богоматери Пентагон Пирамида Хеопса

Слайд 7

В современном дизайне немало строительных фирм выполняют проектирование частных домов, используя принципы и понятия золотого сечения. Такой дом очень удобный и гармоничный в пользовании. Можно выполнить перепланировку комнат или расстановку мебели в золотом сечении. Также можно подбирать цветовые решения. В этом случае соблюдают упрощенное значение золотого сечения – 2/3. Золотое сечение в современном дизайне Основным цветовым фоном следует занять 60% пространства комнаты. Оттеняющий оттенок занимает 30% помещения. Оставшаяся площадь поверхностей закрашивается близкими друг к другу тонами, усиливающими Восприятие выбранного цвета.

Слайд 8

И. И. Шишкин «Корабельная роща» Золотое сечение в живописи На картине И. И. Шишкина ярко освещенная солнцем сосна делит длину картины по золотому сечению. Справа от сосны — освещенный солнцем пригорок. Он делит по золотому сечению правую часть картины по горизонтали. При желании можно с успехом продолжить деление картины по золотому сечению и дальше. Используя пропорции золотого сечения, художники вовлекают зрителя в рассматривание изображения. В такие моменты человек, даже не искушённый в искусстве, подсознательно понимает, что картина ему чем-то нравится, что на неё приятно смотреть.

Слайд 9

Леонардо Да Винчи «Джоконда» Картина Леонардо да Винчи «Джоконда» основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Золотое сечение в живописи Андрей Рублёв «Троица» На картине «Троица» Андрея Рублёва можно увидеть вертикальное золотое сечение.

Слайд 10

Современные фотографы успешно используют золотое сечение в своём творчестве. Применение этого правила позволяет концентрировать взгляд человека на главных точках композиции. Картинка выглядит гармоничной, концептуальной. Зритель с удовольствием рассматривает детали, увлекается сюжетом. Фотография обретает динамику, становится интересной мини-историей с заданной мастером тематикой. Золотое сечение в фотографии

Слайд 11

Исследования поэтических произведений с позиции золотого сечения только начинаются. Рассмотрим, например, стихотворение А.С. Пушкина «Сапожник»: Картину раз высматривал сапожник И в обуви ошибку указал; Взяв тотчас кисть, исправился художник, Вот, подбочась , сапожник продолжал: «Мне кажется, лицо немного криво … А эта грудь не слишком ли нага? Тут Апеллес прервал нетерпеливо: «Суди, дружок, не выше сапога!« Есть у меня приятель на примете: Не ведаю, в каком бы он предмете Был знатоком, хоть строг он на словах, Но черт его несет судить о свете: Попробуй он судить о сапогах! Стихотворение состоит из 13 строк. В нем выделяется две смысловые части: первая в 8 строк и вторая (мораль притчи) в 5 строк (13, 8, 5 — числа Фибоначчи). Характерно, что и первая часть этого стиха (13 строк) по смысловому содержанию делится на 8 и 5 строк, то есть всё стихотворение построено по законам золотой пропорции. Золотое сечение в поэзии

Слайд 12

В 1925 году искусствовед Л.Л.Сабанеев, проанализировав 1770 музыкальных произведений 42 авторов, показал, что подавляющее большинство выдающихся сочинений можно легко разделить на части или по теме, или по интонационному строю, или по ладовому строю, которые находятся между собой в отношении золотого сечения. Причем, чем талантливее композитор, тем в большем количестве его произведений найдено золотых сечений. Композитор и ученый М.А.Марутаев подсчитал количество тактов в знаменитой сонате «Аппассионата» и нашел ряд интересных числовых соотношений. В частности, в разработке – центральной структурной единице сонаты, где интенсивно развиваются темы и сменяют друг друга тональности, — два основных раздела. В первом 43,25 такта, во втором – 26,75. Отношение 43,25:26,75=0,618:0,382=1,618 дает золотое сечение . Золотое сечение в музыке

Слайд 13

Если условно считать рост человека равным 100 %, то, согласно золотому сечению, части целого будут составлять 62 % и 38 %. Это относится как ко всей фигуре человека, так и к отдельным его частям: рукам, лицу, частям лица и т. д. Этот «секрет» лежит в основе правильного эскиза любой модели. Золотое сечение в моде Модели одежды, в которых реализовано «золотое сечение»

Слайд 14

Золотое сечение в природе Начиная с вирусов и растений и заканчивая организмом человека, всюду выявляется золотая пропорция, характеризующая соразмерность и гармоничность их строения. Золотое сечение признано универсальным законом живых систем.

Слайд 15

Золотое сечение в пропорциях тела Кости человека выдержаны в пропорции, близкой к золотому сечению. И чем ближе пропорции к формуле золотого сечения, тем более идеальным выглядит внешность человека. Точное наличие золотой пропорции в лице человека и есть идеал красоты для человеческого взора.

Слайд 16

Идеальные лица с точки зрения Золотого сечения Меган Фокс Екатерина Стриженова Оксана Фёдорова Жанна Фриске Анастасия Заворотнюк Дженифер Лопес

Слайд 17

Экспериментальная работа Исследование со скамейкой В эксперименте участвовало 11 человек. Мы предложили ребятам сесть на скамейку так, как им удобно. Все сели ни с самого края, ни посередине. 63 % всех участников сели в «золотой пропорции»

Слайд 18

Имена учащихся, принявших участие в эксперименте Высота лица/ширина лица Рас-е от подбородка до центральной точки соединения губ/ рас-е от центральной точки соединения губ до основания носа Ширина рта /ширина носа Данил 1,66 1,62 1.5 Марина 1,65 1,3 1,3 Женя 1,6 1,61 1,5 Вика 1,61 1,62 1,5 Полина 1.66 1.3 1.25 Ксюша 1,59 1,66 1,29 Таня 1.7 1.7 1.6 Егор 1,6 1,53 1,7 Ангелина 1,59 1,66 1,38 Кирилл 1.69 1.75 1,3 Миша 1,62 1,75 1,5 Настя 1,62 1,8 1,45 Саша 1,5 1,62 1,3 Миша 1,6 1,5 1,6 Экспериментальная работа «Идеальное лицо»

Слайд 19

Источники информации http://fb.ru/article/243562/zolotoe-sechenie-eto-zolotoe-sechenie-piramidyi-formula-zolotogo-secheniya http://textarchive.ru/c-2062725-p2.html http://studopedya.ru/1-95514.html

Слайд 20

СПАСИБО ЗА ВНИМАНИЕ

Исследовательская работа ученицы 6 класса «В» ГБОУ Гимназии 1257 Соколовой Ксении.

План

1. I.                  Вступление.
2. II.               Что такое «золотое сечение»?

1.  Определение и построение «золотого сечения».

2.  Число φ и ряд Фибоначчи.

3.  История «золотого сечения».

4.   «Золотое сечение» в природе.

5.  «Золотой прямоугольник».

III.     Практическая часть.

1. Экспериментальное подтверждение красоты и гармонии «золотой пропорции».

    2.  Этот циркуль мы делали вместе с дедушкой.

3.  Коллекция «золотых».

IV. Заключение.

V. Список литературы.

        I.            Вступление.

В учебнике по математике, на странице 145, есть статья про «золотое сечение. Информации в учебнике было очень мало. Используется ли «золотое сечение» в современном мире? Так ли оно гармонично, как утверждают античные философы и ученые?  Чтобы ответить на эти и другие вопросы, я решила подробнее ознакомиться с этой темой.

Цель моей работы: доказательство гармонии «золотого сечения» и его присутствия в окружающем нас мире.

 Гипотеза: мы считаем, что «золотое сечение» действительно гармонично, и  человек в своей деятельности постоянно сталкивается с предметами, имеющими в своей основе «золотые пропорции».

Для выполнения поставленной цели мы решали следующие задачи:

1.      Изучить историю вопроса.

2.      Систематизировать теоретические сведения о золотом сечении.

3.      Создать инструмент для определения «золотых пропорций».

4.      Исследовать присутствие золотого сечения в окружающей жизни.

Методы  исследования:

1.           Работа с учебной и научно-популярной литературой.

2.           Социологический опрос.

3.           Наблюдение, сравнение, анализ, аналогия.

4.           Практическая деятельность. 

Объект исследования: «золотое сечение».

Предмет исследования: золотое сечение в окружающем мире.

Актуальность работы заключается в следующем:

1)      пропорциональность в природе, искусстве, архитектуре и в других сферах окружающей нас жизни означает соблюдение определённых соотношений между отдельными частями и является непременным условием гармонии и красоты;

2)      всеобщий характер исследуемого материала;

3)      богатая и увлекательная история исследуемого материала;

4)      сведения о «золотом сечении» впервые встречаются в учебнике 6 класса; возникает желание углубить свои знания по математике, показать значение математики во всех областях окружающей нас жизни.

        I.            Что такое «золотое сечение» ?

1. 1.     Определение и построение «золотого сечения».

Учение об отношениях и пропорциях успешно развивалось в IV в. до н.э. в Древней Греции. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.

Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему. a : b = b : c или с : b = b : а.

Геометрическое изображение золотой пропорции

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки.

Деление отрезка прямой по золотому сечению. BC = 1/2 AB; CD = BC

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

    Как же найти численное выражение «золотой пропорции»?

Пусть х — меньшая часть, тогда кх – большая часть, а(х+кх) – это целый отрезок. Тогда, по определению «золотой пропорции» получим:

х:кх=кх:(х+кх);

Используя основное свойство пропорции, получим:

Разделим обе части равенства на

Приведем уравнение к стандартному виду:

Решение этого уравнения:

Положительный корень уравнения приближенно равен 1,618. Полученное число носит название числа φ (фи).

                      2.   Число φ и ряд Фибинчи.

Это число названо в честь древнегреческого архитектора Фидия, создавшего храм Парфенон в Афинах (по первой букве имени). На самом деле в числе φ бесконечно много знаков после запятой – это бесконечная непериодическая дробь. Можно привести запись этого числа с большим количеством цифр: φ=1,61803398874989484820458683436563811772030917980576286213544…

С историей золотого сечения косвенным образом связано имя итальянского математика монаха Леонардо из Пизы, более известного под именем Фибоначчи (сын Боначчи).

Он много путешествовал по Востоку, познакомил Европу с индийскими (арабскими) цифрами. В 1202 г вышел в свет его математический труд «Книга об абаке» (счетной доске), в котором были собраны все известные на то время задачи. Одна из задач гласила «Сколько пар кроликов в один год от одной пары родится». Размышляя на эту тему, Фибоначчи выстроил такой ряд цифр:

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том, что каждый ее член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13, 8 + 13 = 21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Только это отношение – 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему.

Фибоначчи так же занимался решением практических нужд торговли: с помощью какого наименьшего количества гирь можно взвесить товар? Фибоначчи доказывает, что оптимальной является такая система гирь: 1, 2, 4, 8, 16…

                                    3. История «золотого сечения».

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор, древнегреческий философ и математик (VI в. до н.э.) .

 Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян. И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании. Французский архитектор Ле Корбюзье нашел, что в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют величинам золотого деления. Зодчий Хесира, изображенный на рельефе деревянной доски из гробницы его имени, держит в руках измерительные инструменты, в которых зафиксированы пропорции золотого деления.

В фасаде древнегреческого храма Парфенона, созданного знаменитым древнегреческим архитектором Фидием, присутствуют золотые пропорции.

При его раскопках обнаружены циркули, которыми пользовались архитекторы и скульпторы античного мира. В Неаполе, в Национальном музее, хранится пропорциональный циркуль, найденный при раскопках в Помпеях. Пропорциональный циркуль является необходимым атрибутом архитектора. Он состоит из двух равных по длине ножек, скреплённых винтом наподобие ножниц, и позволяет (минуя вычисления!) для любого отрезка получить  отрезок, находящийся с ним в заданном отношении. Так вот, помпейский циркуль наглухо закреплен в отношении золотого сечения.

 В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления После Евклида исследованием золотого деления занимались Гипсикл (II в. до н.э.), Папп (III в. н.э.) и др. В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры (III в.) сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею. По мнению современников и историков науки, Лука Пачоли был настоящим светилом, величайшим математиком Италии в период между Фибоначчи  и Галилеем. Лука Пачоли был учеником художника Пьеро делла Франчески, написавшего две книги, одна из которых называлась «О перспективе в живописи». Его считают творцом начертательной геометрии.

Лука Пачоли

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями, ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции. Среди многих достоинств золотой пропорции монах Лука Пачоли не преминул назвать и ее «божественную суть» как выражение божественного триединства бог сын, бог отец и бог дух святой (подразумевалось, что малый отрезок есть олицетворение бога сына, больший отрезок – бога отца, а весь отрезок – бога духа святого).

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении. Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

В своих художественных произведениях Леонардо да Винчи конечно же использовал пропорции «золотого сечения». Так например, это соотношение между высотой и шириной лица Моны Лизы на картине «Джоконда».

В то же время на севере Европы, в Германии, над теми же проблемами трудился Альбрехт Дюрер. 

Альбрехт Дюрер. Автопортрет.

Он делает наброски введения к первому варианту трактата о пропорциях. Дюрер пишет: «Необходимо, чтобы тот, кто что-либо умеет, обучил этому других, которые в этом нуждаются. Это я и вознамерился сделать».

Судя по одному из писем Дюрера, он встречался с Лукой Пачоли во время пребывания в Италии. Альбрехт Дюрер подробно разрабатывает теорию пропорций человеческого тела. Важное место в своей системе соотношений Дюрер отводил золотому сечению. Рост человека делится в золотых пропорциях линией пояса, а также линией, проведенной через кончики средних пальцев опущенных рук, нижняя часть лица – ртом и т.д.

Великий астроном XVI в. Иоганн Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

Кеплер называл золотую пропорцию продолжающей саму себя «Устроена она так, – писал он, – что два младших члена этой нескончаемой пропорции в сумме дают третий член, а любые два последних члена, если их сложить, дают следующий член, причем та же пропорция сохраняется до бесконечности».

Построение ряда отрезков золотой пропорции можно производить как в сторону увеличения (возрастающий ряд), так и в сторону уменьшения (нисходящий ряд).

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

         Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа – важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он разработал пропорции Аполлона Бельведерского.

Подверглись исследованию греческие вазы, архитектурные сооружения различных эпох, растения, животные, птичьи яйца, музыкальные тона,

      С. Цейзинг

стихотворные размеры.  

Цейзинг дал определение золотому сечению, показал, как оно выражается в отрезках прямой и в цифрах. Когда цифры, выражающие длины отрезков, были получены, Цейзинг увидел, что они составляют ряд Фибоначчи, который можно продолжать до бесконечности в одну и в другую сторону.

                            4. Золотое сечение в природе.

Среди придорожных трав растет ничем не примечательное растение – цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

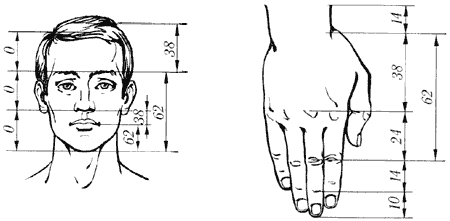
Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

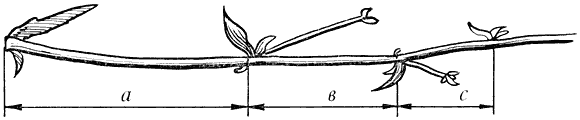
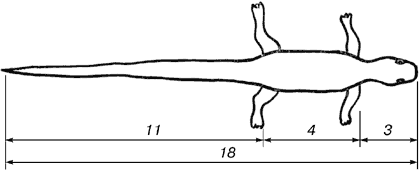
В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы – симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

5.  «Золотой прямоугольник».

Стороны золотого прямоугольника имеют отношение 1,618 к 1. Чтобы построить золотой прямоугольник, начните с квадрата со сторонами, равными двум единицам, потом проведите линию от середины одной стороны квадрата к одной из его вершин, образующих противоположную сторону, как показано на рисунке.

Треугольник EDB является прямоугольным. Около 550 года до Р.Х. Пифагор доказал, что квадрат гипотенузы (X) прямоугольного треугольника равен сумме квадратов двух других его сторон. В данном случае X2 = 22 + I2, или X2 = 5. Длина стороны ЕВ, таким образом, должна быть квадратным корнем из 5. Строя золотой прямоугольник, следующим шагом продлите отрезок CD и постройте на нем отрезок EG, равный квадратному корню из 5, или 2,236 единицы длины, как показано на рис. 3-5. В построенных таким образом прямоугольниках стороны связаны золотым коэффициентом. Таким образом, и прямоугольник AFGC, и прямоугольник BFGD являются золотыми.

Поскольку стороны прямоугольников связаны золотым отношением, следовательно, эти прямоугольники, по определению, являются золотыми прямоугольниками.

                                                     ΙI.            Практическая часть.

                            2.1     Экспериментальное подтверждение красоты и гармонии «золотой пропорции».

Я провела исследование: я нарисовала 7 различных прямоугольников. Среди них я спрятала один прямоугольник, который был сделан по пропорциям «золотого сечения». Затем я расспросила одноклассников, учителей, родных и друзей, какой прямоугольник кажется им наиболее гармоничным?  Всего было опрошено 72 человека. Вот результаты опроса:

«Золотой прямоугольник» на моем чертеже был подписан буквой С. Как видно из приведенной таблицы, подавляющее большинство опрошенных выбрало «золотой прямоугольник». Мы можем подвести итоги: золотое сечение действительно выглядит гармоничным и радует глаз.

                                   2.2     Этот циркуль мы делали вместе с дедушкой.

Но может быть «золотое сечение» забыто, и в наши дни совсем не используется современными дизайнерами, художниками, архитекторами? Как  же это проверить? Я решила создать свой инструмент для определения «золотой пропорции». Мой циркуль сделан по принципу старинного помпейского циркуля, а помог мне его сделать дедушка.

Вам, наверное, будет интересно узнать, как мы это делали?

Сначала мы взяли 2 одинаковые палки длиной по 146 мм.

Затем мы разделили их на 2 неравные части.

Для того, чтобы циркуль показывал пропорции «золотого сечения» я составила уравнение: Пусть х мм – меньшая часть палки, тогда 1,618х мм – большая часть; (х+1,618х) мм – длина всей палки. Зная, что длина нашей палки 146 мм, получим уравнение

Х+1,618х=146;

2,618х=146;

Х=146:2,618;

Х≈56.

         То есть меньшая часть была 56 мм, а большая часть: 56·1,618≈  90 мм.

Соотношение между двумя сторонами получилось 1,618.

Если раздвинуть ножки циркуля, то он всегда покажет пропорции «золотого сечения». Так как  треугольник АОВ и треугольник СOD называются подобными. В подобных треугольниках все стороны пропорциональны.

Поэтому, если

Теперь с помощью этого циркуля я могла определить, где присутствуют «золотые пропорции».

                                                     2.3     Коллекция «золотых».

Мне стало очень интересно, какие предметы сделаны по принципу «золотого сечения». Я ходила и измеряла всё вокруг. И оказалось, что многие предметы из нашей повседневной жизни сделаны по принципу «золотого сечения».

Первым «открытием» оказался мой пропуск в школу. Я обратила внимание, что все банковские карточки и дисконтные карты магазинов одинакового размера и формы. Таких же размеров мой пропуск в школу. Это очень удобно, все карточки можно положить в один футляр. Но когда я испробовала на моём пропуске свой циркуль, оказалось, что это не просто прямоугольник, а «золотой прямоугольник»!

«Золотым прямоугольником»  оказался и спичечный коробок»!

Куриное яйцо также вписывается в «золотой прямоугольник»!

Упаковки некоторых продуктов, например, представленная на фотографии пачка масла, также представляет собой «золотой прямоугольник».

Исследуя историю вопроса, я поняла, что в Древней Греции золотые пропорции использовались в архитектуре. Интересно, а сейчас при проектировании зданий используют ли архитекторы «золотое сечение»?

Внимательно осмотрев здание нашей школы, я решила «поискать» золотые пропорции в наших окнах.

Я тщательно измерила длину и высоту нашего окна.

Оказалось, что высота нашей оконной рамы 232 см, а ширина 144 см. Разделив 232:144=1,6(1), то есть приближенно наше отношение равно числу ϕ.

IΙΙ  Заключение.

Мне очень понравилось работать над темой, посвященной «золотому сечению». В результате работы подтвердилась наша гипотеза о том, что «золотое сечение» действительно гармонично, и  человек в окружающем мире постоянно сталкивается с предметами, имеющими в своей основе «золотые пропорции».

В ходе работы были решены следующие задачи:

1.      Ознакомились с  историей вопроса.

2.      Систематизировали теоретические сведения о золотом сечении.

3.      Создали инструмент для определения «золотых пропорций» — циркуль по примеру помпейского.

4.      Исследовали присутствие золотого сечения в окружающей жизни, обнаружили, что «золотые пропорции» активно используются в современной жизни: в дизайне упаковок продуктов, в архитектуре и т.д.

Я с удовольствием продолжу изучение этого вопроса в дальнейшем.

                                                                           ΙV  Список литературы:

Волошинов А. В. «Математика и архитектура».- М.: «Просвещение». 2000

Виленкин Н. Я. и д.р. «Математика 6 класс».-М.: «Мнемозина». 2011

В. Лаврус «Золотое сечение».- электронная библиотека. «Наука и техника».

Реферат

Золотое сечение

Введение

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Еще в эпоху Возрождения художники открыли, что любая картина имеет определенные точки, невольно приковывающие наше внимание, так называемые зрительные центры. При этом абсолютно неважно, какой формат имеет картина — горизонтальный или вертикальный. Таких точек всего четыре, и расположены они на расстоянии 3/8 и 5/8 от соответствующих краев плоскости.

1. История золотого сечения

Принято считать, что понятие о золотом делении ввел в научный обиход Пифагор. Есть предположение, что Пифагор свое знание золотого деления позаимствовал у египтян и вавилонян.

И действительно, пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона свидетельствуют, что египетские мастера пользовались соотношениями золотого деления при их создании.

Греки были искусными геометрами. Даже арифметике обучали своих детей при помощи геометрических фигур. Квадрат Пифагора и диагональ этого квадрата были основанием для построения динамических прямоугольников.

Платон (427…347 гг. до н.э.) также знал о золотом делении. Его диалог «Тимей» посвящен математическим и эстетическим воззрениям школы Пифагора и, в частности, вопросам золотого деления.

В дошедшей до нас античной литературе золотое деление впервые упоминается в «Началах» Евклида. Во 2-й книге «Начал» дается геометрическое построение золотого деления. После Евклида исследованием золотого деления занимались Гипсикл, Папп и др.

В средневековой Европе с золотым делением познакомились по арабским переводам «Начал» Евклида. Переводчик Дж. Кампано из Наварры сделал к переводу комментарии. Секреты золотого деления ревностно оберегались, хранились в строгой тайне. Они были известны только посвященным.

В эпоху Возрождения усиливается интерес к золотому делению среди ученых и художников в связи с его применением, как в геометрии, так и в искусстве, особенно в архитектуре Леонардо да Винчи, художник и ученый, видел, что у итальянских художников эмпирический опыт большой, а знаний мало. Он задумал и начал писать книгу по геометрии, но в это время появилась книга монаха Луки Пачоли, и Леонардо оставил свою затею.

Лука Пачоли прекрасно понимал значение науки для искусства. В 1496 г. по приглашению герцога Моро он приезжает в Милан, где читает лекции по математике. В Милане при дворе Моро в то время работал и Леонардо да Винчи. В 1509 г. в Венеции была издана книга Луки Пачоли «Божественная пропорция» с блестяще выполненными иллюстрациями (Рис. 2), ввиду чего полагают, что их сделал Леонардо да Винчи. Книга была восторженным гимном золотой пропорции.

Леонардо да Винчи также много внимания уделял изучению золотого деления. Он производил сечения стереометрического тела, образованного правильными пятиугольниками, и каждый раз получал прямоугольники с отношениями сторон в золотом делении (Рис. 3). Поэтому он дал этому делению название золотое сечение. Так оно и держится до сих пор как самое популярное.

Великий астроном XVI в. Иоган Кеплер назвал золотое сечение одним из сокровищ геометрии. Он первый обращает внимание на значение золотой пропорции для ботаники (рост растений и их строение).

В последующие века правило золотой пропорции превратилось в академический канон и, когда со временем в искусстве началась борьба с академической рутиной, в пылу борьбы «вместе с водой выплеснули и ребенка». Вновь «открыто» золотое сечение было в середине XIX в. В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». С Цейзингом произошло именно то, что и должно было неминуемо произойти с исследователем, который рассматривает явление как таковое, без связи с другими явлениями. Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства. У Цейзинга были многочисленные последователи, но были и противники, которые объявили его учение о пропорциях «математической эстетикой».

В конце XIX — начале XX вв. появилось немало чисто формалистических теории о применении золотого сечения в произведениях искусства и архитектуры. С развитием дизайна и технической эстетики действие закона золотого сечения распространилось на конструирование машин, мебели и т.д.

2. Золотое сечение в математике

В математике пропорцией называют равенство двух отношений:

a: b = c: d.

Отрезок прямой АВ можно разделить на две части следующими способами:

.на две равные части — АВ: АС = АВ: ВС;

.на две неравные части в любом отношении (такие части пропорции не образуют);

таким образом, когда АВ: АС = АС: ВС.

Последнее и есть золотое деление или деление отрезка в крайнем и среднем отношении.

Золотое сечение — это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.

a: b = b: c или с: b = b: а.

Практическое знакомство с золотым сечением начинают с деления отрезка прямой в золотой пропорции с помощью циркуля и линейки (Рис. 4).

Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции.

Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE = 0,618…, если АВ принять за единицу, ВЕ = 0,382… Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая — 38 частям.

Свойства золотого сечения описываются уравнением:

x2 — x — 1 = 0.

Решение (Рис. 5)

3. Золотое сечение в природе

Все, что приобретало какую-то форму, образовывалось, росло, стремилось занять место в пространстве и сохранить себя. Это стремление находит осуществление в основном в двух вариантах — рост вверх или расстилание по поверхности земли и закручивание по спирали. Раковина закручена по спирали. Если ее развернуть, то получается длина, немного уступающая длине змеи. Небольшая десятисантиметровая раковина имеет спираль длиной 35 см. Спирали очень распространены в природе. Представление о золотом сечении будет неполным, если не сказать о спирали.

Форма спирально завитой раковины (Рис. 6) привлекла внимание Архимеда. Он изучал ее и вывел уравнение спирали. Спираль, вычерченная по этому уравнению, называется его именем. Увеличение ее шага всегда равномерно. В настоящее время спираль Архимеда широко применяется в технике.

Еще Гете подчеркивал тенденцию природы к спиральности. Винтообразное и спиралевидное расположение листьев на ветках деревьев подметили давно. Спираль увидели в расположении семян подсолнечника, в шишках сосны, ананасах, кактусах и т.д. Паук плетет паутину спиралеобразно. Спиралью закручивается ураган. Молекула ДНК закручена двойной спиралью (Рис. 7).

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

Пьер Кюри в начале нашего столетия сформулировал ряд глубоких идей симметрии. Он утверждал, что нельзя рассматривать симметрию какого-либо тела, не учитывая симметрию окружающей среды.

Закономерности «золотой» симметрии проявляются в энергетических переходах элементарных частиц, в строении некоторых химических соединений, в планетарных и космических системах, в генных структурах живых организмов. Эти закономерности, как указано выше, есть в строении отдельных органов человека и тела в целом, а также проявляются в биоритмах и функционировании головного мозга и зрительного восприятия.

4. Золотое сечение в архитектуре

В книгах о «золотом сечении» можно найти замечание о том, что в архитектуре, как и в живописи, все зависит от положения наблюдателя, и что, если некоторые пропорции в здании с одной стороны кажутся образующими «золотое сечение», то с других точек зрения они будут выглядеть иначе. «Золотое сечение» дает наиболее спокойное соотношение размеров тех или иных длин.

Одним из красивейших произведений древнегреческой архитектуры является Парфенон (Рис.

Парфенон имеет 8 колонн по коротким сторонам и 17 по длинным. Выступы сделаны целиком из квадратов пентилейского мрамора. Благородство материала, из которого построен храм, позволило ограничить применение обычной в греческой архитектуре раскраски, она только подчеркивает детали и образует цветной фон для скульптуры. Отношение высоты здания к его длине равно 0,618. Если произвести деление Парфенона по «золотому сечению», то получим те или иные выступы фасада. Другим примером из архитектуры древности является Пантеон (Рис. 9).

Известный русский архитектор М. Казаков в своем творчестве широко использовал «золотое сечение».

Его талант был многогранным, но в большей степени он раскрылся в многочисленных осуществленных проектах жилых домов и усадеб. Например, «золотое сечение» можно обнаружить в архитектуре здания сената в Кремле (Рис. 10). По проекту М. Казакова в Москве была построена Голицынская больница, которая в настоящее время называется Первой клинической больницей имени Н.И. Пирогова (Рис. 11).

Еще один архитектурный шедевр Москвы — дом Пашкова (Рис. 12) — является одним из наиболее совершенных произведений архитектуры В. Баженова.

. Золотое сечение в живописи

Переходя к примерам «золотого сечения» в живописи, нельзя не остановить своего внимания на творчестве Леонардо да Винчи.

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки.

Он писал справа налево неразборчивым почерком и левой рукой. Это самый известный из существующих образец зеркального письма.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника (Рис. 13).

Вывод

золотой математика сечение

Доверяя глазу больше, чем другим органам чувств, человек в первую очередь учился различать окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения — высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе. Эту мысль разделяли и разделяют многие выдающиеся современные ученые, доказывая в своих исследованиях, что истинная красота всегда функциональна. В их числе и авиаконструкторы. И архитекторы, и антропологи, и многие другие.

Список используемой литературы

1. #»justify»>2. https://ru.wikipedia.org/wiki/%D0% 97% D0% BE % D0% BB % D0% BE % D1% 82% D0% BE % D0% B5_%D1% 81% D0% B5% D1% 87% D0% B5% D0% BD % D0% B8% D0% B5

. http://neutrino.mk.ua/leonardo-da-vinchi/zolotoe-sechenie-universalniy-printsip-garmonii

Руководитель проекта: 

Ганченкова Оксана Алексеевна

Автор исследовательской работы по математике на тему «Золотое сечение» ставит целью своего исследования ознакомится с различной литературой по геометрии и черчению, изучить справочные материалы по теме для более четкого понимания принципа «золотого сечения».

Подробнее о работе:

В данном исследовательском проекте по математике на тему «Золотое сечение» учащийся 6 класса изучает понятие «золотое сечение», рассматривает применение «золотого сечения» в математике, скульптуре, архитектуре, живописи и природе.

Авторская исследовательская работа по математике посвящена изучению взаимосвязи «золотого сечения» и геометрии, выявлению данного понятия в геометрических задачах и нахождению способов их решения. Результаты данного исследования положительно повлияют на формирование научного мировоззрения, установление учащимися межпредметных связей и креативного мышления в научной области.

Оглавление

Введение
1. «Золотое сечение» в математике.
2. «Золотое сечение» в скульптуре.
3. «Золотое сечение» в архитектуре.
4. «Золотое сечение» в живописи.
5. «Золотое сечение» в природе.
6. «Золотое сечение» в геометрических задачах.
Заключение
Литература

Введение

Цель:

воспользовавшись различной литературой по геометрии, по черчению, различными справочными материалами для более подробного изучения темы «Золотое сечение», дать наиболее полное представление о данной теме; рассмотреть применение «золотого сечения» в архитектуре.

Гипотеза: я предполагаю, что данная тема является важной в курсе математики. «Золотое сечение» используется в скульптуре, живописи, математике, архитектуре.

Задачи проекта:

1. Внести понятие «золотое сечение» (немного об истории). Алгебраическое нахождение «золотого сечения», геометрическое построение «золотого сечения».
2. Рассмотреть применение «золотого сечения» в искусстве Древней Греции.
3. Рассмотрим золотую пропорцию и связанные с нею отношения.
4. Показать применение «золотого сечения» в эпоху Возрождения.
5. Частично изучив архитектуру, указав наиболее известные здания с применением золотого сечения.

Я занялся подробным изучением темы «Золотое сечение» после того, как однажды на уроках математики услышал о широком применении «золотого сечения» в архитектуре. Рассмотрел различные энциклопедические справочники по математике, учебные пособия по геометрии и черчению. Средства ЭТ(компьютер, сканер, копир) позволили нам наглядно представить собранный материал воедино.

Работа выполнялась автором самостоятельно, руководитель рекомендовал литературу и давал необходимые рекомендации. Материал можно использовать на факультативных занятиях по предмету.

Золотое сечение в математике

Иоганн Кеплер говорил, что геометрия владеет двумя сокровищами – теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе – с драгоценным камнем.

Теорему Пифагора знает каждый, а вот что такое «золотое сечение» — далеко не все. Расскажем вам об этом «драгоценном камне».

«Золотое сечение» — это такое деление целого на две неравные части, при котором большая часть так относится к целому, как меньшая к большей.

Если длину отрезка АВ обозначить через а, а длину отрезка АС – через х, то а-х длина отрезка СВ, из пропорции (1) принимает вид:

х/а=а-х/х

Из этой пропорции следует, что при золотом сечении длина большего отрезка есть среднее геометрическое или, как часто говорят, пропорциональное длин всего отрезка и его меньшей части:

Х=√х(а-х).

Замечательный пример «золотого сечения» представляет собой правильный пятиугольник — выпуклый и звездчатый.

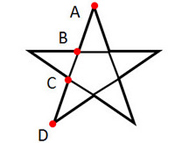
Из подобия треугольников АСDи ABEможем вывести уже известную пропорцию:

AB/AC=AC/BC

Таким образом, звездчатый пятиугольник также обладает «золотым сечением». Внутри пятиугольника можно продолжить строить пятиугольники, и это отношение будет сохранятся.

Звездчатый пятиугольник называется пентаграммой. Пифагорейцы выбрали пятиконечную звезду в качестве талисмана, она считалась символом здоровья и служила опознавательным знаком.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №16»

Пропорция. Золотое сечение

Выполнил(а): ученица 6А класса

Репина Ангелина

Руководитель: учитель математики

Скобычкина Л.Р.

2017 год

СОДЕРЖАНИЕ

Введение 4

1. Теоретическая часть

1.1 Что такое пропорция 6

1.2 Числа Фибоначчи 7

1.3 «Золотое сечение» в архитектуре 7

1.4 «Золотое сечение» в живописи 8

1.5 «Эстетические исследования» Цейзинга 10

1.6 «Золотое сечение» в природе 11

1.7 Пропорции в жизни 12

2. Практическая часть

2.1 Исследование 1 «Золотое сечение» у растений 13

2.2 Исследование 2 «Золотое сечение» в пропорциях тела животных 14

2.3 Исследование 3 «Золотое сечение» в пропорциях тела человека 15

2.4 Исследование 4 «Золотое сечение» и «золотой прямоугольник» в предметах, нас окружающих 16

3. Заключение 20

4. Литература 22

Исследовательская работа по теме «Пропорции. Золотое сечение»

Цель работы: раскрыть для себя тайну «золотого сечения»; доказать, что «золотое сечение» – верх совершенства и гармонии в природе.

Задачи:

1. Изучить понятие «пропорция», «золотое сечение»;

2. Рассмотреть применение пропорции в различных сферах жизни, «золотого сечения » в архитектуре, искусстве, биологии;

3. Исследовать присутствие золотого сечения в окружающей жизни.

Методы исследования:

1. Работа с учебной и научно-популярной литературой, ресурсами сети Интернет.

2. Наблюдение, сравнение, анализ, аналогия.

Объект исследования: пропорция, «золотое сечение»

Гипотеза: Пропорция и золотое сечение являются отображением окружающегося мира.

Предмет исследования: предметы искусства, архитектуры, живописи, пропорции учебников, мебели, фигуры учеников, растений.

Актуальность.

Человек различает окружающие его предметы по форме. Интерес, к форме какого – либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежит сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике, музыке и природе. Поэтому, не только в древние времена скульпторы, художники, музыканты, архитекторы уделяли большое внимание сечению и гармоническому отношению, но и настоящее время помнят и используют это сечение.

Введение

» Красота должна отвечать строгому числу»

Л.Б.Альберти

Окружающий нас мир многообразен…

Вы, наверное, обращали внимание, что мы неодинаково относимся к предметам и явлениям окружающей действительности. Беспорядочность, бесформенность, несоразмерность воспринимаются нами как безобразное и производят отталкивающее впечатление. А предметы и явления, которым свойственна мера, целесообразность и гармония воспринимаются как красивое и вызывают у нас чувство восхищения, радости, поднимают настроение.

Людей с давних времён волновал вопрос, подчиняются ли такие неуловимые вещи как красота и гармония, каким-либо математическим расчётам. Можно ли «проверить алгеброй гармонию»? – как сказал А.С. Пушкин.

Конечно, все законы красоты невозможно вместить в несколько формул, но, изучая математику, мы можем открыть некоторые слагаемые прекрасного.

Впервые с понятием «золотое сечение» я встретилась в курсе математики 6 класса. Меня заинтересовало это понятие, и я решила его изучить. Перед тем как начать работу по теме «Золотое сечение», я провела опрос среди учеников с 7 – 11 классы и учителей нашей школы. Нужно было ответить на вопрос: «Знаете ли вы, что такое «пропорция», «золотая пропорция» или «золотое сечение»?» Результаты опроса изображены на диаграмме.

Меньшая часть учителей знают что такое « Золотая пропорция» и « Золотое сечение», а также и учащиеся с 7 по 11 класс не имеют представления о «Золотом сечении» и « Золотой пропорции». И я решила рассказать вам про это.

1. Теоретическая часть

   1. Пропорция от латинского слова proportiо, означает «соразмерность», определённое соотношение частей между собой.

1) В математике — равенство двух отношений

А : В = С : Д

где А и Д — крайние члены пропорции;

В и С — средние члены пропорции.

2) В современном русском языке слово пропорция имеет оттенок «норма, нужное количество».

Этот оттенок значения выражается в сочетании слова пропорция с предлогами в и без: дать что – либо в пропорции (в нужном количестве), без пропорции (неумеренно).

Учение об отношениях и пропорциях особенно успешно развивалось в 4 веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, развитыми ремёслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке. Теория отношений и пропорций была подробно изложена в «Началах Евклида» (3 век до нашей эры), там, в частности, приводится и доказательство основного свойства пропорции.

Деление отрезка в среднем и крайнем отношении называют золотым сечением. В истории утвердилось ещё одно название – «золотая пропорция».

Пусть, САВ, и производит, как говорят, «золотое сечение» отрезка

АС: АВ =СВ: АС (1)

Золотым сечением называется такое деление отрезка, при котором большая часть так относится к целому, как меньшая часть к большей.

Если длину отрезка АВ обозначить через а, а длину АС – через х, то (а-х)- длину отрезка СВ, и пропорция (1) примет вид:

(2)

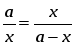
части «золотого сечения» составляют приблизительно 62% и 38% всего отрезка, отношение равно 1,618….

1.2 Числа Фибоначчи

С золотой пропорцией тесно связан ряд чисел Фибоначчи 1,1,2,3,5,8,13,21,34,55,89 и т.д. В этом ряду каждое последующее число является суммой двух предыдущих чисел. Спустя четыре столетия после открытия Фибоначчи ряда чисел И.Кеплер установил, что отношение рядом стоящих чисел в пределе стремится к золотой пропорции Ф. Это свойство присуще не только числам Фибоначчи. Начав с любых двух чисел и построив аддитивный ряд, в котором каждый член равен сумме двух предыдущих (например, ряд 7, 2, 9, 11, 20, …), мы обнаружили, что отношение двух последовательных членов такого ряда также стремится к числу : чем дальше мы будем продвигаться от начала ряда, тем лучше будет приближение. Если взять калькулятор и разделить каждое из них на предыдущее, то получиться: 1:1=1; 2:1=2; 3:2=1,5; 5:3=1,666666; 8:5=1,6; 13:8=1,625; 21:13=1,615384;…

Если делить всё большие и большие числа Фибоначчи, то можно близко подойти к золотому сечению.

1.3 Золотое сечение в архитектуре.

Великолепные памятники архитектуры оставили нам зодчие Древней Греции. И среди них первое место по праву принадлежит Парфенону.

Всю вторую половину V в. до н.э. на Акрополе шло строительство храмов, пропилей (преддверий), алтаря и статуи Афины Воительницы. В 447 году начались работы над храмом Афины – Парфеноном и продолжались до 434 года до н.э. Для создания гармонической композиции на холме его строители даже увеличили холм в южной части, соорудив для этого мощную насыпь.

Как указывает исследователь Г. И. Соколов, протяженность холма перед Парфеноном, длины храма Афины и участка Акрополя за Парфеноном относятся как отрезки золотого сечения.

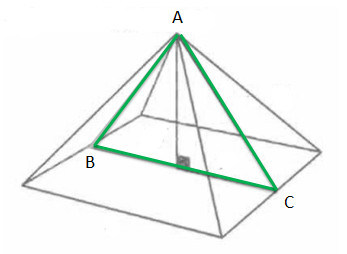
О египетских пирамидах с восхищением писал греческий историк Геродот. Первым европейцем, спустившимся в глубь пирамиды, был римский ученый Плиний Старший. Согласно многим описаниям, эти гигантские монолиты имели совсем иной вид, чем в наше время. Они сияли на солнце белой глазурью отполированных известняковых плит на фоне многоколонных прилегающих храмов. Рядом с царскими пирамидами стояли малые пирамиды жен и членов семьи фараонов.

Среди грандиозных пирамид Египта особое место занимает великая пирамида фараона Хеопса. Она самая крупная и наиболее хорошо изученная. Чего только не находили в ее пропорциях! Число «пи» и золотое сечение, число дней в году, расстояние до Солнца, диаметр Земли и т.п.

Золотое соотношение мы можем увидеть и в здании собора Парижской Богоматери (Нотр-дам де Пари)

В качестве примера «золотого сечения» в России можно полюбоваться фасадом знаменитого Большого театра в Москве.

1.4 «Золотое сечение» в живописи

Леонардо да Винчи. Его личность – одна из загадок истории. Сам Леонардо да Винчи говорил: “Пусть никто, не будучи математиком, не дерзнет читать мои труды”.

Он снискал славу непревзойденного художника, великого ученого, гения, предвосхитившего многие изобретения, которые не были осуществлены вплоть до XX в.

Нет сомнений, что Леонардо да Винчи был великим художником, это признавали уже его современники, но его личность и деятельность останутся покрытыми тайной, так как он оставил потомкам не связное изложение своих идей, а лишь многочисленные рукописные наброски, заметки, в которых говорится “обо всем на свете”.

Он писал справа налево неразборчивым почерком и левой рукой. Это самый известный из существующих образец зеркального письма.

Портрет Монны Лизы (Джоконды) долгие годы привлекает внимание исследователей, которые обнаружили, что композиция рисунка основана на золотых треугольниках, являющихся частями правильного звездчатого пятиугольника. Существует очень много версий об истории этого портрета. Вот одна из них.

Однажды Леонардо да Винчи получил заказ от банкира Франческо де ле Джокондо написать портрет молодой женщины, жены банкира, Монны Лизы. Женщина не была красива, но в ней привлекала простота и естественность облика. Леонардо согласился писать портрет. Его модель была печальной и грустной, но Леонардо рассказал ей сказку, услышав которую, она стала живой и интересной.

Сказка

Жил-был один бедный человек, было у него четыре сына: три умных, а один из них и так, и сяк. И вот пришла за отцом смерть. Перед тем, как расстаться с жизнью, он позвал к себе детей и сказал: “Сыны мои, скоро я умру. Как только вы схороните меня, заприте хижину и идите на край света добывать себе счастья. Пусть каждый из вас чему-нибудь научится, чтобы мог кормить сам себя”. Отец умер, а сыновья разошлись по свету, договорившись спустя три года вернуться на поляну родной рощи. Пришел первый брат, который научился плотничать, срубил дерево и обтесал его, сделал из него женщину, отошел немного и ждет. Вернулся второй брат, увидел деревянную женщину и, так как он был портной, в одну минуту одел ее: как искусный мастер он сшил для нее красивую шелковую одежду. Третий сын украсил женщину золотом и драгоценными камнями – ведь он был ювелир. Наконец, пришел четвертый брат. Он не умел плотничать и шить, он умел только слушать, что говорит земля, деревья, травы, звери и птицы, знал ход небесных тел и еще умел петь чудесные песни. Он запел песню, от которой заплакали притаившиеся за кустами братья. Песней этой он оживил женщину, она улыбнулась и вздохнула. Братья бросились к ней и каждый кричал одно и то же: “Ты должна быть моей женой”. Но женщина ответила: “Ты меня создал – будь мне отцом. Ты меня одел, а ты украсил – будьте мне братьями.

А ты, что вдохнул в меня душу и научил радоваться жизни, ты один мне нужен на всю жизнь”.

Кончив сказку, Леонардо взглянул на Монну Лизу, ее лицо озарилось светом, глаза сияли. Потом, точно пробудившись от сна, она вздохнула, провела по лицу рукой и без слов пошла на свое место, сложила руки и приняла обычную позу. Но дело было сделано – художник пробудил равнодушную статую; улыбка блаженства, медленно исчезая с ее лица, осталась в уголках рта и трепетала, придавая лицу изумительное, загадочное и чуть лукавое выражение, как у человека, который узнал тайну и, бережно ее храня, не может сдержать торжество. Леонардо молча работал, боясь упустить этот момент, этот луч солнца, осветивший его скучную модель…

1.5 В 1855 г. немецкий исследователь золотого сечения профессор Цейзинг опубликовал свой труд «Эстетические исследования». Он абсолютизировал пропорцию золотого сечения, объявив ее универсальной для всех явлений природы и искусства.

Цейзинг проделал колоссальную работу. Он измерил около двух тысяч человеческих тел и пришел к выводу, что золотое сечение выражает средний статистический закон. Деление тела точкой пупа — важнейший показатель золотого сечения. Пропорции мужского тела колеблются в пределах среднего отношения 13 : 8 = 1,625 и несколько ближе подходят к золотому сечению, чем пропорции женского тела, в отношении которого среднее значение пропорции выражается в соотношении 8 : 5 = 1,6. У новорожденного пропорция составляет отношение 1 : 1, к 13 годам она равна 1,6, а к 21 году равняется мужской.

Пропорции золотого сечения проявляются и в отношении других частей тела — длина плеча, предплечья и кисти, кисти и пальцев и т.д.

Справедливость своей теории Цейзинг проверял на греческих статуях. Наиболее подробно он изучил пропорции Аполлона

1.6 Золотое сечение в природе

Среди придорожных трав растет ничем не примечательное растение — цикорий. Приглядимся к нему внимательно. От основного стебля образовался отросток. Тут же расположился первый листок.

Золотое сечение. Цикорий

Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий — 38, четвертый — 24 и т. д. Длина лепестков тоже подчинена золотой пропорции. В росте, завоевании пространства растение сохраняло определенные пропорции. Импульсы его роста постепенно уменьшались в пропорции золотого сечения.

Золотое сечение. Ящерица живородящая

В ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции — длина ее хвоста так относится к длине остального тела, как 62 к 38.

И в растительном, и в животном мире настойчиво пробивается формообразующая тенденция природы — симметрия относительно направления роста и движения. Здесь золотое сечение проявляется в пропорциях частей перпендикулярно к направлению роста.

Природа осуществила деление на симметричные части и золотые пропорции. В частях проявляется повторение строения целого.

Золотое сечение. Яйцо птицы

1.7 Пропорция применяется в любой сфере нашей жизни: при пошиве одежды, при приготовлении еды и т.д. Без знания пропорции невозможно изготовить лекарство.

Например, На 1 л борща идёт:

1)Бульон 600 г

2)Мясо 150 г

3)Картофель 150 г

4)Капуста 70 г

5)Лук 15 г

6)Свекла 8 г

7)Морковь 7 г

1. Практическая часть

Исследование присутствия золотого сечения в окружающей жизни.

Я поставила перед собой следующие цели:

— найти предметы, окружающие нас, которые дают примеры золотого сечения.

— проверить, в каком отношении находятся части тела учеников, и определить ученика с пропорциями «золотого сечения».

2.1 Исследование№1 «Золотое сечение» у растений

Возьмём опять утверждение из школьного учебника: «Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В)».

Чтобы проверить, так ли это, я выбрала 4 различных комнатных растений:

1)Глоксиния

2)Сахарный

3)Огромный цветок (в кабинете математики)

4)У директора

Все эти растения есть в нашей школе, и я посчитала именно их наиболее красивыми. Сделала необходимые измерения между тройками листьев и посчитала соответствующие отношения (с точностью до тысячных).

Данные измерений и вычислений занесены в следующую таблицу:

Из таблицы видно, что полученные отношения получаются достаточно близкими к числу 1,618. Наиболее совершенным с точки зрения математики, оказался цветок под номерами 2 и 4 . Следовательно, действительно расположение листьев на стебле подчиняется «божественной пропорции».

2.2 Исследование №2 «Золотое сечение» в пропорциях тела животных

Кошка – всего – 62 см, корпус – 38,5 см, хвост – 23,5 см (отношения составляют 1,610 и 1,638)

Майский жук – всего – 3,8 см, голова – 1,4 см, корпус – 2,4 см (отношения составляют 1,58 и 1,71)

Фиолетовый шмель-плотник – основная часть корпуса – 1,7 см, верхняя часть корпуса – 1 см; (отношения составляют 1,7 и 1,43)

Муха обыкновенная – всего – 0,9 см, верхняя часть корпуса вместе с головой – 0,6 см (отношения примерно составляют 1,5 и 2)

Моль платяная – всего – 4,2 см, корпус – 3,2 см (отношения – 1,455 и 3,2).

Можно сделать вывод, что пропорции тела кошки, майского жука, фиолетового шмеля-плотника наиболее соответствуют «золотой пропорции».

2.3 Исследование №3 «Золотое сечение» в пропорциях тела человека

Для того чтобы проверить, выполняется ли золотое сечение в пропорциях тела человека я провела исследование среди учащихся 7– 11 классов. У каждого участника были сняты мерки двух видов: мерка от верхней точки головы до талии, мерка от талии до пола. Их отношение сравнивалось с числом отношения золотого сечения.

Из 19-ти человек, участвовавших в исследовании наименьшее отклонение от золотого сечения среди юношей имеют: ученик 6 класса Погожев Игорь (0,074), а также ученик 7 класса Шихов Сергей, Шевченко Максим. Среди девушек наименьшее отклонение от золотого сечения у Репиной Влады, Джамаришвили Арины, Репиной Ангелины, Дрындя Виктории.

Особо хочется выделить ещё двух людей, которые участвовали в исследовании, — это мои папа и мама.

Как видите, у папы и мамы отклонения от «золотой пропорции» минимальные. Может, именно поэтому, как идеальные люди, они дружно и счастливо живут уже много лет?

2.4 Исследование №4 «Золотое сечение» и «золотой прямоугольник» в предметах, окружающие нас.

Напомню, что прямоугольник, стороны которого находятся в золотом отношении, т.е. отношение длины к ширине даёт число 1,618, называется «золотым прямоугольником».

1)Я измерила длину и ширину классной доски:

Длина основной части – 100 см, ширина – 46 см. Отношение ширины к длине равно 2,174.

Длина маленькой части доски – 1 м, а ширина – 72 см, их отношение – 1,389.

Размеры интерактивной доски – 134Х175, отношение длины к ширине равно 1,306.

Размеры деревянной доски – 102Х74, отношение равно 1,378.

2) Я измерила парту в кабинете математики: длина – 110 см, ширина – 50 см. Отношение ширины к длине равно 2,2. Сделала вывод: парты надо менять!

Размеры обеденного стола (обычный стол дома) – 120Х80, отношение размеров составляет 1,5 и оно не равно, но близко к «золотому сечению».

3) Учебники, по которым мы учимся

Для исследования я взяла 4 учебника, измерила размеры и нашла отношение размеров

Учебник длина ширина отношение

«Русский язык» 215мм 165мм 1,303

«Математика» 220мм 170мм 1,294

«Биология» 220мм 140мм 1,57

«Общество» 260мм 195мм 1,333

4) Изучив план школы, я также нашла размеры, отношение которых близки к «золотой пропорции».

Со стороны спортивной площадки выделенные измерения 58,26 м и 41,56 м, их отношение составляет 1,402.

С парадного входа измерения 32,4 м и 20,75 м, отношение данных размеров – 1,567.

5) Кабинет математики имеет размеры 11,14 Х 6,02. Расстояния от доски до первой парты – 3,5 м, а расстояния между партами – по 1 м. Во-первых, отношение длины к ширине равно 1,894. Во-вторых, определим, где, по правилу «золотой пропорции», наиболее «выгодно» сидеть ученику.

Если ученик сидит за первой партой, то расстояния равны 3,5 – 7,64, тогда отношения равны 1,458 и 2,183. Если ученик сидит за второй партой, то – 4,5 – 6,64 и отношения равны 1,678 и 1,476. Если ученик сидит за третьей партой, то – 5,5 и 5,64, отношения – 1,975 и 1,025. Если ученик сидит за четвёртой партой, то – 6,5 и 4,64, отношения – 1,714 и 1,401. И, наконец, если ученик сидит за пятой партой, то – 7,5 и 3,64, отношения – 1,485 и 2,060. Отношения, наиболее близкие к «золотому сечению», получились для второй парты.

Проанализируем, насколько «выгодно» сидеть за второй партой. За второй партой сидят:

6А класс – Булавская Света, Шишман Света, Погожев Игорь, Третьякова Даша, Дьяков ваня

7А класс – Маханько Дмитрий, Оганесян Валера, Абдулвагабова Лейла, Бархударян Лена

7Б класс – Магомедов Марат, Магомедов Руслан, Игнашкин Стас, Хачатрян Артём

5 класс – Маханько Коля, Кудря Женя, Магомедова Лиана, Стрельцов Дима, Мухтарова Аделина.

Успеваемость некоторых из этих учащихся очень низкая, из чего можно сделать вывод: не важно, за какой партой сидит ученик, важно – учиться.

Заключение

Человек различает окружающие его предметы по форме. Интерес к форме какого-либо предмета может быть продиктован жизненной необходимостью, а может быть вызван красотой формы. Форма, в основе построения которой лежат сочетание симметрии и золотого сечения, способствует наилучшему зрительному восприятию и появлению ощущения красоты и гармонии. Целое всегда состоит из частей, части разной величины находятся в определенном отношении друг к другу и к целому. Принцип золотого сечения – высшее проявление структурного и функционального совершенства целого и его частей в искусстве, науке, технике и природе.

Я попыталась исследовать окружающие меня и пропорции своего тела и обнаружила Золотую пропорцию в окружающем нас мире.

ОБЩИЕ ВЫВОДЫ:

• Золотое сечение – это один из основных основополагающих принципов природы;

• Человеческое представление о красивом явно сформировалось под влиянием того, какой порядок и гармонию человек видит в природе.

• Закономерности Золотого сечения заложены в подсознании человека, использовались и используются архитекторами в своих работах.

• Золотое сечение является отображением окружающегося мира

• С возрастом увеличивается количество людей, выбирающих Золотую пропорцию.

• Также Золотое сечение имеет большое применение в нашей жизни. На летательных аппаратах с электромагнитными источниками энергии создаются прямоугольные ячейки с пропорцией золотого сечения. В гидротехнике по золотой спирали изгибают трубу, подводящую поток воды к лопастям турбины. Благодаря этому напор воды используется с наибольшей производительностью.

Человек – венец творения природы… Установлено, что золотые отношения можно найти и в пропорциях человеческого тела. Кроме того, человек сам является творцом, создаёт замечательные произведения искусства, в которых просматривается золотая пропорция.

Список литературы:

1. А. Азевич “Двадцать уроков гармонии” – М., “Школа-Пресс”, 1998

2. Н. Васютинский “Золотая пропорция” – М.,”Молодая гвардия”, 1990

3. М. Гарднер “Математические головоломки и развлечения” – М., “Мир”, 1971

4. Д. Пидоу “Геометрия и искусство” – М., “Мир”, 1989

5. А.П.Савин, В.В.Станцо, А.Ю. Котова “Я познаю мир. Математика” – М.: АСТ: Астрель: Хранитель, 2007

6. Энциклопедический словарь юного математика – М.,1989 Журнал “Квант”, 1973, № 8

7. Журнал “Математика в школе”, 1994, № 2, № 3

8. Энциклопедия для детей. Т.11. Математика. — М.: Аванта+, 1998.

9. Ресурсы Интернет

17

←Вернуться в «Доклады по математике»

Красота, оказывается, порою имеет математическое объяснение.
Пропорции золотого сечения часто используются художниками и скульпторами в соотношениях между
разными элементами картины или скульптуры. Великий Леонардо да Винчи находил соотношение
золотого сечения в пропорциях человеческого тела.

Так чему же равно отношение золотого сечения в математике и как его найти? Разберёмся на примере.

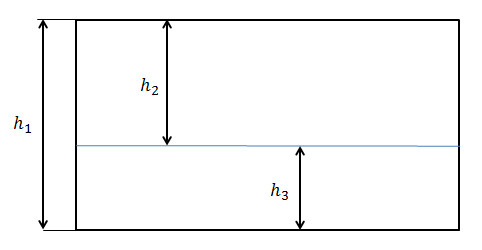
Возьмём лист бумаги и начертим линию горизонта, которая обычно делит небо от земли. Получится,
нечто похожее на рисунок ниже.

Отношение высоты картины h₁ к расстоянию от верхнего края
h₂ равно
отношению расстояния от верхнего края h₂
к расстоянию до нижнего края h₃.
В виде математической записи, это будет выглядеть так:

Найдём числовое значение золотого сечения.

Для этого вернёмся к нашему рисунку. Пусть высота всей картины равна h₁ = 1, а расстояние
от верхнего края до горизонта обозначим за x (h₂ = x). Тогда получим:

=

x² + x − 1 = 0

Положительный корень этого уравнения

≈ 1,618

Это отношение большей части к меньшей в этой пропорции.

Это число равно отношению золотого сечения. Обычно его обозначают греческими буквами
τ (тау) или
φ (фи).
Другие греческие буквы вы можете посмотреть в разделе
«Для учёбы».

Золотое сечение в фигурах

В некоторых фигурах геометрии и стереометрии также присутствует золотое сечение.
Например, в пятиконечной звезде (пентаграмме).

Точка «B» или «С» делит отрезок
«AD» в пропорциях золотого сечения.
Все остальные стороны звезды также поделены в данном соотношении соответственно.

Другой пример золотого сечения был обнаружен в пирамиде Хеопса.

В сечении знаменитого сооружения также заложен принцип золотого сечения.

Сумма двух сторон равнобедренного треугольника «ABC» относится к его основанию
также как сумма всех сторон треугольника к сумме равных сторон. Иными словами: