Всего: 23 1–20 | 21–23
Добавить в вариант
Четыре конденсатора одинаковой электроёмкости C = 25 пФ соединены так, как показано на схеме. Определите электроёмкость полученной батареи конденсаторов. Ответ выразите в пикофарадах.
Систему, состоящую из четырёх одинаковых изначально незаряженных последовательно соединённых конденсаторов, подключают к источнику постоянного напряжения. Дождавшись зарядки конденсаторов, обкладки двух из них замыкают при помощи куска проволоки. Как в результате этого изменятся суммарная электроёмкость данной системы конденсаторов и заряд каждого из двух других конденсаторов?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Суммарная электроёмкость
системы конденсаторов |
Заряд каждого из двух других
конденсаторов |
Систему, состоящую из трёх одинаковых изначально незаряженных последовательно соединённых конденсаторов, подключают к источнику постоянного напряжения. Дождавшись зарядки конденсаторов, обкладки одного из них замыкают при помощи куска проволоки. Как в результате этого изменятся суммарная электроёмкость данной системы конденсаторов и энергия, запасённая в каждом из двух других конденсаторов?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Суммарная электроёмкость
системы конденсаторов |
Энергия, запасённая в каждом из двух других конденсаторов |
В электрической цепи, схема которой изображена на рисунке, ёмкости конденсаторов равны C1 = 1 мкФ, C2 = 2 мкФ, C3 = 3 мкФ, C4 = 4 мкФ, C5 = 5 мкФ, и все они первоначально не заряжены. Какой заряд установится на конденсаторе C5 после подключения к этой цепи источника с напряжением U = 10 В?
Источник: Демонстрационная версия ЕГЭ−2019 по физике
В колебательном контуре, состоящем из двух параллельно соединенных конденсаторов и подключенной к ним катушки индуктивности, происходят свободные электромагнитные колебания. В момент, когда конденсаторы разряжены, один из них отсоединяют. Как после этого изменятся следующие физические величины: запасенная в контуре энергия, частота свободных электромагнитных колебаний, амплитуда напряжения между пластинами второго конденсатора?
Для каждой величины определите соотвествующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) Запасенная в контуре энергия
Б) Частота свободных электромагнитных колебаний
В) Амплитуда напряжения между пластинами второго конденсатора
ИХ ИЗМЕНЕНИЕ
1) Увеличится
2) Уменьшится
3) Не изменится
Участок цепи, схема которого изображена на рисунке, до замыкания ключа К имел электрическую ёмкость 3 нФ. После замыкания ключа электроёмкость данного участка цепи стала равной 4 нФ. Чему равна электроёмкость конденсатора Cx (в нФ)?
Колебательный контур состоит из катушки индуктивности и батареи конденсаторов. В состав батареи входят четыре одинаковых конденсатора, соединённых параллельно. Круговая частота ω свободных электромагнитных колебаний, которые могут происходить в этом контуре, равна 2500 с–1. По разным причинам три конденсатора из четырёх вышли из строя. На сколько изменилась круговая частота свободных электромагнитных колебаний в контуре?
В электрической цепи, схема которой изображена на рисунке, ёмкости конденсаторов равны C1 = 1 мкФ, C2 = 2 мкФ, C3 = 3 мкФ, C4 = 4 мкФ, C5 = 5 мкФ, и все они первоначально не заряжены. Какой заряд установится на конденсаторе C5 после подключения к этой цепи источника с напряжением U = 12 В?
Источник: ЕГЭ по физике 06.06.2022. Основная волна. Разные задачи
Плоский воздушный конденсатор, изготовленный из двух одинаковых квадратных металлических пластин, обладает электрической ёмкостью 96 пФ. Каждую из пластин разрезали пополам вдоль стороны квадрата, собрали из получившихся прямоугольников два конденсатора и соединили их последовательно. Расстояние между пластинами конденсаторов оставили прежним. Определите электрическую ёмкость получившейся системы конденсаторов. Ответ дайте в пФ.
Два одинаковых незаряженных конденсатора ёмкостью 2 мкФ каждый соединили параллельно и зарядили их до напряжения 3 В. Затем конденсаторы разъединили и замкнули выводы одного из них резистором с сопротивлением 100 кОм. Какое количество теплоты выделится в этом резисторе за достаточно большое время?Ответ приведите в микроджоулях.
Школьник решил измерить мощность P, выделяющуюся в резисторе сопротивлением R = 2 кОм, присоединённом к аккумулятору с ЭДС E = 12 В и малым внутренним сопротивлением. Для этого он использовал неидеальный вольтметр с сопротивлением RV = 25 кОм, который подключил параллельно резистору, и неидеальный амперметр с сопротивлением RA = 2 Ом, подключив его последовательно с аккумулятором (см. рис.). На сколько процентов отличается от измеренной мощности P мощность P0, которую школьник бы вычислил бы, используя при измерениях вместо реальных вольтметра и амперметра «идеальные» приборы? Считайте, что ток и напряжение реальные приборы в собранной схеме показывают верно.
Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рис.). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из правого конденсатора диэлектрик вытечет?
Источник: ЕГЭ по физике 08.05.2014. Досрочная волна, резервная волна. Вариант 202
К идеальному источнику тока с ЭДС 3 В подключили конденсатор ёмкостью 1 мкФ один раз через резистор а второй раз — через резистор
Во сколько раз во втором случае тепло, выделившееся на резисторе, больше по сравнению с первым? Излучением пренебречь.
Период свободных колебаний в колебательном контуре, состоящем из конденсатора ёмкостью C и катушки индуктивностью L, равен
Установите соответствие между периодами колебаний и схемами колебательных контуров. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
СХЕМА ЭКСПЕРИМЕНТА
А)
Б)
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Урал. Вариант 5.
Два плоских конденсатора ёмкостью С и 2С соединили параллельно и зарядили до напряжения U. Затем ключ К разомкнули, отключив конденсаторы от источника (см. рис.). Пространство между их обкладками заполнено жидким диэлектриком с диэлектрической проницаемостью ε. Какой будет разность потенциалов между обкладками, если из левого конденсатора диэлектрик вытечет?
Источник: ЕГЭ по физике 08.05.2014. Досрочная волна, резервная волна. Вариант 201
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 1.
Всего: 23 1–20 | 21–23
-
ЕГЭ по физике 2023
- /
-
Теория по физике
- /
- Теория по теме «Конденсатор. Соединение конденсаторов»
- /
Задачи с конденсаторами: сборная солянка
В эту статью вошли задачи всех типов: здесь и определение эквивалентных емкостей, и напряжений между определенными точками схемы, и бесконечные цепочки, и даже исчезновение конденсаторов из схем (бесследное и без последствий).
Задача 1.
Плоский конденсатор разрезают на равные части вдоль плоскостей, перпендикулярных обкладкам. Полученные
конденсаторов соединяют последовательно. Чему равна емкость полученной батaреи конденсаторов, если емкость исходного конденсатора
мкФ?
К задаче 1
Площадь исходного конденсатора:
Площадь нового конденсатора (одного) — в 4 раза меньше исходного (так как площадь меньше):
Теперь соединяем последовательно:
Ответ: 1 мкФ.
Задача 2.
Два плоских конденсатора, емкостью каждый, соединили параллельно. В один из них вставили диэлектрическую пластину с проницаемостью
, заполнившую весь объем конденсатора. Какой емкости и как необходимо подключить третий конденсатор, чтобы емкость системы стала равной
?
Так как первые два конденсатора соединены параллельно, то их емкости надо сложить, чтобы получить эквивалентную емкость:
После введения пластины емкость такого конденсатора стала равна , а эквивалентная емкость стала равна
Теперь к этой конструкции будем присоединять еще один конденсатор. Попробуем присоединить параллельно, тогда
Так как , то
,
.
Теперь присоединяем последовательно, тогда:
Решим неравенство:
Решение — — это решение не имеет смысла,
.
Ответ: , при
, параллельно.
, при
, последовательно.
Задача 3.
Разность потенциалов между точками А и В равна . Емкости конденсаторов
известны. Определить заряды конденсаторов
и разность потенциалов
между точками А и D.
К задаче 3
Так как емкости и
соединены параллельно, то напряжение на них одинаковое. Кроме того, заряды на емкостях
и системе конденсаторов
одинаковы, так как они соединены последовательно. Поэтому
Эквивалентная емкость , поэтому эквивалентная емкость всей схемы – произведение на сумму —
.
Тогда заряд
Но вследствие (1)
Тогда
Находим :
Определим заряды и
:
Ответ: ,
,
,
.
Задача 4.
Определить емкость батареи конденсаторов, показанной на рисунке, если мкФ,
мкФ,
мкФ.
К задаче 4
Сначала два конденсатора подключены параллельно, при этом емкости складываются:
. В конце параллельное соединение
и
:
. Теперь имеем последовательное соединение емкостей
,
и
. Тогда
Можно подставить числа и довести решение до конца:
Ответ: мкФ.
Задача 5.
Найти емкость системы конденсаторов, изображенной на рисунке.
К задаче 5
На рисунке a) емкость оказывается незаряженной, так как схема совершенно симметрична и
, поэтому
.
Рисунок 2 (задача 5)
Поэтому конденсатор не заряжен – разность потенциалов на его выводах нулевая. Следовательно, имеем две веточки, включенные в параллель: в каждой последовательное соединение
и
.
Рисунок 3 (к задаче 5)
Сопротивление одной ветки (емкость двух последовательно включенных конденсаторов – произведение, деленное на сумму):
А двух таких веток в параллель (емкости, включенные параллельно, складываются): .
На рисунке б) – если приглядеться, та же самая ситуация:
К задаче 5 — рисунок 4
Так что, аналогично первой схеме, сопротивление одной ветки с двумя последовательно включенными конденсаторами — , а две такие емкости в параллель дадут
.
Ответ: а) ; б)
.
Задача 6.
Определить емкость Сх бесконечно длинной системы одинаковых конденсаторов, емкостью С каждый, соединенных друг с другом, как показано на рисунке.
К задаче 6, рисунок 1
Выделим в этой цепи повторяющийся элемент:
К задаче 6, рисунок 2
Эти элементы соединены параллельно. Так как емкость цепи бесконечна, то от нее не убудет, если мы один элемент удалим, или выделим. Тогда справа от выделенного элемента цепь с емкостью , и слева – тоже.
К задаче 6, рисунок 3
Можем записать для последовательно включенных емкостей:
Задача 7.
Найти разность потенциалов между точками А и В в схеме, изображенной на рисунке. Емкость мкФ,
мкФ,
мкФ. Напряжение источника
В.
К задаче 7
Емкость верхней ветки:
Емкость нижней ветки:
Заряд верхней ветви (мкКл):
Заряд нижней ветви (мкКл):
Но соединен последовательно с
, поэтому
, и
Аналогично в нижней ветви:
В сумме .
Найдем разность потенциалов между точками и
:
Ответ: B.
Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Проводники и диэлектрики в электростатическом поле
Вещества в природе можно разделить на проводники и диэлектрики.
Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
Типичные проводники — металлы.
Диэлектрическая проницаемость вещества
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Физическая величина, равная отношению модуля напряженности (vec{E}_0) внешнего электрического поля в вакууме к модулю напряженности (vec{E}) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon).
[varepsilon=dfrac{vec{E}_0}{vec{E}}]
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:
[fbox{$C=dfrac{q}{Delta varphi}$}]
Единицы измерения: (displaystyle [text{Ф}]) (фарад).
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электроемкость плоского конденсатора
Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed), где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
[C=dfrac{q}{Delta varphi}=dfrac{sigma S}{Ed}=dfrac{varepsilon_0S}{d}]
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:
[fbox{$C=dfrac{varepsilon_0varepsilon S}{d}$}]
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
-
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
[fbox{$U=U_1+U_2$}]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
[dfrac{q}{C}=dfrac{q}{C_1}+dfrac{q}{C_2}]
Сократив выражение на (Q), получим формулу:
[fbox{$dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}$}]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
[fbox{$C=dfrac{C_1C_2}{C_1+C_2}$}]
-
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
[fbox{$q=q_1+q_2$}]
Так как заряд конденсатора
[q=CU]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
[CU=C_1U+C_2U]
[fbox{$C=C_1+C_2$}]
-
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.
Вычислим эту энергию: начнём с плоского воздушного конденсатора.
Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q), площадь обкладок (S). Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
[F_0 = q_0E_1,]
где (E_1) — напряжённость поля первой обкладки:
[E_1=dfrac{sigma}{2varepsilon_0}=dfrac{q}{2varepsilon_0S}]
Значит
[F_0=dfrac{qq_0}{2varepsilon_0S}]
Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0), с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac{q}{2varepsilon_0S}) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q). В результате получим
[F=dfrac{q^2}{2varepsilon_0S}]
Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2). Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]
Знак правильный: если пластины сближаются ((d_2 < d_1)), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)), то работа силы притяжения получается отрицательной, как и должно быть.
Получаем
[A=dfrac{q^2}{2varepsilon_0S}(d_1-d_2)=dfrac{q^2d_1}{2varepsilon_0S}-dfrac{q^2d_2}{2varepsilon_0S}=dfrac{q^2}{2C_1}-dfrac{q^2}{2C_2}=W_1-W_2]
Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]
где [fbox{$W=dfrac{q^2}{2C}$}, (1)]
Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W). Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).
[fbox{$W=dfrac{qU}{2}$}, (2)]
[fbox{$W=dfrac{CU^2}{2}$}, (3)]
Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
При подготовке к ЕГЭ по физике и решении задач повышенной сложности очень часто обучающиеся сталкиваются с трудностями анализа физических процессов в конденсаторах. Целью данной работы является некоторая систематизация и выделение ключевых позиций при решении задач повышенной сложности по теме «Конденсаторы и их соединение». Реализовывая системно-деятельностный подход к изучению физики, возможно рассмотрение следующих ситуаций анализа решаемых задач, а также вариативных вопросов к ним.
I. Рассмотрим известную задачу, которая раскрывает взаимосвязь физических характеристик конденсатора и последовательность их изменений [2]:
Плоский конденсатор, между пластинами которого находится воздух, заряжен от источника питания. Как меняются заряд конденсатора, напряженность электрического поля, разность потенциалов между пластинами, энергия и плотность энергии электрического поля, если увеличить в n раз расстояние между пластинами в ситуациях, если а) конденсатор отключить от источника питания и б) с включенным источником питания.
Рассмотрим первую ситуацию: изменяем расстояние между пластинами при отключенном источнике.
В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик
— Что остается неизменным в данном процессе. (q = const, заряд на пластинах конденсатора при отключении источника тока)
— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)
Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:
1) Напряженность электрического поля конденсатора E = ϭ/(2ε0) (не изменяется)
2) Разность потенциалов между пластинами C = q/U (С уменьшается, U
увеличивается в n раз)
3) Энергия электрического поля W = qU/2 (U увеличивается в n раз, W
увеличивается в n раз)
4) Плотность энергии ω = ε0E2/2 (не изменяется)
Рассмотрим вторую ситуацию: изменяем расстояние между пластинами при включенном источнике питания.
В ключевых позициях устанавливаем два опорных положения, которые позволяют анализировать изменения физических характеристик
— Что остается неизменным в данном процессе. (U = const, напряжение на пластинах конденсатора при включении источнике тока)
— Что происходит с емкостью конденсатора (Конденсатор плоский: d
увеличивается, C уменьшается)
Анализируем и доказываем, как изменяются физические характеристики и причины их изменения:
1) При неизменном напряжении и уменьшении емкости, заряд конденсатора должен уменьшиться в n раз (анализ C = q/U)
2) Напряженность электрического поля конденсатора E = ϭ/(2ε0) (E
уменьшается в n раз при уменьшении заряда в n раз)
3) Энергия электрического поля W = qU/2 (q уменьшается в n раз, W
уменьшается в n раз)
4) Плотность энергии ω = ε0E2/2 уменьшается в n2 раз (при уменьшении напряженности)
Особое внимание следует обратить на энергетические превращения в конденсаторе. При увеличении расстояния между пластинами совершается положительная механическая работа, но энергия конденсатора уменьшается. Согласно закону сохранения энергии источник должен забирать энергию, равную убыли энергии конденсатора и механической работы внешних сил. Иначе, если источник является аккумулятором, то он будет заряжаться от конденсатора. Если источником является гальванический элемент, то на нем будет выделяться тепло.
Поставленную задачу можно не ограничивать данными изменениями, а можно выполнить анализ при изменении площади пластин конденсатора или замене диэлектрика между пластинами. В результате поможет сформировать у обучающихся целостное и устойчивое представление физических процессов и их характеристик в конденсаторе, варьируя ситуации.
II. Рассмотрим две возможные ситуации при параллельном подключении одного конденсатора к другому, если обкладки конденсаторов соединены одноименными зарядами и разноименными зарядами [2]:
Конденсатор емкостью C1 заряжен до разности потенциалов U1. Какой заряд и каково напряжение будет на обкладках конденсатора, если к нему подключить параллельно другой конденсатор емкостью C2, заряженный до разности потенциалов U2.
Если обкладки конденсаторов соединены одноименными зарядами, то решение задачи сводится к составлению уравнения закона сохранения заряда до соединения и после соединения конденсаторов. Закон сохранения заряда будет ключевым моментом анализа задачи. Второй момент — равенство напряжений на конденсаторах при параллельном подключении, дает возможность упростить и решить данную задачу.
Иначе дело обстоит, если обкладки конденсаторов соединены разноименными зарядами. При соединении двух конденсаторов возникает ситуация, когда при распределении зарядов после подключения происходит перезарядка одного из конденсаторов и смена знаков зарядов на его обкладках. В этом случае при составлении уравнения закона сохранения заряда как ключевого момента следует не забыть изменить знак заряда на противоположный. Положим, в данном примере U2 > U1, то при соединении конденсаторов, первый конденсатор перезарядится, и знаки зарядов на его пластинах сменятся. Поэтому удобно при составлении закона сохранения заряда, принять заряд первого конденсатора, до соединения к нему второго, за отрицательный заряд.
Закон сохранения заряда для данного примера будет выглядеть: -q1+ q2
= q1‘+ q2‘. Последующее равенство напряжений на конденсаторах при параллельном подключении дает возможность упростить и решить данную задачу.
III. Рассмотрим анализ схемы соединения конденсаторов, где их соединения не сводятся к совокупности параллельных и последовательных соединений.
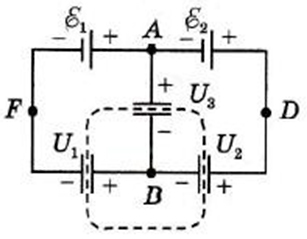
Например, в разветвленной схеме требуется найти напряжения на конденсаторах. Данный пример подробно описан [1]. Из данного примера выделим следующие ключевые моменты:
1) Составляем независимые уравнения, связывающие напряжения на конденсаторах с электродвижущими силами, выбрав точки разности потенциалов.
А) Между точками F и D: Ɛ1+ Ɛ2= U1+ U2
Б) Между точками F и A: Ɛ1= U1+ U3
2) Составляем уравнение алгебраической суммы зарядов в узле точки B:
q1— q2 — q3= 0 или C1U1— C2U2 — C3U3= 0
Система трех независимых уравнений с тремя неизвестными дает их решение. Если схема симметрична (Ɛ1 = Ɛ2, C1 = C2), то U3 (Напряжение между точками A и B) равно нулю, а напряжение U1= U2.
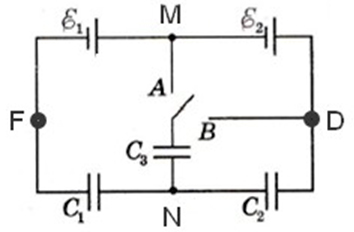
В связи с данным примером, возникает упрощенный анализ схем при переключении в цепи с конденсаторами, например [1]:
Для положения ключа в состоянии A и B между точками F и D выражение Ɛ1 + Ɛ2 = U1 + U2 справедливо в обоих случаях. Следовательно, U2не изменяется при переключении.
Для узла N сумма зарядов в узле равна нулю: q1— q2 ± q3= 0. Следовательно, не изменится заряд третьего конденсатора, а вместе с ним и не изменится напряжение U3.
После переключения U2= U3, конденсаторы соединены параллельно.
В данном примере интересен вывод: точки A и B имеют одинаковый потенциал, следовательно Ɛ2= 0.
IV. Рассмотрим некоторые варианты изменения энергии конденсатора с точки зрения закона сохранения энергии, подробные объяснения которых обсуждаются в источнике [3].
Изменение энергии конденсатора можно произвести от источника питания или путем совершения механической работы внешними силами.
Увеличение энергии конденсатора при зарядке конденсатора в общем виде можно определить из уравнения закона сохранения:
Aист. = ΔWк + A + Q,
где Aист. – работа источника при зарядке конденсатора, ΔWк – изменение энергии конденсатора, A – механическая работа сил электрического поля, Q – выделяющееся тепло. В идеальном случае, при отсутствии потерь энергии от источника: Aист. = ΔWк
Однако наиболее часто встречаются задания, где изменение энергии заряженного конденсатора происходит путем совершения работы внешней силы в ситуациях с отключенным и подключенным источником тока.
Рассмотрим первую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при отключенном источнике питания.
— обращаем внимание на то, что в данной ситуации остается неизменным заряд q конденсатора.
— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε0S/d)
Формируем вывод исходя из формулы энергии при неизменном заряде: W = q2/2C – энергия конденсатора увеличивается. Увеличение энергии произошло за счет работы внешней силы. ΔWк = Aвнеш.
Рассмотрим вторую ситуацию: как изменится энергия конденсатора, если вынуть диэлектрическую пластину из заряженного конденсатора или раздвинуть его обкладки при включенном источнике питания.
— обращаем внимание на то, что в данной ситуации остается неизменным напряжение U на обкладках конденсатора.
— обращаем внимание на то, что емкость при выемке диэлектрика или раздвижении пластин уменьшается емкость конденсатора (C = εε0S/d)
Формируем вывод исходя из формулы энергии при неизменном напряжении: W = CU2/2 – энергия конденсатора уменьшается. Уменьшение энергии произошло за счет того, что источник совершает отрицательную работу, забирая часть заряда с обкладок конденсатора при положительной работе внешних сил:. ΔWк = Aист. + Aвнеш.
Возможны и другие очевидные вариации изменения энергии конденсатора с помощью работы внешних сил.
В данной работе рассмотрена лишь небольшая часть анализа ключевых ситуаций по данной теме. Но все рассмотренные ситуации являются опорными для формирования разбора задач и их решения.
Литература
1. Е.И.Бутиков, А.А.Быков, А.С.Кондратьев. Физика в примерах и задачах, МЦНМО, Пероглиф, 2019, стр. 297-301.
2. А.С.Кондратьев, В.М.Уздин. Физика. Сборник задач, М., ФИЗМАТЛИТ, 2020, стр.67-69.
3. А.С.Кондратьев, Л.А.Ларченкова, В.А.Ляпцев. Методы решения задач по физике. М., ФИЗМАТЛИТ, 2019, стр.149-154.