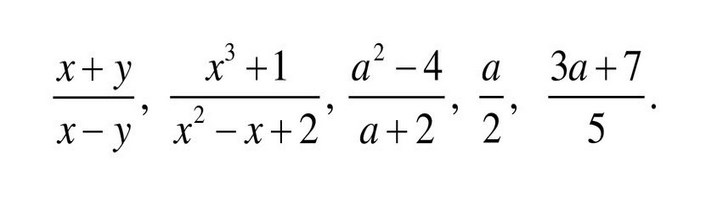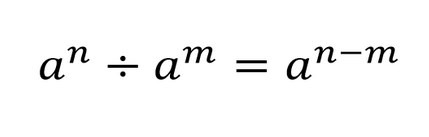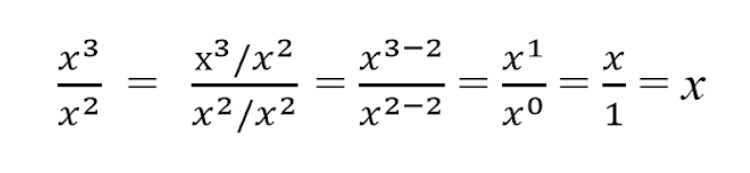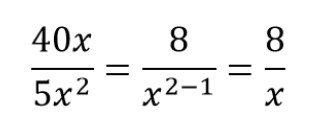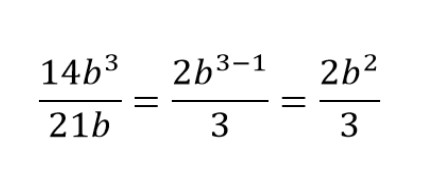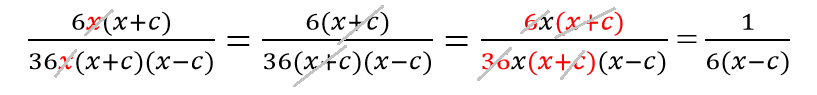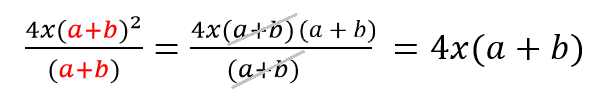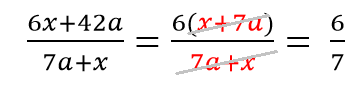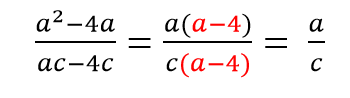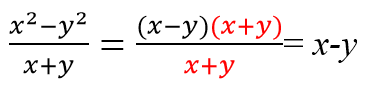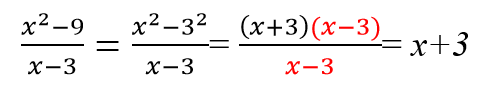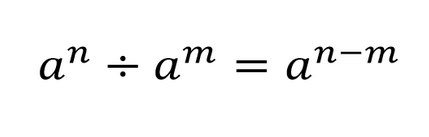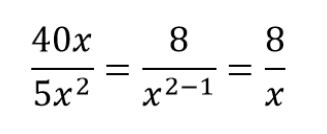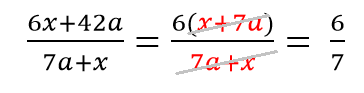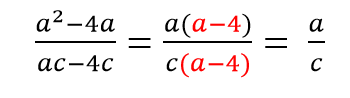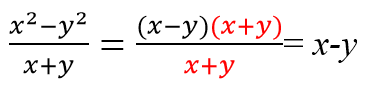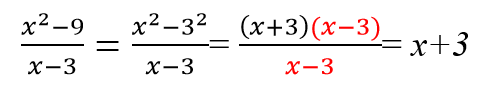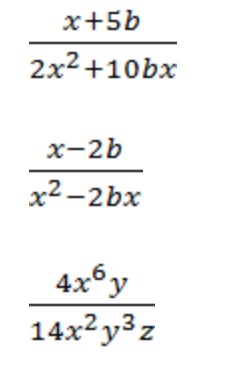Сократите дробь егэ - ExamHelp.top - все самое полезное для учащихся

Определение

Алгебраическая дробь — это дробь, в числителе и/или знаменателе которой стоят алгебраические выражения (буквенные множители). Вот так:

Алгебраическая дробь содержит буквенные множители и степени.

Необыкновенной алгебраическую дробь делают буквы. Если заменить их на цифры, то карета превратится в тыкву — алгебраическая дробь тут же станет обыкновенной.

Если вы засомневались, что должно быть сверху — числитель или знаменатель — переходите по ссылке и освежите знания по теме обыкновенных дробей.

Получай лайфхаки, статьи, видео и чек-листы по обучению на почту

Реши домашку по математике на 5.

Подробные решения помогут разобраться в самой сложной теме.

Сокращение алгебраических дробей

Сократить алгебраическую дробь — значит разделить ее числитель и знаменатель на общий множитель. Общий множитель числителя и знаменателя в алгебраической дроби — многочлен и одночлен.

Сокращение дробей с буквами и степенями проходит в три этапа:

Определите общий множитель.
Сократите коэффициенты.
Поделите все числители и все знаменатели на общий множитель.

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

Следуя формуле сокращения степеней в дробях, сокращаем x³ и x²
Всегда делим на наименьшее значение в степени
Вычитаем: 3 — 1

Получаем сокращенную дробь.

Запоминаем: сокращать можно только одинаковые буквенные множители. Иными словами, сокращать можно только дроби с одинаковыми буквами.

Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Как решаем:

Общий множитель для числителя и знаменателя — 8.
Х и x² делим на x и получаем ответ.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Как решаем:

Общий множитель для числителя и знаменателя — 7.
b³ и b делим на b.
Вычитаем: 3 — 1 и получаем ответ.

Получаем сокращенную дробь.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

сокращайте многочлен в скобках только с таким же многочленом в скобках;
сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.

Запомните: многочлены в алгебраической дроби находятся в скобках. Между этими скобками вклиниться может только знак умножения. Всем остальным знакам там делать нечего.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3).

Вынесение общего множителя при сокращении дробей

При сокращении алгебраических дробей иногда не хватает одинаковых многочленов. Для того, чтобы они появились, вынесите общий множитель за скобки.

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

Найдите число, на которое делятся числа каждого одночлена.
Найдите повторяющиеся буквенные множители в каждом одночлене.
Вынесите найденные буквенные множители за скобку.
Далее работаем с многочленом, оставшимся в скобках.

Алгебра не терпит неточность. Всегда проверяйте, верно ли вынесен множитель за скобки — сделать это можно по правилу умножения многочлена на одночлен.

Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен.

Пример 1.

Как решаем:

Выносим общий множитель 6
Делим 42/6
Сокращаем получившиеся одинаковые многочлены.

Пример 2.

Как решаем: в числителе выносим общий множитель a за скобки, в знаменателе выносим общий множитель c за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Чтобы легко ориентироваться в формулах сокращенного умножения, сохраняйте и заучивайте таблицу. Формулы подскажут вам, как решать алгебраические дроби.

Квадрат суммы	(a+b)² = a² + 2ab + b²
Квадрат разности	(a-b)² = a² — 2ab — b²
Разность квадратов	a² – b² = (a – b)(a+b)
Куб суммы	(a+b)³ = a³ + 3a²b + 3ab² + b³
Куб разности	(a-b)³ = a³ — 3a²b + 3ab² — b³
Сумма кубов	a³ + b³ = (a + b)(a²— ab+b²)
Разность кубов	a³ — b³ = (a — b)(a²+ ab+b²)

Примеры сокращения дробей с помощью формул сокращенного умножения:

Применяем формулу разности квадратов a² − b² = (a − b) (a + b) и сокращаем одинаковые многочлены.

Чтобы раскрыть тему сокращения алгебраических дробей и полностью погрузиться в мир числителей и знаменателей, решите следующие примеры для самопроверки.

Примеры сокращения дробей за 7 и 8 классы

Сократите дроби:

Тема сокращения алгебраических дробей достаточно обширна, и требует к себе особого внимания. Чтобы знания задержалась в голове хотя бы до ЕГЭ, сохраните себе памятку по сокращению дробей. Этот алгоритм поможет не растеряться при встрече с алгебраическими дробями лицом к лицу.

Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
Поделите числитель и знаменатель на общий множитель.
Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.

Источник

Как сокращать алгебраические дроби?

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Определение

Алгебраическая дробь содержит буквенные множители и степени.

Сокращение алгебраических дробей

Если в 7 классе только и разговоров, что об обыкновенных дробях, то 8 класс сокращает исключительно алгебраические дроби.

Сокращение дробей с буквами и степенями проходит в три этапа:

Определите общий множитель.
Сократите коэффициенты.
Поделите все числители и все знаменатели на общий множитель.

Для сокращения степеней в дробях применяем правило деления степеней с одинаковыми основаниями:

Пример сокращения дроби со степенями и буквами:

Следуя формуле сокращения степеней в дробях, сокращаем x 3 и x 2
Всегда делим на наименьшее значение в степени
Вычитаем: 3 — 1

Получаем сокращенную дробь.

Примеры сокращения алгебраических дробей с одночленами:

Пример сокращения №1.

Общий множитель для числителя и знаменателя — 8.
Х и x 2 делим на x и получаем ответ.

Получаем сокращенную алгебраическую дробь.

Пример сокращения №2.

Общий множитель для числителя и знаменателя — 7.
b 3 и b делим на b.
Вычитаем: 3 — 1 и получаем ответ.

Получаем сокращенную дробь.

Сокращение алгебраических дробей с многочленами

Чтобы верно сократить алгебраическую дробь с многочленами, придерживайтесь двух главных правил:

сокращайте многочлен в скобках только с таким же многочленом в скобках;
сокращайте многочлен в скобках целиком — нельзя сократить одну его часть, а другую оставить. Не делайте из многочленов одночлены.

Примеры сокращения алгебраических дробей с многочленами:

Последовательно сокращаем: сначала x, затем (x+c), далее сокращаем дробь на 6 (общий множитель).

Сокращаем многочлены a+b (в дроби их 3). Многочлен в числителе стоит в квадрате, поэтому мысленно оставляем его при сокращении.

Вынесение общего множителя при сокращении дробей

Чтобы легко и непринужденно выносить множитель за скобки, пошагово выполняйте 4 правила:

Найдите число, на которое делятся числа каждого одночлена.
Найдите повторяющиеся буквенные множители в каждом одночлене.
Вынесите найденные буквенные множители за скобку.
Далее работаем с многочленом, оставшимся в скобках.

Для умножения одночлена на многочлен нужно умножить поочередно все члены многочлена на этот одночлен.

Пример 1.

Выносим общий множитель 6
Делим 42/6
Сокращаем получившиеся одинаковые многочлены.

Пример 2.

Как решаем: выносим общий множитель a за скобки и сокращаем оставшиеся в скобках многочлены.

Сокращение дробей. Формулы сокращенного умножения

Перед формулами сокращенного умножения не устоит ни одна дробь — даже алгебраическая.

Квадрат суммы	(a+b) 2 = a 2 + 2ab + b 2
Квадрат разности	(a-b) 2 = a 2 — 2ab — b 2
Разность квадратов	a 2 – b 2 = (a – b)(a+b)
Куб суммы	(a+b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Куб разности	(a-b) 3 = a 3 — 3a 2 b + 3ab 2 — b 3
Сумма кубов	a 3 + b 3 = (a + b)(a 2 — ab+b 2 )
Разность кубов	a 3 — b 3 = (a — b)(a 2 + ab+b 2 )

Примеры сокращения дробей с помощью формул сокращенного умножения:

Применяем формулу квадрата разности (a-b) 2 = a 2 — 2ab — b 2 и сокращаем одинаковые многочлены.

Примеры сокращения дробей за 7 и 8 классы

Чтобы сократить дробь, найдите общий множитель числителя и знаменателя.
Поделите числитель и знаменатель на общий множитель.
Чтобы разделить многочлен на множители, вынесите общий множитель за скобку.
Второй способ разделить многочлен на множители — применить формулы сокращенного умножения.
Выучите все формулы сокращенного умножения — они помогут легко преобразовывать выражения и экономить время при решении задач.
Можно забыть свое имя, но формулу разности квадратов помнить обязательно — она будет встречаться чаще других.
Всегда проверяйте результат сокращения: алгебра — точна, коварна и не любит давать вторые шансы.

Возможно тебе будет полезно — Формулы сокращённого умножения (ФСУ)

Степенные выражения (выражения со степенями) и их преобразование

Рассмотрим тему преобразования выражений со степенями, но прежде остановимся на ряде преобразований, которые можно проводить с любыми выражениями, в том числе со степенными. Мы научимся раскрывать скобки, приводить подобные слагаемые, работать с основанием и показателем степени, использовать свойства степеней.

Что представляют собой степенные выражения?

В школьном курсе мало кто использует словосочетание «степенные выражения», зато этот термин постоянно встречается в сборниках для подготовки к ЕГЭ. В большинства случаев словосочетанием обозначаются выражения, которые содержат в своих записях степени. Это мы и отразим в нашем определении.

Степенное выражение – это выражение, которое содержит степени.

Приведем несколько примеров степенных выражений, начиная со степени с натуральным показателем и заканчивая степенью с действительным показателем.

Самыми простыми степенными выражениями можно считать степени числа с натуральным показателем: 3 2 , 7 5 + 1 , ( 2 + 1 ) 5 , ( − 0 , 1 ) 4 , 2 2 3 3 , 3 · a 2 − a + a 2 , x 3 − 1 , ( a 2 ) 3 . А также степени с нулевым показателем: 5 0 , ( a + 1 ) 0 , 3 + 5 2 − 3 , 2 0 . И степени с целыми отрицательными степенями: ( 0 , 5 ) 2 + ( 0 , 5 ) — 2 2 .

Чуть сложнее работать со степенью, имеющей рациональный и иррациональный показатели: 264 1 4 — 3 · 3 · 3 1 2 , 2 3 , 5 · 2 — 2 2 — 1 , 5 , 1 a 1 4 · a 1 2 — 2 · a — 1 6 · b 1 2 , x π · x 1 — π , 2 3 3 + 5 .

В качестве показателя может выступать переменная 3 x — 54 — 7 · 3 x — 58 или логарифм x 2 · l g x − 5 · x l g x .

С вопросом о том, что такое степенные выражения, мы разобрались. Теперь займемся их преобразованием.

Основные виды преобразований степенных выражений

В первую очередь мы рассмотрим основные тождественные преобразования выражений, которые можно выполнять со степенными выражениями.

Вычислите значение степенного выражения 2 3 · ( 4 2 − 12 ) .

Решение

Все преобразования мы будем проводить с соблюдением порядка выполнения действий. В данном случае начнем мы с выполнения действий в скобках: заменим степень на цифровое значение и вычислим разность двух чисел. Имеем 2 3 · ( 4 2 − 12 ) = 2 3 · ( 16 − 12 ) = 2 3 · 4 .

Нам остается заменить степень 2 3 ее значением 8 и вычислить произведение 8 · 4 = 32 . Вот наш ответ.

Ответ: 2 3 · ( 4 2 − 12 ) = 32 .

Упростите выражение со степенями 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 .

Решение

Данное нам в условии задачи выражение содержит подобные слагаемые, которые мы можем привести: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Ответ: 3 · a 4 · b − 7 − 1 + 2 · a 4 · b − 7 = 5 · a 4 · b − 7 − 1 .

Представьте выражение со степенями 9 — b 3 · π — 1 2 в виде произведения.

Решение

Представим число 9 как степень 3 2 и применим формулу сокращенного умножения:

9 — b 3 · π — 1 2 = 3 2 — b 3 · π — 1 2 = = 3 — b 3 · π — 1 3 + b 3 · π — 1

Ответ: 9 — b 3 · π — 1 2 = 3 — b 3 · π — 1 3 + b 3 · π — 1 .

А теперь перейдем к разбору тождественных преобразований, которые могут применяться именно в отношении степенных выражений.

Работа с основанием и показателем степени

Степень в основании или показателе может иметь и числа, и переменные, и некоторые выражения. Например, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 и ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) . Работать с такими записями сложно. Намного проще заменить выражение в основании степени или выражение в показателе тождественно равным выражением.

Проводятся преобразования степени и показателя по известным нам правилам отдельно друг от друга. Самое главное, чтобы в результате преобразований получилось выражение, тождественное исходному.

Цель преобразований – упростить исходное выражение или получить решение задачи. Например, в примере, который мы привели выше, ( 2 + 0 , 3 · 7 ) 5 − 3 , 7 можно выполнить действия для перехода к степени 4 , 1 1 , 3 . Раскрыв скобки, мы можем привести подобные слагаемые в основании степени ( a · ( a + 1 ) − a 2 ) 2 · ( x + 1 ) и получить степенное выражение более простого вида a 2 · ( x + 1 ) .

Использование свойств степеней

Свойства степеней, записанные в виде равенств, являются одним из главных инструментов преобразования выражений со степенями. Приведем здесь основные из них, учитывая, что a и b – это любые положительные числа, а r и s — произвольные действительные числа:

a r · a s = a r + s ;
a r : a s = a r − s ;
( a · b ) r = a r · b r ;
( a : b ) r = a r : b r ;
( a r ) s = a r · s .

В тех случаях, когда мы имеем дело с натуральными, целыми, положительными показателями степени, ограничения на числа a и b могут быть гораздо менее строгими. Так, например, если рассмотреть равенство a m · a n = a m + n , где m и n – натуральные числа, то оно будет верно для любых значений a , как положительных, так и отрицательных, а также для a = 0 .

Применять свойства степеней без ограничений можно в тех случаях, когда основания степеней положительные или содержат переменные, область допустимых значений которых такова, что на ней основания принимают лишь положительные значения. Фактически, в рамках школьной программы по математике задачей учащегося является выбор подходящего свойства и правильное его применение.

При подготовке к поступлению в Вузы могут встречаться задачи, в которых неаккуратное применение свойств будет приводить к сужению ОДЗ и другим сложностям с решением. В данном разделе мы разберем всего два таких случая. Больше информации по вопросу можно найти в теме «Преобразование выражений с использованием свойств степеней».

Представьте выражение a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 в виде степени с основанием a .

Решение

Для начала используем свойство возведения в степень и преобразуем по нему второй множитель ( a 2 ) − 3 . Затем используем свойства умножения и деления степеней с одинаковым основанием:

a 2 , 5 · a − 6 : a − 5 , 5 = a 2 , 5 − 6 : a − 5 , 5 = a − 3 , 5 : a − 5 , 5 = a − 3 , 5 − ( − 5 , 5 ) = a 2 .

Ответ: a 2 , 5 · ( a 2 ) − 3 : a − 5 , 5 = a 2 .

Преобразование степенных выражений согласно свойству степеней может производиться как слева направо, так и в обратном направлении.

Найти значение степенного выражения 3 1 3 · 7 1 3 · 21 2 3 .

Решение

Если мы применим равенство ( a · b ) r = a r · b r , справа налево, то получим произведение вида 3 · 7 1 3 · 21 2 3 и дальше 21 1 3 · 21 2 3 . Сложим показатели при умножении степеней с одинаковыми основаниями: 21 1 3 · 21 2 3 = 21 1 3 + 2 3 = 21 1 = 21 .

Есть еще один способ провести преобразования:

3 1 3 · 7 1 3 · 21 2 3 = 3 1 3 · 7 1 3 · ( 3 · 7 ) 2 3 = 3 1 3 · 7 1 3 · 3 2 3 · 7 2 3 = = 3 1 3 · 3 2 3 · 7 1 3 · 7 2 3 = 3 1 3 + 2 3 · 7 1 3 + 2 3 = 3 1 · 7 1 = 21

Ответ: 3 1 3 · 7 1 3 · 21 2 3 = 3 1 · 7 1 = 21

Дано степенное выражение a 1 , 5 − a 0 , 5 − 6 , введите новую переменную t = a 0 , 5 .

Решение

Представим степень a 1 , 5 как a 0 , 5 · 3 . Используем свойство степени в степени ( a r ) s = a r · s справа налево и получим ( a 0 , 5 ) 3 : a 1 , 5 − a 0 , 5 − 6 = ( a 0 , 5 ) 3 − a 0 , 5 − 6 . В полученное выражение можно без проблем вводить новую переменную t = a 0 , 5 : получаем t 3 − t − 6 .

Ответ: t 3 − t − 6 .

Преобразование дробей, содержащих степени

Обычно мы имеем дело с двумя вариантами степенных выражений с дробями: выражение представляет собой дробь со степенью или содержит такую дробь. К таким выражениям применимы все основные преобразования дробей без ограничений. Их можно сокращать, приводить к новому знаменателю, работать отдельно с числителем и знаменателем. Проиллюстрируем это примерами.

Упростить степенное выражение 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 .

Решение

Мы имеем дело с дробью, поэтому проведем преобразования и в числителе, и в знаменателе:

3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = 3 · 5 2 3 · 5 1 3 — 3 · 5 2 3 · 5 — 2 3 — 2 — x 2 = = 3 · 5 2 3 + 1 3 — 3 · 5 2 3 + — 2 3 — 2 — x 2 = 3 · 5 1 — 3 · 5 0 — 2 — x 2

Поместим минус перед дробью для того, чтобы изменить знак знаменателя: 12 — 2 — x 2 = — 12 2 + x 2

Ответ: 3 · 5 2 3 · 5 1 3 — 5 — 2 3 1 + 2 · x 2 — 3 — 3 · x 2 = — 12 2 + x 2

Дроби, содержащие степени, приводятся к новому знаменателю точно также, как и рациональные дроби. Для этого необходимо найти дополнительный множитель и умножить на него числитель и знаменатель дроби. Подбирать дополнительный множитель необходимо таким образом, чтобы он не обращался в нуль ни при каких значениях переменных из ОДЗ переменных для исходного выражения.

Приведите дроби к новому знаменателю: а) a + 1 a 0 , 7 к знаменателю a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 к знаменателю x + 8 · y 1 2 .

Решение

а) Подберем множитель, который позволит нам произвести приведение к новому знаменателю. a 0 , 7 · a 0 , 3 = a 0 , 7 + 0 , 3 = a , следовательно, в качестве дополнительного множителя мы возьмем a 0 , 3 . Область допустимых значений переменной а включает множество всех положительных действительных чисел. В этой области степень a 0 , 3 не обращается в нуль.

Выполним умножение числителя и знаменателя дроби на a 0 , 3 :

a + 1 a 0 , 7 = a + 1 · a 0 , 3 a 0 , 7 · a 0 , 3 = a + 1 · a 0 , 3 a

б) Обратим внимание на знаменатель:

x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 2 — x 1 3 · 2 · y 1 6 + 2 · y 1 6 2

Умножим это выражение на x 1 3 + 2 · y 1 6 , получим сумму кубов x 1 3 и 2 · y 1 6 , т.е. x + 8 · y 1 2 . Это наш новый знаменатель, к которому нам надо привести исходную дробь.

Так мы нашли дополнительный множитель x 1 3 + 2 · y 1 6 . На области допустимых значений переменных x и y выражение x 1 3 + 2 · y 1 6 не обращается в нуль, поэтому, мы можем умножить на него числитель и знаменатель дроби:
1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 + 2 · y 1 6 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = = x 1 3 + 2 · y 1 6 x 1 3 3 + 2 · y 1 6 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2

Ответ: а) a + 1 a 0 , 7 = a + 1 · a 0 , 3 a , б) 1 x 2 3 — 2 · x 1 3 · y 1 6 + 4 · y 1 3 = x 1 3 + 2 · y 1 6 x + 8 · y 1 2 .

Сократите дробь: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 , б) a 1 4 — b 1 4 a 1 2 — b 1 2 .

Решение

а) Используем наибольший общий знаменатель (НОД), на который можно сократить числитель и знаменатель. Для чисел 30 и 45 это 15 . Также мы можем произвести сокращение на x 0 , 5 + 1 и на x + 2 · x 1 1 3 — 5 3 .

30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 )

б) Здесь наличие одинаковых множителей неочевидно. Придется выполнить некоторые преобразования для того, чтобы получить одинаковые множители в числителе и знаменателе. Для этого разложим знаменатель, используя формулу разности квадратов:

a 1 4 — b 1 4 a 1 2 — b 1 2 = a 1 4 — b 1 4 a 1 4 2 — b 1 2 2 = = a 1 4 — b 1 4 a 1 4 + b 1 4 · a 1 4 — b 1 4 = 1 a 1 4 + b 1 4

Ответ: а) 30 · x 3 · ( x 0 , 5 + 1 ) · x + 2 · x 1 1 3 — 5 3 45 · x 0 , 5 + 1 2 · x + 2 · x 1 1 3 — 5 3 = 2 · x 3 3 · ( x 0 , 5 + 1 ) , б) a 1 4 — b 1 4 a 1 2 — b 1 2 = 1 a 1 4 + b 1 4 .

К числу основных действий с дробями относится приведение к новому знаменателю и сокращение дробей. Оба действия выполняют с соблюдением ряда правил. При сложении и вычитании дробей сначала дроби приводятся к общему знаменателю, после чего проводятся действия (сложение или вычитание) с числителями. Знаменатель остается прежним. Результатом наших действий является новая дробь, числитель которой является произведением числителей, а знаменатель есть произведение знаменателей.

Выполните действия x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 .

Решение

Начнем с вычитания дробей, которые располагаются в скобках. Приведем их к общему знаменателю:

x 1 2 — 1 · x 1 2 + 1

x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = = x 1 2 + 1 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 — x 1 2 — 1 · x 1 2 — 1 x 1 2 + 1 · x 1 2 — 1 · 1 x 1 2 = = x 1 2 + 1 2 — x 1 2 — 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = x 1 2 2 + 2 · x 1 2 + 1 — x 1 2 2 — 2 · x 1 2 + 1 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2

Теперь умножаем дроби:

4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · 1 x 1 2 = = 4 · x 1 2 x 1 2 — 1 · x 1 2 + 1 · x 1 2

Произведем сокращение на степень x 1 2 , получим 4 x 1 2 — 1 · x 1 2 + 1 .

Дополнительно можно упростить степенное выражение в знаменателе, используя формулу разности квадратов: квадратов: 4 x 1 2 — 1 · x 1 2 + 1 = 4 x 1 2 2 — 1 2 = 4 x — 1 .

Ответ: x 1 2 + 1 x 1 2 — 1 — x 1 2 — 1 x 1 2 + 1 · 1 x 1 2 = 4 x — 1

Упростите степенное выражение x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 .
Решение

Мы можем произвести сокращение дроби на ( x 2 , 7 + 1 ) 2 . Получаем дробь x 3 4 x — 5 8 · x 2 , 7 + 1 .

Продолжим преобразования степеней икса x 3 4 x — 5 8 · 1 x 2 , 7 + 1 . Теперь можно использовать свойство деления степеней с одинаковыми основаниями: x 3 4 x — 5 8 · 1 x 2 , 7 + 1 = x 3 4 — — 5 8 · 1 x 2 , 7 + 1 = x 1 1 8 · 1 x 2 , 7 + 1 .

Переходим от последнего произведения к дроби x 1 3 8 x 2 , 7 + 1 .

Ответ: x 3 4 · x 2 , 7 + 1 2 x — 5 8 · x 2 , 7 + 1 3 = x 1 3 8 x 2 , 7 + 1 .

Множители с отрицательными показателями степени в большинстве случаев удобнее переносить из числителя в знаменатель и обратно, изменяя знак показателя. Это действие позволяет упростить дальнейшее решение. Приведем пример: степенное выражение ( x + 1 ) — 0 , 2 3 · x — 1 можно заменить на x 3 · ( x + 1 ) 0 , 2 .

Преобразование выражений с корнями и степенями

В задачах встречаются степенные выражения, которые содержат не только степени с дробными показателями, но и корни. Такие выражения желательно привести только к корням или только к степеням. Переход к степеням предпочтительнее, так как с ними проще работать. Такой переход является особенно предпочтительным, когда ОДЗ переменных для исходного выражения позволяет заменить корни степенями без необходимости обращаться к модулю или разбивать ОДЗ на несколько промежутков.

Представьте выражение x 1 9 · x · x 3 6 в виде степени.

Решение

Область допустимых значений переменной x определяется двумя неравенствами x ≥ 0 и x · x 3 ≥ 0 , которые задают множество [ 0 , + ∞ ) .

На этом множестве мы имеем право перейти от корней к степеням:

x 1 9 · x · x 3 6 = x 1 9 · x · x 1 3 1 6

Используя свойства степеней, упростим полученное степенное выражение.

x 1 9 · x · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 3 1 6 = x 1 9 · x 1 6 · x 1 · 1 3 · 6 = = x 1 9 · x 1 6 · x 1 18 = x 1 9 + 1 6 + 1 18 = x 1 3

Ответ: x 1 9 · x · x 3 6 = x 1 3 .

Преобразование степеней с переменными в показателе

Данные преобразования достаточно просто произвести, если грамотно использовать свойства степени. Например, 5 2 · x + 1 − 3 · 5 x · 7 x − 14 · 7 2 · x − 1 = 0 .

Мы можем заменить произведением степени, в показателях которых находится сумма некоторой переменной и числа. В левой части это можно проделать с первым и последним слагаемыми левой части выражения:

5 2 · x · 5 1 − 3 · 5 x · 7 x − 14 · 7 2 · x · 7 − 1 = 0 , 5 · 5 2 · x − 3 · 5 x · 7 x − 2 · 7 2 · x = 0 .

Теперь поделим обе части равенства на 7 2 · x . Это выражение на ОДЗ переменной x принимает только положительные значения:

5 · 5 — 3 · 5 x · 7 x — 2 · 7 2 · x 7 2 · x = 0 7 2 · x , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 2 · x — 2 · 7 2 · x 7 2 · x = 0 , 5 · 5 2 · x 7 2 · x — 3 · 5 x · 7 x 7 x · 7 x — 2 · 7 2 · x 7 2 · x = 0

Сократим дроби со степенями, получим: 5 · 5 2 · x 7 2 · x — 3 · 5 x 7 x — 2 = 0 .

Наконец, отношение степеней с одинаковыми показателями заменяется степенями отношений, что приводит к уравнению 5 · 5 7 2 · x — 3 · 5 7 x — 2 = 0 , которое равносильно 5 · 5 7 x 2 — 3 · 5 7 x — 2 = 0 .

Введем новую переменную t = 5 7 x , что сводит решение исходного показательного уравнения к решению квадратного уравнения 5 · t 2 − 3 · t − 2 = 0 .

Преобразование выражений со степенями и логарифмами

Выражения, содержащие с записи степени и логарифмы, также встречаются в задачах. Примером таких выражений могут служить: 1 4 1 — 5 · log 2 3 или log 3 27 9 + 5 ( 1 — log 3 5 ) · log 5 3 . Преобразование подобных выражений проводится с использованием разобранных выше подходов и свойств логарифмов, которые мы подробно разобрали в теме «Преобразование логарифмических выражений».

Формулы степеней и корней.

Формулы степеней используют в процессе сокращения и упрощения сложных выражений, в решении уравнений и неравенств.

Число c является n-ной степенью числа a когда:

Операции со степенями.

1. Умножая степени с одинаковым основанием их показатели складываются:

2. В делении степеней с одинаковым основанием их показатели вычитаются:

3. Степень произведения 2-х либо большего числа множителей равняется произведению степеней этих сомножителей:

(abc…) n = a n · b n · c n …

4. Степень дроби равняется отношению степеней делимого и делителя:

5. Возводя степень в степень, показатели степеней перемножают:

Каждая вышеприведенная формула верна в направлениях слева направо и наоборот.

Операции с корнями.

1. Корень из произведения нескольких сомножителей равняется произведению корней из этих сомножителей:

2. Корень из отношения равен отношению делимого и делителя корней:

3. При возведении корня в степень довольно возвести в эту степень подкоренное число:

4. Если увеличить степень корня в n раз и в тоже время возвести в n-ую степень подкоренное число, то значение корня не поменяется:

5. Если уменьшить степень корня в n раз и в тоже время извлечь корень n-ой степени из подкоренного числа, то значение корня не поменяется:

Степень с отрицательным показателем. Степень некоторого числа с неположительным (целым) показателем определяют как единицу, деленную на степень того же числа с показателем, равным абсолютной величине неположительного показателя:

Формулу a m :a n =a m — n можно использовать не только при m > n , но и при m 4 :a 7 = a 4 — 7 = a -3 .

Чтобы формула a m :a n =a m — n стала справедливой при m=n, нужно присутствие нулевой степени.

Степень с нулевым показателем. Степень всякого числа, не равного нулю, с нулевым показателем равняется единице.

Степень с дробным показателем. Чтобы возвести действительное число а в степень m/n, необходимо извлечь корень n–ой степени из m-ой степени этого числа а:

Формулы степеней.

6. a — n = — деление степеней;

7. — деление степеней;

8. a 1/n = ;

источники:

http://zaochnik.com/spravochnik/matematika/vyrazhenija/stepennye-vyrazhenija/

http://www.calc.ru/Formuly-Stepeney-I-Korney.html

Источник

Грамотное преобразование рациональных выражений

3 августа 2015

Рациональные выражения и дроби — краеугольный пункт всего курса алгебры. Те, кто научатся работать с такими выражениями, упрощать их и раскладывать на множители, по сути смогут решить любую задачу, поскольку преобразование выражений — неотъемлемая часть любого серьёзного уравнения, неравенства и даже текстовой задачи.

В этом видеоуроке мы посмотрим, как грамотно применять формулы сокращённого умножения для упрощения рациональных выражений и дробей. Научимся видеть эти формулы там, где, на первый взгляд, ничего нет. Заодно повторим такой нехитрый приём, как разложение квадратного трёхчлена на множители через дискриминант.

Как вы уже наверняка догадались по формулам за моей спиной, сегодня мы будем изучать формулы сокращенного умножения, а, точнее, не сами формулы, а их применение для упрощения и сокращения сложных рациональных выражений. Но, прежде чем переходить к решению примеров, давайте познакомимся ближе с этими формулами или вспомним их:

${{a}^{2}}-{{b}^{2}}=left( a-b right)left( a+b right)$ — разность квадратов;
${{left( a+b right)}^{2}}={{a}^{2}}+2ab+{{b}^{2}}$ — квадрат суммы;
${{left( a-b right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}}$ — квадрат разности;
${{a}^{3}}+{{b}^{3}}=left( a+b right)left( {{a}^{2}}-ab+{{b}^{2}} right)$ — сумма кубов;
${{a}^{3}}-{{b}^{3}}=left( a-b right)left( {{a}^{2}}+ab+{{b}^{2}} right)$ — разность кубов.

Еще хотел бы отметить, что наша школьная система образования устроена таким образом, что именно с изучением этой темы, т.е. рациональных выражений, а также корней, модулей у всех учеников возникает одна и та же проблема, которую я сейчас объясню.

Дело в том, что в самом начале изучения формул сокращенного умножения и, соответственно, действий по сокращению дробей (это где-то 8 класс) учителя говорят что-то следующее: «Если вам что-то непонятно, то вы не переживайте, мы к этой теме еще вернемся неоднократно, в старших классах так точно. Мы это еще разберем». Ну а затем на рубеже 9-10 класса те же самые учителя объясняют тем же самым ученикам, которые так и не знают, как решать рациональные дроби, примерно следующее: «А где вы были предыдущие два года? Это же изучалось на алгебре в 8 классе! Чего тут может быть непонятного? Это же так очевидно!».

Однако обычным ученикам от таких объяснений нисколько не легче: у них как была каша в голове, так и осталась, поэтому прямо сейчас мы разберем два простых примера, на основании которых и посмотрим, каким образом в настоящих задачах выделять эти выражения, которые приведут нас к формулам сокращенного умножения и как потом применять это для преобразования сложных рациональных выражений.

Сокращение простых рациональных дробей

Задача № 1

[frac{4x+3{{y}^{2}}}{9{{y}^{4}}-16{{x}^{2}}}]

Первое, чему нам нужно научиться — выделять в исходных выражениях точные квадраты и более высокие степени, на основании которых мы сможем потом применять формулы. Давайте посмотрим:

[9{{y}^{4}}={{3}^{2}}cdot {{y}^{4}}={{3}^{2}}cdot {{left( {{y}^{2}} right)}^{2}}={{left( 3{{y}^{2}} right)}^{2}}]

[16{{x}^{2}}={{2}^{4}}cdot {{x}^{2}}={{left( {{2}^{2}} right)}^{2}}cdot {{x}^{2}}={{left( {{2}^{2}}cdot x right)}^{2}}={{left( 4{{x}^{2}} right)}^{2}}]

Перепишем наше выражение с учетом этих фактов:

[frac{4x+3{{y}^{2}}}{{{left( 3{{y}^{2}} right)}^{2}}-{{left( 4x right)}^{2}}}=frac{4x+3{{y}^{2}}}{left( 3{{y}^{2}}-4x right)left( 3{{y}^{2}}+4x right)}=frac{1}{3{{y}^{2}}-4x}]

Ответ: $frac{1}{3{{y}^{2}}-4x}$.

Задача № 2

Переходим ко второй задаче:

[frac{8}{{{x}^{2}}+5xy-6{{y}^{2}}}]

Упрощать тут нечего, потому что в числителе стоит константа, но я предложил эту задачу именно для того, чтобы вы научились раскладывать на множители многочлены, содержащие две переменных. Если бы вместо него был написанный ниже многочлен, как бы мы разложили его?

[{{x}^{2}}+5x-6=left( x-… right)left( x-… right)]

Давайте решим уравнение и найдем $x$, которые мы сможем поставить вместо точек:

[{{x}^{2}}+5x-6=0]

[D=25-4cdot left( -6 right)=25+24=49]

[sqrt{D}=7]

[{{x}_{1}}=frac{-5+7}{2}=frac{2}{2}=1]

[{{x}_{2}}=frac{-5-7}{2}=frac{-12}{2}=-6]

Мы можем переписать трехчлен следующим образом:

[{{x}^{2}}+5xy-6{{y}^{2}}=left( x-1 right)left( x+6 right)]

С квадратным трехчленом мы работать научились — для этого и нужно было записать этот видеоурок. А что делать, если кроме $x$ и константы присутствует еще $y$? Давайте рассмотрим их как еще одни элементы коэффициентов, т.е. перепишем наше выражение следующим образом:

[{{x}^{2}}+5ycdot x-6{{y}^{2}}]

[a=1;b=5y;c=-6{{y}^{2}}]

[D={{left( 5y right)}^{2}}-4cdot left( -6{{y}^{2}} right)=25{{y}^{2}}+24{{y}^{2}}=49{{y}^{2}}]

[sqrt{D}=7y]

[{{x}_{1}}=frac{-5y+7y}{2}=y]

[{{x}_{2}}=frac{-5y-7y}{2}=frac{-12y}{2}=-6y]

Запишем разложение нашей квадратной конструкции:

[left( x-y right)left( x+6y right)]

Итого если мы вернемся к исходному выражению и перепишем его с учетом изменений, то получим следующее:

[frac{8}{left( x-y right)left( x+6y right)}]

Что нам дает такая запись? Ничего, потому что его не сократить, оно ни на что не умножается и не делится. Однако как только эта дробь окажется составной частью более сложного выражения, подобное разложение окажется кстати. Поэтому как только вы видите квадратный трехчлен (неважно, отягощен он дополнительными параметрами или нет), всегда старайтесь разложить его на множители.

Нюансы решения

Запомните основные правила преобразования рациональных выражений:

Все знаменатели и числители необходимо раскладывать на множители либо через формулы сокращенного умножения, либо через дискриминант.
Работать нужно по такому алгоритму: когда мы смотрим и пытаемся выделить формулу сокращенного умножения, то, прежде всего, пытаемся все перевести в максимально возможную степень. После этого выносим за скобку общую степень.
Очень часто будут встречаться выражения с параметром: в качестве коэффициентов будут возникать другие переменные. Их мы находим по формуле квадратного разложения.

Таким образом, как только вы видите рациональные дроби, первое, что нужно сделать — это разложить и числитель, и знаменатель на множители (на линейные выражения), при этом мы используем формулы сокращенного умножения или дискриминант.

Давайте посмотрим на пару таких рациональных выражений и попробуем их разложить на множители.

Решение более сложных примеров

Задача № 1

[frac{4{{x}^{2}}-6xy+9{{y}^{2}}}{2x-3y}cdot frac{9{{y}^{2}}-4{{x}^{2}}}{8{{x}^{3}}+27{{y}^{3}}}]

Переписываем и стараемся разложить каждое слагаемое:

[4{{x}^{2}}={{2}^{2}}cdot {{x}^{2}}={{left( 2x right)}^{2}}]

[6xy=2cdot 3cdot xcdot y=2xcdot 3y]

[9{{y}^{2}}={{3}^{2}}cdot {{y}^{2}}={{left( 3y right)}^{2}}]

[8{{x}^{3}}={{2}^{3}}cdot {{x}^{3}}={{left( 2x right)}^{3}}]

[27{{y}^{3}}={{3}^{3}}cdot {{y}^{3}}={{left( 3y right)}^{3}}]

Давайте перепишем все наше рациональное выражение с учетом этих фактов:

[frac{{{left( 2x right)}^{2}}-2xcdot 3y+{{left( 3y right)}^{2}}}{2x-3y}cdot frac{{{left( 3y right)}^{2}}-{{left( 2x right)}^{2}}}{{{left( 2x right)}^{3}}+{{left( 3y right)}^{3}}}=]

[=frac{{{left( 2x right)}^{2}}-2xcdot 3y+{{left( 3y right)}^{2}}}{2x-3y}cdot frac{left( 3y-2x right)left( 3y+2x right)}{left( 2x+3y right)left( {{left( 2x right)}^{2}}-2xcdot 3y+{{left( 3y right)}^{2}} right)}=-1]

Ответ: $-1$.

Задача № 2

[frac{3-6x}{2{{x}^{2}}+4x+8}cdot frac{2x+1}{{{x}^{2}}+4-4x}cdot frac{8-{{x}^{3}}}{4{{x}^{2}}-1}]

Давайте рассмотрим все дроби.

Первая:

[3-6x=3left( 1-2x right)]

[2{{x}^{2}}+4x+8=2left( {{x}^{2}}+2x+{{2}^{2}} right)]

Вторая:

[{{x}^{2}}+4-4x={{x}^{2}}-4x+2={{x}^{2}}-2cdot 2x+{{2}^{2}}={{left( x-2 right)}^{2}}]

Третья:

[8-{{x}^{3}}={{2}^{3}}-{{x}^{3}}=left( 2-x right)left( {{2}^{2}}+2x+{{x}^{2}} right)]

[4{{x}^{2}}-1={{2}^{2}}cdot {{x}^{2}}-{{1}^{2}}={{left( 2x right)}^{2}}-{{1}^{2}}=left( 2x-1 right)left( 2x+1 right)]

Перепишем всю конструкцию с учетом изменений:

[frac{3left( 1-2x right)}{2left( {{x}^{2}}+2x+{{2}^{2}} right)}cdot frac{2x+1}{{{left( x-2 right)}^{2}}}cdot frac{left( 2-x right)left( {{2}^{2}}+2x+{{x}^{2}} right)}{left( 2x-1 right)left( 2x+1 right)}=]

[=frac{3cdot left( -1 right)}{2cdot left( x-2 right)cdot left( -1 right)}=frac{3}{2left( x-2 right)}]

Ответ: $frac{3}{2left( x-2 right)}$.

Нюансы решения

Итак, чему мы только что научились:

Далеко не каждый квадратный трехчлен раскладывается на множители, в частности, это относится к неполному квадрату суммы или разности, которые очень часто встречаются как части кубов суммы или разности.
Константы, т.е. обычные числа, не имеющие при себе переменных, также могут выступать активными элементами в процессе разложения. Во-первых, их можно выносить за скобки, во-вторых, сами константы могут быть представимы в виде степеней.
Очень часто после разложения всех элементов на множители возникают противоположные конструкции. Сокращать эти дроби нужно крайне аккуратно, потому что при из зачеркивании либо сверху, либо снизу возникает дополнительный множитель $-1$ — это как раз и есть следствие того, что они противоположны.

Решение сложных задач

[frac{27{{a}^{3}}-64{{b}^{3}}}{{{b}^{2}}-4}:frac{9{{a}^{2}}+12ab+16{{b}^{2}}}{{{b}^{2}}+4b+4}]

Рассмотрим каждое слагаемое отдельно.

Первая дробь:

[27{{a}^{3}}={{3}^{3}}cdot {{a}^{3}}={{left( 3a right)}^{3}}]

[64{{b}^{3}}={{2}^{6}}cdot {{b}^{3}}={{left( {{2}^{2}} right)}^{3}}cdot {{b}^{3}}={{left( {{2}^{2}}cdot b right)}^{3}}={{left( 4b right)}^{3}}]

[{{left( 3a right)}^{3}}-{{left( 4b right)}^{3}}=left( 3a-4b right)left( {{left( 3a right)}^{2}}+3acdot 4b+{{left( 4b right)}^{2}} right)]

[{{b}^{2}}-{{2}^{2}}=left( b-2 right)left( b+2 right)]

Вторая:

[9{{a}^{2}}={{3}^{2}}cdot {{a}^{2}}={{left( 3a right)}^{2}}]

[16{{b}^{2}}={{4}^{2}}cdot {{b}^{2}}={{left( 4b right)}^{2}}]

[12ab=3cdot 4ab=3acdot 4b]

Весь числитель второй дроби мы можем переписать следующим образом:

[{{left( 3a right)}^{2}}+3acdot 4b+{{left( 4b right)}^{2}}]

Теперь посмотрим на знаменатель:

[{{b}^{2}}+4b+4={{b}^{2}}+2cdot 2b+{{2}^{2}}={{left( b+2 right)}^{2}}]

Давайте перепишем все рациональное выражение с учетом вышеизложенных фактов:

[frac{left( 3a-4b right)left( {{left( 3a right)}^{2}}+3acdot 4b+{{left( 4b right)}^{2}} right)}{left( b-2 right)left( b+2 right)}cdot frac{{{left( b+2 right)}^{2}}}{{{left( 3a right)}^{2}}+3acdot 4b+{{left( 4b right)}^{2}}}=]

[=frac{left( 3a-4b right)left( b+2 right)}{left( b-2 right)}]

Ответ: $frac{left( 3a-4b right)left( b+2 right)}{left( b-2 right)}$.

Нюансы решения

Как мы еще раз убедились, неполные квадраты суммы либо неполные квадраты разности, которые часто встречаются в реальных рациональных выражениях, однако не стоит их пугаться, потому что после преобразования каждого элемента они практически всегда сокращаются. Кроме того, ни в коем случае не стоит бояться больших конструкций в итогом ответе — вполне возможно, что это не ваша ошибка (особенно, если все разложено на множители), а это автор задумал такой ответ.

В заключение хотелось бы разобрать еще один сложных пример, который уже не относится напрямую к рациональным дробям, однако он содержит все то, что ждет вас на настоящих контрольных и экзаменах, а именно: разложение на множители, приведение к общему знаменателю, сокращение подобных слагаемых. Вот именно этим мы сейчас и займемся.

Решение сложной задачи на упрощение и преобразование рациональных выражений

[left( frac{x}{{{x}^{2}}+2x+4}+frac{{{x}^{2}}+8}{{{x}^{3}}-8}-frac{1}{x-2} right)cdot left( frac{{{x}^{2}}}{{{x}^{2}}-4}-frac{2}{2-x} right)]

Сначала рассмотрим и раскроем первую скобку: в ней мы видим три отдельных дроби с разными знаменателями поэтому первое, что нам необходимо сделать — это привести все три дроби к общему знаменателю, а для этого каждый из них следует разложить на множители:

[{{x}^{2}}+2x+4={{x}^{2}}+2cdot x+{{2}^{2}}]

[{{x}^{2}}-8={{x}^{3}}-{{2}^{2}}=left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)]

Перепишем всю нашу конструкцию следующим образом:

[frac{x}{{{x}^{2}}+2x+{{2}^{2}}}+frac{{{x}^{2}}+8}{left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)}-frac{1}{x-2}=]

[=frac{xleft( x-2 right)+{{x}^{3}}+8-left( {{x}^{2}}+2x+{{2}^{2}} right)}{left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)}=]

[=frac{{{x}^{2}}-2x+{{x}^{2}}+8-{{x}^{2}}-2x-4}{left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)}=frac{{{x}^{2}}-4x-4}{left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)}=]

[=frac{{{left( x-2 right)}^{2}}}{left( x-2 right)left( {{x}^{2}}+2x+{{2}^{2}} right)}=frac{x-2}{{{x}^{2}}+2x+4}]

Это результат вычислений из первой скобки.

Разбираемся со второй скобкой:

[{{x}^{2}}-4={{x}^{2}}-{{2}^{2}}=left( x-2 right)left( x+2 right)]

Перепишем вторую скобку с учетом изменений:

[frac{{{x}^{2}}}{left( x-2 right)left( x+2 right)}+frac{2}{x-2}=frac{{{x}^{2}}+2left( x+2 right)}{left( x-2 right)left( x+2 right)}=frac{{{x}^{2}}+2x+4}{left( x-2 right)left( x+2 right)}]

Теперь запишем всю исходную конструкцию:

[frac{x-2}{{{x}^{2}}+2x+4}cdot frac{{{x}^{2}}+2x+4}{left( x-2 right)left( x+2 right)}=frac{1}{x+2}]

Ответ: $frac{1}{x+2}$.

Нюансы решения

Как видите, ответ получился вполне вменяемый. Однако обратите внимание: очень часто при таких масштабных вычислениях, когда единственная переменная оказывается лишь в знаменателе, ученики забывают, что это знаменатель и он должен стоял внизу дроби и пишут это выражение в числитель — это грубейшая ошибка.

Кроме того, хотел бы обратить ваше отдельное внимание на то, как оформляются такие задачи. В любых сложных вычислениях все шаги выполняются по действиям: сначала отдельно считаем первую скобку, потом отдельно вторую и лишь в конце мы объединяем все части и считаем результат. Таким образом мы страхуем себя от глупых ошибок, аккуратно записываем все выкладки и при этом нисколько не тратим лишнего времени, как это может показаться на первый взгляд.

До новых встреч!

Смотрите также:

Как выполнять сокращение рациональных дробей без ошибок? Простой алгоритм на примере пяти различных задач.
Дробно-рациональные выражения
Тест к уроку «Десятичные дроби» (2 вариант)
Периодические десятичные дроби
Быстрое возведение чисел в квадрат без калькулятора
ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Источник

В9 Алгебраические
дроби Демо вариант

1. Найдите значение выражения $frac{{{(5a^2)}^{3}}cdot {{(6b)}^{2}}}{{{(30a^3b)}^{2}}}$ .

2.
Найдите
значение выражения $frac{{{(11a)}^{2}}-11a}{11a^2-a}$ .

3.
Найдите
значение выражения $frac{7{{(m^5)}^{6}}+11{{(m^3)}^{10}}}{{{(3{{m}^{15}})}^{2}}}$ .

4.
Найдите
значение выражения $frac{9x^2-4}{3x+2}-3x$ .

5.
Найдите
значение выражения $frac{{{(3x)}^{3}}cdot {{x}^{-9}}}{{{x}^{-10}}cdot 2x^4}$ .

6.
Найдите
значение выражения $frac{a^2{{b}^{-6}}}{{{(4a)}^{3}}{{b}^{-2}}}cdot frac{16}{{{a}^{-1}}{{b}^{-4}}}$ .

7.
Найдите
значение выражения $(4a^2-9)cdot (frac{1}{2a-3}-frac{1}{2a+3})$ .

8.
Найдите $frac{p(b)}{p(frac{1}{b})}$ ,
если $p(b)=(b+frac{3}{b})(3b+frac{1}{b})$ .
При .

9.
Найдите ,
если $p(x)=frac{x(6-x)}{x-3}$ при .

10. Найдите $frac{a}{b}$ ,
если $frac{2a+5b}{5a+2b}=1$ .

11. Найдите , если $frac{2a-7b+5}{7a-2b+5}=9$

12. Найдите $frac{a+9b+16}{a+3b+8}$ ,
если $frac{a}{b}=3$ .

13. Найдите значение выражения $(4x^2+y^2-{{(2x-y)}^{2}}):2xy$

14. Найдите значение выражения $({{(3x+2y)}^{2}}-9x^2-4y^2):6xy$ .

15. Найдите значение выражения $({{(4x-3y)}^{2}}-{{(4x+3y)}^{2}}):4xy$ .

16. Найдите значение выражения .

17. Найдите значение выражения .

18. Найдите значение выражения $({{(2x^3)}^{4}}-{{(x^2)}^{6}}):3{{x}^{12}}$ .

19. Найдите значение выражения $18x^7cdot {{x}^{13}}:{{(3{{x}^{10}})}^{2}}$ .

20. Найдите значение выражения ${{(7x^3)}^{2}}:(7x^6)$ .

21. Найдите значение выражения ${{(4a)}^{3}}:a^7cdot a^4$ .

22. Найдите значение выражения $(11a^6cdot b^3-{{(3a^2b)}^{3}}):(4a^6b^6)$ при .

23. Найдите значение выражения ,
если .

24. Найдите значение выражения ,
если , .

25. Найдите значение выражения ,
если .

26. Найдите значение выражения ,
если .

27. Найдите ,
если

28. Найдите ,
если .

29. Найдите
значение выражения при .

30.
Найдите значение выражения $a(36a^2-25)(frac{1}{6a+5}-frac{1}{6a-5})$ при

31. Найдите
значение выражения $(9b^2-49)(frac{1}{3b-7}-frac{1}{3b+7})+b-13$ при .

В9
Преобразование алгебраических дробей вариант №1

$frac{{{(4a^2)}^{3}}cdot {{(5b)}^{2}}}{{{(20a^3b)}^{2}}}$
$frac{{{(11a)}^{2}}-11a}{11a^2-a}$ .
$frac{5{{(m^{4)}}^{3}}+3{{(m^{3})}^{4}}}{{{(2{{m}^{6}})}^{2}}}$ .
$frac{9x^2-64}{3x -8}-3x$ .
$frac{{{(5x)}^{3}}cdot {{x}^{2}}}{{{x}^{4}}cdot 10x}$ .
$frac{a^{-5}{{b}^{-7}}}{{{(3a)}^{2}}{{b}^{-3}}}cdot frac{27}{{{a}^{-7}}{{b}^{-4}}}$ .
$(49a^2-64)cdot (frac{1}{7a -8}-frac{1}{7a +8})$ .
Найдите $frac{p(b)}{p(frac{1}{b})}$ , если $p(b)=(b-frac{1}{b})(-1b+frac{1}{b})$ . при .
Найдите , если $p(x)=frac{x(20-x)}{x -10}$ при .
Найдите $frac{a}{b}$ , если $frac{4a+8b}{4b+8a}=1$ .
Найдите , если $frac{5a-8b+3}{8a-5b+3}=-2$ .
Найдите $frac{a+b+4}{a+3b+8}$ , если $frac{a}{b}=1$ .
$(x^2+16y^2-{{(x +4y)}^{2}}):2xy$ .
$({{(x +4y)}^{2}}-x^2-16y^2):8xy$ .
$({{(3x -2y)}^{2}}-{{(3x +2y)}^{2}}):(-8xy)$ .
.
.
$({{(2x^{3})}^{4}}-{{(3x^{6})}^{2}}):7{{x}^{12}}$ .
$18x^{7}cdot {x^{5}}:{(3{{x}^{6}})^{2}}$ .
${{(5x^5)}^{2}}:50x^{10}$ .
${{(5a)}^{2}}:a^{8}cdot a^6$ .
$(17a^{12}cdot b^3-{{(3a^4b)}^{3}}):(10a^{12}b)$ при .

Найдите
значение выражения , если .
Найдите
значение выражения , если , .
Найдите
значение выражения , если .
Найдите
значение выражения , если .
Найдите , если .
Найдите , если .
Найдите
значение выражения: при .
Найдите
значение выражения $a(49a^2-36)(frac{1}{7a+6}-frac{1}{7a-6})$ при .
Найдите
значение выражения $(9b^2-25)(frac{1}{3b-5}-frac{1}{3b+5})-b -15$ при .

В9
Преобразование алгебраических дробей вариант №2

$frac{{{(3a^2)}^{3}}cdot {{(5b)}^{2}}}{{{(15a^3b)}^{2}}}$ .
$frac{{{(16a)}^{2}}-16a}{16a^2-a}$ .
$frac{7{{(m^{3)}}^{4}}+18{{(m^{4})}^{3}}}{{{(5{{m}^{6}})}^{2}}}$ .
$frac{9x^2-16}{3x +4}-3x$ .
$frac{{{(4x)}^{2}}cdot {{x}^{5}}}{{{x}^{4}}cdot 5x^3}$ .
$frac{a^{-1}{{b}^{9}}}{{{(4a)}^{2}}{{b}^{5}}}cdot frac{16}{{{a}^{-3}}{{b}^{4}}}$ .
$(9a^2-49)cdot (frac{1}{3a +7}-frac{1}{3a -7})$ .
Найдите $frac{p(b)}{p(frac{1}{b})}$ , если $p(b)=(b-frac{7}{b})(-7b+frac{1}{b})$ . при .
Найдите , если $p(x)=frac{x(14-x)}{x -7}$ при .
Найдите $frac{a}{b}$ , если $frac{5a+9b}{5b+9a}=-3$ .
Найдите , если $frac{8a-9b+5}{9a-8b+5}=6$ .
Найдите $frac{a+7b+30}{a+2b+15}$ , если $frac{a}{b}=3$ .
$(25x^2+9y^2-{{(5x +3y)}^{2}}):2xy$ .
$({{(3x -5y)}^{2}}-9x^2-25y^2):(-15xy)$ .
$({{(3x +y)}^{2}}-{{(3x -y)}^{2}}):3xy$ .
.
.
$({{(2x^{2})}^{6}}-{{(5x^{4})}^{3}}):61{{x}^{12}}$ .
$18xcdot {x^{7}}:{(3{{x}^{4}})^{2}}$ .
${{(2x^3)}^{2}}:2x^{6}$ .
${{(3a)}^{4}}:a^{7}cdot a^3$ .
$(11a^{24}cdot b^6-{{(2a^4b)}^{6}}):(a^{24}b)$ при .

Найдите
значение выражения , если .
Найдите
значение выражения , если , .
Найдите
значение выражения , если .
Найдите
значение выражения , если .
Найдите , если .
Найдите , если .
Найдите
значение выражения: при .
Найдите
значение выражения $a(25a^2-81)(frac{1}{5a+9}-frac{1}{5a-9})$ при .
Найдите
значение выражения $(9b^2-16)(frac{1}{3b-4}-frac{1}{3b+4})-b +14$ при .

В9
Преобразование алгебраических дробей вариант №3

$frac{{{(5a^2)}^{3}}cdot {{(4b)}^{2}}}{{{(20a^3b)}^{2}}}$ .
$frac{{{(8a)}^{2}}+8a}{8a^2+a}$ .
$frac{17{{(m^{4)}}^{6}}+7{{(m^{8})}^{3}}}{{{(4{{m}^{12}})}^{2}}}$ .
$frac{x^2-9}{x +3}-x$ .
$frac{{{(2x)}^{4}}cdot {{x}^{-2}}}{{{x}^{5}}cdot 2x^-3}$ .
$frac{a^{-1}{{b}^{7}}}{{{(2a)}^{2}}{{b}^{4}}}cdot frac{6}{{{a}^{-3}}{{b}^{3}}}$ .
$(16a^2-1)cdot (frac{1}{4a +1}-frac{1}{4a -1})$ .
Найдите $frac{p(b)}{p(frac{1}{b})}$ , если $p(b)=(b+frac{4}{b})(4b+frac{1}{b})$ .
При .
Найдите , если $p(x)=frac{x(12-x)}{x -6}$ при .
Найдите $frac{a}{b}$ , если $frac{a+5b}{b+5a}=-1$ .
Найдите , если $frac{a-8b+1}{8a-b+1}=-4$ .
Найдите $frac{a+4b+12}{a+b+6}$ , если $frac{a}{b}=2$ .
Найдите значение выражения $(16x^2+9y^2-{{(4x -3y)}^{2}}):(-6xy)$ .
$({{(3x -5y)}^{2}}-9x^2-25y^2):6xy$ .
$({{(5x +2y)}^{2}}-{{(5x -2y)}^{2}}):2xy$ .
.
.
$({{(2x^{3})}^{6}}-{{(5x^{9})}^{2}}):13{{x}^{18}}$ .
$81x^{8}cdot {x^{10}}:{(3{{x}^{6}})^{3}}$ .
${{(4x^2)}^{2}}:2x^{4}$ .
${{(2a)}^{2}}:a^{3}cdot a$ .
$(15a^{9}cdot b^3-{{(6a^3b)}^{3}}):(3a^{9}b^3)$ при .

Найдите значение выражения , если .
Найдите значение выражения , если , .
Найдите значение выражения , если .
Найдите значение выражения , если .
Найдите , если .
Найдите , если .
Найдите значение выражения: при .
Найдите значение выражения $a(49a^2-81)(frac{1}{7a+9}-frac{1}{7a-9})$ при .
Найдите значение выражения $(25b^2-49)(frac{1}{5b-7}-frac{1}{5b+7})-2b -13$ при .

В9 Преобразование алгебраических дробей

	1 вариант	2 вариант	3 вариант
1.	4	3	5
2.	11	16	8
3.	2	1	1,5
4.	8	-4	-3
5.	12,5	3,2	8
6.	3	1	1,5
7.	16	-14	-2
8.	1	1	1
9.	0	0	0
10.	1	-1,8	-1
11.	-14	-46	-2
12.	0,5	2	2
13.	-4	-15	-4
14.	1	2	-5
15.	3	4	20
16.	-1	-1,6	-25
17.	3	1	2
18.	1	-1	3
19.	2	2	3
20.	0,5	2	8
21.	25	81	4
22.	-4	-53	-67
23.	-32	-70	-20
24.	6	12	12
25.	56	60	84
26.	84	-4	-60
27.	0	14	-16
28.	-9	-62	14
29.	97	174	-645
30.	421,2	-226,8	-513
31.	-88	-288	-123

Источник

Сократите дробь: $frac{x^3+2x^2-9x-18}{(x-3)(x+2) }$ .

Решение задачи

Данный урок демонстрирует решение задачи, которое можно с успехом использовать при подготовке к ОГЭ при решении задач типа ОГЭ 7. По условию необходимо выполнить сокращение дроби с одной неизвестной.

Для начала числитель раскладывается на множители: слагаемые группируются скобками, а далее выносятся общие множители и в первой, и во второй скобках. Полученное выражение состоит из двух слагаемых, в каждом из которых присутствует общий множитель, который и выносится за скобку. Затем применяется основное свойство дроби: если числитель и знаменатель дроби умножить или разделить на одно и то же число, не равное нулю, то получится дробь, равная данной. Согласно этому свойству в дроби сокращается общий множитель. Далее, применяя формулу разности квадратов, преобразовывается числитель. Сокращение образовавшегося в результате преобразования общего множителя и приводит к окончательному ответу.

Источник

Определение

Сокращение алгебраических дробей

Сокращение алгебраических дробей с многочленами

Вынесение общего множителя при сокращении дробей

Сокращение дробей. Формулы сокращенного умножения

Как сокращать алгебраические дроби?

Определение

Сокращение алгебраических дробей

Сокращение алгебраических дробей с многочленами

Вынесение общего множителя при сокращении дробей

Сокращение дробей. Формулы сокращенного умножения

Степенные выражения (выражения со степенями) и их преобразование

Что представляют собой степенные выражения?

Основные виды преобразований степенных выражений

Работа с основанием и показателем степени

Использование свойств степеней

Преобразование дробей, содержащих степени

Преобразование выражений с корнями и степенями

Преобразование степеней с переменными в показателе

Преобразование выражений со степенями и логарифмами

Формулы степеней и корней.

Формулы степеней.

Грамотное преобразование рациональных выражений

Сокращение простых рациональных дробей

Задача № 1

Задача № 2

Нюансы решения

Решение более сложных примеров

Задача № 1

Задача № 2

Нюансы решения

Решение сложных задач

Нюансы решения

Решение сложной задачи на упрощение и преобразование рациональных выражений

Нюансы решения

Решение задачи

Новое и интересное на сайте: