Сравнение чисел в различных системах счисления егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Автор материалов — Лада Борисовна Есакова.

Системы счисления и их разновидности.

Система счисления – это способ представления, записи чисел с помощью письменных знаков. Количество этих самых знаков (цифр), используемых для записи чисел, называется основанием системы счисления.

Различных систем счисления у разных народов существовало великое множество. Но все их можно поделить на непозиционные и позиционные. Позиционные системы в свою очередь подразделяются на однородные и смешанные.

1. Непозиционные системы счисления.

В непозиционных системах счисления число, обозначаемое цифрой, не зависит от положения цифры в записи числа.

Самым простым примером непозиционной системы счисления является единичная (унарная) система счисления. Это запись числа с помощью повторения зарубок на дощечке или узелков на веревке. Все зарубки, узелки или другие «цифры» абсолютно одинаковы, а потому их порядок не имеет значения, число получается простым суммированием количества символов.

Унарной системой счисления до сих пор пользуются маленькие дети, показывая количество на пальцах.

Еще одной используемой до сих пор почти непозиционной системой счисления является Римская:

Она названа почти непозиционной, потому что в Римской системе, кроме обычного сложения цифр в числе, действует правило: если младшая цифра стоит слева от старшей, она вычитается из суммы.
Т.е. число , а число

Непозиционных систем счисления известно очень много, но мы завершим на этом их рассмотрение. Использование непозиционных систем неудобно, а для очень больших чисел практически невозможно, и к тому же нет возможности записать дроби.

2. Позиционные системы счисления.

В позиционных системах счисления число, обозначаемое цифрой, зависит от положения цифры в записи числа.
Самой популярной позиционной системой является, конечно же, десятичная.

Мы видим, что числа 15 и 51 имеют совсем разные значения, хотя состоят из одних и тех же цифр. Разница обусловлена положением цифры в числе.

Но десятичная система ничем не лучше и не хуже другой позиционной системы, она просто привычная. Число 10 выбрано основанием по количеству пальцев на двух руках (для удобства счета). Однако, в Китае популярной была пятиречная система счисления (по количеству пальцев на одной руке), а двадцатиричная система использовалась у Ацтеков, Майя и некоторых народов Африки (по количеству пальцев на ногах и руках).

Еще одной известной позиционной системой счисления является двенадцатиричная (считали фаланги пальцев (кроме большого) на руке. Элементы двенадцатиричной системы сохранились в Англии: 1 фут = 12 дюймов, 1 шиллинг = 12 пенсов.

Ну и, наконец, незаменимая в наш компьютерный век двоичная система. Почему именно двоичная? Да потому что у компьютера только 2 «пальца», точнее два состояния: «есть ток», «нет тока».

2.1. Однородные системы счисления.

В однородной системе в каждой позиции числа может находиться любая цифра. Примером может быть запись числа в любой позиционной системе счисления (десятичной, двоичной и пр.). Т.е. когда мы пишем число в десятичной системе, в любой позиции мы можем написать цифру от 0 до 9.

2.2. Смешанные системы счисления.

В смешанной системе счисления набор используемых цифр может отличаться в зависимости от позиции. В качестве примера удобно рассмотреть запись времени в формате ЧЧ.ММ.СС (часы.минуты.секунды). В качестве часов может быть использовано число от 00 до 23, в качестве минут и секунд – число от 00 до 59.

Системы счисления. Перевод из одной системы в другую.

1. Порядковый счет в различных системах счисления.

В современной жизни мы используем позиционные системы счисления, то есть системы, в которых число, обозначаемое цифрой, зависит от положения цифры в записи числа. Поэтому в дальнейшем мы будем говорить только о них, опуская термин «позиционные».

Для того чтобы научиться переводить числа из одной системы в другую, поймем, как происходит последовательная запись чисел на примере десятичной системы.

Поскольку у нас десятичная система счисления, мы имеем 10 символов (цифр) для построения чисел. Начинаем порядковый счет: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Цифры закончились. Мы увеличиваем разрядность числа и обнуляем младший разряд: 10. Затем опять увеличиваем младший разряд, пока не закончатся все цифры: 11, 12, 13, 14, 15, 16, 17, 18, 19. Увеличиваем старший разряд на 1 и обнуляем младший: 20. Когда мы используем все цифры для обоих разрядов (получим число 99), опять увеличиваем разрядность числа и обнуляем имеющиеся разряды: 100. И так далее.

Попробуем сделать то же самое в 2-ной, 3-ной и 5-ной системах (введем обозначение для 2-ной системы, для 3-ной и т.д.):

0	0	0	0
1	1	1	1
2	10	2	2
3	11	10	3
4	100	11	4
5	101	12	10
6	110	20	11
7	111	21	12
8	1000	22	13
9	1001	100	14
10	1010	101	20
11	1011	102	21
12	1100	110	22
13	1101	111	23
14	1110	112	24
15	1111	120	30

Если система счисления имеет основание больше 10, то нам придется вводить дополнительные символы, принято вводить буквы латинского алфавита. Например, для 12-ричной системы кроме десяти цифр нам понадобятся две буквы ( и ):

0	0
1	1
2	2
3	3
4	4
5	5
6	6
7	7
8	8
9	9
10
11
12	10
13	11
14	12
15	13

2.Перевод из десятичной системы счисления в любую другую.

Чтобы перевести целое положительное десятичное число в систему счисления с другим основанием, нужно это число разделить на основание. Полученное частное снова разделить на основание, и дальше до тех пор, пока частное не окажется меньше основания. В результате записать в одну строку последнее частное и все остатки, начиная с последнего.

Пример 1. Переведем десятичное число 46 в двоичную систему счисления.

Пример 2. Переведем десятичное число 672 в восьмеричную систему счисления.

Пример 3. Переведем десятичное число 934 в шестнадцатеричную систему счисления.

3. Перевод из любой системы счисления в десятичную.

Для того, чтобы научиться переводить числа из любой другой системы в десятичную, проанализируем привычную нам запись десятичного числа.
Например, десятичное число 325 – это 5 единиц, 2 десятка и 3 сотни, т.е.

Точно так же обстоит дело и в других системах счисления, только умножать будем не на 10, 100 и пр., а на степени основания системы счисления. Для примера возьмем число 1201 в троичной системе счисления. Пронумеруем разряды справа налево начиная с нуля и представим наше число как сумму произведений цифры на тройку в степени разряда числа:

Это и есть десятичная запись нашего числа, т.е.

Пример 4. Переведем в десятичную систему счисления восьмеричное число 511.

Пример 5. Переведем в десятичную систему счисления шестнадцатеричное число 1151.

4. Перевод из двоичной системы в систему с основанием «степень двойки» (4, 8, 16 и т.д.).

Для преобразования двоичного числа в число с основанием «степень двойки» необходимо двоичную последовательность разбить на группы по количеству цифр равному степени справа налево и каждую группу заменить соответствующей цифрой новой системы счисления.

Например, Переведем двоичное 1100001111010110 число в восьмеричную систему. Для этого разобьем его на группы по 3 символа начиная справа (т.к. ), а затем воспользуемся таблицей соответствия и заменим каждую группу на новую цифру:

Таблицу соответствия мы научились строить в п.1.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7

Т.е.

Пример 6. Переведем двоичное 1100001111010110 число в шестнадцатеричную систему.

0	0
1	1
10	2
11	3
100	4
101	5
110	6
111	7
1000	8
1001	9
1010	A
1011	B
1100	C
1101	D
1110	E
1111	F

5.Перевод из системы с основанием «степень двойки» (4, 8, 16 и т.д.) в двоичную.

Этот перевод аналогичен предыдущему, выполненному в обратную сторону: каждую цифру мы заменяем группой цифр в двоичной системе из таблицы соответствия.

Пример 7. Переведем шестнадцатеричное число С3A6 в двоичную систему счисления.

Для этого каждую цифру числа заменим группой из 4 цифр (т.к. ) из таблицы соответствия, дополнив при необходимости группу нулями вначале:

Десятичные дроби и смешанные числа в разных системах счисления.

Автор — Лада Борисовна Есакова.

Перевод целых чисел из одной системы счисления в другую обычно не вызывает проблем. А вот необходимость перевести десятичную дробь или смешанное число (число с целой и дробной частью) из системы в систему часто ставит в тупик даже сильных учеников.

1. Перевод смешанного числа в десятичную систему счисления из любой другой.

Для перевода смешанного числа в десятичную систему из любой другой следует пронумеровать разряды числа, начиная с нуля, справа налево от младшего целого разряда. Разряды дробной части нумеруются слева направо от -1 в убывающем порядке. Теперь представим число в виде суммы произведений его цифр на основание системы в степени разряда числа и ответ готов.

Пример 1.

Переведите число 105,4 из восьмеричной системы в десятичную.

Решение:

Пронумеруем целые разряды числа справа налево от 0, дробные – слева направо от -1 :

Посчитаем сумму произведений цифр числа на 8 (основание системы) в степени разряда числа:

Ответ:

2. Перевод десятичных дробей из десятичной системы счисления в любую другую.

Для перевода десятичной дроби из десятичной системы в любую другую следует умножать дробь, а затем дробные части произведений, на основание новой системы пока дробная часть не станет равной 0 или до достижения указанной точности. Затем целые части выписать, начиная с первой.

Пример 2

Переведите десятичное число 0,816 в двоичную систему с точностью до сотых.

Решение:

Умножаем дробь 0,816, а затем дробную часть произведения (0,632) на 2 и выписываем целые части, начиная с первой:

Ответ:

Пример 3.

Переведите десятичное число 0,8125 в восьмеричную систему.

Решение:

Умножаем дробь 0,8125, а затем дробную часть произведения (0,5) на 8 и выписываем целые части, начиная с первой:

Ответ:

3. Перевод смешанных чисел из десятичной системы счисления в любую другую

Если необходимо перевести смешанное число из десятичной системы в любую другую, следует перевести целую и дробную части, а затем записать, разделив десятичной запятой.

Пример 4.

Сколько единиц в двоичной записи десятичного числа 14,125?

Решение:

Переведем целую часть числа в двоичную систему:

Переведем дробную часть числа в двоичную систему:

Соединим целую и дробную части:

14,12510 = 1110,0012

Количество единиц равно 4.

Ответ: 4

Сравнение чисел в различных системах счисления.

Системы счисление:

• Двоичная

• Восьмеричная

• Десятичная

• Шестнадцатеричная

Двоичные числа – каждая цифра обозначает значение одного бита (0 или 1), старший бит всегда пишется слева, индекс обозначает основание системы счисления. Например, .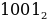

В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7).

Десятичные числа – наиболее привычные для обычного человека в повседневной жизни (от 0 до 9). Обозначаются индексом 10. Например, .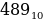

Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными. В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F.

Для того чтобы сравнить числа в различных системах счисления, необходимо выполнить перевод из различных систем счисления в десятичную.
Для перевода чисел в десятичную систему счисления выполняют развернутую запись исходного числа.

• Перевод из двоичной в десятичную.

В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.

В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:

5476 = 5000 + 400 + 70 + 6

Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:

5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100

После равенства числа 5, 4, 7 и 6 – это набор цифр, из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10. Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.

Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после «равно» запись идет в десятичной:

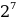
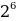
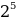
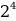
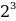
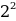
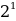
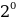
10001001 = 1 *  + 0 *  + 0 *  + 0 *  + 1 * + 0 * + 0 * + 1 *

Результат вычислений дает десятичное число, количественно равное двоичному 10001001:

1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137

То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:

 =

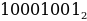
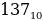
• Перевод из восьмеричной в двоичную.

Для преобразования двоичного числа в восьмеричное надо разбить его на тройки цифр и заменить каждую тройку соответствующей ей одной цифрой из восьмеричной системы счисления. Разбивать двоичное число на тройки следует с конца, а вместо недостающих цифр в начале можно записать нули.

1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135

В примере число 1011101 в двоичной системе приводится к числу 135 в восьмеричной системе счисления.

=

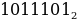
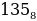
Как перевести восьмеричное число в десятичное? Здесь действует тот же алгоритм, как при преобразовании двоичного числа в десятичное. Однако в случае восьмеричного числа за основание степени берется десятичное число 8:

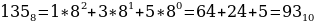
• Перевод из шестнадцатеричную в десятичную.

Перевод из шестнадцатеричной системы счисления в десятичную выполняется аналогично переводу из двоичной и восьмеричной. Только здесь в качестве основания степени выступает число 16, а цифры от A до F заменяются десятичными числами от 10 до 15.

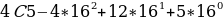
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи, – это число FF.

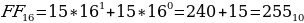
• Перевод из десятичной в двоичную

О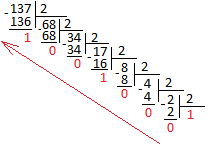 дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим «сбором» двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.

Получаем, что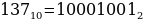

• Преобразование десятичного числа в восьмеричное также похоже на перевод в двоичное, за исключением того, что делить надо на 8

• Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же «алгоритм замещения», что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16

• Перевод двоичного в шестнадцатеричную

При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.

Пример:

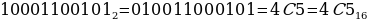
Теперь попробуем прорешать Задание №10 из ОГЭ

№ 10324

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

38₁₆, 75₈, 110100₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

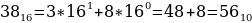
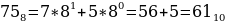
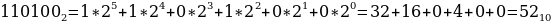
Таким образом, наибольшим среди этих трех чисел является чисто 61.

Ответ: 61.

 № 10325 

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

14₁₆, 26₈, 11000₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

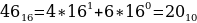
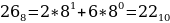
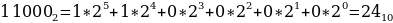
Таким образом, наибольшим среди этих трех чисел является чисто 24.

Ответ: 24.

№ 10329 

Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.

41₁₆, 77₈, 1000010₂.

Решение:

Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.

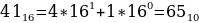
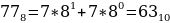
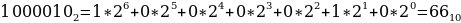
Таким образом, наименьшим среди этих трех чисел является чисто 63.

Ответ: 63.

№1. Ко­ли­че­ство зна­ча­щих нулей в дво­ич­ной
за­пи­си де­ся­тич­но­го числа 222 равно

1) 5

2) 2

3) 3

4) 4

По­яс­не­ние.

1. Пе­ре­ведём 222₁₀ в дво­ич­ную си­сте­му
счис­ле­ния. По­лу­чи­ли: 222₁₀ =11011110₂.

2. Под­счи­та­ем ко­ли­че­ство зна­ча­щих нулей: их 2.

№2. Для каж­до­го из пе­ре­чис­лен­ных ниже
чисел по­стро­и­ли дво­ич­ную за­пись. Ука­жи­те число, дво­ич­ная за­пись ко­то­ро­го
со­дер­жит ровно две еди­ни­цы. Если таких чисел не­сколь­ко, ука­жи­те наи­боль­шее
из них.

1) 8

2) 9

3) 10

4) 11

По­яс­не­ние.

Пред­ста­вим все числа в дво­ич­ной си­сте­ме счис­ле­ния:

8₁₀ = 1000₂,

9₁₀ = 1001₂,

10₁₀ = 1010₂,

11₁₀ = 1011₂.

Из чисел 9 и 10 вы­би­ра­ем число 10, по­сколь­ку оно яв­ля­ет­ся
наи­боль­шим.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

№3. Для каж­до­го из пе­ре­чис­лен­ных ниже
чисел по­стро­и­ли дво­ич­ную за­пись. Ука­жи­те число, дво­ич­ная за­пись ко­то­ро­го
со­дер­жит ровно два зна­ча­щих нуля. Если таких чисел не­сколь­ко, ука­жи­те
наи­боль­шее из них.

1) 7

2) 8

3) 9

4) 10

По­яс­не­ние.

Пред­ста­вим все числа в дво­ич­ной си­сте­ме счис­ле­ния:

7₁₀ = 111₂,

8₁₀ = 1000₂,

9₁₀ = 1001₂,

10₁₀ = 1010₂.

Из чисел 9 и 10 вы­би­ра­ем число 10, по­сколь­ку оно яв­ля­ет­ся
наи­боль­шим.

Пра­виль­ный ответ ука­зан под но­ме­ром 4.

№4. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 307?

1) 5

2) 2

3) 3

4) 4

По­яс­не­ние.

Пе­ре­ве­дем число из де­ся­тич­ной си­сте­мы счис­ле­ния в
дво­ич­ную: нужно де­лить его на 2, пока де­ли­мое не будет мень­ше 2. После за­пи­шем
остат­ки от де­ле­ния на­чи­ная с конца.

307₁₀=100110011₂

№5. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 625?

1) 1

2) 3

3) 5

4) 2

По­яс­не­ние.

Пе­ре­ве­дем число из де­ся­тич­ной си­сте­мы счис­ле­ния в
дво­ич­ную: нужно де­лить его на 2, пока де­ли­мое не будет мень­ше 2. После за­пи­шем
остат­ки от де­ле­ния на­чи­ная с конца.

625₁₀=1001110001₂

№6. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 127?

1) 1

2) 2

3) 6

4) 7

По­яс­не­ние.

Пе­ре­ведём 127 в дво­ич­ную си­сте­му счис­ле­ния и со­счи­та­ем
ко­ли­че­ство еди­ниц:

127₁₀=1111111₂

№7. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 206?

1) 5

2) 2

3) 3

4) 4

По­яс­не­ние.

. В этом числе 5 еди­ниц.

№8. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 1025?

1) 1

2) 2

3) 10

4) 11

По­яс­не­ние.

Пе­ре­ве­дем число в дво­ич­ную си­сте­му счис­ле­ния:

1025₁₀ = 1024 + 1 = 2¹⁰ + 1
= 10000000001₂.

В дво­ич­ной за­пи­си 2 еди­ни­цы.

№9. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 514?

1) 2

2) 3

3) 4

4) 5

По­яс­не­ние.

Пе­ре­ве­дем 514 в дво­ич­ную си­сте­му счис­ле­ния.

В этой за­пи­си 2 еди­ни­цы.

№10. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 255?

1) 1

2) 2

3) 7

4) 8

По­яс­не­ние.

Пе­ре­ве­дем де­ся­тич­ное число 255 в дво­ич­ную си­сте­му
счис­ле­ния:  Итого 8 еди­ниц. Такой ответ
ука­зан под но­ме­ром 4.

Ответ: 4.

       Различные системы счисления

№1. Дано А = A7₁₆, B = 251₈.
Най­ди­те сумму A + B.

1) 101011000₂

2) 101010100₂

3) 101010110₂

4) 101010000₂

По­яс­не­ние.

Пе­ре­ве­дем числа в де­ся­тич­ную си­сте­му счис­ле­ния, вы­пол­ним
сло­же­ние, и пе­ре­ве­дем сумму в дво­ич­ную си­сте­му счис­ле­ния:

A7₁₆ = 10⋅16 + 7 = 167₁₀.

251₈ = 2⋅8² + 5⋅8
+ 1 = 169₁₀.

336₁₀ = 1⋅2⁸ + 1⋅2⁶ +
1⋅2⁴ =
101010000₂.

Также су­ще­ству­ет вто­рой спо­соб:

1. Пе­ре­ве­дем числа в дво­ич­ную си­сте­му счис­ле­ния
(через три­а­ды и тет­ра­ды). А₂ = 1010 0111,

В₂ = 010 101 001.

2. Вы­пол­ним сло­же­ние дво­ич­ных чисел: 10100111 +
10101001 = 101010000.

№2. Ука­жи­те наи­мень­шее четырёхзнач­ное вось­ме­рич­ное
число, дво­ич­ная за­пись ко­то­ро­го со­дер­жит 5 еди­ниц. В от­ве­те за­пи­ши­те
толь­ко само вось­ме­рич­ное число, ос­но­ва­ние си­сте­мы счис­ле­ния ука­зы­вать
не нужно.

По­яс­не­ние.

Наи­мень­шее число из пяти еди­ниц в дво­ич­ной си­сте­ме
счис­ле­ния — 1 1111₂. Пре­об­ра­зу­ем число так, чтобы при пе­ре­во­де
в вось­ме­рич­ную си­сте­му счис­ле­ния по­лу­ча­лось четырёхзнач­ное число.
Для этого нужно, что число со­сто­я­ло из четырёх триад, то есть со­сто­я­ло из
две­на­дца­ти сим­во­лов. Наи­мень­шее число, удо­вле­тво­ря­ю­щее усло­вию за­да­чи:
001 000 001 111₂ = 1017₈.

Ответ: 1017.

№3. Сколь­ко еди­ниц в дво­ич­ной за­пи­си де­ся­тич­но­го
числа 245?

По­яс­не­ние.

Пе­ре­ведём число 245 в дво­ич­ную си­сте­му:

245₁₀ = 2⁷ + 2⁶ +
2⁵ + 2⁴ + 2² + 2⁰ =
11110101₂.

Ответ: 6.

№4. Какое из не­ра­венств вы­пол­ня­ет­ся для чисел А = 164₈,
В = А3₁₆ и С = 2200₄?

1) A<B<C

2) А<С<В

3) В<А<С

4) С<В<А

По­яс­не­ние.

Пе­ре­ве­дем числа в де­ся­тич­ную си­сте­му счис­ле­ния и
затем срав­ним их:

А = 164₈ = 1⋅8² + 6⋅8¹ +
4⋅8⁰ =
64 + 48 + 4 = 116₁₀.

В = A3₁₆ = 10⋅16¹ + З⋅16⁰ =
163₁₀.

С = 2200₄ = 2⋅4³ + 2⋅4² +
0⋅4¹ +
0⋅4⁰ =
2⋅(64
+ 16) = 160₁₀.

По­это­му: А < С < В. Пра­виль­ный ответ ука­зан под
но­ме­ром 2.

№5. Даны два числа: A=9D₁₆ и
B=237₈. Какое из при­ве­ден­ных ниже чисел С в дво­ич­ной си­сте­ме
со­от­вет­ству­ет не­ра­вен­ству: A<C<B?

1) 10011010₂

2) 10011110₂

3) 10011111₂

4) 11011110₂

По­яс­не­ние.

Для того, чтобы ре­шить это за­да­ние, не­об­хо­ди­мо вы­ра­зить
числа А и В в дво­ич­ной си­сте­ме счис­ле­ния. А=10011101₂,
В=10011111₂. Оче­вид­но, что вер­ный ответ: С=10011110₂.

Вто­рой ва­ри­ант, пе­ре­во­дим А и В в де­ся­тич­ную си­сте­му.
По­лу­ча­ем А=157₁₀, В=159₁₀.

По­лу­ча­ем, что С=158₁₀=10011110₂

№6. Как вы­гля­дит число В0С₁₆ в
дво­ич­ной си­сте­ме счис­ле­ния?

1) 110010001010₂

2) 101100001100₂

3) 101100010001₂

4) 101000011100₂

По­яс­не­ние.

Для ре­ше­ния этого за­да­ния можно пойти одним из двух
путей: пе­ре­ве­сти число В0С из шест­на­дца­те­рич­ной в де­ся­тич­ную, а
потом в дво­ич­ную, или за­ме­нить каж­дый раз­ряд шест­на­дца­те­рич­ной си­сте­мы
на че­ты­ре бита дво­ич­ной

( В₁₆ = 1011₂, 0₁₆ =
0000₂, С₁₆ = 1100₂).

№7. Найти сумму двух чисел и за­пи­сать ре­зуль­тат
в дво­ич­ной си­сте­ме счис­ле­ния:

X=110111₂, Y=135₈

1) 11010100₂

2) 10100100₂

3) 10010011₂

4) 10010100₂

По­яс­не­ние.

Пред­ста­вим Y в дво­ич­ной си­сте­ме счис­ле­ния.

Y=135₈=1011101₂.

Най­дем сумму Чисел X и Y (помня, что 0+0=0, 0+1=1,
1+1=10): 110111₂+1011101₂=10010100₂

№8. Зна­че­ние вы­ра­же­ния 11₁₆ +
11₈ : 11₂ в дво­ич­ной си­сте­ме счис­ле­ния
равно

1) 10100₂

2) 110111₂

3) 10101₂

4) 101101₂

По­яс­не­ние.

Пе­ре­ве­дем все числа в де­ся­тич­ную си­се­му счис­ле­ния,
вы­пол­ним дей­ствия и пе­ре­ве­дем ре­зуль­тат в дво­ич­ную си­сте­му счис­ле­ния:

11₁₆ = 16 + 1 = 17₁₀,

11₈ = 8 + 1 = 9₁₀,

11₂ = 2 + 1 = 3₁₀,

17 + 9 : 3 = 17 + 3 = 20₁₀,

20 = 16 + 4 = 10100₂

№9. Чему равна сумма чисел 57₈ и
46₁₆?

1) 1010101₂

2) 125₈

3) АЗ₁₆

4) 75₁₆

По­яс­не­ние.

Пе­ре­ве­дем числа в де­ся­тич­ную си­сте­му счис­ле­ния, и
сло­жим их:

Та­ко­го от­ве­та среди ука­зан­ных ва­ри­ан­тов нет, од­на­ко
можно пе­ре­ве­сти по­лу­чен­ное число в шест­на­дца­те­рич­ную си­сте­му счис­ле­ния:
117_{10} = 7⋅16 + 5= 75_{16}.

№10. Чему равна сумма чисел BA₁₆ и
AB₁₆? Ре­зуль­тат за­пи­ши­те в вось­ме­рич­ной си­сте­ме счис­ле­ния.

1) 228₈

2) 545₈

3) 343₈

4) 104₈

По­яс­не­ние.

Сравнение чисел в различных системах счисления (Готовимся к ЕГЭ)

© 2023 Prezi Inc.
Terms & Privacy Policy

Двоичная система счисления

1. Задание 1 № 6875

Укажите целое число от 8 до 11, двоичная запись которого содержит ровно две единицы. Если таких чисел несколько, укажите наибольшее из них.

2. Задание 1 № 7476

Сколько единиц в двоичной записи десятичного числа 519?

3. Задание 1 № 136

Переведите в двоичную систему десятичное число 99.

4. Задание 1 № 429

Вычислите разность X-Y двоичных чисел, если

Y=1002

Х=10101002

Ответ запишите в двоичной системе.

5. Задание 1 № 409

Вычислите сумму чисел X и Y, если Х=23410, У=5710. Результат представьте в двоичной системе счисления.

6. Задание 1 № 4674

Даны числа: 1, 3, 11 и 33. Укажите среди них число, двоичная запись которого содержит ровно 3 единицы.

Перевод в десятичную системы счисления

1. Задание 1 № 127

Переведите в десятичную систему двоичное число 1010012.

2. Задание 1 № 405

Вычислите сумму чисел х и у при x = B316, у = 1101102. Результат представьте в десятичной системе счисления.

3. Задание 1 № 10277

Вычислите: 101010102 – 2528 + 716. Ответ запишите в десятичной системе счисления.

4. Задание 1 № 13531

Вычислите: 101011102 – 2568 + A16. Ответ запишите в десятичной системе счисления. В ответе запишите только число, основание системы счисления писать не нужно.

5. Задание 1 № 13558

Вычислите: 101011012 − 2558 + D16. Ответ запишите в десятичной системе счисления. В ответе запишите только число, основание системы счисления писать не нужно.

6. Задание 1 № 16376

Вычислите значение выражения B916 − 2718. В ответе запишите вычисленное значение в десятичной системе счисления.

Прямой перевод между шестнадцатеричной/восьмеричной и двоичной СС

1. Задание 1 № 101

Дано А = A716, B = 2518. Найдите сумму A + B. Ответ укажите в двоичной системе.

2. Задание 1 № 7290

Даны 4 целых числа, записанных в различных системах счисления: 3110, F116, 2618, 7118. Сколько среди них чисел, двоичная запись которых содержит ровно 5 единиц?

3. Задание 1 № 8092

Сколько единиц в двоичной записи восьмеричного числа 17318?

4. Задание 1 № 9352

Сколько единиц в двоичной записи шестнадцатеричного числа 12F016?

5. Задание 1 № 105

Переведите число В0С16 в двоичную систему счисления.

6. Задание 1 № 404

Найдите значение выражения 1116 + 118 : 112. Ответ запишите в двоичной системе счисления.

7. Задание 1 № 6405

Переведите в шестнадцатеричную систему счисления двоичное число 101011.

8. Задание 1 № 13585

Сколько единиц в двоичной записи числа 8F16?

Шестнадцатеричная арифметика

1. Задание 1 № 15617

Найдите значение выражения 8F – 80 в шестнадцатеричной системе счисления. В ответе запишите вычисленное значение в десятичной системе счисления.

2. Задание 1 № 15841

Вычислите значение выражения 8F16 − 8B16.

В ответе запишите вычисленное значение в десятичной системе счисления.

3. Задание 1 № 17319

Вычислите значение выражения 8216 + 1E16. Ответ запишите в десятичной системе счисления.

4. Задание 1 № 17365

Вычислите значение выражения 7316 + 2E16. Ответ запишите в десятичной системе счисления.

Сравнение чисел в различных системах счисления

1. Задание 1 № 5227

Сколько верных неравенств среди перечисленных:

100110102 > 25610;

100110102 > 9F16;

100110102 > 2328.

2. Задание 1 № 6761

Даны 4 целых числа, записанных в двоичной системе:

10001011; 10111000; 10011011; 10110100.

Сколько среди них чисел, больших, чем 9A16?

3. Задание 1 № 6940

Даны 4 целых числа, записанных в шестнадцатеричной системе: A8, AB, B5, CA. Сколько среди них чисел, больших, чем 2658?

4. Задание 1 № 4919

Даны 4 целых числа, записанные в двоичной системе:

10001011, 10111000, 10011011, 10110100.

Сколько среди них чисел, больших, чем A416+208?

5. Задание 1 № 13450

Сколько существует натуральных чисел x, для которых выполнено неравенство 110010002 ≤ x ≤ CF16? В ответе укажите только количество чисел, сами числа писать не нужно.