Среднее гармоническое трёх чисел a, b и c вычисляется по формуле h=(frac{frac{1}{a}+frac{1}{b}+frac{1}{c}}{3})^{-1}. Найдите среднее гармоническое чисел frac{1}{4},frac{1}{5} и frac{1}{6}.
Решение:
a=frac{1}{4}\b=frac{1}{5}\c=frac{1}{6}\h=(frac{frac{1}{a}+frac{1}{b}+frac{1}{c}}{3})^{-1}=(frac{frac{1}{frac{1}{4}}+frac{1}{frac{1}{5}}+frac{1}{frac{1}{6}}}{3})^{-1}=(frac{frac{4}{1}+frac{5}{1}+frac{6}{1}}{3})^{-1}=(frac{4+5+6}{3})^{-1}=(frac{15}{3})^{-1}=5^{-1}=frac{1}{5^{1}}=0,2
Ответ: 0,2.
Есть три секунды времени? Для меня важно твоё мнение!
Насколько понятно решение?
Средняя оценка: 4.2 / 5. Количество оценок: 13
Оценок пока нет. Поставь оценку первым.
Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️
Вступай в группу vk.com 😉
Расскажи, что не так? Я исправлю в ближайшее время!
В отзыве оставь любой контакт для связи, если хочешь, что бы я тебе ответил.
Среднее гармоническое
Предлагаемая здесь программа, помимо расчета среднего гармонического, умеет еще и приводить исходные данные к стандартному виду, а так же упорядочивать их по возрастанию или убыванию…
Содержание:
- Определение среднего гармонического и среднего степенного
- Расчет среднего гармонического
- Свойства среднего гармонического
- Прикладное значение среднего гармонического
- Задания ЕГЭ, на тему «Среднее гармоническое»
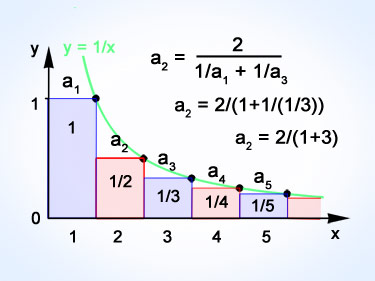
Рис.1. Гармонический ряд и среднее гармоническое
Среднее гармоническое от двух реже трех чисел используется в математике не менее двух с половиной тысяч лет (возможно более 4000 лет). Свойства средних гармонических, арифметических и геометрических величин для двух чисел были детально изучены еще пифагорейцами, поэтому они так же называются классическими пифагорейскими средними.
Свое название среднее гармоническое получило благодаря замечательному свойству гармонического ряда: каждый член ряда, начиная со второго, представляет собой среднее обратно-пропорциональное от двух соседних членов (рисунок). Это свойство гармонического ряда было известно еще во времена Аристотеля.
.
В свете современных представлений:
Среднее гармоническое значение множества положительных вещественных чисел определяется как результат деления количества этих чисел на сумму их обратных величин:
aср.гapм =
Таким образом, мы имеем дело исключительно с положительными вещественными числами ai > 0.
Среднее гармоническое является частным случаем среднего степенного с показателем степени d = — 1.
Среднее степенное значение sd порядка (степени) d от множества заданных чисел a1+ a2+ …+ an определяется формулой:
sd =
(
)
1
d
то есть среднее гармоническое можно представить в следующем виде:
aср.гapм = s-1 =
(
)
-1
Расчет среднего гармонического
Для того чтобы начать онлайн расчет среднего гармонического введите исходные числа в одно из полей ввода-вывода данных.
В первое поле можно ввести последовательность чисел, разделенных точкой с запятой (программа попытается так же преобразовать к стандартному виду, например, вставленную копию последовательности чисел с плавающей точкой, разделенных пробелами, запятой или точкой с запятой).
Во второе поле можно вводить числа по одному — они автоматически будут добавляться к данным первого поля, если расчет не запустился автоматически, кликните по зеленой кнопке, показывающей количество чисел в исследуемом массиве:
Введите исходные данные
Введите число
Что-то пошло не так…
Прямое восхождение не может быть больше 24 часов,
минуты и секунды больше 60,
а склонение по абсолютной величине не должно быть больше 90°
Среднее гармоническое, aср. гарм
Для наглядной демонстрации правила о средних
aср. гарм ≤ aср. геом ≤ a ср. арифм
выводим так же результат расчета среднего арифметического и среднего геометрического:
Среднее арифметическое [1], aср. арифм и
стандартное отклонение σ [2]
Среднее геометрическое [3], aср. геом
aсреднее гармоническое ≤ aсреднее геометрическое ≤ a среднее арифметическое
Если добавить расчет среднего квадратического и степенного, то получиться, что расчет всех средних можно лровести на этой странице (all-means-in-one)
Среднее квадратическое [4], aср.квадр
Среднее степенное [5], aср.степ d с показателем степени d:
Design by Sergey Ov for abc2home.ru
ВНИМАНИЕ! При перезагрузке страницы введенная информация не сохраняется, если Вы не сгенерировали код для записи результатов работы в командной строке:
Сохранить расчет среднего гармонического в истории браузера
Адресную строку с кодом из Ваших данных Вы можете переслать на любое устройство и воспроизвести на нем результаты расчетов
После того как будут введены хотя бы два исходных числа, цвет квадратной кнопки на поле ввода данных должен поменяться с оранжевого на зеленый, и автоматически начнется расчет среднего гармонического и сопутствующих параметров, если это не произошло, то кликните по зеленому полю кнопки.
Страницы по теме «Расчет средних значений»
- Среднее арифметическое — расчет онлайн, определение, формула
- Среднеквадратическое отклонение — расчет онлайн, определение, формула
- Среднее геометрическое — расчет онлайн, определение, формула
- Среднее гармоническое и среднее степенное — расчет онлайн, определения, формулы
- Среднее квадратическое — расчет онлайн, определение, формула
Свойства среднего гармонического
1. Среднее гармоническое значение множества заданных неотрицательных чисел лежит между минимальным и максимальным числами из этого множества.
2. Кроме того среднее гармоническое подчиняется неравенству о средних для множества положительных вещественных чисел
amin ≤ aср. гарм ≤ aср. геом ≤ aср. арифм ≤ a ср.квадр ≤ a max [2*] ,
то есть для любого множества положительных чисел среднее гармоническое никогда не бывает больше среднего арифметического [1]:
n
√
≤
3. Следует запомнить, что среднее гармоническое от двух чисел легко приводится к виду:
aср.гарм 2 =
отсюда в случае двух чисел имеем:
—
среднее арифметическое aср.арифм = ( a1 + a2)/2;
—
среднее геометрическое aср.геом = √a1a2 ,
тогда
aср.гарм = aср.геом · aср.геом / aср.арифм
или
aср.геом = √aср.гарм · aср.арифм
Cреднее гармоническое от трех чисел приводится к следующему виду:
aср.гарм 3 =
3 a1a2a3
a1a2 + a1a3 + a2a3
Прикладное значение среднего гармонического
Согласно закону Ома для участка цепи общее сопротивление параллельно соединенных проводников определяется соотношением:
не трудно догадаться, что среднее сопротивление соединенных такого соединения проводников будет вычисляться в точности как среднее гармоническое.По формуле среднего гармонического вычисляется и средняя емкость последовательно соединенных конденсаторов, а так же индуктивность параллельно соединенных катушек.
В геометрии среднее гармоническое наиболее известным образом связано со свойством вписанной в треугольник окружности — ее радиус равен одной трети от среднего гармонического его высот.
Другой геометрический сюжет — гармонический центр трапеции (Рис.2, точка О) — длина отрезка, проходящего через точку пересечения диагоналей параллельно основаниям, равна среднему гармоническому длин оснований:
xEF =
Рис.2. Гармонический центр трапеции O и всплывающая подсказка для доказательства правила среднего гармонического
Среднее гармоническое широко применяенся в физике, статистике, социологии, финансовой аналитике, там где требуется осреднение и оценка обратно пропорциональных значений от исходных величин. Например, средняя скорость теплохода Vср , плавающего по реке между пунктами A и B с расстоянием S со скоростью V1 вверх против течения и V2 вниз по течению будет определяться по формуле:
Задания ЕГЭ, на тему «Среднее гармоническое»
Задание:
Основания трапеции относятся как 1:2. Через точку пересечения диагоналей проведена прямая, параллельная основаниям.
В каком отношении эта прямая делит площадь трапеции?
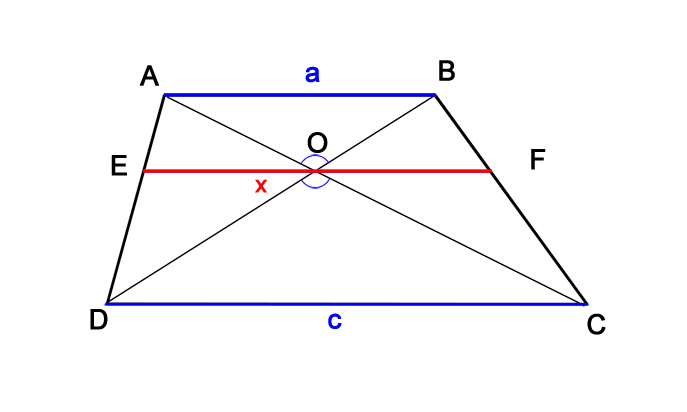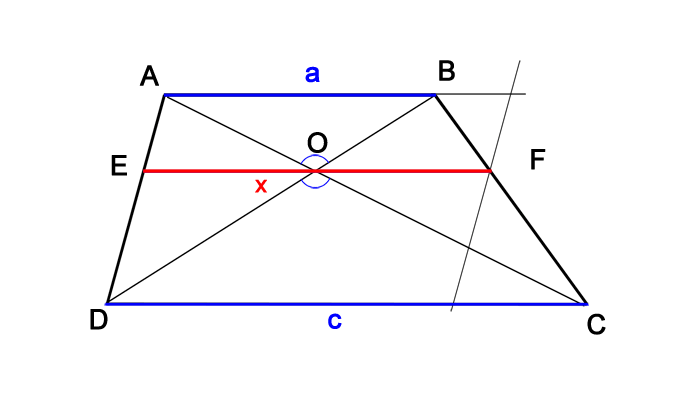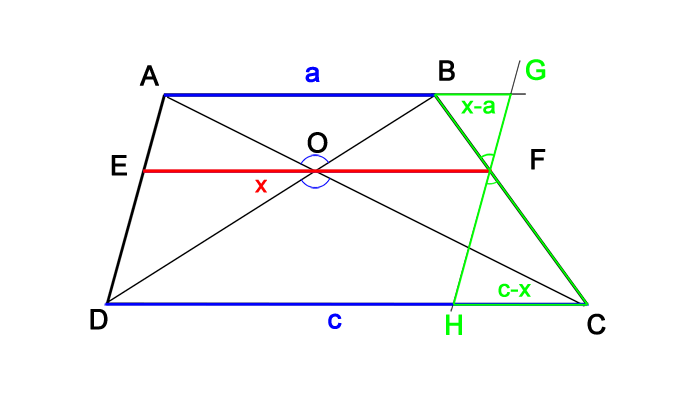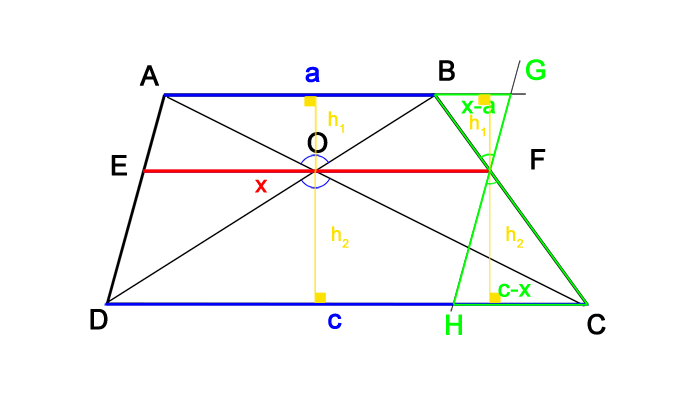
Для решения задачи делается дополнительное построение (Рис.2).
Проведем через точку F прямую FH параллельную стороне DA, а затем продолжим основание АВ до пересечения с этой прямой в точке G, как показано на рисунке.
Треугольники AOB и DOC подобны, их высоты относятся как ac . Треугольники FBG также FCH подобны, их высоты относятся как x — a c — x .
Поскольку рассматриваемые пары треугольников имеют равные высоты, получаем x — a c — x = ac , отсюда:
x =
Найденная длина отрезка является средним гармоническим оснований трапеции.
Поскольку, по условиям задачи с = 2a, получаем x = 2a · 2a / 3a = 4/3·a.
Тогда
SABFE =
· h1 =
· h1 = 7/6·a·h1
SEFCD =
· h2 =
· h2 = 5/3·a·h2
Поскольку треугольники AOB и DOC подобны, их высоты h1 и h2, проведенные соответственно к сторонам и относятся как 1:2 и h2= 2h1.
Таким образом, для искомого отношения площадей трапеций и имеем:
Ответ: 7:20
P.S. На этой странице используется Бета версия программы расчета среднего гармонического, об обнаруженных недочетах, а так же возможных пожеланиях просьба сообщить на форум сайта (окно для входа на форум находится в нижней части страницы).
1. Среднее арифметическое значение (чаще используется термин, просто, «среднее арифметическое» или «среднее») множества заданных чисел определяется как число равное сумме всех чисел множества, делённой на их количество:
aср.арифм =
2. Среднеквадратическое отклонение (стандартное отклонение) значений множества заданных чисел от среднего арифметического определяется как число равное квадратному корню от суммы квадратов разности этих чисел и среднего арифметического, делённой на количество этих чисел:
σ =
√
(a1 — acp)2 + (a2 — acp)2 + …+ (an — acp)2
n
3. Среднее геометрическое значение множества положительных вещественных чисел определяется как результат взаимного умножения этих чисел и извлечения из произведения корня с показателем равным количеству чисел:
aср.геом = n
√
=
Среднее квадратическое значение множества заданных чисел определяется как число равное квадратному корню от суммы квадратов этих чисел, делённой на их количество:
aср.квадр =
√
Можно сказать, что среднее квадратическое равно квадратному корню из среднего арифметического[1] квадратов заданных чисел a1+ a2+ …+ an
5. Среднее арифметическое является степенным средним c d = 1, среднее квадратическое — d = 2, среднее гармоническое можно считать степенным средним порядка d = -1.
● Главная
▸ Статьи
▸ Блог
▸ Копилка
✔ Среднее гармоническое расчет онлайн
Онлайн калькулятор для расчета среднего гармонического двух, трех, четырех и более чисел. Средняя гармоническая величина ( или Среднее гармоническое ) получается от деления числа данных величин на сумму величин обратных данным.
Формулы для нахождения среднего гармонического: 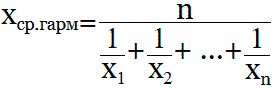
Формула средней гармонической взвешенной:
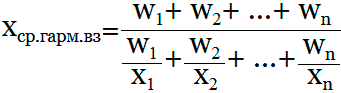
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone — просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android — просто добавьте страницу
«На главный экран»