Старший брат договорился с мишей что в пятницу он будет готовиться к экзамену по физике - ExamHelp.top

Старший брат договорился с Мишей, что в пятницу он будет готовиться к экзамену по физике, решая задачи из сборника. За первую задачу брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?

Спрятать решение

Решение.

Количество минут игры составляет арифметическую прогрессию с первым членом a₁  =  10 и разностью d  =  3, найдем по формуле сумму арифметической прогрессии первых восьми членов:

минуты.

Ответ: 164 минуты.

Источник

Сборник

«Арифметическая
и геометрическая прогрессия в решениях прикладных задач»

Составитель
Маслова Юлия

Ученица
9 класса МАОУ «СОШ № 17»

город
Краснотурьинск

Оглавление.

Прогрессии в медицине………………………………………………………………………………………………..4.

Прогрессии в физике…………………………………………………………………………………………………….7.

Прогрессии в математике……………………………………………………………………………………………..10.

Прогрессии в биологии………………………………………………………………………………………………..14.

Прогрессия в экономике и банковской
системе…………………………………………………………….17.

Интересные задачи……………………………………………………………………………………………………….20

Ответы…………………………………………………………………………………………………………………………23.

Список использованной
литературы…………………………………………………………………………….27.

Интересные факты

При повышении температуры по
арифметической прогрессии, скорость химической реакции растёт по геометрической
прогрессии.

Больной
принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а
в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40
капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием
на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному,
если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Дано:
5,10,15,…40,40,40,35,30,…5.

Решение.

40=5+5(n-1), 5+5n—5=40, 5n=40, n=8

180+180+40=400(капель)

400:250=1,6(пузырька)

Ответ. Больному нужно
купить 2 пузырька лекарства.

Больной, заболевший гриппом, может за день
заразить четырёх человек. Через сколько дней заболеют все учащиеся школы в
количестве 1176 человек?

Лечащий врач Андрея посоветовал своему
пациенту в первый день занятий после операции провести на беговой дорожке 15
минут, а на каждом следующем занятии увеличивать время, проведённое на беговой
дорожке, на 7 минут. За сколько занятий Андрей проведёт на беговой дорожке в
общей сложности 2 часа 25 минут, если будет следовать рекомендациям своего
лечащего врача?

Дима
на перемене съел булочку. Во время еды в кишечник попало 30 дизентерийных
палочек. Через каждые 20 минут происходит деление бактерии (Они удваиваются).

Сколько дизентерийных палочек будет у Димы
кишечнике через 12 часов?.

Сколько граммов опасного вещества оседает
в легких курильщика в среднем в сутки, если с каждой последующей сигаретой это
количество увеличивается в 2 раза и, выкурив третью сигарету, будет равно
0,0008 г.

Курс воздушных ванн начинают с 15 минут в
первый день и увеличивают время этой процедуры в каждый следующий день на 10
минут. Сколько дней следует принимать воздушные ванны в указанном режиме, чтобы
достичь их максимальной продолжительности 1ч 45 мин?

Служившему воину дано вознаграждение за первую рану 1 копейка, за
другую – 2 копейки, за третью – 4 копейки и т.д. По исчислению нашлось, что
воин получил всего вознаграждения 655 руб. 35 коп. Спрашивается число его ран.

Интересные факты

Нейтрон, ударяя по ядру урана, раскалывает
его на 2 части. Затем 2 нейтрона, ударяя по двум ядрам, раскалывает их ещё на 4
части и т. д. — это геометрическая прогрессия.

Задачи

Диаметры пяти шкивов, насажанных на общий
вал, образуют арифметическую прогрессию. Найти диаметры шкивов, если сумма
первого и третьего составляет 268 мм, а второго и четвёртого — 316 мм.

Решение: По условию задачи+=268, Найти.

Составим и решим систему уравнений,
используя формулуd(n-1)

; ;

Подставив полученные значения в формулуd(n-1),
найдём остальные значения

Ответ: 110, 134, 158, 182, 206.

После каждого качания поршня под колоколом
воздушного насоса давления воздуха уменьшается на 0,83 начального давления.
Определить, как велико будет давление воздуха под колоколом после 15 качание,
если первоначальное давление было равно 760 мм ртутного столба.

Решение:
Из условия задачи получаем, что q=0,83;
n=16.

По формуле , значит:

Ответ: 46,45.

Мощности пяти электромоторов составляют
возрастающую геометрическую прогрессию. Мощность первого 5 кВт, а третьего 9,8
кВт. Рассчитать мощности остальных электромоторов (ответ дать в кВт).

Решение:
По условию задачи

Найти .

По условию задачи

Для того, чтобы найти остальные значения,
найдём q,

Ответ: 7; 13,72;
19,208.

Шар, катящийся по жёлобу, в первую
секунду проходит 0,6 м, а путь, пройденный в каждую следующую секунду,
увеличивается на 0,6 м. Сколько секунду будет двигаться шар по шестиметровому
жёлобу?

При свободном
падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше.
Найдите глубину шахты, если свободно падающее тело достигло его дна через 5с
после начала падения.

Решение:
Составим математическую модель задачи: в первую секунду — 5м, во вторую секунду
— 15м, в третью секунду — 25м, в четвертую секунду — 35м, в пятую секунду —
45м. Всего за пять секунд — 5+15+25+35+45=125(м).

Ответ:
глубина шахты 125м.

Два тела, находясь на расстояни153 м друг
от друга, начали двигаться одновременно навстречу друг другу. Первое тело
движется со скоростью 10 м/с, второе в первую секунду прошло 3 м, а в каждую
последующую — на 5 м больше, чем в предыдущую. Через сколько секунд тела
встретятся?

Решение:

Первое
тело движется равномерно, поэтому путь, пройденным этим телом, вычисляется по
формуле: ∙. Движение второго тела
подчиняется законам арифметической прогрессии, где , d
= 5,

Поэтому ∙. +

необходимо найти t.

Из условия задачи
получаем уравнение: , где tN

Второй корень не
удовлетворяет условию .

Ответ:
Тела встретятся через 5 секунд.

Турист, двигаясь по пересечённой
местности, за первый час пути прошёл 800 м, а за каждый следующий час проходил
на 25 м меньше, чем за предыдущий. Сколько времени он потратил на путь, равный
5700м?

Длина,
ширина и высота прямоугольного параллелепипида образуют геометрическую
прогрессию. Обьём параллелепипида равен 216 , а сумма длин всех еего
рёбер равен 104 м. Найдите измерения параллелепипида.

Альпинисты в
первый день восхождения поднялись на высоту 1400м, а затем каждый следующий
день они проходи ли на 100м меньше, чем в предыдущий. За сколько дней они
покорили высоту в 5000м?

Дано: 1400;
1300; …; a1=1400; d=-100; Sn=5000

Найти: n

Решение Sn=
(2a1+ d (n-1))n/2;

5000= (2·1400-100
· (n-1))
n/2;

10000= (2800-100 n+100)
n;

10000= (2900-100 n) n;

100 n2-2900 n+10000=0;

n2-29 n+100=0;

n=25, n=4 – условию задачи удовлетворяет n=4( при
n=25, аn=-1000, но аn>0)

Ответ:
Значит, альпинисты покорили высоту за 4 дня.

Работники нанялись вырыть колодец с таким
условием, чтобы за первый аршин глубины им заплатили 40 копеек, а за каждый
следующий 15-ю копейками больше, чем за предыдущий. Сколько аршин вырыли они,
если за всю работу получили 16 р. 90 к.?

Решение. a1=40, d=15, Sn=1690.

Найти n.

Sn=(2a1+d(n-1))·n:2; n>0;

1690=(80+15(n-1))·n:2;

3380=(65+15n)·n;

15n2+65n-3380=0;

3n2+13n-676=0;

n1=-52/3;

n2=13.
Так как по условию задачи n>0, то n=13.

Ответ. Работники выкопали колодец глубиной
13 аршин.

В правильный треугольник со стороной 32 см
последовательно вписываются треугольники; вершины каждого последующего
треугольника являются серединами сторон предыдущего треугольника. Запишите
формулу n-го
члена полученной прогрессии.

Числа, выражающие длину, ширину и высоту
прямоугольного параллелепипеда, образуют геометрическую прогрессию. Объём параллелепипеда
равен 216 , а диагональ м. Найдите измерения
параллелепипеда, зная, что его диагональ вычисляется по формуле , где a,b,c
— его измерения, а d — длина
диагонали.

Интересные факты:

Интенсивность
размножения бактерий используют… в пищевой промышленности (для приготовления
напитков, кисломолочных продуктов, при квашении, солении и др.) в сельском
хозяйстве (для приготовления силоса, корма для животных и др.) в
фармацевтической промышленности (для создания лекарств, вакцин) в коммунальном
хозяйстве и природоохранных мероприятиях (для очистки сточных вод,ликвидации
нефтяных пятен)

“Потомство
пары мух съест мёртвую лошадь также скоро как лев”. Карл Линней Девятое
поколение одной пары мух наполнило бы куб, сторона которого равна 140 км, или
же составило бы нить, которой можно опоясать земной шар 40 млрд. раз.

Известно, что бактерия в питательной среде
через каждые полчаса делится на две. Сколько бактерий может образоваться из
одной бактерии за 10 часов?

Решение:
Бактерия была одна, следовательно, . Она делится на две,
значит q=2?
а так как время деления полчаса, то за 10 часов произойдёт 20 делений и нам
нужно найти

По формуле

Ответ: ..

Улитка
ползет по дереву. За первую минуту она проползла 30 см, а за каждую следующую
минуту — на 5 см больше, чем за предыдущую. За какое время достигнет улитка
вершины дерева длиной 5,25 м, если считать, что движение начато от его
основания?

Бактерия, попав в живой организм, к концу
20-й минуты делится на две бактерии, а каждая из них к концу следующих 20 минут
делится опять на две и так далее. Найдите число, бактерий, образующихся из
одной бактерии к концу суток.

Решение. В сутках 1440 минут, каждые 20
минут появляется новое поколение — за сутки 72 поколения.

По формуле суммы nпервых
членов геометрической прогрессии, у которой =1, q=2,
n=72,
находим, что

Одно растение одуванчика занимает на земле
площадь 1 кв м и даёт в год около 100 летучих семян.

а) Сколько кв. км площади покроет всё
потомство одной особи одуванчика через 10 лет при прогрессии

б) Хватит ли этим растениям на n-й
год места на поверхности суши земного шара?

Некто поместил пару кроликов в некое
место, огороженное со всех сторон стеной, чтобы узнать, сколько пар кроликов
при этом родится в течении года, если природа кроликов такова, что через месяц
одна пара кроликов производит на свет другую пару, а рождают кролики со 2
месяца после своего рождения.

На
опушке леса живут 4 куницы, которые питаются белками. Белки питаются орехами.
Одна куница съедает 10 белок, каждая белка- 10орехов. Для улучшения плодородия
сосны сибирской (кедр) нужны почвенные бактерии. Для одной сосны 10 бактерий.
Сколько нужно белок, орехов, бактерий, чтобы построить экологическую пирамиду
данного участка леса, используя геометрическую прогрессию.

Дано:

b₁ = 4, b₂ = 40

Найти: b₃ = ?, b₄ = ?
q = 40 / 4 = 10
b₃ = b₁ · qⁿ^-1 = 4 · 10^3-1 = 4 · 10² = 400
b₄ = 4 · 10^4-1 = 4 · 10³ = 4000

Для экологического равновесия этого участка леса необходимо на 4
куницы 40 белок, 400 орехов, 4000 бактерий.

Интересные факты:

Прогрессия имеет очень широкие приложения
в экономике. С её помощью банк производит расчёты с вкладчиком, решает, стоит
ли вкладывать деньги в крупные проекты, доход от которых будет получен через несколько
лет и т.д.

Клиенту в банке предлагают сделать вклад
на условии 2% в месяц. Какая сумма будет на счету через а) 2 месяца, б)
полугодие, в) десять лет, если первоначальная суммавклада равнялась 100 тыс.
руб. (Ответ дайте в рублях, округляя до сотых).

Вклад
составляв 10 000 р., банк дает 10% годовых, срок хранения вклада — 5 лет. Если
вы выбрали стратегию простых процентов, то к концу срока хранения вы получите в
итоге сумму, равную10 000 • (1 + ) , т. е. 15 000 р. Если же вы выбрали
стратегию сложных процентов, то к концу срока хранения вы получите в итоге
сумму, равную 10 000 • ( 1 + )5, т. е. 16 105,1 р.

Клиент
взял в банке кредит в размере 50000 рублей на 5 лет под 20 % годовых. Какую
сумму клиент должен вернуть банку в конце срока?

Два
приятеля положили в банк по 10000 рублей каждый, причем первый положил деньги
на вклад с ежеквартальным начислением 10 %, а второй- с ежегодным начислением
45%. Через год приятели получили деньги вместе с причитающимися им
процентами. Кто получил большую прибыль?

Один гражданин взял в коммерческом банке
кредит на n месяцев с условием, что
в первый месяц он возвращает 1/nчасть
кредита, а за каждый последующий месяц выплата увеличивается на 5 долларов по
сравнению спредыдущем месяцем. Всего он вынужден будет отдать 1995 долларов,
при этом в последний месяц 150 долларов. Сколько денег было взято сначала?

Рабочий обслуживал 6 автоматических
станков, каждый из которых производил 30 деталей в час. Станки последовательно
вводились в рабочий режим через каждые 10 минут. Но в течении пяти лет
конструкция станков была дважды усовершенствована: вначале производительность
была доведена до 36 деталей в час, а потом станки стали вводить в рабочий режим
в 2 раза быстрее. Найти: а) Производительность труда за смену (7 ч) до усовершенствования
и после каждого из двух усовершенствований; б) Месячный (22 дня) заработок
рабочего до усовершенствования и после каждого из двух усовершенствований, если
за каждую деталь в начале оплачивали 0,8 к., после первого усовершенствования —
0, 77к. и 0,75к. после первого усовершенствования.

За изготовление и установку самого нижнего
железобетонного кольца колодца заплатили 26 условных единиц, а за каждое
следующее кольцо платили на 2 у.е. меньше, чем за предыдущее. Кроме того, по
окончании работы было уплачено ещё 40 у.е. Средняя стоимость изготовления и
установки кольца оказалась равной у.е. Сколько колец было
установлено?

Предположим, что в 1776 году, когда
образовались США, 1 доллар был отдан под 10% годовых. В какую сумму он превратился
к 1976 году – 200-летней годовщине образования США?

Используем формулу сложных процентов.

Решение:

Ответ: Более 32 000 000 долларов.

Мама договорилась с Мишей, что в
воскресенье он будет готовиться к экзамену по математике, решая задачи из
пособия . за первую задачу она разрешит ему играть на компьютере 10 минут, а за
каждую следующую задачу ему можно будет играть на 3 минуты больше, чем за
предыдущую. Сколько минут можно будет играть Мише в воскресенье, если он решит
8 задач?

Папа договорился с Олей, что в субботу она
будет учить английские слова. За первое выученное слово он разрешит ей смотреть
телевизор 5 минут, а за каждое следующее слово ей можно будет смотреть
телевизор на 2 минуты больше, чем за предыдущее. Сколько минут можно будет
смотреть телевизор Оле в субботу, если она выучит 12 слов?

При хранении
бревен строевого леса их укладывают как показано на рисунке. Сколько брёвен
находится в одной кладке, если в ее основании положено 12 бревен?

Решение. Составим математическую модель задачи:
1, 2, 3, 4,…,12.

Это
арифметическая прогрессия, а1=1, d=1,аn=12.

Надо найти
n. аn=a1+d(n-1); 12=1+1(n-1);

n=12. Sn=(a1+an)∙n:2;

Sn=(1+12)·12:2;

Sn=78. В одной кладке находится 78 бревен.

Ответ: 78
бревен.

В соревновании по стрельбе за каждый
промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах
— одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за
предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?

Представьте, что вы – учетчик на стройке.
Привезли большое количество бревен строевого леса. Нужно быстро определить,
сколько бревен привезли, чтобы закрыть наряд шоферу. Количество бревен легко
подчитывается по формуле суммы арифметической прогрессии с разностью, равной
единице, если бревна уложены так, как показано на рисунке.

Олегу нужно решить 315 задач. Ежедневно он
решает на одно и то же количество задач больше по сравнению с предыдущем днём.
Известно, что за первый день Олег решил 11 задач. Определите, сколько задач
решил Олег в последний день, если со всеми задачами он справился за 9 дней.

Компания
«Альфа» начала инвестировать средства в перспективную отрасль в 2001
году, имея капитал в размере 3500 долларов. Каждый год, начиная с 2002 года,
она получала прибыль, которая составляла прибыль 100% от капитала предыдущего
года. А компания «Бета» начала инвестировать средства в другую
отрасль в 2004 году, имея капитал в размере 4500 долларов, и, начиная с 2005
года, ежегодно получала прибыль, составляющую 300% от капитала предыдущего
года. На сколько долларов капитал одной из компаний был больше капитала другой
к концу 2008 года, если прибыль из оборота не изымалась?

Справочный материал

Арифметическая прогрессия

Определение. Арифметической прогрессией называется
последовательность, каждый член которой, начиная со второго, равен предыдущему
члену, сложенному с одним и тем же числом. Это число называется разностью
арифметической прогрессии. Каждая арифметическая прогрессия имеет вид: , + d, + 2d, + 3d, … и обозначается знаком: ÷

Свойства арифметической прогрессии:

n-ный (общий) член арифметической прогрессии:

Характеристическое
свойство арифметической прогрессии: каждый член арифметической прогрессии,
начиная со второго, равен среднему арифметическому между предшествующим и
последующим членом.

Если разность арифметической прогрессии d > 0, то прогрессия называется возрастающей, если d < 0 —
убывающей.

Число членов арифметической прогрессии может быть
ограниченным, либо неограниченным.

Если арифметическая прогрессия содержит n членов,
то ее сумму можно вычислить по формуле или

Геометрическая прогрессия

Определение. Числовая последовательность, первый член которой
отличен от нуля, а каждый член, начиная со второго, равен предшествующему
члену, умноженному на одно и то же не равное нулю число, называется
геометрической прогрессией.

Геометрическая прогрессия
имеет вид:

Свойства геометрической прогрессии:

Для того чтобы
задать геометрическую прогрессию (b_n), достаточно знать ее первый
член и знаменатель q.

Последовательность
называется возрастающей (убывающей), если каждый последующий член
последовательности больше (меньше) предыдущего. Таким образом, если q > 0,
то прогрессия является монотонной последовательностью.

Однако, если q =
1, то все члены прогрессии равны между собой. В этом случае прогрессия является
постоянной последовательностью.

Для нахождения
n-ого члена геометрической прогрессии есть формула:.

Характеристическое свойство

последовательность (b_n) является
геометрической прогрессией тогда и только тогда, когда каждый ее член, начиная
со второго, есть среднее геометрическое соседних с ним членов.

Для нахождения
суммы числа членов геометрической прогрессии применяют следующую формулу:

У геометрической прогрессии есть еще одно свойство,
а именно: из определения знаменателя геометрической прогрессии следует, что , т. е. произведение членов,
равноотстоящих от концов прогрессии, есть величина постоянная.

Ответы:

Медицина:

Задача №1

Ответ: 2
пузырька лекарства.

Задача №2

Ответ. За 6 дней.

Задача №3

Ответ. За 5 занятий.

Задача №4

Ответ.30*.

Задача №5

Ответ. 0,0002 г.

Задача №6

Ответ. 10 дней.

Задача №7

Ответ. 16 ран.

Физика:

Задача №1

Ответ: 110, 134, 158, 182, 206.

Задача №2

Ответ: 46,45.

Задача №3

Ответ: 7; 13,72; 19,208.

Задача №4

Ответ: 4.

Задача №5

Ответ:
глубина шахты 125м.

Математика:

Задача №1

Ответ: 5.

Задача №2

Ответ: 8.

Задача №3

Ответ: 2м, 6м, 18м.

Задача №4

Ответ: Значит,
альпинисты покорили высоту за 4 дня.

Задача №5

Ответ. Работники выкопали колодец глубиной
13 аршин.

Задача №6

Ответ:

Задача №7

Ответ: 2, 6 и 18 м.

Биология:

Задача №1

Ответ: ..

Задача №2

Ответ:
Через 10 минут.

Задача №3

Ответ.

Задача №4

а)Ответ: 1012 .

б)Ответ. Нет, Sсуши
= 148 млн.

Задача №5

Ответ: 144.

Прогрессия в экономике и в банковской
системе:

Задача №3

Ответ:
124 416 рублей.

Задача №4

Ответ:
Первый приятель получил большую прибыль.

Задача №5

Ответ: 529.

Задача №6

Ответ: а) 1458 — после первого
усовершенствования станков, а после второго — 1548деталей.
б) до первого усовершенствования — 213р. 84к.

после первого
усовершенствования — 246р. 844к.

после второго
усовершенствования — 255р. 42к.

Задача №7

Ответ: 9 колец.

Задача №8

Ответ: Более 32 000 000
долларов.

Интересные задачи:

Задача №1

Ответ:
164минуты.

Задача №2

Ответ:
192 минуты.

Задача №3

Ответ: 78
бревен.

Задача №4

Ответ. 21 раз.

Задача №5

Ответ: 78 бревен.

Задача №6

Ответ. 59 задач.

Задача №7

Ответ. 704000.

Список использованной литературы:

1.
Алгебра. 9 класс. В 2 ч.Ч.1. Учебник
для общеобразовательных учреждений/А.Г.Мордкович.-9-е изд.,
стер.-М.:Мнемозина,2007-231с.

2. Алгебра. 9 класс : учеб, для общеобразоват.
организаций. Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; под
ред. С. А. Теляковского. — 21-е изд. — М. 2014. — 271 с.

3.
Алгебра. 9 класс, : Учебник для общеобразовательных
учреждений / Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Феактистов И.Е. . -М.:
Мнеозина, 2008, -447с. № 698, 699,702,725,734, 788, 789 (7 задач)

4.
Математика. Алгебра. Функции. Анализ данных.9 кл.:
Учебник для общеобразовательных учебных заведений/ Г.В. Дорофеев , С.Б.
Суворова, Е.А. Бунимович, Л.В. Кузнецова, С.С. Минаева; под ред. Г.В.
Дорофеева. -М. :Дрофа, 2000,-352с.;

5.
Математика.Подготовка к ЕГЭ-2017.Базовый уровень.
40 тренировочных вариантов по демоверсии 2017 года: учебно методическое
пособие/Под редакцией Ф.Ф.Лысенко, С.О. Иванова.-Растов-на
Дону:Легион,2016.-352с.

6.
Перельман Яков Исидорович. Живая математика.
Математические рассказы и головоломки. 2007 год

7.
Пичурин Л.Ф. За страницами учебника алгебры. Книга
для учащихся 7-9 классов средней школы -М.: Просвещение, 1990.-224с.;

8.
Энциклопедический словарь юного математика /Сост.
А.П.Савин.- М.: Педагогика, 1989.-352с.

Источник

1. Бригада маляров красит
забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же
число метров. Известно, что за первый и последний день в сумме бригада
покрасила 60 метров забора. Определите, сколько дней бригада маляров красила
весь забор.

2. Рабочие прокладывают
тоннель длиной 500 метров, ежедневно увеличивая норму прокладки на одно и то же
число метров. Известно, что за первый день рабочие проложили 3 метра тоннеля.
Определите, сколько метров тоннеля проложили рабочие в последний день, если вся
работа была выполнена за 10 дней.

3. Васе надо решить 434
задачи. Ежедневно он решает на одно и то же количество задач больше по
сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач.
Определите, сколько задач решил Вася в последний день, если со всеми задачами
он справился за 14 дней.

4. Турист идет из одного
города в другой, каждый день проходя больше, чем в предыдущий день, на одно и
то же расстояние. Известно, что за первый день турист прошел 10 километров.
Определите, сколько километров прошел турист за третий день, если весь путь он
прошел за 6 дней, а расстояние между городами составляет 120 километров.

5. Грузовик перевозит
партию щебня массой 210 тонн, ежедневно увеличивая норму перевозки на одно и то
же число тонн. Известно, что за первый день было перевезено 2 тонны щебня.
Определите, сколько тонн щебня было перевезено за девятый день, если вся работа
была выполнена за 14 дней.

6. Улитка ползет от одного
дерева до другого. Каждый день она проползает на одно и то же расстояние
больше, чем в предыдущий день. Известно, что за первый и последний дни улитка
проползла в общей сложности 10 метров. Определите, сколько дней улитка
потратила на весь путь, если расстояние между деревьями равно 150 метрам.

7. Вере надо подписать 640
открыток. Ежедневно она подписывает на одно и то же количество открыток больше
по сравнению с предыдущим днем. Известно, что за первый день Вера подписала 10
открыток. Определите, сколько открыток было подписано за четвертый день, если
вся работа была выполнена за 16 дней.

8. Вика решила начать
делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый
следующий день она делала на одно и то же количество приседаний больше, чем в
предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько
приседаний сделала Вика в пятый день?

9. Хозяин договорился с
рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он
заплатит им 4200 рублей, а за каждый следующий метр  — на 1300 рублей больше,
чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если
они выкопают колодец глубиной 11 метров?

10. В первом ряду кинозала
24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в
восьмом ряду?

11.Тренер посоветовал Андрею в первый день
занятий провести на беговой дорожке 15 минут, а на каждом следующем занятии
увеличивать время, проведённое на беговой дорожке, на 7 минут. За сколько
занятий Андрей проведёт на беговой дорожке в общей сложности 2 часа 25 минут,
если будет следовать советам тренера?

12. Врач прописал пациенту
принимать лекарство по такой схеме: в первый день он должен принять 3 капли, а
в каждый следующий день  — на 3 капли больше, чем в предыдущий. Приняв в день
30 капель, он ещё 3 дня пьёт по 30 капель лекарства, а потом ежедневно
уменьшает приём на 3 капли. Сколько пузырьков лекарства нужно купить пациенту
на весь курс приёма, если в каждом содержится 20 мл лекарства (что составляет
250 капель)?

13. В соревновании по
стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные
очки: за первый промах  — одно штрафное очко, за каждый последующий  — на 0,5
очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7
штрафных очков?

14. Улитка ползет вверх по
дереву, начиная от его основания. За первую минуту она проползла 30 см, а за
каждую следующую минуту  — на 5 см больше, чем за предыдущую. За сколько минут
улитка достигнет вершины дерева высотой 5,25 м? В ответе укажите число минут.

15. Альпинисты в первый
день восхождения поднялись на высоту 1400 м, а затем каждый следующий день
поднимались на высоту на 100 м меньше, чем в предыдущий. За сколько дней они
покорили высоту 5000 м?

16.Мать дарит каждой из пяти своих дочерей в
день рождения, начиная с пяти лет, столько книг, сколько дочери лет. Возрасты
пяти дочерей составляют арифметическую прогрессию, разность которой равна 2.
Сколько лет было старшей дочери, когда у них составилась библиотека общей
численностью в 495 книг?

17. Шары одинакового
радиуса расположили один раз в форме правильного треугольника, а другой  — в
форме прямоугольника. Найдите количество шаров, если известно, что и на стороне
треугольника, и на большей стороне прямоугольника располагается на два шара
больше, чем на меньшей стороне прямоугольника.

18. Для асфальтирования
участка длиной 99 м используются 2 катка. Первый каток был установлен в одном
конце участка, второй  — в противоположном. Работать они начали одновременно.
Первый каток в каждую минуту проходил 5 м, а второй каток за первую минуту
прошел 1,5 м, а за каждую следующую минуту проходил на 0,5 м больше, чем за
предыдущую. Через сколько минут катки встретились?

19. В сосуде имеется
несколько одинаковых кранов, которые открывают один за другим через равные
промежутки времени. Через 8 часов после того, как был включен последний кран,
сосуд был заполнен. Время, в течение которого были открыты первый и последний
краны относятся как 5 : 1. Через сколько времени заполнится сосуд, если открыть
все краны одновременно? Ответ дайте в часах.

20. Бригада рабочих могла
выполнить всю работу за 24 ч, если бы работали одновременно все рабочие. однако
по плану в первый час работал один рабочий, во второй час  — 2 рабочих, в
третий  — 3 и т. д. до тех пор, пока в работу не включились все рабочие. И
только несколько часов перед завершением работала вся бригада. Время работы,
предусмотренное планом, было бы сокращено на 6 часов, если бы с самого начала
работы работала бы вся бригада, за исключением пяти рабочих. Найдите количество
рабочих.

21. Часть программы
тренировок Арсения заключается в беге на беговой дорожке. На первой тренировке
необходимо бежать 15 минут, на каждой следующей время пробежки увеличивается на
7 минут. За сколько тренировок Арсений проведёт на беговой дорожке в общей
сложности 2 часа 25 минут, если будет следовать программе? (В ответе укажите
только число.)

22. Занятия йогой начинают
с 15 минут в день и увеличивают на 10 минут время каждый следующий день.
Сколько дней следует заниматься йогой в указанном режиме, чтобы суммарная
продолжительность занятий составила 2 часа?

23.Диаметры пяти шкивов, насаженных на общий
вал, образуют арифметическую прогрессию. Сумма диаметров первого и третьего
шкивов составляет 26,8 см, а второго и четвёртого  — 31,6 см. Сколько
сантиметров составляет диаметр наибольшего шкива?

24. Футбольный мяч катится
так, что за первую секунду он проходит путь 0,6 м, а в каждую следующую секунду
путь увеличивается на 0,6 м по сравнению с предыдущей. Сколько секунд будет
катиться мяч по горке длиной 6 метров?

25. При свободном падении
тело прошло в первую секунду 5 м, а в каждую следующую на 10 м больше. Найдите
глубину шахты, если свободно падающее тело достигло его дна через 5 с после
начала падения.

26. Два велосипедиста,
находясь на расстоянии 153 км друг от друга, начали двигаться одновременно
навстречу друг другу. Первый велосипедист едет со скоростью 10 км/ч, второй в
первый час проехал 3 км, а в каждый последующий  — на 5 км больше, чем в
предыдущий. Через сколько часов велосипедисты встретятся?

27. Улитка, ползая по
пересечённой местности, за первый час проползла 800 мм, а за каждый следующий
час она проползала на 25 мм меньше, чем за предыдущий. Сколько времени она
потратила на путь, равный 5700 мм?

28. В лесу живут белки,
каждая из которых, придя на опушку, съедает 10 орехов. В первый день на опушку
пришли 6 белок. В каждый следующий на опушку приходило на две белки больше.
Сколько орехов съели белки за 30 дней?

29. Старший брат
договорился с Мишей, что в пятницу он будет готовиться к экзамену по физике,
решая задачи из сборника. За первую задачу брат разрешит ему поиграть на своей
приставке 10 минут, а за каждую следующую задачу ему можно будет играть на 3
минуты больше, чем за предыдущую. Сколько минут можно будет поиграть Мише в
воскресенье, если он решит 8 задач?

30. Мама договорилась с
Димой, что в понедельник он будет учить испанские слова. За первое выученное
слово она даст сыну 5 конфет, а за каждое следующее слово на 2 конфеты больше,
чем за предыдущее. Сколько конфет Дима получит от мамы в понедельник, если он
выучит 12 слов?

31. Рихарду необходимо
разобрать 315 квадратных уравнений. Ежедневно он разбирает на одно и то же
количество уравнений больше по сравнению с предыдущем днём. Известно, что за
первый день Рихард разобрал 11 квадратных уравнений, а справился со всеми он за
9 дней. Сколько уравнений Рихард разберёт в последний день?

32. Клиент взял в банке
кредит 100 рублей на n месяцев с условием, что по окончании
первого месяца выплатит банку часть кредита, а
в каждый последующий месяц выплата будет на 5 рублей больше, чем в предыдущий.
Известно, что в последний месяц выплата составила 55 руб. На какой срок был
выдан кредит, если известно, что этот срок превышал полгода?

33. За изготовление и
установку нижнего железобетонного кольца колодца заплатили 234 рубля, а за
каждое следующее кольцо платили на 18 рублей меньше, чем за предыдущее. Кроме
того, по окончании работы была выплачена премия 360 рублей. Средняя стоимость
изготовления и установки одного кольца с учетом премии оказалась равна 202
рубля. Сколько колец было установлено?

34.

При хранении бревен их укладывают, как показано на рисунке.
Сколько бревен находится в одной кладке, если в ее основании положено 12
бревен?

35. При проведении
химической реакции в растворе образуется нерастворимый осадок. Наблюдения
показали, что каждую минуту образуется 0,2 г осадка. Найдите массу осадка (в
граммах) в растворе спустя семь минут после начала реакции.

36. В амфитеатре 13 рядов.
В первом ряду 17 мест, а в каждом следующем на 2 места больше, чем в
предыдущем. Сколько всего мест в амфитеатре?

Решение. Пусть бригада в первый
день покрасила метров забора, во второй  — …
, в последний  — метров забора. Тогда м, а за n дней было покрашено

метров
забора.

Поскольку всего было покрашено 240 метров
забора, имеем: Таким
образом, бригада красила забор в течение 8 дней.

Ответ: 8.

Решение. Пусть рабочие в первый
день проложили  метров тоннеля, во
второй  —  , …, в последний  —  метров
тоннеля. Длина тоннеля  метров.   дней.
Тогда в последний день рабочие проложили

метров.

Таким образом, рабочие в последний день
проложили 97 метров тоннеля.

Ответ: 97.

3.Васе надо решить 434 задачи. Ежедневно он
решает на одно и то же количество задач больше по сравнению с предыдущим днем.
Известно, что за первый день Вася решил 5 задач. Определите, сколько задач
решил Вася в последний день, если со всеми задачами он справился за 14 дней.

Решение. В первый день Вася
решил задач, в последний  — задач. Всего
надо решить задач. Поскольку где имеем:

Тогда

задач.

Ответ: 57.

4. Турист идет из одного
города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то
же расстояние. Известно, что за первый день турист прошел 10 километров.
Определите, сколько километров прошел турист за третий день, если весь путь он
прошел за 6 дней, а расстояние между городами составляет 120 километров.

Решение. В первый день турист
прошел км, во второй  — …,
в последний  — км. Всего он прошел км.
Если каждый день турист проходил больше, чем в предыдущий день, на d км,
то

где дней, км.
Таким образом,

Тогда за третий день турист прошел

Ответ: 18.

Решение. Пусть в первый день
грузовик перевез  тонны щебня, во второй  —  …,
в последний  —  тонн; всего было
перевезено  тонн; норма перевозки
увеличивалась ежедневно на d тонн. Таким образом,

Имеем:

Следовательно, за девятый день было
перевезено 18 тонн щебня.

Ответ: 18.

Решение. Пусть улитка проползла
в первый день  метров, во второй −  …
, в последний −  метров. Тогда  м,
а за n дней проползла  метров.
Поскольку всего она проползла 150 метров, имеем:  откуда  Таким
образом, улитка потратила на весь путь 30 дней.

Ответ: 30.

Решение. В первый день Вера
подписала  открыток, во второй  —  …,
в последний  —  открыток. Всего было
подписано  открыток. Если количество
подписываемых открыток увеличивалось на d каждый день, то

Тогда

Следовательно, за четвертый день было
подписано 22 открытки.

Ответ: 22.

8. Вика решила начать
делать зарядку каждое утро. В первый день она сделала 30 приседаний, а в каждый
следующий день она делала на одно и то же количество приседаний больше, чем в
предыдущий день. За 15 дней она сделала всего 975 приседаний. Сколько приседаний
сделала Вика в пятый день?

Решение. Вика в первый день
сделала 30 приседаний, значит,  во второй  — , …
, в последний  —  приседаний. Тогда  приседаний.
Так как  получим,
что Вика увеличивала на

приседаний
в день.

Зная d, найдем a₅:

Ответ: 50.

Решение. Последовательность цен
за метр  — арифметическая прогрессия с первым членом  и
разностью  Сумма первых n членов
арифметической прогрессии вычисляется по формуле  В
нашем случае имеем:

Тем самым, цена работы составляет 117 700
руб.

Ответ: 117 700.

Решение. Число мест в ряду
представляет собой арифметическую прогрессию с первым членом и
разностью Член арифметической прогрессии с
номером k может быть найден по формуле

Необходимо найти имеем:

Ответ: 38.

11. Тренер посоветовал
Андрею в первый день занятий провести на беговой дорожке 15 минут, а на каждом
следующем занятии увеличивать время, проведённое на беговой дорожке, на 7
минут. За сколько занятий Андрей проведёт на беговой дорожке в общей сложности
2 часа 25 минут, если будет следовать советам тренера?

Решение. Время, проведённое на
беговой дорожке представляет собой арифметическую прогрессию с первым членом
равным 15 и разностью 7. Сумма n членов арифметической
прогрессии может быть найдена по формуле:

Получили квадратное уравнение на n,
решим его:

По условию задачи подходит значение

Ответ: 5.

Решение. На первом этапе приёма
капель число принимаемых капель в день представляет собой возрастающую
арифметическую прогрессию с первым членом, равным 3, разностью, равной 3 и
последним членом, равным 30. Следовательно,

этап, когда число капель в день возрастает продолжается Суммарное
число капель, принятых в этот период, представляет собой сумму арифметической
прогрессии:

Затем в течение трёх дней пациент
принимает ещё

Последний этап приёма начинается с того
момента, когда пациент уменьшит число принимаемых капель на 3, то есть примет в
день 27 капель. Этот этап длится Аналогично
первому этапу:

Таким образом, за весь курс приёма
пациенту нужно принять 165 + 90 + 135 = 390 капель. То есть нужно приобрести не
меньше пузырьков
лекарства. Минимальное количество пузырьков лекарства  — 2.

Ответ: 2.

Решение. Количество начисляемых
штрафных очков представляет собой арифметическую прогрессию с первым
членом a₁  =  1 и разностью d  =  0,5.
Сумма n первых членов этой прогрессии равна
7:

Поскольку n является
положительным числом, стрелок совершил 4 промаха, а значит, 21 попадание.

Ответ: 21.

Решение. Всего улитка проползла
5,25 м или 525 см. Последовательность пройденных расстояний представляет собой
арифметическую прогрессию с первым членом a₁  =  30 и
разностью d  =  5.

Сумма n первых членов этой прогрессии равна
525:

Поскольку n является
положительным числом, получим, что за 10 минут улитка достигнет вершины дерева.

Ответ: за 10 минут.

Решение. Последовательность
пройденных расстояний представляет собой арифметическую прогрессию с первым
членом a₁  =  1400 и разностью d  =  − 100.
Сумма n первых членов этой прогрессии равна
5000:

Следовательно, через 4 дня альпинисты
достигнут вершины.

Ответ: за 4 дня.

16. Мать дарит каждой из
пяти своих дочерей в день рождения, начиная с пяти лет, столько книг, сколько
дочери лет. Возрасты пяти дочерей составляют арифметическую прогрессию,
разность которой равна 2. Сколько лет было старшей дочери, когда у них
составилась библиотека общей численностью в 495 книг?

Решение. Обозначим за x возраст
самой младшей дочери на момент, когда у них стало 495 книг, тогда возраст
остальных дочерей составил x + 2, x + 4, x + 6
и x + 8 лет. Тогда

Решим уравнение:

Это верно при x  =  10, значит, старшей дочери было 18
лет.

Ответ: 18 лет.

Решение. Пусть большей стороне
прямоугольника, как и на стороне треугольника расположено x шаров.
Тогда на меньшей стороне прямоугольника расположено (x − 2) шара, поэтому
всего шаров в прямоугольнике x(x − 2). Количество шаров в
треугольнике представляет собой сумму членов арифметической прогрессии:

Решим уравнение:

Тогда всего шаров было 5 · 3  =  15.

Ответ: 15.

18.Для асфальтирования участка длиной 99 м используются
2 катка. Первый каток был установлен в одном конце участка, второй  — в
противоположном. Работать они начали одновременно. Первый каток в каждую минуту
проходил 5 м, а второй каток за первую минуту прошел 1,5 м, а за каждую
следующую минуту проходил на 0,5 м больше, чем за предыдущую. Через сколько
минут катки встретились?

Решение. Пусть катки встретились
через n минут. Первый каток движется равномерно, поэтому к
моменту встречи пройдет 5n метров. Расстояние, пройденное вторым катком,
является суммой n первых членов арифметической прогрессии с
первым членом 1,5 и разностью 0,5. Тогда S_n + 5n  =  99,
откуда получаем:

Тем самым катки встретятся через 11 минут.

Ответ:11.

Решение. Пусть первый кран
работал (n − 1)d + 8 часов, тогда второй кран работал (n − 2)d + 8
часов, …, n-й кран  — 8 часов. Тогда

Получаем, что для заполнения сосуда требуется 24n часов
работы. Если все краны открываются одновременно, то для заполнения всего сосуда
потребуется часа.

Ответ: 24.

Решение. Пусть всего было n рабочих,
тогда объем работы составляет 24n (считаем, что за 1 час один
рабочий выполняет единицу объема работы). Пусть также время работы по плану
составляло x часов. Тогда:

Найдем количество рабочих из уравнения Получаем:

Ответ: 25 рабочих.

21.Часть программы тренировок Арсения
заключается в беге на беговой дорожке. На первой тренировке необходимо бежать
15 минут, на каждой следующей время пробежки увеличивается на 7 минут. За
сколько тренировок Арсений проведёт на беговой дорожке в общей сложности 2 часа
25 минут, если будет следовать программе? (В ответе укажите только число.)

Решение. Время ежедневных
тренировок на беговой дорожке составляет арифметическую прогрессию с первым
членом a₁  =  15, разностью прогрессии d  =  7.
Сумма прогрессии равна 2 часа 25 минут или 145 минут. Из формулы суммы
арифметической прогрессии получаем:

Ответ: 5.

22.Занятия йогой начинают с 15 минут в день и
увеличивают на 10 минут время каждый следующий день. Сколько дней следует
заниматься йогой в указанном режиме, чтобы суммарная продолжительность занятий
составила 2 часа?

Решение. Продолжительность
занятий составляет арифметическую прогрессию с первым членом a₁  =  15,
разностью d  =  10 и суммой прогрессии S_n  =  120.
Выразим количество дней n (n>0) из формулы суммы
арифметической прогрессии:

Подставим значения в полученное выражение:

Ответ: 4 дня.

23. Диаметры пяти шкивов,
насаженных на общий вал, образуют арифметическую прогрессию. Сумма диаметров
первого и третьего шкивов составляет 26,8 см, а второго и четвёртого  —
31,6 см. Сколько сантиметров составляет диаметр наибольшего шкива?

Решение. Введем обычные
обозначения. Исходя из условия задачи, верны равенства: см, см. Составим и решим систему уравнений, выразив
каждый член арифметической прогрессии через a₁ и d:

Наибольший диаметр имеет пятый шкив, найдем по формуле для 5-го
члена арифметической прогрессии:

см.

Ответ: 20,6.

Решение. Пройденные за каждую
секунду пути составляют арифметическую прогрессию с первым членом a₁  =  0,6
и разностью d  =  0,6. Сумма членов этой прогрессии равна
6. Подставляя, получаем:

Ответ: 4 с.

Пути, пройденные телом за каждую секунду,
представляют собой арифметическую прогрессию с первым членом a₁  =  5
и разностью d  =  10. Путь, пройденный телом за 5 секунд, найдем по
формуле суммы арифметической прогрессии при n  =  5:

26.Два велосипедиста, находясь на расстоянии
153 км друг от друга, начали двигаться одновременно навстречу друг другу.
Первый велосипедист едет со скоростью 10 км/ч, второй в первый час проехал
3 км, а в каждый последующий  — на 5 км больше, чем в предыдущий. Через сколько
часов велосипедисты встретятся?

Решение. Движение второго
велосипедиста составляет арифметическую прогрессию, его путь  — сумма
арифметической прогрессии, количество членов (n>0)  — время движения,
первый член прогрессии a₁ =3, разность прогрессии d =5.
Так как велосипедисты едут навстречу, то 153 км  — сумма их путей за одно и то
же время. Составим уравнение:

Ответ: через 6 ч.

Решение. Движение улитки
составляет арифметическую прогрессию с первым членом a₁=800,
разностью d  =  −25 мм и суммой прогрессии S_n  =  5700 мм.
Выразим количество часов n (n>0) из формулы суммы
арифметической прогрессии:

Подставим значения в полученное выражение:

Заметим, что при n  =  57
последний член прогрессии получится отрицательным, следовательно, n  =  8.

Ответ: 8 часов.

Решение. Растущее количество
белок на опушке составляет арифметическую прогрессию с первым членом a₁  =  6
и разностью d  =  2, посчитав количество белок, которые придут на
опушку за n  =  30 дней по формуле суммы арифметической прогрессии
мы сможем найти количество съеденных орехов:

Подставим значения в полученное выражение:

белок
посетит опушку.

Значит, за 30 дней будет съедено орехов.

Ответ: 10500.

Решение. Количество минут игры
составляет арифметическую прогрессию с первым членом a₁  =  10
и разностью d  =  3, найдем по формуле сумму
арифметической прогрессии первых восьми членов:

минуты.

Ответ: 164 минуты.

Решение. Растущее количество
конфет составляет арифметическую прогрессию с первым членом a₁  =  5,
разностью d  =  2. Сумму первых 12 членов прогрессии

конфеты.

Ответ: 192 конфеты.

Решение. Растущее количество
задач составляет арифметическую прогрессию с первым членом a₁  =  11,
суммой прогрессии S_n  =  315 и количеством членов n  =  9.
Найдем разность арифметической прогрессии из формулы суммы:

Подставим значения в полученное выражение:

задач.

По формуле для девятого члена найдем, сколько задач Рихард
разберёт в последний день:

задач.

Ответ: 59 задач.

Приведем другое решение.

Растущее количество задач составляет
арифметическую прогрессию с первым членом a₁  =  11,
суммой прогрессии S_n  =  315 и количеством членов n  =  9.
Из формулы суммы арифметической прогрессии найдем a_n:

задач.

32.Клиент взял в банке кредит 100 рублей
на n месяцев с условием, что по окончании первого месяца
выплатит банку часть кредита, а
в каждый последующий месяц выплата будет на 5 рублей больше, чем в предыдущий. Известно,
что в последний месяц выплата составила 55 руб. На какой срок был выдан кредит,
если известно, что этот срок превышал полгода?

Решение. Ежемесячные выплаты
составляют арифметическую прогрессию с первым членом и разностью 5.
Тогда за последний месяц клиент выплатил банку руб.,
что составляет 55 руб. Решим уравнение:

Поскольку срок кредитования превышал
полгода, кредит был возвращен банку за 10 месяцев.

Ответ: на 10 месяцев.

Примечание.

Пытливый читатель может заинтересоваться
задачей и выяснить, сколько составила переплата по кредиту. Ответим на этот
вопрос.

В течение 10 месяцев банку
выплачивалась взятой в
кредит суммы, что за 10 месяцев составило 100 рублей. Это сумма, взятая в
кредит у банка. Переплата по кредиту выплачивалась в течение 9 месяцев, 5
рублей в первый месяц и на 5 рублей больше каждый следующий месяц, причем в
последний месяц было выплачено 55 − 10  =  45 рублей. Следовательно,
дополнительные выплаты составляют арифметическую прогрессию, и переплата
составила рублей.

Решение. Пусть за изготовление и
установку всех колец заплатили S_n. Тогда

Средняя стоимость установки одного кольца
с учетом премии равна 202 рубля, а значит, Получаем:

Следовательно, было установлено 9 колец.

Ответ: 9.

34.

Решение. Количества бревен в
рядах представляют собой арифметическую прогрессию с первым членом 12 и
последним членом 1. Найдем сумму этой прогрессии:

Ответ: 78 бревен.

Решение. Масса осадка в растворе
спустя семь минут после начала реакции:

г.

Ответ: 1,4.

Решение. Количества мест в рядах
представляют собой арифметическую прогрессию с первым членом 17. Найдем сумму
этой прогрессии:

Ответ: 377 мест.

Источник

Вариант № 14

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.

Объекты	Салон сотовой связи	Магазин бытовой техники	Магазин «Обувь»	Павильон «Игрушки»
Цифры

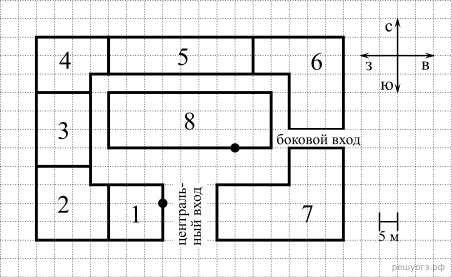
На плане (см. рисунок) изображён торговый комплекс (сторона каждой клетки на плане равна 5 м). Слева от центрального входа расположен магазин «Обувь», к которому примыкает магазин мужской одежды. В северо‐западном углу расположена «Книжная лавка», а в северо‐восточном углу — магазин бытовой техники. Между «Книжной лавкой» и магазином бытовой техники находится павильон «Игрушки». Между книжной лавкой и магазином мужской одежды — салон сотовой связи. Между центральным и боковым входами — магазин женской одежды. В центре торгового комплекса — магазин «Продукты».

Решение. Слева от центрального входа расположен магазин «Обувь», к которому примыкает магазин мужской одежды, следовательно, магазин «Обувь» отмечен цифрой 1. В северо‐западном углу расположена «Книжная лавка», а в северо‐восточном углу — магазин бытовой техники, значит, магазин бытовой техники отмечен цифрой 6. Между «Книжной лавкой» и магазином бытовой техники находится павильон «Игрушки», следовательно, павильон «Игрушки» отмечен цифрой 5. Между книжной лавкой и магазином мужской одежды — салон сотовой связи, значит, салон сотовой связи отмечен цифрой 3.

Ответ: 3615.

2. Стены магазина «Продукты» по всему периметру снаружи замостили декоративной пластиковой плиткой, которая продаётся в упаковках. Одной упаковки хватает на 7 м². Сколько упаковок потребовалось купить, если высота стен равна 4 м, а площадь двери составляет 8 м² (дверь не покрывается пластиковой плиткой)?

Решение. Найдём периметр магазина «Продукты»:

м.

Значит, площадь стен равна

м².

Таким образом, потребовалось купить упаковок. Округляя в большую сторону, получаем ответ — 68 упаковок.

Ответ: 68.

3. Найдите площадь земли (в м²), которую занимает магазин женской одежды.

Решение. Площадь магазина женской одежды равна

м².

Ответ: 675.

4. Между выделенными на плане точками необходимо проложить интернет‐кабель (по потолку). Определите наименьшую возможную длину кабеля (в метрах).

Решение. Найдём наименьшую возможную длину кабеля по теореме Пифагора:

м.

Ответ: 25.

5. Владелец магазина мужской одежды хочет заняться продвижением бренда магазина. В рекламном агентстве предложили три варианта рекламы (см. таблицу).

Тип рекламы	Стоимость создания (руб.)	Стоимость размещения и продвижения за 3 месяца (руб.)	Ожидаемое количество просмотров за месяц	Средний доход от одного просмотра (руб.)
Ролик на YouTube	10 000	30 000	150 000	0,22
ТВ‐ролик	40 000	90 000	300 000	0,23
Рекламные щиты	3 000	50 000	600 000	0,08

Владелец выбрал один вид рекламы, самый выгодный по итогам трёх месяцев. Какую прибыль (в тыс. руб.) принесёт этот вид рекламы за три месяца?

Решение. Рассмотрим все варианты.

1. Стоимость создания и продвижения ролика на YouTube равна

рублей.

Прибыль от ролика на YouTube должна составить

рублей.

2. Стоимость создания и продвижения ТВ‐ролика равна

рублей.

Прибыль от ТВ‐ролика должна составить

рублей.

3. Стоимость создания и размещения рекламного щита равна

рублей.

Прибыль от рекламного щита должна составить

рублей.

Таким образом, самым выгодным вариантом по итогам трёх месяцев являются рекламные щиты. Получим ответ в тысячах — 91.

Ответ: 91.

6. Найдите значение выражения

Решение. Найдём значение выражения:

Ответ: 3328.

7. Значение какого из данных выражений положительно, если известно, что

4)ab

Решение. Заметим, что . Имеем:

Ответ: 3

8. Найдите значение выражения при

Решение. Упростим выражение

Подставим значения :

Ответ: -157

9. Решите уравнение

Решение. Умножим обе части уравнения на 24:

Ответ: −4.

10. В фирме такси в данный момент свободно 30 машин: 1 чёрная, 9 жёлтых и 20 зелёных. По вызову выехала одна из машин, случайно оказавшаяся ближе всего к заказчику. Найдите вероятность того, что к нему приедет жёлтое такси.

Решение. Вычислим вероятность, что приедет желтое такси:

Ответ: 0,3.

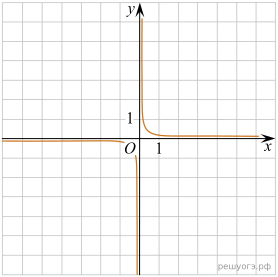
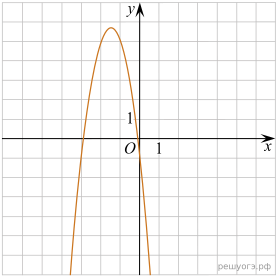
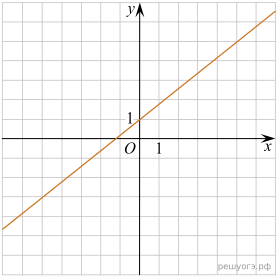
11. Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А) 

Б) 

ГРАФИКИ

В таблице под каждой буквой укажите соответствующий номер.

А	Б	В

Решение. Определим вид графика каждой из функций:

А)  — уравнение параболы, ветви которой опущены вниз

Б)  — уравнение прямой

B)  — уравнение гиперболы

Найдём для каждого графика функцию: A — 2, Б — 3, В — 1.

Ответ: 231.

12. Мощность постоянного тока (в ваттах) вычисляется по формуле P = I²R , где I — сила тока (в амперах), R — сопротивление (в омах). Пользуясь этой формулой, найдите сопротивление R (в омах), если мощность составляет 147 Вт, а сила тока равна 3,5 А.

Решение. Выразим сопротивление из формулы для мощности:

Подставляя, получаем:

Ответ: 12.

13. Решение какого из данных неравенств изображено на рисунке?

В ответе укажите номер правильного варианта.

Решение. Решим каждое из неравенств:

1)   — решений нет.

3)   — верно для всех

Правильный ответ указан под номером 4.

14. Старший брат договорился с Мишей, что в пятницу он будет готовиться к экзамену по физике, решая задачи из сборника. За первую задачу брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?

Решение. Количество минут игры составляет арифметическую прогрессию с первым членом a₁ = 10 и разностью d = 3, найдем по формуле сумму арифметической прогрессии первых восьми членов:

минуты.

Ответ: 164 минуты.

15.

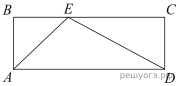
На стороне BC прямоугольника ABCD, у которого AB = 10 и AD = 34, отмечена точка E так, что ∠EAB = 45°. Найдите ED.

Решение. Треугольник ABE — прямоугольный, угол EAB равен 45°, поскольку сумма углов треугольника равна 180°, угол BEA равен Следовательно, треугольник ABE — равнобедренный, поэтому Найдём отрезок Из прямоугольного треугольника CED найдём

Ответ: 26.

16.

Касательные в точках A и B к окружности с центром O пересекаются под углом 18°. Найдите угол ABO. Ответ дайте в градусах.

Решение. Введём обозначение, как показано на рисунке. Касательные, проведённые к окружности из одной точки равны, поэтому следовательно, треугольник ABC — равнобедренный. Откуда Угол между касательной и хордой равен половине дуги, которую он заключает, значит, дуга AB равна 162°. Угол AOB — центральный, поэтому он равен дуге, на которую опирается, следовательно, равен 162°. Рассмотрим треугольник AOB, он равнобедренный, следовательно,

Ответ: 9.

17. В ромбе сторона равна 10, одна из диагоналей — , а угол, лежащий напротив этой диагонали, равен 45°. Найдите площадь ромба, деленную на

Решение. Площадь ромба равна произведению сторон на синус угла между ними:

Ответ:50.

———-

В открытом банке иррациональный ответ.

18. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

Решение. Посчитаем количество клеток внутри закрашенной области: их 18.

Ответ: 18.

19. Какие из следующих утверждений верны?

1) Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.

2) Любые две прямые имеют не менее одной общей точки.

3) Через любую точку проходит более одной прямой.

4) Любые три прямые имеют не менее одной общей точки.

Если утверждений несколько, запишите их номера в порядке возрастания.

Решение. Проверим каждое из утверждений.

1) «Если при пересечении двух прямых третьей прямой соответственные углы равны 65°, то эти две прямые параллельны.» — верно, так как если соответственные углы равны, то прямые параллельны.

2) «Любые две прямые имеют не менее одной общей точки.» — неверно, две прямые имеют не более одной общей точки.

3) «Через любую точку проходит более одной прямой.» — верно, через одну точку проходит множество пересекающихся в этой точке прямых.

4) «Любые три прямые имеют не менее одной общей точки.» — неверно, любые три прямые, которые не совпадают, если и имеют общую точку, то только одну.

Ответ: 13.

20. Решите неравенство

Решение. Преобразуем неравенство:

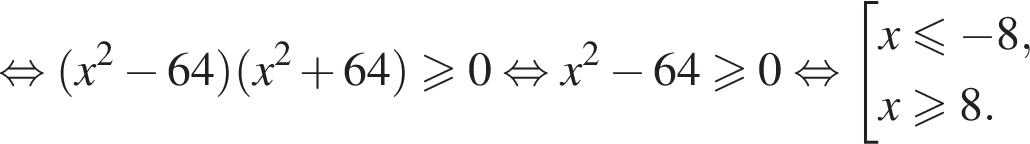
Ответ:

21. Свежие фрукты содержат 78 % воды, а высушенные — 22 %. Сколько требуется свежих фруктов для приготовления 22 кг высушенных фруктов?

Решение. Сухая часть свежих фруктов составляет 22 %, а высушенных — 78 %. Значит, для приготовления 22 кг высушенных фруктов требуется (кг) свежих.

Ответ: 78.

22. Постройте график функции Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.

Решение. Раскрывая модуль, получим, что функцию можно представить следующим образом:

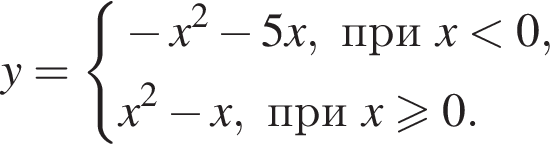
Этот график изображён на рисунке:

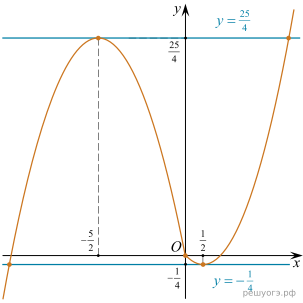
Из графика видно, что прямая имеет с графиком функции ровно две общие точки при и

Ответ: −0,25; 6,25.

23. Найдите площадь выпуклого четырёхугольника с диагоналями 3 и 4, если отрезки, соединяющие середины его противоположных сторон, равны.

Решение. 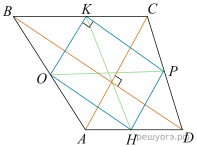Пусть ABCD — данный четырёхугольник, O — середина стороны AB, K — середина стороны BC, P  — середина стороны CD, H — середина стороны DA. Проведём диагонали AC и BD и отрезки OK, KP, PH и HO, последовательно соединяющие середины сторон четырёхугольника. Тогда, по свойству средней линии треугольника, отрезки OK и PH параллельны диагонали AC и равны её половине, а отрезки KP и HO параллельны диагонали BD и равны её половине. Поэтому OKPH — параллелограмм. А так как, по условию задачи, его диагонали KH и OP равны, то OKPH — прямоугольник, и угол OKP — прямой. Отсюда следует, что и угол между диагоналями AC и BD тоже прямой, и, следовательно, площадь четырёхугольника ABCD будет равна половине произведения его диагоналей, то есть

Ответ: 6.

24. В остроугольном треугольнике ABC проведены высоты и . Докажите, что углы и равны.

Решение. 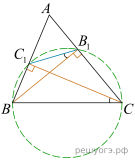Треугольники и имеют общую гипотенузу BC. Поэтому точки лежат на одной окружности. Углы и опираются на одну дугу, и поэтому равны.

25. В треугольнике ABC биссектриса угла A делит высоту, проведённую из вершины , в отношении , считая от точки . Найдите радиус окружности, описанной около треугольника ABC, если .

Решение. 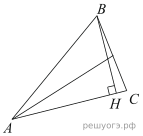Обозначим BH высоту, проведённую из вершины . Биссектриса, проведённая из угла A, делит высоту в отношении, равному отношению AB и AH. Значит, , поэтому . По теореме синусов радиус описанной около треугольника ABC окружности

Ответ: 41.

№ задания	ответ
1	3615
2	68
3	675
4	25
5	91
6	3328
7	3
8	-157
9	-4
10	0,3
11	231
12	12
13	4
14	164
15	26
16	9
17	50
18	18
19	13
20
21	78
22	−0,25; 6,25
23	6
24	—
25	41

Источник

Тренировочный вариант №329 Алекса Ларина ОГЭ 2023 по математике 9 класс с ответами и решением, который вышел на сайте 21 сентября 2022 года, по новой демоверсии ОГЭ 2023 года ФИПИ.

Скачать 2 варианта с ответами

Пробный вариант ОГЭ 2023 состоит из двух модулей: «Алгебра» и «Геометрия». Всего в работе 25 заданий. Модуль «Алгебра» содержит семнадцать заданий: в части 1 — четырнадцать заданий; в части 2 — три задания. Модуль «Геометрия» содержит восемь заданий: в части 1 — пять заданий; в части 2 — три задания.

Тренировочный вариант 329 Ларина ОГЭ 2023 по математике 9 класс

variant-larina-329-oge-2023-mat-9klass

Хозяин дачного участка строит баню с парным отделением. Парное отделение имеет размеры: длина 3,5 м, ширина 2 м, высота 2,1 м. Окон в парном отделении нет. Для прогрева парного отделения можно использовать электрическую или дровяную печь. В таблице (см. выше) представлены характеристики трёх печей.

Для установки дровяной печи дополнительных затрат не потребуется. Установка электрической печи потребует подведения специального кабеля, что обойдётся в 8 000 руб. Кроме того, хозяин подсчитал, что за год электрическая печь израсходует 2400 киловатт‐часов электроэнергии по 4 руб. за 1 киловатт‐час, а дровяная печь за год израсходует 2 м3 дров, которые обойдутся по 1600 руб. за 1 м3.

1)Найдите объём (в м3) парного отопления строящейся бани.

Ответ: 14,7

2)На сколько тысяч рублей дровяная печь, подходящая по отапливаемому объёму парного отделения, обойдётся дешевле электрической с учётом установки?

Ответ: 3

3)На сколько рублей эксплуатация дровяной печи, которая подходит по отапливаемому объёму парного отделения, обойдётся дешевле эксплуатации электрической в течение года?

Ответ: 6400

4)Доставка печи из магазина до участка стоит 600 рублей. При покупке печи ценой выше 20 000 рублей магазин предлагает скидку 5% на товар и 40% на доставку. Сколько будет стоить покупка печи «Огонёк» вместе с доставкой на этих условиях?

Ответ: 20310

5)Хозяин выбрал дровяную печь (см. рис. 1 выше). Чертёж передней панели печи показан на рисунке 2 (см. выше). Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с центром в середине нижней части кожуха (см. рис. 2). Для установки печки хозяину понадобилось узнать радиус закругления арки . Размеры кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в сантиметрах. Результат округлите до десятых.

Ответ: 21,3

10)У бабушки 10 чашек: 3 с красными цветами, остальные с синими. Бабушка наливает чай в случайно выбранную чашку. Найдите вероятность того, что это будет чашка с синими цветами.

Ответ: 0,7

14)Старший брат договорился с Мишей, что в пятницу он будет готовиться к экзамену по физике, решая задачи из сборника. За первую задачу брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?

Ответ: 164

21)Расстояние между городами A и равно 375 км. Город находится между городами А и В. Из города B C A в город выехал автомобиль, а через 1 час 30 минут следом за ним со скоростью 75 км/ч выехал мотоциклист, догнал автомобиль в городе и повернул обратно. Когда он вернулся в B C A , автомобиль прибыл в . Найдите расстояние (в км) от B A до C .

Ответ: 225

23)Прямая AD , перпендикулярная медиане BM треугольника ABC , делит угол BAC пополам. Найдите сторону AB , если сторона AC равна 4 .

Ответ: 2

24)В трапеции ABCD с основаниями AD и BC диагонали пересекаются в точке P . Докажите, что площади треугольников APB и CPD равны.

Тренировочный вариант №3 ОГЭ 2023 по математике 9 класс

Тренировочный вариант №3 ОГЭ 2023 по математике 9 класс с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

ОГЭ математика

149 вариант

1. Установите соответствие между стоимостью и номерами печей.

Заполните таблицу, в бланк ответов перенесите последовательность
трёх цифр без пробелов, запятых и других дополнительных символов.

Стоимость (руб.)	15 000	19 500	18 000
Номер печи

Хозяин дачного участка строит баню с парным отделением. Парное
отделение имеет размеры: длина 3,5 м, ширина 2,2 м, высота 2 м. Окон в парном
отделении нет, для доступа внутрь планируется дверь шириной 60 см, высота
дверного проёма 1,8 м. Для прогрева парного отделения можно использовать
электрическую или дровяную печь. В таблице представлены характеристики трёх
печей.

Номер печи	Тип	Объем помещения	Масса	Стоимость
1	Дровяная	8-12	40	18 000
2	Дровяная	10-16	48	19 500
3	Электрическая	9-15,5	15	15 000

Для установки дровяной печи дополнительных затрат не потребуется.
Установка электрической печи потребует подведения специального кабеля, что
обойдётся в 6500 руб.

2. На сколько рублей покупка дровяной печи, подходящей по объёму
парного отделения, обойдётся дешевле электрической с учётом установки?

3. Во сколько рублей обойдётся покупка электрической печи с
установкой и доставкой, если доставка печи до дачного участка будет стоить 800
рублей?

4. На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько
рублей стала стоить печь?

5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи
показан на рисунке 2.

Печь снабжена кожухом вокруг дверцы топки. Верхняя часть кожуха
выполнена в виде арки, приваренной к передней стенке печки по дуге окружности с
центром в середине нижней части кожуха (см. рис. 2). Для установки печки
хозяину понадобилось узнать радиус закругления арки R. Размеры
кожуха в сантиметрах показаны на рисунке. Найдите радиус закругления арки в
сантиметрах.

6. Найдите значение выражения 

7. На координатной прямой отмечены числа a и b. Укажите
номера неверных утверждений.

1) ab² < 0

2) a − b > 0

3) a + b < 0

4) ab < 0

8. Найдите значение выражения при

9. Решите уравнение .

Если
корней несколько, запишите их в ответ без пробелов в порядке возрастания.

10. Коля выбирает трёхзначное число. Найдите вероятность того, что оно
делится на 4.

11. Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А)

Б)

В)

ГРАФИКИ ФУНКЦИЙ

В таблице под каждой буквой укажите соответствующий номер.

Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:

12. Центростремительное ускорение (в м/c²) вычисляется по
формуле α = ω²R, где ω —
угловая скорость (в с^–1), R — радиус окружности.
Пользуясь этой формулой, найдите радиус R (в метрах), если
угловая скорость равна 10 с^–1, а центростремительное ускорение равно
54 м/c².

13. При каких значениях x значение выражения больше значения выражения ?

В
ответе укажите номер правильного варианта.

1) x > − 10

2) x < − 10

3) x > − 6

4) x < − 6

14. Старший брат договорился с Мишей, что в пятницу он будет
готовиться к экзамену по физике, решая задачи из сборника. За первую задачу
брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую
задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько
минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?

15.

Тангенс острого угла прямоугольной трапеции равен   Найдите её большее
основание, если меньшее основание равно высоте и равно 99.

16. Сторона треугольника проходит
через центр описанной около него окружности. Найдите ,
если . Ответ дайте в градусах.

17. Основания трапеции равны 18 и 12, одна из боковых сторон
равна , а угол между ней и одним из оснований равен 135°. Найдите
площадь трапеции.

18.

На клетчатой бумаге с размером клетки 1 см × 1 см отмечены
точки А, В и С. Найдите расстояние от
точки А до прямой BC. Ответ выразите в сантиметрах.

19. Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его
медианой.

Если
утверждений несколько, запишите их номера в порядке возрастания.

20. Упростите выражение:    .

21. Первый рабочий за час делает на 13 деталей больше, чем второй, и выполняет
заказ, состоящий из 208 деталей, на 8 часов быстрее, чем второй рабочий,
выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?

22. Постройте график функции и определите, при каких
значениях прямая имеет с графиком
ровно три общие точки.

23. Расстояние от
точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из
диагоналей ромба равна 40. Найдите углы ромба.

24. В треугольнике ABC с тупым углом BAC проведены
высоты BB₁ и CC₁. Докажите,
что треугольники AB₁C₁ и ABC подобны.

25. В треугольнике ABC биссектриса BE и
медиана AD перпендикулярны и имеют одинаковую длину, равную
164. Найдите стороны треугольника ABC.

Решение

1. Установите соответствие между стоимостью и номерами печей.

Стоимость (руб.)	15 000	19 500	18 000
Номер печи

Номер печи	Тип	Объем помещения	Масса	Стоимость
1	Дровяная	8-12	40	18 000
2	Дровяная	10-16	48	19 500
3	Электрическая	9-15,5	15	15 000

Решение.

Из таблицы видно, что стоимость для первой печи — 18 000, для
второй — 19 500, а для третьей — 15 000.

Ответ: 321.

Решение.

Вычислим объём помещения:

м³.

Следует, что дровяная печь под номером 2 подходит для установки в
данное парное отделение.

Разница в стоимости нужной дровяной печи и электрической (с учётом
её установки):

рублей.

Получается, на 2 000 рублей покупка дровяной печи, подходящей по
объёму парного отделения, обойдётся дешевле электрической с учётом установки.

Ответ: 2 000.

Решение.

Вычислим стоимость электрической печи:
15 000 + 800 + 6500 = 22 300 рублей.

Ответ: 22300.

4. На дровяную печь, масса которой 48 кг, сделали скидку 10%. Сколько
рублей стала стоить печь?

Решение.

Вычислим сколько стала стоить печь массой 48 кг: 19500 − 19500 · 0,1 = 19500 − 1950 = 17 550.

Ответ: 17 550.

5. Хозяин выбрал дровяную печь (рис. 1). Чертёж передней панели печи
показан на рисунке 2.

Решение.

Проведем радиус как показано на рисунке. Тогда AC = 21,
так как точка С середина по условию. Тогда имеем
треугольник ABC — прямоугольный. По теореме Пифагора найдем
радиус

Ответ: 75.

6. Найдите значение выражения 

Решение.

Приведём в скобках к общему знаменателю:

Ответ: 8.

7. На координатной прямой отмечены числа a и b. Укажите
номера неверных утверждений.

1) ab² < 0

2) a − b > 0

3) a + b < 0

4) ab < 0

Решение.

Проверим все варианты ответа:

1) ab² < 0 — неверно;

2) a − b > 0 — верно;

3) a + b < 0 — верно;

4) ab < 0 — верно.

Ответ: 1.

8. Найдите значение выражения при

Решение.

Преобразуем выражение:

Подставим значение

Ответ: 0,5.

9. Решите уравнение .

Если
корней несколько, запишите их в ответ без пробелов в порядке возрастания.

Решение.

По теореме, обратной теореме Виета, сумма корней равна −8, а их
произведение 12.

Тем самым, это числа −2 и −6.

Ответ: −6−2.

10. Коля выбирает трёхзначное число. Найдите вероятность того, что оно
делится на 4.

Решение.

Трёхзначные числа — числа от 100 до 999 включительно. Их 900 штук,
каждое четвёртое число, начиная со ста делится на 4, поэтому среди данных чисел
225 чисел делится на 4. Следовательно, вероятность выбрать число, делящееся на
4 равна

Ответ: 0,25.

11. Установите соответствие между функциями и их графиками.

ФУНКЦИИ

А)

Б)

В)

ГРАФИКИ ФУНКЦИЙ

В таблице под каждой буквой укажите соответствующий номер.

Запишите в ответ цифры, расположив их в порядке, соответствующем
буквам:

Решение.

Напомним, что если прямая задана уравнением , то:
при тангенс угла наклона прямой к оси абсцисс положителен.

Уравнение задает прямую,
которая пересекает ось ординат в точке -2. Ее график изображен на рисунке 1).

Уравнение задает прямую,
которая пересекает ось ординат в точке +2. Ее график изображен на рисунке 3).

Уравнение задает
прямую, которая пересекает ось ординат в точке -2. Ее график изображен на
рисунке 2).

Тем самым, искомое соответствие: А — 1, Б — 3, В — 2.

Ответ: 132.

Решение.

Выразим радиус из формулы для центростремительного
ускорения:

Подставляя, получаем:

Ответ: 0,54.

13. При каких значениях x значение выражения больше значения выражения ?

В
ответе укажите номер правильного варианта.

1) x > − 10

2) x < − 10

3) x > − 6

4) x < − 6

Решение.

Последовательно получаем:

Правильный ответ указан под номером: 2.

14. Старший брат договорился с Мишей, что в пятницу он будет
готовиться к экзамену по физике, решая задачи из сборника. За первую задачу
брат разрешит ему поиграть на своей приставке 10 минут, а за каждую следующую
задачу ему можно будет играть на 3 минуты больше, чем за предыдущую. Сколько
минут можно будет поиграть Мише в воскресенье, если он решит 8 задач?

Решение.

Количество минут игры составляет арифметическую прогрессию с
первым членом a₁ = 10 и разностью d = 3,
найдем по формуле сумму
арифметической прогрессии первых восьми членов:

минуты.

Ответ: 164 минуты.

15.

Решение.

Заметим, что Тангенс угла равен
отношению противолежащего катета к прилежащему. Следовательно, АВ:  АС =
1:5. Тогда

Поэтому большее основание трапеции равно

Ответ: 594.

Решение.

Угол — вписанный, опирающийся на диаметр,
поэтому он равен 90°. Сумма углов в треугольнике равна 180°,
следовательно,

Ответ: 50.

17. Основания трапеции равны 18 и 12, одна из боковых сторон
равна , а угол между ней и одним из
оснований равен 135°. Найдите площадь трапеции.

Решение.

Пусть дана трапеция ABCD, где AD = 18, BC =
12, AB = , а ∠ABC = 135°.
Опустим перпендикуляр BH на сторону AD. Угол ABH равен:
135° − 90° = 45°. Таким образом, треугольник ABH является
прямоугольным и равнобедренным. Найдем высоту BH:

Площадь трапеции равна произведению полусумму оснований на высоту:

Ответ: 60.

18.

Решение.

Расстояние от точки А до прямой ВС равно
трём сторонам клетки, или 3 см.

Ответ: 3.

19. Укажите номера верных утверждений.

1) Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны.

2) Вертикальные углы равны.

3) Любая биссектриса равнобедренного треугольника является его
медианой.

Если
утверждений несколько, запишите их номера в порядке возрастания.

Решение.

Проверим каждое из утверждений.

1) «Если два угла одного треугольника равны двум углам другого
треугольника, то такие треугольники подобны» — верно по
признаку подобия треугольников.

2) «Вертикальные углы равны» — верно, это теорема
планиметрии.

3) «Любая биссектриса равнобедренного треугольника является его
медианой» — неверно, это утверждение справедливо только для равностороннего
треугольника.

Ответ: 12.

Примечание.

Заметим, что признак подобия треугольников в учебнике геометрии
сформулирован так: «если два угла одного треугольника соответственно равны
двум углам другого, то такие треугольники подобны». В утверждении номер 1
опущено слово «соответственно», что не меняет сути.

20. Упростите выражение:    .

Решение.

1)   .

2)   .

Ответ: −3.

21. Первый рабочий за час делает на 13 деталей больше, чем второй, и
выполняет заказ, состоящий из 208 деталей, на 8 часов быстрее, чем второй
рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй
рабочий?

Решение.

Пусть второй рабочий делает за час x деталей,
тогда первый рабочий делает за час x + 13 деталей. Получаем
уравнение:

Ответ: 13.

22. Постройте график функции и определите, при каких значениях прямая имеет
с графиком ровно три общие точки.

Решение.

Раскрывая модуль, получим, что график функции можно представить
следующим образом:

Этот график изображён на рисунке:

Из графика видно, что прямая имеет с графиком
функции ровно три общие точки при и

Ответ: −1; 0.

Решение.

Введём обозначения, как показано на рисунке. Пусть диагональ  равна
40. Диагонали ромба пересекаются под прямым углом и делятся точкой пересечения
пополам. Рассмотрим треугольник  он прямоугольный, найдём синус
угла   следовательно,
угол  равен 30°. Рассмотрим треугольники  и  они
прямоугольные,  — общая,  следовательно,
эти треугольники равны, откуда  поэтому  Сумма смежных
углов ромба равно 180°, откуда

Ответ: 60°, 60°, 120°, 120°.

Решение.

Углы  и  равны как углы
с взаимно перпендикулярными сторонами. Рассмотрим треугольники  и  они
прямоугольные, углы  и  равны,
следовательно, эти треугольники подобны, откуда  Рассмотрим
треугольники  и  углы  и  равны
как вертикальные,  следовательно,
эти треугольники подобны.

Решение.

Пусть  —
точка пересечения отрезков  и  (см. рис.).
Треугольник  — равнобедренный, так как его
биссектриса  является высотой. Поэтому

; .

По
свойству биссектрисы треугольника

Проведём через вершину прямую,
параллельную . Пусть — точка пересечения
этой прямой с продолжением медианы . Тогда

Из подобия треугольников и следует,
что Поэтому и Следовательно

;

Ответ: ; ;

Извините, обсуждение на данный момент закрыто.

Источник

Количество минут игры составляет арифметическую прогрессию с первым членом a1 = 10 и разностью d = 3, найдем по формуле сумму арифметической прогрессии первых восьми членов:

Ответ: 164 минуты.

ТемаРезультатЗадания1. Числа и вычисленияНе изученаОтработать2. Числовые неравенства, координатная прямаяНе изученаОтработать3. Числа, вычисления и алгебраические выраженияНе изученаОтработать4. Уравнения, неравенства и их системыНе изученаОтработать5. Графики функцийНе изученаОтработать6. Арифметические и геометрические прогрессииНе изученаОтработать7. Алгебраические выраженияНе изученаОтработать8. Треугольники, четырёхугольники, многоугольники и их элементыНе изученаОтработать9. Уравнения, неравенства и их системыНе изученаОтработать10. Окружность, круг и их элементыНе изученаОтработать11. Площади фигурНе изученаОтработать12. Фигуры на квадратной решёткеНе изученаОтработать13. Анализ геометрических высказыванийНе изученаОтработать14. Анализ диаграмм, таблиц, графиковНе изученаОтработать15. Анализ диаграмм, таблиц, графиковНе изученаОтработать16. Простейшие текстовые задачиНе изученаОтработать17. Практические задачи по геометрииНе изученаОтработать18. Анализ диаграммНе изученаОтработать19. Статистика, вероятностиНе изученаОтработать20. Расчеты по формуламНе изученаОтработать

Добавить в вариант

Коля разобрал часы со стрелками и неправильно их собрал: перепутал часовую стрелку с минутной, кроме того, они начали идти в обратную сторону. Коля запустил часы в полдень, выставив точное время. Сколько раз за период с 12:01 до 23:59 такие часы покажут правильное время?

Классификатор: Алгебра. Текстовые задачи

Число х является корнем уравнения Найдите возможные значения Если возможных значений несколько — в ответе укажите их сумму. Если одно — то запишите это число.

Классификатор: Алгебра. Многочлены (делимость, Безу, Виет, бином. ), Методы алгебры. Преобразования выражений

Вписанная в треугольник ABC окружность с центром в точке I касается стороны BC в точке K. На отрезке CK выбираем точку D, на отрезке CD выбираем точке F, на отрезке AC выбираем точку E так, что CD = CE, EF = KD + KF. Найдите ∠EFD, если ∠EID=23°.

Классификатор: Геометрия: планиметрия. Окружности вписанные, Геометрия: планиметрия. Треугольник произвольный, Методы геометрии. Свойства хорд, касательных, секущих

Классификатор: Алгебра. Суммы и произведения

Найдите количество целы x решений неравенства

Если целых решений нет, запишите в ответе 0. Если целых решений бесконечно много, запишите в ответе 9999.

Классификатор: Алгебра: уравнения и неравенства. Неравенства комбинированные, Методы алгебры. Преобразования выражений, Методы алгебры. Разложение на множители

Решите уравнение В ответе укажите число, равное сумме корней уравнения, принадлежащих отрезку при необходимости округлив его до двух знаков после запятой.

Классификатор: Алгебра: тригонометрия. Тригонометрические уравнения, Методы алгебры. Преобразования выражений

Найдите сумму квадратов всех высот треугольника, если известны два его угла α и β и площадь S. Если ответ будет нецелым числом, округлите его до ближайшего целого

Классификатор: Геометрия: планиметрия. Треугольник произвольный, Методы геометрии. Тригонометрия в геометрии

Вычислите значения выражения для каждого решения системы и найдите среди них минимальное. В ответе укажите найденное минимальное значение, при необходимости округлив его до двух знаков после запятой.

Классификатор: Алгебра: уравнения и неравенства. Системы нелинейный уравнений, Методы алгебры. Замена переменной, Методы алгебры. Преобразования выражений

Машина проехала участок пути AB со скоростью υ1 = 40, затем вдвое больший участок пути со скоростью υ2 = 50 и, наконец, третий участок пути, который в три раза больше AB, со скоростью υ3 = 60. Найдите среднюю скорость автомобиля на всём маршруте. В ответе укажите, на сколько процентов найденная средняя скорость больше скорости υ1, при необходимости округлив результат до двух знаков после запятой.

Найдите все целые Значения a, не превосходящие по абсолютной величине 15, при каждом из которых неравен ство

выполняется при всех x из промежутка В ответе укажите сумму всех таких a.

Классификатор: Задачи с параметрами. Уравнения, Методы алгебры. Замена переменной, Методы алгебры. Преобразования выражений

Работники должны были вскопать несколько одинаковых грядок. В первый день работники вскопали 10 грядок, причем каждый вскопал одинаковое количество (не обязательно целое число грядок). На следующий день некоторые работники заболели COVID-19 и на работу вышло только 7 человек. Пришедшие работали половину рабочего дня с такой же производительностью, как и в первый день, и доделали оставшуюся работу. Сколько всего грядок было на подсобном участке?

Будем обозначать трехзначные числа, записанные цифрами a, b, c. Сколько существует трехзначных чисел, таких, что разность делится на 72 без остатка?

Классификатор: Алгебра: числа. Делимость, признаки делимости

Найдите все пары натуральных чисел для которых выполнено равенство

Классификатор: Алгебра: уравнения и неравенства. Уравнения рациональные, Методы алгебры. Косвенные методы в уравнения и неравенствах

Петя строит замок из кубиков. В какой-то момент он изобразил недостроенный замок в трех проекциях: вид спереди, вид сбоку и вид сверху. Какое наименьшее количество кубиков может быть изображено на виде сверху?

Учитель выписал на доске квадратное уравнение Андрей подставил вместо a по очереди все целые числа от 0 до 99 и решил все из получившихся 100 уравнений. Найдите сумму всех получившихся у Андрея действительных корней этих уравнений. При необходимости округлите ответ до сотых.

Классификатор: Алгебра. Квадратный трёхчлен, т. Виета

K середине XXII века человечество освоило 100 обитаемых планет в других звездных системах. От каждой планеты расходится 40 гиперпространственных порталов, и к каждой планете ведёт 40 порталов от других планет. Все порталы строго односторонние, т. если есть портал, ведущий из A в B, то нет портала, ведущего из B в A. Мистер Риггз хочет добраться с Галатеи-37 на Пандору за наименьшее число гиперпространственных прыжков. Сколько прыжков ему может потребоваться (укажите все варианты)?

Какое число окажется на 2022-м месте в бесконечной последовательности 12, 13, 14, 15, 16, 17,. , если в ней удалить все квадраты и кубы каких-либо натуральных чисел (то есть удалить числа 16 = 42, 25 = 52, 27 = 33,

Классификатор: Анализ. Последовательности

Классификатор: Алгебра: тригонометрия. Тригонометрические неравенства, Методы алгебры. Преобразования выражений

Найдите количество натуральных делителей наибольшего целого значения выражения xyz + xy + yz + zx + 2023, если сумма неотрицательных чисел x, y и z равна 2022.

Классификатор: Алгебра: числа. Количество делителей, Методы алгебры. Преобразования выражений

Среди всех вписанных четырёхугольников найдите четырёхугольник ABCD с наименьшим периметром, в котором BC = CD = AD и все попарные расстояния между точками A, B, C и D выражаются целыми числами. Чему равна площадь этого четырёхугольника?

Классификатор: Геометрия: планиметрия. Экстремальные задачи

Тест по теме “Степень с целым показателем”. Для учащихся 8 класса. Содержит 17 вопросов
Действия с геометрическими фигурами, координатами и векторами.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Тест содержит 35 заданий. Задания в тест выбираются случайным образом из общей базы заданий. Критерии: «3» 50-69%, «4» 70-90%, «5» 91-100%. Оценка выставляется сразу после прохождения теста.
Тестовая работа по теме “Графики функций”. Задания в формате ОГЭ (задание № 11), где предлагается установить соответствие между графиками функций и формулами, которые их задают
Данный онлайн тест предназначен для подготовке к ОГЭ по математике задания №13 модуля геометрия. Задания взяты с сайта ФИПИ, но не все. Некоторые задания созданы самим автором.
Тест для учащихся 8 класса и старше. Контактные данные нужны только для отправки моих комментариев (ссылка на страницу VK, электронная почта, WA). Если ответом к вопросу является дробное выражение – в ответе нужно указать десятичную дробь. Тест полезен в качестве проверки знаний при подготовке к экзаменам. Время прохождения ограничено – 30 минут.
Тест составлен из 19 заданий первой части ОГЭ по математике. Предназачен для подготовки к экзамену. Перед выполением внимательно читайте задания!
Тест на проверку знаний по теме “Проценты”. Задания на нахождение числа по проценту, процента по числу и т.д. Тест содержит 12 вопросов с одним вариантом ответа. Правильный ответ – 1 балл. Максимальное количество баллов 12.
Тест составлен из задач открытого банка заданий ОГЭ ФИПИ, раздел “Статистика и теория вероятностей”, предназначен для подготовки к ОГЭ. 7 заданий (каждое генерируется в 6 вариантах). Время прохождения – 20 минут.
Данный тест позволяет проверить уровень владения знаниями по теме Действия с обыкновенными дробями, так же можно использоваать для подготовки к ОГЭ и ЕГЭ

Проверяется умение решать практические задачи, требующие систематического перебора вариантов.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Тест содержит 5 заданий, которые выбираются случайным образом из общей базы заданий. Критерии: “3” – 3 балла, “4” – 4 балла, “5” – 5 баллов. Оценка выставляется сразу после прохождения теста.
В тесте рассматриваются вопросы по теме: “Квадратичная функция”
Тест составлен в соответствии с моделью ОГЭ 2018 года по математике, модуль “Алгебра” (1 часть). Он позволит вам оценить собственный уровень подготовки по алгебре к сдаче экзамена, выявить возможные пробелы, которые необходимо устранить.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2020 году. Данный тест представляет собой модуль «Алгебра»: один из двух модулей ОГЭ по математике. Модуль «Алгебра» содержит четырнадцать заданий части первой.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 году. Данный тест представляет собой модуль «Геометрия».
ОГЭ. Модуль “Алгебра”, часть 1, задания 1-8. Вариант № 1
В тесте проверяется умение строить и читать графики функций.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Тест предназначен для текущего и тематического контроля по математике. Основная задача- отработка практических навыков учащихся для подготовки к ОГЭ.
Тест содержит задачи о печках (№ 1-5 ОГЭ 2021). Генерируется 2 варианта. Время на прохождение – 20 минут.

При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2013 году. Данный тест представляет собой модуль «АЛГЕБРА»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2013 году. Данный тест представляет собой модуль «ГЕОМЕТРИЯ»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2013 году. Данный тест представляет собой модуль «РЕАЛЬНАЯ МАТЕМАТИКА»: один из трех модулей ГИА по математике.
Диагностическая работа по математике для 9 класса в формате ГИА, состоявшаяся 4 октября 2011 г.
Тест содержит задания модуля РЕАЛЬНАЯ МАТЕМАТИКА государственной итоговой аттестации в 9 классе по математике
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2014 году. Данный тест представляет собой модуль «Алгебра»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2014 году. Данный тест представляет собой модуль «Геометрия»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2014 году. Данный тест представляет собой модуль «Реальная математика»: один из трех модулей ГИА по математике.
предлагаю вам вам небольшой экспресс-тест для проверки, как хорошо вы умеете интерпретировать данные, представленные в виде диаграмм и графиков
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2015 году. Данный тест представляет собой модуль «Алгебра»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2015 году. Данный тест представляет собой модуль «Геометрия»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2015 году. Данный тест представляет собой модуль «Реальная математика»: один из трех модулей ГИА по математике.

Тест предназначен для проверки знания теории по теме “Треугольники”при итоговом повторении геометрии 9 класса.Задания составлены из открытого банка заданий ФИПИ по математике.
Демонстрационный аттестационный тест для закончивших 9 классов средней общеобразовательной школы по стандартной программе.
Демонстрационный аттестационный тест для закончивших 11 классов средней общеобразовательной школы по стандартной программе.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2016 году. Данный тест представляет собой модуль «Алгебра»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2016 году. Данный тест представляет собой модуль «Геометрия»: один из трех модулей ГИА по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2016 году. Данный тест представляет собой модуль «Реальная математика»: один из трех модулей ГИА по математике.
Тест с примерами на сложение и вычитание целых чисел с разными знаками. Состоит из 10 вопросов с одним правильным ответом. Правильный ответ – 1 балл. Максимальное количество баллов – 10. Удачи!
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 году. Данный тест представляет собой модуль «Алгебра»: один из трех модулей ОГЭ по математике.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2017 году. Данный тест представляет собой модуль «Реальная математика»: один из трех модулей ГИА по математике.
ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 1
ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 2
ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 3

ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 4
ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 5
ОГЭ. Модуль “Геометрия”, часть 1, задания 9 – 13. Вариант № 6
ОГЭ. Модуль “Алгебра”, часть 1, задания 1-8. Вариант № 2

ОГЭ. Модуль “Алгебра”, часть 1, задания 1-8. Вариант № 3
ОГЭ- 2017 Математика. Демонстрационный вариант. Модули “Алгебра”, «Геометрия», “Реальная математика”
В задании проверяются умения выполнять преобразования и проводить вычисления алгебраических выражений.
Обязательные ответы на все задания теста.
Вновь сгенерированный тест содержит другие вопросы из банка вопросов.
В задании проверяются умения выполнять вычисления и преобразования числовых неравенств. Задания на координатной прямой.
Обязательные ответы на все задания теста.
Вновь сгенерированный тест содержит другие вопросы из банка вопросов.
ОГЭ- 2017 Математика. Вариант 1. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 2. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 3. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 4. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 5. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 6. Модули “Алгебра”, «Геометрия», “Реальная математика”

ОГЭ- 2017 Математика. Вариант 7. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 8. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 9. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 10. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 11. Модули “Алгебра”, «Геометрия», “Реальная математика”
ОГЭ- 2017 Математика. Вариант 12. Модули “Алгебра”, «Геометрия», “Реальная математика”
Данный тест предназначен для подготовки к ОГЭ по математики. Проверка умения выполнять задание №19. Статистика,вероятность.
В тесте проверяется умение выполнять вычисления и преобразования, выполнять пре-
образования алгебраических выражений.
Обязательные ответы на все задания теста.
Вновь сгенерированный тест содержит другие вопросы из банка вопросов.
Уметь решать уравнения, неравенства и их системы.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Арифметические и геометрические прогрессии.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
В тесте проверяется умение выполнять преобразования алгебраических выражений.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.

Умение решать уравнения, неравенства и их системы.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
В тесте проверяется умение выполнять действия с геометрическими фигурами, координатами и векторами.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Действия с геометрическими фигурами, координатами и векторами.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Рассуждения при решении задач, логическая правильность рассуждений, распознавание ошибочных заключений.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Пользоваться основными единицами длины, массы, времени, скорости,площади, объёма; выражать более крупные единицы через более мелкие и наоборот. Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Описывать с помощью функций различные реальные зависимости между величинами; интерпретировать графики реальных зависимостей. Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Решение несложных практических расчетных задач. Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов
Описывать реальные ситуации на языке геометрии. Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Проверяется умение анализировать реальные числовые данные, представленные в таблицах, на диаграммах, графиках.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.
Осуществлять практические расчеты по формулам, составлять несложные формулы, выражающие зависимости между величинами.
Обязательные ответы на все задания теста.
Вновь открытый тест содержит другие вопросы из банка вопросов.

При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2018 году. Данный тест представляет собой модуль «Алгебра»: один из двух модулей ОГЭ по математике. Модуль «Алгебра» содержит четырнадцать заданий части первой.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2018 году. Данный тест представляет собой модуль «Геометрия».
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2018 году. Данный тест содержит 14 заданий модуля “Алгебра” и 6 заданий модуля “Геометрия” первой части ОГЭ. В тесте 20 заданий.
При ознакомлении с демонстрационным вариантом следует иметь в виду, что включённые в него задания не отражают всех элементов содержания, которые будут проверяться с помощью вариантов КИМ в 2019 году. Данный тест содержит 14 заданий модуля “Алгебра” и 6 заданий модуля “Геометрия” первой части ОГЭ. В тесте 20 заданий.

В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!

Источник

Тренировочный вариант 329 Ларина ОГЭ 2023 по математике 9 класс

Тренировочный вариант №3 ОГЭ 2023 по математике 9 класс

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Новое и интересное на сайте: