Точки экстремума функции решу егэ - ExamHelp.top

12. Исследование функций с помощью производной

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Поиск точек экстремума у элементарных функций

(blacktriangleright) Простейшие элементарные функции (ПЭФ) и их производные: [begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{1} & c & 0\&&\
textbf{2} & x^a & acdot x^{a-1}\&&\
textbf{3} & ln x & dfrac1x\&&\
textbf{4} & log_ax & dfrac1{xcdot ln a}\&&\
textbf{5} & e^x & e^x\&&\
textbf{6} & a^x & a^xcdot ln a\&&\
textbf{7} & sin x & cos x\&&\
textbf{8} & cos x & -sin x\[1ex]
hline
end{array} quad quad quad quad
begin{array}{|r|c|c|}
hline & text{Функция } f(x) & text{Производная } f'(x)\
hline
textbf{9} & mathrm{tg}, x & dfrac1{cos^2 x}\&&\
textbf{10} & mathrm{ctg}, x & -,dfrac1{sin^2 x}\&&\
textbf{11} & arcsin x & dfrac1{sqrt{1-x^2}}\&&\
textbf{12} & arccos x & -,dfrac1{sqrt{1-x^2}}\&&\
textbf{13} & mathrm{arctg}, x & dfrac1{1+x^2}\&&\
textbf{14} & mathrm{arcctg}, x & -,dfrac1{1+x^2}\[0.5ex]
hline
end{array}]

(blacktriangleright) Элементарные функции (ЭФ) — любые линейные комбинации простейших элементарных функций (то есть их сумма, разность, умножение на число).

Пример: (f(x)=4cos x +dfrac{x^3}2)

(blacktriangleright) Основные формулы поиска производной ((f=f(x), g=g(x)) – функции):

1. Умножение функции на число: [(ccdot f)’=ccdot f’]

2. Сумма или разность двух функций: [(fpm g)’=f’pm
g’]

(blacktriangleright) Хитрости, упрощающие поиск производной:

I. Т.к. (sqrt[n]{x^m}=x^{frac mn}), то производную этой функции можно искать по формуле (2).

Частный случай: (sqrt x =x^{frac12}): [(sqrt x)’=dfrac1{2sqrt x}]

II. Т.к. (dfrac1{x^a}=x^{-a}), то производную этой функции можно также искать по формуле (2): [left(dfrac1{x^a}right)’=-dfrac a{x^{a+1}}]

(blacktriangleright) Для того, чтобы найти точки экстремума, необходимо схематично изобразить график функции.
В задачах из данной подтемы это можно сделать с помощью производной: найти промежутки возрастания ((f’>0)) и убывания ((f'<0)) функции, критические точки (где (f’=0) или (f’) не существует).

Задание
1

#2390

Уровень задания: Легче ЕГЭ

Найдите точку максимума функции (y = -x^2).

ОДЗ: (x) – произвольный.

1) [y’ = -2x]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [-2x = 0qquadLeftrightarrowqquad x = 0,.] Производная существует при любом (x).

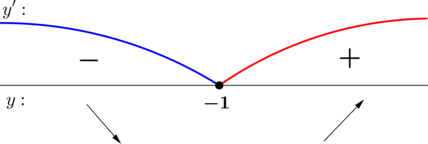
2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика:

Таким образом, (x = 0) – точка максимума функции (y).

Ответ: 0

Задание
2

#2391

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = x^2 + 2x + 2) на отрезке ([-2; 2]).

ОДЗ: (x) – произвольный.

1) [y’ = 2x + 2]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [2x + 2 = 0qquadLeftrightarrowqquad x = -1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-2; 2]):

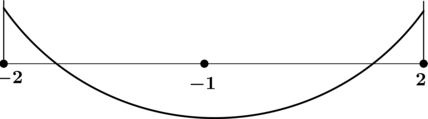
4) Эскиз графика на отрезке ([-2; 2]):

Таким образом, (x = -1) – точка минимума функции (y) на ([-2; 2]).

Ответ: -1

Задание
3

#2392

Уровень задания: Легче ЕГЭ

Найдите точку минимума функции (y = 3x^2 — 6x + pi) на отрезке ([-3; 3]).

ОДЗ: (x) – произвольный.

1) [y’ = 6x — 6]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [6x — 6 = 0qquadLeftrightarrowqquad x = 1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

3) Найдём промежутки знакопостоянства (y’) на рассматриваемом отрезке ([-3; 3]):

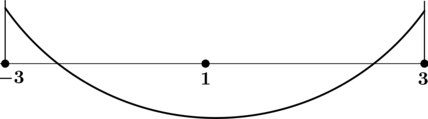
4) Эскиз графика на отрезке ([-3; 3]):

Таким образом, (x = 1) – точка минимума функции (y) на ([-3; 3]).

Ответ: 1

Задание
4

#2691

Уровень задания: Равен ЕГЭ

Найдите точку локального минимума функции (y = x^3 — 3x).

ОДЗ: (x) – произвольный.

1) [y’ = 3x^2 — 3]

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует): [3x^2 — 3 = 0qquadLeftrightarrowqquad x = pm 1,.] Производная существует при любом (x).

2) Найдём промежутки знакопостоянства (y’):

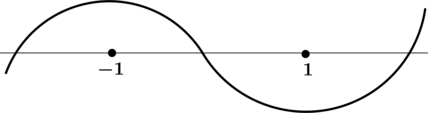
3) Эскиз графика (y):

Таким образом, (x = 1) – точка локального минимума функции (y).

Ответ: 1

Задание
5

#2710

Уровень задания: Равен ЕГЭ

Найдите точку локального максимума функции

(y = x^3 — 15x^2 + 48x + e).

1) (y’ = 3x^2 — 30x + 48 = 3(x^2 — 10x + 16)).

Найдём критические точки (то есть внутренние точки области определения функции, в которых её производная равна (0) или не существует):

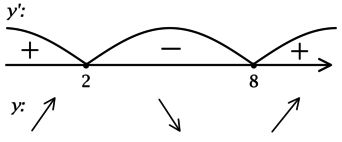
[3(x^2 — 10x + 16) = 0qquadLeftrightarrowqquad x^2 — 10x + 16 = 0,] откуда находим (x_1 = 2, x_2 = . Таким образом, [y’ = 3(x — 2)(x — 8).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

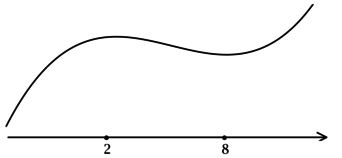
3) Эскиз графика (y):

Таким образом, (x = 2) – точка локального максимума функции (y).

Ответ: 2

Задание
6

#869

Уровень задания: Равен ЕГЭ

Найдите точку локального максимума функции (y = dfrac{1}{3}x^3 — 8x^2 + 55x + 11).

1) (y’ = x^2 — 16x + 55).

(x^2 — 16x + 55 = 0), откуда находим корни (x_1 = 5, x_2 = 11). Таким образом, [y’ = (x-5)(x-11).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

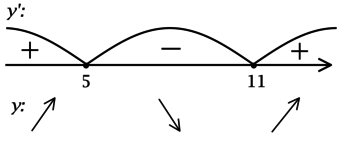
2) Найдём промежутки знакопостоянства (y’):

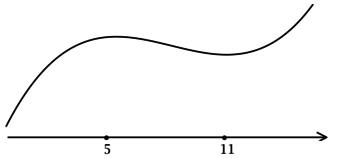
3) Эскиз графика (y):

Таким образом, (x = 5) – точка локального максимума функции (y).

Ответ: 5

Задание
7

#868

Уровень задания: Равен ЕГЭ

Найдите точку локального минимума функции (y = dfrac{1}{3}x^3 — 3x^2 + 8x + 2).

1) (y’ = x^2 — 6x + .

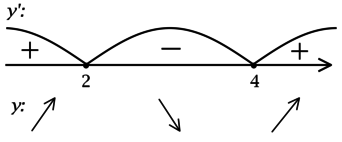
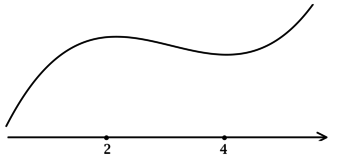
(x^2 — 6x + 8 = 0), откуда находим корни (x_1 = 2, x_2 = 4). Таким образом, [y’ = (x-2)(x-4).] Для того, чтобы найти точки локального максимума/минимума функции, нужно понять, как схематично выглядит её график.

2) Найдём промежутки знакопостоянства (y’):

3) Эскиз графика (y):

Таким образом, (x = 4) – точка локального минимума функции (y).

Ответ: 4

Задачи, при выполнении которых требуется найти точки экстремума у элементарных функций, в ЕГЭ по математике включаются каждый год. Уметь справляться с ними должны школьники, сдающие как базовый уровень экзамена, так и профильный. Научившись безошибочно находить максимум и минимум элементарной функции в задачах ЕГЭ, выпускники смогут выполнить задание и получить конкурентные баллы.

Восполнить пробелы в знаниях и лучше усвоить информацию вам поможет образовательный проект «Школково». Чтобы учащимся было легче справляться с задачами ЕГЭ, в которых необходимо найти минимум и максимум элементарной функции, мы предлагаем прежде всего повторить определения и основные правила. Эту информацию мы разместили в разделе «Теоретическая справка». Здесь собран материал, подготовленный нашими специалистами для выпускников средних школ.

Чтобы закрепить усвоенную информацию и научиться справляться с задачами в ЕГЭ, выполните упражнения, в которых требуется найти точки экстремума у элементарных функций. Богатая подборка задач представлена в разделе «Каталог». Задания здесь регулярно обновляются и дополняются. Выполнить упражнения на нахождение точек экстремума у элементарных функций, которые встречаются в ЕГЭ, можно в режиме онлайн, находясь в Москве или любом другом городе России.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Задание 11 первой части Профильного ЕГЭ по математике — это нахождение точек максимума и минимума функции, а также наибольших и наименьших значений функции с помощью производной.

Вот какие типы задач могут встретиться в этом задании:

Нахождение точек максимума и минимума функций

Исследование сложных функций

Нахождение наибольших и наименьших значений функций на отрезке

Нахождение точек максимума и минимума функций

1. Найдите точку максимума функции $displaystyle y=-{{x^2+289}over{x}}.$

Найдем производную функции.

Приравняем производную к нулю. Получим:

$x^2=289Leftrightarrow left[ begin{array}{c} x=17, hfill \ x=-17. end{array} right.$

Исследуем знаки производной.

В точке x = 17 производная меняет знак с «плюса» на «минус». Значит, x= 17 — точка максимума функции y(x).

Ответ: 17.

2. Найдите точку минимума функции

Найдем производную функции.

Приравняем производную к нулю.

$4x-5+{{1}over{x}}=0Leftrightarrow 4x^2-5x+1=0Leftrightarrow left[ begin{array}{c} x=1, \ x={{1}over{4}}. end{array} right.$

Определим знаки производной.

В точке x = 1 производная меняет знак с «минуса» на «плюс». Значит, x= 1 — точка минимума функции y(x).

Ответ: 1.

Исследование сложных функций

3. Найдите точку максимума функции $y=2^{5-8x-x^2}.$

Перед нами сложная функция $y=2^{5-8x-x^2}.$ Возможно, вы знаете формулы производной сложной функции. Но вообще-то их изучают на первом курсе вуза, поэтому мы решим задачу более простым способом.

Так как функция y=2^t монотонно возрастает, точка максимума функции $y=2^{5-8x-x^2}$ будет при том же x_0 , что и точка максимума функции А ее найти легко.

$t^{$

$t^{$ при x=-4 . В точке x = -4 производная ${{ t}}^{{$ меняет знак с «плюса» на «минус». Значит, x= - 4 — точка максимума функции .

Заметим, что точку максимума функции можно найти и без производной.

Графиком функции является парабола ветвями вниз, и наибольшее значение достигается в вершине параболы, то есть при $x=-frac{8}{2}=-4.$

Ответ: — 4.

4. Найдите абсциссу точки максимума функции $y=sqrt{4-4x-x^2}.$

Напомним, что абсцисса — это координата по

Снова сложная функция. Применяем тот же прием, что и в предыдущей задаче.

Так как функция монотонно возрастает, точка максимума функции $y=sqrt{4-4x-x^2}$ является и точкой максимума функции

Это вершина квадратичной параболы $tleft(xright)=4-4x-x^2;x_0=frac{-4}{2}=-2.$

Нахождение наибольших и наименьших значений функций на отрезке

5. Найдите наибольшее значение функции на отрезке

Мы помним, что наибольшее значение функции на отрезке может достигаться либо в точке максимума, либо на конце отрезка. Эти случаи показаны на рисунке.

Будем искать точку максимума функции с помощью производной. Найдем производную и приравняем ее к нулю.

${3x}^2+4x-4=0;$

$D=64;x=frac{-4pm 8}{6};x_1=frac{2}{3},x_2=-2.$

Найдем знаки производной.

В точке x = - 2 производная равна нулю и меняет знак с «+» на «-«. Значит, x = — 2 — точка максимума функции y(x) . Поскольку при функция y(x) убывает, $y_{max}left(xright)=yleft(-2right)=12.$ В этой задаче значение функции на концах отрезка искать не нужно.

Ответ: 12.

6. Найдите наименьшее значение функции $y={4x}^2-10x+2lnx-5$ на отрезке

Найдем производную функции $y={4x}^2-10x+2lnx-5$ и приравняем ее к нулю.

при $x_1=1,x_2=frac{1}{4}.$

Найдем знаки производной.

Точка x_1=1 — точка минимума функции . Точка $x_2=frac{1}{4}$ не лежит на отрезке Поэтому

и Значит, наименьшее значение функции на отрезке достигается при x=1. Найдем это значение.

$y_{min}left(xright)=yleft(1right)=4-10-5=-11.$

Ответ: -11.

7. Найдите наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

Иногда перед тем, как взять производную, формулу функции полезно упростить.

Мы применили формулу для логарифма произведения. при $x=frac{1}{9}.$

Если то Если , то

Значит, $x=frac{1}{9}$ — точка минимума функции y(x) . В этой точке и достигается наименьшее значение функции на отрезке $left[frac{1}{18};frac{5}{18}right].$

$y_{min}left(xright)=yleft(frac{1}{2}right)=1+3=4.$

Ответ: 4.

8. Найдите наибольшее значение функции на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

Найдем производную функции

Приравняем производную к нулю: $14-frac{7}{{cos}^2x}=0.$

${cos}^2x=frac{1}{2}.$

${cos}^2x=pm frac{1}{sqrt{2}}=pm frac{sqrt{2}}{2}$ . Поскольку $xin left[-frac{pi }{3};frac{pi }{3}right], y$ если $x=pm frac{pi }{4}.$

Найдем знаки производной на отрезке $left[-frac{pi }{3};frac{pi }{3}right].$

При $x=frac{pi }{4}$ знак производной меняется с «плюса» на «минус». Значит, $x=frac{pi }{4}$ — точка максимума функции y(x).

Мы нашли точку максимума, но это еще не все. Сравним значения функции в точке максимума и на конце отрезка, то есть при $x=-frac{pi }{3}$ и $x =frac{pi }{4}.$

$yleft(frac{pi }{4}right)=-7+11=4;$

Мы нашли, что $y_{max}left(xright)=yleft(frac{pi }{4}right)=-7+11=4.$

Заметим, что если вам попадется такая задача в первой части ЕГЭ по математике, то находить значение функции при $-frac{pi }{3}$ не обязательно. Как мы видим, это значение — число иррациональное. А в первой части ЕГЭ по математике ответом может быть только целое число или конечная десятичная дробь.

Ответ: 4.

9. Найдите наименьшее значение функции $y=e^{2x}-{8e}^x+9$ на отрезке [0;2].

Снова сложная функция. Запишем полезные формулы:

${{(e}^{-x})}^{$

${left(e^{cx}right)}^{$

${(e}^{x+a})$

Найдем производную функции $y=e^{2x}-{8e}^x+9.$

если e^x=4. Тогда x=ln4.

При x=ln4 знак производной меняется с «минуса» на «плюс». Значит, x=ln4 — точка минимума функции y(x).

Ответ: -7.

10. Найдите наибольшее значение функции на отрезке $left[0;frac{pi }{2}.right]$

Как всегда, возьмем производную функции и приравняем ее к нулю.

$sinx=frac{sqrt{3}}{2}.$

По условию, $xin left[0;frac{pi }{2}right]$ . На этом отрезке условие $sinx=frac{sqrt{3}}{2}$ выполняется только для $x=frac{pi }{3}.$ Найдем знаки производной слева и справа от точки $x=frac{pi }{3}.$

В точке $x_0=frac{pi }{3}$ производная функции меняет знак с «плюса» на «минус». Значит, точка $x_0=frac{pi }{3}$ — точка максимума функции y(x) . Других точек экстремума на отрезке $left[0;frac{pi }{2}right]$ функция не имеет, и наибольшее значение функции на отрезке $left[{ 0};frac{pi }{{ 2}}right]$ достигается при ${ x=}frac{pi }{{ 3}}.$

$y_{max}left(xright)=yleft(frac{pi }{3}right)=12.$

Ответ: 12.

11.Найдите наименьшее значение функции на отрезке $left[0;frac{pi }{2}right].$

Найдем производную функции и приравняем ее к нулю. — нет решений.

Что это значит? Производная функции не равна нулю ни в какой точке. Это значит, что знак производной в любой точке одинаков, а функция не имеет экстремумов и является монотонной.

Поскольку , получим, что для всех , и функция монотонно возрастает при $xin left[0;frac{pi }{2}right].$

Значит, наименьшее свое значение функция принимает в левом конце отрезка $left[{ 0};frac{pi }{{ 2}}right]$ , то есть при x=0.

$y_{min}left(xright)=yleft(0right)=6.$

Ответ: 6

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 11 Профильного ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Экстремумы функции

С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.

Решение онлайн
Видеоинструкция
Оформление Word
Также решают

Необходимое условие экстремума функции одной переменной

Уравнение f’₀(x^*) = 0 — это необходимое условие экстремума функции одной переменной, т.е. в точке x^* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки x^с, в которых функция не возрастает и не убывает.

Достаточное условие экстремума функции одной переменной

Пусть f₀(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x^* выполняется условие:

f’₀(x^*) = 0

f»₀(x^*) > 0

то точка x^* является точкой локального (глобального) минимума функции.

Если в точке x^* выполняется условие:

f’₀(x^*) = 0

f»₀(x^*) < 0

то точка x^* — локальный (глобальный) максимум.

Пример №1. Найти наибольшее и наименьшее значения функции:
на отрезке [1; 3].

Решение.

Критическая точка одна x₁ = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).

Вычисляем значения функции на концах отрезка и в критической точке.

f(1)=9, f(2)=⁵/₂, f(3)=3 ⁸/₈₁

Ответ: f_min=⁵/₂ при x=2; f_max=9 при x=1

Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).

Решение.

Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±^π/₃+2πk, k∈Z. Находим y’’=2sin(x), вычисляем , значит x=^π/₃+2πk, k∈Z – точки минимума функции; , значит x=-^π/₃+2πk, k∈Z – точки максимума функции.

Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.

Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).

Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x₀ или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.

Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.

Решение. Обозначим x — первое слагаемое. Тогда (49-x) — второе слагаемое.

Произведение будет максимальным: x·(49-x) → max

или

49x — x²

Наибольший объем цилиндра

Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.

Решение:

Объем цилиндра равен: V = πr²H

где H = 2h,

Подставим эти значения в целевую функцию.

V → max

Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса Производная онлайн и приравняем ее к нулю.

dV/dh = 2πR² — 6πh²

dV/dh = 0

2πR² — 6πh² = 0 или R² = 3h²

Откуда

При высоте и радиусе основания размеры цилиндра будут наибольшими.

Источник

Поиск точек экстремума у элементарных функций

Экстремумы функции

Необходимое условие экстремума функции одной переменной

Достаточное условие экстремума функции одной переменной

Наибольший объем цилиндра

Новое и интересное на сайте: