Ставлю 10/10
Все нравится, очень удобный сайт, помогает в учебе. Кроме этого, можно заработать самому, выставляя готовые учебные материалы на продажу здесь. Рейтинги и отзывы на преподавателей очень помогают сориентироваться в начале нового семестра. Спасибо за такую функцию. Ставлю максимальную оценку.
Отлично
Лучшая платформа для успешной сдачи сессии
Познакомился со СтудИзбой благодаря своему другу, очень нравится интерфейс, количество доступных файлов, цена, в общем, все прекрасно. Даже сам продаю какие-то свои работы.
Отлично
Студизба ван лав ❤
Очень офигенный сайт для студентов. Много полезных учебных материалов. Пользуюсь студизбой с октября 2021 года. Серьёзных нареканий нет. Хотелось бы, что бы ввели подписочную модель и сделали материалы дешевле 300 рублей в рамках подписки бесплатными.
Отлично
Отличный сайт
Лично меня всё устраивает — и покупка, и продажа; и цены, и возможность предпросмотра куска файла, и обилие бесплатных файлов (в подборках по авторам, читай, ВУЗам и факультетам). Есть определённые баги, но всё решаемо, да и администраторы реагируют в течение суток.
Отлично
Маленький отзыв о большом помощнике!
Студизба спасает в те моменты, когда сроки горят, а работ накопилось достаточно. Довольно удобный сайт с простой навигацией и огромным количеством материалов.
Хорошо
Студ. Изба как крупнейший сборник работ для студентов
Тут дофига бывает всего полезного. Печально, что бывают предметы по которым даже одного бесплатного решения нет, но это скорее вопрос к студентам. В остальном всё здорово.
Отлично
Спасательный островок
Если уже не успеваешь разобраться или застрял на каком-то задание поможет тебе быстро и недорого решить твою проблему.
Отлично
Всё и так отлично
Всё очень удобно. Особенно круто, что есть система бонусов и можно выводить остатки денег. Очень много качественных бесплатных файлов.
Отлично
Отзыв о системе «Студизба»
Отличная платформа для распространения работ, востребованных студентами. Хорошо налаженная и качественная работа сайта, огромная база заданий и аудитория.
Хорошо
Отличный помощник
Отличный сайт с кучей полезных файлов, позволяющий найти много методичек / учебников / отзывов о вузах и преподователях.
Отлично
Отлично помогает студентам в любой момент для решения трудных и незамедлительных задач
Хотелось бы больше конкретной информации о преподавателях. А так в принципе хороший сайт, всегда им пользуюсь и ни разу не было желания прекратить. Хороший сайт для помощи студентам, удобный и приятный интерфейс. Из недостатков можно выделить только отсутствия небольшого количества файлов.
Отлично
Спасибо за шикарный сайт
Великолепный сайт на котором студент за не большие деньги может найти помощь с дз, проектами курсовыми, лабораторными, а также узнать отзывы на преподавателей и бесплатно скачать пособия.
Отлично
Начертательная геометрия и инженерная графика, ТПУ
Томский политехнический Университет
Лист 1 по начертательной геометрии
Пояснения к задаче 1
Для определения натуральной величины треугольника АВС, требуется сделать две замены плоскостей проекций, т.к. треугольник лежит в плоскости общего положения.
Вначале заменяем плоскость V на V1, располагая ее перпендикулярно плоскости Н и плоскости треугольника АВС. Для этого новую плоскость V1 устанавливаем перпендикулярно горизонтали треугольника – А1.
Строим фронтальную проекцию горизонтали – a’1‘ параллельно оси х, затем строим ее горизонтальную проекцию – a1. Новую ось х1 проводим перпендикулярноa1. Проведя из точек a, b, c, перпендикуляры к оси х1, и откладывая на них (от точек пересечения перпендикуляров с осью х1) z координаты точек, получаем новую фронтальную проекцию треугольника. Так как плоскость треугольника перпендикулярна плоскости V1, то полученные проекции точек будут лежать на одной линии.
При второй замене плоскость H1 располагаем перпендикулярно плоскости V1 и параллельно плоскости треугольника. На эту плоскость треугольник спроецируется в натуральную величину. Ось х2 проводим параллельно линии c1′a1′ b1′ и строим новые горизонтальные проекции точек. Для этого из точек a1′, b1′, c1′ проводим перпендикуляры к оси х2 и от точек пересечения их с осью откладываем yкоординаты точек (т.е. расстояния от горизонтальных проекций точек до оси х1). Полученные проекции точек a1,b1,c1 соединяем прямыми линиями. Построенная проекция треугольника равна его натуральной величине.
Пояснения к задаче 2
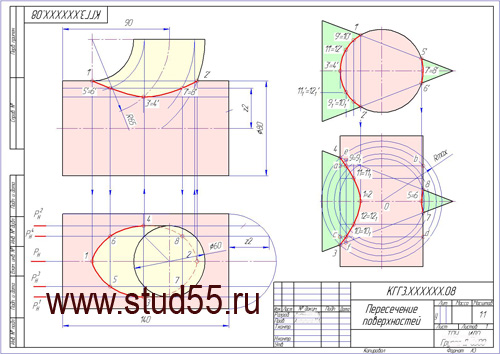
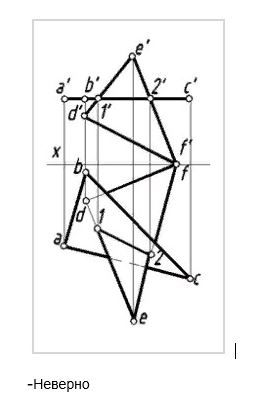
Для построения линии пересечения двух треугольников АВС и DEK необходимо найти две общие точки, принадлежащие тому и другому треугольнику. Эту задачу можно решить, например, определив точки пересечения сторон одного треугольника с плоскостью второго.
Вначале определяем точку пересечения прямой СB (сторона треугольника АВС) с плоскостью треугольника DEK, а затем – точку пересечения прямой DК(сторона треугольника DEK) с плоскостью треугольника АВС
Чтобы определить точку пересечения прямой СB с плоскостью треугольникаDEK, через прямую СB проводим фронтально-проецирующую плоскость Р (РV). Строим линию пересечения плоскости Р с плоскостью треугольника DEK (отмечая точки пересечения сторон KE и DK треугольника с плоскостью Р – точки 1, 2). Плоскость Р пересекает плоскость треугольника по прямой 12 (12, 1’2′). Определяем точку пересечения прямой СB с линией 12 – точку N. На пересечении горизонтальных проекций прямых (cb и 12) получаем горизонтальную проекцию точки N(n). По горизонтальной проекции точки (n) находим ее фронтальную проекцию – n‘ (на фронтальной проекции прямой BС (b’с‘). Аналогично находим точку М (m, m‘), проводя дополнительную горизонтально-проецирующую плоскость R (RV).
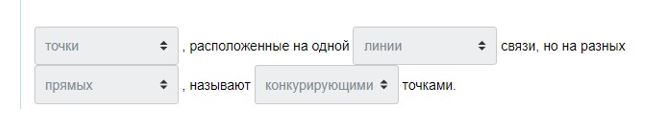
Считая треугольники непрозрачными, определяем их взаимную видимость способом «конкурирующих точек». Конкурирующие точки – точки, принадлежащие разным прямым, но лежащие на общем проецирующим луче.
Для определения видимости на фронтальной плоскости проекций рассмотрим две фронтально-конкурирующие точки 1 и 5. На фронтальной плоскости их проекции совпадают, хотя и принадлежат разным прямым. Точка 1 принадлежит ВС, точка 1 –EK. ВС и EK – скрещивающиеся прямые. Истинное положение этих точек относительно фронтальной плоскости можно выяснить, определив их y координаты. Точка, имеющая большую координату y (точка 5), расположена дальше от плоскостиV, т.е. ближе к нам, и, следовательно, будет видима. Прямая CB, которой принадлежит точка 5, также будет видима, а прямая EK – невидима.
Для определения видимости на горизонтальной плоскости необходимо рассмотреть горизонтально — конкурирующие точки 4 и 6.
Лист 2
Пояснения к задаче 4
Анализ условия задачи показывает, что вырез сделан тремя плоскостями частного положения. Следовательно, решение задачи можно разделить на следующие части – построить линию пересечения конуса: фронтально-фроецирующей плоскостью T (TV); профильной плоскостью Q (QV); горизонтальной плоскостью R (RV).
Секущая плоскость профильная плоскость Q (QV) параллельная высоте конуса, на горизонтальной плоскости проекций проецируется в линию, на которой по высотам находим точки 1, 2, 3, на профильной плоскости в виде параболлы
Секущая плоскость параллельна плоскости проекций R (RV), то плоскость сечения конуса проецируется на плоскость Н в натуральную величину в виде окружности, получаем точки 4, 5, 6.
Фронтально-проецирующей плоскостью T (TV) не параллельна ни к одной из плоскостей проекций, проекциями на гор. и профильной являются эллипсы. По линиям связи находим точки 6,7,8
Пояснения к задаче 5
Метод вспомогательных секущих плоскостей
Построения линии пересечения цилиндра с тором. Для построения линии пересечения заданных поверхностей в качестве вспомогательных плоскостей целесообразно использовать ряд вертикальных плоскостей (Р,Р1, Р2).
Построение начинаем с определения проекций характерных точек 1и 2. Проводим фронтальную плоскость P(PH). Эта плоскость пересекает поверхности по очеркам. Фронтальные проекции точек (1′ и 2′) находим, как точки пересечения очерков. Горизонтальные проекции 1 и 2 определяем, проведя линии связи. Проекции 3′ и 4′ точек, лежащих на экваторе сферы, находим с помощью горизонтальной плоскости T(TV), проходящей через центр сферы.
Ряд вспомогательных фронтальных плоскостей пересекают цилиндр по прямоугольникам и тор по кольцам, с помощью плоскостей Р3, Р4
Определяем положение точек 5, 6, 7, 8 на фронтальной плоскости проекций и по линиям связи на горизонтальной.
Лист №3
Пояснения к задаче 6
Построение линии пересечения цилиндра и конуса вращения.
Точки 1, 2,3, 4, 5, 6, 7, 8 определяются как точки пересечения контурных образующих поверхностей. Остальные точки находим способом вспомогательных сфер. Из точки пересечения осей данных поверхностей (точки O) построим вспомогательную сферу произвольного радиуса. Эта сфера пересечет их по окружностям, горизонтальные проекции этих окружностей − отрезки прямых. Проведенная сфера пересекает конус по окружности диаметра ЕF(ef), а цилиндр − по окружностям диаметра АВ(ab) и диаметра CD(cd). В пересечении окружности EF с окружностями CD и AB получаем соответственно точки 9-10 и 91-101, принадлежащие линии пересечения.
Радиус максимальной секущей сферы будет равен расстоянию от центра O до самой удаленной точки пересечения контурных образующих (от точки 0 до точек 3 и 4). Минимальной секущей сферой должна быть такая сфера, которая касалась бы одной поверхности – в нашем случае касается поверхности цилиндра и радиус равен радиусу основания цилиндра.
Лист 1 и 2 по инженерной графике
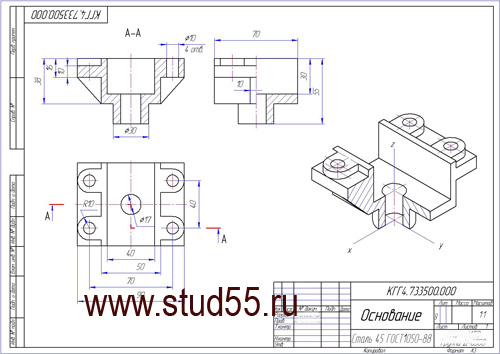
1. По двум данным построить три изображения детали, выполнить рациональные разрезы, нанести размеры. Построить прямоугольную изометрию детали с вырезом ее части (лист 1).
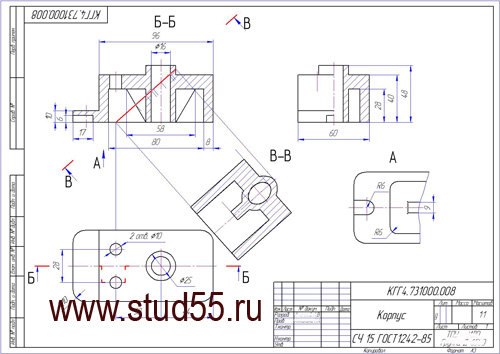
2. По двум данным построить три изображения детали, выполнить рациональные разрезы, нанести размеры. Построить сечения детали заданной наклонной плоскостью (лист 2).
Лист 3
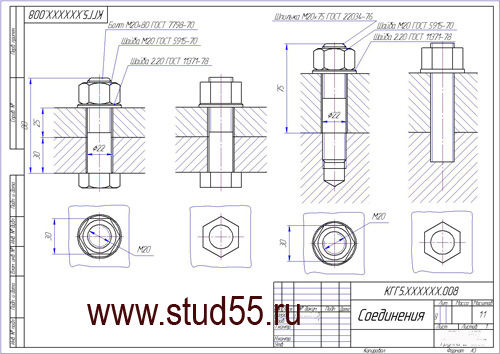
1. Выполнить два изображения соединения болтом по действительным размерам и упрощенное его изображение по ГОСТ 2.315-68.
2. Выполнить два изображения соединения шпилькой по действительным размерам и упрощенное его изображение по ГОСТ 2.315-68. Данные для выполнения задания приведены в табл. 2 для соединения болтом и в табл. 3 для соединения шпилькой.
177 тестовых вопросов по начертательной геометрии и инженерной графике с правильными ответами
1. Масштабы увеличения — 1:2; 1:2,5; 1:4; 1:5; 1:10; 1:15; 1:20; 1:25; 1:40; 1:50; 1:75; 1:100; 1:200; 1:400; 1:500; 1:800; 1:1000
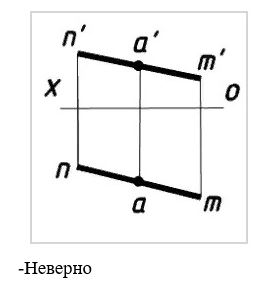
-Неверно
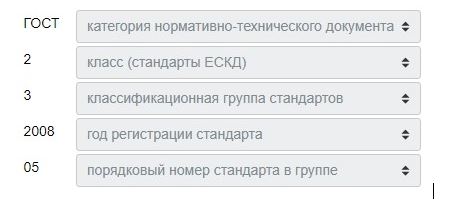
2. Установите правильное соответствие обозначение стандарта:
ГОСТ 2.305-2008 «Изображения, виды, разрезы, сечения».
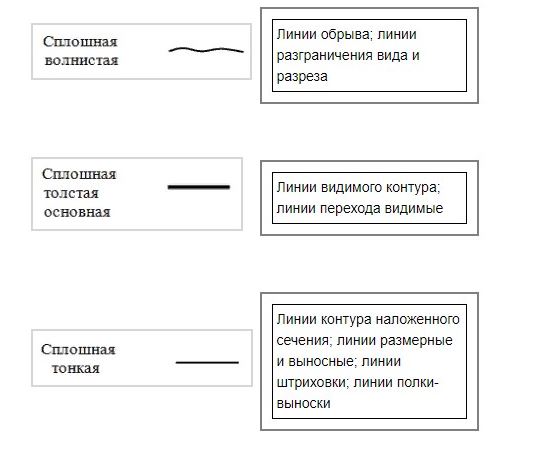
9. Установите правильное соответствие наименования линий чертежа и их основного назначения.
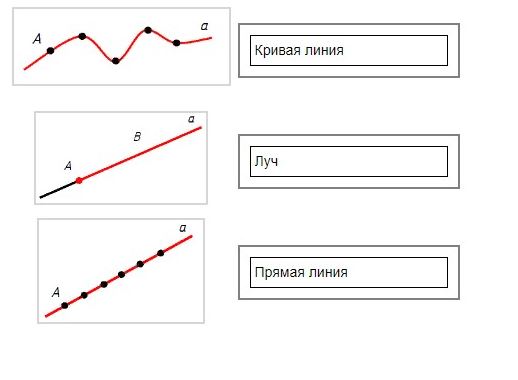
25. Установите правильное соответствие.
37. Французский ученый Гаспар Монж (1746-1818 гг.) основоположник начертательной геометрии.
45. Вставьте пропущенные в тексте слова из предложенных вариантов.
56. Точка А не принадлежит прямой MN.
71. Плоскость, не перпендикулярную и не параллельную ни одной из плоскостей проекций, называют плоскостью
-Общего положения
81. Плоскости пересекаются по прямой параллельной фронтальной плоскости проекций.
89. Высота, на которую поднимается точка по прямой за полный оборот, называется шагом винтовой линии.
-Верно
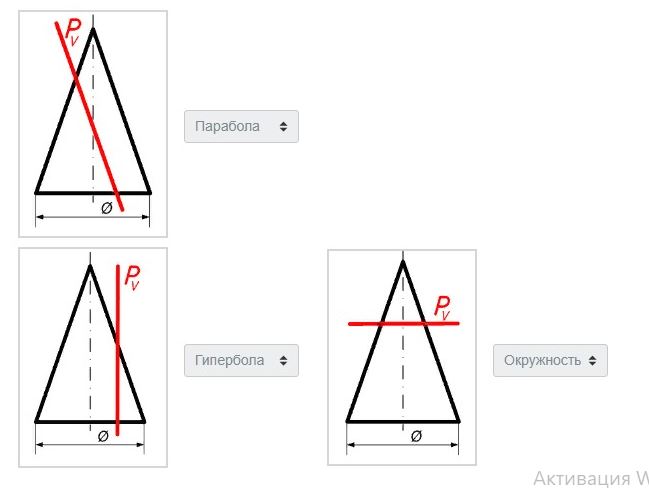
93. Установите правильное соответствие между секущими плоскостями Р и кривыми, которые получаются в сечении.
102. Способ аксонометрического проецирования состоит в том, что фигура вместе с осями прямоугольных координат проецируется на три плоскости.
-неверно
108. Доказано, что сумма квадратов коэффициентов искажения удовлетворяет уравнению:
для прямоугольной аксонометрии m2+n2+k2=2.
-Верно
119. Виды, полученные проецированием предмета на шесть граней куба, если предмет поместить внутрь его, называют
-основные
129. Разрез – изображение предмета, мысленно рассеченного одной или несколькими плоскостями. На разрезе показывается то, что получается в секущей плоскости и что расположено за ней.
-Верно
141. Размеры, которые не подлежат выполнению по данному чертежу и указываются для большего удобства пользования, называются
-Справочными
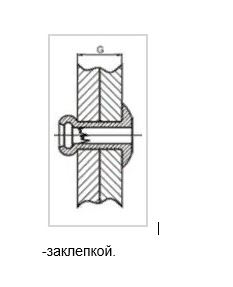
177. На рисунке изображено соединение
| В категории материалов: 6 Показано материалов: 1-6 |
Сортировать по
:
Названию ·
Рейтингу ·
Загрузкам ·
Просмотрам

Просмотров: 27257 / Добавил: mgsu / Дата: 28.02.2012 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5
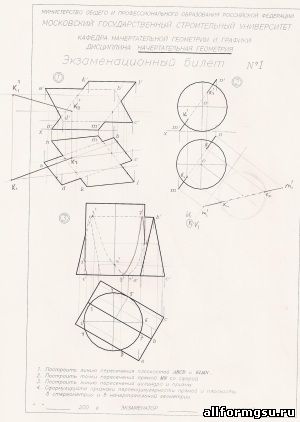
Кафедра начертательной геометрии и графики.
(30 решенных билетов)
Просмотров: 50446 / Добавил: mgsu / Дата: 05.02.2012 / Комментарии: 1
- 1
- 2
- 3
- 4
- 5

Просмотров: 11804 / Добавил: mgsu / Дата: 02.02.2011 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5
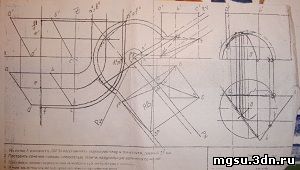
Просмотров: 15658 / Добавил: mgsu / Дата: 19.01.2011 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5
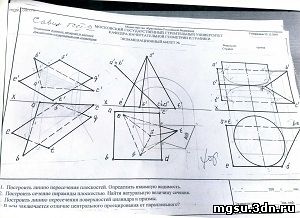
Просмотров: 28528 / Добавил: mgsu / Дата: 19.01.2011 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5

Просмотров: 9657 / Добавил: mgsu / Дата: 19.01.2011 / Комментарии: 0
- 1
- 2
- 3
- 4
- 5
Был(а) на сайте 3 месяца назад
Раздел
Технические дисциплины
ВУЗ
Томский политехнический университет
Каждая работа проверяется на плагиат, на момент публикации
уникальность составляет не менее 40% по системе проверки eTXT.
Всего 2 файла на сумму 200 рублей
Начертательная геометрия и инженерная графика
ИДЗ №1ИДЗ №1 (лист 1 Плоскости, лист 2 Поверхности, лист 3 Поверхности 2) и ИДЗ №2ИДЗ № 2 (лист 1 Основание Сталь 45, лист 2 Корпус СЧ 15, лист 3 Соединения) чертежи
Начертательная геометрия ИДЗ № 1 и ИДЗ № 2 готовые работы
Контрольная работа Контрольная
58
+3
0 покупок
Чертеж Чертеж
44
+1
0 покупок
Чертеж Чертеж
72
0 покупок
Чертеж Чертеж
55
+1
0 покупок
Чертеж Чертеж
51
+3
0 покупок
Реферат Реферат
385
0 покупок
Лабораторная работа Лабораторная
307
0 покупок
Лабораторная работа Лабораторная
310
0 покупок
Лабораторная работа Лабораторная
485
0 покупок
Контрольная работа Контрольная
383
+1
0 покупок
Контрольная работа Контрольная
364
+1
0 покупок
Контрольная работа Контрольная
383
0 покупок
Задача Задача
285
0 покупок
Задача Задача
369
0 покупок
Задача Задача
300
0 покупок
Подборка по базе: Методические для курсовой ПМ.01 (2).doc, 2 курс курсовая.pdf, 1 курс курсовая.pdf, тест по курсу составление резюме Рогова.docx, элина курс диплом.rtf, Кочарян Л.В. ГЛ-18-01 КУРСОВАЯ РАБОТА.pdf, _ 2 курс Методические рекомендации по подготовке и защите курсов, Инструкция по оформлению курсовой работы (ФГОС СПО) 2022.pdf, кур.р 3 курс.docx, Презентация Курсовая.pptx
Г.Ф. Винокурова, Б.Л. Степанов
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
1
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования
«ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Курс лекций для студентов ТПУ всех специальностей
Томск 2009
2
УДК 515
Начертательная геометрия. Курс лекций для студентов ТПУ всех специальностей. – Томск: Изд-во ТПУ, 2009.– 65 с.
Составители: доц., канд. техн. наук Г. Ф. Винокурова доц. Б. Л. Степанов
Рецензент доц., канд. техн. наук Б. А. Франковский
Работа рассмотрена и рекомендована к изданию методическим се- минаром кафедры начертательной геометрии и графики 28 августа 2008 г.
Зав. кафедрой, доц. ______________________С. П. Буркова
3
Лекция 1. Введение. Методы проецирования. Точка. Прямая линия
Введение
Литература
Винокурова Г.Ф., Степанов Б.Л. Начертательная геометрия. Инже- нерная графика: учебное пособие. – 2-е изд. – Томск: Изд. ТПУ, 2008. –
306 с.
А.А. Чекмарев Инженерная графика М.: Высш. шк ., 2000 г.
В.О. Гордон, М.А. Семенцов-Огиевский Курс начертательной гео- метрии М.: Наука, 1988 М.: Высш. шк., 1999 г.
В.С. Левицкий Машиностроительное черчение и автоматизация выполнения чертежей М.:Высш. шк., 2000 г.
Цели и задачи дисциплины
Целью дисциплины является изучение правил изображения на плоскости пространственных фигур и решение инженерно- геометрических задач на плоскостном чертеже; выработка знаний и на- выков, необходимых для выполнения и чтения чертежей отдельных де- талей.
Учебная дисциплина «Начертательная геометрия. Инженерная графика» состоит из двух разделов.
В разделе «Начертательная геометрия» изучаются методы изобра- жения пространственных фигур на плоскости и свойства фигур по их изображениям.
В разделе «Инженерная графика» изучаются правила выполнения и чтения чертежей отдельных деталей и сборочных единиц.
Краткая историческая справка
Основоположник начертательной геометрии – Гаспар Монж.
Годы жизни – 1746 – 1818. Он обобщил ранее накопленный опыт по тео- рии и практике изображений и создал стройную научную дисциплину о прямоугольных проекциях, которую назвал «Начертательная геометрия».
Первый учебник по начертательной геометрии опубликован во
Франции в 1798 г.
С открытием в 1810 г. В Петербурге Института корпуса инженеров путей сообщения наряду с другими дисциплинами там начал препода- ваться курс начертательной геометрии. Первым преподавателем по это- му курсу был ученик Г. Монжа Карл Потье. С 1818 г. Лекции по начер- тательной геометрии стал читать профессор Я. А. Севастьянов, а в 1821г. был опубликован его учебник по начертательной геометрии – первый учебник, изданный на русском языке.
В октябре 1900 г. начались занятия в Томском технологическом институте (ныне Томском политехническом университете). Первую лек- цию по начертательной геометрии 28(16)октября 1900 г. прочел Вален- тин Николаевич Джонс.
4
Методы проецирования
Изображения пространственных объектов на плоскости должны полно и точно отражать геометрические свойства объекта и позволять исследовать его части, что обусловливает ряд требований.
Наиболее важные из них: 1) обратимость, т. е. возможность вос- становить объект по его изображению; 2) простота построения; 3) на-
глядность.
Изображение, удовлетворяющее этим требованиям, получают на основе метода проецирования.
Аппарат проецирования включает в себя центр проекций, проеци- руемый объект, проецирующие лучи и плоскость, на которой получается изображение.
1. Центральное проецирование – это общий случай проецирова- ния геометрических объектов. Проецирование осуществляется из точки S
– центра проецирования на плоскость Р – плоскость проекций. Центр проецирования не должен находиться в плоскости проекций.
Чтобы получить центральную проекцию какой-либо точки (например точки А на рис. 1) необходимо провести проецирующий луч через центр проецирования S и точку А. Точка пересечения луча с плоскостью про- екций (точка а) является центральной проекцией заданной точки А на выбранную плоскость Р.
Рис. 1
Рис. 2
Точки a, b, с,d являются центральными проекциями точек А, В, С D
на плоскости Р.
Свойства центрального проецирования:
1. При центральном проецировании: точка проецируется в точку; прямая, не проходящая через центр проецирования, проецируется в прямую (проецирующая прямая – в точку);
5 плоская фигура, не принадлежащая проецирующей плоскости, проецируется в плоскую фигуру, рис. 2 (фигуры, принадлежащие проецирующей плоскости, проецируются в прямые линии); трехмерная фигура проецируется в двумерную фигуру.
2. При заданном центре проецирования фигуры на параллельных плоскостях подобны.
3. Центральное проецирование устанавливает однозначное соот- ветствие между фигурой и ее изображением.
Центральные проекции имеют большую наглядность, но имеют и недостатки. Они заключаются, например, в сложности построения изо- бражения предмета и определения его истинных размеров. Поэтому этот способ имеет ограниченное применение.
2. Параллельное проецирование можно рассматривать как част- ный случай центрального проецирования.
При этом центр проецирования удален в бес- конечность (S ).При параллельном проеци- ровании применяют параллельные проеци- рующие прямые. Их проводят в заданном на- правлении относительно плоскости проек- ций. Если направление проецирования пер- пендикулярно плоскости проекций, то про- екции называют прямоугольными или орто-
гональными
=90°, в других случаях ко-
соугольными
90° (рис. 3).
Свойства параллельного проецирования:
При параллельном проецировании сохраняются все свойства цен- трального проецирования, которые дополняются новыми:
1. Параллельные проекции взаимно параллельных прямых парал- лельны, а отношение длин отрезков этих прямых равно отношению длин их проекций.
2. Плоская фигура, параллельная плос- кости проекций, проецируется на эту плос- кость в такую же фигуру.
3. Параллельный перенос фигуры в про- странстве или плоскости проекций не изме- няет вида и размеров проекции фигуры.
Применяя приемы параллельного про- ецирования точки и линии, можно строить параллельные проекции поверхности и тела.
Параллельные проекции, как и центральные, не обеспечивают обратимости чертежа.
а
c
b
Рис. 3
Рис. 4
6
При проецировании на одну плоскость проекций между проеци- руемой фигурой и ее проекцией не существует взаимоодназначного со- ответствия. Так, каждому проецируемому предмету при заданном его положении и выбранном направлении проецирования l соответствует единственная его проекция. Однако полученная фигура может быть про- екцией бесконечного множества других фигур, которые отличаются друг от друга по величине и по форме. Из рис. 4 видно, что пространственной точке M соответствует единственная ее проекция на плоскости P точка
m. В то же время точка m является проекцией множества точек, лежащих на проецирующей прямой (M, M
1,
M
2
, M
3
).
Прямолинейный отрезок mn может быть проекцией не только пря- молинейного отрезка M
1
N
1
или M
2
N
2,
но проекцией кривой линии M
3
N
3
и любой плоской фигуры, расположенной в проецирующей плоскости.
Следовательно, изображение пространственной фигуры является не полным. Мы можем правильно понять чертеж тогда, когда он будет сопровождаться дополнительными пояснениями.
Рассмотрим некоторые способы дополнения проекционного изо- бражения, позволяющие сделать его «обратимым», то есть однозначно определяющим проецируемый предмет.
Способ проекций с числовыми отметками
Этот способ лежит в основе построения чертежей планов местно- сти и некоторых инженерных сооружений (плотин, дорог, дамб и т.п.).
Способ заключается в том, что положение любой точки в пространстве определяется ее прямоугольной проекцией на некоторую горизонталь- ную плоскость, принятую за плоскость нулевого уровня (рис. 5). Рядом с проекциями точек (a, b, c) указывают их отметку. Она указывает рас- стояние от точки до плоскости проекций.
Способ векторных проекций
Академик Е.С. Федоров предложил изображать высоты точек при помощи параллельных отрезков на плоскости проекций. Начало этих от- резков находится в проекциях соответствующих точек (рис. 6). Направ- ление всех высотных отрезков произвольно.
Рис. 5
Рис. 6
7
Если точки расположены выше горизонтальной плоскости, высот- ные отрезки, а также числовые отметки считаются положительными, ес- ли ниже отрицательными. Положительные и отрицательные высотные отрезки в «федоровских проекциях» отличаются противоположным на- правлением. Такие чертежи применяют в геологии, горном деле, топо- графии.
Метод прямоугольных проекций (метод Монжа)
Чертеж в системе прямоугольных проекций образуется при про- ецировании предмета не на одну, а на две или три взаимно перпендику- лярные плоскости проекций. Этот способ является частным случаем па- раллельного проецирования. Направление проецирования l перпендику- лярно плоскости проекций. Из точки опускается перпендикуляр на плос- кость проекций. Основание перпендикуляра является прямоугольной
(ортогональной) проекцией точки.
Осуществлять проецирование на две взаимно перпендикулярные плоскости впервые предложил Гаспар Монж.
Такое проецирование обеспечивает обратимость чертежа. Обра-
тимость чертежа – однозначное определение
положения точки в пространстве по ее про-
екциям. Одну из плоскостей принято распола- гать горизонтально ее называют горизон- тальной плоскостью проекций H (от греч. hori-
zon – разграничивающий), другую – ей пер- пендикулярно. Такую вертикальную плоскость называют фронтальной плоскостью проекций
V (от лат. – vertical is – отвесный). Эти плоско- сти проекций пересекаются по линии, которая называется осью проекций х (рис. 7).
Чтобы получить проекции точки на плоскости, опускаем из точки A в простран- стве перпендикуляры (проецирующие лучи) до встречи с плоскостями H и V.
Для полного выявления наружных и внутренних форм деталей и их соединений и для ряда других задач бывает необходимо три и более изображения. Введем в систему плоскостей H и V третью плоскость. Распо- лагаем ее перпендикулярно этим плоскостям.
Новая плоскость называется профильной
плоскостью проекций и обозначается буквой
W. Она пересекает плоскости H и V по осям y и z. Точку пересечения
Рис. 7
Рис. 8
8 всех осей называют началом координат и обозначают буквой O (от ла- тинского слова «origo» начало). Оси x, y, z взаимно перпендикулярны.
Три взаимно-перпендикулярные плоскости делят пространство на восемь частей, восемь октантов (рис. 
В нашей стране принята европейская система расположения про- екций. Ось x направлена от начала координат влево, y вперед (к нам), z вверх (x – ось широт, y – ось глубин, z – ось высот). Обратные направ- ления координатных осей считаются отрицательными.
Точка
Опустим из точки А проецирующие лучи (перпендикуляры) до пе- ресечения с плоскостями проекций H, V и W. Точки пересечения перпен- дикуляров с плоскостями проекций – это проекции точки на каждую из плоскостей проекций (рис. 9):
a горизонтальная;
a
фронтальная;
a
профильная.
Преобразуем его так, чтобы горизонтальная и профильная плос- кости проекций совпали с фронтальной плоскостью проекций, образуя одну плоскость чертежа (рис. 10). В результате получаем чертеж, назы- ваемый эпюр Монжа (от франц. epure чертеж, проект) или комплекс-
ный чертеж.
Рис. 9
Рис. 10
Основные правила ортогонального проецирования точки
1. Положение точки в пространстве определяется тремя координатами
А(x, y, z).
2. Положение точки на плоскости определяется двумя координатами:
a(x, y);
a′(x, z);
a″(y, z).
3. Две проекции точки определяют положение ее третьей проекции; две проекции точки определяют ее положение в пространстве.
4. Две проекции находятся на одном перпендикуляре (линии связи) к оси проекций, их разделяющей.
9
Прямая линия
Линия – это множество всех последовательных положений дви- гающейся точки.
Прямая линия – линия, образованная движением точки, не меняю- щей своего направления.
Прямая линия задается
двумя точками, ей принадлежащими; одной точкой и направлением линии.
Прямая может занимать в пространстве различное положение.
Положение прямой в пространстве
Относительно плоскостей проекции прямая может занимать раз- личные положения: не параллельное ни одной из плоскостей проекций H, V, W; параллельное одной из плоскостей проекций (прямая может и принадлежать этой плоскости); параллельное двум плоскостям проекций, то есть перпендикуляр- ное третьей.
Прямая общего
положения – прямая, не параллельная ни од- ной из плоскостей про- екций (рис. 11).
Прямые частно-
го положения – пря- мые, параллельные или перпендикулярные плоскости проекций.
Прямые частного положения можно разделить на: прямые, параллельные плоскости проекций – прямые уровня; прямые, перпендикулярные плоскости проекций – проецирующие
прямые.
Прямые, параллельные плоскости проекций (прямые уровня)
Горизонтальная прямая (АВ // H)
Фронтальная проекция прямой a b параллельна оси x; профильная проекция a b
параллельнаоси y
W
; длина горизонтальной проекции от- резка равна длине самого отрезка (ab=AB);угол , образованный гори- зонтальной проекцией и осью проекции x, равен углу наклона прямой к фронтальной плоскости проекций; угол , образованный горизонтальной проекцией и осью проекции y
H
, равен углу наклона прямой к профильной плоскости проекций (рис. 12).
Рис. 11
10
Свойства проекций
/ab/ = /АВ/;
(a′b′) // (Оx);
(a′′b′′) // (Oy
w
);
(AB
^
V)=(ab
^
Оx)= ;
(AB
^
W)=(ab
^
Oy
н
)= .
Фронтальная прямая (CD //V)
Горизонтальная проекция прямой cd параллельна оси x; профиль- ная проекция c d
параллельна оси z; длина фронтальной проекции от- резка равна длине самого отрезка (с d =CD);угол , образованный фрон- тальной проекцией и осью проекций x, равен углу наклона прямой к го- ризонтальной плоскости проекций; угол , образованный фронтальной проекцией и осью z, равен углу наклона прямой к профильной плоскости проекций (рис. 13).
Свойст-ва проекций
c
d
=
CD
;
(cd) // (Оx);
(c
d) // (Оz);
(CD^H)=(c
d^Оx)= ;
(CD^W)=(c
d^Оz)= .
Профильная прямая
(EF //W)
Горизонтальная проекция прямой ef параллельна оси y
H
; фронталь- ная проекция e f параллельна оси z; длина профильной проекции отрезка равна длине самого отрезка (e f =EF); углы и , образованные про- фильной проекцией с осямиy
W
и z, равны углам наклона прямой к гори- зонтальной и фронтальной плоскостям проекций соответственно, рис. 14.
Свойства проекций
e
f
=
EF
;
(ef) // (Оy
н
);
(e
f
) = (Оz);
(EF^H)=(e
f
^Оy
w
)= ;
(EF^V)=(e
f
^Оz) = .
Рис. 14
Рис. 12
Рис. 13
11
Если прямая параллельна плоскости проекций, то на эту плос-
кость в натуральную величину проецируется сама прямая и углы накло-
на ее к двум другим плоскостям проекций. Проекции прямой на две дру-
гие плоскости проекций параллельны осям, определяющим данную плос-
кость проекций.
Прямые, перпендикулярные плоскости проекций (проецирующие)
Прямая АВ Н – горизонтально-проецирующая прямая.
Свойства проекций
Проекция a b
перпендику- лярна осиx,проекцияa b
перпендикулярна оси y
w
,
проекции aиbсовпадают.
(AB) H; (AB) // V;
(AB) // W; ab – точка;
a
b
=
a
b
=
AB
;
(a
b)(Оx); (ab)(Оy
w
).
Прямая CD V – фронтально-проецирующая прямая.
Свойства проекций
Проекция cd перпендику- лярна оси x, проекция c d перпендикулярна оси z, проекции с и d совпадают.
(CD) V; (CD) // H;
(CD) // W; c
d
– точка;
cd
=
c
d
=
CD
;
(cd)(Оx); (c
d) (Оz).
Прямая EF W – профильно-проецирующая прямая.
Свойства проекций
Проекция ef перпендику- лярна оси y
H
Кафедра начертательной геометрии и графики ТПУ
Когда был создан Томский технологический институт (в последующем Томский политехнический университет), в нем не было кафедры начертательной геометрии и графики. По начертательной геометрии и графике лекции читали отдельные преподаватели. Первой лекцию по начертательной геометрии и графике прочитал Валентин Николаевич Джонс в октябре 1900 года, он был инженером-технологом.
Кафедра по начертательной геометрии и графики была основана в 1930 году. Доцент С.А.Соколов стал ее первым заведующим. Он заведовал кафедрой до 1937 года. За все время существования кафедры численность преподавателей менялась. Сейчас она составляет 30 человек. На кафедре работают 10 доцентов, 15 старших преподавателей, 4 ассистента. Это Н.А. Антипина, А.И. Озга, Л.Н. Лебедева, Е.В. Белоенко, О.А. Кононова, О.А. Казакова, Р.И. Акимова,Л.Д. Калабухова, Б.А. Франковский, Е.С. Исакова, Н.В. Ватолина, Т.И. Назимок и многие другие.
В университете есть компьютерный класс, созданный весной 1992 года. Сейчас их существует уже три, где у студентов проходят занятия по дисциплине «Компьютерная графика» и они учатся выполнять чертежи на компьютерах.
В университете на базе кафедры существовал факультет повышения квалификации преподавателей и с осени 1970 года здесь начали проводить занятия по специальности «Начертательная геометрия и инженерная графика». Свою квалификацию повышали преподаватели со всей страны. Больше всего было преподавателей из вузов Дальнего Востока, Урала и Сибири. Теперь этот факультет стал Институтом инженерной педагогики.
После того как открылся в университете Институт международного образования, начали проводиться занятия со студентами на английском языке.
На кафедре ежегодно проводится четыре студенческих университетских олимпиады. Так же кафедра ведет активное участие в областных соревнованиях. Команда университета в 1999 году в общем зачете «Инженерная и компьютерная графика» заняла второе место на Всероссийской студенческой олимпиаде.