При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути — со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Ответ:
2
Расстояние между городами A и B равно 470 км. Из города A в город B выехал первый автомобиль, а через 3 часа после этого навстречу ему из города B выехал со скоростью 60 км/ч второй автомобиль. Найдите скорость первого автомобиля, если автомобили встретились на расстоянии 350 км от города Ответ дайте в км/ч.
Ответ:
3
На изготовление 99 деталей первый рабочий тратит на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает второй рабочий?
Ответ:
4
Велосипедист выехал с постоянной скоростью из города A в город B, расстояние между которыми равно 98 км. На следующий день он отправился обратно со скоростью на 7 км/ч больше прежней. По дороге он сделал остановку на 7 часов. В результате он затратил на обратный путь столько же времени, сколько на путь из A в B. Найдите скорость велосипедиста на пути из A в B. Ответ дайте в км/ч.
Ответ:
5
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей за час изготавливает второй рабочий, если известно, что первый за час изготавливает на 1 деталь больше?
Ответ:
6
В сосуд, содержащий 5 литров 12−процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?
Ответ:
7
Две трубы наполняют бассейн за 3 часа 36 минут, а одна первая труба наполняет бассейн за 6 часов. За сколько часов наполняет бассейн одна вторая труба?
Ответ:
8
Из пункта A круговой трассы выехал велосипедист. Через 30 минут он еще не вернулся в пункт А и из пункта А следом за ним отправился мотоциклист. Через 10 минут после отправления он догнал велосипедиста в первый раз, а еще через 30 минут после этого догнал его во второй раз. Найдите скорость мотоциклиста, если длина трассы равна 30 км. Ответ дайте в км/ч.
Ответ:
9
Из двух городов, расстояние между которыми равно 560 км, навстречу друг другу одновременно выехали два автомобиля. Через сколько часов автомобили встретятся, если их скорости равны 65 км/ч и 75 км/ч?
Ответ:
Завершить тестирование, свериться с ответами, увидеть решения.
| Автор | Сообщение | ||||
|---|---|---|---|---|---|
|
Заголовок сообщения: Тренировочный вариант №188
|
|||||
|
http://alexlarin.net/ege/2017/trvar188.html |
||||
  |
|||||
|
|
|||||
|
OlG |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
Спасибо за вариант. _________________ |
||||
  |
|||||
|
Brevno |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
19: Подробности: _________________ |
||||
  |
|||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
18 Подробности: |
||||
  |
|||||
|
OlG |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
16. Подробности: _________________ |
||||
  |
|||||
|
Williams Wolfram |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
Решение задачи 19. Подробности:
|
||||
  |
|||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
15 Подробности: |
||||
  |
|||||
|
OlG |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
17. Подробности: _________________ |
||||
  |
|||||
|
Kirill Kolokolcev |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
14 Подробности: Последний раз редактировалось Kirill Kolokolcev 11 мар 2017, 03:35, всего редактировалось 1 раз. |
||||
  |
|||||
|
OlG |
Заголовок сообщения: Re: Тренировочный вариант №188
|
||||
|
Kirill Kolokolcev писал(а): 14 Подробности: В б) у меня — другой ответ. Подробности: _________________ |
||||
  |
|||||
| Показать сообщения за: Сортировать по: |
Кто сейчас на форуме
|
Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 2 |
|
Вы не можете начинать темы |
|
|
- Главная
-
ЕГЭ
-
Математика профильная
-
Варианты ЕГЭ
-
Вариант 19
Назад

Время
3:55:00Скидки на верхнюю одежду на распродаже составляют 25 %, а на свитера и брюки – 20 %. Вычислите сумму покупки с учетом скидок, состоящей из пальто и двух пар брюк, если без скидки пальто стоило 30 000 рублей, а брюки: одна пара 5 000 рублей, вторая – 6 000 рублей.
Ответ укажите в рублях.
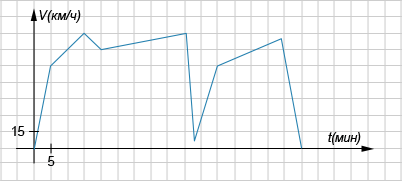
На графике описано прямолинейное движение мотоциклиста: по оси абсцисс отложено время в минутах, по оси ординат – скорость в км/ч. Мотоциклист ехал час из пункта A пункт B, потом повернул обратно. Определите по графику, сколько минут автомобиль ехал со скоростью ниже 75 км/ч по направлению в пункт B.
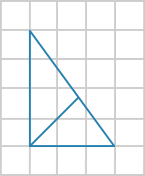
Вычислите высоту прямоугольного треугольника, проведенную к гипотенузе, если треугольник изображён на клетчатой бумаге с размером клетки
1см х 1см. Ответ дайте в см.
В пенале лежат 3 пишущие ручки и 7 не пишущих. Какова вероятность того, что наугад вытянутая из пенала ручка окажется пригодной для письма?
Решите уравнение: 2 · 6(5х+8) = 432.
В треугольнике АВС проведены медианы АМ = 9 см и ВК = 12 см, пересекающиеся в точке О. Найдите величину медианы, проведенной к стороне АС, в треугольнике АОС.
Ответ дайте в см.
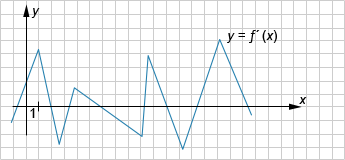
На рисунке изображён график производной функции f(x). Найдите количество точек минимума функции f(x) на промежутке [1;15].
Куб вписан в шар радиусом $2sqrt{3}$см. Найдите сторону куба. Ответ дайте в см.
Найти значение sin (x+y) при условии,что sin x = 0,3 ,cos y = 1.
Перед вами формула для расчета величины сопротивления R(Ом) нити накаливания при температуре t0: R = R0 (1 + αt0). Здесь R0 (Ом) – рабочее сопротивление нити накаливания. Известно, что температурный коэффициент сопротивления вольфрама α = 5·10-3 град-1, величина сопротивления вольфрамовой нити при температуре t0 = 25 0C равна R = 27 Ом. Найдите R0 (Ом).
3 части 5 %-го раствора кислоты смешали с 6 частями 11 %-го раствора такой же кислоты. Какова концентрация получившегося раствора? Ответ дайте в %.
Вычислите значение производной функции
$ y = sin (3x + displaystyle frac{pi}{3})cdot cos(3x + displaystyle frac{pi}{3}) +3x + displaystyle frac{pi}{3} text{в точке } x_0 = displaystyle frac{pi}{18}$
а) Решить уравнение $10^{sin x} = 2^{sin x}cdot 5^{-cos x}$
б) Найдите все корни этого уравнения, принадлежащие отрезку $[-displaystyle frac{5pi}{2}; -pi]$.
ответ
а) Преобразуем исходное уравнение:
$2^{sin x} cdot 5^{sin x} = 2^{sin x} cdot 5^{-cos x} Leftrightarrow 5^{sin x} = 5^{-cos x} Leftrightarrow sin x = -cos x Leftrightarrow tg x = -1$
откуда $x = — displaystyle frac{pi}{4} + pi k, k in Z$
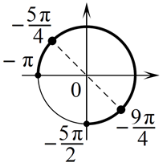
б) С помощью числовой окружности отберем корни, принадлежащие отрезку $[-displaystyle frac{5pi}{2}; -pi]$. Получим числа: $-displaystyle frac{9pi}{4}, -displaystyle frac{5pi}{4}$.
Ответ: а) $x = -displaystyle frac{pi}{4} + pi k, k in Z$, б) $-displaystyle frac{9pi}{4}, -displaystyle frac{5pi}{4}$.
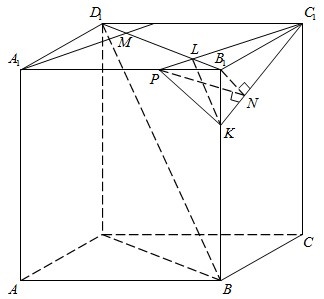
В кубе ABCDA1B1C1D1 все рёбра равны 3. На его ребре BB1отмечена точка K так, что KB=2. Через точки K и C1 проведена плоскость α, параллельная прямой BD1.
а) Докажите, что плоскость α проходит через середину ребра A1B1.
б) Найдите угол наклона плоскости α к плоскости грани BB1C1С.
ответ
а) В плоскости ВВ1DD1 через точку К проведем прямую параллельно BD1. Пусть эта прямая пересекает диагональ B1D1 в точке L. В плоскости основания A1B1C1D1 проведем прямую C1L, пусть она пересекает сторону A1B1 в точке P. Треугольник KPC1 — сечение, проходящее через точки К и С1 параллельно прямой BD1. Действительно, прямая BD1 параллельна плоскости сечения, так как параллельна лежащей в нем прямой KL.
В плоскости основания A1B1C1D1 через точку A1 проведем прямую параллельно C1P. Пусть она пересекает D1В1 в точке M. По теореме Фалеса имеем: B1L: B1D1 = B1K:B1B=1:3 ⇾B1L = 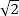
б) Пусть теперь точка N — основание высоты B1N прямоугольного треугольника KB1C1. B1N — является проекцией наклонной PN на плоскость BB1CC1. По теореме о трех перпендикулярах PN перпендикулярна C1K. Тогда угол PNB1 — линейный угол искомого двугранного угла. Имеем:
$PB_1 = displaystyle frac{1}{2}A_1B_1 = displaystyle frac{3}{2}; ; ; S_{B_1C_1K} = displaystyle frac{1}{2}B_1N cdot C_1K = displaystyle frac{1}{2}B_1K cdot B_1C_1; ; ; C_1K = sqrt{3^2 + 1^2} = sqrt{10} \ B_1N = displaystyle frac{B_1K cdot B_1C_1}{C_1K} = displaystyle frac{3}{sqrt{10}}$
$tg PNB_1 = displaystyle frac{PB_1}{B_1N} = displaystyle frac{displaystyle frac{3}{2}}{displaystyle frac{3}{sqrt{10}}} = displaystyle frac{sqrt{10}}{2}$ . Тогда угол между плоскостями = $arctg(displaystyle frac{sqrt{10}}{2})$
Ответ: б) $arctg(displaystyle frac{sqrt{10}}{2})$
Решите неравенство $(x+1)log_36 + log_3(2^x — displaystyle frac{1}{6}) leq x — 1$
ответ
p>Перейдём к неравенству:
$log_3(6^{x+1}(2^x — displaystyle frac{1}{6})) leq log_33^{x-1}; \ begin{cases} 2^x — displaystyle frac{1}{6} > 0, \6^{x+1}(2^x — displaystyle frac{1}{6}) leq 3^{x-1} end{cases}$
Решим второе неравенство системы:
$6cdot 6^x (2^x — displaystyle frac{1}{6})leq displaystyle frac{3^x}{3} \ 2^x (2^x — displaystyle frac{1}{6}) leq displaystyle frac{1}{18}$
Сделаем замену y = 2x; y > 0
$y^2 — displaystyle frac{1}{6}y — displaystyle frac{1}{18} leq 0; \ -displaystyle frac{1}{6} leq y leq displaystyle frac{1}{3}. \ 0< y leq displaystyle frac{1}{3}$
Учитывая первое неравенство системы, получаем: $displaystyle frac{1}{6} < 2^x leq displaystyle frac{1}{3}$.
x ∈ (–log26; –log23].
На отрезке BD взята точка C. Биссектриса BL равнобедренного треугольника ABC с основанием BC является боковой стороной равнобедренного треугольника BLD с основанием BD.
а) Докажите, что треугольник DCL равнобедренный.
б) В каком отношении прямая DL делит сторону AB?
ответ
а) ∠ LBC = ∠LBA = α, ∠ ACB = ∠ABC =2α ,∠LCD = 180 — 2a
∠LDC = α
Поэтому ∠DLC = 180 — ∠LCD — ∠LCD = α = ∠LDC
Треугольник LCD – равнобедренный.
б) Пусть H – точка пересечения DL и AB. Тогда ∠HLB = 180 — ∠BLC — ∠CLD = 180 — (180 — ∠LBC — ∠LCB) — ∠CLD = 2α
Треугольники HLB и LCB подобны по двум углам. Отсюда $displaystyle frac{BH}{BL} = displaystyle frac{BL}{BC}; BH = displaystyle frac{BL^2}{BC}$;
Поскольку cos∠ABC=3/4, BC : AB = 3 : 2 .Пусть AB = 2x, BC = 3x.
Поскольку AL :LC = AB : BC ,находим $AL = displaystyle frac{6x}{5}, CL = displaystyle frac{4x}{5}$. Тогда
$BL = sqrt{AB cdot BC — AL cdot LC} = displaystyle frac{3}{5}sqrt{14}x \ BH = displaystyle frac{9cdot 14x^2}{25cdot 3x} = displaystyle frac{42x}{25} \ BH : HA = 42; : ; 8 = 21; : ; 4$
В этом году Сергей купил ценную бумагу за 7 000 руб. Цена бумаги каждый год увеличивается на 1 500 руб. Сергей может продать ценную бумагу и положить полученную сумму на счет. Каждый год банк будет увеличивать сумму на счете на 15 %. Определите, на какой по счету год после покупки ценной бумаги, Сергею стоит ее продать, чтобы через 35 лет сумма на банковском счету была максимальной.
Найдите все значения параметра а, при которых уравнение $2^x — a = sqrt{4^x — a}$ имеет единственное решение.
ответ
Найдите все значения параметра а, при которых уравнение имеет единственное решение
$2^x — a = sqrt{4^x — a}$
Пусть 2х = t, t > 0
Получаем:
$sqrt{t^2 — 3a} = t — a \ t geq a \ t^2 — 3a = t^2 -2at + a^2 \ a^2 -2at + 3a = 0 \ a^2 + a(3-2t) = 0 \ a(a + 3 -2t) = 0 \ a = 0, ; a + 3 -2t = 0 \ a = 0 text{ или } t = displaystyle frac{a+ 3}{2}$
Подставим в t ≥ a . $begin{cases} a = 0\ t geq 0 end{cases}$или $begin{cases}displaystyle frac{a+3}{2}geq a \ t = displaystyle frac{a+3}{2}end{cases}$ Значит,$begin{cases} a = 0, \ tgeq 0 end{cases}$ или $begin{cases} 3geq a \ t = displaystyle frac{a+3}{2} end{cases}$
Знаем, что t > 0 (при a=0 , t > 0 ) поэтому уравнение имеет единственное решение если – 3 ∠ a ≤3 (вторая система), но а =0 нам не подходит, значит исключаем это решение из окончательного ответа.
Ответ: –3 ∠ a ∠ 0, 0 ∠ a.
Числа 1, 2, 3, 4, 5, 6, 7, 8, 9, 16 произвольно делят на три группы так, чтобы в каждой группе было хотя бы одно число. Затем вычисляют значение среднего арифметического чисел в каждой из групп (для группы из единственного числа среднее арифметическое равно этому числу).
а) Могут ли быть одинаковыми два из этих трёх значений средних арифметических в группах из разного количества чисел?
б) Могут ли быть одинаковыми все три значения средних арифметических?
в) Найдите наименьшее возможное значение наибольшего из получаемых трёх средних арифметических.
ответ
а) Да, могут, если разделить числа так:
Первая группа: 1, 5
Вторая группа: 2, 4, 6, 7, 8, 9, 16
Третья группа: 3
Тогда в первой и третьей группах будет одинаковое значение.
б) Пусть а-среднее арифметическое во всех группах. Пусть в первой группе x чисел, во второй y, в третьей z чисел. Тогда сумма чисел равна: a(x+y+z).
С другой стороны, x+y+z = 10 по условию. Отсюда: 10a.
Посчитаем сумму написанных в условии чисел: 1+2+ 3+ 4+ 5+ 6+ 7+ 8+ 9+ 16=61
Получаем уравнение: $10a = 61leftrightarrow a = 6,1 $. Тогда должно выполняться, что $6,1x; 6,1y; 6,1z$ -целые числа, но это невозможно ни при каких значениях, так как x,y,z принимают значения от 1 до 8. Поэтому не могут.
в) Среднее арифметическое какой-либо из трёх групп должно быть больше 6, так как в противном случае сумма меньше 60, что невозможно.
Если в группе b чисел, то сумма чисел не меньше, чем 6b+1, а среднее арифметическое не меньше, чем $6 +displaystyle frac{1}{b}$
Если все числа составляют отдельную группу, то наибольшего из получаемых трёх средних арифметических будет равно 16. Это не наименьшее значение.
Есть в группе 8 чисел, то две группы будут состоять из одного числа. Если какое-то из них больше 7, то среднее арифметическое большой группы не меньше
$displaystyle frac{61 — (5+6)}{8} = displaystyle frac{50}{8} = displaystyle frac{25}{4} = 6,25$
Если в группе 7 чисел, то среднее арифметическое не меньше, чем $6+ displaystyle frac{1}{7} = displaystyle frac{43}{7}$ Это и есть наименьшее возможное значение. Приведем пример:
Первая группа: 1, 2, 4, 5, 7, 8, 16
Вторая группа: 3, 9
Третья группа: 6
Итоговы ответы:
- да
- нет
- 43/7
Нажми, чтобы завершить тест и увидеть результаты
Пора зарегистрироваться!
Так твой прогресс будет сохраняться.
Регистрация












Начало работы
Привет сейчас ты за 5 шагов узнаешь, как пользоваться платформой
Смотреть
Выбери тест
«Выбери тест, предмет и нажми кнопку «Начать решать»
1 / 6
Вкладки
После выбора предмета необходимо выбрать на вкладке задания, варианты ЕГЭ, ОГЭ или другого теста, или теорию
2 / 6
Задания
Решай задания и записывай ответы. После 1-ой попытки
ты сможешь посмотреть решение
3 / 6
Статистика
Сбоку ты можешь посмотреть статистику и прогресс по предмету
4 / 6
Решение
Нажми, чтобы начать решать вариант. Как только ты перейдешь
на страницу, запустится счетчик времени, поэтому подготовь заранее все, что может тебе понадобиться
5 / 6
Отметки
Отмечай те статьи, что прочитал, чтобы было удобнее ориентироваться в оглавлении
6 / 6
Молодец!
Ты прошел обучение! Теперь ты знаешь как пользоваться сайтом
и можешь переходить к решению заданий
Задание 1
Найдите значение выражения: $$(frac{4}{9}-frac{5}{12}):(frac{3}{8}-frac{4}{9})$$
Ответ: -0,4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(frac{4}{9}-frac{5}{12}):(frac{3}{8}-frac{4}{9})=$$$$frac{4*4-5*3}{36}:frac{3*9-4*8}{72}=$$$$frac{1}{36}*frac{72}{-5}=-frac{2}{5}=-0,4$$
Задание 2
Расстояние от Нептуна – одной из планет Солнечной системы – до Солнца равно 4450 млн км. Как эта величина записывается в стандартном виде?
Варианты ответа:
- $$4.450*10^{6}$$
- $$4.450*10^{7}$$
- $$4.450*10^{8}$$
- $$4.450*10^{9}$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Стандартный вид числа : $$a*10^{n}$$, где $$1leq a <10, n in N$$. Учтем, что 1 млн = $$10^{6}$$. Тогда 4450 млн. км. = $$4,450*10^{3}*10^{6}=4,45*10^{9}$$ км. Данный ответ соответствует 4 варианту.
Задание 3
На координатной прямой отмечено число а. Какое из утверждения для этого числа верно?
- $$a-5<0$$
- $$a-7>0$$
- $$5-a>0$$
- $$8-a<0$$
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Число а располагается между 7 и 8. Пусть а=7,5. Проверим истинность представленных вариантов:
- $$a-5<0Leftrightarrow$$$$7,5-5<0Leftrightarrow$$$$2,5<0$$ — неверно
- $$a-7>0Leftrightarrow$$$$7,5-7>0Leftrightarrow$$$$0,5>0$$ — верно
- $$5-a>0Leftrightarrow$$$$5-7,5>0Leftrightarrow$$$$-2,5>0$$ — неверно
- $$8-a<0Leftrightarrow$$$$8-7,5<0Leftrightarrow$$$$0,5<0$$ — неверно
Верным является только 2 вариант ответа
Задание 4
Найдите значение выражения $$sqrt{5*90}sqrt{50}$$
Ответ: 150
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$sqrt{5*90}sqrt{50}=$$$$sqrt{5*9*10*5*10}=$$$$sqrt{3^{2}*5^{2}*10^{2}}=$$$$3*5*10=150$$
Задание 5
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси — напряжение в вольтах. Определите по графику, за сколько часов работы фонарика напряжение упадёт с 1,2 В до 0,8 В.
Ответ: 10
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1,2 В было в 9 часов, 0,8 В было в 19 часов, следовательно, с 1,2 В до 0,8 В напряжение упадет за 19-9=10 часов
Задание 6
Решите уравнение $$4x+5=-9(8-9x)$$
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$4x+5=-9(8-9x)Leftrightarrow$$$$4x+5=-72+81xLeftrightarrow$$$$4x-81x=-72-5Leftrightarrow$$$$-77x=-77|:(-77)Leftrightarrow$$$$x=1$$
Задание 7
В 6 классе учится 10 мальчиков, остальные ученики — девочки. Контрольную работу успешно написали 60% мальчиков и 90% девочек. Сколько человек учится в 6 классе, если всего контрольную работу успешно написали 24 человека?
Ответ: 30
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
1. 60% мальчиков успешно написали, следовательно, 10*0,6=6 мальчиков
2. 24-6=18 девочек успешно написали, что составляет 90 % от общего числа девочек, тогда:
18 девочек — 90%
х девочек — 100%
$$x=frac{18*100}{90}=20$$ девочек всего
3. Тогда всего детей 20+10=30 человек
Задание 8
На диаграммах показано содержание питательных веществ в сухарях, твороге, сливочном мороженном и сгущенном молоке. Определите по диаграммам, в каком продукте содержание углеводов наибольшее
*к прочему относятся вода, витамины и минеральные вещества
Варианты ответа
- сухари
- творог
- мороженое
- сгущённое молоко
Ответ: 1
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Необходимо выбрать круг, в котором площадь сегмента, характеризующего углеводы, наибольшая. В данном случае это первый вариант — сухари
Задание 9
В среднем на 147 исправных карманных фонариков, поступивших в продажу, приходится три неисправных. Найдите вероятность того, что выбранный наудачу в магазине фонарик окажется исправен
Ответ: 0,98
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если на 147 исправных фонарика 3 неисправных, тогда всего фонариков : 147+3=150 фонариков. Тогда вероятность выбрать исправный фонарик: $$P=frac{147}{150}=0,98$$
Задание 10
Установите соответствие между графиками функций и формулами, которые их задают.
ФОРМУЛЫ
- $$-frac{2}{x}$$
- $$x^{2}-2$$
- $$2x$$
В таблице под каждой буквой укажите соответствующий номер.
Ответ: 231
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В пункте А представлена квадратичная функция вида $$y=ax^{2}+b$$, ей соответствует 2 вариант ответа В пункте Б представлена линейная функция вида $$y=kx$$, ей соответствует 3 вариант ответа В пункте В представлена обратная пропорциональность вида $$y=frac{k}{x}$$, ей соответствует 1 вариант ответа
Задание 11
Даны двадцать чисел, первое из которых равно 10, а каждое следующее больше предыдущего на 4. Найти пятнадцатое из данных чисел.
Ответ: 66
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
В данном случае дана арифметическая прогрессия, первый член которой $$a_{1}=10$$, разность $$d=4$$. Необходимо найти $$a_{15}$$. $$a_{n}=a_{1}+d(n-1)$$, следовательно, $$a_{15}=10+4(15-1)=66$$
Задание 12
Найдите значение выражения $$(a-1):frac{2a-a^{2}-1}{a+1}$$, при $$a=-24$$
Ответ: -0,92
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(a-1):frac{2a-a^{2}-1}{a+1}=$$$$(a-1)*frac{a+1}{-(-2a+a^{2}+1)}=$$$$frac{(a-1)*(a+1)}{-(a-1)^{2}}=$$$$frac{a+1}{-(a-1)}=$$$$frac{-24+1}{-(-24-1)}=-frac{23}{25}=-0,92$$
Задание 13
Чтобы перевести значение температуры по шкале Цельсия в шкалу Фаренгейта, пользуются формулой F=1,8C+32, где C — градусы Цельсия, F — градусы Фаренгейта. Какая температура по шкале Фаренгейта соответствует -8 градусам по шкале Цельсия?
Ответ: 17,6
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Подставим в формулу известные значения: $$F=1,8C+32=$$$$ F=1,8*(-8)+32=$$$$ F=-14,4+32=17,6$$
Задание 14
Решите неравенство $$64-x^{2}<0$$
Варианты ответа:
- $$(—infty ;+infty )$$
- $$(-infty ;-8)cup (8;+infty)$$
- $$(-8;8)$$
- нет решений
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Разложим выражение слева на множители: $$(8-x)(8+x)<0$$. Отметим на координатной прямой точки (пустые, так как неравенство строгое), когда выражение слева равно 0 и расставим знаки значений, которые принимает выражение на полученных промежутках:
Нам необходимы значения меньшие, чем ноль, следовательно, $$xin(-infty ;-8)cup (8;+infty)$$, что соответствует 2 варианту ответа
Задание 15
Какой угол (в градусах) описывает минутная стрелка за 27 минут?
Ответ: 162
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Вся окружность составляет 360 градусов или 60 минут, тогда 1 минута составляет $$frac{360}{60}=6$$ градусов, следовательно, 27 минут составляют $$27*6=162$$ градуса
Задание 16
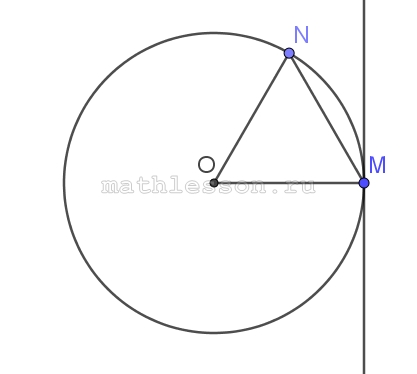
Прямая касается окружности в точке M . Точка O — центр окружности. Хорда MN образует с касательной угол, равный 22°. Найдите величину угла ONM. Ответ дайте в градусах
Ответ: 68
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- OM перпендикулярен касательной (свойство радиуса, проведенного в точку качсания)
- ON=OM (радиусы), тогда $$angle ONM=angle OMN$$
- $$angle OMN=90-22=68$$
Задание 17
Найдите периметр прямоугольника, если в него вписана окружность радиуса 10.
Ответ: 80
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Если в прямоугольник вписана окружность, то данный прямоугольник является квадратом (так как сумма противоположных сторон равна) Радиус вписанной окружности в квадрат равен половине стороны квадрата, то есть сторона квадрата тогда 20 Периметр есть сумма длин всех сторон: $$P=20*4=80$$
Задание 18
Боковая сторона равнобедренного треугольника равна 26, а основание равно 12. Найдите площадь этого треугольника
Ответ: $$48sqrt{10}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Воспользуемся формулой Герона для вычисления площади треугольника. Найдем полупериметр: $$p=frac{26+26+12}{2}=32$$. Тогда площадь треугольника равна: $$S=sqrt{32(32-62)(32-26)(32-12)}=48sqrt{10}$$
Задание 19
В остроугольном треугольнике ABC высота AH равна $$20sqrt{3}$$ , а сторона AB равна 40. Найдите $$cos B$$.
Ответ: 0,5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Из треугольника ABH найдем синус угла B: $$sin B=frac{AH}{AB}=frac{sqrt{3}}{2}$$ Найдем косинус угла B по основному тригонометрическому тождеству: $$cos B=sqrt{1-sin^{2} B}=sqrt{1-frac{3}{4}}=frac{1}{2}$$
Задание 20
Какие из следующих утверждений верны?
- Площадь параллелограмма равна произведению его смежных сторон.
- Площадь прямоугольника равна произведению его смежных сторон.
- Площадь ромба равна произведению его смежных сторон.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов
Ответ: 2
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- Площадь параллелограмма равна произведению его смежных сторон — неверно, произведению смежных сторон на синус угла между ними
- Площадь прямоугольника равна произведению его смежных сторон — верно
- Площадь ромба равна произведению его смежных сторон — ромб — тот же параллелограмм, следовательно, неверно
Задание 21
Упростите выражение: $$frac{a-c}{a^{2}+ac+c^{2}}cdot frac{a^{3}-c^{3}}{a^{2}b-bc^{2}}cdot(1+frac{c}{a-c}-frac{1+c}{c}):frac{c(1+c)-a}{bc}$$
Ответ: $$frac{1}{(a+c)}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Выполним данное задание по действиям:
- $$frac{a-c}{a^{2}+ac+c^{2}}cdot frac{a^{3}-c^{3}}{a^{2}b-bc^{2}}=$$$$frac{a-c}{a^{2}+ac+c^{2}}cdot frac{(a-c)(a^{2}+ac+c^{2})}{b(a-c)(a+c)}$$$$=frac{a-c}{b(a+c)}$$
- $$1+frac{c}{a-c}-frac{1+c}{c}=$$$$frac{ac-c^{2}+c^{2}-a-ac+c+c^{2}}{c(a-c)}=$$$$frac{c+c^{2}-a}{c(a-c)}$$
- $$frac{a-c}{b(a+c)}*frac{c+c^{2}-a}{c(a-c)}*frac{bc}{c(1+c)-a}=frac{1}{(a+c)}$$
Задание 22
Бригада лесорубов должна была за несколько дней заготовить 216 м3 древесины. Первые три дня она выполняла установленную норму, а затем – каждый день заготавливала на 8 м3 больше плана, поэтому за день до срока было заготовлено 232 м3 древесины. Определите плановую дневную норму бригады.
Ответ: 24
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Пусть планировалось добывать х кубических метров в день, в течении у дней. Тогда получаем $$xy=216$$. Но сначала три дня добывали по норме, а потом оставшиеся дни без одного (так как за день до нормы закончили) добывали на 8 больше, то есть $$3x+(y-4)(x+8)=232$$. (y-4 — от того, что три дня уже работали, плюс закончили на 1 день раньше):
$$left{begin{matrix}xy=216\3x+(y-4)(x+8)=232end{matrix}right.Leftrightarrow$$$$left{begin{matrix}xy=216\3x+xy+8y-4x-32=232end{matrix}right.Leftrightarrow$$$$left{begin{matrix}xy=216\8y-x+xy-32=23end{matrix}right. $$
Подставим вместо xy число 216:
$$8y-x+216-32=232Leftrightarrow$$$$8y-x=48Leftrightarrow$$$$x=8y-48$$
Подставим в первое уравнение системы:
$$(8y-48)y=216|:8Leftrightarrow$$$$y^{2}-6y-27=0$$.
Тогда корни данного уравнения 9 и -3. Количество дней не может быть отрицательным, следовательно, $$y=9$$. Найдем х: $$x=8-9-48=24$$
Задание 23
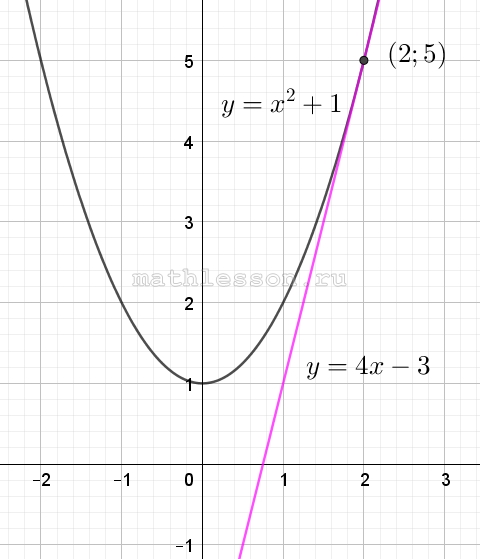
Известно, что графики функций y=x2 +p и y=4x−3 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат
Ответ: (2;5)
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- Так как графики имеют одну точку пересечения, то уравнение : $$x^{2}-p=4x-3$$ должно иметь один корень, то есть дискриминант равен 0:
- $$x^{2}-4x+p+3=0$$ $$D=16-4(p+3)=16-4p+12=4-4p=0$$
- Тогда $$p=1$$.
- Найдем абсциссу точки пересечения: $$x_{0}=-frac{-4}{2}=2$$.
- Найдем ординату (подставим в линейное уравнение): $$y=4*2-3=5$$. То есть точка пересечения будет с координатами (2;5).
- Построим графики функций:
Задание 24
Диагональ равнобедренной трапеции делит пополам угол при её основании. Найдите большее основание трапеции, если её меньшее основание равно 5 см, а высота — 4,8 см.
Ответ: 7,8
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- $$angle BAC=angle CAD$$ (AC — биссектрисса)
- $$angle CAD=angle BCA$$ (накрест лежащие при параллельных), следовательно треугольник ABC — равнобедренный и $$AB=BC=CD=5$$
- Проведем перпендикуляры BM и CH к AD. Из треугольника CHD: $$HD=sqrt{CD^{2}-CH^{2}}=sqrt{5^{2}-4,8^{2}}=1,4$$
- $$AM=HD=1,4$$, тогда $$AD=5+1,4*2=7,8$$
Задание 25
Середины сторон параллелограмма являются вершинами ромба. Докажите, что данный параллелограмм — прямоугольник.
Ответ:
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- $$AB=CD, BC=AD$$ так как дан параллелограмм. Следовательно, $$AM=MB=DL=LC$$, и $$AK=KD=BN=NC$$.
- $$angle A+angle D=180$$. Но $$MK=NK$$, следовательно, треугольники AMK и KLD равны по трем сторонам и $$angle A=angle D$$. Так как они в сумме дают 180, то какждый из них по 90, тогда ABCD — прямоугольник.
Задание 26
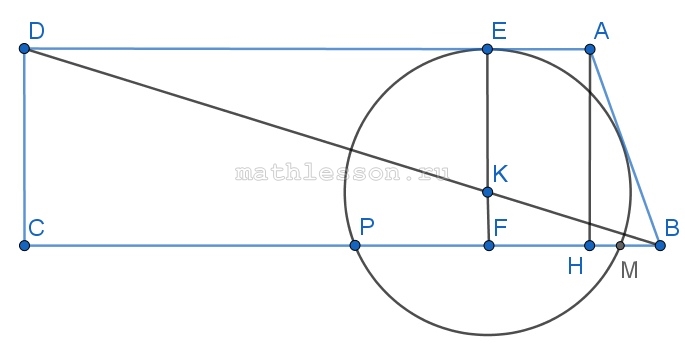
На диагонали BD прямоугольной трапеции ABCD с прямым углом ADС и основаниями ВС и АD, взята точка К так, что ВК : КD = 1 : 3. Окружность с центром в точке К касается прямой АD и пересекает прямую ВС в точках Р и М. Найдите длину стороны АВ, если ВС = 9, АD = 8, РМ = 4.
Ответ: 3
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
- Пусть Е — точка касания, проведем перпендикуляр через E и K (свойство радиуса в точку касания). Пусть EK пересекает CB в точке F
- Так как $$EFperp PM$$, то $$FP=FM$$ (из равенства треугольников KFP и KFM). Так же $$KE=KP=K=R$$ (радиусы)
- Треугольники KED и KFB подобный (так как дана трапеция), тогда $$frac{KF}{KE}=frac{KB}{KD}=frac{1}{3}$$, тогда $$KF=frac{1}{3}KE=frac{R}{3}$$
- из треугольника PKF: $$KP^{2}=PF^{2}+KF^{2}$$ или $$R^{2}=frac{1}{9}R^{2}+4$$. Отсюда $$R=frac{3}{sqrt{2}}$$
- Опустим $$AHperp BC$$ (AH пересекает BC в точке H). Тогда $$AH=EK+KF=frac{4}{3}R=2sqrt{2}$$, $$HB=BC-AD=1$$
- Из треугольника AHB: $$AB=sqrt{1^{2}+(2sqrt{2})^{2}}=3$$
Пробные варианты по математике профильного уровня в формате ЕГЭ 2023 из различных источников.
Варианты составлены в соответствии с демоверсией 2023 года
Пробные варианты ЕГЭ 2023 по математике (профиль)
| egemath.ru | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| time4math.ru | |
| вариант 1-2 | |
| yagubov.ru | |
| вариант 33 (сентябрь) | ege2022-yagubov-prof-var33 |
| вариант 34 (октябрь) | ege2022-yagubov-prof-var34 |
| вариант 35 (ноябрь) | ege2022-yagubov-prof-var35 |
| вариант 36 (декабрь) | ege2022-yagubov-prof-var36 |
| math100.ru (с ответами) | |
| variant 180 | скачать |
| variant 181 | скачать |
| variant 182 | скачать |
| variant 183 | скачать |
| variant 184 | скачать |
| variant 185 | скачать |
| variant 186 | скачать |
| variant 187 | скачать |
| variant 188 | скачать |
| alexlarin.net | |
| Вариант 400 | проверить ответы |
| Вариант 401 | проверить ответы |
| Вариант 402 | проверить ответы |
| Вариант 403 | проверить ответы |
| Вариант 404 | проверить ответы |
| Вариант 405 | проверить ответы |
| vk.com/ege100ballov | |
| вариант 1 | скачать |
| вариант 2 | скачать |
| вариант 3 | скачать |
| вариант 4 | скачать |
| вариант 5 | скачать |
| вариант 6 | скачать |
| вариант 7 | скачать |
| vk.com/shkolkovo_easy_math | |
| Вариант 1 | решение |
| Вариант 2 | решение |
| Вариант 3 | решение |
| Вариант 5 | решение |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий.
Часть 1 содержит 11 заданий с кратким ответом базового и повышенного уровней сложности.
Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Связанные страницы:
Пробные варианты ЕГЭ 2022 по математике (профильный уровень)
Сборник задач по стереометрии для 10-11 классов
Задание 10 по профильной математике — новые задачи по теории вероятностей в ЕГЭ-2022
Тест по теме «Производная» 11 класс алгебра с ответами
Основные тригонометрические тождества и формулы